Theories and Applications for Sequencing Randomly Selected Clones

Abstract

Theory is developed for the process of sequencing randomly selected large-insert clones. Genome size, library depth, clone size, and clone distribution are considered relevant properties and perfect overlap detection for contig assembly is assumed. Genome-specific and nonrandom effects are neglected. Order of magnitude analysis indicates library depth is of secondary importance compared to the other variables, especially as clone size diminishes. In such cases, the well-known Poisson coverage law is a good approximation. Parameters derived from these models are used to examine performance for the specific case of sequencing random human BAC clones. We compare coverage and redundancy rates for libraries possessing uniform and nonuniform clone distributions. Results are measured against data from map-based human-chromosome-2 sequencing. We conclude that the map-based approach outperforms random clone sequencing, except early in a project. However, simultaneous use of both strategies can be beneficial if a performance-based estimate for halting random clone sequencing is made. Results further show that the random approach yields maximum effectiveness using nonbiased rather than biased libraries.

Genomic mapping and sequencing have benefited greatly from the development of stable large-insert cloning platforms, such as the bacterial artificial chromosome (BAC) clone (Shizuya et al. 1992). Sequencing random clones has recently been discussed, both as a primary strategy and/or in the role of augmenting map-based sequencing. By random clone sequencing, we mean that large-insert clones are randomly selected from a library without a priori knowledge of their positions in the genome. They are then sequenced by standard shotgun techniques and assembled into contigs (i.e., sets of contiguous clones) using sequence comparison methods. Because positional information is not known in advance, there is no guarantee that a clone will extend a contig or will not be fully redundant with respect to clones already sequenced. This random-clone approach contrasts with map-based sequencing, by which clone selection is guided by a preexisting physical map. Here, redundancy and contig information are known at the outset, enabling some optimization of the selection procedure. For example, if constant minimal redundancy can be maintained, map-based sequencing is essentially a linear coverage process.

As with map-based sequencing, issues for random clone sequencing revolve largely around performance, as measured by such parameters as rates of progress and redundancy accumulation. These parameters have not been empirically quantified for random sequencing because there remains a lack of substantial data for large genomes. Conversely, map-based sequencing is better understood from an empirical standpoint. For example, a map-based approach was employed for the Caenorhabditis elegans sequencing project (C. elegans Sequencing Consortium 1998) and has figured prominently in the Human Genome Project (Sanger Centre and Washington University Genome Sequencing Center 1998). These projects provide a good benchmark of the map-based approach for large genomes.

As for mathematical modeling, the random-sequencing scenario described above has not been specifically addressed. Theoretical developments have concentrated mainly on mapping techniques, for example, the seminal work of Lander and Waterman (1988) for the fingerprint method and later models for other procedures (Arratia et al. 1991; Barillot et al. 1991; Zhang and Marr 1993; Port et al. 1995; Schbath 1997). Owing to considerations of similarity, it has been postulated that mapping models could be directly applied to random clone sequencing (Lander and Waterman 1988; Roach 1995). However, a subtle issue related to clone overlaps arises. Mapping models are necessarily based on the ability of the method to detect overlaps for contig assembly. In particular, a prescribed clone-length fraction necessary for detection θ₀ > 0 accounts for the fact that some percentage of overlaps will go undetected (the full description of nomenclature is given in Table 1). A measure of overlap itself, for example, as characterized by library depth ϕ is not considered. However, for random clone sequencing, contig assembly relies on ex post facto sequence comparison, which can be assumed to detect all overlaps (θ₀ ➞ 0). Application of mapping theory, for instance, the Lander and Waterman model with θ₀ = 0, would not explicitly account for library depth. Modeling liability of this idealization, if any, has not been established.

Table 1.

Nomenclature

Symbol	Meaning
b	number of bases from one cut site to the next in a uniformly distributed library
i	number of sequenced clones
e	Euler's constant (≈2.71828)
m	user-specified level of restriction site bias
n	number of expected restriction sites per specified segment length
N	total number of clones in a multi-fold library
s	restriction enzyme specificity (number of bases)
χ	distance in bases along linearly arranged genome
θexp	experimentally determined average overlap of sequenced clones (%)
G	linear genome length in bases (∼3 Gb for human genome)
L0	nominal clone length in bases (∼170,000 for BAC clones)
θ0	required threshold to detect clone overlap in a mapping project (%)
L(i)	effective bases of genome covered after sequencing i clones
C(i)	effective percentage of genome covered after i clones = L(i)/G
θ(i)	redundancy after sequencing i clones
fn	Poisson probability density function for restriction site distribution
R(i)	rate of progress after sequencing i clones
ϕ	library depth
μavg	Poisson average number of restriction sites per specified segment length

In this report, we formulate a theory for the random-clone-sequencing procedure described above. Our primary purpose is to provide a mechanism to estimate performance of an actual sequencing project based on this paradigm. Moreover, we also evaluate the importance of library depth as a modeling factor and, thus, the applicability of mapping models to this problem. We focus on two types of libraries: one generated by random means, for example, mechanical shearing, and one created by partial digest using a restriction enzyme. The former is expected to have essentially a uniform clone distribution because there is no preference for cut sites, whereas the latter depends upon the inherent nonuniformity of restriction sites throughout a genome and could have appreciable bias in the distribution of clones. We apply the theory to the particular case of human BAC sequencing using a randomly generated library and a library created by partial digest with HindIII. We refer to these as the randomly generated and HindIII libraries, respectively. Map-based results from human-chromosome-2 BAC data are used for comparison. No account is made of genome-specific or nonrandom phenomena; therefore, theory and results are considered to be first-order approximations.

RESULTS

Assessment of the Importance of Library Depth

If we set Θ₀ = 0 in the Lander and Waterman (1988) model to simulate perfect overlap detection, the main difference between it and our model in equation 3 is consideration of library depth. For perfect detection, Lander-Waterman coverage reduces to the well-known Poisson coverage expression L(i) = G − Ge^−L₀i/G. Equation 3 yields the same result if we allow clone size to vanish (L₀ ➞ 0). Thus, the importance of considering library depth diminishes with clone size, at least in the approximate context of these models.

The physical interpretation is that L₀ ➞ 0 tends toward an idealized point model, for which partial overlap of one clone with another is not possible. For the point model, clones only overlap completely or not at all. As would be expected, one identically recovers the Poisson coverage law if our model is derived without accounting for partial overlap. Because clone size is usually small relative to genome size, it appears from equation 3 that library depth is actually a secondary consideration compared to the other variables. A corollary is that random clone sequencing can often be reasonably approximated by the Poisson coverage expression.

Assessment of the Importance of Clone Size Variation

Actual clone sizes in any library can be expected to vary somewhat; however, uniform clone size has been a standard theoretical assumption (e.g., Lander and Waterman 1988; Barillot et al. 1991; Zhang and Marr 1993; Port et al. 1995; Roach 1995). We use data from chromosome-2 BAC clones to evaluate the effect upon the present model. Table 2 indicates an average clone length of 181.8 kb, with a 19-kb standard deviation. A rudimentary test is to determine difference in coverage over one standard deviation in clone size, that is, for 181.8 ± 9.5 kb (the test is more conservative than it may initially seem because the size distribution is entirely concentrated at a single point for each case). Equation 3 yields a maximum difference below 10% when evaluated over the whole sequencing project. As with library depth, variation of clone size does not appear to be a primary factor in modeling random clone sequencing.

Table 2.

Overlapping BAC Clones from Chromosome 2 RPCI-11 Library

Clone name	GenBank accession no.	Size (Kb)	Overlap (%)
H_NH0140K04	AC005033	165.6	31.2
H_NH0019M18	AC007238	183.9	8.0
H_NH0059I21	AC006327	158.4	41.6
H_NH0074G24	AC007314	164.5	15.5
H_NH0083A12	AC007239	205.3	40.7
H_NH0086N01	AC007677	197.7	15.7
H_NH0090D01	AC007092	200.8	21.8
H_NH0148A10	AC007558	162.4	26.1
H_NH0150O02	AC008273	178.0	15.1
H_NH0154L24	AC006985	176.0	61.0
H_NH0182H09	AC007242	168.0	81.2
H_NH0206M19	AC007877	172.6	15.9
H_NH0252C12	AC006368	171.1	18.1
H_NH0260K08	AC007077	182.0	18.3
H_NH0263G22	AC006037	149.2	71.3
H_NH0288C18	AC007382	184.0	56.3
H_NH0308G20	AC007278	184.1	11.8
H_NH0309N08	AC007279	219.0	37.0
H_NH0323F11	AC007880	178.3	31.6
H_NH0332L11	AC005538	193.4	76.5
H_NH0334G22	AC007250	181.7	8.1
H_NH0343N14	AC006461	181.2	20.6
H_NH0355F16	AC007681	194.7	24.1
H_NH0359K10	AC007386	176.7	16.5
H_NH0372J12	AC007387	199.4	17.9
H_NH0374F15	AC008173	235.1	17.6
H_NH0386G20	AC007560	174.4	28.8
H_NH0394E01	AC007561	219.2	51.6
H_NH0395B14	AC007388	189.4	19.8
H_NH0407F02	AC007252	177.7	19.5
H_NH0436C12	AC006464	159.3	37.4
H_NH0445A14	AC007099	160.1	22.0
H_NH0449G16	AC007684	196.9	19.0
H_NH0481J13	AC007743	194.5	27.1
H_NH0485G02	AC007970	169.3	18.0
H_NH0493L16	AC007002	177.4	21.0
H_NH0510C23	AC007971	146.7	28.2
H_NH0518G12	AC007367	213.8	7.8
H_NH0523H20	AC005041	191.2	27.1
H_NH0536I18	AC007283	163.6	22.2
H_NH0548P06	AC007006	189.6	40.9
H_NH0559J05	AC006385	173.5	34.3
H_NH0569H17	AC007179	159.6	17.4

DISCUSSION

Performance Early in a Project

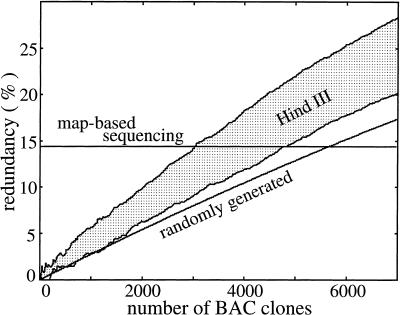
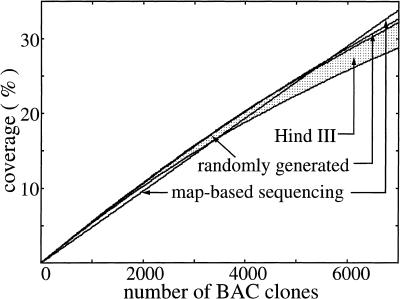
Results from 7000 randomly sequenced human BAC clones are used to evaluate performance early in a project. Modeling constants are genome length G = 3 Gb, nominal clone size L₀ = 170 kb (derived from a genomewide sampling of Genome Sequencing Center BAC clones), and library depth ϕ = 10×. Other parameters are as discussed in Methods; in particular, the average value of redundancy for map-based sequencing is θ_exp = 14.4%. Figures 1 and 2 show redundancy and coverage results, respectively, for each approach. They confirm that randomly sequenced BACs, regardless of library type, initially yield comparable rates of coverage and lower redundancy compared to map-based sequencing. After some number of clones, the advantage shifts to the map-based approach. From a redundancy standpoint, this crossover occurs at approximately 5600 clones for the randomly generated library and between 2900 and 4800 clones for the HindIII library. In terms of coverage, the numbers are comparable: 5600 nonbiased clones and between 3500 and 5400 HindIII clones. The upper limit for performance crossover is about 5600 BAC clones, using a randomly generated library. At this point, a total of ∼one-fourth of the genome has been covered. This value is also a reasonable estimate for the mouse genome because its parameters are nominally the same as for the human genome. Figure 2 also indicates that performance is essentially independent of library type and bias level for the first several thousand clones. In fact, rate of progress for the first 10%–15% of the genome is essentially fixed. This observation suggests that conventional restriction digest libraries could effectively be used for random clone sequencing while mapping work is in progress.

Figure 1.

Expected redundancy for the first 7000 BAC clones using both map-based and randomly selected BAC sequencing approaches. The randomly generated library appears as a single curve and the HindIII library appears as a shaded region resulting from low- and high-restriction site-bias estimates. The top bound denotes high bias; the bottom corresponds to low bias. Results for map-based sequencing are given by the horizontal line.

Figure 2.

Effective expected coverage for map-based and randomly selected BAC sequencing for the first 7000 BAC clones. The shaded area denotes the HindIII library; high bias is represented by the lower of the bounding curves.

Simultaneous Random, Map-Based Sequencing

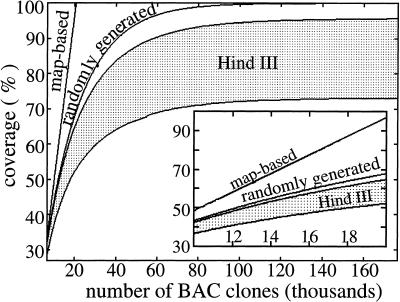
In a general scenario, random and map-based sequencing could be conducted simultaneously. At the time of this writing, ∼50% of map-based human sequencing was complete, well past the 5600 clone crossover juncture. However, Figure 3 (inset) suggests that sequencing from the random library would still be justified because its coverage rate, as deduced from the slope, remains comparable to the map-based approach. Conversely, suitability of the HindIII library depends strongly on bias. For low bias, the coverage rate is slightly less than that for a random library; however, the rate is much decreased at higher bias.

Figure 3.

Predicted coverage up to 176,000 BAC clones (∼10 genome equivalents). The inset shows a magnified view in the 30%–45% range of coverage. HindIII coverage is denoted by the shaded area; the high-bias simulation is the lower of the bounding curves.

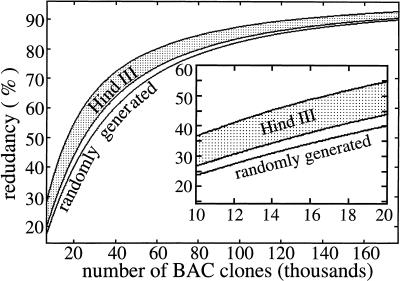
To determine when random clone sequencing should be halted, the following procedure can be applied. First, specify minimum acceptable performance in terms of model parameters; then evaluate the resulting number of clones obtained for each parameter. Choose the lowest value as the stopping point. If finished sequence is already available, as in this case, subtract the equivalent number of already-sequenced clones to obtain the number of clones that can still be sequenced within the original constraints. Consider the following example: Random sequencing is performed while its rate of coverage is at least half that of map-based sequencing and its redundancy is <50%. We work the problem for a random library because it is already clear that this will yield a higher number of clones. Using θ_exp = 0.144 from Table 2, rate of progress for map-based sequencing is computed as R = 0.856L₀ per BAC clone. Taking half this value indicates that random clone sequencing should be continued until R falls to 0.428L₀ per BAC. Solving equation 4 for i and substituting R = 0.428L₀ yields ∼15,000 clones as one possible stopping point. The other possibility is given by the number of clones for 50% redundancy, which can be read directly from Figure 4 as ∼28,000. Our prescribed coverage rate governs the problem; so we choose 15,000 as the maximum number of randomly sequenceable BAC clones. At 50% coverage, the equivalent number of already-sequenced BAC clones is about 12,000, which means 15,000–12,000 or 3000 BACs could still be sequenced within our original performance constraints.

Figure 4.

Predicted redundancy up to 176,000 bacterial artificial chromosome (BAC) clones (∼10 genome equivalents). The inset shows a magnified view in the lower redundancy region. The map-based redundancy of 14.4% coincides with the abscissa in both plots.

Extrapolation to Higher Coverage

Figures 3 and 4 extend the simulation to 10 genome equivalents (176,000 BACs) to examine results at higher coverage levels. There has been considerable debate on the efficacy of a clone map for sequencing (Green 1997; Weber and Myers 1997); however, Figures 3 and 4 clearly show its superior performance at higher coverage levels. Specifically, map-based clone sequencing behaves linearly, whereas random clone sequencing is an asymptotic process. The random library displays better coverage and lower redundancy than the best HindIII library and converges to full coverage. All bias estimates predict the HindIII library falling short of 100% coverage due to unrepresented regions of the genome.

Summary

Performance of map-based sequencing is superior to random clone sequencing, except early in a project. Moreover, a randomly generated library can be expected to outperform a restriction digest library, perhaps by a significant margin. These conclusions are likely true for many combinations of organism, clone type, enzyme, etc. Results suggest that sequencing via map-based and random strategies simultaneously is reasonable, especially if a suitable performance-based estimate for halting random clone sequencing is made.

Other cases of interest can be treated by applying the same procedures shown here for human BAC clones. Of special interest is the whole-genome shotgun method, which is now being used for large genomes (Adams et al. 2000). The procedure relies on random fragmentation so that a uniform subclone distribution can reasonably be assumed. Here, L₀ is the subclone length. Because this value is considerably small compared to genome size, a point model can readily be assumed, permitting usage of the Poisson coverage approximation discussed above.

METHODS

Models for map-based and random clone sequencing are derived here. Solomon (1978) and Hall (1988) are good introductions to the general topic of coverage theory, which encompasses these processes.

Empirical Model of Map-Based Sequencing

A clone library supported by a physical map can be characterized by the average overlap of the sequenced clones θ_exp. We estimate this parameter empirically using 43 human-chromosome-2 BAC clones sequenced at the Genome Sequencing Center. Table 2 shows derived overlap and size data for these clones, which originate from the RPCI-11 library (Osoegawa et al. 1998). In the present context, our documentation system for clone lengths and finishing boundaries has the effect of tallying overlaps twice. Therefore, the average overlap of 28.9% calculated from Table 2 must be divided in half, yielding θ_exp = 14.4%. This group of clones is taken as representative of the overall map-based sequencing process for human BAC clones. In other words, overlap is assumed to be a constant given by θ(i) = θ_exp. Therefore, the coverage added by each sequenced clone, that is, the rate of progress is R(i) = (1 − θ_exp)L₀ and the total coverage L(i) is simply iR(i).

Random-Sequencing Model for a Randomly Generated Library

Random fragmentation implies that all base positions are equally likely to be breakage sites, which results in a uniform clone distribution. We assume a constant clone size of L₀ bases, a genome length of G bases, and a library depth of ϕ. The standard equation of expected value is employed for estimating coverage L = Σp_ɛL_ɛ, where L_ɛ is the coverage contributed by a particular event ɛ and p_ɛ is its probability of occurrence. Three events are considered: the new event, in which the clone does not overlap any established sequence (all added sequence is new); the partial event, in which part of the clone overlaps established sequence; and the buried event, in which the entire clone is buried in previously generated sequence. The coverage after randomly sequencing a clone is then Σ(pL)_new + Σ(pL)_partial + Σ(pL)_buried. Then define a segment length b, the average number of bases from one breakage site to the next. Because clone ends are synonymous with breakage sites, clones must overlap in units that are multiples of b. The number of clones in a library N = ϕG/L₀, equals the number of right (or left) clone ends, and therefore, the number of uniformly distributed breakage sites. By definition, b can be computed by dividing the genome length by the number of breakage sites, yielding b = G/N = L₀/ϕ. A clone end can only occupy discrete positions given by multiples of b; so the total number of possible positions is K = N − ϕ + 1 and the probability of any given position is p = K⁻¹. This expression accounts for so-called end effects (Port et al. 1995; Roach 1995) and prevents clones from running off the end of the genome. No such constraint exists for circular genomes (Parke 1997).

The length of unique sequence after i clones have been sequenced is L_i, where L_i = l_ib. For the new event, the length after sequencing another clone is L_new = L_i + L₀ and the number of ways to obtain this event is K − (l_i + ϕ − 1). For the buried event, the length remains the same as it was before the clone was sequenced, that is, L_buried = L_i, and the number of ways this could occur is l_i − ϕ + 1. These combinations yield p_new = (K − l_i − ϕ + 1)/K and p_buried = (l_i − ϕ + 1)/K. Length for the partial event is simply L_new minus the amount of overlap, that is, L_partial = L_i + L₀ − h b, where h is the number of b-length segments of overlap. Because the new clone is, at most, equal in length to the established sequence, this can happen a total of h = ϕ − 1 ways on either side of the established sequence. Therefore, the partial event can be written as ∑(pL)_partial = 2∑^ϕ−1_h=1(L_i + L₀ − h · b)/K. Using a summation identity, this expression reduces to ∑(pL)_partial = 2(ϕ − 1)(L_i + L₀)/K − (ϕ − 1)L₀/K. Taking all of these events and simplifying, the final recursion for coverage is L_i+1 = L_i + [1 − L_i/(G − L₀ + L₀/ϕ]L₀. Rearranging, we obtain

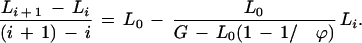1

The left hand side is a finite difference approximation of the rate of change of coverage with respect to the number of clones sequenced. Eqn. (1) is therefore a discrete analog of the differential equation

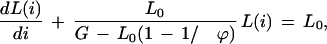2

which can be solved using e^{L₀i/[G−L₀(1−1/ϕ)]} as an integrating factor (Martin and Reissner 1956). Initial conditions require that the first clone sequenced yields coverage equal to its own length, L(1) = L₀, which leads to the final coverage expression

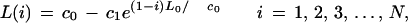3

where c₀ = G − L₀(1 − 1/ϕ) and c₁ = c₀ − L₀. Various performance parameters can be derived from this equation. For example, in the ideal case of end-to-end clone placement, coverage is simply L₀i, which allows redundancy to be defined in a normalized sense as θ(i) = 1 − L(i)/(L₀i). Rate of progress, R(i), can be calculated by differentiation as

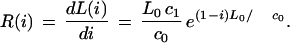4

Random-Sequencing Model for a Restriction Digest Library

Modeling the sequencing process for a restriction digest library must account for nonuniform clone distribution, which arises from the natural restriction-site bias of a genome. Rather than attempt to derive an exact solution for this case, it is more expedient to employ Monte-Carlo simulation (Press et al. 1991). A set of restriction sites is first established according to an appropriate nonuniform-probability-density function. Sequence coverage is then simulated by randomly selecting a site as a left clone end. Based upon local site distribution and nominal clone length, the right end is then determined, after which cumulative coverage is recomputed. Iteration is continued until a user-specified stopping point is encountered.

Poisson probability density functions provide a suitable model for restriction sites in the sense that a large segment size can be specified, for example, 4^s where s is enzyme specificity, while the probability of a site occurring in any neighborhood of a segment is small. Because site bias cannot be known a priori (Green 1997), we follow the methodology of Port et al. (1995) and Schbath (1997) in using simple functions to model bias. We select (m + 1)x^m, where m is the user-specified bias level and x is the distance along the linearly arranged genome. This function conserves the total number of sites in a genome to μ_avgG/4^s, where μ_avg is an empirically sampled value of the number of restriction sites in a segment. A general variable-rate Poisson process for restriction site distribution is then given by

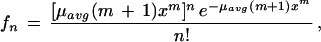5

where n is the number of sites expected per segment. Global distribution of sites is computed along 0 < x ≤ G using equation 5; however, the local distribution in each segment is taken to be uniform. No coverage is allowed between base position 1 and the first restriction site x₁. Thus, bias yields a segment x₁ − 1, which cannot be covered by sequence due to lack of representation in the library.

As with the uniform distribution model, other performance parameters can be obtained using coverage results. Redundancy is computed exactly as defined for the uniform model. For rate of progress, no closed-form expression is available. However, it can be calculated by finite difference approximation (Tannehill et al. 1997). Due to the nonsmooth nature of Monte-Carlo simulation, it may be necessary to average out local fluctuations by computing each difference over a large set of clones. We note that this introduces an additional component of numerical error (Tannehill et al. 1997).

As applied specifically to a HindIII human BAC library, the parameters are s = 6 (because this enzyme is a 6-cutter recognizing AAGCTT) and a segment size of 4096 bases. To estimate μ_avg, 868 finished sequences from the Genome Sequencing Center encompassing ∼105 megabases were analyzed for AAGCTT. We found μ_avg ≈ 1.25, implying ∼916,000 total sites for a 3-Gb genome size. A coefficient of dispersion of 1.046 indicates that Poisson modeling is acceptable (Sokal and Rohlf 1981). We assume lower- and upper-bound functions for bias as 3√x/2 and 3x², respectively.

A code using this model was tested with m = 0 and results compared well to equation 3. This method is computationally intensive because each restriction site and its coverage status must be stored explicitly and these arrays are traversed for each succeeding clone. Placing a clone in the genome and computing coverage require approximately L₀/4^s and G/4^s operations, respectively. Because clone ends must be restriction sites, the simulated length of a clone will vary in a range of ∼4^s around the nominal value of L₀. Exceptions are that near the end of the genome, a clone may be much smaller because it cannot run off the end, and in restriction-site-poor areas, a clone can be significantly longer because it must extend to the next restriction site.