No apparent ecological trend to the flight-initiating jump performance of five bat species

SUMMARY

The jump performance of five insectivorous bat species (Miniopterus schreibersii, Myotis blythii, Myotis capaccinii, Myotis myotis and Rhinolophus blasii) was filmed using a high-speed camera. All study bats jumped using a similar technique, with the wing musculature providing the force. The bats jumped off the wrist joint of their wings, typically with their feet already off the ground. Contrary to expectations, jump performance did not correlate with ecology and was instead strongly determined by body size. In general, the larger bats produced more jump force, left the ground at higher speeds and jumped higher than the smaller bats. The differences in force production disappeared when the data were corrected for body size, with the exception of Myotis capaccinii, which produced significantly less force. Scaling of jump performance with body size measured here was compared against two existing muscle performance scaling models. The model suggesting that muscle contraction velocity is proportional to muscle length was better supported than that based on muscle cross-sectional area. Both models, however, failed to accurately predict the scaling of jump forces, with the slope of the relationship being significantly steeper than predicted, highlighting the need for further investigations of vertebrate muscle performance scaling. The results of this study indicate that a bat's jumping ability is a secondary locomotor ability that uses the strongly selected-for flight apparatus with no apparent ecological trend present, i.e. flight so dominates bat locomotor morphology that other locomotor abilities tend to be derivative.

INTRODUCTION

The ability to take-off is crucial for all volant animals, as this marks the transition from terrestrial, arboreal or aquatic to aerial locomotion. For many species of bat, taking-off is not particularly challenging, as they roost in caves, attic spaces or trees and only need to drop into space to initiate flight. Indeed, landing upside-down on a horizontal surface is the real acrobatic challenge they face (Riskin et al., 2009). Several bat species, however, spend a significant proportion of their foraging time on the ground (Altringham, 1996; Riskin et al., 2006; Schutt et al., 1997) and must become airborne again with gravity working against them. Furthermore, all bats can potentially crash onto the ground and an ability to quickly return to flight will improve their survival chances, particularly as the terrestrial crawling ability of most bats seems to be poor because of their modified hindlegs (Riskin et al., 2005). Although a number of bat species are known to jump into the air, only two studies, and then concerning only one species (the vampire bat, Desmodus rotundus), have quantitatively investigated this behaviour in bats (Altenbach, 1979; Schutt et al., 1997).

In general, however, animal jumping is well studied, occurring in a wide range of species from tiny insects to large vertebrates (e.g. Alexander, 1995; Caple et al., 1983; Demes et al., 1996; Gabriel, 1984; Harris and Steudel, 2002; James et al., 2007; Schutt et al., 1997; Toro et al., 2003). A jump (as opposed to continuous hopping) is generally considered to be a single discrete kinematic event. This allows the animal's mechanical performance to be relatively easily parameterised (i.e. jump distance or height, take-off speed, jump force). Specialist jumping species typically have several adaptations that improve their performance: both leg length and the musculature associated with jumping are increased (Gabriel, 1984; James et al., 2007). In addition, keeping weight at the extremities of the legs to a minimum and having additional leg joints allows further improvements in jump performance (Alexander, 1995). Humans roll onto the ball of their foot during a jump, allowing the section of foot between the heel and the ball to act as an additional leg segment (Alexander, 1995). Many specialist jumpers also employ energy storage mechanisms. Small insects often make use of a catapult-type mechanism, deforming an elastic structure to store energy before releasing a ‘catch’ to propel them through the air (Alexander, 2003). Larger vertebrates, however, rely on counter-movement prior to the jump to stretch tendons, thus storing energy, which is released during the jump (Alexander, 2003). Even humans (non-specialist jumpers) make use of tendon stretching counter-movement to improve jump height (James et al., 2007).

The jumping technique used by bats is unusual amongst vertebrates because the power is generated by the forelimbs instead of the hindlegs (Schutt et al., 1997). In contrast, birds generate approximately 80–90% of their take-off speed from their hindlegs, with the wings continuing the initial movement generated by the legs (Earls, 2000). Bats, however, possess extensively modified hindleg and pelvic bones (Neuweiler, 2000; Riskin et al., 2005), which have left them with relatively poor terrestrial locomotion. Many bat species are documented as landing on the ground during foraging, and then resuming flight once the prey is captured (e.g. Arlettaz, 1996; Bell, 1982; Fiedler, 1979; Siemers and Ivanova, 2004; Vaughan, 1976), but it is their forelimbs and powerful wing musculature that generate the necessary forces to propel them back into the air, the hindlimbs only being used to orientate the body over the pectoral limbs, which generate the jump force (Schutt et al., 1997). The vampire bat D. rotundus is considered to be one of the most agile bats on the ground. Therefore, perhaps unsurprisingly, previous studies investigating bat jumping have tended to focus on D. rotundus (Altenbach, 1979; Schutt et al., 1997). Schutt and colleagues found that D. rotundus typically generates a force of 6.51 times their body weight, giving them a take-off speed of 2.38 m s^–1 (Schutt et al., 1997). The unique foraging ecology of D. rotundus (feeding on the blood of larger mammals) could influence its jumping performance and it may not, therefore, be a good exemplar of all bat species. A study by Siemers and Ivanova comparing the take-off times of three Rhinolophidae species, Rhinolophus blasii, R. euryale and R. mehelyi, however, did not detect any ecological trend in jump performance even though R. blasii spends significantly more time on the ground than the other two species (Siemers and Ivanova, 2004). In quantifying take-off performance, the study used the time taken to cover a given distance, which perhaps lacked the resolution necessary to identify any interspecific ecologically driven differences in take-off performance. Therefore, a more comprehensive study is required before uniformity (no ecological trend) in ground take-off performance in bats may be concluded.

The aim of our study was to determine whether a bat's foraging behaviour affects its jump performance. We hypothesised that gleaning bats would have a better jumping ability (i.e. higher jumps made at faster speeds and higher jump forces) than hawking bats as they spend a larger proportion of their time on or near the ground catching their prey. In addition, we investigated the scaling of jump performance in bats and compared this with the theoretical scaling models of Hill (Hill, 1950) and Richard and Wainwright (Richard and Wainwright, 1995).

MATERIALS AND METHODS

Filming of bat jumps

Bats were caught using a harp trap on three separate evenings (24 August 2006, 25 August 2006 and 25 August 2007) as they exited a roosting cave at Maronea, Rhodope Prefecture, Greece. The bats were then released onto a flat platform (±5 deg) from which they could take-off. The bats were escaping from their captors and therefore it was assumed that they would be performing their take-off with maximal performance. To encourage the bats to leave the platform in a perpendicular direction to the camera view, a white sheet was hung behind the platform; this also improved the visibility of the bat in the footage. The platform was illuminated using floodlights (Nightsearcher, Portsmouth, UK). The take-off jumps were filmed using a Trouble Shooter camera (Fastec Imaging, San Diego, CA, USA), running at either 125 or 250 frames s^–1 (Fig. 1). Before the jump the forearm length and body mass (M_b) of the bat were measured.

Fig. 1.

Selected frames from high-speed video footage of Miniopterus schreibersii jumping from a platform to initiate flight. The use of the forearms to generate the force of the jump is clearly visible. Also note that the first wing beat after jumping tends to have a reduced amplitude, compared with a more typical wing beat. Frames are 16 ms apart.

Study species

Data were collected from five species of bat.

Myotis blythii, Tomes 1857 (N=5) and Myotis myotis, Borkhausen 1797 (N=12), two closely related large bat species. Both of these bats have flexible foraging strategies including ground gleaning and aerial hawking, depending on the availability of food (Arlettaz, 1996). These bats were predicted to have intermediate jumping performance compared with the other species because they are able to glean prey from the ground.

Myotis capaccinii, Bonaparte 1837 (N=15), a much smaller bat, with a highly specialised trawling foraging behaviour, gaffing insects and small fish from the surface of ponds (Aihartza et al., 2008). Myotis capaccinii was predicted to have poor jumping performance because it is a specialist trawler.

Miniopterus schreibersii, Kuhl 1817 (N=17), which forages at high altitudes, hawking insects in flight (Norberg and Rayner, 1987). Miniopterus schreibersii was predicted to have the poorest jump performance, as it specialises in hawking insects out of the air.

Rhinolophus blasii, Peters 1866 (N=6), a small, ground-gleaning species, sometimes even pursuing prey items across the ground (Siemers and Ivanova, 2004). Rhinolophus blasii was predicted to perform the best in the jumping experiments because of its frequent ground gleaning.

Video analysis

Video footage of the bats jumping to initiate flight was digitised using Tracker 3.10 (Brown, 2009). The shoulder joint of the bat was tracked as a proxy for the centre of mass (CoM) of the bat. Although not ideal, given a bat's CoM is known to vary in location throughout locomotor activities such as flight (Iriarte-Diaz and Swartz, 2008), this gave the best consistently viewable landmark close to the CoM. The timing of key events in each jump was recorded: the start of the jump (first frame showing vertical movement), the wrist joint leaving the ground (signalling the end of the jump) and the start of both first and second downstrokes. Video footage was scaled and rotated relative to the vertical using a checkerboard and a plumb line. Any footage in which the bat obviously jumped towards or away from the camera, or was obscured, making tracking difficult, was disregarded.

Data analysis

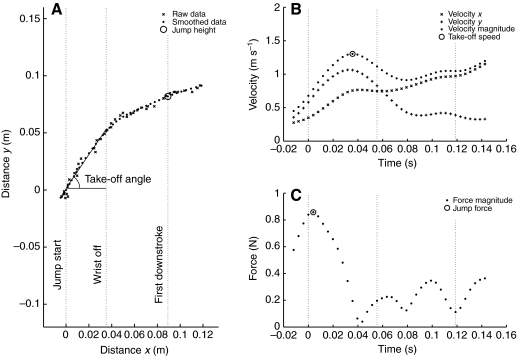
All subsequent data and statistical analyses were performed using Matlab® R2007a (The MathWorks Inc., Natick, MA, USA). The data were smoothed using a fourth-order Butterworth filter with a cut-off frequency of 12.5 Hz. The cut-off frequency was selected by plotting the residuals (i.e. a measure of the difference between the smoothed data and the original) over a large range of potential cut-off frequencies for the data of the first few jumps analysed. The cut-off frequency that was the best compromise between maximising noise reduction and minimising the signal distortion (that all smoothing introduces) was selected [see p. 42 of Winter (Winter, 1990)]. The following kinematic variables (Fig. 2) were then calculated for each bat from the smoothed data: take-off angle (deg; the angle travelled by the bat above horizontal between the start of the jump and the wrist leaving the ground, which was calculated from the slope of a linear least-squares fit to the data); jump height (m; defined as the height above ground obtained at the start of the first downstroke, as this marks the transition between the bat being a projectile and actively flying); maximum take-off speed (m s^–1; between the start of the jump and the wrist leaving the ground); and jump force, which was calculated as:

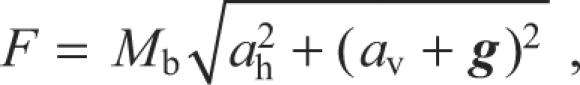(1)

where F is jump force (N), M_b is body mass (kg), a_h is horizontal acceleration (m s^–2), a_v is vertical acceleration (m s^–2) and g is gravitational acceleration (m s^–2). The maximum value between the start of the jump and the onset of the first downstroke was then taken as the jump force. The ratio of jump force to the bat's weight was also calculated.

Fig. 2.

Example kinematic data from a Myotis myotis jump. (A) Raw and smoothed positional data of the bat's centre of mass (CoM). Definitions of take-off angle and jump height are also indicated. (B) Velocity of the bat's CoM, including the point taken as representative of the bat's take-off speed. (C) Force acting upon the bat's CoM, including the point taken to be the bat's jump force. All plots are shown with vertical dashed lines to indicate key events in the jump sequence. From left to right, the lines signify the jump start, wrist off the ground and the first downstroke.

As the velocities and accelerations are derived from the estimated position of the CoM, the process of video digitisation may introduce error into the estimates of kinematic variables. Digitising video footage is dependent upon the selection of a reliable landmark on the animal (in this case the shoulder joint). To estimate the error associated with video digitisation here, a test piece of footage was digitised five times and the standard deviations of the kinematic variable means were calculated. The standard deviations due to the digitisation process were 0.3 mm (0.33% of the mean) for jump height position, 0.027 m s^–1 (2.01% of the mean) for take-off speed and 2.07 m s^–2 (4.87% of the mean) for peak acceleration. These errors are unlikely to be systematic and therefore should not cause bias between species comparisons. The jump forces calculated here, however, should be regarded as estimates rather than direct measurements, such as those derived from a force plate.

Differences in the kinematic variables for each species were tested using one-way ANOVA and Tukey post hoc tests. The scaling relationships of the forearm length, jump height, take-off speed and jump force were also tested using least-squares regression. Least-squares regression was chosen over reduced major axis (RMA) as RMA can artificially inflate the slopes if the r² is low.

The scaling exponents (slopes) from the regression analyses were then tested against exponents predicted from the literature. A summary of the scaling predictions based on two distinct geometric models, the first being the classic Hill (Hill, 1950) model and the second a newer model from Richard and Wainwright (Richard and Wainwright, 1995), is given in table 1 of Toro et al. (Toro et al., 2003). The experimental scaling exponents from our study were tested against the predictions from both models. The models differ in their predictions of the relationship between velocity and increasing size. Hill's model predicts that velocity does not increase with increasing body size (Hill, 1950), whereas Richard and Wainwright's model predicts that velocity will increase 1:1 with increasing length (Richard and Wainwright, 1995).

Table 1.

Summary of means (±s.e.) and ANOVA results for the jump kinematic variables of five species of insectivorous bat

Published data (Schutt et al., 1997) for the vampire bat D. rotundus were plotted on the figures for comparative purposes. The data for D. rotundus, however, were not included in the statistical analyses as they were collected using a different methodology.

RESULTS

All the bats in the study followed a similar pattern during a take-off jump (Fig. 1). First, a small amount of counter-movement was observed in the footage, signalling the start of a jump. This was followed by a rapid jump using the wing musculature to propel the bat off its wrists. The bat's feet tended to leave the ground before the wrists. Once the wrist left the ground (end of the jump) the wings were quickly brought upwards and the first downstroke started, which tended to have a smaller amplitude than subsequent downstrokes. The bats then typically flew off at an angle shallower than the angle of the initial jump.

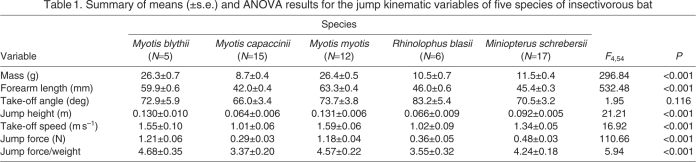
There was no detectable difference in the take-off angle used by the bats (Fig. 3A, Table 1), with all bats typically jumping at an angle between 70 and 80 deg from horizontal. The jump height achieved at the onset of the first downstroke varied considerably amongst species (Fig. 3B, Table 1), with the larger bats (M. blythii and M. myotis) jumping twice the height of the smaller M. capaccinii and R. blasii. Miniopterus schreibersii jumped higher than M. capaccinii, but not significantly higher than R. blasii. Take-off speed (Fig. 3C, Table 1) and jump force (Fig. 3D, Table 1) produced similar results to jump height, with the larger bats generally outperforming the smaller species. When jump force was corrected for body weight (N) (Fig. 3E, Table 1), however, the differences between the bats in the study were much smaller, with all species producing a force of between 3.5 and 4.5 times their body weight. Only the force to weight ratio produced by M. capaccinii was significantly lower than that of any of the other bats. The comparative data for D. rotundus suggest that it is likely to outperform all the bat species in this study in terms of take-off speed, jump force and the ratio of jump force to body weight (Fig. 3). Indeed, although the absolute jump force produced by D. rotundus is not much larger than that of M. blythii and M. myotis, when compared with its body weight the difference is striking. Desmodus rotundus is able to produce a force over 6 times larger than its body weight whilst jumping (Schutt et al., 1997).

Fig. 3.

Kinematic variables for jumping bat species. Myotis blythii (Mb, N=5), Myotis capaccinii (Mc, N=15) Myotis myotis (Mm, N=12), Rhinolophus blasii (Rb, N=6) and Miniopterus schrebersi (Ms, N=17). Data for Desmodus rotundus (Dr) are included for comparative purposes (Schutt et al., 1997). (A) Take-off angle. (B) Jump height. (C) Take-off speed. (D) Jump force. (E) Jump force/weight. Letters above the bars indicate significant differences (P<0.05) determined from the Tukey post hoc analyses. Bars with the same letters are not significantly different from each other and all data are shown with standard error bars.

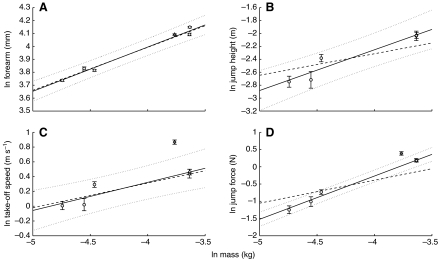
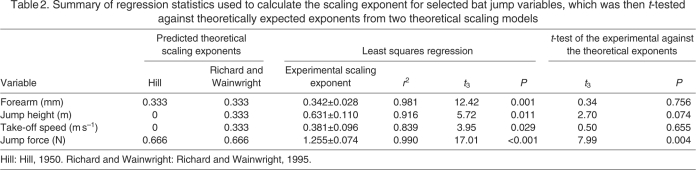
The scaling relationships investigated were all significantly different from zero (Fig. 4, Table 2). The scaling exponents from the regression of the bats' forearm length, jump height and take-off speed against M_b, however, were not significantly different from the predicted exponents from Richard and Wainwright's model (Richard and Wainwright, 1995) (Fig. 4, Table 2). In contrast, the calculated scaling exponents were different from those expected using Hill's model (Hill, 1950), which predicts no relationship between jump height or speed and M_b. Both the scaling models predict that jump force should scale as M ^0.66_b. The calculated exponents, however, showed positive allometry (Fig. 4D, Table 2), with larger bats generating higher forces than expected by the models. The comparative data of D. rotundus show that whilst it clearly falls within the 95% confidence limits for the scaling of forearm length (geometrically similar to the other bat species), it produces a greater than expected take-off speed and jump force.

Fig. 4.

Least-squares regression of bat jump variables against body mass for the five species of insectivorous bat (circles). Data from Desmodus rotundus (Schutt et al., 1997) (diamonds) are included for comparative purposes and are not used in the calculation of the regression lines. (A) Forearm length. (B) Jump height. (C) Take-off speed. (D) Jump force. All data are shown with standard error bars. Solid lines are the calculated regression slopes and dashed lines are the slopes from the predicted scaling exponents (Table 2). Dotted lines represent 95% confidence limits.

Table 2.

Summary of regression statistics used to calculate the scaling exponent for selected bat jump variables, which was then t-tested against theoretically expected exponents from two theoretical scaling models

DISCUSSION

Contrary to what was originally hypothesised, the jumping ability of the study bats appears to be driven more by their body size than by their foraging strategy, with the strongly selected-for and highly developed flight musculature providing a secondary ability of propelling the bat into the air from the ground. A potential exception to the lack of an obvious ecological trend in jump performance is perhaps D. rotundus, which has an extraordinary jumping ability possibly due to its highly unique sanguivorous foraging strategy.

The jumping technique used by the study bats for initiating flight (Fig. 1) is consistent with the technique previously described for D. rotundus (Altenbach, 1979; Schutt et al., 1997). The jump force is produced by the forearms and directed onto the ground through the wrist joint, with the hindlimbs leaving the ground first. This jump technique is completely different from the take-off of birds. Birds generate a large proportion of their take-off speed with their hindlegs, and the wings are used to continue the initial movement (Earls, 2000). In our study of bats, a small amount of counter-movement was typically observed before the start of each jump. Larger jumping animals often use counter-movement before jumping to stretch tendons, storing energy and improving the overall jump performance (Alexander, 2003). The bats may have been able to make some use of this technique, even though they are not specialist jumpers, given humans (also non-specialists at jumping) have been shown to improve jump performance through pre-jump tendon stretching (James et al., 2007).

The bats in the present study that typically feed near the ground or vegetation (gleaners) were expected to have a better jumping performance (i.e. higher jumps and faster take-off speeds) than the bats that feed in open areas (hawkers). The results, however, do not support this hypothesis, with the larger bats tending to outperform the smaller bats in absolute terms, with no clear ecological trend apparent (Fig. 3, Table 1). Rhinolophus blasii (a ground gleaner) was predicted to outperform both M. schreibersii (a fast-flying hawker) and M. capaccinii (a trawler) as it spends a significantly larger portion of time foraging on the ground. The three bats, however, had similar jump abilities, with the performance of R. blasii and M. capaccinii being indistinguishable. Indeed, M. schreibersii actually had a faster take-off speed than R. blasii (Fig. 3C, Table 1). Myotis capaccinii did not show a particularly reduced jumping performance despite possessing exceptionally large feet; extra weight at the extremities tends to reduce jumping performance (Alexander, 1995). The results support earlier evidence from a study of three Rhinolophid species, which also found no ecological trend in jump performance (Siemers and Ivanova, 2004).

The scaling exponent of forearm length against M_b was not significantly different from that expected for geometric similarity (0.33), a fundamental assumption of both scaling models tested here (Hill, 1950; Richard and Wainwright, 1995) (Fig. 4, Table 2). Furthermore, as there is generally an isometric scaling of muscle mass with M_b for mammals (Alexander et al., 1981; Schmidt-Nielsen, 1984), the percentage of the muscle mass available to the bats for jumping should be the same for all species. The scaling of both jump height and take-off speed with M_b supports the geometric model of Richard and Wainwright (Richard and Wainwright, 1995), rather than Hill's model (Hill, 1950). This suggests that the muscles involved in bat jumping behave so that any increase in length causes a 1:1 increase in contraction velocity. This predicted 1:1 relationship is based on the assumption that sarcomere length is constant within muscles during ontogeny (Richard and Wainwright, 1995). The scaling relationships determined here, however, are interspecific, which implies that sarcomere length must be relatively constant across the bat species studied. Both models (Hill, 1950; Richard and Wainwright, 1995) fail to predict the scaling of jump force, as larger bats were able to produce relatively more force (F∝M ^1.255±0.074_b) than the models predicted (F∝M ^0.66_b). These results differ from a study of 12 Anolis lizard species (Toro et al., 2003), which found that peak force did scale as predicted by the models. Lizard jump speed, however, was not predicted by either model, which also contrasts with the bat results, as the scaling of bat take-off speed was not significantly different from the predictions of Richard and Wainwright's model (Richard and Wainwright, 1995). These inconsistencies highlight the fact that the scaling of muscle performance and how it relates to animal kinematics are likely to vary across taxa.

An exception to the lack of an ecological influence on take-off performance is perhaps D. rotundus, which seems to outperform the bats in this study (Fig. 3). The jump force and take-off speed of D. rotundus are clearly greater than would be expected based on the scaling relationships for the other five species of bat, as they fall far outside the 95% confidence limits (Fig. 4). Vampire bats frequently take on 50% of their body mass in blood during feeding; thus, their extraordinary jumping ability may have evolved to cope with this increase in body mass, ensuring they can still get airborne (Altenbach, 1979). Indeed, Harris and Steudel found that fat mass relative to lean body mass explained most of the variation in the jump velocity of cats (Harris and Steudel, 2002). Desmodus rotundus falls well within the confidence intervals for the scaling of forearm length against M_b (Fig. 4), whereas other specialist jumpers have elongated limbs to improve jumping (James et al., 2007), suggesting that the improved performance of D. rotundus is not related to limb morphology but perhaps to muscle physiology. Schutt and colleagues propose that during a D. rotundus jump different muscle fibre types are sequentially recruited, which may help maximise jump performance (Schutt et al., 1997). Whether this suggested sequential recruitment of muscle fibres occurs in all bats or perhaps only D. rotundus remains unknown. Another explanation for the exceptional jump performance of D. rotundus compared with the bats in this study, however, may relate to differences in methodology. The data in the study of Schutt and colleagues (Schutt et al., 1997) were collected using a force plate, whereas this study utilised high-speed video footage. Nevertheless, the two techniques are known to produce comparable results (Arampatzis et al., 2000; Saini et al., 1998; Thirunarayan et al., 1996). Therefore, the difference in the jump performance of D. rotundus is likely to be due to ecological pressures and not methodological differences.

The data presented here show that, contrary to expectations, there is no obvious ecological trend to the jumping performance of the study bats. Rather, the bats' jump performance seems to correlate with their body mass, with the strongly selected-for wing musculature providing the necessary force for take-off from the ground. It is likely that selection for flight performance is dominant in shaping the forelimbs and associated musculature of bats, with the relationship between the two tightly constrained to provide an aerodynamic optimum and, hence, similar levers and motors for jumping with. Comparisons of the bat data with scaling models are supportive of the model of Richard and Wainwright (Richard and Wainwright, 1995), except when considering force production. This failure of existing models to predict the scaling of jump force and the apparent differences between taxa indicate that further investigations of bat jumping, and vertebrate muscle performance in general, are required.