Abstract
Tuberculosis (TB) is a deadly infectious disease caused by Mycobacterium tuberculosis (Mtb). No available vaccine is reliable and, although treatment exists, approximately 2 million people still die each year. The hallmark of TB infection is the granuloma, a self-organizing structure of immune cells forming in the lung and lymph nodes in response to bacterial invasion. Protective immune mechanisms play a role in granuloma formation and maintenance; these act over different time/length scales (e.g. molecular, cellular and tissue scales). The significance of specific immune factors in determining disease outcome is still poorly understood despite incredible efforts to establish several animal systems to track infection progression and granuloma formation.
Mathematical and computational modeling approaches have recently been applied to address open questions regarding host-pathogen interaction dynamics, including the immune response to Mtb infection and TB granuloma formation. This provides a unique opportunity to identify factors that are crucial to a successful outcome of infection in humans. These modelling tools not only offer an additional avenue for exploring immune dynamics at multiple biological scales, but also complement and extend knowledge gained via experimental tools. We review recent modelling efforts in capturing the immune response to Mtb, emphasizing the importance of a multi-organ and multi-scale approach that has tuneable resolution. Together with experimentation, systems biology has begun to unravel key factors driving granuloma formation and protective immune response.
Tuberculosis (TB) is a deadly infectious disease in humans caused by the bacteria Mycobacterium tuberculosis (Mtb)1. An estimated 2 billion people, or one-third of the world’s population, are infected with Mtb, and approximately 2 million people died of TB in 2008. A unique feature of Mtb is its ability to persist in the infected host during a latent clinical state. About 90% of those infected with Mtb have asymptomatic, latent TB infection (sometimes called LTBI) with a 10% lifetime chance of progressing to TB disease (or active TB)1, 2. If untreated, the death rate for active TB is more than 50%2. In addition, the presence of HIV/AIDS increases the risk of reactivation of latent TB by 10% per year. Antibiotics reduce the risk of reactivation, but do not lead to cure. A vaccine does exist (not used in the USA or UK) but the efficacy is variable at best3. Thus, there is a global urgency to understand this disease ranging from the epidemiology to genetic levels. This article briefly summarizes some of the successes that systems biology approaches, in particular mathematical and computational modelling, have had on exploring the within-host dynamics of this world-health problem.
IMMUNOBIOLOGY AND PATHOGENESIS OF TB
When considering the dynamics of an infectious disease, there are many perspectives of interest, e.g. how it spreads through a population (epidemiology), the dynamics of the bacterial genetics in different portions of the world, or how the host and pathogen interact. Although we and others have explored TB from these and other perspectives4-6, our focus here will be to review studies exploring the host immune response to infection with Mtb. The immunological processes by which the host controls this infection are incompletely understood. Mtb is a small non-motile bacterium that primarily infects the lungs in adult humans. TB infection begins when the mycobacteria reach the pulmonary alveoli, where they invade and replicate within a phagocytic cells termed macrophages1 7. Mtb divides every 16 to 24 hours, an extremely slow rate compared to typical bacteria, which divide on the order of minutes8. Mtb has evolved ways to evade many protective host immune mechanisms; as a consequence, Mtb is able to multiply almost unchecked within a resting macrophage. Bacteria are also internalized by another phagocytic cell type, dendritic cells, at the site of infection; these cells are less permissive for Mtb replication and are specialized for transporting bacteria to local, draining lymph nodes (LNs) to initiate T cell priming and an adaptive immune response by the host. This response is required to contain infection, but is unable to clear it. The failure to clear bacteria elicits a unique immune response at the site of infection, the appearance of granuloma, the hallmark of Mtb infection.
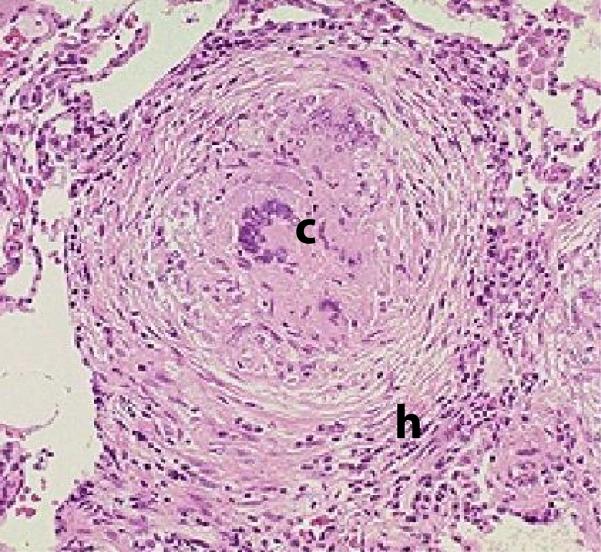
A granuloma appears as a spherical collection of macrophages, T cells, B cells and other immune cells with the goal of immunologically restraining and physiologically containing bacterial infection (Figure 1). The typical spatial arrangement of cells is a ring of T-cells surrounding a core of infected macrophages. Granuloma form in response to a cascade of cytokine and chemokine signals9 at the site of infection. Initially they form in the lungs, but later can be observed in LNs as well. To complicate matters, there are various types of human (primate) TB granulomas (caseous, necrotic, fibrotic, etc) and ranges in between these10. Many questions regarding the form and function of granuloma remain unanswered, yet granulomas remain as the central player to understanding prevention, treatment and therapy for TB. Ultimately, formation and maintenance of “good” or “working” granuloma are essential for control of Mtb infection. What defines “good” is not known.
Figure 1. Example of a typical granuloma.
Note: the letter c denotes the central necrotic core and infected macrophages surrounded by a rim of lymphocytes (letter h)14, 39.
Animal models of tuberculosis
Mtb infects most mammals. There are several established animal models for Mtb, including mice, zebrafish, guinea pigs, rabbits, and monkeys11. However, immunologic reagents are only readily available for mice and non-human primates (NHP). Mice are most commonly used, and the availability of genetically identical and engineered mice has proven invaluable in addressing the roles of various cells and cytokines in control of infection. Two limitations to the mouse model are the lack of latent infection (infection is chronic and progressive in mice) and the pathology: mouse granulomas are not similar in structure to human granulomas. NHPs are similar to humans in almost all aspects, with active TB, latent infection and reactivation TB observed, as well as pathology and granulomas that are identical to humans12, 13. The immunologic reagents available for monkeys allow one to obtain quantitative and qualitative data on cell populations and functions in the lungs and LNs10, 12-14. However, the peculiar slow-progression of TB in NHPs (and humans) makes comprehensive data collection particularly difficult (and expensive) for scientists. Studies in animal models and some human data have identified various necessary immune factors important in control of Mtb infection, but sufficient conditions have yet to be uncovered. A protective immune response requires priming and activation of antigen-specific CD4+ and CD8+ T-cells, production of chemokines to impact recruitment of cells to the infection site, production of cytokines (e.g. IFN-γ, IL-12, TNF, IL-10) some of whose role is to activate macrophages, and macrophage effector molecules that kill bacteria (such as nitric oxide). These factors all comprise the granuloma, but the role of spatial information within granuloma for these effector cells and molecules is not currently available. Yet, it is likely the balance, location and concentrations of these and numerous other factors within the granuloma that dictates the outcome of infection and disease.
WHAT CAN SYSTEMS BIOLOGY DO FOR TB RESEARCH?
Experimental biology has and will continue to be a successful and necessary approach to exploring infection with Mtb and other pathogens. However, many questions in tuberculosis remain unanswered: Which collection of immune factors is responsible for determining whether an individual develops active TB or latent infection? Where is latent infection established and where does it reactivate? What events occur in the LN that affect control at the level of the lung, and vice versa, and how do these physiological compartments communicate? What factors affect timing of initiation of the immune response in the LN and lung? What new approaches for treatment and control might be useful? Difficulties in approaching these questions experimentally include the number and expense of experiments required to fully explore all these interacting factors and various outcomes, the time required to do experiments in the most relevant animal system (the NHP), and the difficulty in integrating data from multiple experiments and from experiments aimed at various organs and at various length (molecular, cellular, tissue, organism, population) and time scales (e.g. seconds to lifetimes) into a comprehensive view. For example, molecular data on TNF binding over a period of minutes, granuloma formation over a period of days (mice) to weeks (NHP), T cell priming in the LN (days), and cellular trafficking among multiple organs are all necessary components of understanding granuloma formation and ultimately the immune response to Mtb. While there is no “standard dataset” available for model development, numerous types of data are available in the literature. Some of these are summarized in Table 1. Using a systems biology approach, data from both animal and computational systems can be integrated and synthesized to explore a complex biological system and address relevant questions. One goal of this approach is to create a computational model system that reflects human biology, providing an opportunity to perform experiments that are impractical or not feasible in vivo or in vitro as well as generate testable hypotheses.
TABLE 1.
experimental data availability based on scale/organ modeled in TB infection
| Scale/ Compartment |
Data Available | Techniques | Data Not Available |
|---|---|---|---|
|
Individual
Granuloma |
|
Flow cytometry, ELISPOT, Luminex, Immuno-Histo- Chemistry (IHC), In-Situ Hybridization (ISH), in vivo and in vitro cytotoxicity assays, gene-knockout (deletion) & cell and cytokine depletions |
|
|
Individual Lymph
Node |
|
Flow cytometry, ELISPOT Luminex, in vivo and in vitro cytotoxicity assays , 2-photon microscopy |
|
A Systems Biology Approach to Understanding Immunity to Mtb
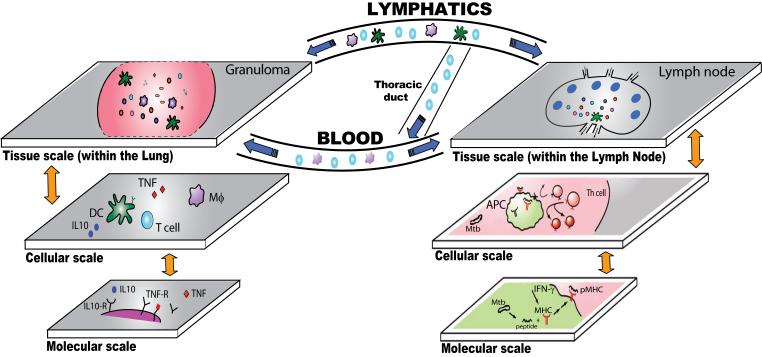
We believe that for the study of the immune response during Mtb infection, a multi-organ (compartment) and multi-scale quantitative approach is necessary to capture the unique, complex and interdependent interactions between Mtb and the host and to allow us to integrate information across length and time scales. A general paradigm for understanding the immune response during Mtb infection and guiding development of a computational framework is shown in Fig. 2 and Table 2.
Figure 2. Multi-scale, multi-compartment view of the immune response to Mtb infection.
Mtb introduced into the lung (left side of figure) is taken up by dendritic cells (DCs) and macrophages (Mϕs). DCs travel through the lymphatics to a draining lymph node (LN) bringing bacteria with them. In the LN, display of peptide-MHC (pMHC) complexes by DCs (APCs) leads to T helper cell (Th) priming. These cells travel to the lung via blood. Granulomas form in the lung and later, LNs (not shown). In both the lung and LN, molecular events (e.g., pMHC binding, IL-10 and TNF-receptor binding) influence cell behaviour (e.g., display of pMHC complexes, cell survival or activation) and cell behaviour influences tissue level events (e.g., T cell priming and granuloma formation). Within a granuloma, T cells secrete cytokines such as IFN-γ which activates macrophages to destroy the bacteria with which they are infected40. Cytotoxic T-cells can also directly kill infected cells, by secreting perforin and granulysin7. This leads to inhibition or killing of bacilli as well. Another feature of the granuloma in primates is the extensive cell death within the tissue, called necrosis, that develops in the center of the granuloma41. Importantly, bacteria are not always eliminated within the granuloma, but can become dormant, resulting in a latent infection1. Information flows both “bottom-up” and “top-down” (orange arrows) and “to and from” compartments (blue arrows).
TABLE 2.
Some published models relevant to understanding the immune response during TB
| Model category | Biology | Biological scale | Time scale |
Length scale | Model type | Ref. |
|---|---|---|---|---|---|---|
|
Lymph node
models |
Peptide-MHC binding | Molecular | 10−1-102 s | 10−9-10−8 m | Statistical | 42, 43 |
| Antigen uptake and presentation by single APC |
Molecular/ single cell |
101-103 s | 10−5 m | Deterministic, continuous (ODE) |
43, 44 | |
| Priming of single T cell by APC |
Molecular Multiple cells |
101-102 s | 10−3-10−2 m | Deterministic, continuous (ODE) |
5, 43 | |
| Cell interactions and T cell priming in LN |
Cell/Tissue | 104-105 | 10−3-10−2 m | Stochastic, discrete (ABM) |
38, 45-51 | |
|
Granuloma
models |
TNF secretion and binding by single cells |
Single cell | 1-101 s | 10−6-10−5 m | Deterministic, continuous (ODE) |
23 |
| TNF secretion and binding by cells in granuloma |
Cell/Tissue | 1-101 s | 10−3-10−2 m | Deterministic, continuous (PDE) |
23 | |
| Cell interactions in the lung to form granuloma |
Cell/Tissue | 102-103 s | 10−3 m | Stochastic, discrete (ABM) |
21, 22, 37 | |
| Lung models | Cell interactions in the lung |
Tissue/Organ | 1 day | 10−1 m | Deterministic continuous (ODE,PDE) |
16-20, 30, 31 |
|
Lymphatic/
organ models |
LN to other organ models |
Organ/Body | 105-106 s | 10−2-1 m | Deterministic (Two compartmental ODE systems) |
24-26, 52-54 |
Two important aspects of model development are highlighted in the figure. First, the biological processes that are relevant to the immune response occur at different length scales; molecular, cellular, and tissue level scales are shown. Thus, models that include relevant detail at multiple scales are important. Models developed and validated with experimental data at individual physiological scales are then linked to form a multi-scale model and allow information to flow in particular directions. If the results from a model developed at the smallest scale are passed to the model developed at the next larger scale, the information flow is “bottom-up”. This can be done in various ways: the larger scale model may contain the entire smaller scale model, for example, or may simply use a parameter that is calculated in the smaller scale model. Alternatively, the linking may also need to incorporate information flow that is “top-down” if changes at larger scales affect behaviour at smaller scales. Analysis can begin at any scale (the “middle-out” approach, as pointed out by the Nobel laureate Sydney Brenner): “Analysis must start somewhere, but it doesn’t really matter where. In the best of all systems-biological world, we will eventually meet up, anyway”15. The multi-scale model allows the relevance of events at that one scale to be observed at higher or lower scales as well. Second, models need to incorporate events occurring in both the lung and the draining LN, necessitating a multi-organ (compartment) model. Indeed, it is likely that the movement of cells between these compartments determines the speed and efficiency of an immune response.
Importantly, models developed should have tuneable-resolution, by which we mean the ability to fine-grain or coarse-grain model components at will. For example, to answer questions about how a particular cytokine’s binding kinetics affect granuloma formation, immune system models that explicitly include molecular processes involving this cytokine are most useful, but those models do not need extensive detail in the LN compartment and a relatively coarse-grained treatment there may suffice. Since models are often used to answer different questions at different times, then the accessibility to a model that allows for fine-graining in some scale(s) of interest and coarse-graining in others is desired. In addition, such tuneable resolution yields some computational assistance as well: it can improve debugging, increase the speed of computation and assist in analysis.
LESSONS LEARNED FROM DIFFERENT MODELS AIMED AT UNDERSTANDING THE IMMUNE RESPONSE DURING TB
Over the past decade we have developed a series of mathematical and computational models in an effort to qualitatively and quantitatively characterize the immune response to Mtb infection in lung16-23, and in lung and LN24-26. Table 2 summarizes our work and the work of others in this area. In addition, we have integrated experimental data into the development and testing of our models (for examples, see Table 1) allowing us to make predictions regarding mechanisms, dynamics and data that are currently open questions for TB researchers. We will focus on a few models to highlight key findings that different models reveal, while emphasizing the importance of each approach.
Single Organ Models
The past 20 years saw a boom in the use of mathematical models to study within-host-pathogen interactions; most of these models explore viruses such as HIV-1/AIDS and Hepatitis C interacting with the immune system27, 28 and use a system of nonlinear, ordinary differential equations (ODEs) to describe time course behavior of cells and other system elements. The first model published to capture within-host dynamics during a bacterial infection explored Mtb infection dynamics at the site of infection20, and next generation models included additional cell types and cytokines that play a role in the immune response in the lung environment18, 19. To develop these models, we created equations that were based on known interactions of immune cells in the lung during infection with Mtb. We used data from literature to estimate parameter values when available and performed uncertainty and sensitivity analysis29 to define the parameter space. In addition, we validated our models using known experimental results for gene knock-out and depletions from mouse, NHP and humans. In this way, we ensured that the models behaved according to known dynamics. Once tested, the model was used to make predictions regarding dynamics and data currently not available.
Few other studies have been done on modelling within-host dynamics of TB30, 31. Magombedze et al30 built an ODE system based on our previously published work but with the emphasis on analytical results (e.g., bifurcation analysis). Day et al31 built a model to understand the environment in the lung during infection and introduced two novelties to host-pathogen modeling: first, they represented macrophages by activation phenotypes (classically versus alternatively activated macrophages, CAM vs AAM) and, second, they focus on the concept of switching time (i.e., the time needed to switch from an AAM-dominated to a CAM-dominated lung environment during infection). They argued that the biological relevance of increasing switching times is that a delay in CAM presence in lung may be responsible for Mtb gaining an initial “foothold”.
Modeling makes predictions about processes that are currently not possible to observe experimentally. A key modeling contribution to our understanding of Tb regards the cytokine IL-10. This is a cytokine that serves to down-regulate the immune response, suppressing excessive inflammation during infection. During mouse deletion and depletion studies, it was determined that this molecule had no strong effect on disease outcome for Mtb32. Our studies suggested something different- a subtle phenotype that was missed. Our simulations of IL-10 deletion and depletion showed that the system went from an asymptotically stable steady state to a less stable oscillatory state- one that was easily missed with experimental approaches. This suggests that IL-10 is an important stabilizer of the system that was later confirmed with experiments performed based on our work 33, 34. Another key result made possible by the mathematical formulation was to show how selective deletion of CD8+ T cell subsets. As a second example, models suggested a differential contribution for CD8+ T cell effectors that are cytotoxic as compared with those that produce IFN-γ; it is not possible to delete one subset or the other in experiments, but this can be done in the model. We also predicted the minimum levels of effector memory cells of each T cell subset (CD4+ and CD8+) that provide effective protection following vaccination19.
As useful as these temporal models are in predicting certain aspects of immunity, they cannot recapitulate details of granuloma formation because they do not include a way to capture spatial structure. It was recognized in the early 90’s that cellular automata models were a way to capture stochastic, discrete events occurring in the immune system35. After the development of object oriented programming, agent-based models (ABMs) appeared and provided more flexibility in capturing agents (cells, etc) and their behaviours36. The first ABM to describe the immune response to a pathogen was developed for Mtb and specifically to characterize mechanisms that control granuloma formation and function22. Next generation models have included additional cell types (e.g., effector CD8+ T cells and regulatory T cells), cytokines (e.g., TNF) and chemokines (e.g., CCL5, CCL10) as data on those became available21. By defining simple rules of interactions between cells (macrophage and effector T cells), bacteria (Mtb) and environment (a 2-D grid representing a 2 mm by 2 mm section of lung tissue), unique spatially-specific mechanisms emerge as important immune control factors in TB infection (figure 3A). Here again, model rules were based on experimental data regarding cell-cell interactions that were available and the model was tested against cell depletion and deletion data for humans, primates and mouse systems. Currently, there are no experimental methods available to observe the dynamics of individual granuloma formation over a long time in primates and humans. Thus, our models are the first to look at the dynamics of granuloma formation in the lung from initial infection onwards.
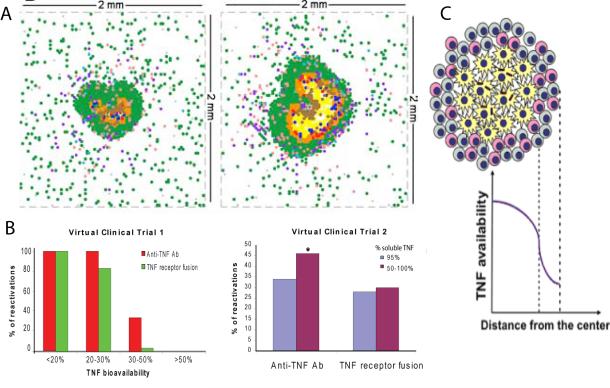
Figure 3. Individual scale models to understand the role of TNF in TB.
A. 2-D ABM simulation of a granuloma showing baseline solid granuloma and a necrotic TNF−/− granuloma21. B. Virtual clinical trial of anti-TNF therapy shows the number of reactivations per 100 virtual patients using two types of anti-TNF treatments and two different reactivation thresholds 18. C. Prediction of a TNF gradient in a granuloma due to secretion and uptake kinetics by different cells types 23
Cytokines have multiple actions, but one cannot experimentally separate these effects of an individual molecule , We used the ABM of a granuloma to separate the multiple known activities of the cytokine TNF (macrophage activation; regulation of apoptosis; chemokine and cytokine production; and regulation of cellular recruitment via trans-endothelial migration) and study how each contributes alone and in combination to granuloma formation, maintenance, and ultimately pathology21. Key insights from these ABMs include identifying a key role in granuloma formation of chemokine diffusion kinetics, macrophage overcrowding within the granuloma, arrival time of T cells from the LN, as well as location and number of T cells within the granuloma. For example by shortening the arrival time of effector T cells at the infection site (lung), lower bacterial loads and clearance could be obtained. This suggests that a specific vaccine could be effective in TB. After our initial work, to our knowledge, only one other study has been published targeting the impact of spatial effects and inherently stochastic processes on TB granuloma formation37 . Warrender et al37 used a platform called CyCells simulator, obtaining results very similar to the previously published ABM of Segovia et al22, although their focus was on early events in Mtb infection driving disease outcome.
In addition to modelling the immune response in the lung, immune responses in LNs have also been studied. Nearly all of these models are not TB-specific, but do give insights into the DC-T cell interaction (c.f Table 2). One of the most useful outputs of these simulations is a prediction of the number and dynamics of primed T cells produced in the LN and available to travel to a site of infection38.
Multi-Organ Models
Multi-organ models are needed to capture important processes such as cellular activation and immune cell priming that occur in the LN, leading to trafficking of cells back to sites of infection 24-26 (Fig. 2). This involves linking models describing individual physiological compartments together with consideration of scaling and flow between compartments. Typically, little to no experimental data is available describing these events. Thus, the models have to be validated individually and then linked. Multi-compartmental approaches suggested that delays in either DC migration to the LN or T cell trafficking to infection sites could dramatically alter infection outcomes, leading to either bacterial clearance or overgrowth if not regulated properly. A natural progression towards a next generation multi-organ model builds into the ABM formulation some of the mechanisms of T cell priming in LNs. A first-time hybrid multi-organ model couples a discrete/stochastic system to a continuous/deterministic system (manuscript in preparation). Building a hybrid model is a first step before moving on to the final development, which is to link two compartment ABMs. This remains an open problem.
Multi-scale Models and Tuneable Resolution
We have published multi-scale mathematical models addressing the effects of host genetics and demographic factors on TB epidemics4, and investigated how multiple polymorphisms interact to determine individual susceptibility to TB5. Fallahi-Sichani et al23 recently developed a multi-scale PDE granuloma model that includes TNF/TNF receptor binding and trafficking processes (see Figure 3B). This model represents a first attempt to quantify impact of immune cell organization on TNF bioavailability within granuloma— data that are presently not obtainable in vivo or in vitro. Organization of immune cells and molecular level mechanisms (i.e., TNF/TNF receptor binding) are identified as important factors regulating bioavailability. One great advantage of this modelling approach is that the action of several known drugs could be tested on a molecular level basis, and not simply at a phenomenological level as in Marino et al18 (see Figure 3C). Indeed, we are currently extending this work by incorporating molecular scale TNF dynamics into a multi-scale tuneable-resolution ABM of the granuloma to learn how TNF dynamics influence granuloma development at each scale (in preparation).
CONCLUSION
Despite all of the experimental and theoretical work on TB, it remains the main killer by infectious disease in the world. Specific open questions are as basic as how treatment works and what factors are important for vaccine development. A systems biology approach, integrating both modelling and experimental aspects, is essential; however, challenges remain in both areas. Development of multi-scale, multi-compartment models with tuneable resolution requires significant effort in model development and validation. Experimental techniques are needed that allow, for example, measuring in vivo and real-time cell and bacterial counts during infection progression, or tracking cells moving within a single organ (lung) or, more elusively, between organs over long time and large space. Collaboration between experimental and modelling colleagues is crucial to achieve our goal of unravelling mechanisms of TB infection, prevention, treatment and cure.
SIDEBAR 1: Immunology terminology.
Monocyte: cell produced in the bone marrow that circulates throughout the bloodstream. Monocytes leave the bloodstream in response to infection and inflammation, and develop into macrophages or dendritic cells.
Macrophage: functions as a patrol cell and engulfs and kills foreign infectious invaders. Macrophages also stimulate T cells to destroy these invaders.
Dendritic cell: cell that functions as part of the adaptive immune system. Dendritic cells are called antigen presenting cells (APCs) because of their ability to present antigens to B- and T-cells. Antigen presentation helps T- and B-cells to recognize pathogens and respond faster the next time infection occurs.
T-cell: type of lymphocyte that helps to orchestrate the immune system by killing pathogens and producing or helping to produce cytokines and chemokines.
B-cell: type of lymphocyte that produces antibodies that bind antigens.
Antigen: a substance or molecule that is recognized by the immune system as a bacterium or virus.
Cytokines interferon-γ, interleukin-12, tumor necrosis factor and interleukin-10 (IFN-γ, IL-12, TNF, IL-10): molecules produced by cells. Cytokines interact with cells of the immune system in order to regulate the body’s response to disease and infection.
Chemokine: molecules manufactured by cells and tissues that stimulate movement and activation of immune system cells to the area where the chemokine is produced.
SIDEBAR 2: Mathematical and Modeling Terminology.
Differential Equations (DEs): a mathematical equation usually describing a deterministic relation of some continuously varying quantities (modeled by functions) and their rates of change in space and/or time (expressed as derivatives). There are two major types: Ordinary Differential Equations (ODEs) and Partial Differential Equations (PDEs).
ABM, Agent-Based Model: class of computational models for simulating the actions and interactions of autonomous agents (either individual or collective entities) in a heterogeneous environment where possibly global, system-wide dynamics and patterns emerge from the local, likely stochastic, individual-level interactions.
Hybrid model: a representation in which multiple types of mathematical models are used simultaneously to describe a system (ODE, PDE, ABM, etc)
Multi-scale model: a model that allows for explicit consideration of events at a variety of length and/or time scales.
Multi-Compartment model: a model that allows for variables to be allocated in different environments that may correspond to different organs or tissues (compartments may each also have multiple scales of interest). Each of the above representations can be represented as a compartmental model.
Tuneable-resolution: a model that includes the ability to fine-grain or coarse-grain particular sub-models ‘at will’.
Acknowledgements
This work was supported by grants from the NIH: R33HL092844, R33HL092853 and N01 AI50018.
Contributor Information
Simeone Marino, Dept. of Microbiology and Immunology, University of Michigan Medical School, Ann Arbor, MI, USA.
Jennifer Linderman, Dept. of Chemical Engineering, College of Engineering, University of Michigan, Ann Arbor, MI, USA.
Denise E. Kirschner, Dept. Microbiology and Immunology, University of Michigan Medical School, Ann Arbor, MI, USA.
Further Reading/Resources
- 1.MultiscaleModelingWorkingGroup 2010 http://www.imagwiki.org/mediawiki/index.php?title=Multiscale_Modeling_Working_Groups.
References
- 1.Kumar V, Robbins SL. Robbins basic pathology. 8th ed Saunders/Elsevier; Philadelphia, PA: 2007. [Google Scholar]
- 2.Onyebujoh PR, W. GA. World Health Organization Disease Watch: Focus: Tuberculosis. 2006.
- 3.Colditz GA, Brewer TF, Berkey CS, Wilson ME, Burdick E, et al. Efficacy of BCG Vaccine in the Prevention of Tuberculosis: Meta-analysis of the Published Literature. JAMA. 1994;271(9):698–702. [PubMed] [Google Scholar]
- 4.Murphy BM, Singer BH, Anderson S, Kirschner D. Comparing epidemic tuberculosis in demographically distinct heterogeneous populations. Math Biosci. 2002;180:161–185. doi: 10.1016/s0025-5564(02)00133-5. [DOI] [PubMed] [Google Scholar]
- 5.Chang ST, Linderman JJ, Kirschner DE. Effect of multiple genetic polymorphisms on antigen presentation and susceptibility to Mycobacterium tuberculosis infection. Infect Immun. 2008;76(7):3221–3232. doi: 10.1128/IAI.01677-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Young D, Stark J, Kirschner D. Systems biology of persistent infection: tuberculosis as a case study. Nat Rev Microbiol. 2008;6(7):520–528. doi: 10.1038/nrmicro1919. [DOI] [PubMed] [Google Scholar]
- 7.Houben EN, Nguyen L, Pieters J. Interaction of pathogenic mycobacteria with the host immune system. Curr Opin Microbiol. 2006;9(1):76–85. doi: 10.1016/j.mib.2005.12.014. [DOI] [PubMed] [Google Scholar]
- 8.Cox RA. Quantitative relationships for specific growth rates and macromolecular compositions of Mycobacterium tuberculosis, Streptomyces coelicolor A3(2) and Escherichia coli B/r: an integrative theoretical approach. Microbiology. 2004;150(Pt 5):1413–1426. doi: 10.1099/mic.0.26560-0. [DOI] [PubMed] [Google Scholar]
- 9.Flynn JL, Chan J. Immunology of tuberculosis. Annu Rev Immunol. 2001;19:93–129. doi: 10.1146/annurev.immunol.19.1.93. [DOI] [PubMed] [Google Scholar]
- 10.Fuller CL, Flynn JL, Reinhart TA. In situ study of abundant expression of proinflammatory chemokines and cytokines in pulmonary granulomas that develop in cynomolgus macaques experimentally infected with Mycobacterium tuberculosis. Infect Immun. 2003;71(12):7023–7034. doi: 10.1128/IAI.71.12.7023-7034.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Flynn JL, Chan J. What’s good for the host is good for the bug. Trends Microbiol. 2005;13(3):98–102. doi: 10.1016/j.tim.2005.01.005. [DOI] [PubMed] [Google Scholar]
- 12.Lin PL, Pawar S, Myers A, Pegu A, Fuhrman C, et al. Early events in Mycobacterium tuberculosis infection in cynomolgus macaques. Infect Immun. 2006;74(7):3790–3803. doi: 10.1128/IAI.00064-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lin PL, Rodgers M, Smith L, Bigbee M, Myers A, et al. Quantitative comparison of active and latent tuberculosis in the cynomolgus macaque model. Infect Immun. 2009;77(10):4631–4642. doi: 10.1128/IAI.00592-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lin PL, Myers A, Smith L, Bigbee C, Bigbee M, et al. Tumor necrosis factor neutralization results in disseminated disease in acute and latent Mycobacterium tuberculosis infection with normal granuloma structure in a cynomolgus macaque model. Arthritis Rheum. 2010;62(2):340–350. doi: 10.1002/art.27271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Noble D. The music of life : biology beyond the genome. Oxford University Press; Oxford ; New York: 2006. [Google Scholar]
- 16.Ganguli S, Gammack D, Kirschner DE. A metapopulation model of granuloma formation in the lung during infection with mycobacterium tuberculosis. Math Biosci Eng. 2005;2(3):535–560. doi: 10.3934/mbe.2005.2.535. [DOI] [PubMed] [Google Scholar]
- 17.Gammack D, Doering CR, Kirschner DE. Macrophage response to Mycobacterium tuberculosis infection. J Math Biol. 2004;48(2):218–242. doi: 10.1007/s00285-003-0232-8. [DOI] [PubMed] [Google Scholar]
- 18.Marino S, Sud D, Plessner H, Lin PL, Chan J, et al. Differences in reactivation of tuberculosis induced from anti-TNF treatments are based on bioavailability in granulomatous tissue. PLoS Comput Biol. 2007;3(10):1909–1924. doi: 10.1371/journal.pcbi.0030194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Sud D, Bigbee C, Flynn JL, Kirschner DE. Contribution of CD8+ T cells to control of Mycobacterium tuberculosis infection. J Immunol. 2006;176(7):4296–4314. doi: 10.4049/jimmunol.176.7.4296. [DOI] [PubMed] [Google Scholar]
- 20.Wigginton JE, Kirschner D. A model to predict cell-mediated immune regulatory mechanisms during human infection with Mycobacterium tuberculosis. J Immunol. 2001;166(3):1951–1967. doi: 10.4049/jimmunol.166.3.1951. [DOI] [PubMed] [Google Scholar]
- 21.Ray JC, Flynn JL, Kirschner DE. Synergy between individual TNF-dependent functions determines granuloma performance for controlling Mycobacterium tuberculosis infection. J Immunol. 2009;182(6):3706–3717. doi: 10.4049/jimmunol.0802297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Segovia-Juarez JL, Ganguli S, Kirschner D. Identifying control mechanisms of granuloma formation during M. tuberculosis infection using an agent-based model. J Theor Biol. 2004;231(3):357–376. doi: 10.1016/j.jtbi.2004.06.031. [DOI] [PubMed] [Google Scholar]
- 23.Fallahi-Sichani M, Schaller MA, Kirschner DE, Kunkel SL, Linderman JJ. Identification of key processes that control tumor necrosis factor availability in a tuberculosis granuloma. PLoS Comput Biol. 2010;6(5):e1000778. doi: 10.1371/journal.pcbi.1000778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Marino S, Kirschner DE. The human immune response to Mycobacterium tuberculosis in lung and lymph node. J Theor Biol. 2004;227(4):463–486. doi: 10.1016/j.jtbi.2003.11.023. [DOI] [PubMed] [Google Scholar]
- 25.Marino S, Myers A, Flynn JL, Kirschner DE. TNF and IL-10 are major factors in modulation of the phagocytic cell environment in lung and lymph node in tuberculosis: a next-generation two-compartmental model. J Theor Biol. 2010 doi: 10.1016/j.jtbi.2010.05.012. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Marino S, Pawar S, Fuller CL, Reinhart TA, Flynn JL, Kirschner DE. Dendritic cell trafficking and antigen presentation in the human immune response to Mycobacterium tuberculosis. J Immunol. 2004;173(1):494–506. doi: 10.4049/jimmunol.173.1.494. [DOI] [PubMed] [Google Scholar]
- 27.Dahari H, Layden-Almer JE, Kallwitz E, Ribeiro RM, Cotler SJ, et al. A mathematical model of hepatitis C virus dynamics in patients with high baseline viral loads or advanced liver disease. Gastroenterology. 2009;136(4):1402–1409. doi: 10.1053/j.gastro.2008.12.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wodarz D, Nowak MA. Mathematical models of HIV pathogenesis and treatment. Bioessays. 2002;24(12):1178–1187. doi: 10.1002/bies.10196. [DOI] [PubMed] [Google Scholar]
- 29.Marino S, Hogue IB, Ray CJ, Kirschner DE. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J Theor Biol. 2008;254(1):178–196. doi: 10.1016/j.jtbi.2008.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Magombedze G, Garira W, Mwenje E. Modelling the human immune response mechanisms to mycobacterium tuberculosis infection in the lungs. Math Biosci Eng. 2006;3(4):661–682. doi: 10.3934/mbe.2006.3.661. [DOI] [PubMed] [Google Scholar]
- 31.Day J, Friedman A, Schlesinger LS. Modeling the immune rheostat of macrophages in the lung in response to infection. Proc Natl Acad Sci U S A. 2009;106(27):11246–11251. doi: 10.1073/pnas.0904846106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Jung YJ, Ryan L, LaCourse R, North RJ. Increased interleukin-10 expression is not responsible for failure of T helper 1 immunity to resolve airborne Mycobacterium tuberculosis infection in mice. Immunology. 2003;109(2):295–299. doi: 10.1046/j.1365-2567.2003.01645.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Turner J, Gonzalez-Juarrero M, Ellis DL, Basaraba RJ, Kipnis A, et al. In vivo IL-10 production reactivates chronic pulmonary tuberculosis in C57BL/6 mice. J Immunol. 2002;169(11):6343–6351. doi: 10.4049/jimmunol.169.11.6343. [DOI] [PubMed] [Google Scholar]
- 34.Higgins DM, Sanchez-Campillo J, Rosas-Taraco AG, Lee EJ, Orme IM, Gonzalez-Juarrero M. Lack of IL-10 alters inflammatory and immune responses during pulmonary Mycobacterium tuberculosis infection. Tuberculosis (Edinb) 2009;89(2):149–157. doi: 10.1016/j.tube.2009.01.001. [DOI] [PubMed] [Google Scholar]
- 35.Seiden PE, Celada F. A model for simulating cognate recognition and response in the immune system. J Theor Biol. 1992;158(3):329–357. doi: 10.1016/s0022-5193(05)80737-4. [DOI] [PubMed] [Google Scholar]
- 36.Bauer AL, Beauchemin CA, Perelson AS. Agent-based modeling of host-pathogen systems: The successes and challenges. Inf Sci (Ny) 2009;179(10):1379–1389. doi: 10.1016/j.ins.2008.11.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Warrender C, Forrest S, Koster F. Modeling intercellular interactions in early Mycobacterium infection. Bull Math Biol. 2006;68(8):2233–2261. doi: 10.1007/s11538-006-9103-y. [DOI] [PubMed] [Google Scholar]
- 38.Linderman JJ, Riggs T, Pande M, Miller M, Marino S, Kirschner DE. Characterizing the dynamics of CD4+ T cell priming within a lymph node. J Immunol. 2010;184(6):2873–2885. doi: 10.4049/jimmunol.0903117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Diedrich CR, Mattila JT, Klein E, Janssen C, Phuah J, et al. Reactivation of latent tuberculosis in cynomolgus macaques infected with SIV is associated with early peripheral T cell depletion and not virus load. PLoS One. 2010;5(3):e9611. doi: 10.1371/journal.pone.0009611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Kaufmann SH. Protection against tuberculosis: cytokines, T cells, and macrophages. Ann Rheum Dis. 2002;61(Suppl 2):ii54–58. doi: 10.1136/ard.61.suppl_2.ii54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Grosset J. Mycobacterium tuberculosis in the extracellular compartment: an underestimated adversary. Antimicrob Agents Chemother. 2003;47(3):833–836. doi: 10.1128/AAC.47.3.833-836.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Chang ST, Ghosh D, Kirschner DE, Linderman JJ. Peptide length-based prediction of peptide-MHC class II binding. Bioinformatics. 2006;22(22):2761–2767. doi: 10.1093/bioinformatics/btl479. [DOI] [PubMed] [Google Scholar]
- 43.Chakraborty AK, Kosmrlj A. Statistical mechanical concepts in immunology. Annu Rev Phys Chem. 2010;61:283–303. doi: 10.1146/annurev.physchem.59.032607.093537. [DOI] [PubMed] [Google Scholar]
- 44.Chang ST, Linderman JJ, Kirschner DE. Multiple mechanisms allow Mycobacterium tuberculosis to continuously inhibit MHC class II-mediated antigen presentation by macrophages. Proc Natl Acad Sci U S A. 2005;102(12):4530–4535. doi: 10.1073/pnas.0500362102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Riggs T, Walts A, Perry N, Bickle L, Lynch JN, et al. A comparison of random vs. chemotaxis-driven contacts of T cells with dendritic cells during repertoire scanning. J Theor Biol. 2008;250(4):732–751. doi: 10.1016/j.jtbi.2007.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Baldazzi V, Paci P, Bernaschi M, Castiglione F. Modeling lymphocyte homing and encounters in lymph nodes. BMC Bioinformatics. 2009;10:387. doi: 10.1186/1471-2105-10-387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Beltman JB, Maree AF, Lynch JN, Miller MJ, de Boer RJ. Lymph node topology dictates T cell migration behavior. J Exp Med. 2007;204(4):771–780. doi: 10.1084/jem.20061278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Bogle G, Dunbar PR. Simulating T-cell motility in the lymph node paracortex with a packed lattice geometry. Immunol Cell Biol. 2008;86(8):676–687. doi: 10.1038/icb.2008.60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Bogle G, Dunbar PR. Agent-based simulation of T-cell activation and proliferation within a lymph node. Immunol Cell Biol. 2010;88(2):172–179. doi: 10.1038/icb.2009.78. [DOI] [PubMed] [Google Scholar]
- 50.Jansson A, Harlen M, Karlsson S, Nilsson P, Cooley M. 3D computation modelling of the influence of cytokine secretion on Th-cell development suggests that negative selection (inhibition of Th1 cells) is more effective than positive selection by IL-4 for Th2 cell dominance. Immunol Cell Biol. 2007;85(3):189–196. doi: 10.1038/sj.icb.7100023. [DOI] [PubMed] [Google Scholar]
- 51.Zheng H, Jin B, Henrickson SE, Perelson AS, von Andrian UH, Chakraborty AK. How antigen quantity and quality determine T-cell decisions in lymphoid tissue. Mol Cell Biol. 2008;28(12):4040–4051. doi: 10.1128/MCB.00136-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Bajaria SH, Webb G, Cloyd M, Kirschner D. Dynamics of naive and memory CD4+ T lymphocytes in HIV-1 disease progression. J Acquir Immune Defic Syndr. 2002;30(1):41–58. doi: 10.1097/00042560-200205010-00006. [DOI] [PubMed] [Google Scholar]
- 53.Bajaria SH, Webb G, Kirschner DE. Predicting differential responses to structured treatment interruptions during HAART. Bull Math Biol. 2004;66(5):1093–1118. doi: 10.1016/j.bulm.2003.11.003. [DOI] [PubMed] [Google Scholar]
- 54.Hogue IB, Bajaria SH, Fallert BA, Qin S, Reinhart TA, Kirschner DE. The dual role of dendritic cells in the immune response to human immunodeficiency virus type 1 infection. J Gen Virol. 2008;89(Pt 9):2228–2239. doi: 10.1099/vir.0.83600-0. [DOI] [PMC free article] [PubMed] [Google Scholar]