Integrative modeling of the cardiac ventricular myocyte

Abstract

Cardiac electrophysiology is a discipline with a rich 50-year history of experimental research coupled with integrative modeling which has enabled us to achieve a quantitative understanding of the relationships between molecular function and the integrated behavior of the cardiac myocyte in health and disease. In this paper, we review the development of integrative computational models of the cardiac myocyte. We begin with a historical overview of key cardiac cell models that helped shape the field. We then narrow our focus to models of the cardiac ventricular myocyte and describe these models in the context of their subcellular functional systems including dynamic models of voltage-gated ion channels, mitochondrial energy production, ATP-dependent and electrogenic membrane transporters, intracellular Ca dynamics, mechanical contraction, and regulatory signal transduction pathways. We describe key advances and limitations of the models as well as point to new directions for future modeling research.

INTRODUCTION

Cardiac electrophysiology is a discipline with a rich history, extending from the early 1960s, of experimental research coupled with integrative modeling. The goal of this modeling has been to achieve a quantitative understanding of the relationships between molecular function and the integrated behavior of the cardiac myocyte in health and disease. Some of the most fundamental advances in computational cell biology, including formulation of dynamic models of voltage-gated ion channels, mitochondrial energy production, ATP-dependent and electrogenic membrane transporters, intracellular Ca dynamics, ligand-gated receptors, and signal transduction pathways have emerged from this field. Our goal in this paper is to review the development of these models, as well as point to new directions for future modeling research.

As a result of the close interplay between modeling and experiments, we have a remarkably deep understanding of cardiac myocyte function. The most fundamental property of cardiac myocytes is that they are electrically excitable cells. Rhythmic electrical activity of the heart is initiated by pacemaking cells within the sinoatrial (SA) node. Frequency entrainment of these oscillations is assured by electrical coupling of neighboring SA node cells via gap junctions.¹ This oscillatory wave of electrical depolarization propagates into and through the right and left atria, initiating atrial contraction and filling of the right and left ventricles. The depolarization wave is then conducted through cells of the atrioventricular (AV) node and the Purkinje fiber system to initiate electrical depolarization and contraction of the ventricles. A major focus of molecular cardiobiology has been to identify and model the ion transport mechanisms whose interactions give rise to the electrical excitability of cardiac myocytes. We will review modeling of these processes and will focus primarily on modeling of the cardiac ventricular myocyte.

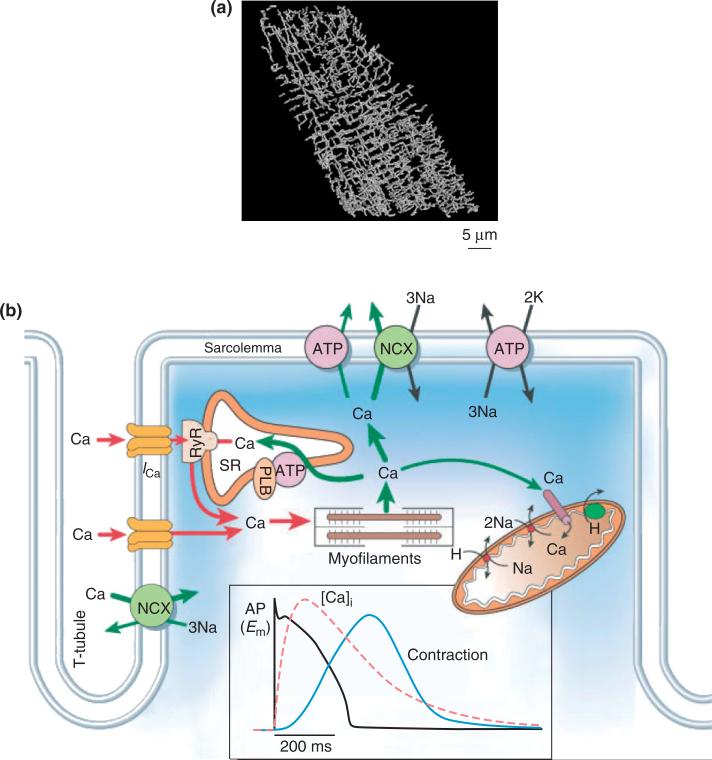
Figures 1 and 2 show several important structural aspects of the ventricular myocyte. These are t-tubules, the network and junctional sarcoplasmic reticulum (NSR and JSR, respectively), mitochondria, and the contractile apparatus. T-tubules are invaginations of the sarcolemma extending deep into the cell. A reconstruction of the t-tubule network by Soeller and Cannell² is shown in Figure 1(a), and a schematic illustration of the functional organization of the t-tubule is shown in Figure 1(b).³ The SR is a luminal organelle located throughout the interior of the cell. It is involved in uptake, sequestration, and release of Ca in a process known as intracellular Ca cycling. The JSR is the portion of the SR most closely approximating the t-tubules (Figure 1(b)), the distance between these structures being ~12–15 nm.⁴ This region of close approximation is known as the dyad or the dyadic space. L-type Ca channels (LCCs) are preferentially located in the sarcolemmal portion of the dyad. The majority of the RyRs are found in the JSR directly opposed to the LCCs. When LCCs open in response to membrane depolarization, Ca flows into the dyadic space. Ca may then bind to the RyRs, inducing them to open and release Ca stored in the JSR. This process is known as Ca-induced Ca release (CICR). The resulting rise in cytosolic Ca regulates a wide range of processes including muscle contraction, properties of the cardiac action potential (AP), mitochondrial ATP production, intracellular signaling processes, and gene expression. We will review models of CICR and Ca cycling.

FIGURE 1.

(a) Reconstruction of the three-dimensional t-tubular system in a rat ventricular myocyte (Reprinted with permission from Ref 2. Copyright 1999 American Heart Association). (b) Ca transport in ventricular myocytes (Reprinted with permission from Ref 3. Copyright 2002 Macmillan Magazines Ltd.). Inset shows time course of action potential, Ca transient, and contraction.

FIGURE 2.

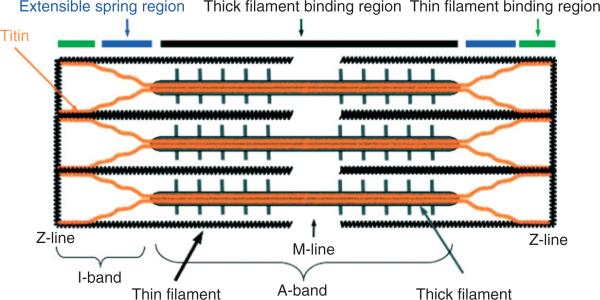
Schematic representation of the cardiac sarcomere. The sarcomere is made up of thick (myosin) filaments (A-band) and thin (actin) filaments (I-band), which are interconnected by titin (with segments shown by colored bars on the top). The Z-line is the boundary between sarcomeres and the M-line is central portion of the A-band (Reprinted with permission from Ref 5. Copyright 2008 The Company of Biologists).

In cardiac myocytes, mitochondria are located near the major ATP-utilizing processes (i.e., cross-bridge cycling and muscle contraction, and pumping of Ca into the NSR). Mitochondria sense and are regulated by local levels of Ca near the dyad. Our understanding of the processes by which mitochondrial energy production is regulated in the cardiac myocyte is advancing rapidly.^6–9 We will review models of mitochondrial energy production and its coupling to membrane transport processes.

The fundamental unit of contraction of the cardiac muscle fiber is the sarcomere⁵ (Figure 2)—the contractile apparatus between adjacent Z-lines (or Z-disks). Figure 2 shows the region of overlap of thick (myosin) and thin (actin) filaments. Myocyte contraction is accomplished by the sliding motion of the thick and thin filaments relative to one another in this region in response to elevated levels of intracellular Ca. We will describe recent approaches to modeling of cardiac myocyte muscle contraction.

The proteins that underlie membrane currents, CICR, energy production, and contraction, are regulated via a variety of signaling pathways. The activation of signaling cascades results in posttranslational modifications of target proteins (e.g., phosphorylation of LCCs) which alter their functional properties and/or regulate protein trafficking and gene transcription, and hence, the abundance of certain functional proteins. Cell signaling pathways are complex, involving cascades of signaling molecules, multiple protein targets, and interactions among different pathways. Two of the most thoroughly studied signaling pathways in the cardiac myocyte are the β-adrenergic and Ca/calmodulin-dependent kinase II (CaMKII) pathways, and models of each have been developed. We will review models of cell signaling in the cardiac myocyte.

MODELS OF THE CARDIAC MYOCYTE ACTION POTENTIAL

Processes Underlying the Cardiac Action Potential

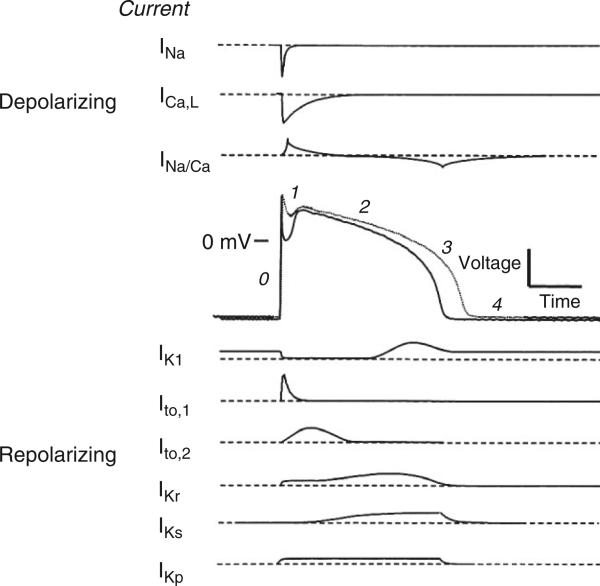
Figure 3 illustrates the major ionic currents giving rise to the mammalian cardiac AP.¹⁰ Currents mediating the AP upstroke (Phase 0) are the fast inward sodium (Na) current¹¹ (I_Na), and to a lesser extent the L-type Ca current¹² (I_CaL). The Phase 1 notch, apparent in ventricular myocytes isolated from epi- and mid-myocardial regions but largely absent in those from the endocardium, is produced by activation of the voltage-dependent transient outward potassium (K) current¹³ (I_to,1). A transient voltage-independent Ca-activated chloride current (I_to,2) may also contribute to the Phase 1 notch¹⁴; however, whether this current contributes to shaping the human AP remains controversial.¹⁵ During the Phase 2 plateau, membrane conductance is very low, with the plateau potential and duration being regulated by a delicate balance between inward and outward currents. The major inward plateau current is I_CaL, major outward plateau currents are the rapid and slow-activating delayed rectifier currents (I_Kr and I_Ks, respectively),^16,17 and the plateau K current is I_Kp.¹⁸ The initial portion of repolarization Phase 3 results from activation of I_Kr and I_Ks, and the later phase is due to the inward rectifier K current I_K1.¹⁹

FIGURE 3.

Schematic of the membrane currents that underlie a ventricular action potential (AP) shown with a control (solid line) and failing (dotted line) AP with phases labeled. (Reprinted with permission from Ref 10. Copyright 1999 Elsevier).

At least three major ion pumps and exchangers play an important role in shaping properties of the cardiac AP, Ca transient, and in long term regulation of intracellular ion concentrations. These are the sarcolemmal Na–K pump, the Na–Ca exchanger, and the SR Ca-ATPase. The sarcolemmal Na–K pump,^20,21 present in virtually all mammalian cell membranes, hydrolyzes one ATP in order to extrude three Na ions while importing two K ions on each cycle. The net charge movement of this electrogenic pump generates outward membrane current, which influences both AP duration (APD) and resting potential. This pump functions to keep intracellular Na low, and thereby maintains the transmembrane Na gradient by extruding Na that enters during each AP. During diastole, the sarcolemmal Na–Ca exchanger is believed to import three Na ions for every Ca ion extruded, yielding a net inward charge movement²² (see Ref 23 for recently proposed alternative transport modes). It is the principal means by which Ca that enters the cell during the AP is extruded from the myocyte. It is driven by transmembrane voltage and intra- and extracellular Na and Ca ion concentrations. It can also function in reverse mode during the AP, in which case it extrudes Na and imports Ca, thus generating a net outward current.^24,25 The duration of reverse mode Na–Ca exchange, and hence its effect on AP shape, has been shown to vary with species, heart failure, and other factors.^26,27 The second major cytoplasmic Ca extrusion mechanism is the SR Ca-ATPase, which pumps Ca released from the JSR back into the NSR. The SR Ca-ATPase has both forward and reverse components.²⁸

Early Models of the Cardiac AP

The foundation of quantitative modeling of the cardiac AP was established in the early 1960s by Denis Noble, who presented the first computational models of a cardiac myocyte—the Purkinje cell.^29,30 These models were developed to investigate the mechanisms underlying long duration APs observed in cardiac myocytes. To do this, the Hodgkin and Huxley description of the squid giant axon AP³¹ was modified. The model was able to explain the long plateau phase as a balance between a maintained inward Na current and a slowly activating outward K current. Either a stable resting potential or a stable oscillation could be produced by adjusting the relative Na and K conductances, thereby mimicking the long duration, slow, oscillatory APs of the cardiac Purkinje fiber. While this model provided insight into the fundamental process involved in long duration APs, it is now known that the inward current during the plateau phase is primarily due to membrane Ca permeability. These models were subsequently extended by McAllister et al.³² However, the experimental data on which this and other models of this era were based were flawed due to an inability to establish adequate spatiotemporal voltage clamp, and to control for changes in K concentration in the extracellular clefts of multicellular preparations.³³

The first computational model of the mammalian cardiac ventricular myocyte was developed by Beeler and Reuter in 1977.³⁴ The model described four distinct membrane currents: (1) the fast inward sodium current I_Na; (2) a slow inward current I_s carried predominantly by Ca; (3) a time-independent inward rectifier potassium current I_K1; and (4) a time-dependent outward K current I_X1. Membrane currents were modeled using the Hodgkin–Huxley formalism. Properties of the model AP were shown to agree qualitatively with those measured experimentally. The Beeler–Reuter model is significant in being the first attempt to quantify mechanisms of the ventricular cell AP. The model reinforced the concepts that the AP plateau phase is controlled by a balance between K(I_X1) and Ca (I_s) currents, and repolarization is controlled by inactivation of I_s coupled with slow activation of I_X1. The model was the first to describe the time-varying concentration of an intracellular ionic species (Ca) within its ‘small distribution volume’ as a dynamic state variable.

Subsequent elaboration of these and other models led to the development of the landmark DiFrancesco–Noble (DN) model of the cardiac Purkinje fiber.³⁵ This model was groundbreaking in that it described: (1) hyperpolarizing-activated, Na and K permeant G_f conductance that contributes to pacemaking in Purkinje fibers; (2) time-varying concentration of K in the extracellular cleft, and intracellular concentrations of Na, K, and Ca; (3) activity of the Na–K pump and Na–Ca exchanger; and (4) voltage- and Ca-dependent inactivation of the Ca current. It introduced models of the transport of Ca into the NSR by the SR Ca-ATPase, diffusion of Ca from NSR to JSR, and CICR from the JSR. This model established the conceptual framework on which all subsequent models of the myocyte have been built. Modifications of the DN model soon led to the development of SA node^36–39 and atrial cell models.^38,40

Computational modeling of the cardiac myocyte has advanced significantly since the days of the DN model. Tables 1 and 2 are updates to a summary of existing cardiac myocyte models first presented by Wilders.⁴¹ Models of rabbit SA node cells,^{1,36,37,39,42–48} some of which describe regional variations in cell properties,^1,44–46 have been developed. Insight into the relationship between spontaneous diastolic Ca release and the AP firing rate has been gained through the use of computational modeling to better understand mechanisms of a complex integrative theory of SA node pacemaking—the ‘Ca Clock Hypothesis’.^47,48 Models of both rabbit^38,40 and human^49,50 atrial cells as well as rabbit AV node cells⁵¹ and human Purkinje fibers⁵² have been developed. Tremendous advances have been made in modeling of the cardiac ventricular myocyte (Table 2). These advances are the focus of the remainder of this review.

TABLE 1.

Purkinje, SA Node, Atrial, and AV Node Cell Models Based on Tables 1 and 2 of Wilders⁴¹

	Authors	Species
Purkinje cell models	Noble29	Generic
	Noble30	Generic
	McAllister et al.32	Generic
	DiFrancesco and Noble35	Generic
	Stewart et al.52	Human
Sinoatrial node cell models	Yanagihara et al.53	Rabbit
	Bristow and Clark54	Rabbit
	Irisawa and Noma55	Rabbit
	Noble and Noble36	Rabbit
	Noble et al.37	Rabbit
	Rasmusson et al.56	Bullfrog
	Wilders et al.57	Rabbit
	Noble et al.39	Rabbit
	Dokos et al.58	Rabbit
	Cai et al.1	Rabbit
	Demir et al.42	Rabbit
	Dokos et al.43	Rabbit
	Endresen et al.59	Rabbit
	Zhang et al.44	Rabbit
	Zhang et al.45	Rabbit
	Kurata et al.60	Rabbit
	Garny et al.61	Rabbit
	Sarai et al.62	Rabbit
	Lovell et al.46	Rabbit
	Maltsev et al.47	Rabbit
	Vinogradova et al.48	Rabbit
	Mangoni et al.63	Mouse
	Maltsev and Lakatta64	Rabbit
Atrial cell models	Hilgemann and Noble40	Rabbit
	Earm and Noble38	Rabbit
	Lindblad et al.65	Rabbit
	Courtemanche et al.50	Human
	Nygren et al.49	Human
	Ramirez et al.66	Canine
	Aslanidi et al.67	Rabbit
	Maleckar et al.68	Human
AV node cell models	Liu et al.69	Rabbit
	Inada et al.51	Rabbit

TABLE 2.

Ventricular Myocyte Models Based on Tables 1 and 2 of Wilders⁴¹

Authors	Species	Parent Model Authors	Novel Features
Beeler and Reuter34	Mammal	McAllister et al.32	First ventricular cell model
Noble et al.70	Guinea pig	Earm and Noble38	Based on voltage-clamp recordings in isolated cells
Luo and Rudy71	Guinea pig	Beeler and Reuter34	Based on voltage-clamp recordings in isolated cells, pumps/exchangers, Ca buffers
Nordin72	Guinea pig	DiFrancesco and Noble35	Updated currents and Ca cycling, myoplasmic compartments, homeostatic system
Luo and Rudy73,74	Guinea pig	Luo and Rudy71	Updated currents based on wide array of isolated myocyte data, variable ionic concentrations
Jafri et al.75	Guinea pig	Luo and Rudy73	Dyadic subspace, mode-switching L-type Ca channel (LCC) Markov model
Noble et al.76	Guinea pig	Noble et al.70	Dyadic space, length- and tension-dependent processes
Priebe and Beuckelmann77	Human	Luo and Rudy73	First human model
Winslow et al.78	Canine	Jafri et al.75	First canine model, Ca mediated prolongation of action potential (AP) in heart failure
Pandit et al.79	Rat	Demir et al.42	First adult rat model, transmural variations
Hund et al.80	Guinea pig	Luo and Rudy73	Ionic charge conservation constraints
Puglisi and Bers81	Rabbit	Luo and Rudy73	Heart failure, user-friendly graphical interface
Bernus et al.82	Human	Priebe and Beuckelmann77	Efficient, reduced model for use in tissue simulations
Fox et al.83	Canine	Winslow et al.78	Updated K and Ca currents, show ionic bases of APD alternans
Greenstein and Winslow84	Canine	Winslow et al.78	Stochastically simulated local control of sarcoplasmic reticulum (SR) Ca release
Cabo and Boyden85	Canine	Luo and Rudy73	Remodeling in epicardial border zone of infarct, drug effects on AP
Matsuoka et al.86	Guinea pig		Integrated contraction and ATP-mediated effects
Iyer et al.87	Human	Winslow et al.78	Updated currents, Markov models including INa
Matsuoka et al.88	Guinea pig	Matsuoka et al.86	ATP metabolism
Bondarenko et al.89	Mouse		Markov models, apex/septum variations
Shannon et al.90	Rabbit	Puglisi and Bers81	Luminal SR Ca-dependent RyR, submembrane Ca space
ten Tusscher et al.91	Human		Updated currents, transmural variations
Hund and Rudy92	Canine	Luo and Rudy73	CaMKII regulation, chloride handling
Greenstein et al.93	Canine	Greenstein and Winslow84	Simplified local control of SR Ca release
Cortassa et al.94	Guinea pig	Winslow et al.78	Integrated mitochondrial bioenergetics and contraction
Crampin and Smith95	Guinea pig	Luo and Rudy73	EC coupling with pH regulation
Crampin et al.96	Rat	Pandit et al.79	EC coupling with pH regulation
Mahajan et al.97	Rabbit	Shannon et al.90	Markovian LCC, fast rate Ca alternans
Pasek et al.98	Guinea pig	Nordin,72 Noble et al.,76 and Faber and Rudy99	Diffusive transverse-axial tubule system, heterogeneous ion channel distribution
Wang and Sobie100	Neonatal mouse	Bondarenko et al.89	Neonatal currents and Ca cycling
Hashambhoy et al.101	Canine	Greenstein and Winslow84	CaMKII regulation, LCC phosphorylation (ICaL facilitation)
Korhonen et al.102	Mouse embryonic cardiomyocyte		E9-E11 myocytes, Ca oscillations underlying pacemaking and EC coupling
Korhonen et al.103	Neonatal rat		Radial Ca diffusion between sarcolemma, SR, and nucleus
Grandi et al.104	Human	Shannon et al.90	Updated K currents and Ca handling, Na accumulation
Koivumaki et al.105	Mouse	Bondarenko et al.89	CaMKII regulation of EC coupling

Modern Computational Models of the Ventricular Myocyte AP

The first ventricular cell models based on voltage-clamp recordings obtained from isolated myocytes were reported in 1991. The ability to record from isolated cells greatly enhanced spatiotemporal control of voltage clamp and also enabled control of extracellular ion concentrations. These models were the Oxsoft HEART Version 3.3 ventricular cell model by Noble et al.,⁷⁰ and the Luo–Rudy Phase I ventricular myocyte model.⁷¹ Both models were based on experimental data from small mammalian hearts, primarily that of guinea pig.

The Noble model was derived from prior atrial cell models,^38,40 which were in turn modifications of the 1985 DN model.³⁵ This model was shown to approximate AP and Ca transient waveforms measured in isolated ventricular myocytes, and was also used to investigate the role of the Na–Ca exchange current in shaping AP characteristics. While this model provided significant insights into processes regulating AP shape, its impact was limited due to the lack of full publication of model equations.

In 1991, Luo and Rudy published the Luo–Rudy Phase I model of the guinea pig ventricular cell.⁷¹ The model described six distinct membrane currents: (1) fast inward Na current I_Na; (2) the slow inward current I_si (from Beeler and Reuter³⁴); (3) a time-dependent delayed rectifier K current I_K; (4) a time-independent inward rectifier current I_K1; (5) the plateau K current; and (6) a background K current. Intracellular Ca cycling, sarcolemmal Na–Ca exchange, Na–K pumping, and temporal variation of intracellular ion concentrations were not described in this model. The Luo–Rudy Phase I model represented a step forward in that: (1) descriptions of ionic currents were carefully based on existing experimental data; (2) model equations were fully published, enabling model implementation by other investigators; and (3) the model was able to account for a range of experimental measurements on ventricular cell responses. Its shortcomings were that it retained the original slow inward current description of the Beeler–Reuter model and did not describe any aspect of intracellular Ca cycling.

Another landmark was the formulation of the Luo–Rudy Phase II model.^73,74 The model included the following changes: (1) sarcolemmal Na–K and Ca pumps; (2) Na–Ca exchange; (3) Ca buffers; (4) a non-specific Ca-activated current; and (5) CICR and Ca cycling. Because of the extent to which formulations of membrane currents and model predictions have been validated against experimental data, and the full publication of model equations, the Luo–Rudy Phase II model and its subsequent enhancements have become the most extensively used cardiac ventricular cell models.

Publication of the Luo–Rudy Phase II model marked the beginning of an era in which computational models of the cardiac ventricular myocyte have become increasingly biophysically detailed. Development of new experimental techniques has provided extensive data describing the functional components within the cardiac myocyte. Many advances in integrative modeling of the ventricular myocyte have resulted from quantitative modeling of these components and their addition to existing models. This has sometimes required the solution of thousands of differential equations or the stochastic simulation of up to ~10⁶ single channels in a single cell. These computations are now tractable. Some important advances in modeling of the ventricular myocyte are described in the following section. In this short review, we cannot possibly do justice to all the important work that has brought us to where we are today. We have therefore chosen to focus on development of major new functional components, their integration into whole cell models, and the insights that have been obtained from these advances in modeling capabilities.

MODELING FUNCTIONAL COMPONENTS OF THE CARDIAC VENTRICULAR MYOCYTE

Modeling Voltage-Gated Ionic Currents

For many years, Hodgkin–Huxley models have been the standard for describing voltage-dependent membrane ion current dynamics.³¹ These models introduced the concept of activation and inactivation gates, and related the current through an ensemble of channels to the state of these gates. The brilliance of Hodgkin and Huxley is that they developed experimental techniques for measuring properties of activation and inactivation using the voltage-clamp recording technique.

More recent data obtained using new experimental approaches for measuring single-channel openings and closings have shown that Hodgkin–Huxley models have significant limitations, often due to the assumption that channel gates behave independently. This assumption can be relaxed by using continuous-time Markov chain models¹⁰⁶ to describe channel gating and ionic currents. Markov chain models are comprised of a number of different states, loosely corresponding to different conformations of channel protein(s) as they undergo activation and inactivation, with transition rates between certain states being voltage-dependent. While a Hodgkin–Huxley model can be expanded to an equivalent Markov chain representation,¹⁰⁷ often many single-channel behaviors such as mean open time, first latency, and a broad range of other kinetics behaviors are not well described using this equivalent model.^108,109

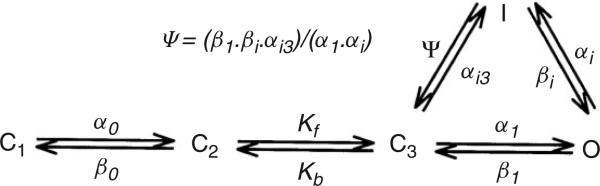
An example of a Markov chain model of the HERG and HERG+hKCNE2 channel is shown in Figure 4. This model was used by Mazhari et al.¹¹⁰ to interpret their experimental data regarding the functional role of co-expression of hKCNE2 with HERG (the two molecular components of I_Kr). Markov models are parameterized by the state transition rates. These rates reflect the free energy profile between two protein conformations¹⁰⁷ and must be determined experimentally. This is done through application of various voltage-clamp protocols, recording current responses, and adjusting the transition rates using minimization algorithms to yield a best fit to the data. In some instances, single-channel patch-clamp recordings have been used to constrain Markov models. Markov models of ion currents are now used extensively. Applications have included quantitative modeling of the effects of channel mutation,^111–114 drug–channel interactions,^115–118 channel phosphorylation,^101,119 and channel-subunit nteractions¹¹⁰ on myocyte responses. These whole cell models have been shown to have predictive value.

FIGURE 4.

State diagram of the HERG and HERG+hKCNE2 Markov model. C_l, C₂, and C₃ are closed states, O is the open state, and I is the inactivated state (Reprinted with permission from Ref 110. Copyright 2001 American Heart Association).

Now there are many Markov membrane current models that, for each current, can differ radically in their number of states and interconnection topology (e.g., I_Na,^114,119,120 I_Kr,^{110,113,121,122} and I_CaL^75,97,123). If several channels in a single cell model are modeled using the Markov formulation, the aggregate number of state equations may become large. Consequently, use of Markov models imposes increased computational load. However, the advent of faster, multicore processors and graphics processing units is making this less of a problem at both the cellular and tissue levels. In addition, use of complex state models at the cellular level does not impose a major additional computational load when simulating these models stochastically because the Markov property assures that the future evolution of the process state depends only on the nature of the current state and not on the number of states in the model.

Modeling Sarcolemmal Membrane Transporters

The first myocyte model to explicitly describe membrane transporter function was the DN model.³⁵ The Na–K pump, Na–Ca exchanger, and the SR Ca-ATPase were modeled as algebraic functions of the relevant intracellular and extracellular Na, Ca, and K concentrations. These models were refined and constrained using experimental data in the work of Luo and Rudy.⁷³ In 1998, Shannon et al.¹²⁴ proposed a new model of the SR Ca-ATPase that included forward- and reverse-current components, each with its own Ca-binding constant and peak forward and reverse rates. This model is now used extensively, and has been integrated into the models of Winslow et al.,⁷⁸ Puglisi and Bers,⁸¹ Shannon et al.,⁹⁰ and Grandi et al.¹⁰⁴ Recently, carefully constrained Markovian models of the Na–K pump,¹²⁵ the SR Ca-ATPase,¹²⁶ and Na–Ca exchanger²³ have been published but have not yet been incorporated in whole cell models. The first model of intracellular pH regulation, based on phenomenological representations of transmembrane acid fluxes in guinea pig, was developed by Leem et al.¹²⁷ More recently, Crampin et al.⁹⁶ and Crampin and Smith⁹⁵ have developed models of the sarcolemmal: (1) Na–H ion exchanger; (2) Na–HCO₃ cotransporter; (3) Cl/OH exchanger; and (4) the anion exchanger. Models of pH regulation have been incorporated into the Luo–Rudy model and used to study the effects of acidosis in ischemia on excitation–contraction (EC) coupling. Results predict that changes in cytosolic Ca transients in acidosis are primarily due to direct inhibition of the Na–Ca exchanger and a rise in intracellular Na levels.

Modeling Intracellular Calcium Cycling and Calcium-Induced Calcium-Release

At rest, low levels of Ca in the dyad lead to a low RyR open probability. During the initial stages of the AP, voltage-gated LCCs in the sarcolemmal membrane open and Ca (‘trigger Ca’) enters the dyadic space. This Ca binds to RyRs, increasing their open probability and producing CICR. The amount of Ca released from the JSR is significantly greater than the amount of trigger Ca.¹²⁸ The ratio of Ca released from JSR to the amount of trigger Ca entering the myocyte is referred to as the EC coupling gain. Graded release refers to the phenomenon, originally observed by Fabiato et al.,¹²⁹ that Ca release from JSR is graded according to the amount of trigger Ca entering the cell via LCCs.

Many advances in cardiac myocyte models over the past decade have resulted from improved descriptions of the underlying mechanisms of CICR. In 1998, Jafri et al.⁷⁵ presented a model of the guinea pig ventricular myocyte whose membrane currents were largely based on those of the Luo–Rudy Phase II model. This model was the first to incorporate mechanistic Markov models for both LCCs and RyRs, and was also the first to implement a ‘restricted subspace’, a single compartment representing the total volume of all dyads into which all Ca fluxes through RyRs and LCCs are directed. The major prediction of this model was that experimentally measured interval-force (transient) and frequency-force (steady-state) relationships could be explained by the interplay between RyR inactivation and SR Ca load dynamics. Shortly thereafter, this Ca subsystem was modified for canine in the model of Winslow et al.⁷⁸ The model predicted that negative feedback produced by Ca release from the JSR and the subsequent Ca-dependent inactivation of LCCs was a powerful factor regulating APD. This prediction was subsequently validated by studies of Alseikhan et al.¹³⁰ in which APD was shown to be dramatically prolonged by knockout of Ca binding to calmodulin and the resulting ablation of Ca-dependent inactivation of LCCs.

While the models described above successfully predict mechanisms underlying experimentally observed Ca transients and APs in both normal and diseased cells, they cannot reproduce graded SR Ca release because they are ‘common pool’ models. As defined by Stern¹³¹ in 1992, common pool models are those in which LCC trigger Ca enters the same cytosolic Ca pool into which SR Ca is released. The rapid increase of Ca in this pool in turn leads to non-physiological regenerative, all-or-none rather than graded Ca release. Stern elegantly demonstrated that common pool models cannot achieve both high gain and graded Ca release.¹³¹

One way to circumvent this problem is to model SR Ca release flux as a phenomenological function of LCC influx and/or membrane potential.^{74,83,89,91,92,97} Doing so removes the positive feedback effect inherent to common pool models. Models incorporating this phenomenological mechanism have been successful in describing many myocyte behaviors. However, as with any phenomenological approach, the predictive power of such models must always be questioned. By formulating a model in which it was assumed that a single LCC can trigger SR Ca release only from a locally apposed cluster of RyRs, Stern demonstrated that graded release arises as the result of statistical recruitment of release clusters.¹³² This process is known as local control of Ca release. Discrete Ca release events can now be measured experimentally, and are known as Ca sparks.¹³³ The first comprehensive model of the myocyte based on the theory of local control was developed by Greenstein and Winslow.⁸⁴ This model includes a population of dyadic Ca release units in which local interactions of individual sarcolemmal LCCs and nearby RyRs are simulated stochastically. This multiscale approach to model construction resulted in the ability to reproduce experimentally observed behaviors on both microscopic (single-channel gating and discrete Ca release events) and macroscopic scales (graded SR Ca release, voltage-dependent EC coupling gain, whole cell Ca transients, and APs). Application of the model demonstrated that local control is an essential property for stability of APs when the LCC inactivation process depends more strongly on local Ca than on membrane potential. Subsequently, a simplified local control model of CICR^134–136 was formulated by applying a carefully chosen set of approximations that allow for the ensemble behavior of Ca release units to be represented by a low dimensional system of ordinary differential equations. Incorporation of this coupled LCC–RyR model into that of Greenstein and Winslow⁸⁴ yielded the ventricular myocyte model of Greenstein et al.⁹³ which could reproduce all the core features of its predecessor, but without the computationally expensive stochastic simulations, making it a candidate for use in large-scale tissue simulations.¹³⁷ This model was able to predict aspects of the underlying relationship between macroscopic EC coupling gain and single-channel properties of LCCs measured experimentally.¹³⁸

The rabbit ventricular myocyte model of Shannon et al.⁹⁰ was the first to introduce a subsarcolemmal Ca compartment, based on experiments that suggested Ca-dependent transport mechanisms are sensing elevated Ca levels.^26,139 Another novel feature of the Shannon et al.⁹⁰ rabbit model was the formulation of an RyR model with dynamics that depend on both cytosolic and SR luminal Ca levels. This model was modified from that of Stern et al.¹⁴⁰ so that Ca binding to the luminal site increased the affinity of the cytosolic activation site, while decreasing the affinity of the cytosolic inactivation site for Ca. This novel regulatory feature underlies the ability of the Shannon et al.⁹⁰ model to reproduce experimentally characterized relationships between SR Ca load and properties of SR Ca release,^141,142 and assigns an important role to the (partial) depletion of luminal JSR Ca level in the dynamic regulation and termination of SR Ca release. Using this model, Shannon et al.¹⁴³ demonstrated that the role of RyR regulation by luminal Ca may be to adjust steady-state SR Ca level in response to alteration in RyR Ca sensitivity, as originally proposed by Eisner et al.¹⁴² Despite the success of this model, its reliance in part on cytosolic Ca-dependent inactivation for termination of SR Ca release conflicts with recent experiments,^144–146 and the underlying mechanisms of SR release termination remain controversial and not well understood.

Modeling Metabolism

The first computational models of metabolic dynamics of substrate utilization and energy transfer in cardiac myocytes were formulated in the late 1970s by Garfinkel and coworkers.^147,148 These pioneering comprehensive models, encompassing about 90 biochemical reactions, were formulated with individual biochemical reactions described by either mass action laws or Michaelis–Menten kinetics.^149,150 Several pathways, such as glycolysis, β-oxidation, and oxidative phosphorylation, were included in these early formulations. The models also accounted for compartmentalization, transport of intermediary metabolites between compartments, and regulatory interactions such as the effect of ATP and ADP on the activity of glycolytic enzymes.^148,151,152 Model simulations supported the idea that adenine nucleotides were key regulators of cellular energy production,¹⁵³ in agreement with studies of isolated mitochondria,¹⁵⁴ which described how ‘respiratory control’ of energy metabolism is coupled to cellular energy demand through the effects of adenine nucleotide phosphorylation potential on mitochondrial oxygen consumption.

However, subsequent results obtained with ³¹P NMR showed that bulk ATP and phosphocreatine levels were relatively insensitive to changing workload conditions in the short term, challenging the ‘respiratory control’ mechanism for matching energy supply with demand.¹⁵⁵ As an alternative, Saks and coworkers hypothesized that energy transfer dynamics occurred at the sites of energy production and consumption, introducing the concept of ‘intracellular energetic units’.¹⁵⁶ A model accounting for generation of gradients of ADP around myofibrils, where active ATP consumption occurs during contractile activity, was postulated.¹⁵⁷ The linear dependence of the respiratory rate with workload, as measured through changes in cardiac volume in the Frank–Starling mechanism, could be quantitatively explained with such a model of reaction–diffusion of adenine nucleotides and creatine metabolites. This model further assumed that the creatine kinase reaction is operating far from equilibrium at the sites of energy consumption and in the mitochondrial intermembrane space.¹⁵⁸ The subsequent work of van Beek¹⁵⁹ challenged this notion and concluded that a combination of cytoplasmic phosphate buffering reactions (creatine kinase and glycolysis) predominates to influence the adaptation rate. A model of ADP diffusion and interconversion of ADP/ATP with creatine could reproduce the fast response.^160,161

Ischemia–reperfusion represent a major challenge for computational modeling of myocardial metabolism. Initial work was done by Ch'en et al.¹⁶² They developed a model describing proton transport across the sarcolemmal membrane, and lumped biochemical reactions accounting for glycogen degradation into lactate, creatine kinase equilibrium, and ATP hydrolysis, including pH-associated changes. Simulations of contractile failure and contracture after 5 min of total ischemia reproduced experimental data on the consumption of internal glycogen stores and the exhaustion of creatine phosphate followed by ATP depletion.¹⁶² However, most mathematical expressions used in this model were phenomenological rather than mechanistic. Further model development has focused on a more detailed representation of pH regulation and generation of pH gradients, and oxidative phosphorylation in cardiomyocytes.^163,164

In 2003, Cortassa et al.¹⁶⁵ formulated a mechanistic model of mitochondrial energy production that included Ca transport, regulation of tricarboxylic acid cycle dehydrogenases by calcium, and the electrochemical driving forces that describe the fundamental relationship between mitochondrial membrane potential and respiratory rate, as observed in isolated mitochondria treated with oligomycin and rotenone and titrated with the uncoupler FCCP (carbonyl cyanide p-trifluoromethoxyphenylhydrazone).¹⁶⁶ By simulating extra-mitochondrial Ca pulses, this model could also reproduce the temporal profile of NADH changes associated with alterations in pacing frequency in intact cardiac muscle.¹⁶⁷ Using a similar approach, Nguyen and Jafri¹⁶⁸ modified the Ca transport rate equations and added phosphate transport. The resulting model simulates a linear relationship between mitochondrial Ca and cytoplasmic Ca that the authors used to reproduce experimental data from the Lemasters group.¹⁶⁹ Beard and coworkers developed a model of mitochondrial function including linear force–flow relations between respiration and its driving forces, and potassium and phosphate ion dynamics. The model is able to simulate respiratory rates and NADH levels that are observed with isolated mitochondria in the presence of different levels of inorganic phosphate.^170,171

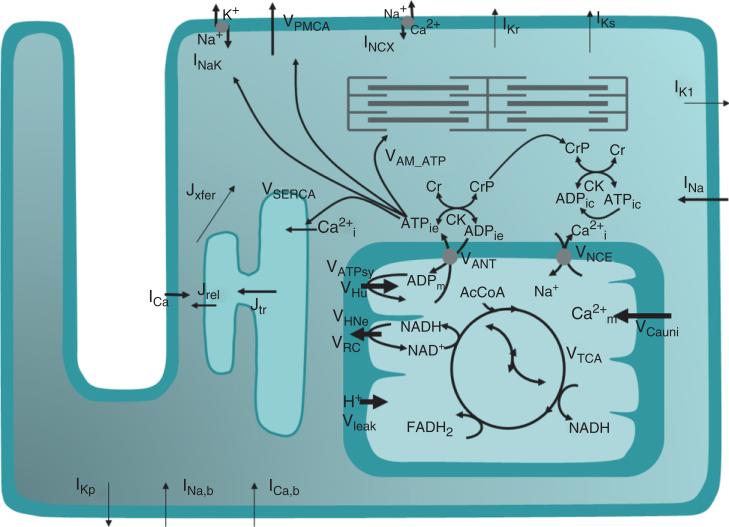
Integrating mitochondrial energetics into models of cardiomyocyte function is the natural step forward to understand heart physiology and pathophysiology. Simulations of NADH and mitochondrial Ca transients, following an increase in workload, were achieved by changing the stimulation frequency by the ‘Kyoto’ model in which Korzeniewski's mitochondrial metabolic model was coupled to the electrophysiological model of Noma.⁸⁸ Model simulations were able to show that ~23% of the increase in the rate of ATP synthesis in response to an increase in workload was met by Ca activation of dehydrogenases, whereas the remaining 77% was assigned to ‘respiratory control’.¹⁷² The excitation–contraction coupling and mitochondrial energetic (ECME) model⁹⁴ (Figure 5) was built by integrating the mitochondrial energetics¹⁶⁵ and EC coupling models, the latter describing the dynamics of electrophysiological and contractile processes in the guinea pig.¹⁷³ The ECME substantiates the participation of mitochondria in Ca buffering,¹⁷⁴ which is transported across the inner mitochondrial membrane through the Ca uniporter and the mitochondrial Na–Ca exchanger. One of the main contributions of the ECME model has been to clarify the role of ADP and Ca as two main signaling mechanisms participating in matching energy supply with demand at different workloads in heart trabeculae.^167,175 Further studies of metabolic control performed with the ECME model at rest or working conditions revealed the importance of the myofibrilar ATPase activity as a rate-controlling step of mitochondrial respiration; the regulatory function of adenine nucleotides in the response of bioenergetic processes could also be demonstrated in the context of integrated cardiomyocyte function.¹⁷⁶ Extensions of the ECME model have been used to investigate mechanisms of oxidative stress.^177–181

FIGURE 5.

General scheme of the excitation–contraction coupling-mitochondrial energetics guinea pig model including membrane currents, sarcolemmal ion transport, Ca compartmentalization, and mitochondrial function.

Modeling Excitation–Contraction Coupling

The heart cell can be considered a coupled electromechanical system in which the AP triggers an increase in intracellular Ca and contraction of the myofilaments that allows the heart to pump. Troponin is the largest buffer of Ca in the cell, and affinity of the Ca-binding regulatory sites on troponin is thought to be a function of force generated by the myofilaments. The Ca transient is in fact altered when developed force is changed.¹⁸² Therefore, including myofilament binding of Ca is not only crucial for modeling force generation by the myocyte, but is also important for realistic modeling of cytosolic Ca transients and Ca cycling. Here, we provide an overview of myofilament modeling. More complete descriptions may be found elsewhere.^183,184

In cardiac muscle, each troponin molecule can bind Ca at two high-affinity and one low-affinity binding sites. The lower affinity site serves a regulatory function because, in the steric hindrance model, Ca binding produces an allosteric shift of troponin/tropomyosin on the thin filament to allow actin–myosin interactions. Troponin/tropomyosin units connect end-to-end and form two-strand helices that wrap around the thin filaments in the myofilaments of the myofibrils. Myosin protrudes from the thick filaments, and when allowed, forms crossbridges with the actin in the thin filament. While the steric hindrance model is generally accepted, the detailed mechanisms remain controversial.^23,185

Many different myofilaments models are being developed by numerous groups.^88,186–193 The diversity reflects both the lack of consensus regarding the appropriate mathematical formalisms needed to describe the biophysics, as well as controversies regarding which mechanisms are most salient to muscle responses.¹⁸³ Here, we review a subset of force generation models that describe both the cardiac AP and function of the myofilaments in order to illustrate the progression of the field:

The Hilgemann–Noble (HN) model⁴⁰ of rabbit atrium incorporated one ordinary differential equation to represent Ca-based activation, and a second to represent crossbridge binding. This formulation was presented as an abstract description of force generation, and some aspects of the model are now known to be inconsistent with current data. For example, in the HN model, binding of Ca to both high- and low-affinity sites affects activation, whereas it is now known that only low-affinity sites are regulatory in cardiac muscle. By assuming multiple binding sites, the HN model exhibited an increased Ca sensitivity and Hill coefficient similar to cardiac muscle. This basic formulation was carried on to models later developed by Noble and coworkers,³⁸ including model extensions for describing SL sensitivity.⁷⁶

The Hunter–McCulloch–ter Keurs (HMT)¹⁸⁶ model couples a mechanistic myofilament activation model to a fading memory crossbridge model that uses a convolution integral approach. The model includes active force with SL dependence and passive tissue properties. Simulated responses have been compared with a wide range of experimental measures. The HMT model has been refined¹⁹⁴ and extended¹⁹⁵ recently by incorporation within a model of the rat myocyte AP formulated by Pandit et al.⁷⁹ The combined model has been used to investigate the putative mechanisms of the slow force response, a secondary prolonged increase in force beyond the Frank–Starling response. The combined model has also been used as the basis of a multiscale electromechanical model of the rat left ventricle¹⁹⁶ that has been used to investigate how cellular-level behaviors affect work transduction, stress and strain homogeneity at the whole ventricle level.

The Rice-Jafri-Winslow (RJW) model integrated the myofilament model of Rice et al.¹⁸⁸ into the model of the guinea pig AP formulated by Jafri et al.⁷⁵ This model reproduced experimentally measured properties of mechanical restitution and post-extrasystolic potentiation. These phenomena are examples of interval–force relations in which changing the temporal spacing between APs can produce dramatic changes in developed force.¹⁸⁴ An important finding from this work was that altering the pacing protocol affected the amplitude of the Ca transient and force generation to a relatively small degree, while the cooperative properties of the myofilaments produced a much larger relative change in developed force. The model included a phenomenological representation of cooperative interactions between neighboring troponin/tropomyosin units, including effects of SL. However, the RJW model was limited since only isometric force protocols could be simulated.

The RJW model has been refined and expanded to reproduce a wider variety of experimental protocols in the Rice et al. model.¹⁸² Importantly, active contraction and re-lengthening can be simulated, and passive muscle properties are included to simulate muscle strips and isolated myocytes, two common experimental preparations. The model includes phenomenological representations of cooperative interactions between neighboring troponin/tropomyosin units and cycling crossbridges that are computationally efficient. While phenomenological approximations are employed, the overall model structure attempts to map well to the underlying biophysics. Thus, parameter definitions are intuitive and easily modified, as compared to highly lumped or abstracted parameters in fully phenomenological models. The model has been extended recently by Campbell et al.¹⁹⁷ to replicate canine epicardial, endocardial, and mid-myocardial myofilament responses. These cell models have been composed into a tissue model to investigate the heterogeneous layers in the ventricles.¹⁹⁸ Tran et al.¹⁹⁹ have modified the Rice et al. model to include binding and release of metabolites: ATP, ADP, Pi, and H.

Modeling Regulation via Cell Signaling

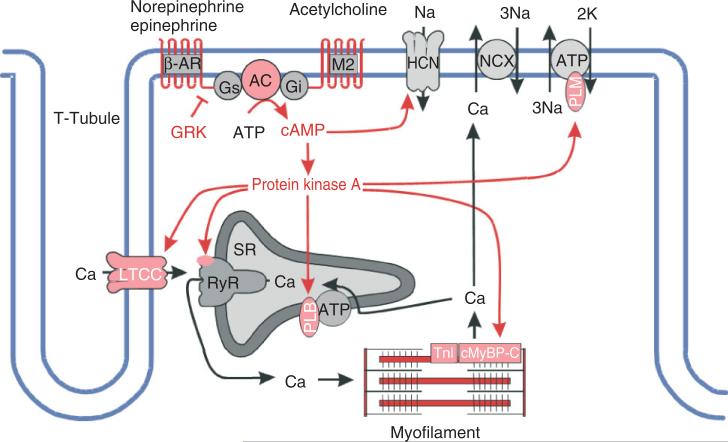
Cardiac ion channels as well as proteins involved in CICR and EC coupling are primary targets for regulation via cell signaling pathways. The most widely studied pathway is that of the β-adrenergic signaling cascade (Figure 6). The ‘fight or flight’ response increases cardiac contractility and output via the release of neurotransmitters and hormones by the sympathetic nervous system. Norepinephrine and epinephrine bind to β-adrenergic receptors (β-ARs) on the myocyte surface. These are G-protein-coupled receptors which trigger the activation of adenylyl cyclase (AC), leading to the production of cyclic AMP (cAMP), which in turn activates protein kinase A (PKA). The numerous targets of PKA-mediated phosphorylation include LCCs, RyRs, phospholamban (PLB, a regulator of the SR Ca-ATPase), the myofilament protein troponin I, and phospholemmen (a subunit of the Na–K pump).^3,200,201 Early attempts to model the effects of PKA-mediated phosphorylation of these targets on the properties of CICR and the AP involved modeling the stimulated cell by altering the function of the target proteins based on the measured effects of phosphorylation. Greenstein et al.²⁰² developed a model of the canine ventricular myocyte in the presence of 1 μM isoproterenol (a β-AR agonist). This model could explain PKA-mediated changes in AP shape, dissected the specific effects of PKA-mediated phosphorylation of LCCs and RyRs on the voltage-dependent gain of CICR, and predicted a mechanism by which increasing levels of LCC phosphorylation could lead to increased frequency of early afterdepolarizations.²⁰³ However, this model did not describe the dynamics of the β-adrenergic signaling pathway. Saucerman et al.²⁰⁴ developed a differential-algebraic model of the dynamics of the β-adrenergic signaling pathway, and incorporated it into the rabbit myocyte model of Puglisi and Bers.⁸¹ This model was used to understand and predict effects of specific molecular perturbations (e.g., expression changes in AC and β-AR density) on cAMP dynamics and contractility via changes in function of target proteins resulting from altered phosphorylation dynamics. Recently, the model of Saucerman et al.²⁰⁴ was incorporated into the guinea pig ventricular model of Faber and Rudy⁹⁹ in a study of the role of β-adrenergic agonists and antagonists in long-QT syndrome.²⁰⁵

FIGURE 6.

Protein kinase A signaling pathways in cardiac myocytes (Reprinted with permission from Ref 200. Copyright 2008 Springer Science+Business Media). See text and Figure 2 of Ref 200 for further details.

An important Ca cycling regulatory mechanism of recent interest is the signaling pathway involving CaMKII, whose target proteins include LCCs, RyRs, PLB, and the SR Ca-ATPase, as well as Na and K channels.²⁰⁶ Evidence suggests that CaMKII is directly associated with its target proteins^207,208 and that CaMKII activity is elevated in heart failure.²⁰⁹ CaMKII becomes activated when its autoregulatory domain is bound by Ca-bound calmodulin (CaM), thereby exposing its catalytic domain. In addition, the phosphorylation of a CaMKII monomer by a neighboring monomer (within the dodecameric enzyme) renders the molecule ‘autonomous”, where its kinase activity no longer depends on Ca binding,²¹⁰ therefore the net activity of CaMKII has a complex dependence on Ca dynamics in the local vicinity of its target proteins.

The first model of the cardiac myocyte to integrate the role of CaMKII was presented by Hund and Rudy.⁹² In this model, CaMKII transitions from an inactive to an active state in response to elevated subspace Ca levels, and may also enter the trapped state in which it remains active for some time following the decline of subspace Ca. CaMKII activity is assumed to modify the function of LCCs, RyRs, PLB, and the SR Ca-ATPase. The model predicted that CaMKII plays an important role in the rate-dependent increase of the cytosolic Ca transient, but does not play a significant role in rate-dependent changes of APD. Grandi et al.¹¹⁹ developed a model of CaMKII overexpression in the rabbit ventricular myocyte, including the role of CaMKII phosphorylation of fast Na channels, LCCs, and I_to,1. The CaMKII-dependent alteration of I_Na enhanced/stabilized its inactivation, but at the same time increased the late, non-inactivating component of current, revealing an important mechanism by which I_Na may modulate different properties of the AP at different pacing rates (APD at slow rates and upstroke velocity at fast rates). Combining CaMKII's effect on I_Na with that on I_CaL and I_to,1 revealed a net effect of APD reduction with CaMKII, as measured in experiments.²¹¹ Saucerman and Bers²¹² incorporated models of CaM, CaMKII, and calcineurin (CaN) into the Shannon et al.⁹⁰ model in order to better understand the functional consequences of the different affinities of CaM for CaMKII and CaN during APs. The model predicted that in the cardiac dyad, Ca levels lead to a high degree of CaM activity which results in frequency-dependent CaMKII activation and constitutive CaN activation, whereas the lower Ca levels in the cytosol only minimally activate CaM, which allows for gradual CaN activation, but no significant activation of CaMKII. Recently, Hashambhoy et al.¹⁰¹ described dynamic CaMKII phosphorylation of LCCs in the context of the stochastic, local control canine ventricular myocyte model of Greenstein and Winslow.⁸⁴ In this model it is assumed that a single CaMKII holoenzyme is tethered to each LCC, and each CaMKII monomer can transition among a variety of activity states (see Figure 2 of Hashambhoy et al.¹⁰¹), and CaMKII monomers can catalyze the phosphorylation of individual LCCs. This model demonstrated that CaMKII-dependent shifts of LCC gating patterns into high-activity gating modes may be the underlying mechanism of a variety of experimentally observed phenomena associated with I_CaL facilitation. Hashambhoy et al.²¹³ further expanded this model to include CaMKII-dependent regulation of RyRs and demonstrated that under physiological conditions, CaMKII phosphorylation of LCCs ultimately has a greater effect on RyR (leak) flux and APD than phosphorylation of RyRs.

CONCLUSION

Integrative modeling of the cardiac myocyte is advancing rapidly into exciting new areas. The ever accelerating pace of model development can be attributed, in part, to the availability of published model source codes in their original electronic form. These are often made available on the World Wide Web either directly by the model authors or via a model repository such as CellML (models.cellml.com). Here, we note some important new directions for future research.

Recently, Silva et al.²¹⁴ constructed an atomic-level model of the I_Ks alpha-subunit KCNQ1, and used results from molecular dynamics simulations to constrain a Markov model of the I_Ks current, including KCNE1 β-subunit interactions. This line of work holds great promise for developing ‘first principles’ Markov models of channel gating and for predicting effects of channel point mutations on gating behavior.

Myocyte modeling has proceeded in a ‘top down’ fashion. The first step was to understand the voltage-gated membrane currents and transporters that shape the cardiac AP. Modeling of these currents has now reached an advanced level. Consequently, a new direction of research is to characterize and model the intracellular signaling pathways that modulate these primary effectors of the cardiac AP. Development of such models will be challenging, since both the dynamics of the signaling pathway itself and the actions of key signaling proteins on their molecular targets must be modeled. Models of the β-adrenergic and CaMKII signaling pathways are now under development. Other key pathways, such as the nitric oxide signaling pathway, remain to be developed.

Ca cycling and release plays a key role in both EC coupling and regulation of characteristics of the cardiac AP. In particular, the cardiac ryanodine receptor is a complex channel whose function is modulated in many different ways, including by phosphorylation, interactions with accessory subunits, potentially interactions with adjacent RyRs, JSR Ca, and a wide variety of point mutations. Altered function of RyRs is associated with increased JSR Ca leak in heart failure^214–216 and arrhythmic activity in diseases such as catecholaminergic polymorphic ventricular tachycardia and arrhythmogenic right ventricular cardiomyopathy type 2.²¹⁷ However, it has been notoriously difficult to characterize and model the behavior of these channels.

Incorporation of models of mitochondrial energetics into whole myocyte models has shed new light on the mechanisms involved in matching energy supply and demand in the heart. Looking forward, there are several important areas of further metabolic model development. The addition of computational descriptions to describe switching between different substrates, for example, due to the transcriptional activation of enzymes responsible for fatty acid metabolism, which occurs in association with cardiac disease, will be important. More refined models of the properties of Krebs cycle enzymes and the mitochondrial respiratory chain complexes will also be required in order to understand how newly discovered posttranslational modifications might impact energy flux. Another important area will be to model the interactions between metabolism and intracellular redox regulation, including effects on antioxidant pathways. Finally, models to take into account spatial considerations and information transfer between organelles (e.g., mitochondria–SR; mitochondria–nucleus) are needed for a better understanding of whole cell systems’ interactions.

Development of these models will be a key step forward in integrative modeling of the myocyte.