Heart Rate Variability and Respiratory Sinus Arrhythmia Assessment of Affective States by Bivariate Autoregressive Spectral Analysis

Abstract

The study of emotions elicited by human-computer interactions is a promising field that could lead to the identification of specific patterns of affective states. We present a heart rate variability (HRV) assessment of the autonomic nervous system (ANS) response and respiratory sinus arrhythmia during PC-mediated stimuli by means of standard and multivariate autoregressive spectral methods. 35 healthy volunteers were exposed to computer-mediated tasks during data collection. The stimuli were designed to elicit: relaxation (R), engagement (E) and stress (S); half of the subjects were exposed to E before S (RES) while the other to S before E (RSE). HRV measures clearly separate the ANS response among R, S and E. Less significant differences are found between E and S in RSE, suggesting that S stimuli may cause a lasting response affecting the E period. Results from the bivariate analysis indicate a disruption of the cardio-respiratory coupling during non-relax conditions.

1. Introduction

The impact of computational devices in modern everyday life has raised an increasing interest on the study of emotions elicited by human-computer interactions, with particular focus on better understanding the link between emotional responses and learning processes mediated by computers. Many studies have shown interesting results that support the feasibility to detect affective states by means of psycho-physiological data acquisitions and analysis, with the critical purpose to transform the correlation between biological signals and emotional reactions into additional inputs for innovative human-computer interactions [1-5].

In particular, heart rate variability (HRV) measured as the variations of the time interval between two consecutive cardiac beats registered by means of electrocardiogram (ECG), is influenced by multiple neural and hormonal inputs that generate specific observable rhythms in the series. These rhythms provide a quantitative noninvasive measure of the autonomic nervous system regulatory action. Moreover the quantification of respiratory sinus arrhythmia (RSA), the influence of respiration on heart rate, provides information about the mechanisms involved in respiratory coupling [6].

Transfer function analysis [7,8] has been used in cardiovascular modeling in order to describe the relationship between different cardiac variables in different frequency bands, thus focusing on various underlying physiological mechanisms. In particular, the coherence function can be considered as a measure of the strength of the linear coupling between the two time series. As nonzero coherence values are likely to occur at some frequency even in the case of complete uncoupling between two time series, a threshold level has to be defined in order to assess whether the two series are significantly coupled or not. Previous studies [9] showed that the use of surrogate series, preserving the power spectrum of the original series but being structurally uncoupled, are recommended to avoid false coupling detections in the presence of oscillations occurring at nearby frequencies but produced by different mechanisms.

Accordingly, the aim of our study is to evaluate the autonomic nervous system response and the mechanical and autonomic effect of respiration on heart rate [10] during different digital stimuli efficient in simulating good elicitors of the targeted affective states [11-12].

2. Methods

2.1. Experimental Protocol

A group of 35 healthy volunteers (20 to 25 years old) is considered in this study. Each subject was monitored during the following experimental conditions:

1. Baseline (B): fixation of a white screen (3 mins)

2. Relaxation (R): fixation of relaxing panoramas slides (10 mins)

3. Engagement (E): detective story reading on the PC screen (10-15 mins)

4. Stress (S): frustrating task performance (i.e. stroop task) (4 mins)

In order to account for possible effects due to the sequential order of the emotion-induced conditions, the sample was split into two groups: half of the subjects (RES group) were exposed to E before S, whereas the other half (RSE group) to S before E. Such setting allows for evaluation of both effects of Engagement on Stress and vice versa, as well as the effects of Engagement and Stress on Relaxation. The entire session was repeated for each student after one month.

Every subject was briefed in the Lab in order to become more familiar with the Lab environment and equipment. When the subject reached a comfortable status, he/she was asked to start the experiment. Since during the stress task subjects have to speak, they were instructed to loudly read statements written on some relaxation and engagement slides, in order to fairly compare stress to the other conditions.

2.2. Signal Acquisition and Preprocessing

ECG and respiration signals were continuously acquired with subjects sitting and interacting in front of a personal computer. The ECG electrodes and respiration belts were connected to a multi-modality device for real-time computerized biofeedback and data acquisition (Flexcomp Infinity™ encoder, Thought Technology Ltd., Montreal, Canada). Every channel was acquired at 256 Hz sampling rate. The ECG signal was analyzed with custom software developed using Matlab (The Mathworks, Inc.; Natick, MA) in order to detect the R peaks and calculate the RR series as the time interval between two consecutive R peaks, detected by a traditional derivative threshold procedure. The respiratory signal was low-pass filtered and sampled in correspondence to the R waves, thus deriving the respiratory series. All data analysis was performed at the Neuroscience Statistic Research Laboratory, Department of Anesthesia (Massachussetts general hospital).

2.3. Autoregressive Spectral Analysis

Spectral analysis was performed by means of autoregressive (AR) spectral methods with custom software. The Levinson–Durbin recursion was used to identify the coefficients of the autoregressive model [13] and the order was chosen (between 4 and 12) according to the Akaike figure of merit. The AR spectral decomposition procedure was applied to calculate the power of the oscillations embedded in the series [14]. The rhythms were classified [15] as very low frequency (VLF, <0.04 Hz), low-frequency (LF, from 0.04 to 0.15 Hz) and high frequency (HF, from 0.15 to 0.5 Hz) oscillations. The power was expressed in absolute (LF_RR, LF_resp and HF_RR, HF_resp) and in normalized units [e.g. RR series: LF_nu and HF_nu as 100*LF_RR/(σ² _RR-VLF_RR) and 100*HF_RR/(σ² _RR-VLF_RR), where σ² _RR was the RR variance and VLF_RR was the VLF power expressed in absolute units].

2.4. Bivariate AR Yule-Walker Algorithm

A bivariate autoregressive model was employed to study the interaction between RR and respiration [8]. The model is defined as

$$X\left(n\right)=-\sum _{k=1}^{M}A\left(k\right)\cdot X(n-k)+w\left(n\right)$$ (1)

where M is the order and is set at 14, and

$$X\left(n\right)=\left[x_1\right(n\left)x_2\right(n\left)\right],A\left(k\right)=\left[\begin{array}{cc}\hfill a_{11}\left(k\right)\hfill & \hfill a_{12}\left(k\right)\hfill \\ \hfill a_{21}\left(k\right)\hfill & \hfill a_{22}\left(k\right)\hfill \end{array}\right],w\left(n\right)=\left[w_1\right(n\left)w_2\right(n\left)\right].$$

x₁(n) and x₂(n) are the RR and respiration respectively, w(n) represents the white noise and a_ij (k) represents the autoregressive coefficients. We used a recursive algorithm to determine the coefficients of the autoregressive model; spectral components are determined from these coefficients.

The coherence γ² as a function of frequency f is evaluated as

$${\gamma }^2\left(f\right)=\frac{{\mid P_{x_1{x}_2}\left(f\right)\mid }^2}{P_{x_1}\left(f\right)P_{x_2}\left(f\right)}$$ (2)

where P_x1 (f) and P_x2 (f) are the auto-spectral density functions of RR and respiration respectively. P_x1x2 (f) is the cross spectral density between RR and respiration.

The transfer function as a function of frequency for the model in Eqn (1) is obtained as

$$\text{Gain}(x_j\to x_i)=H_{ji}\left(f\right)=\frac{-\sum _{k=1}^M{a}_{ij}\left(k\right)e^{-l2\pi fk}}{1+\sum _{k=1}^M{a}_{ii}\left(k\right)e^{-l2\pi fk}}$$ (3)

with i = 1,2; j = 1,2; $l=\sqrt{-1}$.

2.5. Surrogate Data Analysis

For each pair of respiratory and RR series, we generated an ensemble of 100 pairs of AR surrogate time series preserving the power spectrum of the original ones but being completely uncoupled, as generations of two linearly independent stochastic processes [9].

These surrogates were obtained by fitting an AR model to each of the two original series, using pairs of independent white noises as model inputs to produce completely uncoupled surrogate series. The order of the model used to fit the data was optimized by means of the Akaike criterion.

The coherence was then estimated between each pair of surrogate series and its empirical sampling distribution computed accordingly at each frequency of the signal bandwidth. The threshold for zero coherence was set at the 95th percentile of the coherence sampling distribution.

2.6. Statistical Analysis

Median, 5^th, 25^th, 75^th and 95^th percentiles were computed for the group, for each index considered, for each epoch. Statistical analysis was performed to compare the R, S, E emotional states and B, using a paired t- test with Bonferroni multiple comparison correction (p<.05).

3. Results

Table I reports the median, 25^th and 75^th percentile values of mean, variance and spectral analysis indexes obtained from the RR series and respiration separately, during all the experimental conditions for both the RES and RSE groups. Mean RR significantly decreased during S compared to B and E in both groups. Moreover a significant decrease in HF_nu and a parallel increase in LF_RR and LF_nu indexes was also observed during both E and S compared to B. Interestingly, HF_RR and LF_nu indexes showed significant differences between E and S phases only in the group which performed E before S (RES group).

TABLE 1.

SPECTRAL ANALYSIS RESULTS OBTAINED IN 35 SUBJECTS FROM THE RR SERIES DURING THE 4 EXPERIMENTAL CONDITIONS

	RES				RSE
	B	R	E	S	B	R	E	S
mean [ms]	837(763-906)	822(791-913)	839(762-913)	764(691-858)*#	827(729-940)	824(720-910)	846(740-879)	757(711-834)*#
var [ms*10−3]	2.37(1.5-4.4)	3.14(1.8-5.0)	3.17(1.8-5.3)*	3.40(2.3-4.4)	2.08(1.2-2. 9)	2.42(1.7-3.7)	3.12(1.5-4.1)*	2.43(1.8-3.8)
LFRR [ms2]	896(489-1519)	777(457-1594)	1271(531-2029)*	1597(937-2473)*	656(369-1221)	614(380-1017)	1062(617-2140)*	1316(760-2106)*
HFRR [ms2]	437(193-1494)	470(191-1319)	398(139-1159)	269(161-533)*#	236(144-731)	307(133-865)	248(96-504)	202(110-437)
LFnu [%]	55.0(38.7-80.2)	60.4 (45.5-77.6)	70.8(56.4-80.2)*	78.7(69-92.3)*#	65.6(41.8-84.4)	63.2(42.1-76.7)	81.9(63.8-89.0)*	82.6(72.6-92.4)*
HFnu [%]	43.4(24.4-64.4)	39.2(22.8-56.0)	28.8(18.9-42.9)*	22.1(12.9-37)*	31.6(14.8-58)	36.0(21.5-56.0)	18.0(10.8-33.8)*	15.8(8.0-23.4)*
LF/HF [−]	1.40(.64-4.16)	1.63(.87-3.96)	2.56(1.47-4.56)	4.15(2.79-18.5)	2.07(.73-5.69)	1.76(0.75-3.63)	4.99(1.93-8.86)	5.37(3.16-14.3)
LFresp[*103]	79.3(15.1-179)	35.4(8.6-62.0)	38.6 (11.0-105)	66.1 (37.9-112.5)	11.9(2.2-53.3)	20.9(5.1-158.7)	34.8(7.0-94.3)	57.9 (39.0-145.0)
HFresp [*103]	86.9 (56.6-20.3)	101.1(51.2-193)	95.6 (46.9-183.8)	128.6(66.7-264)	73.7(25.2-211)	62.6(22.2-180)	52.2(24.7-134.4)	92.5(45.7-238.4)

Median (25^th-75^th percentile) are shown;

^*:p<0.05 paired t-test with Bonferroni correction vs B ;

^#:p<0.05 paired t-test with Bonferroni correction vs E

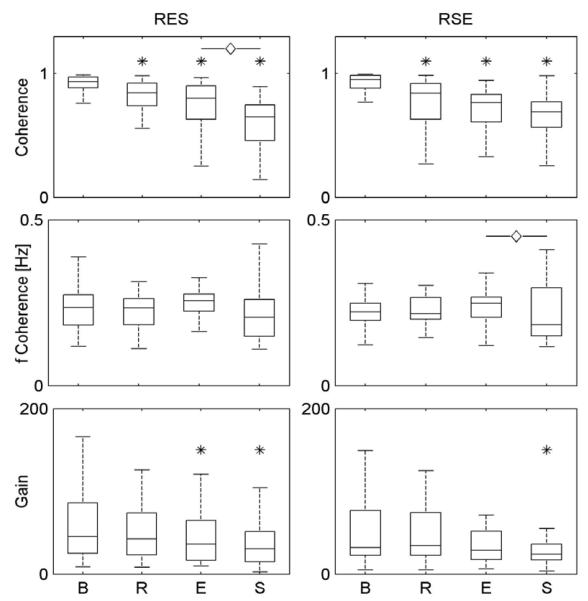
Fig.1 shows the values of coherence and gain of the transfer functions from respiration to RR interval, sampled at HF for the two groups of subjects (RES and RSE). We presented the results relevant to E before that to S even for RSE group for better visual comparison of the two groups. We found that even if the coherence between the respiratory and RR series significantly decreased during S compared with the other protocol phases, its value was upon the threshold level set by means of AR surrogates to reject the hypothesis of uncoupling in 93% of the series. Interestingly, in the RES group the gain of the transfer function from respiration to RR interval (the RSA gain) significantly decreased during E and S compared to B, while in the RSE group a significant decrease was found only with S. Moreover, significant differences were found between S and E phases in both groups.

Fig. 1.

The box-and-whisker plots summarize the results relevant to the bivariate AR analysis for the coherence and gain estimation performed on the RES and RSE groups at B, R, E and S phases. The symbol * indicates p<0.05 vs B; ◇: p<0.05 vs E.

4. Discussion

We have reported a preliminary quantitative analysis where standard autoregressive spectral and bivariate algorithms have been applied to R-R interval and respiratory time series with the goal to identify changes in the autonomic nervous system response and respiratory sinus arrhythmia as associated to three target affective states elicited by specific computer-mediated stimuli. Surrogate data analysis was further performed in order to accept or reject the hypothesis of uncoupling between the two time series.

Our results demonstrated that both standard and bivariate AR spectral analysis were able to detect significant differences in the autonomic response between the target phases of the protocol; moreover, the observed trends generally reflect the ones assessed through psychological self-rated tests [16]. In this sense the results give reasonable perspectives regarding an effective use of HRV and RSA measures in order to characterize the target states in question.

Significant differences were found between the two groups of subjects. In particular, standard spectral analysis was able to detect significant differences in the autonomic nervous system response between E and S in RES group only; accordingly we hypothesized that the stress-related stimuli cause a more lasting response influencing the E phase of the RSE group. The bivariate AR analysis was also able to identify differences between RES and RSE groups: while in RSE the gain of the transfer function significantly decreased during both E and S compared to B, in the RSE group a significant decrease was found only during S. Because there is a sequence effect, RES gradually improves the arousal reactions from the first to the last epoch, while RSE shows how engagement after stress is affected by the lingering stress arousal. This has important implications in setting up sequential stimuli, and/or using a randomized experimental design.

In conclusion, this preliminary study showed that the influence of stress and engagement states on heart rate and respiration could be identified by means of spectral and bivariate AR methods; accordingly these signal processing methods could be able to play a key role in the identification of specific affective states elicited by human-computer interactions.