Abstract
The evolution of cooperation through partner choice mechanisms is often thought to involve relatively complex cognitive abilities. Using agent-based simulations I model a simple partner choice rule, the ‘Walk Away’ rule, where individuals stay in groups that provide higher returns (by virtue of having more cooperators), and ‘Walk Away’ from groups providing low returns. Implementing this conditional movement rule in a public goods game leads to a number of interesting findings: 1) cooperators have a selective advantage when thresholds are high, corresponding to low tolerance for defectors, 2) high thresholds lead to high initial rates of movement and low final rates of movement (after selection), and 3) as cooperation is selected, the population undergoes a spatial transition from high migration (and a many small and ephemeral groups) to low migration (and large and stable groups). These results suggest that the very simple ‘Walk Away’ rule of leaving uncooperative groups can favor the evolution of cooperation, and that cooperation can evolve in populations in which individuals are able to move in response to local social conditions. A diverse array of organisms are able to leave degraded physical or social environments. The ubiquitous nature of conditional movement suggests that ‘Walk Away’ dynamics may play an important role in the evolution of social behavior in both cognitively complex and cognitively simple organisms.
Keywords: group selection, multilevel selection, Walk Away, conditional movement, contingent movement, migration, social dilemma
Introduction
The relationship between mobility and cooperation has been a topic of study in the evolutionary and behavioral sciences for decades. This interest has generated a number of conceptually related literatures using terms such as mobility, migration, dispersal, population viscosity, and movement. The historical view has been that mobility undermines the evolutionary viability of cooperation, with early models showing that low but non-zero migration rates are most favorable for the evolution of cooperation (Maynard Smith, 1964; Wilson, 1987; Wright, 1931). More recent work has painted a more ambiguous picture, showing that low mobility/high viscosity limits the evolution of cooperation because it leads to higher levels of competition among kin (Taylor, 1992; Wilson et al., 1992, West, 2002). It is now becoming clear that cooperation can be viable despite the kin competition limitations, but this depends on the population structure and the ways that individuals influence their environments (Lion & Gandon, 2009; Lehmann & Rousset, 2010). It has been shown that cooperative acts that expand carrying capacity are not subject to the same negative effects from kin competition (Platt & Bever, 2009) and that the negative effects of kin competition are limited when groups expand via budding (Gardner & West, 2006) or expansion of territory (Lehmann et al., 2006). Helping has also been shown to be limited to non-dispersers (Mouden & Gardner, 2008) and less fecund individuals (Johnstone, 2008) in other models of the evolution of cooperation under limited dispersal.
Conditional movement is an important and much neglected form of mobility with regard to the evolution of cooperative traits since it enables individuals to respond to local conditions. This affords greater opportunities for taking advantage of potentially beneficial so cial environments and dispersing when those environments become degraded by the increasing presence of defectors. Conditional movement is also evolutionarily ancient and phylogenetically widespread (Sorkin, 1974; Glagolev, 1984), suggesting that it is likely to be a strategy available to most organisms. Although conditional movement has been included in a number of models (Enquist & Leimar, 1993; Dugatkin & Wilson, 1992), the role of conditional movement in promoting cooperation has been neglected until recent work on environmental feedback (Pepper & Smuts, 2002; Pepper, 2007; Pepper & Smuts, 2000) and the Walk Away strategy (Aktipis 2004; Aktipis 2008) have shown that the ability to leave degraded environments can favor the evolution of cooperation.
Explanations for the evolution of cooperation
The literature on the evolution of cooperation seems to be unified around the basic question: can cooperation evolve when defection pays? The literature suggests a complicated answer to this question, with two primary ‘solutions’ taking center stage: namely kin selection (Hamilton, 1964a; Hamilton, 1964b), and reciprocity (Trivers, 1971). Group selection as a force promoting cooperation has alternately been lauded (Wilson, 1983; Wilson & Wilson, 2007; Wynne-Edwards, 1962), sullied (Dawkins, 1976; Williams, 1966) and considered uncontroversial and mathematically equivalent to kin selection (Hamilton, 1975; Queller, 2004; West, et al., 2007). Yet another class of explanations, those involving partner choice (Aktipis, 2004; Aktipis, 2008; Ashlock et al., 1996; Bull & Rice, 1991; Connor, 1992; Enquist & Leimar, 1993; Friedman & Hammerstein, 1991; Nesse, 2009; Noe & Hammerstein, 1994; Sachs et al., 2004), are receiving increasing attention.
Despite these varied approaches, a common thread joins these explanations: assortment, or the preferential interactions of cooperators with one another, promotes the evolution of cooperation (Hamilton, 1971; Fletcher & Doebeli, 2009). Assortment increases the likelihood that cooperators are the recipients of benefits, making cooperation more viable. It is assortment that promotes the evolution of cooperation via kin selection (Hamilton, 1975). Other processes such as kin recognition (Buston & Balshine, 2007; Grafen, 1990; Hepper, 1991; Holmes, 2004; Komdeur & Hatchwell, 1999) can promote assortment, therefore leading to selection for cooperation. Assortment is also at work in reciprocity, where conditional cooperation limits benefits to defectors and amplifies benefits to cooperators, although reciprocity may be limited by the requirement that individuals have extensive memory abilities to keep track of interaction partners (Aktipis, 2006; Axelrod & Hamilton, 1981; Axelrod, 1984; Axelrod, 1997; Cox et al., 1999; Hammerstein, 2003; Vos & Zeggelink, 1994). Partner choice strategies selectively exclude defectors from the benefits of interacting with cooperators, which promotes assortment and favors cooperation (Aktipis, 2004; Bergmüller et al., 2007; Bull & Rice, 1991; Connor, 1992; Enquist & Leimar, 1993; Friedman & Hammerstein, 1991; Nesse, 2009; Noe & Hammerstein, 1994; Sachs et al., 2004).
Much confusion arises because explanations for the evolution of cooperation are often presented as competing hypotheses, while in reality they invoke mechanisms operating at very different levels. Kin selection and group selection describe the ultimate level, i.e., the selection of cooperative traits due to assortment from common descent or other processes. In contrast, reciprocity and partner choice explanations describe the proximate cognitive and behavioral processes that enable assortment of cooperators. These processes are not mutually exclusive. In fact, behavioral/cognitive adaptations such as conditional cooperation and partner choice increase assortment and influence population structure, making the operation of kin and group selection more likely.
Social selection and partner choice in the evolution of cooperation
Social selection is the evolutionary process that arises from individuals exerting choice over interaction partners (West-Eberhard, 1979). There has been renewed interest in the role of social selection in the evolution of cooperation and prosocial tendencies (Nesse, 2009). Partner choice has been shown to be important in a variety of contexts (Aktipis, 2004; Bergmüller et al., 2007; Bull & Rice, 1991; Connor, 1992; Enquist & Leimar, 1993; Friedman & Hammerstein, 1991; Nesse, 2009; Noe & Hammerstein, 1994; Sachs et al., 2004) and has been shown to increase cooperation in experimental economics games (Barclay & Willer, 2007; Boone & Macy, 1999; Orbell et al.,1984).
Partner choice can be complex, involving the ability to represent a complicated network of agents and/or dynamically alter group composition (Ashlock et al., 1996; Vanberg & Congleton, 1992; Yamagishi et al., 1994; Yamagishi & Hayashi, 1996; Hamilton & Taborsky, 2005; Eldakar et al., 2007; Eldakar & Wilson, 2008). Other simpler strategies such as opting out of interactions entirely (Hauert et al., 2002; Szabó & Hauert, 2002; Brandt et al., 2006) have been explored as well. The ‘loner’ strategy explored by Hauert and colleagues is different from the Walk Away strategy of selectively leaving uncooperative partners (Aktipis, 2004; Aktipis, 2008) in one critical respect: in loner models, individuals receive a payoff when not participating, while in the only way to accumulate payoffs is to interact with other players. Environmental feedback models are also examples of partner choice; in these models individuals stay only in regions of high quality, where this quality is directly influenced by the altruistic behavior of agents in that region (Pepper & Smuts, 2002; Pepper, 2007; Pepper & Smuts, 2000).
Conditional movement strategies such as ‘Walk Away’ offer a simple mechanism for partner choice that requires little or no cognitive complexity: individuals just respond to the state of the current social environment, leaving if levels of cooperation are insufficient. This fit between the environmental demands and the decision rule promotes adaptive behavior in the face of little information (Todd & Gigerenzer, 2003), making these simple rules good candidates for ‘rules of thumb’ in a variety of biological contexts (Hutchinson & Gigerenzer, 2005). Rules that can operate with limited information are often necessary in conditional movement contexts including foraging (McNamara & Houston, 1985; McNamara & Houston, 1980).
The role of conditional mobility in the evolution of cooperation was first explored by Enquist & Leimar (1993), who concluded that conditional mobility restricts the evolution of cooperation by making free riders more efficient at moving through and exploiting a population of cooperators. However, their results, as well as the results of the dyadic Walk Away model (Aktipis, 2004), demonstrate that defectors only have an advantage when search times for new partners are low. Nevertheless, the two models derive very different conclusions: Enquist and Leimar conclude that mobility restricts cooperation while the dyadic Walk Away model shows that conditional movement promotes cooperation under a variety of parameter values. This is likely to be due both to differences in interpretation of results and differences in implementation. The Walk Away model is an agent-based model with explicit space, individual movement rules and an endogenous fitness function, while Enquist and Leimar’s model is analytical. It is often the case that spatial (and/or agent-based) models result in different results than analytical models because, in these models, decentralized processes can drive associations among individuals. This can be critical in models of the evolution of cooperation because the association of cooperators with one another drives selection for cooperation. In the dyadic Walk Away model (Aktipis, 2004), associations between partners were a result of individual movement rules only, while Enquist & Leimar’s (1993) model, coalition time was a parameter that was varied exogenously.
Methods Overview
In this paper, I explore the evolutionary viability of a partner choice rule that has low cognitive requirements and is powerful in promoting assortment: the Walk Away rule. In the dyadic version of Walk Away model, cooperative Walk Away agents outperformed defectors as well as Tit-for-Tat and PAVLOV (Aktipis, 2004). Here this framework is extended to a group-wise context in which agents play public goods games in endogenously formed groups. Agents have the ability to detect and leave low quality social environments (i.e., groups with a large proportion of defectors in a public goods game). These Walk Away agents lack any memory capacity, recognition, or conditional cooperation and are unable to follow or seek out likely cooperators. Individuals simply decide whether or not to stay in a group based on the payoffs they receive in that group (see Figure 1). Groups, however, do not possess a mechanism to choose which agents can enter or stay in the group.
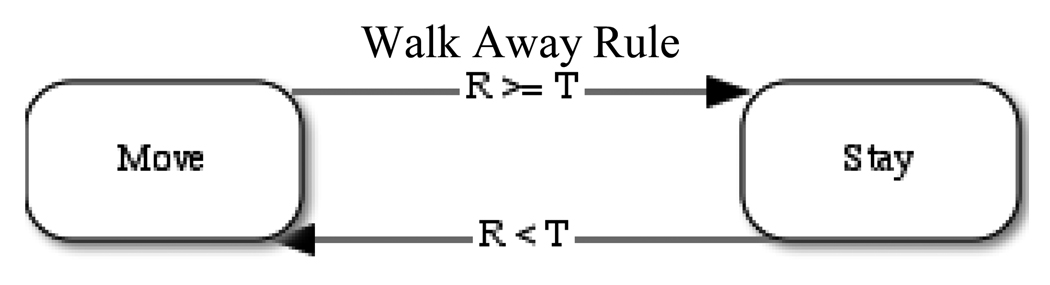
Figure 1.
The Walk Away strategy is illustrated in the above state transition figure. Agents can occupy one of two states: “move” or “stay,” indicated by boxes; arrows indicate possible state transitions. Agents stay in a group if and only if the return (R) received from the group meets or exceeds the agent’s threshold (T). Cooperators in the “stay” state contribute to the group each time period and stay in their current location. Defectors in the “stay” state simply remain in the group, contributing nothing each time period. In the “move” state, agents move one step each time period and do not contribute. Agents switch to the “stay” state when they encounter another agent (or agents) and continue to stay only if the benefit received from the group exceeds their threshold.
In the present Walk Away model, group size emerges from interactions between group properties (local cooperation), individual level rules (the staying threshold of agents) and population level features (the likelihood that a new group member is a cooperator). Analytical models can be used for probabilistic conditional movement models, but are less tractable for models such as the current one, where agents have a threshold for leaving groups. Agent based models are appropriate for contexts such as these in which interactions among individual level, group level and population level processes generate complex feedback loops (Hammond & Axelrod, 2006).
Agent based models of the evolution of cooperation in groups provide an alternative to exogenously varying migration rate, group size or number of groups, instead allowing these features to emerge from the behavior of individuals (e.g., Avilés, 2002; Avilés, 1998; Marshall & Rowe, 2003; Ramos-Fernández et al., 2006) and allowing for novel and unexpected phenomena. Spatial structure (Durrett & Levin, 1994) and self-structuring processes, such as those generated by dispersal (Lion & Van Baalen, 2008), generate feedback loops between ecological and evolutionary processes that have been shown to affect the evolution of cooperation.
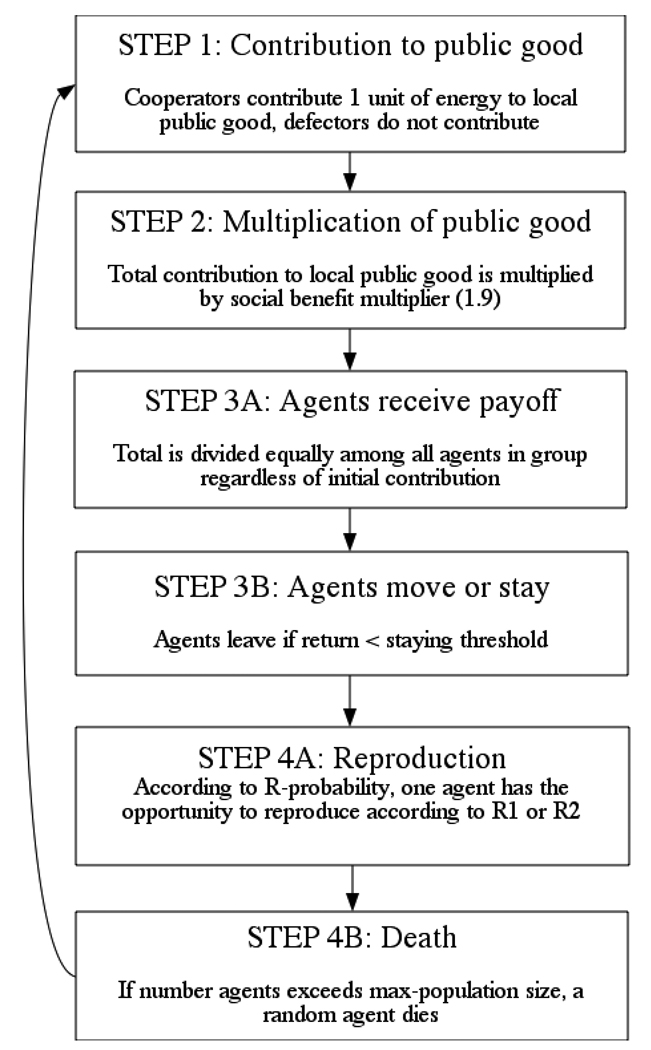
The basis of the current model is a spatially-based public goods game. The basic schedule and processes of the model are illustrated in Figure 2 and more technical details following the standardized ODD protocol for describing individual and agent based models (Grimm & Railsback, 2005; Grimm et al., 2006) can be found in Appendix A. Agents on the same patch participate in voluntary contributions to a local public good (Step 1), with cooperators contributing 1 unit and defectors contributing nothing. After all contributions have been made, the total contributions are multiplied by the social benefit multiplier, which is 1.91 (Step 2), making the interaction a social dilemma even if groups are made up of only 2 agents. Next, this total is divided equally among group members, regardless of initial contribution, giving each group member the same return (R) from the public goods game (though defectors have a higher net payoff then cooperators in the same group) (Step 3A). Cooperators can have negative net payoffs and agents not in a group neither contribute nor receive payoffs. After receiving the return from interacting with the group, agents stay on the present patch (i.e., remain in the current group) if the return (R) received in the previous step exceeds their staying threshold (T), and move if the return is below threshold or if no other agents occupy the current patch (Step 3B). Finally, agents have the opportunity to reproduce according to a threshold-based reproduction scheme (R1) or payoff proportional reproduction scheme (R2), and the population size is reduced if the total number of agents exceeds the carrying capacity of 500 agents (Step 4). Agents remain in the game if their energy becomes negative.
Figure 2.
Diagram indicating the basic schedule of the model. A detailed model description can be found in Appendix A.
The group-wise Walk Away model is designed as a general model of conditional movement in response to the quality of the local social environment. It is not based on observations of a particular species. How ever, several observations about mobility in various species provided a basis for the assumptions of this model. Conditional mobility is phylogenetically widespread and evolutionarily ancient (Glagolev, 1984) in forms including chemotaxis (Sorkin, 1974) and foraging (Stephens et al., 2007). In social animals, the exploitation of resources is known to affect social organization and behavior (Waite & Field, 2007). In humans, conditional movement away from uncooperative social partners has been observed in experimental settings (Barclay & Willer, 2007; Boone & Macy, 1999; Orbell et al., 1984).
Results
The two primary questions answered by this model are 1) does the inclusion of conditional movement affect the viability of cooperation? and, 2) does conditional movement lead cooperation to be selected when overall rates of movement/migration are high? Because one of the goals of this model is to explore whether cooperation can evolve when agents have high migration rates (resulting from conditional movement), the agents’ thresholds were systematically varied rather than allowing them to evolve.
Cooperator Viability (with death and reproduction)
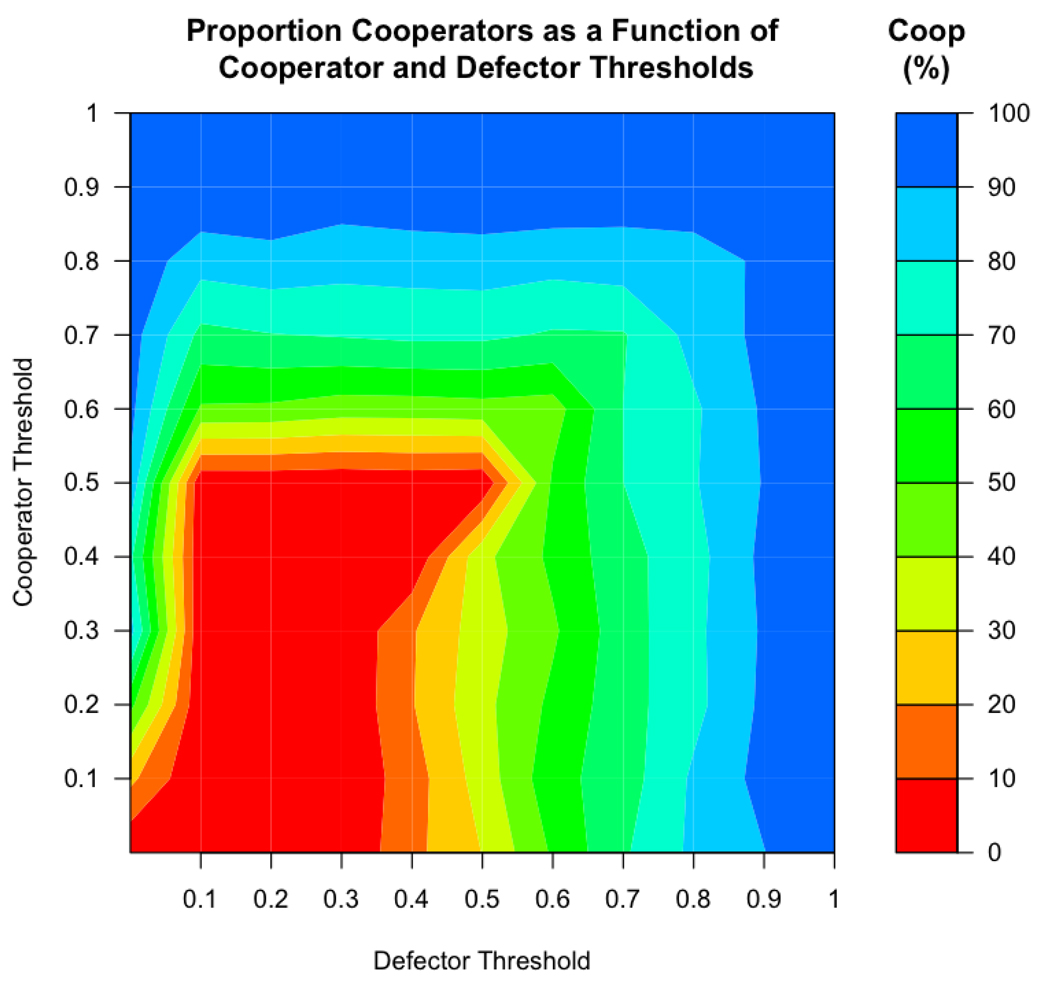
With high staying thresholds, agents stay only in groups with very high levels of cooperation. In contrast, agents with low thresholds are more ‘tolerant’ of groups with defectors. Cooperators were most successful when thresholds of cooperators and/or defectors are high, i.e., agents were intolerant of defection. In these simulations (Figure 3) a mixed population of c ooperators and defectors was maintained over the majority of the parameter space. Defectors dominated the population when the thresholds of both cooperators and defectors were low (but not when defector threshold was 0).
Figure 3.
When the threshold of cooperators or the threshold of defectors was higher, cooperators were more successful. When the threshold of both strategies was low, defectors outperformed cooperators (except when defector’s threshold was 0). This figure shows the outcomes with 0 noise.
Cooperator success when cooperators have high thresholds is fairly intuitive: when cooperators had high thresholds, they were able to leave groups with growing numbers of defectors. However, cooperators’ success when defectors had high thresholds is somewhat puzzling at first glance. Why do cooperators do better when defectors are pickier? When defectors readily left fairly cooperative groups (i.e., when defectors had high thresholds), they did not spend long periods of time in groups where they might have otherwise been able to benefit from exploiting cooperators. Further, defectors with high thresholds left groups, after which they were less likely (than cooperators) to be able to form successful and stable groups.
Cooperators were also somewhat successful when defectors had thresholds of 0. In these cases, defectors were infinitely tolerant of other defectors so they never left groups, even after they had been completely taken over by defectors, giving these defectors no mechanism by which to colonize new groups. This enabled cooperators to be relatively successful when defector threshold was 0 and there was no noise (however, this effect disappeared when noise was introduced to the threshold, see below).
In biological and cognitive systems, errors often occur in information processing and behavior. In order to model the potential for such errors or noise, variation was introduced into the staying threshold of agents, such that the threshold used by a given agent varied between time periods around a mean (reported on the graph) with a standard deviation of 0.1. This made the likelihood that an agent would stay in a group probabilistic around the reported mean.
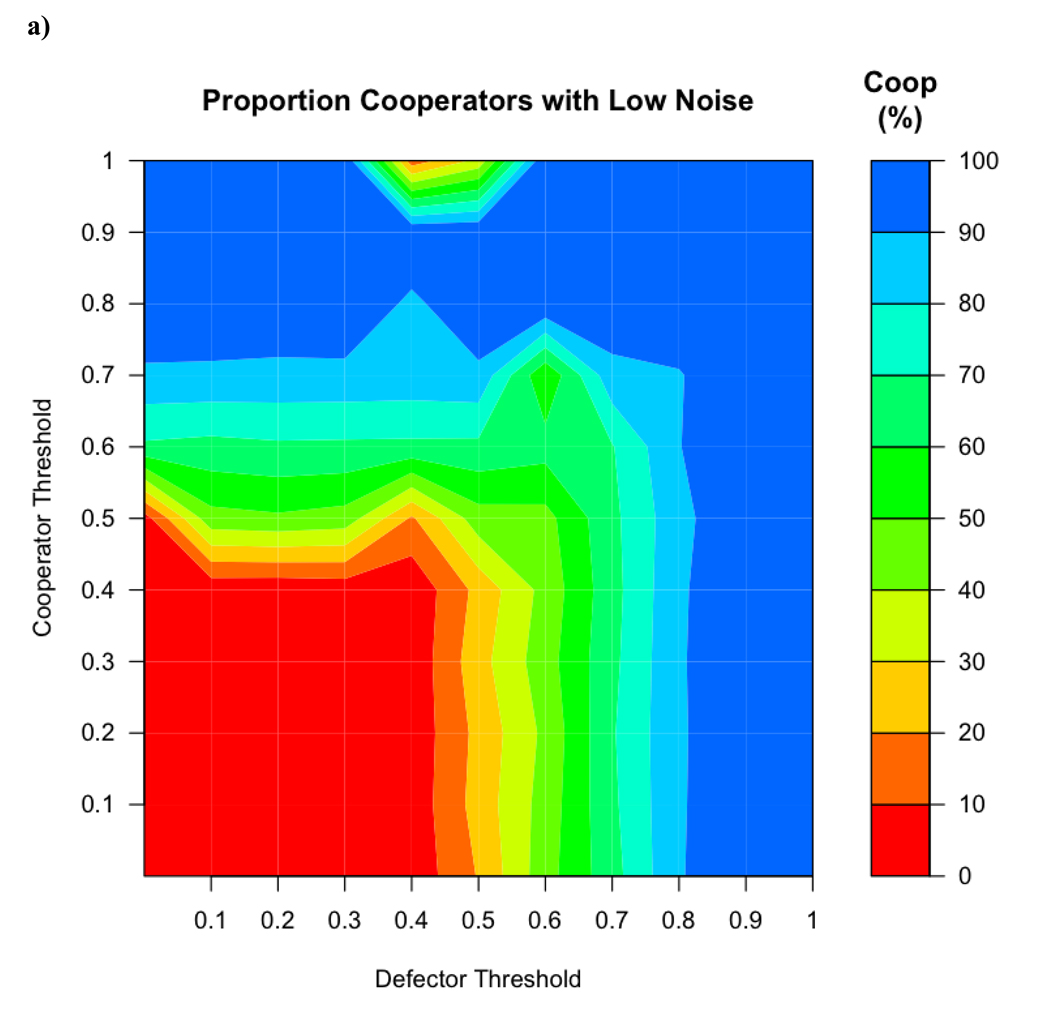
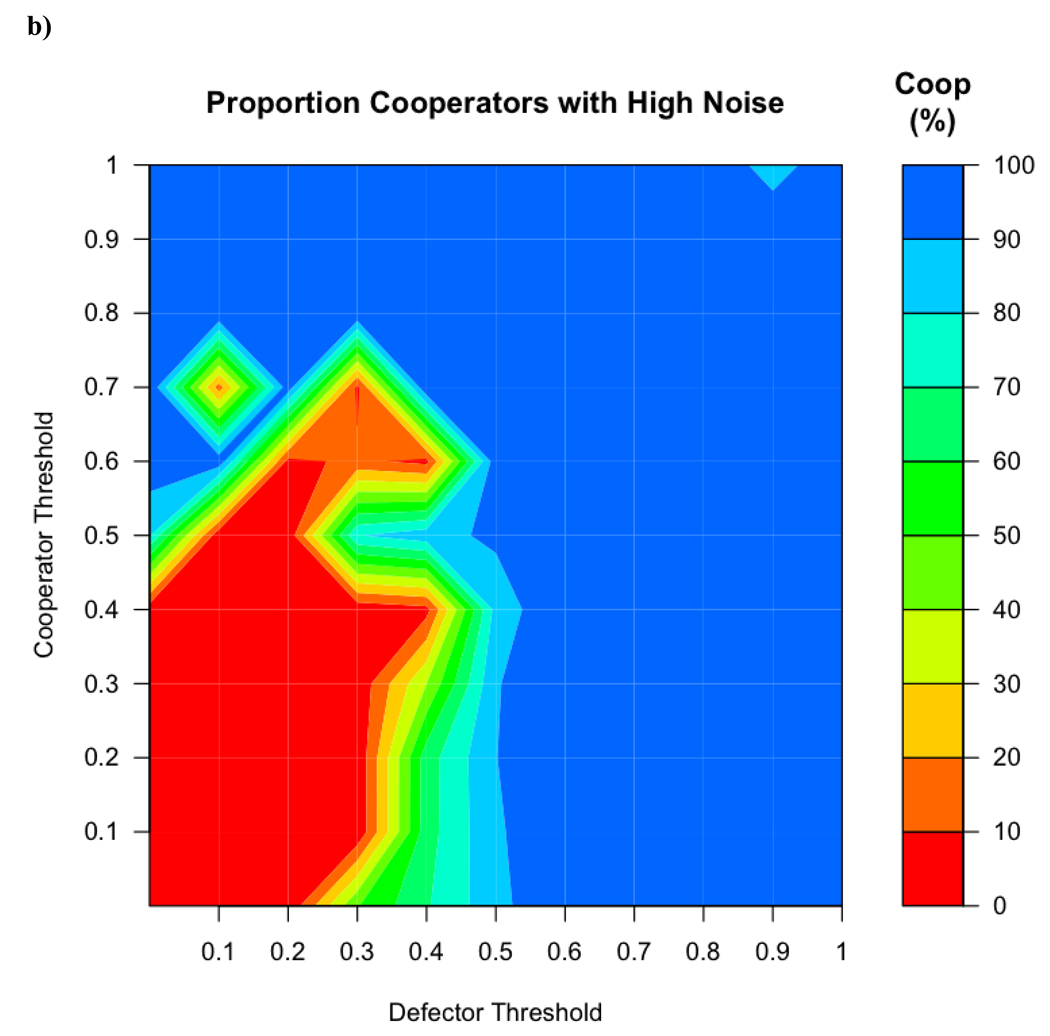
The addition of error resulted in smaller regions with a mixed population and larger areas with only cooperators and only defectors. In addition, the moderate success of cooperators when the average initial defectors threshold was 0 disappears (see Figure 4a). This is because defectors probabilistically used a threshold higher than 0, giving them a way to leave previously colonized groups and take over new ones.
Figure 4.
a) When variability (with a SD of 0.1) was introduced into the threshold used by the agents, the regions of cooperator success at high thresholds expands. b) When variability was increased to SD = 0.3, this region is even larger and the region in which cooperators and defectors coexist becomes smaller.
When the standard deviation was increased from 0.1, the region favoring cooperators became larger. When the standard deviation of the variation was raised to 0.3, cooperators were overwhelmingly successful, but defectors were still successful at threshold values lower than 0.5 for both cooperators and defectors (Figure 4b).
Migration
In the present model, the emergent rate of migration varies across staying thresholds and across evolutionary time, influencing and being influenced by evolutionary dynamics. Cooperation is strongly selected in regions with initially high emergent migration rates, although these migration rates decrease after selection has favored cooperators.
Because there can be high variability between time periods in migration events, the average rate of migration over the final 100 time periods of runs is used, and migration is calculated as the rate of emigration from groups (the number of agents leaving divided by the number agents leaving and staying). In these simulations, there was a noise level with SD = 0.1 (as in Figure 4a) in the agents’ thresholds and the initial proportion of cooperators was 0.05.
Emergent migration rate before selection (no death or reproduction)
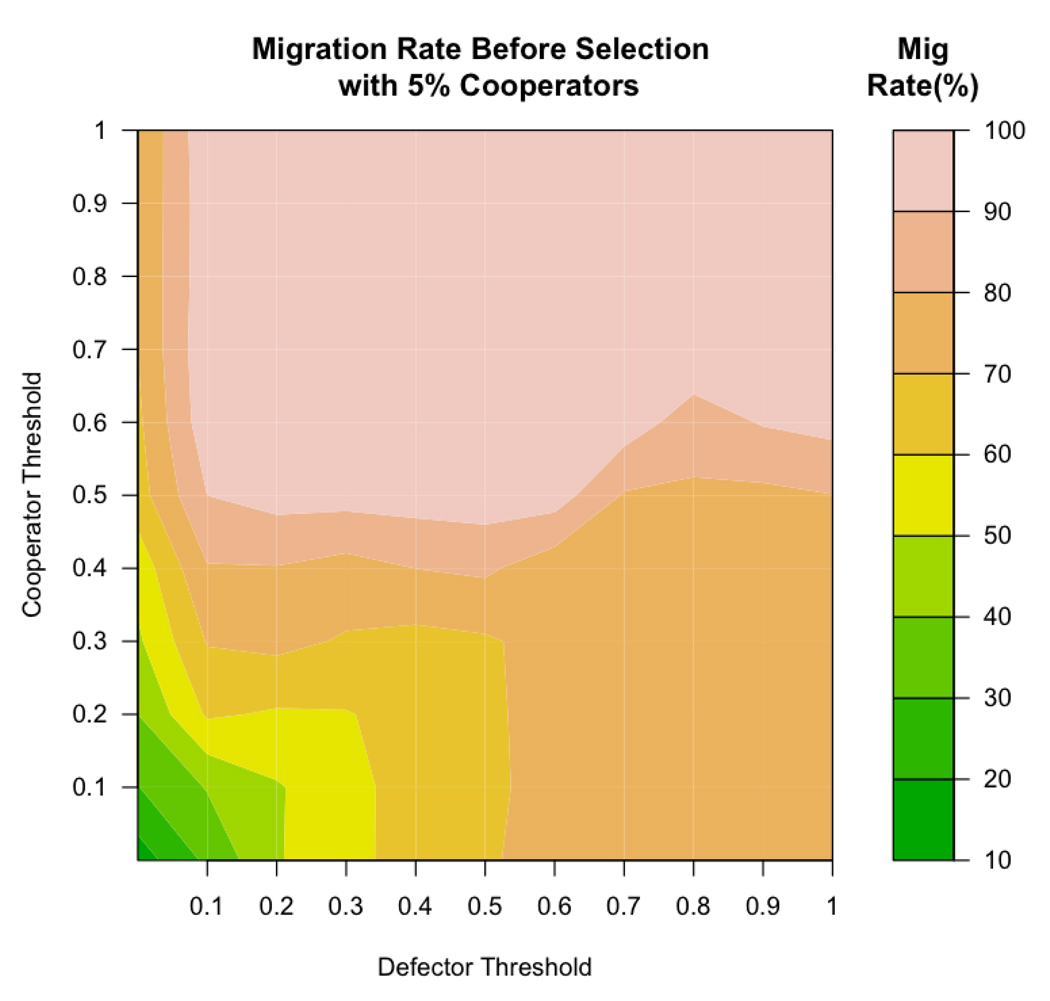
In order to establish a baseline for the rate of migration in the initial population, a set of simulations without reproduction and death were run for 1,000 time periods (long enough for the migration rate to reach equilibrium) with 5% cooperators and 95% defectors. The emergent migration rate at each combination of cooperator and defector thresholds is reported in Figure 5. Note that the lowest migration rates emerged when agents had low thresholds (when agents were more tolerant of low levels of cooperation). Very high levels of migration resulted when agents, especially cooperators, had high thresholds.
Figure 5.
These results from non-evolutionary runs show that migration rates before selection are very high for most cooperator and defector thresholds when the proportion of cooperators is 5% (the starting proportion for all simulations reported in this paper).
Interestingly, it is exactly the regions with high initial migration rates in Figure 5 (70 – 99% migration) in which the evolution of cooperation was favored in earlier reported runs (compare to Figure 4a). This is in contrast to the results of traditional analytical models that show that high migration does not allow cooperation to evolve (Maynard Smith, 1964; Wright, 1931). In the present simulations, high migration rate is not a barrier to the evolution of cooperation; instead it is a population-level manifestation of high thresholds. Interestingly, it is exactly the high thresholds of these agents that both result in an initially high migration r ate and enable cooperation to be selected in the long term.
Emergent migration rate after selection (with death and reproduction)
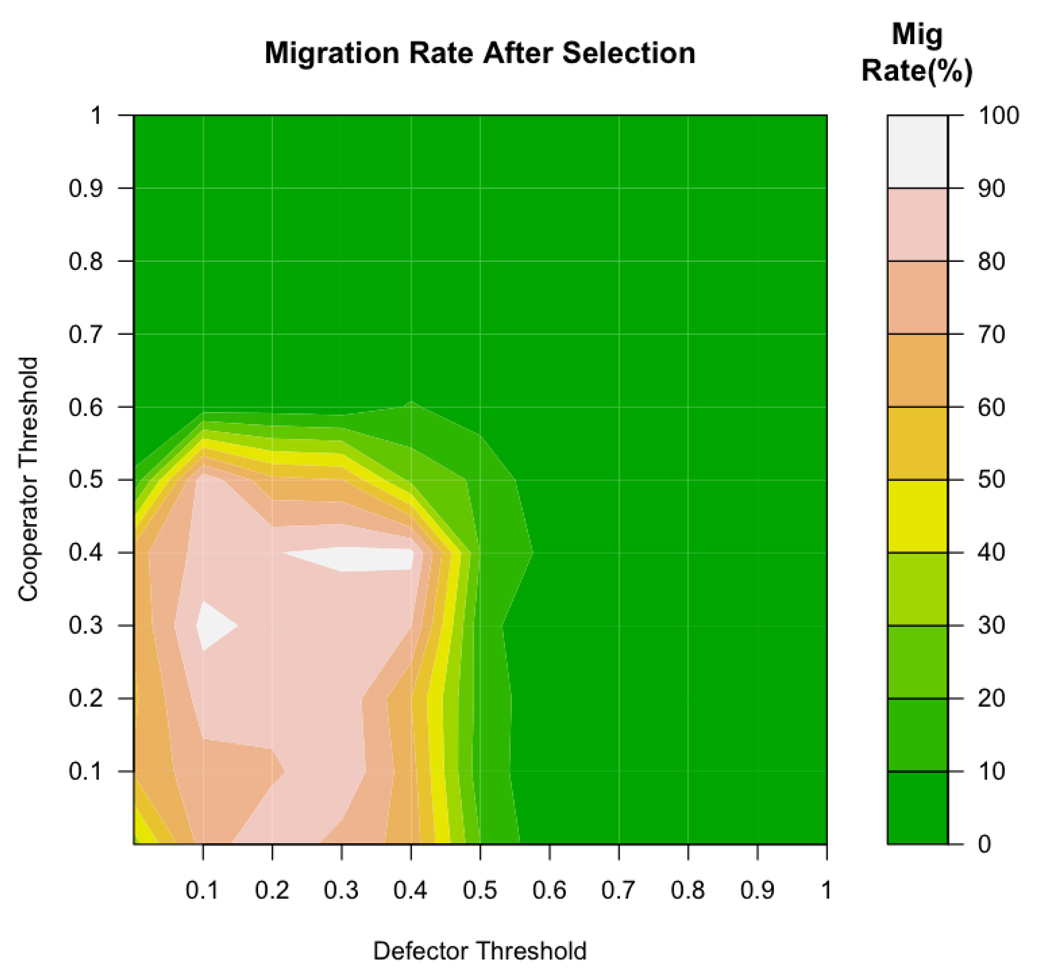
Adding the evolutionary elements of reproduction and death led to selection for cooperators over much of the parameter space (as described in earlier sections). As the proportion of cooperators increased, groups became on average more cooperative, leading to less Walking Away and therefore a lower emergent migration rate. Figure 6 shows this emergent migration rate after selection has acted for 50,000 time periods.
Figure 6.
In evolutionary simulations, migration rate patterns are nearly opposite to those present before the action of selection (see Figure 5). When agents have low thresholds, final migration rate is high because defectors dominate. When the thresholds of either cooperators or defectors are high, relatively low rates of migration result because cooperators come to dominate the population.
Interestingly, the regions with higher initial rates of migration (Figure 5) had lower final rates of migration in the evolutionary simulations (Figure 6). As noted above, cooperators were actually selected more strongly over the region where emergent migration rates were high. Once cooperators were selected, the migration rate decreased because more cooperative groups led to fewer agents ‘Walking Away’ in the overall population.
The results presented above suggest that the rate of migration itself is less important than the reasons for that migration. To the extent that migration occurs as a result of conditional movement away from uncooperative groups, high levels apparently do not restrict the evolution of cooperation.
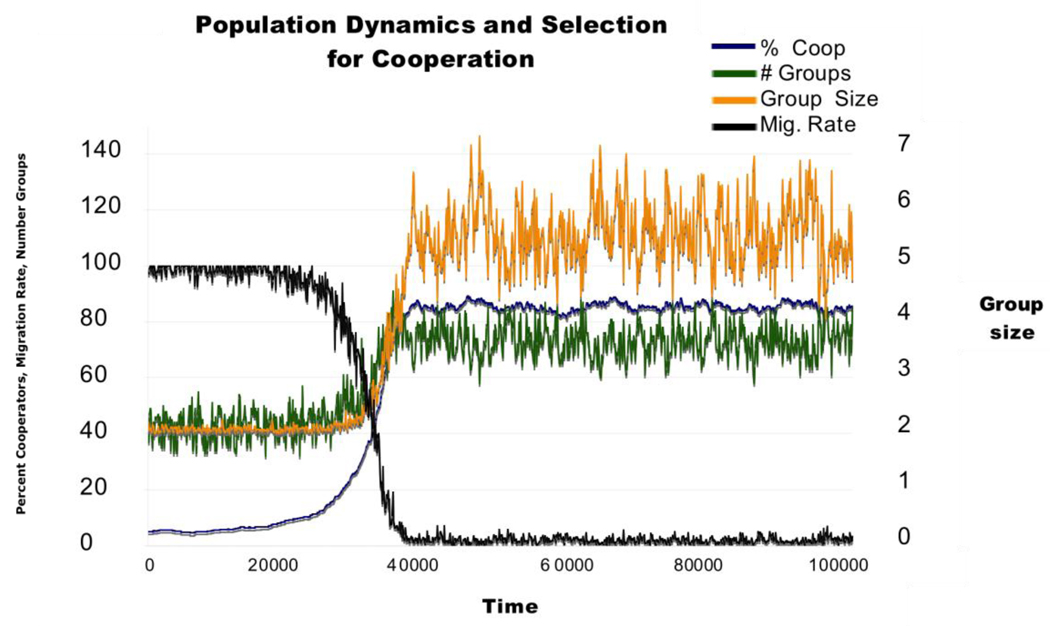
This can also be seen in Figure 7, which shows the changes over time in a typical run (with agents having thresholds of .7) and in the two screen shots illustrating the spatial structure before (Figure 8a) and after (Figure 8b) the evolutionary transition from low to high levels of cooperation. This evolutionary transition is accompanied by a transition in spatial structure from high rates of migration with mostly moving individuals and occasional small, ephemeral groups to low rates of movement with larger and more stable groups. These large groups are stable as long as the proportion of cooperators remains above the staying threshold of the agents within that group. As within group selection favors defectors, this leads groups to dissolve, generating periods of increased migration, new group formation, and positive assortment. This dynamic helps to maintain cooperation despite within group selection favoring defectors
Figure 7.
The evolutionary transition from low to high levels of cooperation (blue line) is mirrored by a spatial transition from high to low rates of migration (black line), more groups (green line) and larger group size (yellow line). This plot shows the changes in each variable over the first 100,000 time periods of a run with cooperator and defector thresholds of 0.7. Percent cooperators, migration rate and number of groups are indicated on the left axis and group size is indicated on the right axis.
Figure 8.
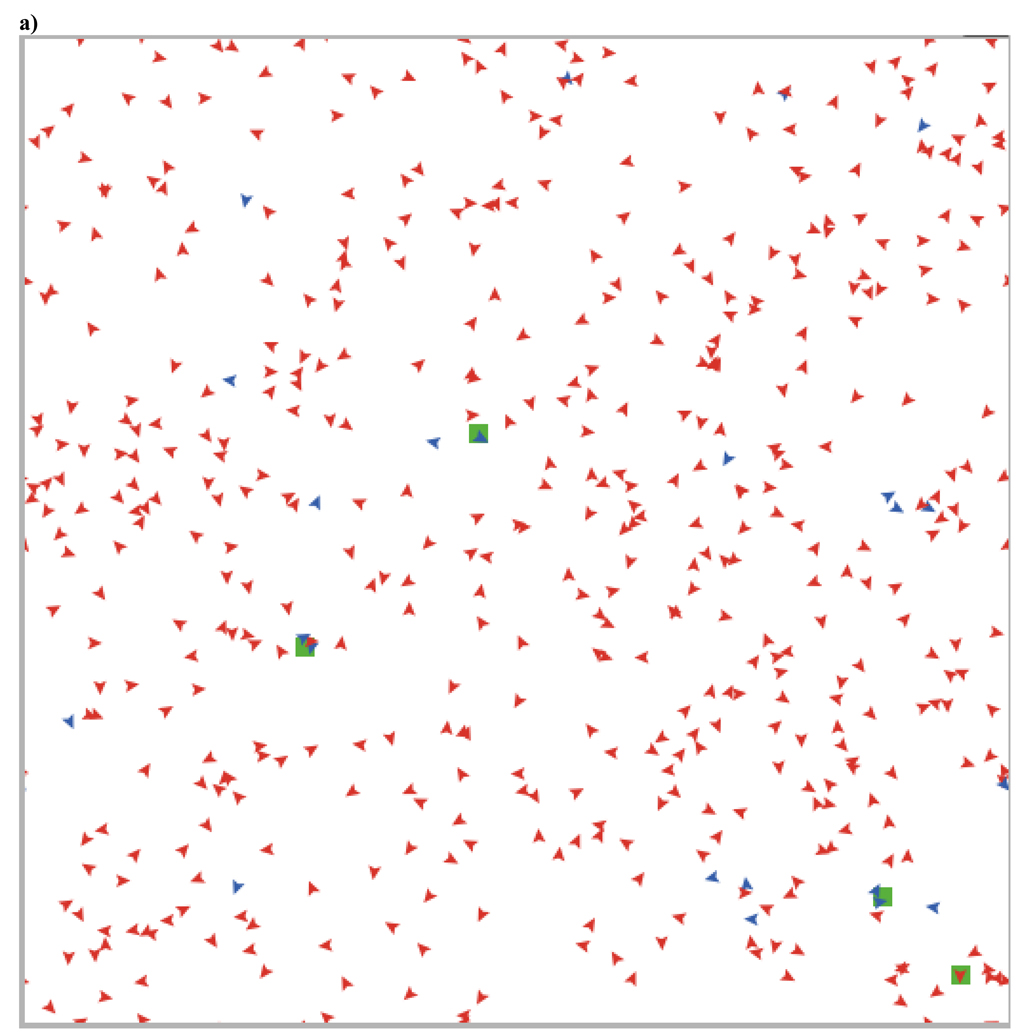
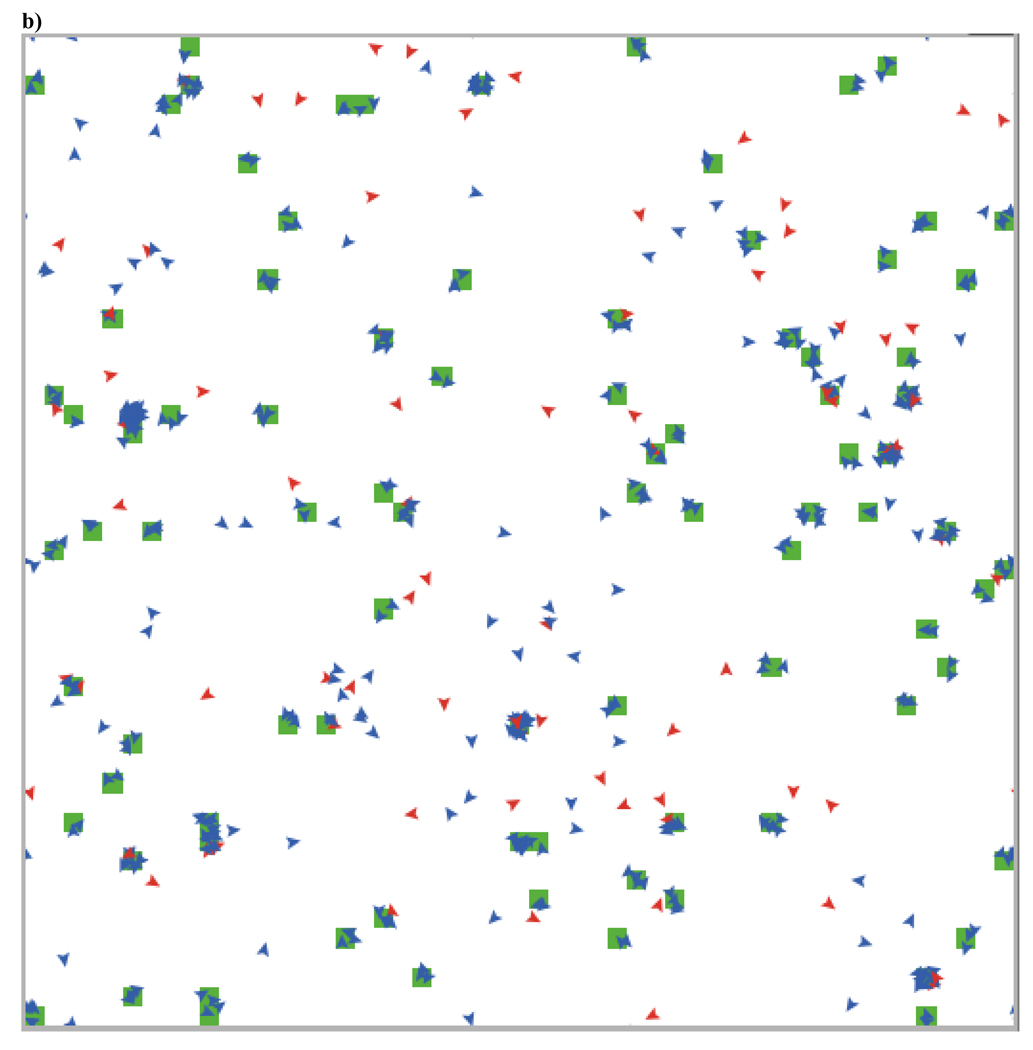
a) This screen shot from 200 time periods into a run with agents having thresholds of .7 shows the initial state of the population. Simulations begin with 95% defectors (red), and the proportion of cooperators (blue) remains low for many time periods. Initially, most agents are moving and the minority are in groups that last longer than one time period (indicated by the green patch color). Groups of cooperators tend to be more stable than groups of defectors, leading cooperators to preferentially interact with one another (i.e., assort). This generates positive selection for cooperators. b) After 40,000 time periods, cooperators make up the vast majority of the population and most agents are in long-lasting groups. These groups remain stable as long as the proportion of cooperators in that group is above .7. This instability of groups with increasing proportions of defectors results in new group formation and competition between these groups, which maintains cooperators in high proportions indefinitely.
Discussion
The findings of this paper can be considered within the broader work on the evolution of cooperation and dispersal/mobility. In historical models of group selection, including Maynard Smith’s haystack model (1964), Wright’s island model (1931) and models based on the Price equation (1970), too much migration or mixing undermines assortment, leading to selection for defectors. However, conditional movement can actually increase assortment, as demonstrated by Pepper (2007), leading to the unexpected finding that high rates of move ment can actually generate strong selection for cooperation.
Despite surface level similarities to reciprocity models, Walk Away is critically different in that agents do not possess the ability to remember outcomes of previous rounds or change from cooperation to defection. Walk Away promotes cooperation for a different reason: it amplifies existing assortment due to genetic identity by descent (i.e., kinship) through its effects on group stability. Through simple, decentralized processes, it leads to the dissolution of groups as within-group competition increases and it increases between-group competition by amplifying assortment within groups. This allows cooperation to be selected even when there are very high rates of migration and agents do not possess complex cognitive abilities.
It has been shown that periodic group reformation events, in which all individuals are randomly redistributed to groups, can favor altruism when they occur as defectors are just beginning to invade altruistic groups (Fletcher & Zwick, 2004; Fletcher & Zwick, 2007). The Walk Away rule presented here can promote the effective timing of these group reformation events without centralized control; the groups simply dissolve as levels of defection rise and agents leave.
In a recent widely received paper on the evolution of eusociality, Nowak, Tarnita and Wilson (2010) argue that the evolution of eusociality should be understood not in terms of kin selection, but instead as a series of steps beginning with “the formation of groups within a freely mixing population.” According to their model, traits that improve the quality of the local/shared environment are then selected, and finally a reduction in dispersal evolves which creates the kin structure characteristic of eusocial colonies. Although their model describes dispersal as a non-conditional trait, conditional movement may play an important role in the process that are described as underling this transition to eusociality. In the Walk Away model, a shift to more cohesive and persistent groups (Figure 8) is driven by improved quality of the returns from the public good, accomplishing the first step of increased “cohesion and persistence,” as well as increasing selection favoring cooperation (driven by the assortative effects of the Walk Away strategy) and finally reducing the likelihood of dispersal. This suggests that Walk Away dynamics might contribute both to the proximate and ultimate mechanisms underlying changes in population structure and cooperation in the transition to eusociality.
Given the complex dynamics underlying this model, what conclusion can be drawn about the underlying relationship between migration rate and cooperation? The results of this model show that there is not a simple underlying relationship between the two. Migration rate emerges from both the current level of cooperation and the agents’ thresholds, with migration rate being high when agents regularly encounter groups with insufficient levels of cooperation (lower than their thresholds). If agents spend most of their time in groups with sufficient levels of cooperation (equal or greater than their thresholds) then migration rate will be low. This means that the migration rate can tell an observer about the mismatch between agents ‘expectations’ (i.e., thresholds) for cooperation and the actual level of cooperation they encounter, but it cannot give direct information about the level of cooperation or the threshold that agents have. However, because conditional movement promotes assortment (Pepper, 2007), finding high rates of movement may be able to tell us that selection is currently favoring cooperation.
Individual mobility plays an important role in a variety of processes studied by behavioral ecologists and sociobiologists including foraging, individual dispersal and large-scale migration. Although it is a challenge to use modeling results to inform observational work, the results of this model do suggest that the use of conditional (rather than unconditional/probabilistic) movement should be explored and ascertained in populations that are the subject of field study. This may be done by examining the factors that induce individuals to leave their current social group and disperse/join new groups. If individuals exhibit conditional movement in response to the quality of the social environment or components of the physical environment that are socially determined, this would indicate that the population is or has the potential to be a Walk Away population. One example of a Walk Away population are water striders, aquarius remigis. Female water striders avoid interactions with highly aggressive males by refusing to mate, hiding or leaving pools with aggressive males (as reviewed by Eldakar et al. 2010). This free movement increases the variation in male aggressiveness among groups (Eldakar et al. 2009a; Eldakar et al. 2010), which can lead to higher overall fitness of less aggressive males (Eldakar et al. 2009b).
In general, if individuals in a natural population exhibit conditional movement in response to social conditions as water striders do, it is reasonable to hypothesize that this conditional movement may be leading to selection for more cooperative social traits. If high rates of movement are observed in these populations, this may be an indication that selection is actively favoring cooperative traits via the effects of conditional movement on assortment (Pepper 2007). The construction of specific Walk Away models based on the underlying features of the population being studied (e.g., the thresholds, cooperation/consumpt ion levels and population structure) are an additional option for researchers interested in the effects of conditional movement on social evolution in their species of study. This is an important direction for future work and I welcome collaborations along these lines.
Limitations to Walk Away
There are, however, limitations to the capacity of conditional movement to promote the evolution of cooperation. The present results suggest that when individuals have low thresholds and are therefore relatively ‘tolerant’ of defectors, defectors can continue to persist in the population. Selection for cooperation in this model relies on individuals who are ‘picky’ about the groups they will or will not remain members of. Interestingly, intolerance of defection leads to an initial populations structure with mostly loners, similar to the “wall flower ecology” observed in (Ashlock et al., 1996), but the long term effect of intolerance for defection is a final population made up of highly cooperative agents interacting in relatively large groups.
Another limitation of conditional movement for promoting cooperation has been shown in previous work- the necessity of relatively high search times for new partners. Enquist and Leimar’s (1993) excellent and systematic analysis of the effects of varying search time clearly demonstrates that low search times tip the scales in favor of defectors. Similarly, low densities can generate higher search times, limiting the viability of conditional movement (Aktipis, 2004). When search time for new group or partners is very low, conditional movement rules do not favor cooperation as strongly because defectors are more easily able to move on to new regions or groups after exploiting their current group.
Yet another limitation of conditional movement for promoting cooperation is that it must be useable by cooperators, not just defectors. If conditional movement is employed only by defectors (and cooperators do not move conditionally), defectors are, unsurprisingly, successful (Dugatkin & Wilson, 1992). Along similar lines, preliminary results from a variation of the present model suggest that the thresholds of defectors may evolve more quickly than the thresholds of cooperators, perhaps allowing defectors to more readily take advantage of cooperators.
Walk Away in human social evolution
It has been suggested that the ability to leave current partners and seek out new ones might have played an important role in cooperative behaviors in humans and other animals (Connor, 1992; Noe & Hammerstein, 1994; Nesse 2009). In humans, it has been shown that humans use something like a Walk Away strategy when given the opportunity in experimental economics settings (Barclay & Willer, 2007; Boone & Macy, 1999; Hauk, 1999; Orbell & Dawes, 1993; Yamagishi & Hayashi, 1996). To the extent that humans do use such a strategy in the laboratory, this suggests that something like Walk Away might have played a role in the evolution of cooperation in humans.
However, the effectiveness of Walk Away is likely to be constrained by a variety of behavioral and cognitive systems that may have evolved for the purposes of modifying conditional movement rules, especially in organisms with complex social adaptations such as humans. For instance, the ability to enter into commitments (Nesse, 2001) and bond with others (Carter et al., 2006) could be considered systems that constrain Walk Away behavior in oneself and others in circumstances where it may be beneficial to stay in the face of immediate costs, or to induce others to do so. Other factors such as the threat of punishment certainly can serve as deterrents to leaving. Also, it is not uncommon for social, cultural and political institutions to constrain the ability of individuals to leave their current groups. To the extent that humans use a Walk Away-type rule, it is likely to be buried beneath a host of complex cognitive rules and behaviors. These complex rules might, however, be built upon a very simple and evolutionarily ancient foundation, to Walk Away from low quality social environments. The results of this conditional movement model have other potentially important implications for human social evolution. It has previously been assumed that migration rates among early human groups were too high to allow for sufficient levels of genetic assortment for cooperation to favored via between-group selection (Brown & Armelagos, 2001; Richerson & Boyd, 1998). However, if movement is conditional, as in the Walk Away strategy, this can increase positive assortment, rather than decreasing it. If humans used a strategy like Walk Away when deciding whether or not to migrate from one group to another, this would have increased assortment, making between-group selection a viable force in human social evolution. Because high rates of movement can promote assortment, the potential role of between-group selection in human social evolution cannot be dismissed (as it has been) on the grounds that there was ‘too much’ migration between groups and ‘too little’ stability of groups. Indeed, the results of the present model demonstrate that cooperation can be selected under very high migration rates and very low stability of groups.
Walk Away in unicellular entities
The Walk Away rule is important for other reasons as well: it is simple, viable in contexts with limited information, evolutionarily ancient and phylogenetially widespread, playing a role in foraging behavior (MacArthur & Pianka, 1966) and processes such as chemotaxis (Glagolev, 1984; Koshland, 1980). It might therefore underlie the evolution of cooperation in a variety of species with low cognitive complexity and high rates of mobility.
Evidence also suggests that cancer cells are capable of leaving degraded environments through switching from a more sedentary (epithelial) phenotype to a motile (mesenchymal) phenotype. This transition is induced by low levels of oxygen (i.e., hypoxia) which upregulates HIF-1, causing a variety of changes in cell architecture that enable it to leave its local environment and move quickly through tissue (Harris, 2002; Lester et al., 2005; Li et al., 2009; Semenza, 2009). These hypoxia induced processes may enable cancer cells to conditionally leave regions with ‘exploitative’ cells that consume high levels of oxygen and/or produce low levels of angiogenic factors (‘public goods’ that induce the formation of new blood vessels). This may lead to cycles of invasion and metastasis as cancer cells degrade their local somatic environments. Depending on the population structure of cells within the neoplasm (i.e., density, genetic heterogeneity, group structure) this Walk Away process could actually lead somatic evolution to favor cancer cells that cooperate with their local ‘group’ to more effectively extract resources from their host and/or more effectively compete with other aggregations of cells.
These implications are worthy of further study as it is already known that somatic evolutionary dynamics underlie neoplastic progression (Merlo et al., 2006; Nowell, 1976; Pepper et al., 2009) and that the local microenvironment of tumors influences the evolution of cell motility and other behavioral phenotypes (Anderson et al., 2006; Anderson et al., 2009; Gerlee & Anderson, 2009; Polyak et al., 2009). Further, restoration of oxygen (i.e., improvement of the local microenvironment) has been shown to limit cell motility and metastasis (Mazzone et al., 2009), strongly suggesting that conditional cell movement is a contributing factor in metastasis. In collaboration with other computational biologists and cancer researchers, I have begun to explore the role of conditional movement in dynamics of cancer progression and determine whether feedback between cell motility and the quality of the tumor microenvironment influences the underlying spatial and evolutionary dynamics. This work will employ a variety of methods including evolutionary spatial models based on realistic assumptions about neoplastic cells, somatic phylogeography of tissue samples, assays of tissue samples to assess hypoxia and other components of degraded microenvironment, intra-vital microscopy to observe cell motility in animal models, and gene expression studies to detect the signatures of motile cells (e.g., using RNA fluorescent in situ hybridization). Future simulations should allow for testing the viability of different proposed interventions on environmentally induced cell motility with the goal of reducing the likelihood of invasion and metastasis in patients with cancer.
Conclusions
Conditional movement is cognitively simple, evolutionarily ancient and widespread across biological systems, making its inclusion in models of cooperation necessary if we are to understand the evolution of social behavior in organisms capable of responding to their local environments. The results of the simulations reported here demonstrate that a simple conditional movement rule, Walk Away, can promote the evolution of cooperation in groups. The Walk Away rule (in contrast to unconditional movement) leads to greater stability of more cooperative groups, generating assortment and positive selection for cooperation. Perhaps even more importantly, the present simulations suggest that conditional movement in the form of a very simple Walk Away strategy can favor the evolution of cooperation, even at high rates of movement/migration. The Walk Away model, and models of conditional movement more generally, may aid our understanding the evolution of social behavior and the emergence of mobility in a variety of biological systems. Future work will investigate the roles of processes such as commitment and bonding that may act to modify Walk Away rules in more complex cognitive organisms. Further, specialized conditional movement models are being developed to investigate the implications of environmentally induced cell motility in cancer.
Table 1.
Overview of state variables associated with each type of entity. Bold indicates the independent variable and arrows indicate dependent variables.
| Entity | State variable | Description |
|---|---|---|
| Global | • Social benefit Multiplier | Amount by which agents’ contribution to the local public good are multiplied before being distributed to all local residents |
| • R-probability | Probability per time step that one agent (whose energy is above R-threshold) will reproduce | |
| • R-threshold | Minimum energy required for agent to reproduce | |
| • Population size | Number of agents | |
| ➢ Proportion cooperators | The proportion of cooperators in the total population | |
| ➢ Migration rate | The emergent rate of migration that results from individual movement decisions | |
| • | ||
| Patches | • Location | Coordinates of the patch |
| • Resource | Amount of resources available on patch | |
| Agents | • Public good behavior | Either cooperation (investment in public good) or defection (free riding) |
| • Staying threshold | The payoff required from local public goods interaction for agent to stay in current location | |
| • Energy | Amount of energy accumulated by agent through payoffs from public goods interactions | |
| • Heading | Direction of agent movement | |
| • Location | Coordinates of agent | |
Table 2.
Initial and default values for all variables. Bold indicates the independent variable and arrows indicate dependent variables.
| Entity | State variable | Initial/Default Value | Units |
|---|---|---|---|
| Global | • Social benefit multiplier | 1.9 | N/A |
| • R-probability | .002 | probability | |
| • R-threshold | 1000 | energy | |
| • Population size | 500 | count | |
| ➢ Proportion cooperators | .05 | proportion | |
| ➢ Migration rate | 0 | rate per time | |
| • | |||
| Patches | • Location | (−25 – 25, −25 – 25) | coordinates |
| • Resource | 0 | energy | |
| Agents | • Public good behavior | C or D | |
| • Staying threshold | N/A | ||
| • Energy | Uniform between 0–2000 | energy | |
| • Heading | Random between 0–359 | degrees | |
| • Location | Random coordinates | Continuous | |
Acknowledgements
Thank you to John Pepper, Carlo Maley, Matthew Herron and Robert Kurzban for helpful comments on earlier drafts of this paper. This project was supported by a NSF Graduate Research Fellowship a nd National Cancer Institute grants F32CA144331 and R01CA140657.
Appendix A: Model Description
Purpose
This model was developed to explore the conditions under which the ‘Walk Away’ strategy promotes the evolution of cooperation and describe the aggregate migration patterns that emerge from a population of agents using the Walk Away strategy.
State variables and scales
In this model, time and space are both represented discretely. During each time period, agents and ‘patches’ (lattice locations) execute the commands described in the schedule. Space is represented as discrete locations in a 2-dimensional 51×51 lattice. Agents interact in public goods games with agents on the same lattice location. All movement is determined by individual-level decisions of agents to leave insufficiently cooperative groups.
Process overview and scheduling
This model proceeds in discrete time steps, and entities execute procedures according to the following ordering:
- AGENTS contribute to local patch public good game or free ride. This procedure runs only if there is at least one additional agent on the present patch.
- If a cooperator/contributor, transfer 1 unit of energy to patch
- If a defector/free rider, do not transfer energy to patch
- PATCHES multiply total contributions according to social benefit multiplier
- Total contributions amount to the total number of units of energy transferred from resident agents
- AGENTS:
- Play public goods game
- Cooperators place a unit of energy on patch, contributing to the public good, defectors do not
- Total contribution is multiplied by the multiplier (1.9)
- Resultant energy is divided equally among members of the group (all agents in current patch)
- Defectors get a net payoff of 1.9 * proportion cooperators in current group, cooperators get this same net payoff minus 1 because of their initial contribution to the public good.
- Move if payoff received is less than threshold or if there are no other agents on the current patch
- Movement entails the agent moving forward one unit in space in the direction of the current heading
- When a gent moves forward one step, heading is changed to the right up to 10 degrees in a uniform distribution and then to the left in the same fashion
- Global POPULATION processes:
- According to R-probability (the aggregate reproduction rate), one agent is given the opportunity to reproduce and does so according to R1 or R2:
-
R1.Threshold-based: if energy above R-threshold (fixed)
-
R2.Proportional to energy: if energy is above a random number chosen from a uniform distribution between 0 and 2* R-threshold
-
R1.
- If number of total agents exceeds max-population, a random agent dies
Design concepts
Emergence
Group size, the number of groups, the stability of groups and the migration rate emerge from the individual-level movement decisions of the agents. Because agents leave insufficiently cooperative groups, higher rates of migration emerge when cooperative agents are rare and agents are intolerant of defectors (i.e., they have a high staying threshold).
Evolutionary adaptation
The only trait that evolution acts on in this model is cooperation/contribution to the public good. The staying threshold of agents is varied among runs (independently for cooperators and defectors), but does not change within runs.
Fitness
Fitness is modeled impl icitly through differential survival and reproduction due to accumulation of energy/payoffs from public goods interactions.
Prediction
Agents lack the ability to predict outcomes of future interactions or integrate information across time periods
Sensing
Agents know only the payoff they received from the most recent public goods interaction on their local patch and have no information about payoffs in neighbouring groups or from past time steps.
Interaction
Agents interact in public goods games only with those on the same patch (i.e., lattice location).
Stochasticity
Decisions to move are guided by agents’ thresholds. In some conditions there is no stochasticity in movement decisions, and in others there is a high or low level noise. Further, direction of movement is stochastic (with small changes to the heading each time period) and components of the reproduction and death algorithms are stochastic.
Collectives
Agents occupying the same patch constitute a group and participate in public goods games, affecting each others’ fitness through these interactions.
Observation
Simulations were run for 50,000 time steps unless otherwise noted. The proportion of cooperators is measured in the final time step. Because there is high variability between time steps in migration events, the average rate of migration over the final 100 time periods of runs is used, and migration is calculated as the rate of emigration from groups (the number of agents leaving divided by the number agents leaving and staying).
Initialization
All runs were initialized according to default parameters in the table below. Agents were randomly placed on the lattice, no groups were explicitly created at the beginning of runs. Cooperator and defector staying thresholds were varied independently among runs.
Appendix B: Generalizability
Threshold-based vs. proportional reproduction
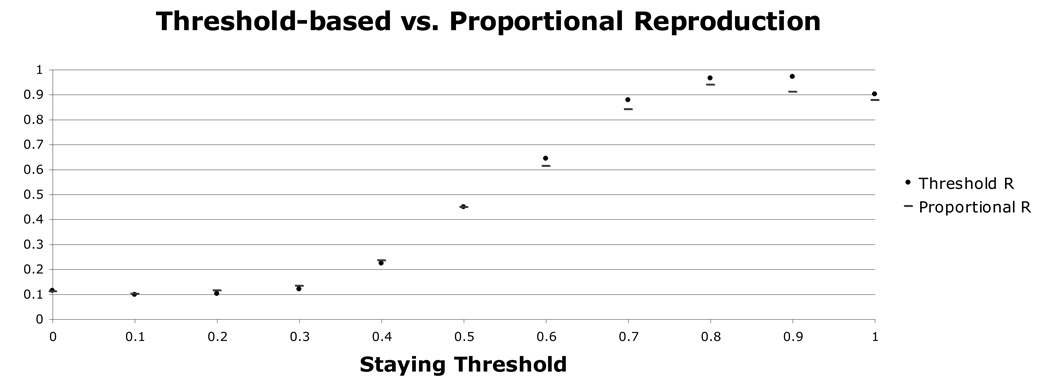
In the model results reported in the primary text, reproduction was threshold based, i.e., agents had to accumulate a certain amount of energy (through payoffs from the public goods interactions) in order to have the opportunity to reproduce. Here, an alternative reproduction algorithm (R2) is compared to the threshold based reproduction algorithm (R1) in several abbreviated runs (5,000 time periods with initial proportion cooperators set to .5) in order to test whether the results generalize to other reproduction schemes. In the alternative reproduction scheme (R2), the likelihood of an agent’s reproducing was proportional to their current energy (rather than requiring energy to be above a threshold, as in R1). More specifically, in R2, reproduction occurred if energy level was above a random number chosen from a uniform distribution between 0 and 2* R-threshold (see Appendix A for more details). Figure 9 reports the proportion cooperators under both R1 and R2. These two reproduction algorithms generated similar outcomes; the difference in proportion cooperators between these two conditions was never more than .1 and was near 0 for most thresholds.
Figure 9.
Altering the reproduction algorithm has little effect on the outcome of the simulations. High staying thresholds lead to high proportions of cooperators for both threshold based and proportional reproduction algorithms.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
A multiplier of 2 is typically used in public goods games because it generates a social dilemma in the group sizes typically used. However, this multiplier does not generate a social dilemma when there are only two individuals in a group. For this reason, a multiplier of 1.9 was used.
Bibliography
- Aktipis CA. Know when to walk away: contingent movement and the evolution of cooperation in groups. Journal of Theoretical Biology. 2004;231:249–260. doi: 10.1016/j.jtbi.2004.06.020. [DOI] [PubMed] [Google Scholar]
- Aktipis CA. Recognition memory and the evolution of cooperation: how simple strategies succeed in an agent-based world. Adaptive Behavior. 2006;14:239–247. [Google Scholar]
- Aktipis CA. Dissertation. University of Pennsylvania; 2008. When to Walk Away and when to stay: cooperation evolves when agents can leave unproductive partners and groups. [Google Scholar]
- Anderson A, Rejniak KA, Gerlee P, Quaranta V. Microenvironment driven invasion: a multiscale multimodel investigation. Journal of Mathematical Biology. 2009;58:579–624. doi: 10.1007/s00285-008-0210-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson A, Weaver A, Cummings P, Quaranta V. Tumor morphology and phenotypic evolution driven by selective pressure from the microenvironment. Cell. 2006;127:905–915. doi: 10.1016/j.cell.2006.09.042. [DOI] [PubMed] [Google Scholar]
- Ashlock D, Smucker MD, Stanley EA, Tesfatsion L. Preferential partner selection in an evolutionary study of Prisoner's Dilemma. Molecular Biosystems. 1996;37:99–125. doi: 10.1016/0303-2647(95)01548-5. [DOI] [PubMed] [Google Scholar]
- Avilés L. Cooperation, nonli near dynamics and the levels of selection. presented at The Second International Conference on Complex Systems; Nashua, NN. 1998. [Google Scholar]
- Avilés L. Solving the freeloaders paradox: genetic associations and frequency-dependent selection in the evolution of cooperation among nonrelatives. Proceedings of the National Academy of Sciences. 2002;99:14268–14273. doi: 10.1073/pnas.212408299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Axelrod R. The evolution of cooperation. New York: Basic Books; 1984. [Google Scholar]
- Axelrod R. The complexity of cooperation: Agent-based models of competition and collaboration. Princeton: Princeton University Press; 1997. [Google Scholar]
- Axelrod R, Hamilton WD. The evolution of cooperation. Science. 1981;211:1390–1396. doi: 10.1126/science.7466396. [DOI] [PubMed] [Google Scholar]
- Barclay P, Willer R. Partner choice creates competitive altruism in humans. Proceedings of the Royal Society of London, Series B. 2007;274:749–753. doi: 10.1098/rspb.2006.0209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergmüller R, Johnstone RA, Russell AF, Bshary R. Integrating cooperative breeding into theoretical concepts of cooperation. Behavioural Processes. 2007;76:61–72. doi: 10.1016/j.beproc.2007.07.001. [DOI] [PubMed] [Google Scholar]
- Boone RT, Macy MW. Unlocking the doors to prisoner's dilemma: dependence, selectivity, and cooperation. Social Psychology Quarterly. 1999;62:32–52. [Google Scholar]
- Brandt H, Hauert C, Sigmund K. Punishing and abstaining for public goods. Proc Natl Acad of Sci USA. 2006;103:495–497. doi: 10.1073/pnas.0507229103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown RA, Armelagos GJ. Apportionment of racial diversity: a review. Evolutionary Anthropology. 2001;10:34–40. [Google Scholar]
- Bull JJ, Rice WR. Distinguishing mechanisms for the evolution of cooperation. J of Theoretical Biology. 1991;149:63–74. doi: 10.1016/s0022-5193(05)80072-4. [DOI] [PubMed] [Google Scholar]
- Buston PM, Balshine S. Cooperating in the face of uncertainty: A consistent framework for understanding the evolution of cooperation. Behavioural Processes. 2007;76:152–159. doi: 10.1016/j.beproc.2007.01.020. [DOI] [PubMed] [Google Scholar]
- Carter CS, Ahnert L, Grossmann KE, Hrdy SB, Lamb ME, Porges SW, Sachser N. Attachment and bonding: A new synthesis. The MIT Press; 2006. [Google Scholar]
- Connor RC. Egg-trading in simultaneous hermaphrodites: an alternative to Tit-for-Tat. J of Evolutionary Biology. 1992;5:523–528. [Google Scholar]
- Cox SJ, Sluckin TJ, Steele J. Group size, memory and the interaction rate in the evolution of cooperation. Current Anthropology. 1999;40:369–377. [Google Scholar]
- Dawkins R. The selfish gene. Oxford: Oxford University Press; 1976. [Google Scholar]
- Dugatkin LA, Wilson DS. Rover: A strategy for exploiting cooperators in a patchy environment. The American Naturalist. 1992;138:687–701. [Google Scholar]
- Durrett R, Levin S. The Importance of being discrete (and spatial) Theoretical Population Biology. 1994;46:394–363. [Google Scholar]
- Eldakar OT, Farrell DL, Wilson DS. Selfish punishment: Altruism can be maintained by competition among cheaters. J of Theoretical Biology. 2007;249:198–205. doi: 10.1016/j.jtbi.2007.07.024. [DOI] [PubMed] [Google Scholar]
- Eldakar OT, Wilson DS. Selfishness as second-order altruism. Proceedings of the National Academy of Sciences. 2008;105:6982–6986. doi: 10.1073/pnas.0712173105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eldakar OT, Dlugos MJ, Pepper JW, Wilson DS. Population structure mediates sexual conflict in water striders. Science. 2009a;326:816. doi: 10.1126/science.1180183. [DOI] [PubMed] [Google Scholar]
- Eldakar OT, Dlugos MJ, Wilcox RS, Wilson DS. Aggressive mating as a tragedy of the commons in the water strider. Aquarius remigis, Behavioral Ecology and Sociobiology. 2009b;64:25–33. [Google Scholar]
- Eldakar OT, Wilson DS, Dlugos MJ, Pepper JW. The role of multilevel selection in the evolution of sexual conflict in the water strider. Aquarius remigis, Evolution. 2010;64:3183–3189. doi: 10.1111/j.1558-5646.2010.01087.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- El Mouden C, Gardner A. Nice natives and mean migrants: the evolution of dispersal-dependent social behaviour in viscous populations. J of Evolutionary Biology. 2008;21:1480–1491. doi: 10.1111/j.1420-9101.2008.01614.x. [DOI] [PubMed] [Google Scholar]
- Enquist M, Leimar O. The evolution of cooperation in mobile organisms. Animal Behaviour. 1993;45:747–757. [Google Scholar]
- Fletcher JA, Zwick M. Strong altruism can evolve in randomly formed groups. J of Evolutionary Biology. 2004;228:303–313. doi: 10.1016/j.jtbi.2004.01.004. [DOI] [PubMed] [Google Scholar]
- Fletcher JA, Doebeli M. A simple and general explanation for the evolution of altruism. Proceedings of the Royal Society of London, Series B: Biol Sci. 2009;276:13–19. doi: 10.1098/rspb.2008.0829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fletcher JA, Zwick M. The evolution of altruism: Game theory in multilevel selection and inclusive fitness. J of Theoretical Biology. 2007;245:26–36. doi: 10.1016/j.jtbi.2006.09.030. [DOI] [PubMed] [Google Scholar]
- Friedman JW, Hammerstein P. To trade or not to trade; that is the question. In: Selten R, editor. Game Equilibrium Models I: Evolution and Game Dynamics. Berlin: Springer-Verlag; 1991. pp. 257–275. [Google Scholar]
- Gardner A, West SA. Demography, altruism, and the benefits of budding. J of Evolutionary Biology. 2006;19:1707–1716. doi: 10.1111/j.1420-9101.2006.01104.x. [DOI] [PubMed] [Google Scholar]
- Gerlee P, Anderson ARA. Evolution of cell motility in an individual-based model of tumour growth. J of Theoretical Biology. 2009;259:67–83. doi: 10.1016/j.jtbi.2009.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glagolev A. Motility and taxis in prokaryotes. Harwood Academic Publishers; 1984. [Google Scholar]
- Grafen A. Do animals really recognize kin? Animal Behaviour. 1990;39:42–54. [Google Scholar]
- Grimm V, Berger U, Bastiansen F, Eliassen S, Ginot V, Giske J, Goss-Custard J, Grand T, Heinz S, Huse G. A standard protocol for describing individual-based and agent-based models. Ecological Modelling. 2006;198:115–126. [Google Scholar]
- Grimm V, Railsback SF. Individual-based modeling and ecology. Princeton: Princeton University Press; 2005. [Google Scholar]
- Hamilton IM, Taborsky M. Contingent movement and cooperation evolve under generalized reciprocity. Proceedings of the Royal Society of London, Series B. 2005;272:2259–2267. doi: 10.1098/rspb.2005.3248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamilton WD. The genetical evolution of social behavior II. J of Theoretical Biology. 1964a;7:17–52. doi: 10.1016/0022-5193(64)90039-6. [DOI] [PubMed] [Google Scholar]
- Hamilton WD. The genetical evolution of social behavior I. J of Theoretical Biology. 1964b;7:1–16. doi: 10.1016/0022-5193(64)90038-4. [DOI] [PubMed] [Google Scholar]
- Hamilton WD. Selection of selfish and altruistic behavior in some extreme models. In: Eisenberg, Dillon, editors. Man & Beast: Comparative Social Behavior. Washington, DC: Smithsonian Press; 1971. [Google Scholar]
- Hamilton WD. Innate social aptitudes of man: an approach from evolutionary genetics. In: Fox R, editor. Biosocial Anthropology. London: John Wiley & Sons; 1975. pp. 133–155. [Google Scholar]
- Hammerstein P. Why is reciprocity so rare in social animals? A protestant appeal. In: Hammerstein P, editor. Genetic and cultural evolution of cooperation. United States of America: MIT and Freie Universität Berlin; 2003. pp. 83–93. [Google Scholar]
- Hammond RA, Axelrod R. Evolution of contingent altruism when cooperation is expensive. Theoretical Population Biology. 2006;69:333–338. doi: 10.1016/j.tpb.2005.12.002. [DOI] [PubMed] [Google Scholar]
- Harris A. Hypoxia--a key regulatory factor in tumour growth. Nat Rev Cancer. 2002;2:38–47. doi: 10.1038/nrc704. [DOI] [PubMed] [Google Scholar]
- Hauert C, De Monte S, Hofbauer J, Sigmund K. Volunteering as red queen mechanism for cooperation in public goods games. Science. 2002;296:1129. doi: 10.1126/science.1070582. [DOI] [PubMed] [Google Scholar]
- Hepper PG. Kin recognition. Cambridge, UK: Cambridge University Press; 1991. [Google Scholar]
- Holmes WG. The early history of Hamiltonian-based research on kin recognition. Annales Zoologici Fennici. 2004;41:691–711. [Google Scholar]
- Hutchinson JMC, Gigerenzer G. Simple heuristics and rules of thumb: where psychologists and behavioral biologists might meet. Behavioural Processes. 2005;69:97–124. doi: 10.1016/j.beproc.2005.02.019. [DOI] [PubMed] [Google Scholar]
- Johnstone RA. Kin Selection, Local Competition, and Reproductive Skew. Evolution. 2008;62:2592–2599. doi: 10.1111/j.1558-5646.2008.00480.x. [DOI] [PubMed] [Google Scholar]
- Komdeur J, Hatchwell B. Kin recognition: function and mechanism in avian societies. Trends in Ecology & Evolution. 1999;14:237–241. doi: 10.1016/s0169-5347(98)01573-0. [DOI] [PubMed] [Google Scholar]
- Koshland D. Bacterial chemotaxis as a model behavioral system. 1st ed. Raven Press (ID); 1980. [Google Scholar]
- Lehmann L, Perrin N, Rousset F. Population Demography and the Evolution of Helping Beaviors. Evolution. 2006;60:1137–1151. [PubMed] [Google Scholar]
- Lehmann L, Rousset F. How life history and demography promote or inhibit the evolution of helping behaviours. Phil. Trans. R. Soc. B. 2010;365:2599–2617. doi: 10.1098/rstb.2010.0138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lester R, Jo M, Campana W, Gonias S. Erythropoietin promotes MCF-7 breast cancer cell migration by an ERK/mitogen-activated protein kinase-dependent pathway and is primarily responsible for the increase in migration observed in hypoxia. J of Biological Chemistry. 2005;280:39273–39277. doi: 10.1074/jbc.M509446200. [DOI] [PubMed] [Google Scholar]
- Li Y, Qiu X, Zhang S, Zhang Q, Wang E. Hypoxia induced CCR7 expression via HIF-1alpha and HIF-2alpha correlates with migration and invasion in lung cancer cells. Cancer Biology and Therapy. 2009;8:322–330. doi: 10.4161/cbt.8.4.7332. [DOI] [PubMed] [Google Scholar]
- Lion S, Gandon S. Habitat saturation and the spatial evolutionary ecology of altruism. J of Evolutionary Biology. 2009;22:1487–1502. doi: 10.1111/j.1420-9101.2009.01769.x. [DOI] [PubMed] [Google Scholar]
- Lion S, Van Baalen M. Self-structuring in spatial evolutionary ecology. Ecology Letters. 2008;11:277–295. doi: 10.1111/j.1461-0248.2007.01132.x. [DOI] [PubMed] [Google Scholar]
- MacArthur RH, Pianka ER. On optimal use of a patchy environment. The American Naturalist. 1966;100:603. [Google Scholar]
- Marshall JAR, Rowe JE. Viscous populations and their support for reciprocal cooperation. Artificial Life. 2003;9:327–334. doi: 10.1162/106454603322392497. [DOI] [PubMed] [Google Scholar]
- Maynard Smith J. Group selection and kin selection. Nature. 1964;201:1145–1147. [Google Scholar]
- Mazzone M, Dettori D, Leite de Oliveira R, Loges S, Schmidt T, Jonckx B, Tian Y, Lanahan A, Pollard P, Ruiz de Almodovar C, et al. Heterozygous deficiency of PHD2 restores tumor oxygenation and inhibits metastasis via endothelial normalization. Cell. 2009;136:839–851. doi: 10.1016/j.cell.2009.01.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McNamara JM, Houston A. The application of statistical decision theory to animal behaviour. J of Theoretical Biology. 1980;85:673. doi: 10.1016/0022-5193(80)90265-9. [DOI] [PubMed] [Google Scholar]
- McNamara JM, Houston AI. Optimal foraging and learning. J of Theoretical Biology. 1985;117:231–249. [Google Scholar]
- Merlo L, Pepper JW, Reid B, Maley C. Cancer as an evolutionary and ecological process. Nature Reviews Cancer. 2006;6:924–935. doi: 10.1038/nrc2013. [DOI] [PubMed] [Google Scholar]
- Nesse RM. The Moral Brain. Netherlands: Springer; 2009. Runaway Social Selection for Displays of Partner Value and Altruism; pp. 211–231. [Google Scholar]
- Nesse RMM. Evolution and the capacity for commitment. Russell Sage Foundation Publications; 2001. [Google Scholar]
- Noe R, Hammerstein P. Biological markets: supply and demand determine the effect of parner choice in cooperation, mutualism and mating. Behavioral Ecology and Sociobiology. 1994;35:1–11. [Google Scholar]
- Nowak MA, Tarnita CE, Wilson EO. The evolution of eusociality. Nature. 2010;466:1057–1062. doi: 10.1038/nature09205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nowell P. The clonal evolution of tumor cell populations. Science. 1976;194:23–28. doi: 10.1126/science.959840. [DOI] [PubMed] [Google Scholar]
- Orbell JM, Schwartz-Shea P, Simmons RT. Do cooperators exit more readily than defectors? American Political Science Review. 1984;78:147–162. [Google Scholar]
- Pepper JW. Simple models of assortment through environmental feedback. Artificial Life. 2007;13:1–9. doi: 10.1162/artl.2007.13.1.1. [DOI] [PubMed] [Google Scholar]
- Pepper JW, Smuts BB. Dynamics in human and primate societies: agent-based modeling of social and spatial processes. Oxford University Press; 2000. The evolution of cooperation in an ecological context: an agent based model; pp. 45–76. Available from: http://portal.acm.org/citation.cfm?id=344762. [Google Scholar]
- Pepper JW, Smuts BB. A mechanism for the evolution of altruism among nonkin: positive assortment through environmental feedback. The American Naturalist. 2002;160:205–213. doi: 10.1086/341018. [DOI] [PubMed] [Google Scholar]
- Pepper J, Scott Findlay C, Kassen R, Spencer S, Maley C. Cancer research meets evolutionary biology. Evolutionary Applications. 2009;2:62–70. doi: 10.1111/j.1752-4571.2008.00063.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Platt TG, Bever JD. Kin competition and the evolution of cooperation. Trends in Ecology & Evolution. 2009;24:370–377. doi: 10.1016/j.tree.2009.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polyak K, Haviv I, Campbell IG. Co-evolution of tumor cells and their microenvironment. Trends In Genetics. 2009;25:30–38. doi: 10.1016/j.tig.2008.10.012. [DOI] [PubMed] [Google Scholar]
- Price GR. Selection and covariance. Nature. 1970;227:520–521. doi: 10.1038/227520a0. [DOI] [PubMed] [Google Scholar]
- Queller DC. Social evolution: Kinship is relative. Nature. 2004;430:975–976. doi: 10.1038/430975a. [DOI] [PubMed] [Google Scholar]
- Ramos-Fernández G, Boyer D, Gómez V. A complex social structure with fission-fusion properties can emerge from a simple foraging model. Behavioral Ecology and Sociobiology. 2006;60:536–549. [Google Scholar]
- Richerson P, Boyd R. The evolution of ultrasociality. In: Eibl-Eibesfeldt I, Salter FK, editors. Indoctrinability, ideology and warfare. New York: Berghahn Books; 1998. pp. 71–96. [Google Scholar]
- Sachs JL, Mueller UG, Wilcox TP, Bull JJ. The evolution of cooperation. The Quarterly Review of Biology. 2004;79:135–160. doi: 10.1086/383541. [DOI] [PubMed] [Google Scholar]
- Semenza GL. Defining the role of hypoxia-inducible factor 1 in cancer biology and therapeutics. Oncogene. 2009;29:625–634. doi: 10.1038/onc.2009.441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sorkin E. Chemotaxis: its biology and biochemistry. New York: S. Karger; 1974. [Google Scholar]
- Szabó G, Hauert C. Evolutionary prisoner's dilemma games with voluntary participation. Physical Review E. 2002;66:062903. doi: 10.1103/PhysRevE.66.062903. [DOI] [PubMed] [Google Scholar]
- Taylor P. Altruism in viscous populations – an inclusive fitness model. Evolutionary Ecology. 1992;6:352–356. [Google Scholar]
- Todd PM, Gigerenzer G. Bounding rationality to the world. Journal of Economic Psychology. 2003;24:143–165. [Google Scholar]
- Trivers RL. The evolution of reciprocal altruism. The Quarterly Review of Biology. 1971;46:35–57. [Google Scholar]
- Vanberg VJ, Congleton RD. Rationality, morality and exit. American Political Science Review. 1992;86:418–431. [Google Scholar]
- Vos HD, Zeggelink E. Reciprocal altruism in human social evolution: the viability of altruism with a preference for "old-helping-partners". Evolution and Human Behavior. 1994;18:261–278. [Google Scholar]
- Waite TA, Field KL. Foraging with others: Games social foragers play. In: Stephens DW, Brown JS, Ydenberg RC, editors. Foraging: Behavior and ecology. Chicago: University of Chicago Press; 2007. pp. 331–362. [Google Scholar]
- West SA, Griffin AS, Gardner A. Evolutionary explanations for cooperation. Current Biology. 2007;17:R661–R672. doi: 10.1016/j.cub.2007.06.004. [DOI] [PubMed] [Google Scholar]
- West SA, Pen I, Griffin AS. Cooperation and competition between relatives. Science. 2002;296:72–75. doi: 10.1126/science.1065507. [DOI] [PubMed] [Google Scholar]
- West-Eberhard MJ. Sexual Selection, Social Competition, and Evolution. Proceedings of the American Philosophical Society. 1979;123:222–234. [Google Scholar]
- Williams GC. Adaptation and natural selection. Princeton, NJ: Princeton University Press; 1966. [Google Scholar]
- Wilson DS. The group selection controversy: history and current status. Anuual Review of Ecology and Systematics. 1983;14:159–187. [Google Scholar]
- Wilson DS, Wilson EO. Rethinking the theoretical foundation of sociobiology. The Quarterly Review of Biology. 2007;82:327–348. doi: 10.1086/522809. [DOI] [PubMed] [Google Scholar]
- Wilson DS. Altruism in mendelian populations derived from sibling groups: the haystack model revisited. Evolution. 1987;41:1059–1070. doi: 10.1111/j.1558-5646.1987.tb05876.x. [DOI] [PubMed] [Google Scholar]
- Wright S. Evolution in mendelian populations. Genetics. 1931;16:97–159. doi: 10.1093/genetics/16.2.97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wynne-Edwards VC. Animal dispersion in relation to social behavior. New York: Hafner Publishing Co.; 1962. [Google Scholar]
- Yamagishi T, Hayashi N. Selective play: social embeddedness of social dilemmas. In: Liebrand W, Messick D, editors. Frontiers in Social Dilemma Research. Berlin: Springer; 1996. pp. 363–384. [Google Scholar]
- Yamagishi T, Hayashi N, Jin N. Prisoner's dilemma networks: Selection strategy versus action strategy. In: Schulz U, Albers W, Mueller U, editors. Social dilemmas and cooperation. Berlin: Springer-Verlag; 1994. pp. 233–250. [Google Scholar]