Monkeys (Macaca Mulatta and Cebus Apella) and Human Adults and Children (Homo Sapiens) Compare Subsets of Moving Stimuli Based on Numerosity

Abstract

Two monkey species (Macaca mulatta and Cebus apella) and human children and adults judged the numerousness of two subsets of moving stimuli on a computer screen. Two sets of colored dots that varied in number and size were intermixed in an array in which all dots moved in random directions and speeds. Participants had to indicate which dot color was more numerous within the array. All species performed at high and comparable levels, including on trials in which the subset with the larger number of items had a smaller total area of coloration. This indicated a similarity across species to use the number of items in the subsets, and not dimensions such as area or volume, to guide decision making. Discrimination performance was constrained by the ratio between the subsets, consistent with other reports of numerousness judgments of stationary stimuli. These results indicate a similarity in numerical estimation ability for moving stimuli across primate species, and this capacity may be necessary for naturally occurring experiences in which moving stimuli must be summed.

Introduction

Animals show an impressive collection of quantitative abilities. When presented with stimuli in a variety of formats, they can quantify and in some cases even enumerate those stimuli. For example, some animals show counting-like abilities as they label or create sets to match a cardinal value (e.g., Matsuzawa, 1985; Capaldi and Miller, 1988; Boysen and Berntson, 1989; Pepperberg, 1994, 2006; Boysen et al., 1995; Beran and Rumbaugh, 2001; Xia et al., 2001; Roberts et al., 2002; Tomonaga and Matsuzawa, 2002). Some animals are sensitive to arithmetic manipulations in which sets of items are increased or decreased in number through addition and subtraction of items (e.g., Boysen and Berntson, 1989; Call, 2000; Hauser et al., 2000; Beran, 2001, 2004; Sulkowski and Hauser, 2001; Beran and Beran, 2004; Flombaum et al., 2005). And, there is widespread phylogenetic evidence for so-called relative numerousness judgments in which two sets are compared on the basis of the quantities within them. A number of species have shown successful performance including great apes (Boysen and Berntson, 1995; Boysen et al., 1999; Anderson et al., 2005; Hanus and Call, 2007), monkeys (Thomas and Chase, 1980; Brannon and Terrace, 2000; Judge et al., 2005; Santos et al., 2005; Brannon et al., 2006; Cantlon and Brannon, 2006; Beran, 2007; Addessi et al., 2008; Evans et al., 2009), pigeons (Roberts and Mitchell, 1994; Emmerton et al., 1997; Emmerton, 1998), dolphins (Kilian et al., 2003; Jaakkola et al., 2005), parrots (Pepperberg, 2006; Aïn et al., 2009), horses (Uller and Lewis, 2009), dogs (Ward and Smuts, 2007), voles (Ferkin et al., 2005), fish (Dadda et al., 2009), and salamanders (Uller et al., 2003).

Within the set of studies that involve judgments between sets of stimuli, however, there must be a distinction made between those studies that require animals to discriminate the number of items from those studies that afford other stimulus properties that could successfully guide performance. For example, many studies have used homogeneous food items as the stimuli to be discriminated (e.g., Beran, 2001, 2004; Hanus and Call, 2007; Aïn et al., 2009; Evans et al., 2009), and this allows the animal to make the quantity judgment using the total amount of stimuli rather than the number of stimuli. Other studies control for non-numerical properties, so that quantity judgments must be made on the basis of the number of items in sets, and some species succeed in these tests showing that their judgments are truly numerical and could be rightly called numerousness judgments (e.g., Brannon and Terrace, 2000; Judge et al., 2005; Emmerton and Renner, 2006; Jordan and Brannon, 2006a; Beran, 2007; Tomonaga, 2007).

In some cases, the numerical processing of non-human animals has been directly compared to that of humans on the same task. For example, monkeys and human children have shown some similarities in the way they process numerical stimuli in a bisection task, in which they had to classify stimuli as being of large or small numbers (Jordan and Brannon, 2006b; Beran et al., 2008). Humans and monkeys also show similarities in their ordinal sequencing of stimuli based on numerical properties (e.g., Cantlon and Brannon, 2006). They show semantic congruity effects where they are faster to choose the correct response when there is congruity between the task rule (such as “choose smaller” or “choose larger”) and the magnitude of the choice sets (small or large numbers of dots; see Cantlon and Brannon, 2005). Humans, monkeys, and chimpanzees also all show the same perceptual illusion of overestimating the quantity of items in sets on the basis of the spatial arrangement of those items (Beran, 2006). These reports all suggest that human and non-human primates are highly similar with regard to their abilities for numerical processing. However, these direct comparisons between human and non-human primates have overwhelmingly relied on rhesus monkey subjects, and so a broader comparison across primate species is needed when direct comparison to humans is made. In addition, direct comparisons between non-primate species are warranted as well.

One explanation for the consistent success of many species in discriminating quantities is that access to a representational system for non-exact enumeration or quantification of stimuli is phylogenetically widespread and evolutionarily ancient. Analog magnitude estimation seems to underlie many performances by animals, including those that involve estimating continuous and discrete amounts (for overviews, see Gallistel and Gelman, 2000; Cantlon et al., 2009). When humans are prevented from counting stimuli, they too show this approximate number sense by representing sets inexactly, with greater variability as a function of increasing set size, as expected by Weber's Law (e.g., Whalen et al., 1999; Huntley-Fenner and Cannon, 2000; Cordes et al., 2001; Huntley-Fenner, 2001; Beran et al., 2006).

Despite judging many kinds of stimuli according to their numerical properties, one type of judgment remains relatively uninvestigated – judging moving stimuli. Quantifying moving stimuli may be particularly important in natural situations. Keeping track of the members of a group to which one belongs or summing the number of moving items such as competitors, predators, or prey are all important parts of the daily life of many species. Enumerating moving stimuli also may be considered harder than stationary stimuli because of the increased concern that any individual element will “overcontribute” to the estimation or count of that array because its movement through space leads to it being counted or added to the estimate more than once. Violation of the one-to-one correspondence principle of counting (Gelman and Gallistel, 1978) would lead to increased errors.

Despite the potential importance of quantifying moving stimuli, little experimental research has examined how well animals or even humans can judge the numerosity of moving sets of stimuli. In one study with 6-month-old infants, arrays of moving dots were presented on a screen, and when the number of dots changed across trials, infants dishabituated to those arrays, suggesting they perceived the change in numerosity (Wynn et al., 2002). Importantly, this study showed that it was changes in numerosity that led to dishabituation rather than changes to some other stimulus property. In one study with animals, Beran (2008) reported that rhesus monkeys and capuchin monkeys could choose the larger of two discrete and spatially separated sets of moving dots located within different areas on a computer screen, and numerosity controlled that discrimination rather than some other property of the stimulus sets (such as the amount of pixilation of each set or the amount of chaotic movement). A subsequent experiment in that report required the monkeys to choose the larger number of dots when both choice sets also contained distracter items that moved along with the target items in each spatial array. However, monkeys never had to differentiate items into subsets within one array and decide which subset was larger. In addition, although adult humans were included for comparison in one of the experiments, no direct comparison of monkeys and humans (young and old) discriminating subsets of moving stimuli has been conducted. That was the aim of this study.

We presented rhesus monkeys (Macaca mulatta), capuchin monkeys (Cebus apella), and humans (Homo sapiens) with a numerical discrimination task in which a single set of moving stimuli was presented, and participants had to judge which of two subsets within that larger array was more numerous. Thus, the task extends beyond that of the Beran (2008)study where the discrimination occurred between arrays that were spatially separate on the screen. In the present task, subjects not only had to sum and enumerate moving objects but they also had to distinguish items in each of two colors from each other when all items were present in a single, spatially overlapping visual group of moving items.

Human participants were of two age groups, undergraduate students and 4- to 5-year-old children. We chose to test children at this age because by this age children are old enough to count sets of stimuli and form estimations of sets, and because we wanted to determine whether this kind of estimation could occur for moving sets of stimuli. We were not attempting to chart the developmental progression of this ability to judge relative numerousness of moving sets. Instead, we wanted to determine whether such judgments could be made by human children at this point of development, during which other mathematical abilities are emerging, or whether these judgments are too difficult and do not emerge until later in development.

For all groups, controls were included that required use of the number of items rather than the total area of those items for correct completion of trials. Sets ranged from 1 to 12 items across the experiments, and movement varied in direction and speed for each item within each set. In this way, participants had to enumerate elements within sets while taking into account individual item movement.

Materials and Methods

Participants

Six male rhesus monkeys were tested: Obi (5 years old), Han (6 years old), Chewie (9 years old), Murph (15 years old), Lou (15 years old), and Willie (23 years old). Five capuchin monkeys (C. apella) also were tested: Logan (male, 3 years old), Liam (male, 5 years old), Wren (female, 6 years old), Nala (female, 6 years old), and Lily (female, 11 years old). Fifty adult humans between the ages of 18 and 36 years (mean = 21.0; SD = 4.1) were tested, and 22 children between the ages of 44 and 68 months (mean = 54.5 months; SD = 6.8 months) were tested. All monkeys had been trained to respond to computer-generated stimuli using a joystick response input (Evans et al., 2008), and all had participated in previous numerical tasks. With the exceptions of Chewie, Lou, and Lily, all monkeys participated in the previous study that involved summing and enumerating multiple sets of moving items on the computer screen (Beran, 2008). Adult humans all had experience using computers, and children were confirmed to be proficient enough with the test system with the specific modifications we made for their testing (see below).

Apparatus

For monkeys, trials were presented on a Compaq DeskPro with an attached 17-inch color monitor. Joystick responses were made with a Gravis GamePad Pro digital joystick mounted vertically to the cage. The test program was written in Visual Basic for Windows. Details of this testing system are reported elsewhere (Rumbaugh et al., 1989; Richardson et al., 1990; Washburn and Rumbaugh, 1991). For adult humans, the same exact program was presented, but participants responded through mouse clicks rather than joystick responses. For children, a laptop computer was used so that it could be taken to where the children were tested, and key presses were used, with small icons representing each response option affixed to the relevant keys on the keyboard.

Design and procedure

These experiments were performed in accordance with relevant institutional and national guidelines and regulations for the testing of humans and non-human animals. The research with humans was conducted with approval of the Georgia State University Institutional Review Board, and informed consent was provided by all participants or their parents or legal guardians. The research with animals was conducted with approval of the Georgia State University Institutional Animal Care and Use Committee.

Monkey procedure

All monkeys were tested individually while physically (but not visually) isolated from all other animals in their living quarters. The monkeys had continuous access to the computer program for blocks of time from 2 to 12 h in length, and the computer apparatus was attached to the cage of each animal at all times. Monkeys chose when to work and when to rest, and they were not deprived of water or regular feedings at any point during the study. Thus, the number of trials completed in a session was determined solely by each monkey.

Monkeys manipulated a joystick with their hand to move a cursor on the computer screen, and they initiated each trial by moving the cursor into contact with a rectangle in the center of the screen. The rectangle then disappeared and an array of dots colored blue and red appeared in the top center of the screen. Each dot was drawn with a diameter of 4–12 mm, randomly determined by the program. There were two trial types. Congruent trials were those in which the subset with the larger number of dots also was the subset with the larger total area of those dots in that color (calculated as the total area of pixilation in that color). Incongruent trials were those in which the subset with the larger number of dots contained the smaller total area (i.e., the subset with more dots had a smaller total area). These trial types necessarily occurred for a smaller range of numerical differences given the constraints on individual dot sizes.

At the bottom left and bottom right of the screen were two 36 mm × 36 mm colored squares – one was red and one was blue. These were the match choices, and the correct response was the color square that matched the color of the larger quantity of dots within the dot array at the top of the screen. Monkeys made a response by moving the cursor into contact with either the red or blue square. When a monkey made a correct response it received a Bio-Serv food pellet through use of an automated pellet dispenser attached to the computer. An incorrect response led to a 20-s timeout during which the screen remained blank. A 1-s inter-trial interval occurred in both cases before the next trial was presented.

Monkeys completed two training phases before moving to the test phase. In the first training phase, the dot array consisted of one to four stationary dots in one color (red or blue) and one to four stationary dots in the other color. The number of each color of dots could not be equal. When a monkey completed a session at greater than 80% accuracy in choosing the larger subset, it then moved to the second training phase. In that phase, dots also remained stationary, but now all possible combinations of red and blue dots ranging from 1 to 12 dots of each color were presented, except for equal numbers of both colors. Again, monkeys continued in this training stage until completing a session at greater than 80% correct.

In the test phase, after the initiation stimulus was contacted the array of blue and red dots appeared within a black border (78 mm × 78 mm). These dots also were drawn with a diameter of 4–12 mm, with the diameter of each dot randomly determined by the program on each trial. This helped to dissociate area and number cues for each set. Each dot also was given an initial, randomly selected trajectory and began moving on the screen as soon as it appeared. Movement took place at one of four randomly selected speeds, and a given dot moved in a straight line until it came into contact with one of the walls of the rectangular outline, at which point it was redirected, appearing as if it had deflected off of the wall. All dots in both colors appeared at once and were moving immediately. When dots approached each other, their movement created the illusion that they passed through (or over/under) each other (in other words, they did not bounce off of each other), with one dot randomly being chosen as the one to cross over the other (see Video S1 in Supplementary Material for a short video of the task). Thus, the monkeys saw two immediately visible, randomly moving sets of stimuli. The cursor appeared directly between the two rectangles and could be moved by a monkey into contact with either the red or the blue square. Contact constituted the selection by the monkey and ended a trial. Dot movement continued throughout the entire trial, and the stimuli remained on the screen until a monkey made a response. There was no time limit to how fast the monkeys had to respond. Each monkey completed either three or four sessions in the test phase so that a sufficiently large data set would be available for analysis. During this phase, there were no training trials presented, so all trials involved two subsets of moving stimuli. For the rhesus monkeys, this led to trial counts of 3,035 trials for Murph, 2,937 trials for Lou, 5,105 trials for Willie, 4,565 trials for Chewie, 2,129 trials for Han, and 1,776 trials for Obi. For the capuchin monkeys, this led to trial counts of 1,690 trials for Liam, 2,242 trials for Lily, 2,854 trials for Logan, 1,904 trials for Nala, and 1,791 trials for Wren.

Adult human procedure

Adult humans performed the exact same test phase as the monkeys. They did not do the two training phases because they were explicitly instructed to pick the larger of the two sets of colored dots within each array. They made responses by clicking the red and blue squares rather than using a joystick. Correct responses led to the addition of one point to a summary score presented on the screen. Incorrect responses led to the loss of two points in that summary score as well as a 5-s timeout during which the screen was blank. These point values were selected to motivate participants to make their best possible responses in an effort to accumulate points. To prevent giving adults unlimited time to try to count the dots in each subset, they were only given 2 s to make a response. If they did not make a response within 2 s, the trial was cleared and the next trial began. However, this occurred only rarely (1.6% of the trials). The time limit also was the upper maximum for nearly all response times produced by the monkeys. Each adult human participant completed 100 trials in the experiment.

Children's procedure

All trials were initiated by the experimenter with a key press on the keyboard. This was necessary to ensure that the children were ready for the trial and were ready to attend to the screen. Children made responses by key press rather than mouse or joystick. They were told that they had to decide whether there were more pink or blue dots and then press the same colored key on the keyboard, and they also began immediately with the final phase given to the monkeys (i.e., there was no training). Pink and blue stimuli were used because those colors were also part of an unrelated experiment conducted immediately prior to this one, although it had nothing to do with numerical estimation. Pink and blue key presses were on keys that were directly in line with the corresponding colored squares on the bottom left and bottom right of the screen. Correct responses led to the presentation of a smiley face in the center of the screen and a happy chuckle sound. Incorrect responses led to an unhappy face on the screen and a beeping sound. Children were given as long as they needed to make a response. This was necessary because they showed variable levels of motor skill in pressing the keys, and so a time limit would have precluded many valid choice responses. Additionally, if needed, the children could tell the examiner their response and then the examiner would push the corresponding key for them. Regardless of how well they were performing, after every 10 trials children were allowed to chose a sticker and place it on their sticker page. All other details of the procedure were identical to the tasks give to the other groups of participants.

Children worked for one session for as long as they were willing to engage in the task. Thus, they completed variable numbers of trials. Of the 22 children that were tested, data were analyzed from 19 of those children. The data from three children were excluded due to early discontinuation. Those children completed only a small number of trials (7, 11, and 22 trials). All other children completed at least 50 trials (mean = 79 trials).

We should note that the use of different input methods for participants’ responses was intentional. Monkeys could only respond through use of the joysticks, whereas adult humans are more familiar with mouse clicks. And, as mentioned, for testing children at this age we had to be flexible with regard to the form of input response they were willing to make. Joystick responses were found to be difficult for some children at this age in earlier pilot studies, and so this necessitated the variability allowed for children's responding. We were not interested in measuring response times for this experiment, and so a consistent input mode was considered less important than finding modes that were comfortable for each species and age group.

Results

All rhesus monkeys required either two or three sessions to reach criterion in Phase 1 (trial range = 1,955–4,077 trials). Five of six rhesus monkeys reached criterion in one session in Phase 2, whereas the sixth monkey required four sessions (trial range = 1,724–5,919 trials). Capuchin monkeys required two to six sessions to reach criterion in Phase 1 (trial range = 941–3,120 trials). Four of five capuchin monkeys reached criterion in one session in Phase 2, whereas the fifth monkey required four sessions (trial range = 314–1,745 trials).

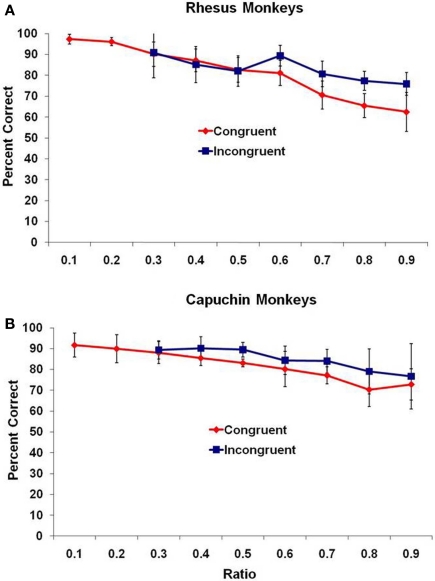
On the test trials, overall, all three species performed at levels significantly above chance for all possible differences between subset quantities (all p < 0.05 as assessed with a binomial test). Even looking at only the first 100 trials, 7 of 11 monkeys were significantly above chance (p < 0.05, binomial test), and this number of trials matches the number performed by adult humans. Performance of the two monkey species overall is presented in Figure 1 as the mean percentage of trials correct (with 95% confidence intervals) as a function of the ratio (small set divided by large set) between the two sets, with all trials binned into one of nine bins ranging from a ratio of 0.10 to a ratio of 0.90. An assessment using ratio is ideal because it includes both the effect of magnitude and difference between sets. For each species, the data are presented from the two trial types – congruent and incongruent trials.

Figure 1.

Mean performance for (A) rhesus monkeys and (B) capuchin monkeys for the two trial types, presented as a function of the ratio between subsets. Bars indicate 95% confidence intervals.

For the rhesus monkeys (Figure 1A), there was a significant negative correlation of ratio and mean percentage of trials correct for both congruent and incongruent trial types, r(7) = −0.99, p < 0.001, and r(5) = −0.84, p < 0.01, respectively. For the capuchin monkeys (Figure 1B), there was a significant negative correlation of ratio and mean percentage of trials correct for both congruent and incongruent trial types, r(7) = −0.98, p < 0.001, and r(5) = −0.92, p = 0.004, respectively. The accuracy of the monkeys decreased as the ratio approached 1.0.

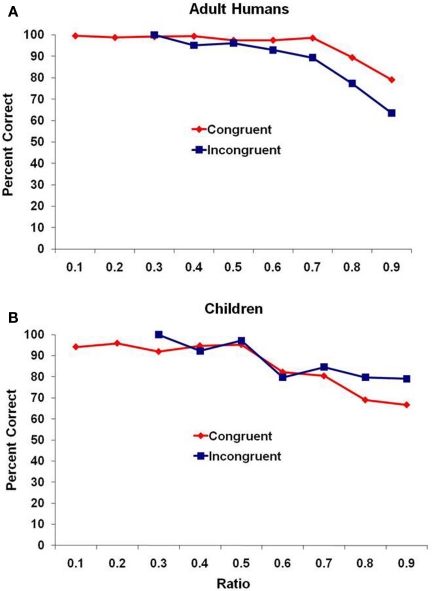
Figure 2 presents performance for the adult humans and children. Here, because of the smaller number of trials completed by each participant, we combined all of the trials for each age group rather than reporting mean performance and again binned those trials in the same way as with the monkeys. Similar results were obtained. For the adults (Figure 2A), there was a significant negative correlation of ratio and mean percentage of trials correct for both congruent and incongruent trial types, r(7) = −0.83, p = 0.006, and r(3) = −0.82, p = 0.025, respectively. For the children (Figure 2B), there was not a significant correlation of ratio and mean percentage of trials correct for congruent trials r(7) = −0.48, p = 0.19, but there was a significant negative correlation for the incongruent trial type, r(3) = −0.90, p = 0.006.

Figure 2.

Performance for (A) adult humans and (B) human children for the two trial types, presented as a function of the ratio between subsets. Data are combined across all participants because of the smaller number of trials completed by each participant compared to the monkey test.

We also compared performance on each trial type (congruent and incongruent) across species controlling for the effect of ratio by using ANCOVA. For congruent trials, there was a significant difference in performance across species, F(3,31) = 16.82, p < 0.001. Post hoc paired-samples t-tests where the ratios were used to pair the samples from each species were used to determine which species differed from each other. We applied the Bonferroni correction to account for the use of repeated tests, and the corrected alpha level was set at 0.008. Adult humans outperformed all other species, all t(df = 6) > 4.37, p < 0.005. No other statistically significant differences were found between any two species. For incongruent trials, ANCOVA indicated that there was no difference in performance across species, F(3,23) = 1.51, p = 0.24.

Discussion

The results of this experiment indicate three main points. First, all groups of participants performed at high levels in the experiment. They distinguished which of two sets of moving stimuli was more numerous. More importantly, all groups showed that performance was highly correlated with the ratio between sets, and this indicates something about the nature of the representations that are used in these kinds of tasks. Variability in responding on the basis of both set size (magnitude) and the quantitative difference between sets suggests that all of these groups relied on an approximate representation of the quantities in each color. Thus, the present results with two species of monkeys and two age groups of humans match previous research that shows similar analog magnitude signatures in the performance of animals (see Gallistel and Gelman, 2000; Brannon et al., 2006; Cantlon et al., 2009).

The second finding was that performance on incongruent trials, in which continuous aspects of the trial such as total area or amount could not be used to choose the larger set, was equivalent to performance on congruent trials and above chance levels. Such a comparison was necessary to indicate whether the judgments made by these groups were, in fact, likely to be numerical in nature. It is not surprising that this is true for humans, given that they are immersed, even at young ages, in an environment in which numerosity is relevant. More surprising was that both monkey species performed well on the incongruent trials. However, this finding may be explained by the previous experiences of the monkeys on other similar computer tasks requiring judgments of moving stimuli, as those tasks also involved dissociating number from continuous dimensions of trial stimuli so that only number was reliably associated with the correct response. In addition, it is important to remember that monkeys did many more trials than humans, and this too likely led to their greater emphasis on responding to number.

The third finding was that, overall, there was much similarity in the performance across groups. The only advantage shown by humans over monkeys occurred in the congruent condition, and then only for the adult humans. Such an advantage might have been the result of adult humans applying additional strategies to their choice behavior. The most likely one of these was to use both number and area as cues to guide responding which would account for the specific outperformance of adults over the other groups on the congruent condition. Adult humans also may still have been attempting to count the arrays given the 2-s time window for making judgments. It seems unlikely, however, at least for the high ratio trials where adults showed the performance advantage. On these trials, they would have had to not only count but also track and avoid double counting many more items than has been shown possible in object tracking experiments (e.g., Pylyshyn, 1989). Despite the relatively moderate performance advantage shown by adults in a few situations, performance was very similar across the four groups. Thus, the results indicate another cross-species continuity with regard to quantity representation, namely that for enumerating and comparing sets of moving stimuli even when they were spatially contiguous.

As noted earlier, this ability to estimate moving quantities would seem to be an important skill in a variety of natural situations in which one has to take into account a dynamic array that can change in its arrangements through movement without changing in its number. That a variety of primates, including humans and New and Old World monkeys species, can perform this task show that the capacity is phylogenetically widespread among the order Primates, and we would predict even broader than that. Given the competencies shown by many species in judging relative quantities in various kinds of visual formats as outlined in the introduction, it seems reasonable to expect that birds, rodents, and other non-primate mammals could succeed on this task as well, although performance may differ somewhat in degree of competence.

The children we tested clearly performed as well as these highly experienced monkeys and, in the incongruous condition, as well as adult humans. Little previous research has looked at how well young children enumerate moving stimuli, and these results suggest that the emergence of such skills occurs before 4 years of age. It will be important to test even younger children, and better establish what basic competencies are necessary to perform this kind of task. We tested children who were mastering the counting routine, but such mastery may not be necessary. In fact, the data suggest that it would not, as children (like adults and monkeys) showed a pattern of decreasing performance as the ratio between sets increased, and this suggests that children were not relying on specific, cardinal numerical values but rather relied on an approximate number system for judging the quantities (see Jordan and Brannon, 2006b). This system does not seem to require formal counting abilities as it has been shown in much younger children (e.g., Brannon and Van de Walle, 2001). The present study extends this approximate representation of number to moving stimuli, and also to the segregation and comparison of subsets within arrays of moving stimuli.

When asked to judge which of two sets of spatially contiguous but moving sets of stimuli was more numerous, monkeys and humans all succeeded. The performance of all groups on this task matched that reported in other studies that required comparing and discriminating quantities. There was a signature distance effect and magnitude effect that indicated easier discrimination when sets were more disparate than when they are more similar and easier when sets were smaller overall than when they were larger (e.g., Moyer and Landauer, 1967). As such, it reflects that both monkey species and humans of both age groups were relying on an approximate number sense to make these judgments (e.g., Cantlon et al., 2009). Those discriminations are made through sensitivity to approximate number, and this approximate number sense is shared across species and, as indicated in the present study, across a variety of visual presentation formats that require numerical estimation and comparison.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at http://www.frontiersin.org/Comparative%20Psychology/10.3389/fpsyg.2011.00061/abstract