Minimization of Imaging Gradient Effects in Diffusion Tensor Imaging

Abstract

A new, sample independent optimization criterion for minimizing the effect of the imaging gradients, including the directional awareness they create, is defined for diffusion tensor imaging (DTI) experiments. The DTI linear algebraic framework is expanded to a normed space to design optimal diffusion gradient schemes (DGS) in an integral fashion without separating the magnitude and direction of the DGS vectors. The feasible space of DGS vectors, for which the estimation equations are determinate, thus a hard constraint for the optimization, is parametrized. Newly generated optimal DGSs demonstrate on an isotropic sample and an ex-vivo baboon brain that the optimization goals are reached as well as a significant increase in estimation performance.

I. INTRODUCTION

The diffusion tensor imaging (DTI) is an important technique that is being used extensively in clinical and research environments. Its importance stems from its capability of inferring the tissue microstructure by representing the measurements of the spin motion using magnetic resonance imaging (MRI). With this information, it is possible to monitor different conditions such as multiple sclerosis [1], [2], cancer [3], Alzheimer’s disease [4], and spinal cord injury [5]. DTI is also the basis of fiber tracking algorithms [6], [7] that found a wide variety of application areas [8].

The origin of DTI is the adaptation of the work of Torrey [9], which resulted in Bloch–Torrey or modified Bloch equations, to the pulsed-gradient spin-echo (PGSE) experiment by Stejskal and Tanner [10]. In essence, the measurements in [10] rely on a pair of strong magnetic field gradients that sensitize the signal to the motion of the spins. The gradients attenuate the nuclear magnetic resonance (NMR) signal’s peak as a function of the newly added gradients.

With the invention of MRI creating the ability of applying the magnetic field gradients as three dimensional vectors, the spin motion, which was only described in NMR experiments as a scalar quantity, is calculated as a three dimensional construct. The modeling of NMR diffusion experiments was directly adapted to MRI using a tensor algebraic framework in [11], [12]. The diffusion tensor estimated by DTI is a symmetric tensor of rank two and thus is a quadratic form that is represented by a symmetric matrix D. In simplest terms, DTI presents the general tendency of the incoherent spin motion with ellipsoids.

Whether seen as matrices or quadratic forms, these objects are elements of a vector space. In [13] the DTI estimation equations were written appropriately using linear algebra. The imaging gradients were not included in the formulation, in a sense parallel to the adaptation from NMR experiments that do not possess any gradients other than the diffusion encoding ones.

Considering that physically any magnetic field gradient affects the signal according to the motion of the spin packets and that the magnitude of the imaging gradients is inversely proportional to the field of view (FOV), it is imperative that a complete DTI model includes the effect of the imaging gradients, especially for the experiments with small FOV. The inclusion was presented for the tensor algebraic framework in [12]. The same task is accomplished in a much less tedious fashion with the minimalist linear algebraic framework introduced in [14], [15]. The framework is more utilitarian than the tensor algebraic one: it provided a set of necessary conditions for the design of the DTI experiments that guarantee the uniqueness of solutions for linear and nonlinear estimation [16]–[18]. Moreover, it reveals modeling incongruities that are exposed in detail in [14], [15], [19] and are also summarized in Appendix A–C. Most importantly, it created the basis of this manuscript’s foundation: the normed space that allows the description of a sample independent, geometric optimization problem to design more efficient DTI experiments and the parametrization of the feasible space where the search for the optimal diffusion gradient vectors scheme takes place.

The design of DTI experiments consists of finding a diffusion gradient scheme (DGS) in the 3D space i.e., a set of at least six vectors that define the diffusion encoding magnetic field gradient magnitude and direction.

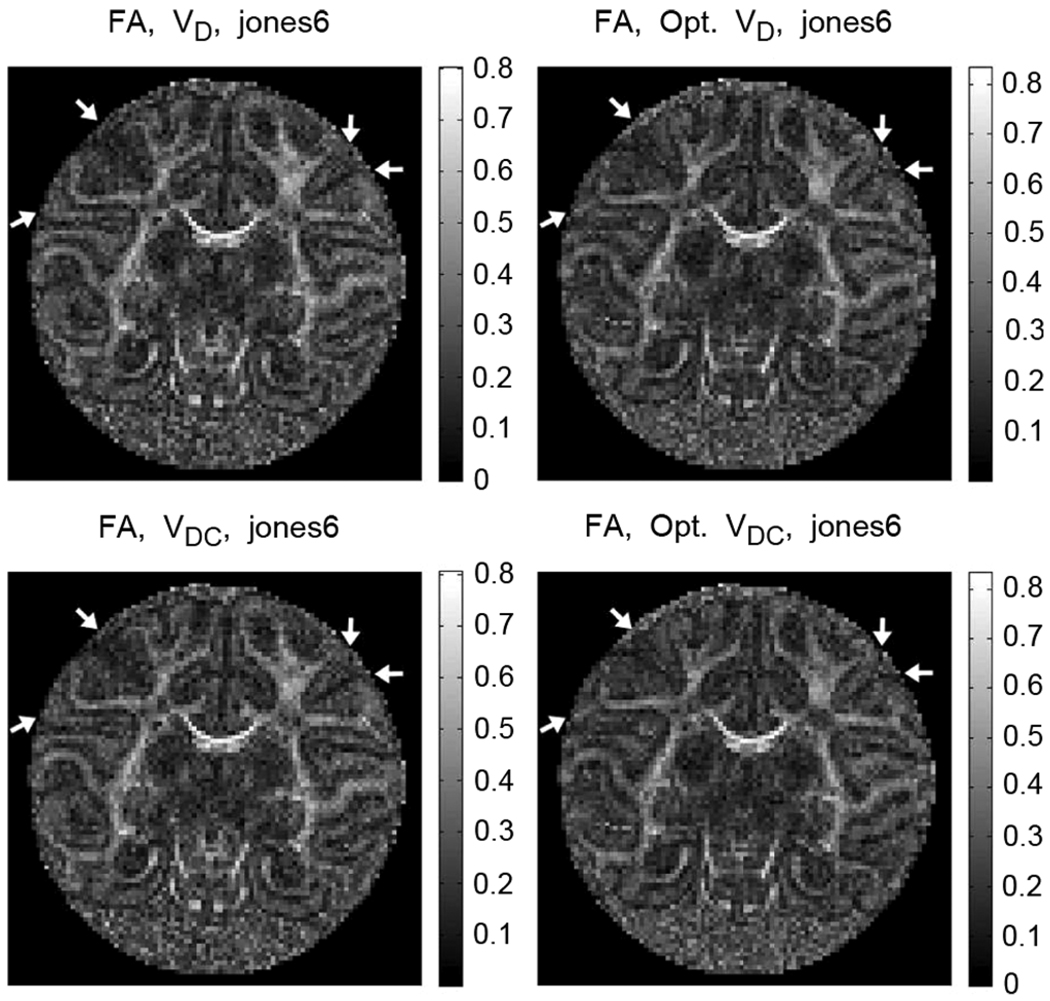
In a scenario where the effect of the imaging gradients is neglected, experiments conducted with an isotropic sample using a given DGS and any other scheme obtained by rotating the original DGS as a group should give identical results. Clearly, the imaging gradients introduce a directional awareness. The DTI parameters (e.g., the eigenvalues) obtained from a given DGS and its rotated version will not be the same due to the additional encoding created by the imaging gradients in different strengths for each scheme. The situation is more complicated for anisotropic samples, specifically for tissues with a geometric structure constraining the motion of the spins where the directional awareness is highly enhanced. Under these circumstances, if, for example, the sample orientation changes for any reason, e.g., during a longitudinal time study, the affected eigenvalues and eigenvectors will cause inconsistencies for the fiber tracking algorithms [20]. Moreover, depending on their alignment with respect to the imaging gradients, fine structure might become undetectable (see Fig. 4) in a detrimental manner, e.g., for tractography.

Fig. 4.

The fractional anisotropy maps obtained using nonoptimal and optimal versions of Jones6 DGS. On the right column, the arrows point to the structures that become visible when the optimal DGS is utilized. The structures on the left side of each image are the subcortical U-fibers that are not identifiable with the nonoptimal Jones6 DGS. The U-fiber, couple of pixels away from the left top arrow in its direction, is not distinguishable in nonoptimal schemes. The optimal DGS provides also better separability of the adjacent gyri as shown on the right side of the images with the arrows.

The essence of the optimization process is to design new DGSs with their cones (formed by their vectors, see Fig. 1 in Section II) oriented in such a manner that minimizes the effect of the imaging gradients. With this in hand, the optimal DGSs allow ignoring the imaging gradients in the estimation equations with higher fidelity and consequently addressing the modeling incongruities.

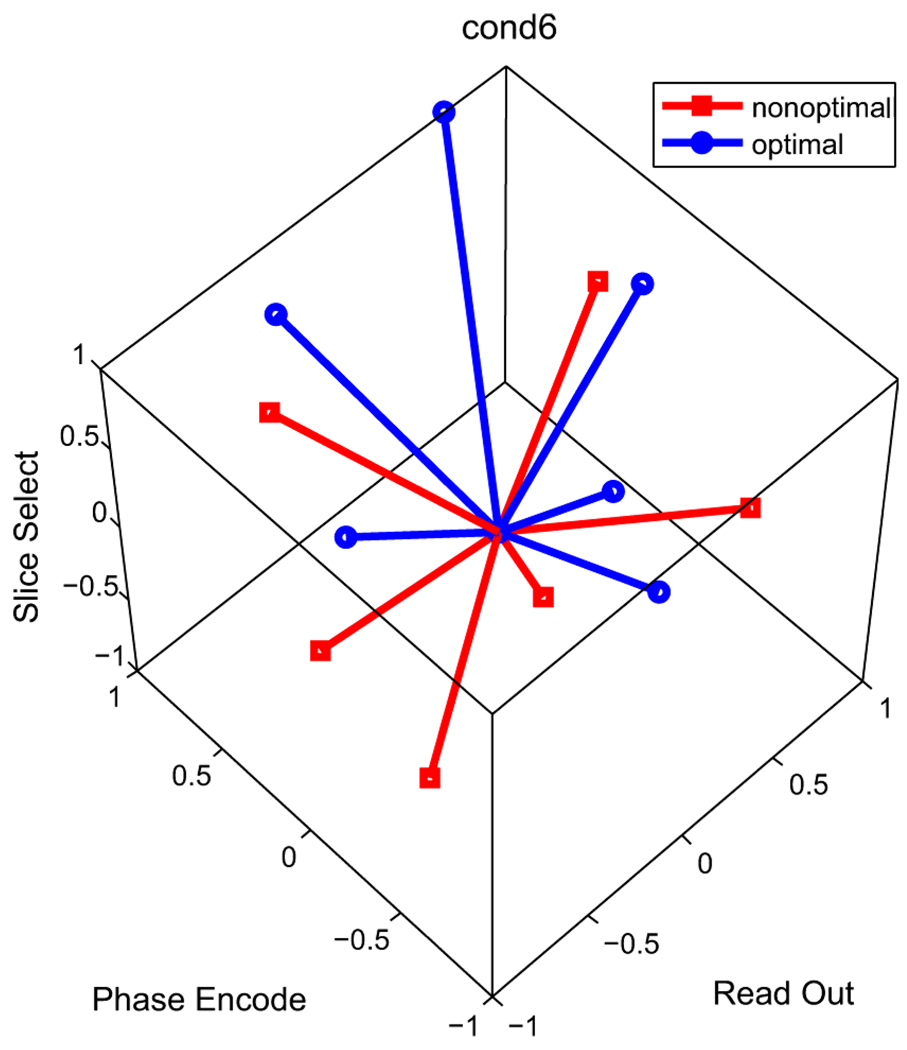
Fig. 1.

Cond6 DGS and its optimized version (see Tables V and VI). Notice that the cones are different but the schemes are not completely antipodal to each other. In the optimization problem the gradients are confined to the cube [−1, 1]³ to respect the hardware limitations.

In Section II-A, the vector and operator norms that are used to define the optimization criterion for this purpose are presented. It is natural that the optimized DGS have vectors with different magnitudes favoring the directions that minimize and balance the effect of the imaging gradients. The factorization of the switching times and DGS vectors for the DTI estimation equations described in [14] and [15] provides that capability (see (29) and the discussion below it). In brief, with the new framework the DGS vectors are not constrained to the unit sphere as it is traditionally done in the existing DTI experiment designs. In consequence, the optimization presented in this manuscript is integral: there is no separate optimization of the vector magnitudes and directions as its done in [21]–[25].

However, the choice of the DGS vectors is not arbitrary. First of all, the newly designed DGS must make the coefficient matrix of the estimation equation full rank. Otherwise, the DTI experiment will collect redundant data leading to a set of underdetermined equations [14], [16] regardless of whether least squares or nonlinear estimation is used [17]. The optimization is therefore constrained to the feasible DGS space where the rank condition is guaranteed. The constraint is implemented by utilizing the linear parametrization of Section II-B [19]. Second, as there is a natural tendency in the optimization to enhance the diffusion sensitizing gradients to make the imaging gradients negligible, the DGS vectors must be prevented from breaching the hardware limits. The objective function in Section II-D includes a hard constraint that limits the magnitude of the magnetic field gradients.

Most important of all, the optimization problem presented in Section II is sample independent, quite different and novel than the existing optimization criterions [21]–[25]. It is founded on bounding the difference between the eigenvalues of diffusion matrix D calculated with and without including the imaging gradients in the estimation equations. Whereas the eigenvalues are uniquely dependent on the characteristics of the sample, the bound is solely dependent on coefficient matrices of the DTI estimation equations that are completely independent of the sample. As the eigenvalues are the building blocks of the anisotropy indices due their invariance under similarity transformations (e.g., rotations), bounding their difference to minimize their directional awareness is an effective choice for providing consistency. The advantage of the optimal DGSs is demonstrated with the fractional anisotropy index on a fixed baboon brain in Fig. 4 of Section IV.

As the coefficient matrices are functions of the pulse sequence parameters (e.g., the echo time) and imaging gradients defined by the slice FOV, orientation, position etc., the optimization problem possesses a different solution for different parameter values. Therefore each time a new experiment is conducted, the optimal DGS must be computed on-the-fly. The implementation is provided in Section III-B.

The optimization generates new DGSs by using the existing DGSs in the literature as the starting points for the numerical optimization routine. The newly generated DGSs are tested with the experimental setups of Section III that consist of a water tube and a fixed baboon brain. In Section IV, the results are analyzed and compared with the results from the nonoptimal schemes.

II. DEFINITION OF THE OPTIMIZATION PROBLEM

The linear algebraic framework derived in [14] and [15], which is summarized in Appendix A, formulates the governing DTI estimation equations by deriving explicitly the coefficient matrix V of the equations as shown in (31). The matrix is the sum of three matrices corresponding respectively to the diffusion gradients, imaging gradients and the cross terms between them

$$V=b_t{V}_g+V_I+V_{C(g)}.$$ (1)

The matrix V_I from (31) is for imaging gradients and is constant with equal rows. V_D ≐ b_t V_g is conveniently factorized as a function of the gradient switching times, b_t from (33) and the matrix V_g defined in (30) as a function of the DGS denoted by g. V_C(g) given in (32) represents the cross terms between the imaging and diffusion gradients. Since the imaging gradients are fixed for the experiment, V_C is also a function of g.

In the case where the imaging gradients are neglected the equations take the form

$${\mathrm{\gamma }}^2{V}_{D}d={\mathrm{\gamma }}^2{b}_t{V}_{g}d=p$$ (2)

where the entries of p are the logarithms of the measurements shown in (37), d ∈ ℝ⁶ represents the six elements of the (symmetric) diffusion quadratic form D [see (17)] and γ is the gyromagnetic ratio.

A. Normed Space and the Error Bound

The central idea is to treat (1) as a matrix perturbation of V_D in (2): V = V_D + (V_I + V_C) and use the following theorem.

Theorem 1 ([26]): Let A ∈ ℝ^m×m be nonsingular and let à = A + E be a perturbation of A. For p ∈ ℝ^m let A d = p and let ║ · ║ be an operator norm. If there is a vector d̃ such that à d̃ = p, then

$$\frac{\parallel d-\tilde{d}\parallel }{\parallel \tilde{d}\parallel }\le \parallel A^{-1}E\parallel .$$ (3)

The theorem provides an upper bound on the relative error between the entries of the solutions d̃ from (1), i.e., V, and d from V_D as in (2) using any vector norm and the corresponding operator norm

$$\frac{\parallel d-\tilde{d}\parallel }{\parallel \tilde{d}\parallel }\le \parallel V_D^{-1}(V_I+V_C)\parallel .$$ (4)

In this work, the Frobenius norm F is adopted due to the following property for a symmetric matrix D with eigenvalues λ = [λ₁, λ₂, λ₃]

$$F(D)={\left[{\displaystyle \sum _i^3{\lambda }_i^2}\right]}^{1/2}=\parallel \lambda {\parallel }_2.$$ (5)

F(D) is computed as a R-weighted norm for d ∈ ℝ⁶

$$\begin{array}{cc}F(D)\hfill & =\parallel d{\parallel }_R\doteq \sqrt{d^{T}Rd}\hfill \\ \hfill & =\sqrt{d_1^2+d_2^2+d_3^2+2(d_4^2+d_5^2+d_6^2)}\hfill \end{array}$$

with

$$R=\left[\begin{array}{cc}\hfill I_3\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 2I_3\hfill \end{array}\right]$$

where I₃ is 3 × 3 identity matrix. It can be shown that the compatible operator Frobenius norm is given by

$$\begin{array}{cc}\parallel V{\parallel }_R\hfill & ={\parallel R^{1/2}V{R}^{-1/2}\parallel }_2\hfill \\ \hfill & =\sqrt{r_{\sigma }(R^{-1/2}{V}^{T}RV{R}^{-1/2})}\hfill \end{array}$$ (6)

with r_σ denoting the spectral radius of a matrix. The Frobenius norm also possesses the following important property:

Theorem 2 ([26], p. 205): Let d and d̃ ∈ ℝ⁶ represent two symmetric n × n matrices with eigenvalues λ₁ ≥ λ₂ ≥ · · · ≥ λ_n and λ̃₁ ≥ λ̃₂ ≥ · · · ≥ λ̃_n, respectively. Then

$${\left[{\displaystyle \sum _i^n{({\lambda }_i-{\tilde{\lambda }}_i)}^2}\right]}^{1/2}\le \parallel d-\tilde{d}{\parallel }_R.$$

The (4), (5), and Theorem 2 are now combined to place a bound on the relative error of eigenvalues

$$\frac{{\left[{\displaystyle \sum _i^3{({\lambda }_i-{\tilde{\lambda }}_i)}^2}\right]}^{1/2}}{{\left[{\displaystyle \sum _i^3{\tilde{\lambda }}_i^2}\right]}^{1/2}}\le \parallel V_D^{-1}(V_I+V_C){\parallel }_R.$$ (7)

The goal of the optimization algorithms is to find a DGS that will minimize the right-hand side of (7). This is a geometric search for schemes that define cones that are optimally “stretched” and “oriented” with respect to the fixed imaging gradient vectors (see Fig. 1).

The left-hand side of the inequality (7) is unknown before the measurements and reflects uniquely the sample’s diffusion properties. In contrast, the right-hand side is solely determined by the magnetic field gradient vectors and their activation times. Therefore, the upper bound is completely independent of measurement values and properties of the diffusion at any given location including the eigenvectors and eigenvalues. The bound guarantees the generation of optimal schemes that provide impartial experimental results for two different samples imaged with the same pulse sequence parameters. It is an extremely sound choice for an objective function that does not possess any sample dependence (tissue properties, orientation, location in the sample, etc.) of the existing optimization criterions [21]–[25].

The advantage of a formulation that separates the timings and the strengths of the gradients (as V_D = b_t V_g) presented in [14], [15] now becomes clear. When the gradient pulses are approximated by boxcar functions, b_t defined in [14] [different than the definition of b-value used in the literature, see (33)] is a factor for the on and off times of the gradient pulses and is independent of their strength. This prevents the restriction of optimizing the b-value and the direction of the diffusion gradient vectors separately, so it is more integral and sound. Each of the DGS vectors (i.e., each acquisition) will have its own b-value defined by the product of its magnitude and b_t. The search for an optimal solution, then, transforms into a true vectorial optimization geometrically balancing the effect of the imaging gradients. This is different and much more general than restricting the gradients to the unit sphere in order to use a single b-value for all of them.

B. Parametrization of the Feasible Space

Regardless of how the estimation is computed, with or without the incorporation of the imaging gradients, using linear or nonlinear methods [17], any DGS, g, must create a full rank V_g, (thus a full rank V_D) [16] in concert with the conditions of Theorem 1. In addition, the full version of Theorem 1 in [26] asserts that provided V_D is nonsingular, if $\parallel V_D^{-1}(V_I+V_C)\parallel$ is small, the sum of all three matrices, V, will also be nonsingular. Therefore the optimization problem must respect the full rank condition for V_g.

The constraint is satisfied by using the following parametrization of the set of admissible diffusion gradient vectors. It can be shown that when the DGS

$$g=\left[\begin{array}{ccc}\hfill g_{1x}\hfill & \hfill g_{1y}\hfill & \hfill g_{1z}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill g_{mx}\hfill & \hfill g_{my}\hfill & \hfill g_{mz}\hfill \end{array}\right]\in {ℝ}^{m\times 3}$$

is transformed to ḡ = g P with the 3 × 3 matrix P, V_g transforms via a matrix M, which is a function of P, to

$$V_{\overline{g}}=V_{(gP)}=V_{g}M.$$ (8)

The calculations are routine and use the linearity of h following from its definition (16):

$$h(G_{iD}P+G_I)=h(G_{iD})P+h(G_I).$$ (9)

The transformation obviously leaves V_I intact since the imaging gradients are not modified. V_g and V_C change because they are functions of the diffusion gradients. M is given in (12), shown at the bottom of the page, with the property that det(M) = (det(P))⁴. This implies that det(V_ḡ) = det(V_g) (det(P))⁴. Hence, V_ḡ will be nonsingular if and only if P is nonsingular. Thus, P is the parameter that describes the feasible gradient schemes. The original DGS, g, acts like a “pivot” and new admissible schemes are generated by changing P in the set of non-singular matrices. All of the schemes that can be obtained from a given pivot form a congruence class, with each member characterized by an element of the set of nonsingular matrices.

The feasible DGS set is characterized by the parametrization of the set of nonsingular matrices via polar decomposition: P = U Q. Here U is an orthogonal matrix (“angle”) and Q is a positive definite matrix (“magnitude”) [27]. In addition, Q is parametrized by q ∈ ℝ⁶ using the Cholesky decomposition

$$Q={\widehat{Q}}^T\widehat{Q}={\left[\begin{array}{ccc}\hfill q_1\hfill & \hfill q_4\hfill & \hfill q_6\hfill \\ \hfill 0\hfill & q_2& \hfill q_5\hfill \\ \hfill 0\hfill & 0& \hfill q_3\hfill \end{array}\right]}^T\left[\begin{array}{ccc}\hfill q_1\hfill & q_4& q_6\\ \hfill 0\hfill & \hfill q_2\hfill & \hfill q_5\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill q_3\hfill \end{array}\right].$$

In this work, the orthogonal part of the parametrization is confined to the set of rotation matrices using the Euler angles (ψ, θ, ϕ) ∈ [0, 2π] × [0, π] × [0, 2π] = Ω

$$U=\left[\begin{array}{ccc}\hfill \text{cos}(\varphi )\hfill & \hfill -\text{sin}(\varphi )\hfill & \hfill 0\hfill \\ \hfill \text{sin}(\varphi )\hfill & \hfill \text{cos}(\varphi )\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & 1\end{array}\right]\times \left[\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \text{cos}(\theta )\hfill & \hfill -\text{sin}(\theta )\hfill \\ \hfill 0\hfill & \hfill \text{sin}(\theta )\hfill & \hfill \text{cos}(\theta )\hfill \end{array}\right]\times \left[\begin{array}{ccc}\hfill \text{cos}(\psi )\hfill & \hfill -\text{sin}(\psi )\hfill & \hfill 0\hfill \\ \hfill \text{sin}(\psi )\hfill & \hfill \text{cos}(\psi )\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right].$$ (10)

However, the entirety of the feasible DGS space is not reachable starting from a single good DGS using the linear parametrization of (8). There are gradient schemes such that ḡ = g P does not hold

$$\begin{array}{c}\tilde{g}=\left[\begin{array}{ccc}1\hfill & 0\hfill & 0\hfill \\ 0\hfill & 1\hfill & 0\hfill \\ 0\hfill & 0\hfill & 1\hfill \\ \frac{1}{\sqrt{2}}\hfill & \frac{1}{\sqrt{2}}\hfill & 0\hfill \\ 0\hfill & \frac{1}{\sqrt{2}}\hfill & \frac{1}{\sqrt{2}}\hfill \\ \frac{1}{\sqrt{2}}\hfill & 0\hfill & \frac{1}{\sqrt{2}}\hfill \end{array}\right],\hfill \\ \dot{g}=\left[\begin{array}{ccc}\frac{(1+\sqrt{5})}{2}\hfill & 1\hfill & 0\hfill \\ \frac{(1+\sqrt{5}}{2}\hfill & -1\hfill & 0\hfill \\ 0\hfill & 1\hfill & \frac{(1+\sqrt{5})}{2}\hfill \\ 0\hfill & \frac{(-1-\sqrt{5})}{2}\hfill & -1\hfill \\ -1\hfill & 0\hfill & \frac{(1+\sqrt{5})}{2}\hfill \\ 1\hfill & 0\hfill & \frac{(1+\sqrt{5})}{2}\hfill \end{array}\right].\hfill \end{array}$$ (11)

$$M=\left[\begin{array}{cccccc}\hfill P_{11}^2\hfill & \hfill P_{12}^2\hfill & \hfill P_{13}^2\hfill & \hfill 2P_{11}{P}_{12}\hfill & \hfill 2P_{12}{P}_{13}\hfill & \hfill 2P_{11}{P}_{13}\hfill \\ \hfill P_{21}^2\hfill & \hfill P_{22}^2\hfill & \hfill P_{23}^2\hfill & \hfill 2P_{21}{P}_{22}\hfill & \hfill 2P_{22}{P}_{23}\hfill & \hfill 2P_{21}{P}_{23}\hfill \\ \hfill P_{31}^2\hfill & \hfill P_{32}^2\hfill & \hfill P_{33}^2\hfill & \hfill 2P_{31}{P}_{32}\hfill & \hfill 2P_{32}{P}_{33}\hfill & \hfill 2P_{31}{P}_{33}\hfill \\ \hfill P_{11}{P}_{21}\hfill & \hfill P_{12}{P}_{22}\hfill & \hfill P_{13}{P}_{23}\hfill & \hfill P_{12}{P}_{21}+P_{11}{P}_{22}\hfill & \hfill P_{13}{P}_{22}+P_{12}{P}_{23}\hfill & \hfill P_{13}{P}_{21}+P_{11}{P}_{23}\hfill \\ \hfill P_{21}{P}_{31}\hfill & \hfill P_{22}{P}_{32}\hfill & \hfill P_{23}{P}_{33}\hfill & \hfill P_{22}{P}_{31}+P_{21}{P}_{32}\hfill & \hfill P_{23}{P}_{32}+P_{22}{P}_{33}\hfill & \hfill P_{23}{P}_{31}+P_{21}{P}_{33}\hfill \\ \hfill P_{11}{P}_{31}\hfill & \hfill P_{12}{P}_{32}\hfill & \hfill P_{13}{P}_{33}\hfill & \hfill P_{12}{P}_{31}+P_{11}{P}_{32}\hfill & \hfill P_{13}{P}_{32}+P_{12}{P}_{33}\hfill & \hfill P_{13}{P}_{31}+P_{11}{P}_{33}\hfill \end{array}\right].$$ (12)

Although $M=V_{\dot{g}}^{-1}{V}_{\tilde{g}}$ exists, there is no P that provides M as in (12), shown at the bottom of the page. Consequently, the search is forcefully restricted to the congruence classes represented by different pivots. Since the classes are disjoint and disconnected, there is no way to find a global minimizer starting from a single pivot scheme with the linear parametrization. The strategy for covering the feasible DGS space is described in Section III-B. The investigation of more complicated parametrizations that will enable the discovery of a global optimum is the subject of future research.

C. Hardware Constraints

Intuitively speaking, if V_D has large entries, the effect of V_I and V_C will be reduced. Clearly, without any boundaries on the hardware limits, the solution of the minimization problems tends towards strong diffusion gradients in order to make V_D dominant. The main hardware constraint is the upper limit for the strength of the diffusion gradients, G_max. The value cannot be higher than the maximum value imposed by the system. Alternatively, the user can set it at a lower level for satisfactory amplifier performance. The constraint, which is incorporated in the objective function below (13), guarantees that the limit is not violated in the search for the optimal DGSs.

D. Objective Function

At the heart of each optimization problem lays the choice of an adequate objective function. The analysis of the previous sections provided the foundation for including the minimization of the estimation differences in the objective function. The R-norm condition number of V_D is added for handling the perturbation of the measurements (e.g., due to noise) and for increasing the robustness and the numerical stability, which is also valid for nonlinear estimation

$$10\parallel {(b_t{V}_{(gP)})}^{-1}(V_I+V_{C(gP)}){\parallel }_R+b_t^2\parallel V_{(gP)}{\parallel }_R\parallel V_{(gP)}^{-1}{\parallel }_R+100\left|\underset{i=1,\dots ,m}{\text{max}}\parallel g_{i}P{\parallel }_1-G_{\text{max}}\right|.$$ (13)

The last portion defines the hardware constraint that confines the diffusion gradients to the cube [−G_max, G_max]³. The largest weight, 100, was assigned to it to guarantee that the optimal DGS vectors have the largest allowed magnitudes to maximally attenuate the effect of the imaging gradients, which assists reaching the main goal with the second largest weight, 10. The choice of the weights was accomplished by trial and error while monitoring the magnitude of the DGS vectors after each trial. The degree of freedom in the weight assignment provides application-specific flexibility. The process relies both on the problem at hand, theoretical and experimental results, as well as on the experience of the designer. The investigation of weight determination methods is left as a future research topic.

The search is performed over the variables (ψ, θ, ϕ, q) ∈ Ω × ℝ⁶. that parametrize P as in Section II-B.

III. EXPERIMENTAL SETUP, OPTIMIZATION, AND ANALYSIS

Although the main purpose of the DTI method is the discovery of microstructure, first and foremost, the estimation procedures must work properly for the simplest case of diffusion with known characteristics: an isotropic sample. For that reason, a polypropylene centrifuge tube by FisherBrand (Cat. No. 05-539-6) filled with tap water at room temperature, with an inner diameter at the slice of 2.7 cm was chosen as the phantom.

A fixed baboon brain immersed in 4% paraformaldehyde was used for testing the optimization procedures on biological tissue. The primate was prematurely delivered at 125th day and sacrificed at 59th day after delivery. All animal husbandry, handling, and procedures were performed at the Southwest Foundation for Biomedical Research, San Antonio, Texas. Animal handling and ethics were approved to conform to American Association for Accreditation of Laboratory Animal Care (AAALAC) guidelines. Further details of the sample preparation are described in [28].

A. Experimental Setup

The experiments were carried out on a 4.7T MR scanner (Varian NMR Systems, Palo Alto, CA) with a gradient system of bore size of 15 cm, maximum gradient strength of 45 gauss/cm and rise time of 0.2 ms using a quadrature birdcage coil (Varian NMR Systems, Palo Alto, CA) with 63 mm inner diameter size. DTI data were obtained using the standard spin-echo multislice sequence with in-house modifications that store all of the relevant parameters, including the timing and amplitudes of all of the crusher gradients. The images were 128 × 128 pixels with a field of view 64 × 64 mm². The slice thickness was 1 mm for the water sample and 0.5 mm for the baboon brain. The repetition time T_R = 1 s, echo times T_E = 35 ms (water) T_E = 30.5 ms (baboon brain), diffusion pulse separation Δ = 18 ms and diffusion pulse duration δ = 6 ms were used.

Center-symmetric diffusion gradient schemes with 12 diffusion gradient vectors were used to obtain data. Initial nonoptimal DGSs were constructed by appending to the six vector gradient schemes [29] their central symmetric part: Tetrahedral (geometrically, the scheme is build on the four tetrahedral vectors of [30] by adding two more elements and is different from the scheme presented in [30]), Cond6, Jones noniso (without the last vector) renamed as Cond* because it yields to a V_g with a good condition number, Jones (N = 6), Muthupallai, (which is equal to Icosahedron (ICOSA6) scheme from [31]), Downhill Simplex Minimization (DSM) and Dual Gradient. Also a modified version of the Muthupallai scheme, denoted by MUTM is included in the experiments. The DGSs are provided in Table V with the modified entries of MUTM in bold. Maximum diffusion gradient strengths of g_diff = 12 gauss/cm (water) and g_diff = 21 gauss/cm (baboon brain) were used. With boxcar approximation, at maximum diffusion gradient, the value of the scalar coefficient for the water and baboon brain were respectively: ${\mathrm{\gamma }}^2{b}_t{g}_{\text{diff}}^2=593.61\mathrm{s}/{\text{mm}}^2$ and ${\mathrm{\gamma }}^2{b}_t{g}_{\text{diff}}^2=1817.94\mathrm{s}/{\text{mm}}^2$. The ex vivo tissue experiments were carried out consecutively after leaving the sample in the scanner for approximately 12 h to reach a stable temperature.

TABLE V.

Non-Optimal DGSs [14], [15], [29]

cond6			cond*
0.755	0.26	0.602	1	0	0
−0.479	0.711	0.515	0	1	0
−0.394	−0.63	0.669	0	0	1
−0.616	−0.262	−0.743	0.707	0.707	0
0.558	−0.741	0.375	0	0.707	0.707
−0.954	−0.067	0.292	0.707	0	0.707
dsm			dualgr
0.91	0.416	0	0.707	0.707	0
0	0.91	0.416	0.707	0	0.707
0.416	0	0.91	0	0.707	0.707
0.91	−0.416	0	0.707	−0.707	0
0	0.91	−0.416	0.707	0	−0.707
−0.416	0	0.91	0	0.707	−0.707
mutm			jones6
0.851	0.526	0	1	0	0
0.851	−0.526	0	0.446	0.895	0
0	0.526	0.851	0.447	0.275	−0.851
0	−0.851	−0.526	0.448	−0.723	−0.525
−0.526	0	0.851	0.447	−0.724	0.526
0.526	0	0.851	−0.449	−0.277	−0.85
muthup			tetra
0.851	0.526	0	0.577	0.577	0.577
0	0.851	0.526	−0.577	−0.577	0.577
0.526	0	0.851	0.577	−0.577	−0.577
0.851	−0.526	0	−0.577	0.577	−0.577
0	0.851	−0.526	0.707	0.707	0
−0.526	0	0.851	0.707	0	0.707

B. Implementation of the Optimization

Optimal gradient schemes were generated using each of the diffusion gradient schemes listed in Section III-A, which are explicitly given in Table V, with six vectors as the pivot DGS g in the objective function of (13). Standard Matlab Optimization Toolbox (Mathworks, Natick, MA) routine fmincon was used to solve the optimization problems.

The initial condition supplied to the numerical routines plays a crucial role in the convergence of the algorithm. In this work, for each pivot, several initial conditions obtained by changing Euler angles in multiples of π/4 rad, equivalent to rotating the pivots, were evaluated. The “magnitude” of the pivot was left untouched having in mind from Section II-D that the vectorial approach deals with the strengths of the gradients automatically. After the algorithm converged for each initial condition of every pivot, which takes between 2.5 to 3.1 s with the computer hardware described in Section III-C, the best of the congruence class optimal solutions was selected as listed in Tables VI and VII.

TABLE VI.

Optimal DGSs Used With the Water Tube.

Opt. cond6			Opt. cond*
−0.384	−0.513	−0.845	−0.5	1	−0.543
0.519	−1	−0.573	−0.828	−0.904	−0.541
0.859	0.96	−0.768	0.959	−0.135	−0.871
0.188	0.502	1	−0.939	0.0682	−0.767
−0.0932	1	−0.534	0.0928	−0.734	−0.999
0.996	0.223	−0.23	0.325	0.612	−1
Opt. dsm			Opt. dualgr
−1	0.461	0.00318	−1	0.995	0.0199
−0.0034	0.995	0.446	−1	0.0501	0.981
−0.464	0.047	0.999	0	0.996	1
−1	−0.432	0.0116	−1	−0.946	−0.0193
0.00325	0.958	−0.465	−1	0	−0.98
0.45	0.0337	0.993	0	0.945	−0.961
Opt. mutm			Opt. jones6
−0.314	1	0.898	−0.923	0.144	0.749
−0.727	−0.755	1	−0.295	1	0.39
0.807	0.11	0.362	−0.988	0.479	−0.295
−0.705	−0.946	−0.173	−0.885	−0.613	−0.109
0.922	−0.843	−0.173	−0.129	−0.771	0.689
0.278	−0.692	1	−0.232	−0.228	−1
Opt. muthup			Opt. tetra
−0.993	0.609	0.0362	−0.727	0.822	0.82
−0.0265	0.978	0.639	0.906	−0.811	0.993
−0.627	0.0379	1	−0.976	−0.887	−1
−0.975	−0.578	0.00126	0.796	0.876	−0.813
−0.00332	0.943	−0.583	−1	1	−0.106
0.59	0.0187	0.977	−0.933	−0.0333	1

TABLE VII.

Optimal DGSs Used With the Baboon Brain

Opt. cond6			Opt. cond*
−0.0455	0.825	−0.872	−0.619	1	−0.556
0.935	0.309	−0.999	−0.795	−0.974	−0.528
0.681	1	1	0.985	−0.177	−0.858
−0.172	−0.977	0.845	−1	0.0185	−0.767
−0.304	0.852	0.812	0.135	−0.814	−0.981
0.944	0.208	0.464	0.259	0.582	−1
Opt. dsm			Opt. dualgr
−0.107	−0.931	−0.753	−0.727	0.13	−0.853
0.938	−0.737	−0.061	0.21	0.48	−1
0.669	0.0439	−1	0.0455	−0.505	−1
−0.616	−0.137	−0.952	0.165	0.985	0
0.175	−1	0.497	−0.772	0.635	0.147
0.999	0.532	−0.22	−0.937	−0.35	0.147
Opt. mutm			Opt. jones6
−0.974	−0.865	−0.679	−1	0.13	−0.587
−1	0.959	−0.336	−0.392	−0.777	−0.761
0.395	−0.142	−0.851	−0.969	−0.631	0.166
−0.257	1	0.697	−0.824	0.466	0.499
0.992	0.741	−0.366	−0.158	1	−0.218
−0.228	0.799	−0.993	−0.106	−0.231	0.999
Opt. muthup			Opt. tetra
−1	0.262	−0.395	0.655	−0.5	−0.3
−0.347	−0.294	−1	0.365	1	0.0692
−0.17	0.731	−0.808	−0.907	−0.165	−0.686
−0.376	0.908	0.256	−0.113	−0.336	0.916
−0.663	−0.751	−0.054	0.177	−0.918	−0.226
0.681	0.00759	−0.722	0.47	−0.1	−0.744

It should be emphasized that the optimized schemes are not universal, they are specific to the parameters of the experiments: FOV, slice thickness, timing of the gradients, etc. For a new experiment, the optimization algorithm must be run to find the optimal solution corresponding to the new parameters.

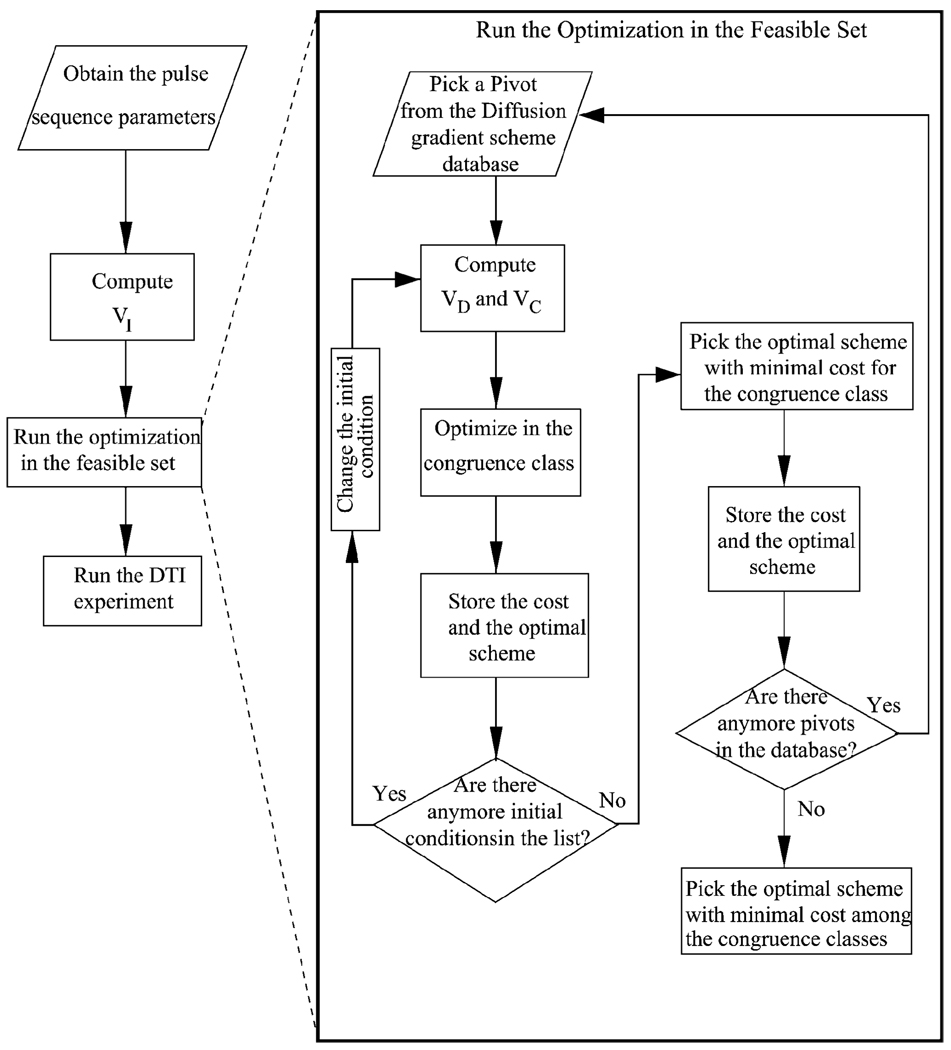
Practically, the optimization is implemented in real time as described in the flowchart of Fig. 2. In the beginning, all of the pulse sequence parameters are obtained from the MR console based on the physical size, orientation and location of the slices, and the pulse sequence times (e.g., T_E), including the timing of the imaging gradients. V_I is calculated using these data. If a connected parametrization of the feasible set is discovered in future, the optimization will be executed using it. However, the current linear parametrization describes the feasible space as the union of disjoint and disconnected congruence classes. The optimization routines must run separately for each of the congruence classes. The larger the number of representative pivots (i.e., the number of classes), the larger will be the covered portion of the feasible space. For this reason, the congruence classes of interest are defined by a list of representative pivots. As the convergence of numerical optimization routines depends crucially on the initial conditions, different initial conditions are obtained by multiplying the representative pivot with an invertible matrix before running the optimization algorithms. Once the list of initial conditions is completed in a congruence class, the optimal solution that results in the minimum cost among all is chosen as the optimizer for that class. Afterwards, the next pivot in the database is subjected to the same procedure. The loop is repeated until the cost is found for each congruence class. Finally, the optimal solution with minimal cost between all of these is selected. The optimal DGS is provided as input to the MR scanner and the DTI experiment is executed.

Fig. 2.

Flowchart for implementing the optimization procedure in real time during DTI experiments. On the left is the overall setup. On the right is description of the algorithm inside the box “Run the Optimization” for the case of current linear parametrization of the feasible space that can only describe disconnected congruence classes. If the feasible space can be parametrized in a connected fashion, the search in disconnected sets will not be necessary.

The search can be sped up by keeping in a database the optimal solutions corresponding to sets of pulse sequences and imaging parameters. In the beginning of the experiment, after the operator chooses all of the parameters, the optimization starts from the initial condition equal to the optimal solution that corresponds to the parameters closest to those of the current experiment. If the parameter space is sampled densely enough, numerical routines will quickly convergence to the optimal solution.

C. Analysis of the Experimental Results

In-house Mathematica (Wolfram Research, Champaign, IL) code was used to compute components of V as described in [14], using the parameter values written to the console computer’s hard disk by in-house additions to the pulse sequence. In-house Matlab (Mathworks, Natick, MA) programs were utilized for the estimation of d at each pixel, for graphical representation and maps of related results on a two quad core 2.3 GHz Intel Xeon cpu and 8 GB memory Dell Precision Workstation 490 running Windows XP 64-bit operating system. Standard Matlab Image Processing Toolbox routines, Sobel edge detection and morphological reconstruction were used to detect the signal region of the phantom in non-diffusion weighted images for each gradient scheme. The edges were removed to obtain a region free of susceptibility artifacts and the intersection of all regions was taken to obtain the circular area with 2022 pixels for the water sample and 6080 pixels for the baboon brain.

Among several estimation methods such as weighted and non-weighted least squares, total fitting [32] and nonlinear optimization (constrained and unconstrained), nonweighted least squares is chosen because of its speed and simplicity. The nonlinear estimation is investigated in [17]. In the computation of V_C and V_I the phase-encoding gradient value of 0 was selected as described in [14].

IV. ANALYSIS RESULTS

Table I summarizes the numerical values of the cost function (13) at different stages of the optimization procedure: The pivot DGSs are the ones listed in Section III-A, the initial condition is found by rotating the pivots as explained in Section III-B and the last row is the optimal solution. For Muthupallai, DSM, Dual Gradient and Tetrahedral, the original DGS as the initial condition has resulted in the optimal cost as shown in the appropriate columns of Table I. The optimal scheme initiated from Jones6 had the lowest cost for both of the samples.

TABLE I.

Value of the Cost Function for the Pivot, Initial, and Optimized Schemes

Water Sample
	cond6	cond*	dsm	dualgr	mutm	jones6	muthup	tetra
Pivot	50.18	5.921	13.81	34.48	35.13	5.085	19.81	45.33
Initial	40.64	20.64	13.81	34.48	21.71	12.96	19.81	45.33
Opt.	25.35	5.177	4.546	4.348	9.437	4.241	4.41	12.53
Baboon Brain
Pivot	37.51	5.052	12.69	33.26	30.7	3.757	18.6	42.14
Initial	33.39	19.63	10.05	4.011	27.93	7.146	6.53	12.13
Optimal	18.89	4.35	3.445	3.571	7.671	3.259	3.513	10.59

Due to different imaging parameters, the optimization yielded different DGSs for the water sample and baboon brain. The center symmetric counterparts of the DGSs listed in Tables VI and VII are appended to them to obtain the NoCroT schemes (see [14], [15], the Appendix A–C). The new twelve gradient DGSs are used in the experiments respectively on both samples.

There are three levels for the inclusion of the imaging gradients in the estimation equations: “all gradients” (V_DC) as in (39), NoCroT as in (42) and “diffusion gradients only” as in (2). Since NoCroT becomes equivalent to neglecting all of the imaging gradients in the case of center-symmetric DGSs [see (42)], the estimation using the experimental data was carried out with two methods: “all gradients” and NoCroT (equivalently V_D).

The main goal of the optimization defined in (7) is the minimization of the differences between the eigenvalues (Δλ_i = λ_i – λ̃_i) estimated by excluding and including the imaging gradients (λ_i and λ̃_i) as in (2) and as in (40), respectively. Table II shows that the eigenvalue difference obtained from the nonoptimal DGSs ((Δλ_i)_Non) is higher than the ones from the optimal DGSs ((Δλ_i)_Opt), for the water sample and the overall baboon brain including individually the region of interests (ROIs) displayed in Fig. 3. This observation holds regardless of the ROIs that are specifically chosen to be physically near each other and to depict different levels of microstructure: cerebrospinal fluid (CSF) is similar to an isotropic sample, white matter (WM) possess structure and corpus callosum (CC) is highly organized. In short, the optimization goal has been reached.

TABLE II.

Percent Change Between Non-Optimal and Optimal Differences Between the Eigenvalues, Δλ_i = λ_i − λ̃_i, From V_D and V_DC

100 × ((Δλi)Non – (Δλi)Opt)/(Δλi)Non
	cond6	cond*	dsm	dualgr	mutm	jones6	muthup	tetra
Water	68.71	10.91	−209	79.99	85.86	47.03	88.31	48.08
	44.99	−104.6	−18.45	112.3	10.01	95.58	166.5	47.2
	17.04	−54.24	29.26	74.41	44.19	38.64	39.11	46.36
Brain	−142.1	83.65	31.83	−12.44	110.2	64.35	2.794	73.97
	−80.93	−70.82	39.07	−32.53	51.83	69.1	20.44	149.6
	80.14	315.5	47.04	62.08	99.2	11.91	37.97	75.11
CSF	197.8	328.1	58.2	79.18	107	122.2	44.08	62.39
	−35.2	−311.4	86.51	−72.34	208.3	81.64	5.018	146.3
	105	−1727	−15.63	31.15	79.35	21.34	36.51	70.98
WM	143.8	67.5	60.17	471.2	98.76	55.42	−29.67	74.64
	−93.53	−4.371	28.73	6.909	38.75	36.69	17.83	138.6
	60.67	226.7	1.596	41.84	240.4	76.01	31.51	70.36
CC	−545.3	−129.2	90.69	224.3	96.49	74.79	−0.2668	101.4
	125.8	−24.55	792.5	273.1	184.7	3.054	848.7	105.1
	145	−320.8	0.7862	68.16	49.22	43.91	34.76	67.36

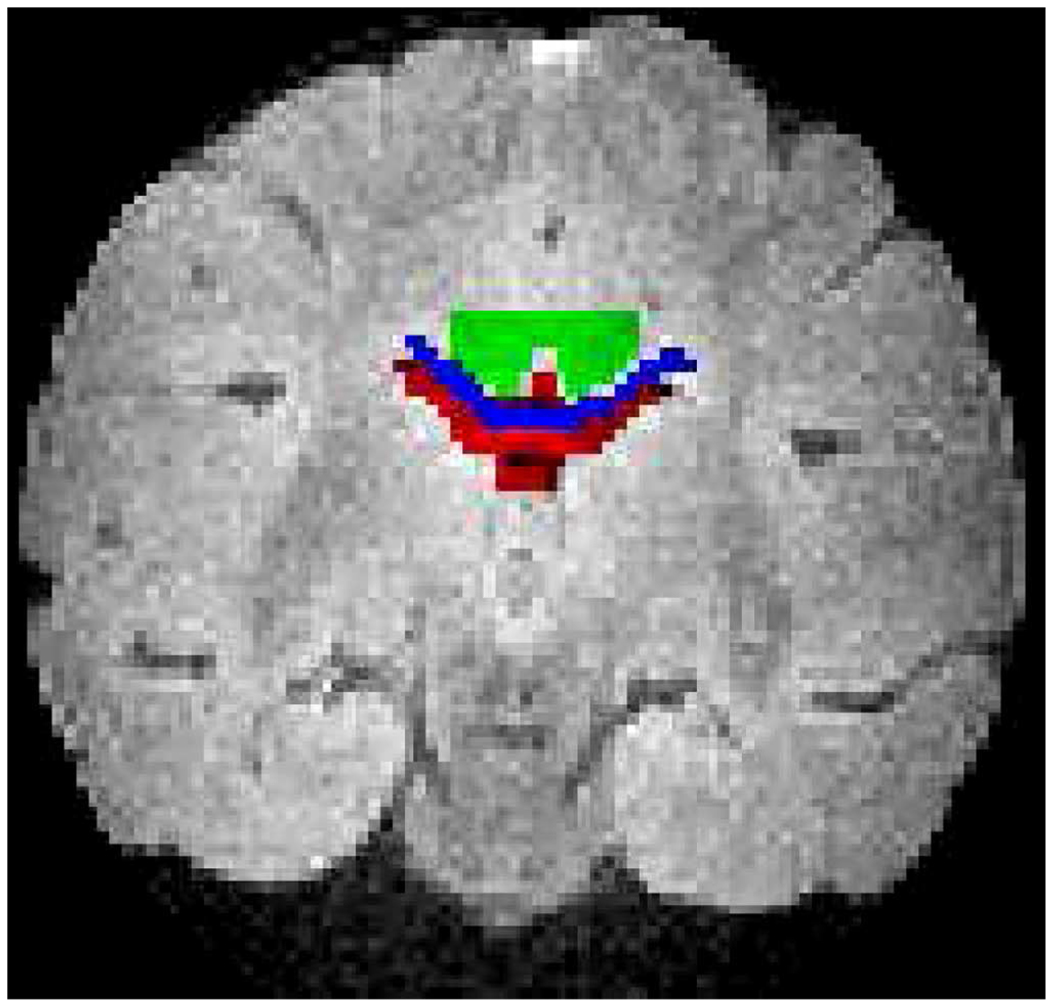
Fig. 3.

The T₂-weighted image of the baboon brain and the regions of interest used in the analysis: CSF in red (n_roi = 82), WM in green (n_roi = 86), and the CC in blue (n_roi = 53).

Aside from the specific goal, it is also important to judge the overall performance of the newly designed DGSs. As DTI is a model matching method, the most relevant performance measure is the model matching error, the difference between the model S of (19) and the m measurement values Ŝ_i

$$\parallel \chi {\parallel }_2^2=\frac{1}{m}{\displaystyle \sum _{i=1}^m{(S_i-{\widehat{S}}_i)}^2.}$$ (14)

χ̄ denotes the mean of the pixel residuals [14] from the signal region. Table III shows that the model matching error is reduced by using the optimized DGS for both samples, including different structures of the baboon brain. For example, in the isotropic sample the error is reduced by 46.96% for the dual gradient scheme, by 28.97%, 14.15%, and 16.46% in CSF, WM, and CC respectively for the Cond* scheme. These results are highly significant. But despite the success, the model matching error for “all gradients” method is larger compared to the less “complete” model NoCroT.

TABLE III.

Percent Change in the Model Matching Error

100 × (χ̄Non − χ̄Opt)/χ̄Non
		cond6	cond*	dsm	dualgr	mutm	jones6	muthup	tetra
Water	VDC	30.75	37.36	9.271	46.96	−8.979	12.41	17.63	52.36
	VD	31	35	9.728	46.55	6.978	12.31	18.1	62.5
Brain	VDC	22.83	17.85	6.936	1.703	17.23	4.257	2.016	9.192
	VD	15.22	11.33	4.174	1.029	11.21	2.979	1.469	9.625
CSF	VDC	24.26	28.97	14.53	3.14	21.82	14.54	7.437	2.633
	VD	18.19	14.34	8.016	3.238	10.74	8.744	4.828	−0.5225
WM	VDC	19.41	14.15	5.055	1.402	14.32	4.797	2.109	9.191
	VD	12.1	3.751	−1.351	3.467	10.79	4.617	4.719	7.749
CC	VDC	15.13	1646	7.221	−6.688	6.165	1.941	−2.423	1.661
	VD	4.222	8.603	1.285	−6.669	−7.782	−0.3637	−5.418	2.659

The eigenvalues obtained from the optimal DGSs are smaller compared to their non-optimal counterparts. For most of the optimal DGSs the standard deviation of the eigenvalues is also lower up to 7% (with the exception of Cond6 and Modified Muthupallai with 43% and 55%, respectively). In other words, the precision for the optimal DGSs is increased.

In addition, in [15] and [14] the negative eigenvalues of the water sample and CC estimated with “all gradients” for Tetrahedron DGS completely disappear for the optimal version. The negative eigenvalues are physically meaningless because their existence violates the Fick’s law of diffusion. In the case of the overall baboon brain sample, all of the nonoptimal DGSs, except DSM and Jones6, exhibit negative eigenvalues. The number of the negative eigenvalues are either eliminated (Dual Gradient and Muthupallai) or reduced by up to 70% with the optimal DGSs. In the CSF, nonoptimal Cond6 and Tetrahedron estimate negative eigenvalues whose numbers are reduced by up to 80% with the optimal schemes and in the WM they are completely eliminated. These observations demonstrate that the newly obtained DGSs are more robust than the DGSs in the literature.

One of the issues that motivated this research was to overcome the indeterminateness of the phase-encoding gradient values in the estimation equations, which is briefly summarized in Appendix A–C. As first noted in [14] and [15], the eigenvectors of the water sample tend to align themselves according to the value of the phase-encode gradient used in the coefficient matrices (V_I and V_C) for the nonoptimal schemes. The observation persists for nonlinear estimation [17] as well. The experimental results of the water sample show that the bias exists also for the optimal schemes for both least squares and nonlinear estimation [17]. It can only be concluded that the problem originates from a fundamental level of modeling that is beyond the scope of this manuscript.

Since the only physically known fact is the isotropic nature of the water sample, the only way to assess the accuracy performance is to investigate the anisotropy index fractional anisotropy (F A). Table IV summarizes the percent change of the mean value of F A $(\overline{FA})$ between the nonoptimal and optimal schemes. For the optimal DGSs, $\overline{FA}$ is lowered (with the exception of Cond*) for “all gradients” estimation up to 57.54%. However, this consistency is not observed for NoCroT: Cond6 and Modified Muthupallai report lowering of $\overline{FA}$ (up to 23.65%) but Dual Gradient and Tetrahedron DGSs show a significant increase (up to 48.3%) while the other schemes have small increases (up to 6.8%). Like the model matching error, $\overline{FA}$ estimated by V is higher than the one from NoCroT. This is an indication of the deficiency of a complete DTI model [14].

TABLE IV.

Percent Change in the Anisotropy Indices of the Water Sample

$100\times ({\overline{FA}}_{Non}-{\overline{FA}}_{Opt})/{\overline{FA}}_{Non}$
	cond6	cond*	dsm	dualgr	mutm	jones6	muthup	tetra
VDC	32.17	−20.97	12.65	39.45	57.54	19.1	21.28	27.54
VD	23.65	−6.573	−2.922	−42.2	20.11	−6.549	−6.801	−48.3

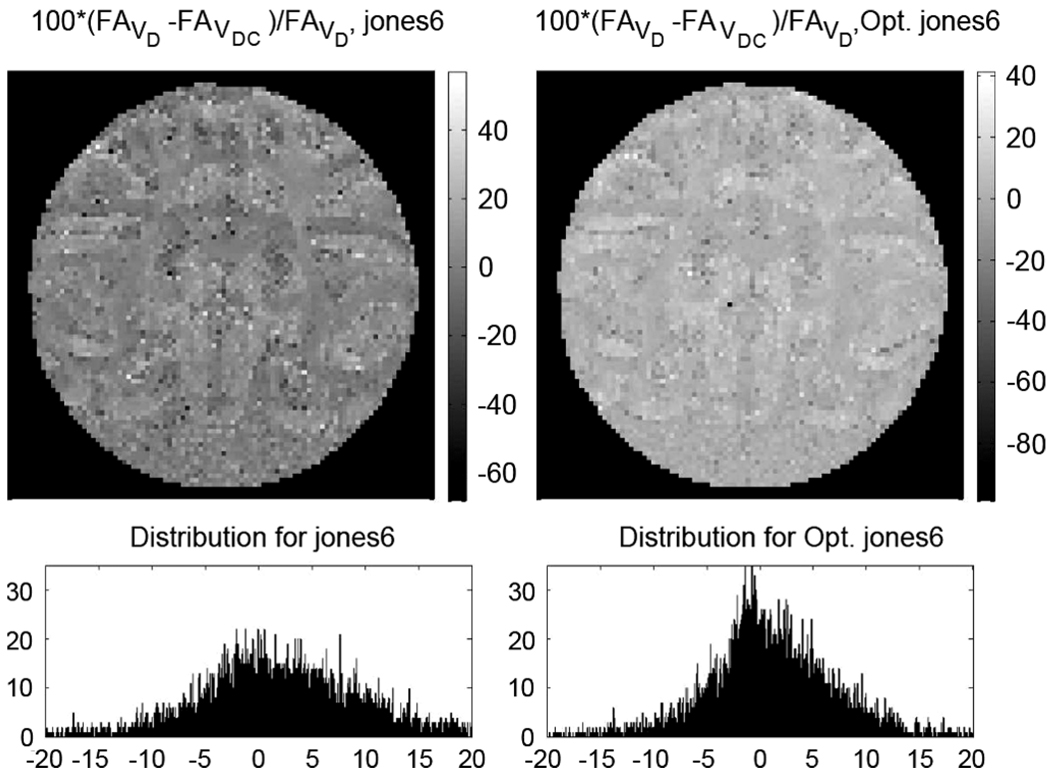
For the ex vivo sample, the true F A values are unknown but the F A maps of Fig. 4 present a great deal of information about the anatomical structure with known characteristics. The optimal DGS elucidates the subcortical U-fibers, which are not visible with the nonoptimal DGS. Also, the separation of the adjacent gyri is much better with the optimal scheme. Fig. 5 shows that the minimization of the eigenvalue difference, which is the main aim of the optimization criterion, reflects well on the fractional anisotropy. The relative F A difference for optimal DGS is lower and more homogenous over the baboon brain than the one from the nonoptimal version.

Fig. 5.

The relative difference between the fractional anisotropy maps obtained using “all gradients,” V, and “diffusion gradients only,” V_D (equivalently NoCroT) for the non-optimal and optimal versions of Jones6 DGS: 100 × (F A_VD – F A_V)/F A_VD. The distribution of the difference is highly concentrated around 0 on the second row right column for the optimal DGS, whereas for the nonoptimal scheme it is much more dispersed as shown on the left column. For the optimal DGS, the F A values obtained with and without the imaging gradients in the calculations are homogenously closer than the ones from the nonoptimal DGS.

V. CONCLUSION AND FUTURE DIRECTIONS

As it is summarized in the Appendix A–C, [14] and [15] show that the DTI model equations cannot be resolutely written when the imaging gradients are needed to be included to obtain a complete model. The following, which is realized in [14], is one of the motivators of this work:

The decrease of the accuracy for the inclusion of all of the gradients validates the existence of modeling incongruities in Diffusion Tensor Imaging model.

The profound challenge is to overcome DTI’s theoretical inability to provide the account of the imaging gradients for a complete model, using the best available theoretical information within the model itself. Motivated by the lack of an exact description, this manuscript created a new and robust method for designing appropriate DGSs that minimize the effect of the imaging gradients in the DTI equations by positioning and orienting the cone defined by the diffusion gradient vectors so that the imaging gradients appear not be in place. The goal, which was initiated by the usage of the center symmetric DGSs in [14] and [15], also encompasses the elimination of the directional awareness created by the imaging gradients.

Although the optimization objective-bringing closer the eigenvalues estimated with and without the inclusion of the imaging gradients-was achieved with the bonus of model matching error reduction for the optimal DGSs, for the water sample the more complete model, “all gradients,” V, still reports higher model matching error and higher anisotropy than the calculations that ignore the imaging gradients, i.e., NoCroT. In other words despite quantitative improvements with the optimized DGSs, qualitatively the behavior of the DTI model remains the same whether optimal or nonoptimal DGSs are used.

The model matching error and water sample’s anisotropy is consistently lowered for estimation with V throughout the optimal DGSs. This a benefit of the optimization procedure for “all gradients.” But the increase in $\overline{FA}$ for the majority of the optimal DGSs in NoCroT despite the consistent reduction of model matching error and attained optimization objective, is a reflection of modeling incongruities of the DTI method. Moreover, these observations are also valid for nonlinear estimation [17], fortifying the last remark. Therefore, the DTI model is not powerful enough to capture adequately the essence of the diffusion-weighted MRI signal.

Despite these deficiencies, the simplicity of DTI method makes it still a useful protocol. The optimization method introduced in this manuscript improved the quality of the information obtained by DTI: The superior anatomical resolution provided by the optimal DGS originates from the elimination of the directional awareness and establishes a stronger foundation for the fiber tracking algorithms (see Fig. 4). Also, the optimal DGS minimized the effect of the modeling incongruity by bringing closer the results obtained with and without the imaging gradients for the eigenvalues and consequently for the F A map (see Fig. 5).

In brief, the optimization problem furnished valuable tools to maximize the usefulness of the DTI method.

In this work, the optimization problem was posed for DGSs with six vectors mainly because Theorem 1 and 2 are valid for square matrices. The addition of the six center symmetric counterparts is for taking advantage of NoCroT method. The twelve vector DGSs force the usage of least squares estimation rather than matrix inversion. For acquisitions with arbitrary number of DGS vectors (m > 6), a different and more complicated perturbation theorem [33] concerning the least squares estimation comes into play. Further investigations of this subject are left for future research with important considerations for clinical practice. For example, the adoption of the manuscript’s optimization framework can significantly influence the results of [34] and [35] where the organization and acquisition order of DGSs are arranged to minimize the impact of partial scans, e.g., due to patient motion, for salvaging efficiently the results that would otherwise be lost.

APPENDIX A

BRIEF DERIVATION OF THE DTI ESTIMATION EQUATIONS IN THE LINEAR ALGEBRAIC FRAMEWORK

In this section, the derivation of the coefficient matrix V that is presented in full details in [14] is concisely reviewed.

A) The Estimation Equation

The solution of Stejskal and Tanner for the NMR pulsed-gradient spin-echo (PGSE) experiments [10] has been directly translated to MR-DTI experiments in [11] and [12]. The translation in [11], (3), is written here in its most general form by replacing the spin-echo image S₀ with S_p that is related to the proton density

$$S(G,t)=S_p\text{exp}\left(-{\mathrm{\gamma }}^2{\displaystyle {\int }_0^{t}h(G,\zeta )D{[h(G,\zeta )]}^{T}d\zeta }\right)$$ (15)

where G(·) = [G_x(·) G_y(·) G_z(·)] denotes the time course of the magnetic field gradient vector, γ is the gyromagnetic ratio, S denotes the signal intensity at each pixel. The initial time, 0, is taken in this manuscript as the time “immediately following the 90° pulse” [36]. The time t is chosen to be T_E, the echo time. The analytic form of the vector valued function h for the PGSE imaging experiment is derived by incorporating the unit step function for the sign change created by the π-pulse

$$h(G,\zeta )={\displaystyle {\int }_0^{\zeta }G(\xi )d\xi -2u(\zeta -\tau ){\displaystyle {\int }_0^{\tau }G(\xi )d\xi }}$$ (16)

where τ is the time of the π-pulse and u(·) denotes the unit step function.

By the appearance of D as a quadratic from acting on h in (15), D is a symmetric 3 × 3 matrix that is represented as a vector d ∈ ℝ⁶

$$d={[d_1\cdots d_6]}^T\mapsto D=\left[\begin{array}{ccc}\hfill d_1\hfill & \hfill d_4\hfill & \hfill d_6\hfill \\ \hfill d_4\hfill & \hfill d_2\hfill & \hfill d_5\hfill \\ \hfill d_6\hfill & \hfill d_5\hfill & \hfill d_3\hfill \end{array}\right].$$ (17)

For a fixed h ∈ ℝ³, the argument of the exponential function in (15) becomes a linear function of D and therefore it is expressed as the product of a row vector υ_i and d

$${\upsilon }_{i}d={\displaystyle {\int }_0^{t}h(G_i,\zeta )D{[h(G_i,\zeta )]}^{T}d\zeta }$$ (18)

where the subscript i corresponds to the acquisition with the i^th diffusion gradient vector. Equation (15) transforms to

$$S({\upsilon }_{i}d)\doteq S_p\text{exp}(-{\mathrm{\gamma }}^2{\upsilon }_{i}d)=S_i$$ (19)

and after the application the logarithm, the linear estimation equation is obtained

$${\mathrm{\gamma }}^2{\upsilon }_{i}d=-\text{ln}\left(\frac{S_i}{S_p}\right)=\text{ln}{S}_p-\text{ln}{S}_i.$$ (20)

Here, the substraction on the right is preferred to emphasize the reduction of propagation of errors in numerical implementation. Stacking the row vectors υ_i to form a matrix V and using m, measurements to form a vector

$$p_r={[\text{ln}(S_p)-\text{ln}(S_1),\dots ,\text{ln}(S_p)-\text{ln}(S_m)]}^T$$ (21)

the linear equations for the estimation of the diffusion matrix are written as

$${\mathrm{\gamma }}^{2}Vd=p_r.$$ (22)

This expression is the true governing equation for DTI experiments and consequently the optimization problem is posed based on the coefficient matrix V.

Ideally, in order to obtain an impartial observation, S_p ought to be obtained from an imaging experiment other than DTI. Nevertheless, S_p can be estimated by adding another (minimum seventh) acquisition

$$\begin{array}{cc}\left[\begin{array}{cc}\hfill {\upsilon }_1\hfill & \hfill -1\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill {\upsilon }_7\hfill & \hfill -1\hfill \end{array}\right]\left[\begin{array}{c}\hfill d\hfill \\ \hfill \frac{\text{ln}(S_p)}{{\mathrm{\gamma }}^2}\hfill \end{array}\right]\hfill & =[V-\mathrm{𝟙}]\left[\begin{array}{c}\hfill d\hfill \\ \hfill \frac{\text{ln}(S_p)}{{\mathrm{\gamma }}^2}\hfill \end{array}\right]\hfill \\ \hfill & =-\frac{1}{{\mathrm{\gamma }}^2}\left[\begin{array}{c}\hfill \text{ln}(S_1)\hfill \\ \hfill ⋮\hfill \\ \hfill \text{ln}(S_7)\hfill \end{array}\right].\hfill \end{array}$$ (23)

The augmented coefficient matrix uses V rather than V_D that is used by Papadakis et al. [32] in the method called total fitting.

However, in practice, the image obtained without any diffusion gradients, S₀, is used to replace S_p as described in the Appendix A–C.

B) Components of V

The magnetic gradient vector G, is the sum of two components corresponding to the diffusion sensitizing gradients and to the imaging gradients

$$G_i=G_{iD}+G_I.$$

Using this decomposition and the linearity of h from (16)

$$h(G_D+G_I)=h(G_D)+h(G_I)$$

V is formulated in (31) with three components corresponding to diffusion gradients V_D, imaging gradients V_I, and the cross terms between them, V_C. V is calculated explicitly by calculating each of the components as follows.

Although the vector G_iD changes at each acquisition, G_I defined by the MR slice parameters (slice thickness, field of view) is fixed. Without loss of generality, the coordinate frame is taken as the frame defined by the read-out (x = ro), phase-encode (y = pe), and slice select (z = ss) axes

$$G_I(\xi )=[{\beta }_{ro}(\xi ){\beta }_{pe}(\xi ){\beta }_{ss}(\xi )]$$ (24)

where each β describes the on-off times and the strength of each gradient channel as shown in Fig. 6. Similarly, G_iD is written as a product of a scalar function and of a vector (not necessarily of unit norm)

$$G_{iD}(\xi )={\beta }_D(\xi )g_i.$$ (25)

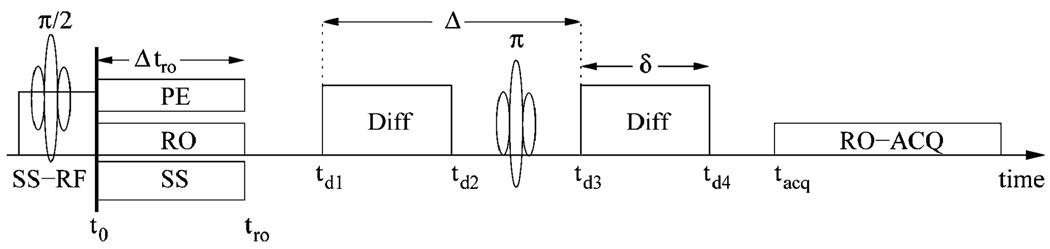
Fig. 6.

The pulsed-gradient spin-echo pulse sequence and the definition of the variables used in the calculations. RO is for read-out, PE for phase-encode, SS is the slice select gradient and ACQ stands for the digital to analog conversion acquisition.

The calculation in (16) is systematically carried for different gradient types using the scalar valued integral

$${\mu }_{*}(\zeta )={\displaystyle {\int }_0^{\zeta }{\beta }_{*}(\xi )d\xi }-2u(\zeta -\tau ){\displaystyle {\int }_0^{\tau }{\beta }_{*}(\xi )d\xi }$$ (26)

to obtain from (16)

$$h(G_{*},\zeta )={\mu }_{*}(\zeta )g_{*}={\mu }_{*}(\zeta )[g_{*x}{g}_{*y}{g}_{*z}].$$ (27)

The asterisk can be any of the labels ro, pe, ss for imaging or D for diffusion gradients.

The calculation of V_I in (31) only requires one row vector

$${\displaystyle {\int }_0^t[{\mu }_{ro}^2{\mu }_{pe}^2{\mu }_{ss}^{2}2{\mu }_{ro}{\mu }_{pe}2{\mu }_{pe}{\mu }_{ss}2{\mu }_{ro}{\mu }_{ss}]d\zeta .}$$ (28)

On the other hand V_D is calculated as the product of a scalar and a matrix

$$V_D=b_t{V}_g$$ (29)

where V_g is the m × 6 matrix

$$\left[\begin{array}{cccccc}\hfill g_{1x}^2\hfill & \hfill g_{1y}^2\hfill & \hfill g_{1z}^2\hfill & \hfill 2g_{1x}{g}_{1y}\hfill & \hfill 2g_{1y}{g}_{1z}\hfill & \hfill 2g_{1x}{g}_{1z}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill g_{mx}^2\hfill & \hfill g_{my}^2\hfill & \hfill g_{mz}^2\hfill & \hfill 2g_{mx}{g}_{my}\hfill & \hfill 2g_{my}{g}_{mz}\hfill & \hfill 2g_{mx}{g}_{mz}\hfill \end{array}\right]$$ (30)

$$\begin{array}{cc}V=\hfill & {\displaystyle {\int }_0^t}\left[\begin{array}{ccc}\hfill h_x^2(G_{1D})\hfill & \hfill \cdots \hfill & \hfill 2h_x(G_{1D})h_z(G_{1D})\hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill ⋮\hfill \\ \hfill h_x^2(G_{mD})\hfill & \hfill \cdots \hfill & \hfill 2h_x(G_{mD})h_z(G_{mD})\hfill \end{array}\right]d\zeta +{\displaystyle {\int }_0^t}\left[\begin{array}{ccc}\hfill h_x^2(G_I)\hfill & \hfill \cdots \hfill & \hfill 2h_x(G_I)h_z(G_I)\hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill ⋮\hfill \\ \hfill h_x^2(G_I)\hfill & \hfill \cdots \hfill & \hfill 2h_x(G_I)h_z(G_I)\hfill \end{array}\right]d\zeta +2{\displaystyle {\int }_0^t}\left[\begin{array}{ccc}\hfill h_x(G_{1D})h_x(G_I)\hfill & \hfill \cdots \hfill & \hfill h_x(G_{1D})h_z(G_I)+h_x(G_I)h_z(G_{1D})\hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill ⋮\hfill \\ \hfill h_x(G_{mD})h_x(G_I)\hfill & \hfill \cdots \hfill & \hfill h_x(G_{mD})h_z(G_I)+h_x(G_I)h_z(G_{mD})\hfill \end{array}\right]d\zeta \hfill \\ \hfill & =V_D+V_I+V_C=b_t{V}_g+V_I+V_{C(g)}.\hfill \end{array}$$ (31)

$$V_C=2{\displaystyle {\int }_0^t{\mu }_D}\left[\begin{array}{cccccc}\hfill {\mu }_{ro}{g}_{1x}\hfill & \hfill {\mu }_{pe}{g}_{1y}\hfill & \hfill {\mu }_{ss}{g}_{1z}\hfill & \hfill ({\mu }_{pe}{g}_{1x}+{\mu }_{ro}{g}_{1y})\hfill & \hfill ({\mu }_{pe}{g}_{1y}+{\mu }_{ss}{g}_{1z})\hfill & \hfill ({\mu }_{ss}{g}_{1x}+{\mu }_{ro}{g}_{1z})\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill {\mu }_{ro}{g}_{mx}\hfill & \hfill {\mu }_{pe}{g}_{my}\hfill & \hfill {\mu }_{ss}{g}_{mz}\hfill & \hfill ({\mu }_{pe}{g}_{mx}+{\mu }_{ro}{g}_{my})\hfill & \hfill ({\mu }_{pe}{g}_{my}+{\mu }_{ss}{g}_{mz})\hfill & \hfill ({\mu }_{ss}{g}_{mx}+{\mu }_{ro}{g}_{mz})\hfill \end{array}\right]d\zeta .$$ (32)

(see (31) and (32) at the bottom of the page) and b_t is calculated using (26) and (27):

$$\begin{array}{cc}{b}_t\hfill & ={\displaystyle {\int }_0^t{\left({\displaystyle {\int }_0^{\zeta }{\beta }_D(\xi )d\xi -2u(\zeta -\tau ){\displaystyle {\int }_0^{\tau }{\beta }_D(\xi )d\xi }}\right)}^{2}d\zeta }\hfill \\ \hfill & ={\displaystyle {\int }_0^t{\mu }_D^2(\zeta )d\zeta .}\hfill \end{array}$$ (33)

For example, the scalar factor of rectangular diffusion gradient pulses is b_t = δ² (Δ – δ/3) and for trapezoidal pulses it is ${\delta }^2(\mathrm{\Delta }-\delta /3)-\delta t_{\text{rise}}^2/6+t_{\text{rise}}^3/30$ where δ is the length of the pulses, Δ is the time between them, and t_rise is the time for the gradients to reach a specified value.

Note that b_t involves only the switching times of the gradients, and the b-value given in the literature is equal to the product of ${\mathrm{\gamma }}^2{b}_t\parallel g_i{\parallel }_2^2$. The factorization of V_D in (29) with a pure function of switching times, b_t, and V_g that is a function of the diffusion gradient vectors is the key factor for the definition and the implementation of the geometric optimization problem (13) in Section II-D.

The cross terms matrix, V_C(g) is calculated as a function of the diffusion gradient scheme g as shown in (32). Finally, (22) is written explicitly as

$${\mathrm{\gamma }}^2(b_t{V}_g+V_I+V_{C(g)})d=p_r.$$ (34)

C) Estimation With the Spin-Echo Image S₀

The reference image obtained without diffusion gradients, S₀, is obtained by turning off the diffusion gradients resulting in the row vector υ_I of (28) in for the calculation of (18)

$$S_0=S_p\text{exp}(-{\mathrm{\gamma }}^2{\upsilon }_{I}d).$$ (35)

Since S_p is not directly available, the usual approach is to replace it by writing (19) as

$$S({\upsilon }_{i}d)\doteq S_0\text{exp}(-{\mathrm{\gamma }}^2({\upsilon }_i-{\upsilon }_I)d)=S_i.$$ (36)

Applying the logarithm to this equation yields

$${\mathrm{\gamma }}^2({\upsilon }_i-{\upsilon }_I)d=-\text{ln}\left(\frac{S_i}{S_0}\right)=\text{ln}{S}_0-\text{ln}{S}_i.$$ (37)

With

$$p={[\text{ln}(S_0)-\text{ln}(S_1),\dots ,\text{ ln}(S_0)-\text{ln}(S_m)]}^T$$ (38)

the linear equations are written as

$${\mathrm{\gamma }}^2(V-V_I)d={\mathrm{\gamma }}^2{V}_{DC}d=p.$$ (39)

D) No Cross Terms Estimation: NoCroT

The main difference between the diffusion-weighted NMR and MRI experiments is that in the former the estimation is based on a single point-the peak of the signal-whereas the DTI model uses the pixel intensity (15) and (19) that originates from the entirety of the k-space lines.

The read-out and the slice select gradients, and therefore β_ro and β_ss in (24), have fixed values in Fig. 6 and in all of the computations of Appendix A–B. However, the phase-encode gradient, thus β_pe, changes at each k-space line. It is, therefore, not clear which value of the phase-encoding gradient to utilize in the estimation equations. When the equations are solved for different phase-encode gradient strengths, the eigenvectors align with the direction dictated by those strengths [14] regardless of whether least squares or nonlinear estimation [17] is utilized. Taking the strength to be equal to zero is equivalent to completely neglecting the phase-encode gradient which defeats the purpose of deriving a complete model.

Moreover, because the imaging gradients do not possess null moments, the integral of µ_ro, µ_pe and µ_ss do not form a plateau around T_E in (15). In consequence [14], each of the k-space sample points collected during the readout acquisition period is differently diffusion sensitized. In other words, V_C(g) in (32) and V_I in (28) and (31) are in fact not well defined.

The resolution of this indeterminateness proposed in [14], [15] relies on the properties of the coefficient matrices originating from (30) and (32): when the sign of the DGS is changed, V_D remains the same, because V_g = V_(−g) while the cross terms matrix changes sign, V_C(−g) = −V_C(g). Experiments performed with center-symmetric DGSs, i.e., with (g, −g) = (g₁, …, g_m/2, −g₁, …, −g_m/2) result in

$${\mathrm{\gamma }}^2\left[\begin{array}{c}\hfill b_t{V}_g+V_{C(g)}\hfill \\ \hfill b_t{V}_{(-g)}+V_{C(-g)}\hfill \end{array}\right]d=\left[\begin{array}{c}\hfill p_1\hfill \\ \hfill p_2\hfill \end{array}\right].$$ (40)

The sum of the equations in (40) yield

$$\begin{array}{cc}2{\mathrm{\gamma }}^2{b}_t{V}_{g}d\hfill & =\left[\begin{array}{c}\hfill 2\text{ln}{S}_0-\text{ln}{S}_1-\text{ln}{S}_{(m/2+1)}\hfill \\ \hfill ⋮\hfill \\ \hfill 2\text{ln}{S}_0-\text{ln}{S}_{m/2}-\text{ln}{S}_m\hfill \end{array}\right]\hfill \\ \hfill & =p_1+p_2(\text{NoCroT}).\hfill \end{array}$$ (41)

This is equivalent to solving the following set of inconsistent equations:

$${\mathrm{\gamma }}^2\left[\begin{array}{c}\hfill V_D\hfill \\ \hfill V_D\hfill \end{array}\right]d=\left[\begin{array}{c}\hfill p_1\hfill \\ \hfill p_2\hfill \end{array}\right]$$ (42)

by least squares estimation. Hence, the center-symmetric gradient schemes guarantee that the NoCroT portion of the complete set of DTI estimation equations is equivalent to completely neglecting the imaging gradients from the equations.

The cross terms matrix, V_C, does not appear in (41) or (42), hence the name “No Cross Terms:” NoCroT is adopted. The central assumption behind the NoCroT strategy is that irrespective of the true nature of the indeterminateness, the sign change in the DGS causes a sign change in V_C. The correct way to choose the center-symmetric diffusion gradients is to first select 6 vectors that will ensure the full rank condition on V_g [16], [18] and then add their center-symmetric counterparts to obtain V_(g,−g) with full rank.

APPENDIX B

SUMMARY OF THE RESULTS

In this section, Tables II–IV are presented.

APPENDIX C

GRADIENT SCHEMES USED IN THE EXPERIMENTS

In this section, Tables V–VII are presented.