Validity of the Actical for estimating free-living physical activity

Abstract

The purpose of this study was twofold: (1) develop a refined 2-regression model for the Actical which predicts METs every 15 s, and (2) compare the refined and 2008 Crouter 2-regression models and the Klippel and Heil equations during free-living activity. To develop the refined 2-regression model, 48 participants (mean ± SD; age 35 ± 11.4 years) performed 10-min bouts of various activities ranging from sedentary to vigorous intensity. An Actical accelerometer was worn on the left hip, and a Cosmed K4b² was used to measure oxygen consumption. For the free-living measurements, 29 participants (age, 38 ± 11.7 years; BMI, 25.0 ± 4.6 kg m⁻²) were monitored for approximately 6 h during work (N = 23) or leisure time (N = 9) while wearing an Actical and Cosmed. Actical prediction equations were compared against the Cosmed for METs and time spent in sedentary behaviors, light physical activity (LPA), moderate PA (MPA), vigorous PA (VPA), and moderate and vigorous PA (MVPA). The refined 2-regression model developed used an exponential regression equation and a linear equation to predict METs every 15 s for walking/running and intermittent lifestyle activities, respectively. Based on the free-living measurement, the refined 2-regression model was the only method that was not significantly different from the Cosmed for estimating time spent in sedentary behaviors, LPA, and MVPA (P > 0.05). On average, compared to the Cosmed, the refined 2-regression model and the Klippel and Heil equations had similar mean errors for average METs.

Introduction

Over the past decade, the use of accelerometer-based activity monitors for objective measurement of physical activity (PA) has become more widespread. These devices have been used in the US National Health and Nutrition Examination Survey (Troiano et al. 2008) and the Canadian Health Measures Survey (Tremblay et al. 2007). Accelerometers have advantages over self-report measures such as being able to track the intensity, duration, and frequency of free-living PA, without relying on participants to recall their activity. In addition, estimated values for energy expenditure (EE) and time spent in light PA [LPA; <3 metabolic equivalents (METs)], moderate PA (MPA; 3–6 METs), and vigorous PA (VPA; ≥6 METs) can be estimated with minimal subject burden.

Currently, there are several types of accelerometer-based activity monitors, but the Actical and ActiGraph (formerly Manufacturing Technology Incorporated ActiGraph and Computer Science Applications Inc.) accelerometers are two of the most commonly used in research studies. These devices have some distinct differences, however, which preclude the equations developed on one device from being used on the other. For example, they have different filters that result in different count values for the same activity. They also have different specifications for the minimum epoch that can be used. With the Actical, the shortest epoch setting is 15 s, while the ActiGraph can collect and store count data every second. Thus, it is important to consider each device separately.

The Actical accelerometer, while widely used, has only a few calibration equations relating the accelerometer counts to EE: four for children (Puyau et al. 2004; Pfeiffer et al. 2006; Corder et al. 2005; Evenson et al. 2008) and three for adults (Heil 2006; Crouter and Bassett 2008; Klippel and Heil 2003). Most of the equations for the Actical use a single regression equation to relate the accelerometer counts and EE. In addition, these equations were typically developed on a small number of activities and/or subjects, which limits their validity under free-living conditions. Recently, Crouter and Bassett (2008) developed a 2-regression model for the Actical accelerometer, which incorporated three parts: (1) an inactivity threshold below which the individual was credited with 1 MET; (2) when the inactivity threshold was exceeded and the coefficient of variation (CV) of four consecutive 15-s epochs was ≤13% (indicating that the individual was performing continuous walking or running) a walk/run regression equation was used; and (3) when the inactivity threshold was exceeded and the CV was >13% (indicating that the individual was performing an intermittent lifestyle activity), a lifestyle regression equation was used. By distinguishing between continuous walking/running and intermittent lifestyle activities, the 2008 Crouter 2-regression model provided a substantial improvement over the Klippel and Heil equations (Klippel and Heil 2003) developed for the Actical (Crouter and Bassett 2008). Specifically, for estimating METs, the 2008 Crouter 2-regression model was within 0.10 METs [root mean-square error (RMSE), 0.58] of measured METs across 17 different structured activities, and the Klippel and Heil equations were significantly different from measured METs with a mean error of 0.8 METs (RMSE, 1.19–1.25). In addition, the 2008 Crouter 2-regression model provided the closest estimate of time spent in LPA, MPA, and VPA during structured activity bouts (Crouter and Bassett 2008).

A limitation to the 2008 Crouter 2-regression model for the Actical is that it may have a problem detecting continuous walking and running bouts when the activity bout starts in the middle of a minute on the Actical clock (Crouter et al. 2009; Kuffel et al. 2008). Specifically, this is due to the 2-regression model being developed on structured activity bouts and the model was trained to look at each minute of data when the activity started and stopped exactly on the minute of the Actical clock, which is not how PA is performed in free-living situations. Thus, when a walking/ running bout starts or stops in the middle of a minute, it will have a high CV, resulting in that minute being misclassified as an intermittent lifestyle activity, which ultimately results in an overestimation of EE and time spent in MPA and VPA.

The purpose of this study was twofold: (1) develop a refined 2-regression model for the Actical, which will examine each 15-s epoch and all combinations of the three adjacent epochs, so that a walking/running bout could be detected to the nearest 15 s, and (2) compare the refined 2-regression model for the Actical to the 2008 Crouter 2-regression model and the Klippel and Heil equations (Klippel and Heil 2003) to indirect calorimetry during a 6-h free-living measurement period.

Methods

Development of refined 2-regression model for the Actical

This was part of a larger study and the participant characteristics and methods are published elsewhere (Crouter and Bassett 2008; Crouter et al. 2006a, b, 2008a,b, 2009). In addition, the subjects and data used to develop the refined 2-regression model for the Actical are the same as those used for the development and cross-validation of the original 2008 Crouter 2-regression model. For a complete description see Crouter and Bassett (2008). Briefly, 48 participants [24 men and 24 women; mean (SD) age = 35 (11.4) years, height = 172.7 (9.7) cm, weight = 73.1 (19.6) kg, BMI = 24.2 (4.8) kg m⁻², and resting VO₂ = 3.5 (0.9) ml kg⁻¹ min⁻¹) from The University of Tennessee, Knoxville, and surrounding community volunteered to participate in the study. The procedures were reviewed and approved by the University of Tennessee Institutional Review Board before the start of the study. Each participant signed a written informed consent and completed a Physical Activity Readiness Questionnaire before participating in the study.

Prior to testing, participants had their height and weight measured (in light clothing, without shoes) using a stadiometer and physician’s scale, respectively. Participants then performed one of three structured physical activity routines, which consisted of six activities (Table 1). Each routine was performed by 20 participants (2 participants performed all three routines and 8 performed two routines). Each activity was performed for 10 min with a 1–2 min break between activities. The activities were performed in order from the lowest to the highest intensity. During all testing, an Actical accelerometer was worn on the left hip and metabolic data were measured simultaneously using a portable indirect calorimeter (Cosmed K4b², Rome, Italy).

Table 1.

Activities performed in each routine

Routine 1	Routine 2	Routine 3
Lying	Slow track walk (~3 mph)	Vacuuming
Standing	Fast track walk (~4 mph)	Sweeping/mopping
Computer work	Basketball	Washing windows
Filing papers	Racquetball	Washing dishes
Ascending/descending stairs	Slow track run (~5 mph)	Lawn mowing
Stationary cycling (~100 Watts)	Fast track run (~7 mph)	Raking grass/leaves

Indirect calorimetry

The Cosmed K4b² is a lightweight device, which has been shown to be valid for measuring VO₂ and VCO₂, compared to the Douglas Bag method, during cycle ergometry (McLaughlin et al. 2001). Prior to each test the oxygen and carbon dioxide analyzers and the flow turbine were calibrated according to the manufacturer’s instructions, which consisted of a room air calibration, gas calibration, volume calibration, and a delay calibration. During each test, a gel seal was used to help prevent air leaks from the face mask. Data from the Cosmed were stored in memory and downloaded to a laptop computer at the completion of each test.

Actical accelerometer

The Actical accelerometer is a small (28 × 27 × 10 mm) device that uses an omni-directional accelerometer and weighs 17 g. The Actical can measure accelerations in the range of 0.05–2.0 G and is sensitive to movements in the range of 0.35–3.5 Hz. The Actical was worn at waist level attached to a belt in the left anterior axillary line. The device was initialized using 15-s epochs and the time was synchronized with a digital clock so the start time could be synchronized with the Cosmed K4b². At the conclusion of each test, the Actical data were downloaded to a laptop computer for subsequent analysis. Three Actical accelerometers were used during the study and the device used was picked at random for each participant. The Actical accelerometers were calibrated at the factory, where calibration offset factors were entered into the memory. At the end of the study, the Actical accelerometers were returned to be recalibrated and it was found to be within 1% of the initial calibration.

Data analysis

For each activity, minutes 4–9 were averaged and used for the analysis. Breath-by-breath data were collected by the Cosmed K4b², which were averaged over a 1-min period. For each minute of measurement, the VO₂ (ml min⁻¹) was converted to VO₂ (ml kg⁻¹ min⁻¹) and then to METs (1 MET = 3.5 ml kg⁻¹ min⁻¹).

For the development of the refined 2-regression model, all participants and activities were used, except for cycling. Cycling was excluded because waist-mounted accelerometers were not able to detect this activity.

Following the same principles that were used to develop the 2008 Crouter 2-regression model, each activity for each participant was classified into groups based on the CV value of four consecutive 15-s epochs: CV from 0.1 to 13% (CV ≤ 13) and CV of >13%. For activities such as lying, sitting, and standing, where the counts could be zero for a full minute (thus, a CV cannot be calculated), they were placed in the CV > 13 group for the purpose of developing the regression equation. We chose to include lying, sitting, and standing in the CV > 13 group for several reasons. First, they are more representative of intermittent lifestyle activities; while the majority of the time their counts were below the sedentary cut point, this was not always the case. Also, by including them in the model, it helped to anchor the y axis and improved the predictive validity for activities with low activity counts. For example, during the development of the 2008 2-regression model for the Actical (Crouter and Bassett 2008), if the lying, sitting, and standing activities were not included, the y axis crossing was greater than three METs. This would result in predicting zero minutes of light activity since once could not predict a MET value below 3. The same was true when developing the refined 2-regression model for the Actical; thus, inclusion of sedentary activities in the development of the lifestyle equation is necessary. Regression analysis was then used to develop a walk/run equation and a lifestyle equation that predicted EE (METs) for each 15-s epoch.

To overcome the potential problem of misclassifying walking/running bouts that start or stop in the middle of a minute on the Actical clock, each 15-s epoch and all combinations of the three adjacent 15-s epochs were examined to determine whether each 15-s epoch was part of a walking/ running bout or intermittent lifestyle activity bout. Specifically, each 15-s epoch was examined in the following manner: 15-s epoch of interest and (1) the three preceding 15-s epochs, (2) the two preceding 15-s epochs and one 15-s epoch that followed, (3) the one preceding 15-s epoch before and the two 15-s that followed, and (4) the three 15-s epochs that followed. After the four CV values were calculated, the lowest CV of these four was used. If the CV was ≤13% it was deemed to be part of a continuous walking/ running bout, and the walk/run equation was used. In contrast, if the CV was >13%, then the intermittent lifestyle activity equation was used. By examining each 15-s epoch separately in this way, we could determine whether the epoch was part of a continuous walking/running bout lasting 1 min or longer (Appendix Tables 1, 2).

Table 2.

Physical characteristics of the participants in the 6-h free-living study [mean ± SD (range)]

Variable	Male (N = 12)	Female (N = 17)	All Participants (N = 29)
Age (year)	26 ± 4.9 (23–54)	25 ± 4.6 (20–55)	25 ± 4.6 (20–55)
Height (cm)	180.4 ± 9.1 (159.8–193.5)	162.4 ± 6.7 (153.1–172.9)	169.8 ± 11.9 (153.1–193.5)
Body Mass (kg)	83.0 ± 16.4 (52.6–122.3)	64.8 ± 9.9 (45.4–85.7)	72.3 ± 15.6 (45.4–122.3)
BMI (kg m−2)	25.5 ± 4.9 (20.6–37.4)	24.7 ± 4.6 (19.4–36.3)	25.0 ± 4.6 (19.4–37.4)

BMI body mass index

Six-hour validation study

Subjects

A total of 12 males and 17 females from Cornell University and the surrounding community volunteered to participate in a 6-h free-living study, to examine the validity of the refined 2-regression model and other Actical equations. The procedures were reviewed and approved by the Institutional Review Boards at Cornell University and The University of Tennessee, Knoxville before the start of the study. Prior to beginning the study, each participant signed a written informed consent and completed a Physical Activity Readiness Questionnaire. Participants were excluded from the study if they had any contraindications to exercise. The physical characteristics of the participants are shown in Table 2.

Procedures

Prior to testing, participants had their height and weight measured (in light clothing, without shoes) using a stadiometer and a physician’s scale, respectively. The participant was then fitted with a portable metabolic measurement system (Cosmed K4b², Cosmed, S.r.l., Italy) and an Actical accelerometer on the left hip. Three Actical accelerometers, which were different from the ones used to develop the 2008 and refined 2-regression models, were used during the study and the device used was picked at random for each participant. Breath-by-breath oxygen uptake (VO₂) and accelerometer data were collected simultaneously for a 5 to 6-h period except for an intermittent (10–15 min) break every 2 h to change the battery of the Cosmed system and to allow the participant to drink water if needed. A total of 23 participants were measured while they were at work and 9 were measured during their leisure time outside of the working day. Three participants completed both conditions. Throughout the 6-h measurement period, an investigator monitored their activity, but did not directly influence the activities they performed. The participants were asked to go about their normal routine. The Cosmed K4b² and Actical accelerometer were worn and calibrated as described above.

Data analysis

Breath-by-breath data were collected by the Cosmed K4b², which were averaged over a 1-min period. For each minute of measurement, the VO₂ (ml min⁻¹) was converted to METs. We chose to calculate METs in two different ways. This is due to the research literature suggesting that the standard definition of a MET (1 MET = 3.5 ml kg⁻¹ min⁻¹) does not always hold true in the general population, especially in obese individuals (Byrne et al. 2005; Kozey et al. 2010a, b). Thus, we present METs as the measured VO₂/3.5 ml kg⁻¹ min⁻¹ (MET_standard) and as measured VO₂/predicted RMR (MET_predictedRMR). Since we did not have a measured RMR on the participants, we chose to use the Harris–Benedict equation to predict RMR (Harris and Benedict 1919).

For the Actical, CV was calculated for each minute by using four consecutive 15-s epochs within a minute (2008 Crouter 2-regression model). We also examined the 15-s epoch and all combinations of the three adjacent epochs (refined 2-regression model). Energy expenditure (METs) was then calculated based on the CV values for the 2008 Crouter 2-regression model (Crouter and Bassett 2008) and refined Crouter 2-regression model for each minute of the measurement period. In addition, the Actical software has two equations to predict METs from the activity counts per minute. These equations were developed by Klippel and Heil (2003): one uses a single regression line (Klippel and Heil 1-regression equation) and the other uses a 2-regression equation (Klippel and Heil 2-regression equation). The MET levels for each minute of measurement were also calculated using both Klippel and Heil equations so that they could be compared against the 2008 and Refined Crouter 2-regression models. The Klippel and Heil regression equations were developed on 24 adults, who performed ten activities ranging from supine rest to treadmill running (Klippel and Heil 2003). These equations are unpublished, but preliminary results using these equations have been presented in an abstract (Klippel and Heil 2003). The methodology and subjects used to develop the equations are presented by Heil (2006) in an article that published the Actical activity energy expenditure (AEE) equations.

For the Cosmed data and each accelerometer prediction equation, average time spent in sedentary behaviors, LPA, MPA, VPA and moderate-to-vigorous PA (MVPA) were calculated, as well as an average MET value for the measurement period.

Statistical treatment

Statistical analyses were carried out using SPSS version 17.0 for Windows (SPSS Inc., Chicago, IL, USA). For all analyses, an alpha level of 0.05 was used to indicate statistical significance. All values are reported as mean ± standard deviation (SD). Pairwise comparisons with Bonferroni adjustments were used to compare actual (MET_standard and MET_{predicted RMR}) and predicted METs from the accelerometer equations and time spent in sedentary behaviors, LPA, MPA, VPA, and MVPA.

Modified Bland–Altman plots were used to graphically illustrate the variability in individual error scores (actual minus predicted) during the 6-h measurement period for average MET value, sedentary behaviors, LPA, and MVPA (Bland and Altman 1986). This allowed for the mean error score and 95% prediction interval (95%PI) to be shown. Prediction equations that show a tight prediction interval around zero are deemed to be more accurate. Data points below zero signify overestimations, while points above zero signify underestimations.

Results

Development of refined 2-regression model for the Actical

Similar to the 2008 Crouter 2-regression model, when CV ≤ 13% (continuous walking or running), an exponential regression equation was used. However, when CV > 13% (intermittent lifestyle activity), a linear regression line was used (the 2008 2-regression model used a cubic equation on the natural log of the count per 15-s values). The threshold for sedentary activity was changed to 35 counts 15 s⁻¹, and a second cut point was added at 85 counts 15 s⁻¹. Thus, when the counts were less than or equal to 35 counts 15 s⁻¹, then the individual was credited with 1 MET, and when they were greater than 35 but less than 85, then the individual was credited with 1.83 METs. This is similar to the count thresholds established by Heil (2006). The rationale is that the Actical is less sensitive in this count range and the counts do not increase in a linear fashion relative to EE through this range. For example, activities that had individual participant counts values between 35 and 85 counts per 15 s include filing papers (average 1.56 METs), vacuuming (3.37 METs), washing windows (2.86 METs), washing dishes (1.98 METs), sweeping and mopping (3.32 METs), and raking grass/leaves (3.69 METs). This shows that for a small change in the Actical counts there can be a wide range in EE, reducing the predictive validity of a regression equation in this range. Therefore, the refined 2-regression model to predict gross EE (METs) from the Actical counts would consist of four parts:

• If the counts per 15 s are ≤35, EE = 1.0 METs

• If the counts per 15 s are >35 but <85, EE = 1.83 METs

• If the counts per 15 s are ≥85

  1. and the CV of the counts per 15 s are ≤13%, the EE (METs) = 2.522276 × [exp(0.00055462 × Actical counts per 15 s)] (R² = 0.925; SEE = 0.135);

  2. and the CV of the counts per 15 s are >13%, then EE (METs) = 2.1724798 + (0.0072286 × Actical counts per 15 s) (R² = 0.797; SEE = 1.092).

• Finally, once a MET value has been calculated for each 15-s epoch within a minute on the Actical clock, the average MET value of four consecutive 15-s epochs within each minute is calculated to obtain the average MET value for that minute.

Six-hour validation study

On average, participants were monitored for 300.7 ± 0.8 min. Mean measured and predicted METs and time spent in sedentary behaviors, LPA, MPA, and VPA during the 6-h measurement period are shown in Table 3.

Table 3.

Mean (SD) energy expenditure (METs) and time (min) spent in sedentary behaviors (SB), light physical activity (LPA), moderate physical activity (MPA), and vigorous physical activity (VPA) during the 6-h measurement period for the Cosmed K4b² and each prediction equation

	Cosmed METstandard	Cosmed METpredictedRMR	2008 Crouter 2-regression model	Refined 2-regression model	Klippel and Heil 1-regression	Klippel and Heil 2-regression
EE (METs)	1.90 (0.68)	2.10 (0.78)*	2.70 (0.86)*,#	1.82 (0.56)#	1.92 (0.54)	2.06 (0.67)
SB	167.5 (99.4)	151.0 (103.3)*	115.0 (76.9)*,#	158.7 (81.9)	155.5 (83.7)	155.5 (83.7)
LPA	117.1 (74.0)	115.5 (66.2)	80.7 (35.0)	116.3 (58.7)	81.4 (43.0)*,#	82.3 (43.3)*,#
MPA	47.2 (50.0)	63.4 (55.8)*	133.2 (76.6)*,#	60.6 (57.6)	99.3 (74.6)*,#	98.4 (74.2)*,#
VPA	4.4 (11.4)	6.4 (16.5)	7.3 (11.0)	0.6 (1.5)	0.0 (0.0)	0.0 (0.0)

^*Significantly different from Cosmed MET_standard

^#Significantly different from Cosmed MET_predictedRMR (P < 0.05)

On average, the Cosmed had a mean MET_standard value during the measurement period of 1.9 ± 0.7 METs, which was significantly different from the MET_predictedRMR value of 2.1 ± 0.78 METs (P < 0.001). The 2008 Crouter 2-regression model significantly overestimated the average MET_standard by 0.8 ± 0.5 METs (P < 0.001), while the other equations were all within 0.2 METs and not significantly different from the MET_standard (P > 0.05). The 2008 Crouter 2-regression model significantly overestimated MET_predictedRMR by 0.6 ± 0.5 METs (P < 0.001) and the refined Crouter 2-regression model significantly underestimated MET_predictedRMR by 0.3 ± 0.4 METs (P = 0.011), while the other equations were within 0.2 METs of MET_predictedRMR (P > 0.05).

On average, when using MET_standard there were 167.5 ± 99.4 min in sedentary behaviors, which was significantly different from the time in sedentary behaviors when using MET_predictedRMR (151.0 ± 103.3 min) (P = 0.005). The 2008 Crouter 2-regression model significantly underestimated the mean MET_standard time in sedentary behaviors by 52.5 ± 53.3 and 34.8 ± 48.4 min (P < 0.001), while the other equations were within 12 min (P > 0.05). The 2008 Crouter 2-regression model significantly underestimated the mean MET_predictedRMR value by 36.0 ± 61.9 min (P = 0.037), while the other equations were within 8 min (P > 0.05) of the MET_predictedRMR time.

For LPA, the MET_standard time of 117.1 ± 74.0 min was not significantly different from the MET_predictedRMR LPA time (115.5 ± 66.2 min) (P > 0.05). The Klippel and Heil 1- and 2-regression equations significantly underestimated the MET_standard LPA time by 35.7 ± 52.2 and 34.8 ± 52.0 min, respectively (P < 0.01), while the 2008 Crouter 2-regression model underestimated by 36.4 ± 80.5 min (P = 0.232) and the refined 2-regression model was within 0.8 ± 39.8 min (P = 1.00). When using MET_predictedRMR, the Klippel and Heil 1- and 2-regression equations significantly underestimated MET_predictedRMR time by 34.1 ± 48.8 and 33.2 ± 48.8 min, respectively (P < 0.008), while the 2008 and refined 2-regression model were not significantly different from MET_predictedRMR LPA time (P > 0.05).

For MPA, the MET_standard time of 47.2 ± 50.0 min was significantly less than the MET_predictedRMR MPA time of 63.4 ± 55.8 min (P = 0.021). The refined 2-regression model was within 13.4 ± 34.3 min of the Cosmed MPA value (P = 0.970). The other equations significantly overestimated MET_standard MPA time by 51–86 min (P < 0.001). When using MET_predictedRMR, he refined 2-regression model was within 2.8 ± 38.3 min (P = 1.00). The other equations significantly overestimated MET_predictedRMR MPA time by 35–70 min (P < 0.001).

For VPA, none of the equations were significantly different from the mean MET_standard value of 4.4 ± 11.4 min or the MET_predictedRMR value of 6.4 ± 16.5 min (P > 0.05). However, it should be noted that the Klippel and Heil 1 and 2-regression equations failed to predict any VPA for any subject.

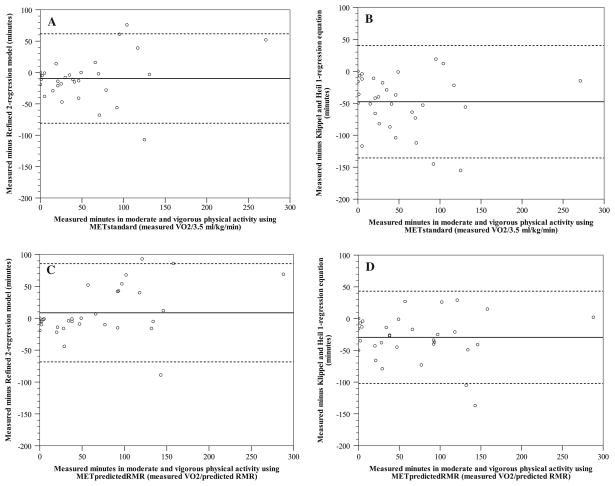
Bland–Altman plots for average MET value (Appendix figures 1a–d) and time spent in sedentary behaviors (Appendix figures 2a–d), LPA (Appendix figures 3a–d), and MVPA (Fig. 1a–d) show wide individual variation for the prediction equation. Plots are only shown for the refined 2-regression model and Klippel and Heil 1-regression equation, compared to both MET_standard and MET_predictedRMR. Table 4 shows the mean bias, 95% PI, and shared variance for each prediction model for time spent in sedentary behaviors, LPA, MVPA, and average MET value during the 6-h measurement. In addition, due to the small amount of VPA, it was combined with the MPA and is shown as combined MVPA. In general, the use of MET_predictedRMR tended to provide a closer mean estimate, compared to using MET_standard; however, the use of MET_predictedRMR had little effect on the 95% PI and in about half of the cases the use of MET_predictedRMR increased the 95% PI compared to using MET_standard. In general, for sedentary behaviors, as the measured time increases, the underestimation of each prediction equation increases (r² range; 0.31–0.45). For LPA, both the 2008 2-regression model and Klippel and Heil equations showed a trend to overestimate LPA, when measured time was less than 100 min for the 6-h period, and underestimate LPA when measured time was greater than 100 min for the 6-h period (r² range; 0.67–0.81). The refined 2-regression model has a similar trend for LPA, but the over- and underestimations were not as great as the other equations (r² = 0.25–0.38). For MVPA, the refined 2-regression model had a small trend to underestimate as time increased (r² = 0.20); however, there was no trend seen for the other prediction models (r² range; 0.01–0.07). Lastly, for the average MET value during the 6-h measurement, all the prediction models tended to overestimate the MET_standard value. When using the MET_predictedRMR value, all prediction models, except for the 2008 2-regression model, tended to underestimate the mean MET value. Regardless of whether MET_standard or MET_predictedRMR was used, there was a trend for the prediction models to underestimate at the higher average MET values (r² range 0.01–0.57).

Fig. 1.

Modified Bland–Altman plots depicting error scores for time spent in moderate and vigorous physical activity (criterion minus estimate) for a MET_standard (measured VO₂/3.5 ml kg⁻¹ min⁻¹) and refined Crouter 2-regression model, b MET_standard and Klippel and Heil 1-regression equation, c MET_predictedRMR (measured VO₂/predicted RMR using Harris–Benedict equation) and refined Crouter 2-regression model, and d MET_predictedRMR and Klippel and Heil 1-regression equation. The solid line represents the mean bias and the dashed lines represent the 95% prediction interval of the individual observations

Table 4.

Mean bias ± 95% prediction interval (measured minus prediction) and shared variance (r²) for time (min) spent in sedentary behaviors (SB), light physical activity (LPA), moderate and vigorous physical activity (MVPA), and average MET value during the 6-h measurement period

	2008 Crouter 2-regression model	Refined 2-regression model	Klippel and Heil 1-regression	Klippel and Heil 2-regression
SB METstandard	52.5 ± 106.5; r2 = 0.41	8.78 ± 87.1; r2 = 0.34	11.9 ± 86.7; r2 = 0.31	11.9 ± 86.7; r2 = 0.31
SB METpredictedRMR	36 ± 123.5; r2 = 0.45	−7.7 ± 105.8; r2 = 0.38	−4.6 ± 104.8; r2 = 0.35	−4.6 ± 104.8; r2 = 0.35
LPA METstandard	36.4 ± 160.6; r2 = 0.81	0.8 ± 79.5; r2 = 0.38	35.7 ± 104.2; r2 = 0.68	34.8 ± 103.6; r2 = 0.67
LPA METpredictedRMR	34.8 ± 144.4; r2 = 0.77	−0.8 ± 89.1; r2 = 0.25	34.1 ± 97.7; r2 = 0.58	33.2 ± 97.5; r2 = 0.57
MVPA METstandard	−88.9 ± 111.4; r2 = −0.01	−9.6 ± 71.3; r2 = 0.07	−47.7 ± 87.9; r2 = −0.01	−46.8 ± 86.9; r2 = −0.01
MVPA METpredictedRMR	−70.8 ± 87.9; r2 = −0.02	8.6 ± 77.0; r2 = 0.20	−29.5 ± 72.6; r2 = −0.01	−28.6 ± 72.1; r2 = −0.01
Avg. METstandard	−0.79 ± 0.93; r2 = −0.01	−0.09 ± 0.37; r2 = 0.32	−0.01 ± 0.72; r2 = 0.36	−0.16 ± 0.78; r2 = 0.10
Avg. METpredictedRMR	−0.59 ± 0.90; r2 = 0.01	0.28 ± 0.43; r2 = 0.52	0.19 ± 0.82; r2 = 0.57	0.05 ± 0.82; r2 = 0.27

MET_standard, measured VO₂/3.5 ml kg ⁻¹ min⁻¹; MET_predictedRMR, measured VO₂/predicted RMR (Harris–Benedict equation)

Discussion

This study describes the validity of four different prediction equations for the Actical accelerometer during a 6-h free-living measurement period. The main findings are that the refined 2-regression model is a significant improvement over the 2008 Crouter 2-regression model, and it also provides the closest estimate of sedentary behaviors, LPA, and MVPA to the Cosmed, compared to the other equations. Except for the 2008 Crouter 2-regression model, the equations gave similar estimates for the mean MET value.

There are some distinct differences between the 2008 and refined 2-regression models, which contribute to the differences seen during the free-living measurements. First, the refined 2-regression model examines each 15-s epoch and all combinations of the three surrounding epochs, which results in less misclassification of continuous walking/running. As a result, an estimate of mean EE and MVPA closer to that from the Cosmed is obtained. A second difference between the 2-regression models is how they define sedentary behavior. For the 2008 Crouter 2-regression model, a cut point of <10 counts min⁻¹ was used, but this was shown to significantly underestimate the Cosmed values. Thus, for the refined 2-regression model, we used an approach similar to the Klippel and Heil equations (Klippel and Heil 2003) in that we now credit an individual with 1 MET when the individual is below the inactivity threshold (35 counts 15 s⁻¹), and when the counts.15 s⁻₁ are greater than 35 but less than 85, we credit the individual with 1.83 METs.

To our knowledge, this is the first study to examine the validity of the Actical during free-living activity, measured by indirect calorimetry. There have been similar studies performed using other techniques and devices; however, it is difficult to make direct comparisons. A study by Strath et al. (2003) investigated the validity of five different Acti-Graph single regression equations during a 6-h free-living period using the Cosmed as the criterion measure. They found that the ActiGraph equations under- or overestimated LPA by approximately 26–77 min (10–29%), MPA by approximately 18–77 min (28–120%), and VPA by approximately 0–5 min (0–83%), although there was no single equation that was consistently better than the others across the three activity categories. Their data suggest that depending on the outcome of interest (e.g. LPA or MPA), the appropriate equation to maximize accuracy should be chosen. In addition, as in the current study, Strath et al. found very little time in VPA, as measured by the Cosmed. The equations in the current study have similar validity, but the refined 2-regression model worked consistently well for sedentary behaviors, LPA, and MVPA. In contrast, the Klippel and Heil 1- and 2-regression equations worked well only for sedentary behaviors.

Recently, several investigators have suggested that the traditional definition of 1 MET equalling 3.5 ml kg⁻¹ min⁻¹ overestimates the average RMR of most individuals, especially in those who are obese (Byrne et al. 2005; Kozey et al. 2010a, b). Instead of using the standard 3.5 ml kg⁻¹ min⁻¹, these investigators suggest using measured or predicted RMR. Given that many investigators calculate METs by dividing measured VO₂ by 3.5 ml kg⁻¹ min⁻¹, we chose to compare the prediction equations to both MET_standard and MET_predictedRMR. Since we did not measure RMR, a limitation to our approach was that we used the Harris–Benedict prediction equation (Harris and Benedict 1919) to estimate RMR, which also has prediction errors associated with it that may have contributed to the errors between the accelerometer prediction equations and MET_predictedRMR. Overall, the use of MET_predictedRMR resulted in a 10% (0.2 METs) higher average MET value compared to MET_standard, for the 6-h measurement period. However, this had only a small effect on the accuracy of the equations for estimating time spent in sedentary behaviors, LPA, MPA, and VPA. In addition, while some of the equations did have closer estimates of time spent in the PA intensity categories compared to MET_predictedRMR, versus using MET_standard, there was no change in the 95% PIs. Future work is needed to fully understand the errors associated with using 3.5 ml kg⁻¹ min⁻¹ for RMR rather than a measured or predicted value.

This study has several strengths and weaknesses. The strengths of the study include separate groups being used for the development and validation of the refined 2-regression model. On average, the validation group used in the 6-h study was approximately 10 years younger and had a slightly higher BMI than the group used to develop the 2-regression model. Thus, future studies should examine the validity of these equations in older populations as factors such as movement patterns and types of activities performed may alter the performance of the equations. Another strength of the study is the use of free-living activity to validate the equations. While the individuals were slightly constrained by the Cosmed, they were instructed to perform their typical activities that included office work, working at a dairy plant, playing golf, and step aerobics classes. These were not structured activities as are typically used and were performed as the individual typically would. Lastly, the number of participants used in the developmental study (N = 48) was larger than in most studies of this type; however, the use of more subjects would allow for a more robust equation to be developed, which in theory should improve the accuracy of the equation across a broader range of individuals.

In conclusion, this study shows that the refined 2-regression model is a significant improvement over the 2008 Crouter 2-regression model for measuring free-living PA with the Actical accelerometer. In addition, the refined 2-regression model provided similar mean estimates of EE to the Klippel and Heil 1- and 2-regression equations while providing the closest estimates for time spent in sedentary behaviors, LPA, and MVPA, compared to the Cosmed.