Abstract
Modern microelectrode arrays make it possible to simultaneously record population neural activity. However, methods to analyze multiunit activity (MUA), which reflects the aggregate spiking activity of a population of neurons, have remained underdeveloped in comparison to those used for studying single unit activity (SUA). In scenarios where SUA is hard to record and maintain or is not representative of brain’s response, MUA is informative in deciphering the brain’s complex time-varying response to stimuli or to clinical insults. Here, we present two quantitative methods of analysis of the time-varying dynamics of MUA without spike detection. These methods are based on the multiresolution discrete wavelet transform (DWT) of an envelope of MUA (eMUA) followed by information theoretic measures: multiresolution entropy (MRE) and the multiresolution Kullback–Leibler distance (MRKLD).We test the proposed quantifiers on both simulated and experimental MUA recorded from rodent cortex in an experimental model of global hypoxic–ischemic brain injury. First, our results validate the use of the eMUA as an alternative to detecting and analyzing transient and complex spike activity. Second, the MRE and MRKLD are shown to respond to dynamic changes due to the brain’s response to global injury and to identify the transient changes in the MUA.
Index Terms: Brain injury, cardiac arrest (CA), discrete wavelet transform (DWT), envelope, Kullback–Leibler distance (KLD), multiresolution, multiunit activity (MUA), Shannon entropy
I. INTRODUCTION
Recent advances in extracellular microelectrode technology enable researchers to record action potentials (spikes) simultaneously from a population of multiple neurons [1]–[5]. The large-scale recording of a population makes it easier to gain a deeper understanding of how populations of neurons respond to natural or applied stimuli or insults to the brain. Study of large populations of neurons can be accomplished through simultaneous recording from population of neurons, or multiunit activity (MUA) or local field potential (LFP) [1], [2].
Conventional approach, however, has been to record and analyze single unit activity (SUA) as a single neuron’s response in an experiment [2]–[5]. The use of SUA is hampered, especially when SUA is hard to separate or when if it turns out to be difficult to record from the same neuron for sufficiently long periods [6], [7]. In experiments where the brain’s response is transient or time varying, such as when brain is injured, recording or analyzing SUA can be ineffective. Compared to SUA, MUA may be a better measure of a population of neurons around the electrode under such circumstances [1], [6], [8]. MUA may also be useful for investigating the interaction among multiple neurons [2], [6], [8], [9].
Here, we present novel quantitative methods to assess the time-varying dynamics of MUA. We use a continuous representation of MUA by constructing an envelope of the MUA signal (eMUA). Such an envelope reflects the changing dynamics of all spike activities regardless of the magnitude of spike potentials or the number of neurons. Amplitude envelope of population activity bypasses the need for spike detection and isolation. Moreover, eMUA is a nonstationary signal that has detailed and coarse temporal features. For such signals, the wavelet transform has proven itself as a way to deal with local changing features in both time and frequency. Theory of multiresolution discrete wavelet transform (DWT) has been developed to optimally decompose complex time-varying signals into orthonormal scales [10]. DWT has emerged as a very popular tool for the analysis of complex physiological signals that invariably are time varying and exhibit unique features at various frequencies or scales [11]–[17]. Here, we use the multiresolution DWT to decompose the eMUA signal into different scales. Next, to quantify the embedded information content of the eMUA signal, we calculate its entropy [18]. Two of the most popular measures are the Shannon entropy and the relative entropy. Numerous studies have used entropy [19]–[22] and relative entropy, referred to as Kullback–Leibler distance (KLD) [23], to measure the discrepancy between two distributions [24], [25] of complex physiological signals.
In our paper, two complementary methods of multiresolution wavelet-based entropy of MUA are developed: the multiresolution entropy (MRE) and the multiresolution KLD (MRKLD). The former provides the degree of uncertainty associated with the time-varying eMUA, while the latter captures the local variation in the dynamics of eMUA by comparing the distributions of the wavelet coefficients of successive eMUA windows.
The remainder of the paper is organized as follows: In Section II, the eMUA is first developed and next the multiresolution-based entropy measures for eMUA are formulated. Section III presents MUA simulations followed by analysis of cortical MUA obtained during experiments to study the brain’s response to global hypoxic–ischemic injury as an example. Section IV presents the conclusion.
II. MULTIRESOLUTION ENTROPIES FOR MUA
A. Envelope of MUA
High-pass filtering yields the high-frequency spike activity of multiple neurons while filtering out the low-frequency LFPs. In most studies using MUA, a spike-detection scheme is used to discriminate spikes from the underlying noise. Using spike detection, neural activity can be converted into a binary sequence and subsequent firing rate can be estimated [6], [26], [27].
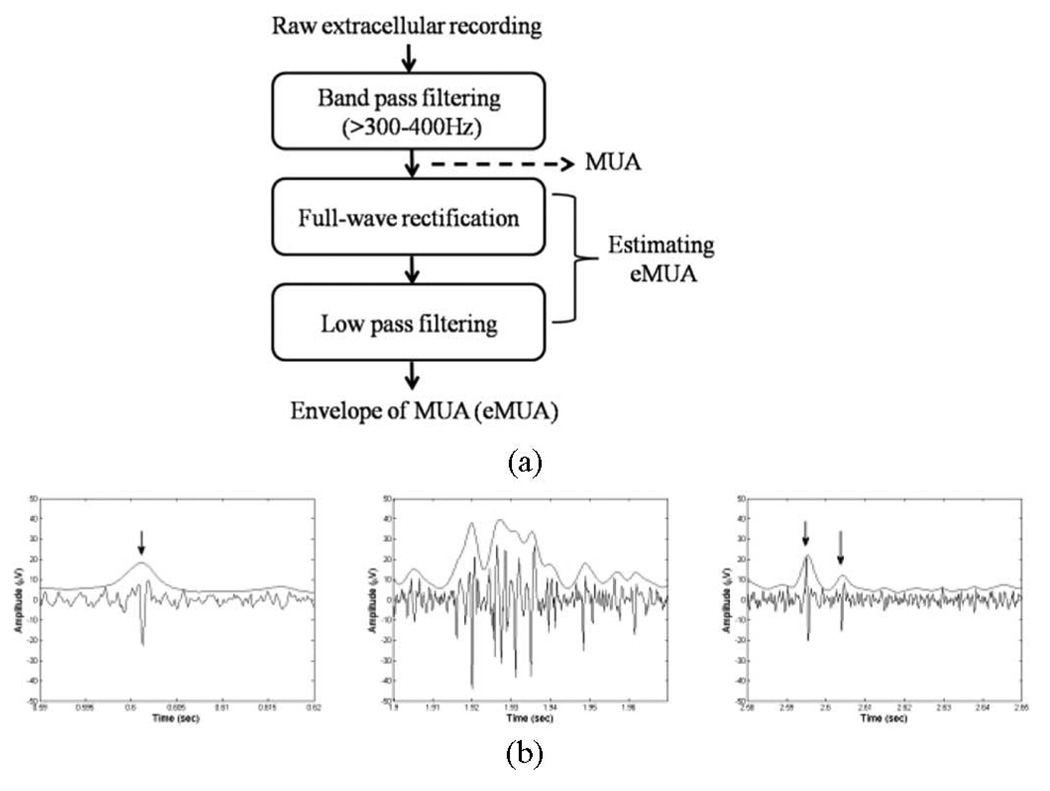
In contrast, we represent the filtered MUA as a continuous waveform by obtaining an envelope of the underlying high-frequency population activity, represented as a voltage. As shown in Fig. 1(a), the filtered MUA is first full-wave rectified (i.e., taking absolute values of the signal). Subsequent low-pass filtering (cutoff < 500 Hz) is carried out [6], [9], [28]. Finally, the eMUA is obtained. Following Fig. 1(b) shows that the eMUA captures distinctive spikes, including hard-to-separate multiple-spike trains. The upper trace is the eMUA signal and the lower one is the MUA signal. Arrows indicate the occurrences of spikes. Fig. 1(b)–(d) shows the filtered MUA and its corresponding eMUA. Fig. 1(b) indicates the raw cortical MUA recording from an anesthetized rat.
Fig. 1.
(a) Block diagram for extracting the eMUA. MUA signal is obtained by bandpass filtering of a raw extracellular recording. Following full-wave rectification and low-pass filtering are carried out to estimate the eMUA signal. (b) Examples of MUA recordings and their corresponding eMUA. Arrows indicate the occurrence of spike activities.
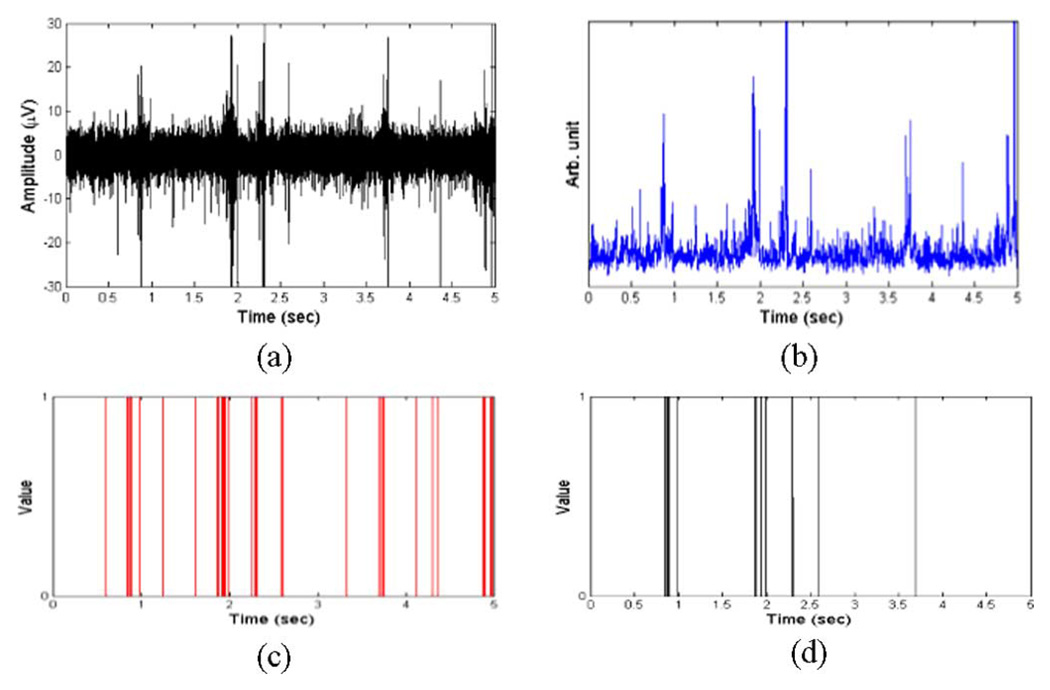
Fig. 2(a)–(d) shows the MUA, eMUA, spike sequences from multiple neurons after spike detection from MUA, and the primary clustered SUA after spike sorting, respectively. While the multiple neuron spike sequence in Fig. 2(c) treats distinct spikes as a binary sequence (on/off), the eMUA signal in Fig. 2(b) reflects the time-varying and transient spike information that preserves the number and magnitude of all spikes. Moreover, we can observe that SUA in Fig. 2(d) does not account for the population response since it loses firing information from small amplitude spike activity. On the other hand, the eMUA signal provides an envelope of the time-varying neural response of all neurons in the population.
Fig. 2.
(a) Bandpass-filtered MUA signal (300 Hz–3 kHz) with a sampling frequency of 6.1 kHz. These signals were recorded from cortex of rat using microelectrodes (described in Section III-B). (b) eMUA for signal in (a). This was obtained by full-wave rectification, low-pass filtering (cutoff frequency 150 Hz). (c) Multiple neuron spike train recorded by single-channel microelectrode obtained after spike detection. (d) Primary clustered SUA after spike sorting. The resulting eMUA preserves the population response, i.e., neural spike activities of multiple neurons, contained in the filtered MUA signal.
B. DWT of eMUA
The eMUA is divided into a number of segments using a sliding temporal window [29]. Let s(i) denote an eMUA signal. For a given {s(i) : i = 1, …, N}, a sliding temporal window w ≤ N and a sliding interval Δ ≤ w are defined. Then, the nth sliding window of the eMUA is represented as
| (1) |
where n = 0, 1, …, [(N − w + 1)/Δ] and [x] denotes the integer part of x.
Since eMUA is, in general, nonstationary and time-varying, we use the multiresolution DWT for analysis due to its ability to localize signal characteristics in both time and frequency domains [15], [30]. In this way, both coarse changes occurring over longer time scales as well as finer transitions occurring at shorter time scales can be adequately represented. We incorporate DWT to characterize the eMUA. The signal is decomposed over j levels by the DWT. A set of wavelet coefficients, DWTj [sn (i)], is obtained from the eMUA signal in a sliding window sn (i)
| (2) |
where ck for k = 1, 2, …, j + 1 are the sets of wavelet coefficients corresponding to the j-level DWT.
The next step involves estimating the probability distribution of the wavelet coefficients. We introduce the set {Im, m = 1, …, M} of disjoint intervals for each window DWTj [sn (i)] as follows:
| (3) |
Then, pn (m), is the probability that the wavelet coefficient belongs to the interval Im within DWTj [sn (i)]. It is evaluated as a ratio of number of the wavelet coefficients of DWTj [sn (i)] within Im and the total number of the wavelet coefficients in DWTj [sn (i)], i.e., pn (m) = nm/N, where nm is the number of times of DWTj [sn (i)] found within mth interval and N is the total number of wavelet coefficients in DWTj [sn (i)].
C. Entropy Measures of eMUA
The MRE of the time-varying eMUA is calculated as follows:
| (4) |
where 0 ≤ pn (m) ≤ 1 and . The entropy of the wavelet coefficients reflects the underlying uncertainty associated with the time-varying eMUA signal.
Further, we develop a second measure to detect changes in the entropy of eMUA. Such a measure is useful as it can be used to interpret changes in the complexity of the underlying time-varying physiological process. Our approach is to characterize the dissimilarity in dynamics of two consecutive eMUA windows. Using the relative entropy measure [31]–[33], the amount of discrepancy between the wavelet coefficients of consecutive sliding windows is measured. Taking the distribution of wavelet coefficients of the previous window as a reference, r(m), MRKLD of the signal of interest is obtained as
| (5) |
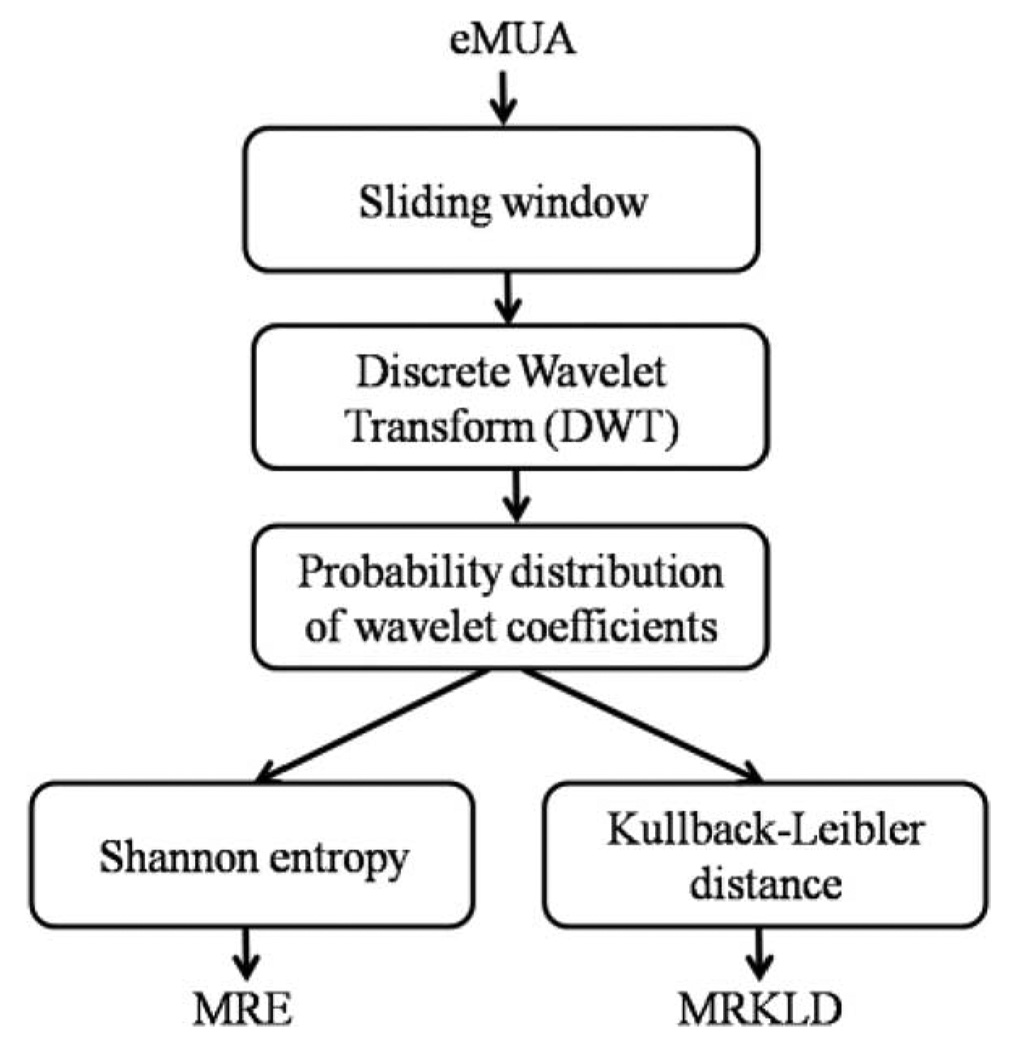
The resultant MRKLD can detect the transition between two successive windows, i.e., nth and (n−1)th windows of the eMUA signal. The MLKLD is nonnegative, asymmetric, and zero if the distributions match exactly. The greater the variation of the local dynamics is between consecutive eMUA temporal windows, the greater the MRKLD value. Block diagram describing MRE and MRKLD is shown in Fig. 3.
Fig. 3.
Block diagram of the proposed measures, i.e., MRE and MRKLD.
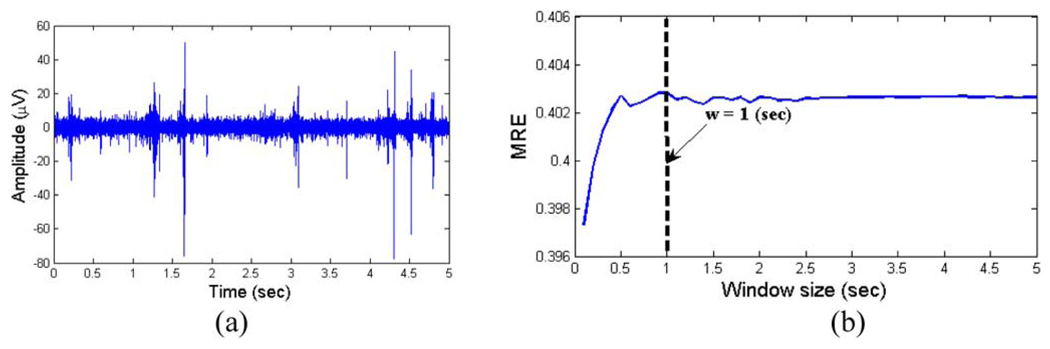
The window size was chosen empirically, as discussed in [29]. We calculated the MRE for a 5-s-long segment of the actual cortical MUA [see Fig. 4(a)] for variable nonoverlapping window sizes w. We started with w = 0.1 s and incremented it steps of 0.1 s up to w = 5 s. The effects of window size are demonstrated in Fig. 4(b). As can be seen in Fig. 4(a), MRE approaches a steady-state value for window sizes > 1 s. Thus, w > 1 s provides an unbiased estimate of entropy.
Fig. 4.
Effect of window size on the MRE. (a) 4 s of actual baseline MUA was chosen to evaluate the time-dependent MRE. (b) Resulting MRE plot versus window size. The plots indicate that the selection of w > 1 s is appropriate for avoiding a bias.
III. RESULTS
We first examined the MRE and MRKLD of a simulated eMUA signal synthesized from experimental recordings. Next, we applied these measures to the actual MUA recorded from rodent cortex in experimental studies of neurological responses to global hypoxic–ischemic injury and recovery after cardiac arrest (CA) (the experimental details follow in Section III-B, and were previously described in [34] and [35]).
A. Simulation Studies
To test the performance of the measures, i.e., MRE and MRKLD, a synthetic MUA signal was used. The synthetic MUA was modeled by combining three SUAs and background noise. The sampling frequency for the simulated MUA was 10 kHz. Three spike templates for the three SUAs were obtained from cortical single neurons of an anesthetized rat. Each spike template was recorded from different neurons and the temporal sequence of each spike template was designed by a integrate-and-fire model with refractory period of 2 ms [36], [37]. To mimic the signal conditions of the actual MUA signals, noise with a Gaussian probability distribution was added. The SNR is defined as the ratio between the absolute peak amplitude of the spiking activity and the standard deviation of the noise [38]. In the simulation, SNR was set to 5.
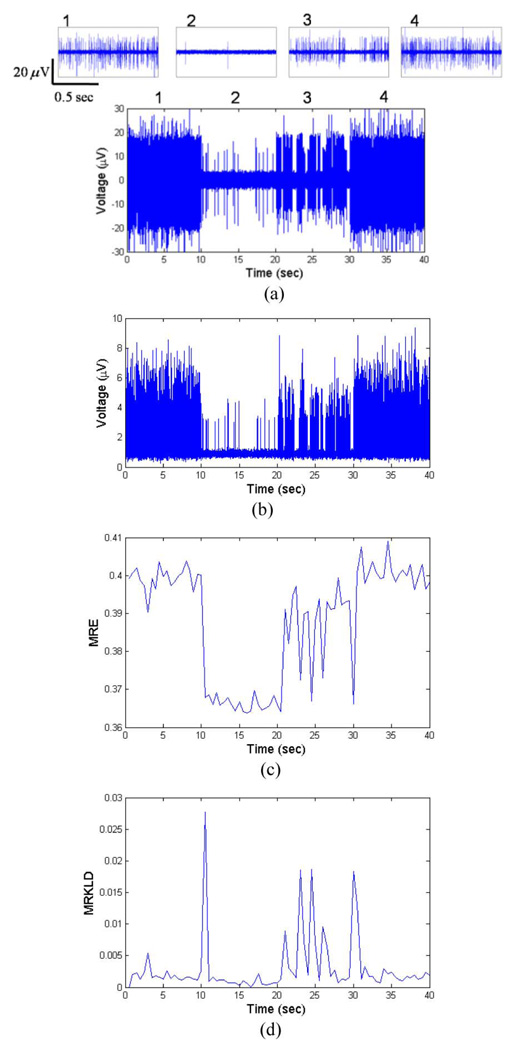
By combining the three SUAs, we obtained the simulated MUA segment for 40 s. To simulate the time-varying MUA pattern, the firing rates of three SUAs were varied every 10 s. To imitate abrupt neural activity changes, the firing-rate parameter was held constant for 10 s, then changed significantly for the following time periods. During the initial 10 s period, the firing rate of each SUA was 50 spikes/s. Between 10 and 20 s, the firing rate is 3 spikes/s. For the following 10 s, burst firing activity of neurons was included to reflect similar experimental recordings. During last 10 s, the firing rate of each SUA is set to 50. Fig. 5(a) shows the resultant simulated MUA. Fig. 5(b) depicts the eMUA signal obtained from the signal shown in Fig. 5(a) by a full-wave rectification, followed by low-pass filtering with 150 Hz cutoff frequency. Zero-phase forward and reverse low-pass filtering was carried out using a second-order Butterworth filter. Note that the eMUA signal not only retains the high-frequency activity of a population of neurons, but also includes small spike activities which might be ignored in typical spike detection. In calculating the MRE for the simulated eMUA, the parameters were: sliding-window length w = 1 s, sliding step Δ = 1s, M = 20. The Daubechies wavelet function [39] was used as the mother wavelet, as daughter wavelets are orthogonal and suitable for representing nonstationary signals. The number of decomposition levels in DWT was set to 5, in accordance with the experimental sampling frequency and to avoid the redundancy of using a greater number of levels. Fig. 5(c) shows the time evolution of MRE of the simulated eMUA. In Fig. 5(c), we can observe that MRE is indicative of different firing rates. In addition, MRE reflects the variable dynamics of the bursting activity during 20–30 s.
Fig. 5.
Synthetic MUA and the time evolutions of MRE and MRKLD. (a) Synthetic MUA is constructed by convolving three spike templates and three spike train modeled a Poisson process, along with the addition of Gaussian noise (SNR = 5). Each 10 s period has the distinct firing rate (period 1: 0–10 s, period 2: 10–20 s, period 3: 20–30 s, and period 4: 30–40 s). The upper traces show the enlarged synthetic MUA of corresponding numbered periods. (b) eMUA signal is obtained by a full-wave rectification, followed by low-pass filtering at 150 Hz. (c) Time evolution of MRE for the simulated eMUA. (d) Time evolution of MRKLD for the simulated eMUA. In calculating the time-dependent entropy-based measures, the sliding-window length w = 1s, the sliding step Δ = 1s, and M = 20 were used. The arrows in (d) identify the transition points in the varying dynamics of the synthetic MUA signal.
In Fig. 5(d), the time evolution of MRKLD of the simulated eMUA is shown. At each transition of firing pattern, the corresponding MRKLD value was high, implying a high degree of discrepancy between successive dynamics. For the bursting activities during the 20–30 (s) period, MRKLD detected the transient changes of short-length bursting activities. Thus, MRKLD is well suited for detecting the transient dynamics of underlying MUA such as significant changes in the firing activity and occurrence of complex neural activity. Fig. 5(c) and (d) shows that the MRE and MRKLD can identify state changes with respect to the actual times of transition.
B. Experimental Studies on Cortical MUA Following Hypoxic–Ischemic Brain Injury
Our work on MUA analysis is motivated by experiments that use microelectrodes to record from injured brain. We investigate the cortical multiunit spiking activity from rats subjected to hypoxic–ischemic brain injury due to CA and subsequent recovery after cardiopulmonary resuscitation (CPR). Our long-term goal is to identify the neural response to injury, and this response is assessed by recording and analyzing the MUA in the cortex of the injured animal.
The brain injury studies were carried out under a protocol approved by the Institutional Animal Care and Use Committee of the Johns Hopkins Medical Institution. We have previously reported on the asphyxic CA and resuscitation protocol [34], [40]. This rat model has been validated to study multiple aspects of brain injury after asphyxic CA including duration of injury and temperature manipulation.
The experimental protocol is as follows. Five adult male Wistar rats (300 ± 25 g) were used. The rats were anesthetized by 1% isoflurane in 50%:50% N2:O2. After anesthesia, a stereotaxic frame (David Kopf Instruments, Tujunga, CA) was used to place the silicon-based 16-channel microelectrode array (Neuronexus Technologies, Ann Arbor, MI) into the parietal cortex of the rats. The cortical MUA was continuously recorded with 6.1 kHz sampling frequency (RX 5, Tucker-Davis Technologies, Alachua, FL) and followed by a fourth-order Butterworth bandpass filtering with forward–backward, zerophase lag with cutoff frequencies of 300–3000 Hz. EEG signal was also recorded simultaneously.
Baseline recording of 10 min was followed by a 5 min anesthetic washout to ensure no significant residual effect of isoflurane on the physiological signals. After washout, CA was induced via asphyxia by pharmacological paralysis and clamping of the tracheal tube for 7 min. During the injury phase, CA was defined by two parameters: the time to pulselessness (MAP < 10 mmHg) and the time to return of spontaneous circulation (ROSC) during resuscitation (MAP > 50 mmHg). Resuscitation was initiated by unclamping the endotracheal tube, restarting mechanical ventilation with 100% oxygen, administering epinephrine, sternal chest compressions (attempting to generate systolic arterial pressure peaks of > 50 mmHg) until ROSC. Further experimental details can be found in [35] and [40].
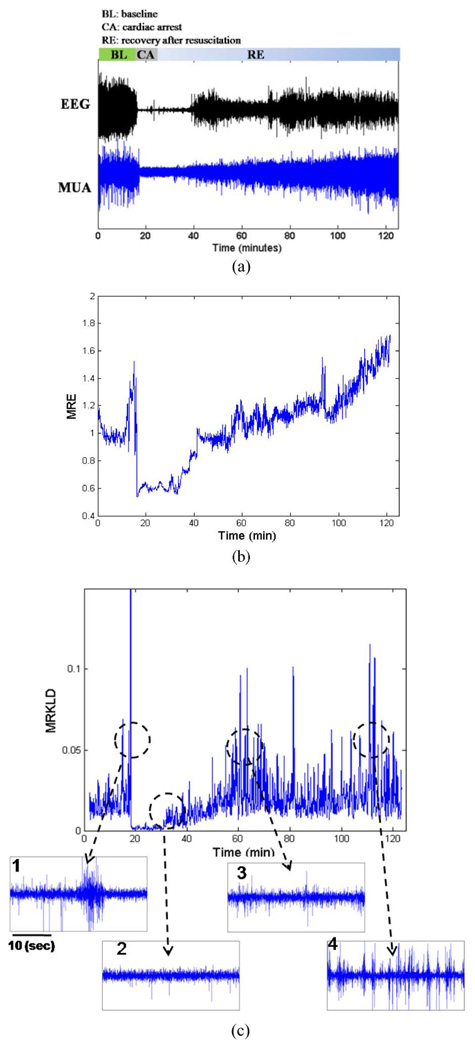
Fig. 6(a) demonstrates the actual MUA recording from cortical population of a rat as well as the simultaneous EEG recording during baseline, brain injury, and recovery. The recorded MUA can be divided into three distinct phases. The first phase consists of a 10-min baseline recording and a 5-min anesthesia washout period, which is further characterized by spontaneous firing of MUA. The second phase consists of 7 min duration of hypoxia after CA. This phase was characterized by a significant reduction of MUA. Around 35–40 min, the spike activity gradually increased, indicative of recovery of neural activity postinjury. This pattern suggests that neural population activity is strongly related to the status of recovery. We observed that the population activity during the initial recovery phase had smaller spike amplitudes and sparse firing. In addition, during the late recovery phase, the MUA signal exhibited a characteristic busting pattern.
Fig. 6.
Raw EEG and cortical MUA recordings of a rat before, during, and after hypoxic–ischemic brain injury due to cardiac arrest and multiresolution entropies (MRE and MRKLD) of eMUA. (a) Raw EEG(upper trace) and cortical bandpass-filtered MUA (lower trace). The raw recordings consist of 10 min baseline recording, 5 min washout, 7 min CA, and the subsequent recovery period (BL: baseline, CA: cardiac arrest, RE: recovery). (b) Time course of MRE for the cortical eMUA shown in (a). (c) Time course of MRKLD for the cortical eMUA shown in (a). The four lower traces show the enlarged actual MUA of abrupt increases in MRKLD compared to previous one.
The main aim in this experimental study was to quantify the time-varying cortical MUA before, during, and after hypoxic–ischemic brain injury. Previous studies have used EEG signals to track the hypoxic–ischemic brain injury as a suitable marker for neurological status early after the injury [13], [29]. This study explored the role of underlying activity at the neuronal population level. We calculate multiresolution entropies of the eMUA. The parameters used in the calculation of the time-dependent entropies were as follows: sliding-window length w = 5s, sliding step Δ = 5s, M = 20, and decomposition scale r = 5 in DWT.
Fig. 6(b) and (c) shows the time courses of multiresolution entropies, i.e., MRE and MRKLD, respectively. Fig. 6(b) depicts the time evolution of MRE, normalized to its average value over the baseline recording period. Compared with the baseline period, we can observe the sudden decrease of MRE at the onset of CA. Nearly 18 min into recovery, MRE gradually increased, suggesting the reappearance of neural activity. MRE tends to increase during the recovery duration. In Fig. 6(c), the time evolution of MRKLD is shown. The MRKLD increased as the brain recovers from the ischemic insult.
The MRE profiles during the recovery periods of five rats are summarized in Table I. One channel out of 16-channel microelectrode array that has a highest baseline firing rate was chosen per rat. Table I lists the averaged MRE for each rat during early and late recovery periods. For 5-min-long segment in Table I, we obtained the 60 samples of MRE. Based on the central limit theorem, the MREs can be assumed to be normally distributed.
TABLE I.
Statistical Results of MRE Value (Mean ± SD) for Different Time
| Rat ID | MRE | |||
|---|---|---|---|---|
| 25–30 min post-CA | 35–40 min post-CA | 60–65 min post-CA | 100–105 min post-CA | |
| Rat #1 | 0.93±0.07▽,◇,◆ | 0.96±0.07◇, ◆ | 1.20±0.08◆ | 1.59±0.09 |
| Rat #2 | 0.93±0.03*,◇, ◆ | 0.99±0.03◇, ◆ | 1.47±0.05◆ | 1.67±0.07 |
| Rat #3 | 0.65±0.03*,◇, ◆ | 0.71±0.03◇, ◆ | 0.93±0.03◆ | 1.06±0.06 |
| Rat #4 | 0.84±0.05*,◇, ◆ | 0.94±0.07◇, ◆ | 1.36±0.06◆ | 1.50±0.06 |
| Rat #5 | 0.78±0.07◇, ◆ | 0.79±0.04◇, ◆ | 0.89±0.04◆ | 0.97±0.05 |
Note: The MRE values are normalized with respect to that of baseline recording and are in arbitrary unit.
t-test with 35–40 min post-CA, p < 0.001;
t-test with 60–65 in post-CA, p < 0.001;
t-test with 100–105 min post-CA, p < 35–40 min with p < 0.05.
Thus, the t-test, which assumes normality of the underlying distribution, was used in the analysis. Since, the recovery pattern is being studied over time and we tested if there was a difference between successive time durations, we used a two-tailed test. We can observe that MRE tends to increase as the recovery progresses. For comparison, we carried out a nonparametric bootstrap test using the median value of eMUA with a bootstrap resample size of 500 shown in Table II. The analysis demonstrated that the median value of eMUA does not always follow the same trend as the MRE, especially during initial recovery when dynamic changes to brain’s physiological state occur to restore neural activity from a period of relative absence of electrical activity. For example, in rats 3 and 5, while the MRE is able to track the increasing trend of recovery between 25 and 40 min postinjury, eMUA does not reflect the same trend adequately.
TABLE II.
Statistical Results of the Nonparametric Bootstrap Test on eMUA
| Rat ID | Median of eMUA | |||
|---|---|---|---|---|
| 25–30 min post-CA | 35–40 min post-CA | 60–65 min post-CA | 100–105 min post-CA | |
| Rat #1 | 1.0718*,◇, ◆ | 1.2704◇, ◆ | 1.3576◆ | 1.6598 |
| Rat #2 | 0.9831▽, ◇, ◆ | 1.0275◇, ◆ | 1.3297◆ | 1.6186 |
| Rat #3 | 0.9821◆ | 0.8280◇, ◆ | 0.9653◆ | 1.1617 |
| Rat #4 | 1.0558◇, ◆ | 1.0719◇, ◆ | 1.2045◆ | 1.3346 |
| Rat #5 | 1.3195 | 0.9628◇, ◆ | 1.0012◆ | 1.0623 |
Note: The bootstrap resampling size of 500 was used.
t-test with 35–40 min post-CA, p < 0.001,
t-test with 60–65 in post-CA, p < 0.001;
t-test with 100–105 min post-CA, p < 0.001,
t-test with 35–40 min with p < 0.01.
IV. CONCLUSION
We have presented an eMUA-based quantitative measure that can capture time-varying dynamics of neural activity. The eMUA signal used in this study is useful in analyzing population responses to stimuli or brain dysfunction. Considering the time-varying and nonstationary nature of eMUA, we used multiresolution-based DWT to detect and localize the varying temporal-spectral dynamics of the signal. It is well known that information-theory-based metrics can provide more useful insights about the information embedded in neurological signals when compared to standard frequency analyses [16], [17], [29], [34]. The combination of distribution of wavelet coefficients and information theoretic measures are shown to be very effective for describing both the spectral and temporal changes of the eMUA. The resultant MRE is capable of exploring global quantification of dynamics of the time-varying eMUA and MRKLD serves to detect the local dynamic transitions in the MUA. To our knowledge, this study is the first to explore a time-varying MUA without the detection of spikes and to demonstrate its application to a clinically important problem. Finally, the quantitative measures developed, MRE and MRKLD, were shown to be useful in assessing the electrophysiological response of a population of neurons under simulated and in vivo experimental conditions.
Acknowledgments
This work was supported in part by the National Institutes of Health under Grant R01 HL071568, and in part by the Korean Research Foundation Grant funded by Korean Government (MOEHRD) under Grant KRF-2007-357-D00188.
Biographies

Young-Seok Choi (M’07) received the B.S. degree in electronic and electrical engineering from Hanyang University, Seoul, Korea, in 2000, and the Ph.D. degree in electrical and computer engineering from Pohang University of Science and Technology (POSTECH), Pohang, Korea, in 2007.
From 2007 to 2010, he was a Postdoctoral Fellow in the Department of Biomedical Engineering, Johns Hopkins School of Medicine, Baltimore, MD. Since July 2010, he is with the Neural Interface Research Team, Electronics and Telecommunications Research Institute, Daejeon, Korea, where he is currently a Senior Researcher. His current research interests include neural signal processing, brain–computer interface, neural interface, and neural engineering.

Matthew A. Koenig is currently the Associate Medical Director of Neurocritical Care, Queen’s Medical Center, and Assistant Professor of Medicine at the John A. Burns School of Medicine, Honolulu, HI. Dr. Koenig received his M.D. from the University of Maryland in 2001. After training in Neurology and Neurocritical Care at the Johns Hopkins Hospital, he was a Research Associate in the Biomedical Instrumentation and Neuroengineering Laboratory, Johns Hopkins University, under N. Thakor. His current research interests include physiologic mechanisms of brain recovery after global hypoxia–ischemia using multimodality fMRI, and electrophysiologic tools.

Xiaofeng Jia received the M.D. degree from Zhejiang University, Hangzhou, China, in 1994, and the M.S. degree in surgery, in 1997, and the Ph.D. degree in surgery (orthopedics), in 2003, both from Fudan University, Shanghai, China.
Since 2007, he has been a Faculty member in the Department of Biomedical Engineering, Physical Medicine, and Rehabilitation, Johns Hopkins University School of Medicine, Baltimore, MD. His current research interests include novel application of neuroelectrophysiology for detection and restoration of spinal cord and peripheral nerve injury, therapeutic hypothermia after global ischemia.
Dr. Jia is a member of the American Academy of Orthopedic Surgeons, the American Association for Hand Surgery, the Society of Critical Care Medicine, the American Heart Association. He is a recipient of the 2008 Annual Research Awards from the American Association for Hand Surgery and the 2009 Top 20 Scientific Exhibits of American Academy of Orthopedic Surgeons.

Nitish V. Thakor (S’78–M’81–SM’89–F’97) is currently a Professor of biomedical engineering and neurology at Johns Hopkins School of Medicine, Baltimore, MD, where he directs the Laboratory for Neuroengineering. His current research interests include neural diagnostic instrumentation, neural signal processing, optical and MRI imaging of the nervous system, and micro- and nanoprobes for neural sensing. He is the Director of a Neuroengineering Training Program funded by the National Institute of Health (NIH). He has authored or coauthored more than 190 refereed journal papers and generated 11 patents and carries out research funded mainly by the NIH, the National Science Foundation (NSF), and the Defense Advanced Research Projects Agency (DARPA).
Dr. Thakor is the Editor-in-Chief of the IEEE Transactions on Neural and Rehabilitation Engineering. He was the IEEE Conference Chair for the American Medical Association (AMA)–IEEE Medical Technology Conference and was a Distinguished Lecturer. He is a recipient of a Research Career Development Award from the NIH and a Presidential Young Investigator Award from the NSF. He is a Fellow of the American Institute of Medical and Biological Engineering and the Founding Fellow of the Biomedical Engineering Society. He is also a recipient of the Centennial Medal from the University of Wisconsin School of Engineering, the Honorary Membership from Alpha Eta Mu Beta Biomedical Engineering student Honor Society, and the Distinguished Alumnus Award from the Indian Institute of Technology, Bombay, India.
Footnotes
Color versions of one or more of the figures in this paper are available online at http://ieeexplore.ieee.org.
Contributor Information
Young-Seok Choi, Department of Biomedical Engineering, Johns Hopkins School of Medicine, Baltimore, MD 21205 USA. He is now with the Neural Interface Research Team, Electronics and Telecommunications Research Institute, Daejeon, 305700 Korea (bluecula@etri.re.kr)..
Matthew A. Koenig, Neurology Department, Johns Hopkins University School of Medicine, Baltimore, MD 21287 USA. He is now with the Neurocritical Care, Queen’s Medical Center and Medicine, John A. Burns School of Medicine, Honolulu, HI 96813 USA (mkoenig95@gmail.com).
Xiaofeng Jia, Department of Biomedical Engineering and Physical Medicine and Rehabilitation, Johns Hopkins School of Medicine, Baltimore, MD 21205 USA (xjia1@jhmi.edu)..
Nitish V. Thakor, Department of Biomedical Engineering, Johns Hopkins School of Medicine, Baltimore, MD 21205 USA (nitish@jhu.edu)..
REFERENCES
- 1.Buzsaki G. Large-scale recording of neuronal ensembles. Nat. Neurosci. 2004 May;vol. 7:446–451. doi: 10.1038/nn1233. [DOI] [PubMed] [Google Scholar]
- 2.Brown EN, Kass RE, Mitra PP. Multiple neural spike train data analysis: State-of-the-art and future challenges. Nat. Neurosci. 2004 May;vol. 7:456–461. doi: 10.1038/nn1228. [DOI] [PubMed] [Google Scholar]
- 3.Dayan P, Abbott LF. Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems. Cambridge, MA: MIT Press; 2001. [Google Scholar]
- 4.Lewicki MS. A review of methods for spike sorting: The detection and classification of neural action potentials. Network. 1998 Nov.vol. 9:R53–R78. [PubMed] [Google Scholar]
- 5.Rieke F, Warland D, Steveninck RR, Bialek W. Spikes: Exploring the Neural Code. Cambridge, MA: MIT Press; 1997. [Google Scholar]
- 6.Super H, Roelfsema PR. Chronic multiunit recordings in behaving animals: Advantages and limitations. Prog. Brain Res. 2005;vol. 147:263–282. doi: 10.1016/S0079-6123(04)47020-4. [DOI] [PubMed] [Google Scholar]
- 7.Nicolelis MA, Dimitrov D, Carmena JM, Crist R, Lehew G, Kralik JD, Wise SP. Chronic, multisite, multielectrode recordings in macaque monkeys. Proc. Nat. Acad. Sci. USA. 2003 Sep.vol. 100:11041–11046. doi: 10.1073/pnas.1934665100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zeitler M, Fries P, Gielen S. Assessing neuronal coherence with single-unit, multi-unit, and local field potentials. Neural. Comput. 2006 Sep.vol. 18:2256–2281. doi: 10.1162/neco.2006.18.9.2256. [DOI] [PubMed] [Google Scholar]
- 9.Stark E, Abeles M. Predicting movement from multiunit activity. J. Neurosci. 2007 Aug.vol. 27:8387–8394. doi: 10.1523/JNEUROSCI.1321-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mallat SG. A theory for multiresolution signal decomposition—The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989 Jul.vol. 11(no. 7):674–693. [Google Scholar]
- 11.Ubeyli ED, Ilbay G, Sahin D, Ates N. Analysis of spike-wave discharges in rats using discrete wavelet transform. Comput. Biol. Med. 2009 Mar.vol. 39:294–300. doi: 10.1016/j.compbiomed.2009.01.004. [DOI] [PubMed] [Google Scholar]
- 12.Ubeyli ED. Statistics over features: EEG signals analysis. Comput. Biol. Med. 2009 Aug.vol. 39:733–741. doi: 10.1016/j.compbiomed.2009.06.001. [DOI] [PubMed] [Google Scholar]
- 13.Shin HC, Tong S, Yamashita S, Jia X, Geocadin RG, Thakor NV. Quantitative EEG and effect of hypothermia on brain recovery after cardiac arrest. IEEE Trans. Biomed. Eng. 2006 Jun.vol. 53(no. 6):1016–1023. doi: 10.1109/TBME.2006.873394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Nenadic Z, Burdick JW. Spike detection using the continuous wavelet transform. IEEE Trans. Biomed. Eng. 2005 Jan.vol. 52(no. 1):74–87. doi: 10.1109/TBME.2004.839800. [DOI] [PubMed] [Google Scholar]
- 15.Kim KH, Kim SJ. A wavelet-based method for action potential detection from extracellular neural signal recording with low signal-to-noise ratio. IEEE Trans. Biomed. Eng. 2003 Aug.vol. 50(no. 8):999–1011. doi: 10.1109/TBME.2003.814523. [DOI] [PubMed] [Google Scholar]
- 16.Al-Nashash HA, Paul JS, Ziai WC, Hanley DF, Thakor NV. Wavelet entropy for subband segmentation of EEG during injury and recovery. Ann. Biomed. Eng. 2003 Jun;vol. 31:653–658. doi: 10.1114/1.1575757. [DOI] [PubMed] [Google Scholar]
- 17.Rosso OA, Blanco S, Yordanova J, Kolev V, Figliola A, Schurmann M, Basar E. Wavelet entropy: A new tool for analysis of short duration brain electrical signals. J. Neurosci. Methods. 2001 Jan.vol. 105:65–75. doi: 10.1016/s0165-0270(00)00356-3. [DOI] [PubMed] [Google Scholar]
- 18.Shannon CE. A mathematical theory of communication. Bell Syst. Tech. J. 1948;vol. 27:379–423. [Google Scholar]
- 19.Ferenets R, Lipping T, Anier A, Jantti V, Melto S, Hovilehto S. Comparison of entropy and complexity measures for the assessment of depth of sedation. IEEE Trans. Biomed. Eng. 2006 Jun.vol. 53(no. 6):1067–1077. doi: 10.1109/TBME.2006.873543. [DOI] [PubMed] [Google Scholar]
- 20.Barbieri R, Frank LM, Nguyen DP, Quirk MC, Solo V, Wilson MA, Brown EN. Dynamic analyses of information encoding in neural ensembles. Neural Comput. 2004 Feb.vol. 16:277–307. doi: 10.1162/089976604322742038. [DOI] [PubMed] [Google Scholar]
- 21.Tiesinga PH, Fellous JM, Jose JV, Sejnowski TJ. Information transfer in entrained cortical neurons. Network. 2002 Feb.vol. 13:41–66. [PubMed] [Google Scholar]
- 22.Bruhn J, Lehmann LE, Ropcke H, Bouillon TW, Hoeft A. Shannon entropy applied to the measurement of the electroencephalographic effects of desflurane. Anesthesiology. 2001 Jul.vol. 95:30–35. doi: 10.1097/00000542-200107000-00010. [DOI] [PubMed] [Google Scholar]
- 23.Gray RM. Entropy and Information Theory. New York: Springer-Verlag; 1990. [Google Scholar]
- 24.Kopitzki K, Warnke PC, Timmer J. Quantitative analysis by renormalized entropy of invasive electroencephalograph recordings in focal epilepsy. Phys. Rev. E. 1998 Oct.vol. 58:4859–4864. [Google Scholar]
- 25.Quiroga RQ, Arnhold J, Lehnertz K, Grassberger P. Kulback-Leibler and renormalized entropies: Applications to electroencephalograms of epilepsy patients. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 2000 Dec.vol. 62:8380–8386. doi: 10.1103/physreve.62.8380. [DOI] [PubMed] [Google Scholar]
- 26.Buchwald JS, Grover FS. Amplitudes of background fast activity characteristic of specific brain sites. J. Neurophysiol. 1970 Jan.vol. 33:148–159. doi: 10.1152/jn.1970.33.1.148. [DOI] [PubMed] [Google Scholar]
- 27.Logothetis NK. The underpinnings of the BOLD functional magnetic resonance imaging signal. J. Neurosci. 2003 May 15;vol. 23:3963–3971. doi: 10.1523/JNEUROSCI.23-10-03963.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Moran A, Bar-Gad I. Revealing neuronal functional organization through the relation between multi-scale oscillatory extracellular signals. J. Neurosci. Methods. 2010 Jan.vol. 186:116–129. doi: 10.1016/j.jneumeth.2009.10.024. [DOI] [PubMed] [Google Scholar]
- 29.Bezerianos A, Tong S, Thakor N. Time-dependent entropy estimation of EEG rhythm changes following brain ischemia. Ann. Biomed. Eng. 2003 Feb.vol. 31:221–232. doi: 10.1114/1.1541013. [DOI] [PubMed] [Google Scholar]
- 30.Indiradevi KP, Elias E, Sathidevi PS, Nayak SD, Radhakrishnan K. A multi-level wavelet approach for automatic detection of epileptic spikes in the electroencephalogram. Comput. Biol. Med. 2008 Jul.vol. 38:805–816. doi: 10.1016/j.compbiomed.2008.04.010. [DOI] [PubMed] [Google Scholar]
- 31.Kullback S. The Kullback-Leibler distance. Amer. Statist. 1987 Nov.vol. 41:340–340. [Google Scholar]
- 32.Kullback S. Information Theory and Statistics. NewYork: Wiley; 1959. [Google Scholar]
- 33.Kullback S, Leibler RA. On information and sufficiency. Ann. Math. Stat. 1951;vol. 22:142–143. [Google Scholar]
- 34.Jia X, Koenig MA, Nickl R, Zhen G, Thakor NV, Geocadin RG. Early electrophysiologic markers predict functional outcome associated with temperature manipulation after cardiac arrest in rats. Crit. Care Med. 2008 Jun.vol. 36:1909–1916. doi: 10.1097/CCM.0b013e3181760eb5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Jia X, Koenig MA, Shin HC, Zhen G, Pardo CA, Hanley DF, Thakor NV, Geocadin RG. Improving neurological outcomes post-cardiac arrest in a rat model: Immediate hypothermia and quantitative EEG monitoring. Resuscitation. 2008 Mar.vol. 76:431–442. doi: 10.1016/j.resuscitation.2007.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Zhang PM, Wu JY, Zhou Y, Liang PJ, Yuan JQ. Spike sorting based on automatic template reconstruction with a partial solution to the overlapping problem. J. Neurosci. Methods. 2004 May 30;vol. 135:55–65. doi: 10.1016/j.jneumeth.2003.12.001. [DOI] [PubMed] [Google Scholar]
- 37.Quiroga RQ, Nadasdy Z, Ben-Shaul Y. Unsupervised spike detection and sorting with wavelets and superparamagnetic clustering. Neural Comput. 2004 Aug.vol. 16:1661–1687. doi: 10.1162/089976604774201631. [DOI] [PubMed] [Google Scholar]
- 38.Brychta RJ, Tuntrakool S, Appalsamy M, Keller NR, Robertson D, Shiavi RG, Diedrich A. Wavelet methods for spike detection in mouse renal sympathetic nerve activity. IEEE Trans. Biomed. Eng. 2007 Jan.vol. 54(no. 1):82–93. doi: 10.1109/TBME.2006.883830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Daubechies I. Ten Lectures on Wavelets. Philadelphia, PA: Soc. Ind. Appl. Math; 1992. [Google Scholar]
- 40.Geocadin RG, Muthuswamy J, Sherman DL, Thakor NV, Hanley DF. Early electrophysiological and histologic changes after global cerebral ischemia in rats. Mov. Disord. 2000;vol. 15:14–21. doi: 10.1002/mds.870150704. [DOI] [PubMed] [Google Scholar]