In Vivo Dynamic Strains of the Ovine Anterior Mitral Valve Leaflet

Abstract

Understanding the mechanics of the mitral valve is crucial in terms of designing and evaluating medical devices and techniques for mitral valve repair. In the current study we characterize the in vivo strains of the anterior mitral valve leaflet. On cardiopulmonary bypass, we sew miniature markers onto the leaflets of 57 sheep. During the cardiac cycle, the coordinates of these markers are recorded via biplane fluoroscopy. From the resulting four-dimensional data sets, we calculate areal, maximum principal, circumferential, and radial leaflet strains and display their profiles on the averaged leaflet geometry. Average peak areal strains are 13.8±6.3%, maximum principal strains are 13.0±4.7%, circumferential strains are 5.0±2.7%, and radial strains are 7.8±4.3%. Maximum principal strains are largest in the belly region, where they are aligned with the radial direction during diastole switching into the circumferential direction during systole. Circumferential strains are concentrated at the distal portion of the belly region close to the free edge of the leaflet, while radial strains are highest in the center of the leaflet, stretching from the posterior to the anterior commissure. In summary, leaflet strains display significant temporal, regional, and directional variations with largest values inside the belly region and toward the free edge. Characterizing strain distribution profiles might be of particular clinical significance when optimizing mitral valve repair techniques in terms of forces on suture lines and on medical devices.

1. Introduction

The mitral valve is a sophisticated three-dimensional structure, consisting of the annulus, two leaflets, and the chordae tendinae that originate from the papillary muscles and insert into the leaflets. In the healthy heart, the mitral valve ensures unidirectional blood flow from the left atrium into the left ventricle. Throughout the cardiac cycle, the mitral valve experiences complex mechanical loading. Particularly during systole, the leaflets undergo large deformation [35, 37].

Malfunctioning mitral valves are associated with high mortality and morbidity. Fortunately, several of the disease scenarios can be treated either medically, interventionally, or surgically [4]. Throughout the past decades, surgical mitral valve repair has become the procedure of choice [41]. Different strategies such as leaflet resection [9, 14], leaflet augmentation [1], edge-to-edge repair [27], neo-chordae, chordal cutting, chordal shortening [9, 11], and papillary muscle repositioning [23] have been proposed as repair techniques to restore mitral valve competence. In addition, medical devices such as annuloplasty rings or mitral clips are implanted in support of the repair or as the sole solution [8, 10]. While these interventions aim at restoring valve function, it is likely that they alter normal loading conditions and associated deformations [29]. It has been shown that alterations in mechanical loading may result in valvular remodeling, which, in turn, might affect normal valve function [33]. In addition, abnormal loading patterns on the valve may impair long-term repair durability [7, 38].

A common measure for the deformation of a body is strain. In a series of studies, in vitro leaflet strains were reported over the entire cardiac cycle of bovine anterior and posterior mitral valve leaflets, both under normal and disease conditions [18, 19, 20, 30]. These studies demonstrate the sensitivity of leaflet strains to alterations in mitral valve geometry and loading. Only recently, piezoelectric transducers were used to quantify ovine anterior mitral valve leaflet strains in vivo [36]. In addition, computational studies can also help to understand the complex mechanics of heart valves in silico [12, 31, 32, 39, 40]. In vitro and in vivo studies provide valuable insight into mitral valve function. However, existing studies only report local strain values from the center of the leaflet. Understanding of the mechanical state of the leaflet outside the center may be crucial for the evaluation of repair techniques in terms of repair durability [15]. In this study, we provide a more complete picture of anterior mitral leaflet strains. This knowledge will help to characterize mitral valve mechanics more accurately and provide guidance to improve long-term durability of surgical treatments and medical devices. In the past two decades, we have established different ovine models to study various aspects of mitral valve mechanics under pathological and normal conditions [5, 6, 17]. In living sheep, we track surgically implanted tantulum markers throughout several consecutive cardiac cycles via video fluoroscopy. In the current study this technique is combined with a continuum mechanical approach to reconstruct strain profiles across the entire anterior mitral leaflet throughout the complete cardiac cycle. To address both the engineering community and clinical community, we report areal strains and maximum principal strains which might be more intuitive to engineers [20], and circumferential and radial strains which are more intuitive to cardiac surgeons [6, 36]. Since the choice of the appropriate reference configuration has been discussed controversially in the literature [18, 21, 36], we also explore the sensitivity of the strain calculation with respect to different reference states.

2. Methods

2.1. Animal Experiments

All animals received humane care in compliance with the Principles of Laboratory Animals Care formulated by the National Academy of Sciences and published by the National Institutes of Health (DHEW [NIH] Publication 85 to 23, revised 1985). This study was approved by the Stanford Medical Center Laboratory Research Animals Review Committee and conducted according to Stanford University policy.

Prior to data acquisition we pre-medicate 57 adult, male Dorsett-hybrid sheep intramuscularly with ketamine and anesthetize them with sodium thiopental. We intubate and ventilate the sheep with inhalational isoflurane. Following a left thoractomy, under cardiopulmonary bypass and cardioplegic arrest, we implant 23 miniature radiopaque tantulum markers onto the anterior mitral leaflet and the surrounding annulus, see Figure 1. After all markers are placed, we close the left atrium before weaning the animals off cardiopulmonary bypass. For biplane videofluoroscopic imaging of the markers in the beating heart, we transfer the animals to the experimental catheterization laboratory. In the right lateral decubitus position, we acquire the marker coordinates from biplane videofluoroscopy under open chest conditions at a sampling frequency of 60Hz. Using catheter micromanometer pressure transducers, we simultaneously record atrial, ventricular, and aortic pressures. To obtain four-dimensional marker coordinates, we merge the biplane images off-line via a semi-automated image processing and digitization software developed in our laboratory [31].

Figure 1.

Animal in decubitus position during videofluoroscopic imaging, left. Cameras C1 and C2 record two-dimensional X-ray images of the beating heart. Merging these two data sets, we obtain the three-dimensional coordinates of 23 markers from which we reconstruct the leaflet surface, right. We implanted seven markers close to the mitral leaflet free edge, grey, nine on the central belly region of the leaflet, black, and seven on the anterior section of the mitral annulus, white. The markers have an average weight of 3.2mg with an outer diameter of 1.1mm and inner diameter of 0.6mm.

2.2. Temporal interpolation

The sampling frequency of our biplane videofluoroscopy system is fixed at 60Hz for all animals. Since the animals have different heart rates, the number of data time points acquired over a cardiac cycle varies with each animal. To create average leaflet geometries and strain profiles, we map all 57 data sets into four time intervals between end-diastole, end-isovolumic contraction, end-systole, end-isovolumic relaxation, and end-diastole of the next beat. Based on the different average interval lengths, these four intervals are further subdivided into five, thirteen, seven, and fifteen segments, respectively, see Figure 2. Within each of these four intervals, we perform a linear temporal interpolation between the experimentally acquired raw data points to create temporally aligned data sets of hemodynamic and kinematic data at the five, thirteen, seven, and fifteen segment points, thus representing the cardiac cycle through n_time = 40 discrete time points.

Figure 2.

Average left ventricular pressure with representative time points. Squares indicate the three analyzed reference states for the strain calculations referenced in Figure 3. Reference states R1, R2, and R3 correspond to minimum left ventricular pressure, black square, end-diastole, grey square, and leaflet separation, white square, respectively. The black diamond indicates maximum left ventricular pressure referenced in Figure 6. Black circles indicate the time points referenced in Figure 7.

2.3. Spatial interpolation

From the time-aligned data sets, at each of the n_time = 40 discrete time points, we create a triangular facet mesh, see Figure 1. We characterize the leaflet as a thin membrane and quantify its strain state exclusively in terms of its membrane or in plane strains [2]. For each three-noded membrane element, n_nod = 3, we interpolate the reference configuration X(θ¹, θ²) and the current configuration x(θ¹, θ²) in terms of the reference and current nodal positions X_I and x_I.

$$\begin{array}{c}\hfill \mathit{X}({\theta }^1,{\theta }^2)={\displaystyle {\sum }_{I=1}^{n_{\text{nod}}}}{N}_I({\theta }^1,{\theta }^2){\mathit{X}}_I\\ \hfill \mathit{x}({\theta }^1,{\theta }^2)={\displaystyle {\sum }_{I=1}^{n_{\text{nod}}}}{N}_I({\theta }^1,{\theta }^2){\mathit{x}}_I\end{array}$$ (1)

Herein, N_I are the linear shape functions parameterized in terms of the local curvilinear coordinates θ^α, with α = 1, 2. From their partial derivatives with respect to the curvilinear coordinates ∂N_I/∂θ^α we calculate the set of covariant base vectors in the reference configuration G_α and in the current configuration g_α.

$$\begin{array}{c}\hfill {\mathit{G}}_{\alpha }({\theta }^1,{\theta }^2)={\displaystyle {\sum }_{I=1}^{n_{\text{nod}}}}\frac{\partial N_I}{\partial {\theta }^{\alpha }}{\mathit{X}}_I\\ \hfill {\mathit{g}}_{\alpha }({\theta }^1,{\theta }^2)={\displaystyle {\sum }_{I=1}^{n_{\text{nod}}}}\frac{\partial N_I}{\partial {\theta }^{\alpha }}{\mathit{x}}_I\end{array}$$ (2)

The scalar product between the individual covariant base vectors introduces the covariant surface metrics of the reference configuration G_αβ and of the current configuration g_αβ.

$$\begin{array}{ccc}{G}_{\alpha \beta }={\mathit{G}}_{\alpha }·{\mathit{G}}_{\beta }\hfill & & \hfill g_{\alpha \beta }={\mathit{g}}_{\alpha }·{\mathit{g}}_{\beta }\end{array}$$ (3)

Using the contravariant spatial surface metric g^αβ = [g_αβ]⁻¹, i.e., the inverse of the covariant spatial surface metric g_αβ, we map the covariant base vectors g_β onto their contravariant counterparts g^α.

$$\begin{array}{ccc}{\mathit{g}}^{\alpha }=g^{\alpha \beta }{\mathit{g}}_{\beta }\hfill & & g^{\alpha \beta }={\mathit{g}}^{\alpha }·{\mathit{g}}^{\beta }={[g_{\alpha \beta }]}^{-1}\hfill \end{array}$$ (4)

We then introduce the Euler-Almansi membrane strains e as the differences between the contravariant current and reference surface metrics g_αβ and G_αβ in terms of the contravariant spatial base vectors g^α.

$$\begin{array}{ccc}\mathit{e}=e_{\alpha \beta }{\mathit{g}}^{\alpha }\otimes {\mathit{g}}^{\beta }\hfill & & e_{\alpha \beta }=\frac{1}{2}[g_{\alpha \beta }-G_{\alpha \beta }]\hfill \end{array}$$ (5)

By solving the corresponding eigenvalue problem, we calculate the principal strains λ^e,

$$[e_{\alpha \beta }-{\lambda }^e{g}_{\alpha \beta }]n^{\beta }=0_{\alpha }$$ (6)

where n^β are the contravariant principal strain directions. From the corresponding characteristic equation

$$\begin{array}{ccc}{\lambda }^{e2}-I_e\lambda +{\mathit{\text{II}}}_e=0\hfill & & {\lambda }_{1,2}^e=\frac{1}{2}[I_e\pm \sqrt{I_e^2-4{\mathit{\text{II}}}_e}]\hfill \end{array}$$ (7)

we obtain the maximum and minimum principal strains ${\lambda }_{\text{max}}^e=\text{max}\{{\lambda }_{1,2}^e\}\text{ and }{\lambda }_{\text{min}}^e=\text{min}\{{\lambda }_{1,2}^e\}$ using the following expressions for the invariants I_e and II_e.

$$\begin{array}{ccc}{I}_e={\text{tr}}_g(\mathit{e})=e_{\alpha \beta }{g}^{\alpha \beta }\hfill & & {\mathit{\text{II}}}_e={\text{det}}_g(\mathit{e})=\text{det}(e_{\alpha \beta })/\text{det}(g_{\alpha \beta })\hfill \end{array}$$ (8)

To determine the circumferential and radial strain components e^cc and e^rr, we map the Euler-Almansi strain e onto the circumferential and radial directions n^c and n^r in the current configuration.

$$\begin{array}{ccc}{e}^{\text{cc}}={\mathit{n}}^{\mathrm{c}}·\mathit{e}·{\mathit{n}}^{\mathrm{c}}\hfill & & e^{\text{rr}}={\mathit{n}}^{\mathrm{r}}·\mathit{e}·{\mathit{n}}^{\mathrm{r}}\hfill \end{array}$$ (9)

The radial direction n^r is defined as the vector pointing from the mid-trigonal marker to the geometric center of the leaflet; the circumferential directions n^c is defined orthogonal to it, passing through the leaflet center, see Figure 1. Finally, for each time point we calculate the Euler-Almansi areal strains

$$e^{\text{areal}}=\frac{\text{da}-\text{dA}}{\text{da}}$$ (10)

as the relative changes in triangular area, where dA and da are the areas of each triangular element in the reference and current configurations. From the Euler-Almansi areal strain e^areal, we can calculate the area stretch

$${\nu }^{\text{area}}=\frac{\text{da}}{\text{dA}}=\frac{1}{[1-e^{\text{areal}}]}$$ (11)

which, in classical continuum mechanics, is known as the norm of the projection of the unit normal to the corresponding triangular facet element in the reference configuration, projected with the cofactor of the deformation gradient. If we assume that the leaflet is incompressible, changes in thickness direction

$${\nu }^{\text{thick}}=\frac{\text{dA}}{\text{da}}=1-e^{\text{areal}}$$ (12)

would follow directly from the incompressibility constraint ν^thick = 1/ν^area.

2.4. Local Strains in the Belly Region

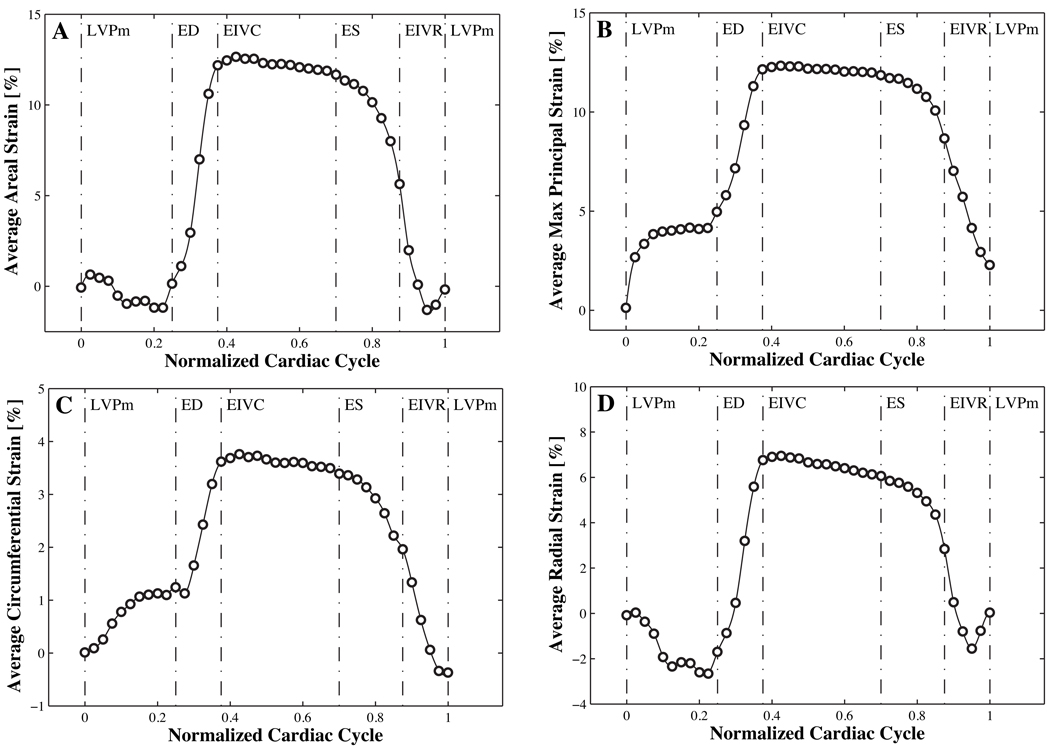
For a quantitative comparison with previously reported data [36], we extract peak strain values averaged over the belly region from the raw data sets and report areal strains e^areal according to equation (10), maximum principal strains ${\lambda }_{\text{max}}^e$ according to equation (7), and circumferential and radial strains e^cc and e^rr according to equation (9), see Figure 3 left. Using a second order central difference scheme, we calculate strain rates as the first temporal derivatives of the strains. To calculate the left and right boundary values, we apply a one-sided second order downwind and upwind scheme, respectively, see Figure 3 right. Since different reference configurations have been proposed in the literature, we report these strains and strain rates for three commonly used reference configurations, R1 at minimum left ventricular pressure [36], R2 at end-diastole, and R3 at leaflet separation [21], see Figure 2. To illustrate temporal strain variations throughout the cardiac cycle, we extract average areal, maximum principal, circumferential, and radial strains using the reference configuration R1, see Figure 4.

Figure 3.

Average peak strains and average peak strain rates in the belly region. Means ± standard deviations of areal, maximum principal, circumferential, and radial strains and their corresponding strain rates displayed for three different reference states. Reference states R1, R2, and R3 correspond to minimum left ventricular pressure, black, end-diastole, grey, and leaflet separation, white, respectively. Strains and strain rates display similar means and standard deviations, irrespective of the reference state R1, R2, or R3.

Figure 4.

Average strains in the belly region over the normalized cardiac cycle. Time aligned areal, maximum principal, circumferential, and radial strains in the belly region are averaged over 57 animals. Average areal and maximum principal strains with peak values of 12.3% and 12.7% are significantly larger than average circumferential and radial strains with peak values of 3.8% and of 7.0%.

2.5. Global Strains in the Entire Leaflet

For visualization purposes, we employ a custom-designed approximating subdivision algorithm to create a smooth leaflet surface [16]. The subdivision is based on the original mesh created from the 23 experimentally acquired marker coordinates, see Figure 1. Marker coordinates are temporally averaged throughout the cardiac cycle as described in Section 2.2. To iteratively create finer surface meshes, we compute the coordinates of the (k+1)-th refinement level as the weighted averages of the nodal coordinates of the k-th refinement level. The newly generated nodes ${\mathit{x}}_I^{\mathrm{k}+1}$ are computed as follows.

$${\mathit{x}}_I^{\mathrm{k}+1}=[3{\mathit{x}}_0^{\mathrm{k}}+{\mathit{x}}_{I-1}^{\mathrm{k}}+3{\mathit{x}}_I^{\mathrm{k}}+{\mathit{x}}_{I+1}^{\mathrm{k}}]/8$$ (13)

The old nodes ${\mathit{x}}_0^{\mathrm{k}}$ are assigned new coordinates ${\mathit{x}}_0^{\mathrm{k}+1}$ according to

$${\mathit{x}}_0^{\mathrm{k}+1}=[1-\upsilon w]{\mathit{x}}_0^{\mathrm{k}}+w{\displaystyle {\sum }_{I=1}^{\upsilon }}{\mathit{x}}_I^{\mathrm{k}}$$ (14)

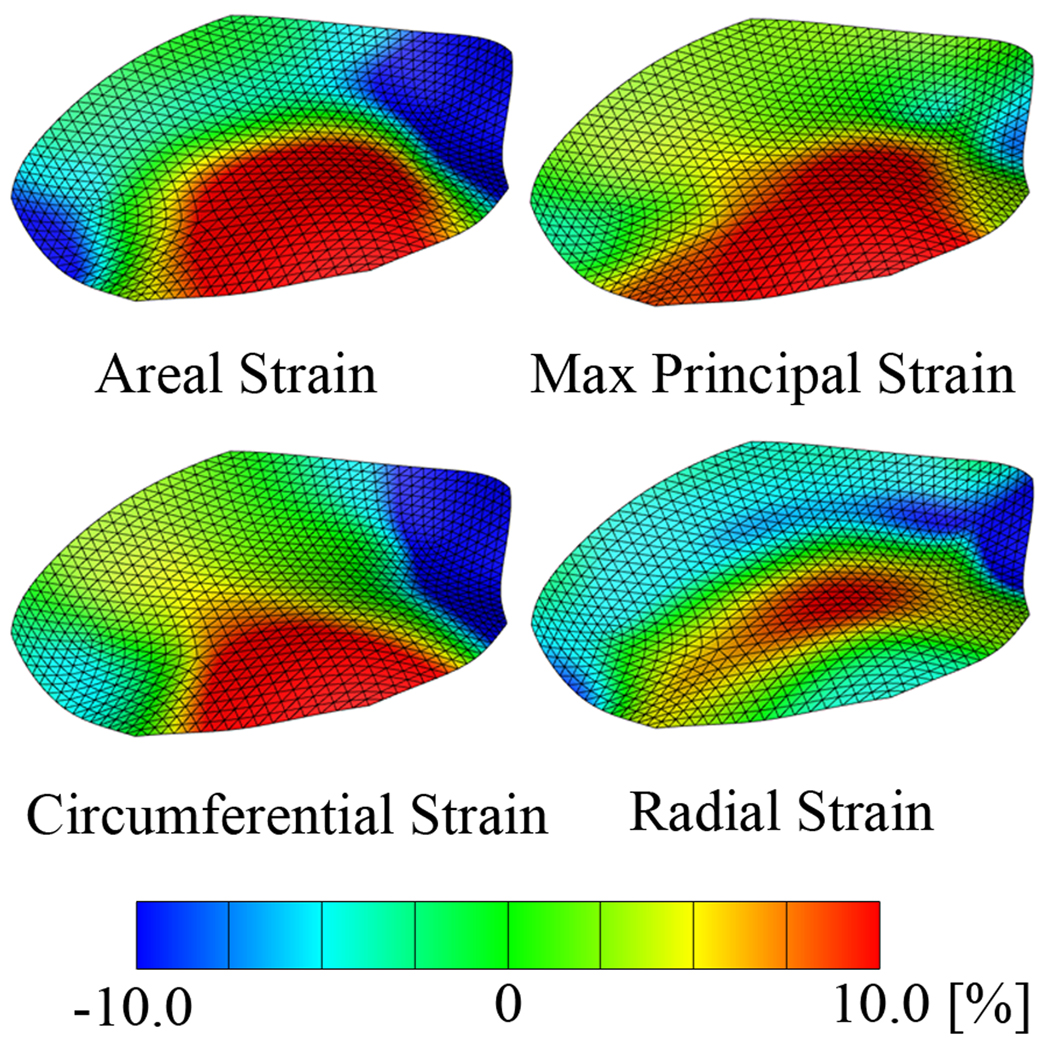
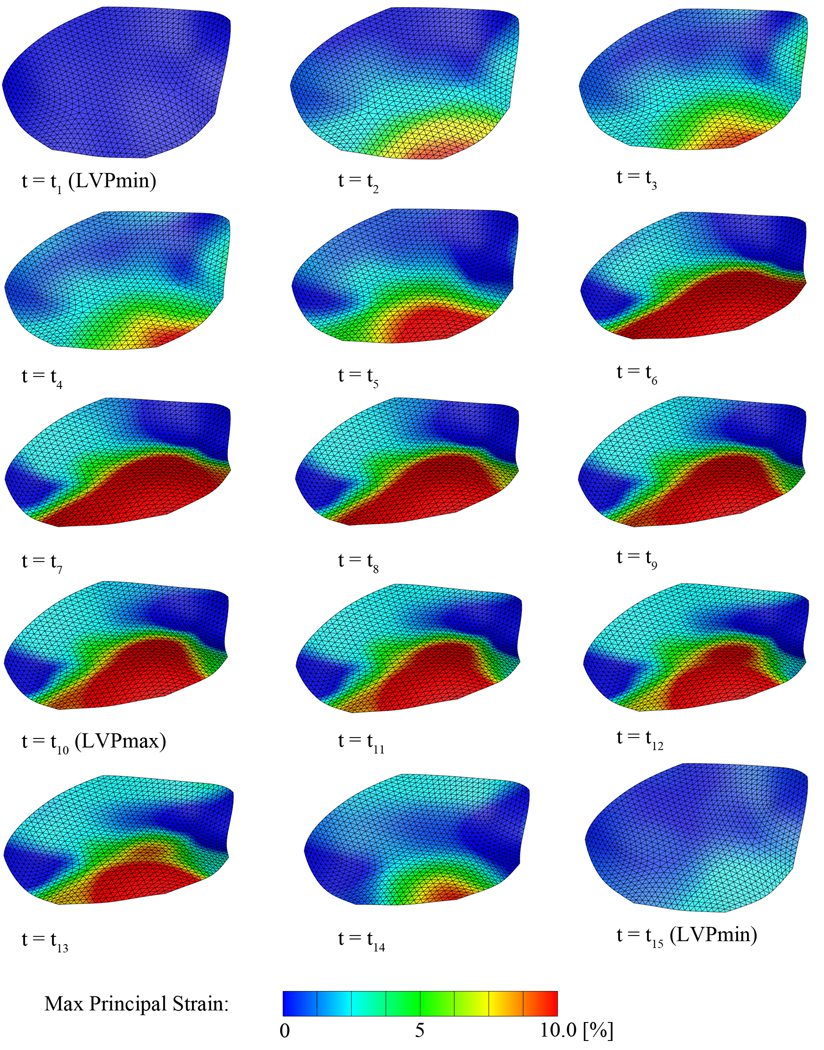
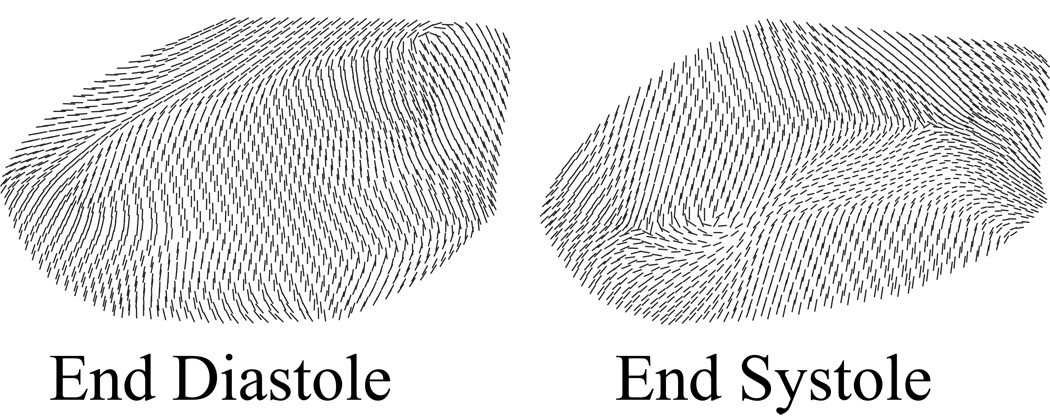
where w is a weighting function and υ denotes the valence of the node under consideration, i.e., the number of edges connected to it. We employed this subdivision algorithm in three refinement steps to create a smooth representation of the three-dimensional leaflet surface which consists of 1017 nodes and 1920 elements, see Figure 5. Using this smoothened average leaflet representation we extract areal strains e^area, maximum principal strains ${\lambda }_{\text{max}}^e$ , circumferential strains e^cc, and radial strains e^rr at maximum left ventricular pressure, averaged over 57 animals using the spatial interpolation of Section 2.3, see Figure 6. To illustrate the temporal strain variation throughout the cardiac cycle, we display the maximum principal strains ${\lambda }_{\text{max}}^e$ , averaged over 57 animals using the temporal and spatial interpolations of Sections 2.2 and 2.3, see Figure 7. Last, to demonstrate changes in maximum principal strain directions throughout the cardiac cycle, we illustrate the maximum principal strain directions n^β associated with the maximum principal strains ${\lambda }_{\text{max}}^e$ according to equation (6) at end diastole and end systole, see Figure 8.

Figure 5.

Average maximum principal strains upon successive mesh refinement. The original mesh shown on the left consists of 23 nodes and 30 triangular facet elements such that each node corresponds to the original marker position. The mesh is iteratively refined to 1017 nodes and 1920 elements in three consecutive subdivision steps. Upon mesh refinement, the resulting leaflet surface shows increased smoothness and resembles mitral valve leaflet geometry more closely. The convergence study of the surface subdivision algorithm shows that further refinement beyond the third subdivision does not reveal noticeable changes.

Figure 6.

Average areal strains, maximum principal, circumferential, and radial strains at maximum left ventricular pressure. Geometric data of 57 animals are temporally interpolated and then averaged. Strains are calculated from the averaged data set on the approximated leaflet surface after three levels of subdivision.

Figure 7.

Average maximum principal strains over the entire cardiac cycle. Geometric data of 57 animals are temporally interpolated and then averaged. Strains are calculated from the averaged data set on the approximated leaflet surface after three levels of subdivision. The first plot at t₁ corresponds to the leaflet in the reference state and is therefore strain free. Time points t₁ to t₁₅ correspond to the time points indicated as black circles in Figure 2.

Figure 8.

Average maximum principal strain directions at end diastole and end systole. Strains are calculated from the averaged data set on the approximated leaflet surface after three levels of subdivision. At end diastole, maximum principal strains at the annulus and close to the free edge are oriented circumferentially, while maximum principal strains in the belly region are oriented radially. At end systole, maximum principal strains at the annulus and close to the free edge are oriented more radially, while maximum principal strains in the belly region are oriented more circumferentially.

3. Results

For 57 animals, we collect four-dimensional marker coordinates and hemodynamic data. We interpolate these data in time and space to calculate Euler-Almansi strain tensors. We extract areal and maximum principal strains relevant to the engineering community, and circumferential and radial strains relevant to the clinical community. All animals display physiological hemodynamics with a maximum left ventricular pressure of 97.2±7.8mmHg, see Figure 2, and a cardiac cycle length of 681.5±103.4ms. All mitral valves exhibit normal leaflet motion with no apparent valvular dysfunction assessed by epicardial echocardiography.

3.1. Local Strains in the Belly Region

Figure 2 illustrates three reference configurations commonly used in the literature, R1 at minimum left ventricular pressure, R2 at end-diastole, and R3 at leaflet separation. Figure 3 displays the comparison of these reference configurations in terms of average peak strains and average peak strain rates of areal, maximum principal, circumferential, and radial strains in the belly region. Mean values and standard deviations of the different strain types and strain rates vary only insignificantly for the different reference configurations. We conclude that strain and strain rate are almost insensitive to the choice of the reference configuration, R1, R2, or R3. Since minimum left ventricular pressure is unproblematic to determine experimentally and has been successfully used in the past [36], we personally recommend state R1 as the most reproducible reference configuration. All following results are therefore based on the reference configuration R1.

Figure 4 shows the average belly strains over the normalized cardiac cycle. As expected, areal, maximum principal, circumferential, and radial strains are positive during most of the cycle. However, all strain plots display slightly negative values shortly after isovolumic relaxation. While circumferential strains show a distinct positive peak toward end diastole, radial strains display a noteworthy negative deflection. With continuing systole, the strains rise to their peak values before starting a slow decrease during the second half of systole. During diastole strains drop rapidly to a local minimum toward the end of the cardiac cycle. The quantitative comparison between areal, maximum principal, circumferential, and radial strains shown in Figure 4 agrees with the average peak values displayed in Figure 3. As indicated through the solid black bars in Figure 3 and through the maximum values in Figure 4, belly average peak areal strains are 12.7 +/− 8.7%, belly average peak maximum principal strains are 12.3±4.5%, belly average peak circumferential strains are 3.8 +/− 3.6%, and belly average peak radial strains are 7.0 +/− 4.2%. All peak strains occur at the same time, at t=0.42 of the normalized cardiac cycle, slightly after the phase of isovolumetric contraction.

3.2. Global Strains in the Entire Leaflet

Figure 5 summarizes the average maximum principal strains upon successive mesh refinement to demonstrate the convergence of our custom designed subdivision surface algorithm. Figure 5, left, displays the original mesh with 23 nodes and 30 elements which is successively refined to create a smooth representation of the three-dimensional leaflet surface. Sufficient smoothness is obtained within three steps, with a final mesh consisting of 1017 nodes and 1920 elements illustrated in Figure 5, right.

Figure 6 illustrates the average areal, maximum principal, circumferential, and radial strains at maximum left ventricular pressure. Areal, maximum principal, and circumferential strain profiles display largest tensile strains of more than 10% in an area ranging from the belly towards the free edge. The radial strain profile displays largest tensile strains in the belly region spanning from the anterior to the posterior commissure, while radial strains near the free edge are slightly compressive. Global average peak areal strains are 13.8±6.3% and their strain rates are 432.1±174.3%/s, global average peak maximum principal strains are 13.0±4.7% and their strain rates are 247.9±112.2%/s, global average peak circumferential strain are 5.0 ±2.7% and their strain rates are 111.5±58.6%/s, and global average peak radial strain are 7.8±4.3% and their strain rates are 332.2±149.8%/s.

Figure 7 displays the averaged maximum principal strains over the entire cardiac cycle; videos of all four strain components throughout the cardiac cycle can be found in the supplemental materials. Starting at t₁, the leaflet is in the diastolic position, almost fully opened. With progressing time, the leaflet undergoes a configurational change accompanied by localized tensile strains in the center of the free edge. The increasing transvalvular pressure during systole pushes the leaflet into its systolic position, giving rise to increasing tensile strains close to the leaflet edge and toward the belly region. During systole, peak strains do not change significantly, however, the size of the tensile area increases from early systole to mid systole at t₇. From mid systole to mid diastole, tensile strains gradually decrease back to zero.

Figure 8 shows the average maximum principal strain directions at end diastole and at end systole. At end diastole, maximum principal strains at the annulus and close to the free edge are oriented circumferentially, while maximum principal strains in the belly region are oriented radially. At end systole, however, maximum principal strains at the annulus and close to the free edge are oriented more radially, while maximum principal strains in the belly region are oriented more circumferentially.

4. Discussion

Preceding the discussion, we would like to point out that since our markers are implanted on the atrial leaflet surface, their digitized centers do not lie exactly within the leaflet’s mid-surface. Our strain calculation might therefore introduce errors, particularly in regions of high curvature [16, 26].

4.1. Relation to Previous Studies

When comparing the belly strains of the current study (CS) to the results reported in previous in vivo studies [36] (S), we find a good agreement concerning average peak areal strain (CS: 13.8%, S: 15–20%), average peak circumferential strain (CS: 5.0%, S: 2.5–3.3%), and average peak radial strain (CS: 7.8%, S: 15%–20%). In addition, reported average peak strain rates agree well with our circumferential strain rate (CS: 111.5%/s, S: 100–130%/s) and radial strain rate (CS: 332.2%/s, S: 300–400%/s). Our average strains over the entire cardiac cycle closely resemble reported single animal raw data, qualitatively and quantitatively [36]. Small deviations might be attributed to the different marker locations in the two studies. Previously reported in vitro data show qualitatively similar average peak values and strain vs. time curves [18, 19, 30]. However, all reported strains are slightly larger than ours. This might be caused by the general difference between porcine and ovine valves, and by the incapability of in vitro models to accurately reproduce the mechanical and hemodynamic environment of the mitral valve. In agreement with previous reports [21, 22, 24], we find that in the belly region, the leaflet displays higher mechanical strength in circumferential direction than in radial direction, giving rise to significantly different circumferential and radial strain profiles. These findings underline the pronounced anisotropic character of the mitral leaflet, manifesting itself in the heterogeneity of the maximum principal strain directions, which can be attributed to the highly organized microstructure [3, 25].

4.2. Advantage over Previous Studies

Local strains in porcine and ovine mitral valve leaflets have been reported in the past measured in vitro using a left heart simulator [18, 19, 30]. Although, these in vitro studies have enhanced our knowledge concerning mitral valve disease and repair, they are per se incapable of reproducing all aspects of the complex mechanical and hemodynamic environment of the mitral valve. The first study to characterize the mechanical state of the mitral valve in vivo used sonocrystals to quantify anterior mitral leaflet strains in the beating ovine heart [36]. The knowledge gained from this experiment has since been valuable to both basic understanding of valve mechanics and medical device design. In addition to these studies, our methodology provides a high spatial resolution based on a larger marker array distributed over the entire anterior mitral leaflet. The large number of animals included in our analysis provides a higher confidence than previous studies.

4.3. Global Strains in the Entire Leaflet

We quantify average areal, maximum principal, circumferential, and radial strains for 57 animals. These average strain maps on an average anterior mitral leaflet geometry allow us to characterize leaflet kinematics throughout the entire cardiac cycle. Regional strain variations are illustrated by means of different strain patterns at maximum left ventricular pressure. While high circumferential strain dominates the mechanics close to the free edge of the leaflet, radial strains are highest in the center of the belly reflecting the circumferential collagen organization and the reduced thickness of the valve tissue [3, 25]. The proposed methodology allows us to elicit the mechanics of leaflet tissue, not only in the belly region, but throughout the entire leaflet surface, and to provide information about the qualitative and quantitative strain state, for instance, close to the free edge of the leaflet and in the septal region. In a complementary study, using a similar methodology, we are currently exploring the dynamics of the mitral annulus in terms of annular geometry, strains, and curvature [6, 34] in analogy to a recent study in the literature [13].

4.4. Clinical significance

Information about the mechanical state of the entire mitral leaflet might be important when evaluating current medical devices and techniques for mitral valve repair. In most cases, long-term repair failures are the result of disruption at leaflet, chordal, or annular suture lines. Therefore, the information presented in this work would allow the optimization of potential intervention sites in order to reduce strain on medical devices or suture lines. A profound scientific understanding of leaflet strain kinematics is essential to systematically increase repair durability.

4.5. Conclusion

In summary, the present study demonstrates significant temporal, regional, and directional variations of mitral leaflet strains. From an engineering point of view, average peak maximum principal strains of ~13% in combination with the maximum principal strain directions in end systole and end diastole might be most interesting. From a clinical point of view, the average peak circumferential and radial strains of ~5% and ~8% in the belly region might be most relevant. To our knowledge, this is the first study to characterize strain profiles across the entire anterior mitral leaflet in the beating heart. We believe that the reported strain values and strain profiles will provide crucial information to quantify existing repair techniques and devices, and to support engineers and clinicians in the endeavor of improving current treatment strategies.