cis Element/Transcription Factor Analysis (cis/TF): A Method for Discovering Transcription Factor/cis Element Relationships

Abstract

We report a simple new algorithm, cis/TF, that uses genomewide expression data and the full genomic sequence to match transcription factors to their binding sites. Most previous computational methods discovered binding sites by clustering genes having similar expression patterns and then identifying over-represented subsequences in the promoter regions of those genes. By contrast, cis/TF asserts that B is a likely binding site of a transcription factor T if the expression pattern of T is correlated to the composite expression patterns of all genes containing B, even when those genes are not mutually correlated. Thus, our method focuses on binding sites rather than genes. The algorithm has successfully identified experimentally-supported transcription factor binding relationships in tests on several data sets from Saccharomyces cerevisiae.

An unprecedented opportunity exists to decipher transcriptional regulation by combining computational analysis of large-scale gene expression with knowledge of complete genomic sequence. The logical basis for this research is the now well-established fact that gene expression is controlled by specific interactions between regulatory proteins, transcription factors, and short sequences in the regulatory regions of genes to which they bind, cis elements (Arnone and Davidson 1997). Taking a reverse perspective, several computational techniques have used expression data to help focus the search for cis elements within the vast expanse of genomic sequence (for review, see Zhang 1999). We describe a simple computational approach that identifies cis elements and the factors that are likely to bind them by finding a high correlation between the expression of a given transcription factor and the sum of expression patterns of a group of genes that share a motif in their regulatory regions. Describing the mechanisms behind gene regulation has enormous implications for understanding development and designing therapies for genetic diseases in humans but the first steps are now focused on defining the primary level of regulatory interactions.

Microarray technology has permitted genomewide expression data to be collected in a single experiment (Schena et al. 1995; Lockhart et al. 1996; DiRisi et al. 1996). For instance, in Saccharomyces cerevisiae, several public databases exist that report the expression level of virtually every transcript at different points during a developmental or metabolic time course (e.g., Chu et al. 1998; Spellman et al. 1998). With the complete sequence of S. cerevisiae available, it is also possible to retrieve the putative upstream regulatory sequence of any gene.

One important approach to identifying cis elements has been to cluster genes according to their expression patterns and then search for potential regulatory motifs in the upstream regions of gene clusters (Brazma et al. 1998; Roth et al. 1998; Spellman et al. 1998; van Heldon 1998; Zhang 1999). Spellman et al. (1998) used cDNA microarrays to measure mRNA transcript levels in synchronized yeast cells at several time points in the cell cycle. Genes were grouped into expression profiles using Pearson correlation and their upstream regions were searched for over-represented, degenerate motifs using a modified Gibbs sampling algorithm. The technique yielded cis elements that are known to play a role in cell-cycle regulation, suggesting it could predict novel binding sites with functional roles.

However, motif searching based on clustered genes eliminates useful data when gene regulation is complex. For instance, the expression pattern of a particular gene may be due to a combination of different regulatory elements conferring different effects at different times or in different tissues (Yuh et al. 1998; Flores et al. 2000; Halfon et al. 2000; Xu et al. 2000). Thus, genes may share certain functional cis elements in their regulatory regions but still differ in their overall expression due to other, nonshared, cis elements.

In a method developed independently, Bussemaker et al. (2001) assumed that each binding site makes an additive contribution to the expression of a gene in a given experimental setting. That is, G_i = Σ_j N_ij C_j, where G_i is the normalized expression value of gene i at a given experimental point, N_ij is the number of times binding site B_j appears on the promoter region of gene i, and C_j is the coefficient for binding site B_j for a particular experiment. An important assumption of this method is that each binding site B contributes the positive or negative influence on expression for every gene as represented by its coefficient. That implies, for example, that if two binding sites B and B‘ happen to have the same coefficients and if a promoter for gene G has both, then replacing each instance of B by B‘ will result in the same expression level of gene G.

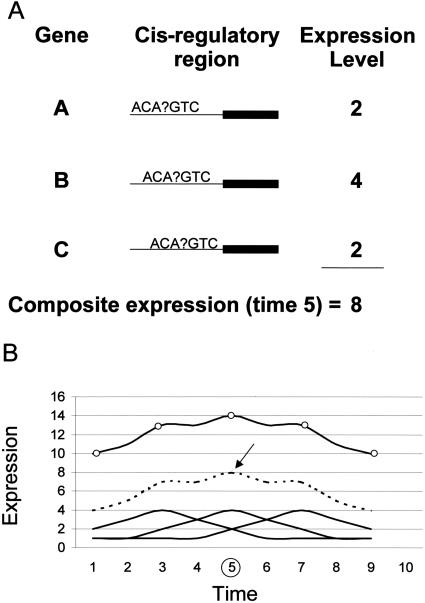
We have developed a technique that decomposes promoter regions into reading frames of modest length (e.g., 6–7 bp) that represent the entire set of nondegenerate potential cis elements for a given set of expressed genes. For each such motif z, we add other motifs having degeneracy at each possible position of z. Those are the set of potential cis elements. (We conducted some computational experiments with motifs as large as 16, with 10 degenerate elements.) Then, we calculate correlations between the expression of known transcription factors and the composite expression of genes with respect to specific potential cis elements (Fig. 1). In an experiment, the composite expression with respect to a motif z is defined as the sum of all expression values of those genes containing z in their promoter regions. The expression pattern of a known transcription factor is then compared with the composite expressions of each potential cis element found in the promoters of the genes under study. The motifs whose composite expression correlates best (over a series of experiments) to a transcription factor constitute the best candidate binding sites for that transcription factor.

Figure 1.

The method for correlating a transcription factor with a regulatory motif is based on creating a composite expression of genes for each putative cis element. The regulatory region of all expressed genes are scanned and each frame of a given size (in this case seven) is regarded as a potential cis element. (A) At each time point, a composite expression pattern is generated by adding the expression value of genes carrying a given motif in their regulatory regions (in this case, the summation for ACA?GTC is shown at time 5 where ? can be any base). (B) A series of time points is analyzed and, systematically, composite expression patterns based on potential motifs are compared with the expression of each transcription factor. The expression patterns of genes with ACA?GTC in their promoters, shown as solid lines, is summed to create a composite expression pattern, the broken line directly above. Transcription factor expression, depicted as a solid line with circles, is shown to correlate well with the composite pattern. The best correlations are considered the best transcription factor-binding site hypotheses.

The weighted value of cis element motifs, which we call the composite expression, is not influenced by genes whose promoters have the cis element but are not expressed (in contrast, see Bussemaker et al. 2001). The basis for this formulation is that a cis element may induce expression on some promoters but not on others that, for instance, lack other cis elements needed for expression or contain bound repressor elements. This is one way to account for combinatorial mechanisms in gene regulation. In our algorithm, the composite weight of a cis element is not a measure of how well the motif explains overall expression but rather has meaning only in its correlation to the expression of a single transcription factor over a series of experiments.

A critical assumption of our approach is that there is a quantitative response to a transcription factor’s expression level by at least some of its immediate downstream targets. This assumption incorporates two potential effects. (1) As a transcription factor increases in concentration, the mRNAs it induces also increase in concentration (DiRisi et al. 1997; Chu and Herskowitz 1998). For instance, a reporter gene fused to a promoter with GCN4-responsive cis elements showed increases in activity that were proportional to increases in GCN4 mRNA levels during histidine starvation (Albrecht et al. 1998). (2) Alternatively, a transcription factor may induce more genes at a higher concentration, possibly due to low-affinity binding sites requiring high transcription factor concentration for induction (Driever et al. 1989).

Another one of our assumptions is that mRNA expression accurately reflects relative levels of transcription factor proteins. Although there is not a strict concordance between RNA expression and protein concentration, numerous studies have shown that there is usually a very good correlation between the RNA expression level of a transcription factor and its protein concentration.

Correlations between a transcription factor and a composite expression pattern can be computed with data from a series of microarray experiments, which may be conducted at various times during a developmental process, under differing conditions, or on different cell types in a multicellular organism. Positive correlations predict induction, whereas negative correlations predict repression. At present, we restrict our analysis of program performance to induction and defer repression to future work. Because of the number of correlations that are measured, it is likely that some correlations do in fact arrive by chance. However, we consider false correlations acceptable if the correct binding sites rank within the top 10 highest candidates. Here, we evaluate our program on several data sets from experiments on yeast comparing our results with known transcription factor binding sites.

RESULTS

Theoretical Basis of the cis/TF Program

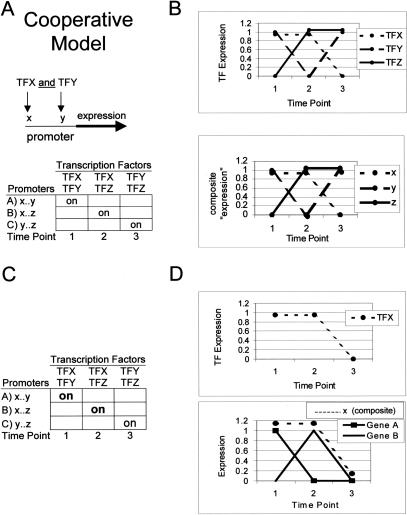
An attractive feature of correlating transcription factor expression with composite gene expression is that it accommodates complex mechanisms of gene regulation (including boolean AND/OR circuits and even circuits with amplifiers). Figure 2A shows an example of combinatorial gene regulation; any two of three transcription factors binding to their respective sites on the same promoter leads to gene expression. Although none of the genes shares the same expression pattern, the composite expression pattern of genes grouped by cis elements does correlate with the transcription factors that bind them (Fig. 2A,B).

Figure 2.

How the program operates under cooperative gene regulation in which two transcription factors binding to their respective cis elements are necessary to induce expression. (A) The top row in the table shows a hypothetical case in which different pairs of transcription factors are expressed at three time points. In the leftmost column are promoters containing the binding sites for transcription factors [e.g., transcription factor X (TFX) binds cis element x]. The internal cells illustrate gene expression patterns given expression of transcription factors and composition of gene promoters. (B) Expression patterns of the transcription factors (TFs; top) and the composite expression of genes grouped by the presence of cis elements in their promoters (x,y,z). A comparison of the top graph and the bottom graph shows that transcription factors correlate with composite patterns to reveal the correct binding relationships. (C,D) Breakdown of composite expression pattern construction. (C) A hypothetical case of cooperative binding as in A and B but with expression of genes with cis element x in bold. (D) Expression of TFX is in the top graph. The expression patterns of the two genes with cis element x are shown as solid lines in the bottom graph and their composite expression is the broken line immediately above. A comparison shows that TFX expression correlates with the composite expression of genes with cis element x in their promoter although TFX alone is not sufficient to induce expression.

The technique does not assume that a transcription factor will always induce a gene with its target binding site. Figure 2, C and D, shows the genes that comprise one composite expression pattern in more detail. The gene in the first row of Figure 2C contains the binding site for transcription factor X (denoted x) but the gene is not expressed at time 2 when transcription factor X is expressed (because of the absence of transcription factor Y). However, the gene in the second row, which has a promoter containing binding sites x and z, does express at time 2, contributing to composite expression of the genes with binding site x in their promoters. Summed together, the two genes match the expression of transcription factor X (Fig. 2D).

The lack of any correlated gene expression in this example shows that clustering would not succeed. Algorithms that assume cis elements contribute to expression in an additive fashion would be misled by genes with promoters that contain a transcription factor-binding site but are still not induced because not all transcription factors needed for expression are present.

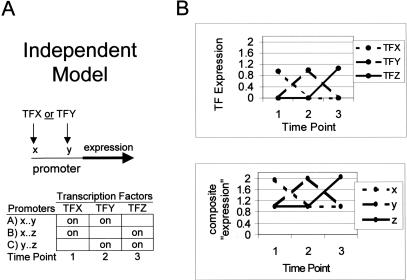
Figure 3A models an example of independent regulation; any one of multiple transcription factors binding to their respective sites can lead to induction. Our program predicts the correct association between transcription factors (Fig. 3B) and their binding sites even though the mechanism of transcriptional activation is different from the cooperative model shown in Figure 2. In this case, an additive model leads to the correct inference (because additivity is a generalization of disjunction). Although no gene clusters exist in this example, our simulations (data not shown) suggest that clustering often performs well under a model of independent induction.

Figure 3.

(A,B) The case depicts independent gene regulation in which the binding of any one of three transcription factors is sufficient to cause gene expression. (A) As in Fig. 2, the table illustrates how genes with given promoters are induced (internal cells) under a hypothetical transcription factor expression pattern (top row). (B) Transcription factor expression (top) also correlates well with composite expression patterns under the independent binding model.

Algorithm Testing: Evaluation Criteria

We tested our algorithm on three yeast data sets, including two derived from analysis of the mitotic cell cycle (Spellman et al. 1998; Cho et al. 1998) and one from analysis of the steady-state expression of nearly 300 yeast knockout lines (Hughes et al. 2000). We evaluated the program's performance by comparing algorithm results with documented binding sites for specific transcription factors from SCPD (Zhu and Zhang 1999) and TRANSFAC (Wingender 2000) as well as the published literature. We set four criteria for establishing valid program predictions and for making a comparison between our results and documented transcription factor-binding sites: (1) For the Spellman et al. (1998) data set (see Methods), a transcription factor value is considered to be nonzero if its value is at least a factor of 2 greater than or less than the reference level (the red/green ratio must be <0.5 or >2), (2) a transcription factor had five significant data points in any data set (at least five experiments contained a nonzero value of that transcription factor), (3) correlations had a null probability of 0.05 or less (see Methods), and, (4) the documented binding sites to which we compared sites predicted by the program had been narrowed down to a consensus region. We searched for hits (defined as a match in at least five positions) in the top 10 correlating motifs. We trained our program on the knockout lines to determine the minimum number of data points required (see Methods).

Overall Performance

In the knockout lines (the training set), there were 11 transcription factors that fit the criteria for comparison. Of the 11 transcription factors, the program's predictions matched the documented binding site in four cases, giving a success rate of about 36% in finding the expected answer within the top 10 motifs (Table 1). Of these, three motifs overlapped in six positions and one overlapped in five positions. Two other transcription factors failed to meet the training criteria but showed close matches, including GCN4, which ranked 38th among top correlating sites, and GCR1, which matched at only four sites.

Table 1.

cis/TF's Matches to Documented TF Binding Sites

TF	Rank	Correlation (r value)a	Significance level	Program prediction	Documented siteb
Knockout lines
STE12	4	0.89	0.001	?TGAAACc	ATGAAA
BAS1	7	0.52	0.01	?GAGTCA	GAGTCA
PDR3	5	0.65	0.05	CGCGG?T	TCCG(C,T)GGA
MET28	4	0.87	0.001	?GTCACG	TCACGTG
GCR1d	2	0.99	0.001	ACCA?CC	C(A,T)TCC
GCN4d	38	0.50	0.01	TGACTC?	TGANTNe
Total evaluated: 11
Cell cycle (high density arrays)
MET32	2	0.99	0.001	CT?TGGC	AACTGTGG
GCN4	2	0.95	0.001	CTGAC?C	TGANTNe
Total evaluated: 6
Cell cycle (cDNA arrays)
PHO4	1	0.95	0.002	CACG?G	CACGT(T,G)
Total evaluated: 9

^aProbability that the correlation is different from zero. 

^bTaken from SCPD. 

^c“?” denotes a position where the program allowed any base. 

^dThese two did not meet criteria for successful hits. 

^eApproximately one-half of the 20 documented GCN4 binding sites in SCPD contained the sequence TGACTC. 

In data from high-density oligonucleotide arrays generated by Cho et al. (1998), two documented binding sites were found by the algorithm out of six transcription factors that fit the comparison criteria, giving a success rate of 33% (Table 1). In a data set using cDNA arrays on yeast expression in the cell cycle, the algorithm found one documented binding site out of nine possible candidates, the lowest hit rate at about 10% (Table 1).

Detailed Results: Knockout Lines

An example of the program's output for the knockout lines is shown in Table 2. A detailed analysis provides further support for some of the program's inferences. For instance, a high scoring binding site predicted for STE12 includes five of the six bases in the SCPD consensus binding site (Table 2). Additionally, binding sites for STE12 on several promoters (SCPD) show support for the degeneracy of the A in the first position and a well-conserved C in the seventh position, which is not part of the consensus site (Table 3).

Table 2.

Detail of cis/TF's Output

TF/Motif rank	Correlation (r)	Program predictions	Consensus site
STE12
1	0.929085	?GTCGCA
2	0.929085	GTCGCA?
3	0.911508	CGGT?TC
4	0.890778	?TGAAAC	ATGAAA
5	0.890778	TGAAAC?
6	0.887036	GTC?CAT
7	0.880103	GTC?AGC
8	0.879187	GGTC?AC
9	0.879041	CGATA?T
10	0.876010	CTTCG?G
MET28
1	0.899350	G?CCGGT
2	0.887494	?GTGACC
3	0.880627	GTGACC?
4	0.867763	?GTCACG	TCACGTG
5	0.867763	GTCACG?
6	0.865051	CGGTC?C
7	0.862943	?CACGAC
8	0.862943	CACGAC?
9	0.852736	GGC?CCA
10	0.852028	GGTCA?G
BAS1
1	0.6048632	GGTC?CG
2	0.6038906	C?GAGTC
3	0.5608319	CAG?GTC
4	0.5487359	GG?CACG
5	0.5385006	GA?TCAC
6	0.5337829	CTGAG?C
7	0.5166461	?GAGTCA	GAGTCA
8	0.5166461	GAGTCA?
9	0.5148253	TGA?TCA
10	0.5051281	?GTCACG

Table 3.

Binding Sites for STE12

STE12 targets	Putative binding site on target genes
Ty1	TGAAACG
Ty2	TGAAACG
YCL027	GAAACA
YCL027	GAAACG
YDR461	TGAAACC
YFL026	TGAAACA
YNL145	ATGAAACa
YNL145	TTTTCATTTGAAACAb

Source of data: Saccharomyces cerevisiae Promoter Database (SCPD). 

^aThe sequence listed is the reverse complement of the motif listed in SCPD. 

^bNote that the reverse complement of this sequence also contains the motif ATGAAAA. 

In several cases, two or more high-ranking motifs for a single transcription factor were similar in sequence, suggesting that the algorithm detected additional degeneracy in core binding sites. For instance, 8 of the top 10 ranking sequences for BAS1 were at least close matches to the documented binding site. The seventh and eighth highest-ranking motifs were exact matches to the six bases in the documented consensus site whereas the second highest ranking motif matched the consensus site in five positions. Five other top ranking sites overlapped the documented site in five or six positions and included degeneracy in one of several positions (see the 3rd, 5th, 6th, 9th and 10th ranking sequences). In the case of MET28, the second and third ranking sequences were similar to the best match (the fourth sequence) with two base changes.

In other cases, only one top-correlating motif matched the documented binding site with no closely related sequences among the highest correlating motifs. An example is STE12 (Table 2). Although we cannot rule out that these nonmatching sequences are alternate binding sites, we assume they are false positives, possibly binding sites that are frequently found on the same promoters as the target motif.

For several binding sites, the program predicted degeneracy in a position that was identified as conserved in the documented binding site. In other cases, the sequence predicted by the algorithm only partially overlapped the consensus site. For instance, in the case of MET28, the last five positions of the motif that the algorithm identified, ?GTCACG, overlap with the first five positions in the MET28 documented site, TCACGTG. We expect these differences because consensus sites are generally determined from a relatively small set of sequences. They may not represent the full range of degeneracy in a binding site whereas our algorithm's analysis of binding sites generally includes information from many promoters.

It has been shown that MET28 forms a complex over its binding site with CBF1, a general transcription factor, and another specific factor, MET4 (Kuras et al. 1997). Therefore, we expected the algorithm to identify the same binding motif for MET4 and MET28 (Table 2). The algorithm did identify the TCACG motif for MET4 as it did for MET28. However, in the case of MET4, the correlation was not significantly different from zero.

Permutation Test

To assess whether the above success rate could have been achieved by chance alone, we devised a permutation test using data from the knockout lines to analyze the program's rate of false positives. The test randomly swapped expression patterns among genes whereas the links to their upstream regulatory sequence remained unaltered. The random reassignment should effectively scramble the signals between gene expression and upstream sequence on which our program relies. However, the test does not alter potential biases in the base composition of upstream regulatory sequences. We ran the permutation test several times to assess the success rate for 100 transcription factors using the same criteria listed above. Of 100 transcription factors examined in the permutation test, there were two matches, indicating that the rate of false positives is well below our hit rate. Thus, the program's success appears to be based on real biological signals in the data.

Another test of the algorithm was based on evidence that most known yeast cis elements are found within 600 bp of the start of transcription of the regulated gene (Roth et al. 1998). As a null test, we analyzed the correlation of transcription factors with cis elements found in the region from −1 to −600 proximal to the start of translation, which should contain most cis elements. We compared that result to a separate analysis using a 600-bp region distal to the start of translation, defined as the sequence from −1400 to −2000, which should contain few, if any, transcription factor-binding motifs. For the proximal region, the correlation for a known transcription factor/cis element relationship, BAS1/GAGTCA, was similar to when 2000 bp was used. The correct binding site had the highest correlation. For the distal region (−1400 to −2000), the 10 motifs with the highest correlations did not include the documented binding site. This result provides further evidence that the correlations between transcription factors and putative cis elements that we are detecting using cis/TF appear to be based on meaningful biological signals and not general sequence bias in nontranscribed regions.

DISCUSSION

Overview

With no a priori knowledge of the sequence of a transcription factor-binding site or its location in a promoter region, cis/TF is able to identify the binding sites of known transcription factors and determine their positive regulatory effect. Our early tests show that the program is able to identify documented binding sites for transcription factors in three separate data sets generated by two different types of microarrays. Our predictions do not imply that a particular transcription factor is sufficient or necessary to cause expression of a gene whose promoter contains the identified motif. For instance, more than one transcription factor may be required for gene induction, or, alternate transcription factors may induce the same expression (Arnone and Davidson 1997; Yuh et al. 1998). Thus, the assumptions in our algorithm do not preclude complex regulatory mechanisms.

Although the program has proved effective for well-documented transcription factors, some transcription factors may not follow this pattern. One possibility is that a transcription factor's function may require cofactors that vary in expression temporally or spatially in a way that is not correlated with the transcription factor itself. In addition, a transcription factor may be constitutively expressed but regulated strictly post-transcriptionally. Our algorithm would not be able to discover the binding sites of such transcription factors nor would the algorithm make successful predictions concerning transcription factors that do not vary in expression.

In some cases, a transcription factor may have the same quantitative effect on induction at moderate and high expression levels (i.e., a threshold effect). However, even when a transcription factor has a threshold effect, a general correlation between a transcription factor and a composite expression can still exist: Above a certain threshold an inducing transcription factor can lead to high levels of downstream target genes, and below the threshold it will lead to low or no detectable levels of downstream targets. Partial violations of our program's assumptions such as threshold regulatory effects or some level of post-transcriptional regulation may still lead to high enough correlations to give the correct answer. Our program requires further testing with many transcription factors and in other organisms to see how often its assumptions are valid.

Program Performance and Data Sets

The success rate of our program varied significantly among the different data sets used. The program performed best with the knockout line data, achieving a success rate of almost 40% in providing the expected answer within the top 10 motifs. The distinguishing feature of this data set was the use of replicate microarray measurements and the calculation of a confidence value for each data point. The other data sets did not use replicate experiments to assess variability in microarray measurements. It seems likely that a reduction in experimental noise by use of replicates and confidence values enabled our program to perform better on this data set, emphasizing the importance of high quality data.

The knockout lines also contained more information with 300 different conditions to compare. However, the vast majority of the different knockout lines did not contribute to transcription factor-binding site correlations. Typically, only 20–30 different knockout expression profiles were informative because low confidence in transcription factor measurements eliminated many data points and many lines showed no variation in expression. The program was able to find correct transcription factor/cis element relationships when as few as five different expression profiles were used for correlations. Thus, the algorithm does not require an unrealistically large set of different expression profiles.

Coregulation

By use of our technique, transcription factors that have a similar expression pattern will often share the same predicted binding site. For instance, our program assigned the same binding site to BAS1, GLN3, and TEA1. At least two of these transcription factors are involved in amino acid biosynthesis, and all share a similar expression pattern in the knockout data set. In such cases, different experimental conditions may be required to generate differing transcription factor expression profiles, or, direct molecular analyses may be necessary to analyze DNA binding sites. In other cases, the program's assignment of shared predicted binding sites might also give clues to molecular interactions. For instance, if transcriptional cofactors were included in the analysis, the program should list a DNA-binding protein and a necessary cofactor with a similar expression pattern as sharing the same cis element.

Clearly, our technique is a starting point for cis element discovery and not a replacement for direct experimentation. Its purpose is to generate a short list of potential binding sites for a known transcription factor. Other techniques could be used in complement to further refine the list of candidate binding sites, such as algorithms that detect a nonrandom distribution of potential motifs in genomic DNA (e.g., Wagner 1997). The power of our technique is linking potential new cis elements to the transcription factors that bind them. This added information suggests a much more specific set of hypotheses for testing results that could bring biologists a step closer to deciphering genetic pathways.

METHODS

Data set training

The algorithm was initially trained on data from a genomewide expression of sporulating yeast (Chu et al. 1998), matching the transcription factor NDT80 to its known core binding site, CACAAA (Chu and Herskowitz 1998). Further training on the Rosetta knockout lines (Hughes et al. 2000) led to a minimal number of data points requirement and a simplification of the weighting scheme for composite expressions. After setting the minimal data points criteria, the sporulation data and another data set on the diauxic shift (DiRisi et al. 1997) led to only two results that could be compared. Therefore, these data sets were not included in the analysis.

Gene Expression Data sets

For the cDNA microarrays, we used log₂ ratios (experimental time point value over the reference state value). For the data set of Spellman et al. (1998), data points with less than a twofold increase or decrease in expression were considered to be zero, following the authors' convention. The knockout line data set (Hughes et al. 2000) was also generated using cDNA arrays but replicates allowed the authors to include a significance value (P) for each data point based on variation among replicates. We used only data points with a 95% confidence level or higher but did not set a minimum increase or decrease in expression. In the data set of Cho et al. (1998), we used the raw expression values generated by DNA oligonucleotide arrays. We set a minimum expression value of 500 to minimize computation time.

Composite Expression

Our approach is to correlate transcription factor expression with a summed or composite expression pattern. This composite expression is calculated as follows: the upstream regulatory sequence of size N (we used 500) bases from the translational start site for each yeast gene was obtained from the Saccharomyces Genome Database (Cherry et al. 2000). Every k base pair frame in the regulatory regions and the reverse complement of regulatory regions of expressed genes was catalogued so that each gene's regulatory region provided 2(N − [k − 1]) frames (some of which were identical in sequence). In experiments presented here, we used k = 7. Then, we took each potential cis element z and created degenerate cis elements consisting of z with a single wild card at every possible position. For instance, from the motif ACCGATG we create: ?CCGATG, A?CGATG, AC?GATG, ACC?ATG, ACCG?TG, ACCGA?G, and ACCGAT?. Each wild-card motif matches four nondegenerate motifs. For example, AC?GATG matches ACAGATG, ACCGATG, ACTGATG, and ACGGATG.

To calculate composite expression patterns and correlations, we used the following formulas: Let E_gt be the expression level of gene g at time t. Let G_z = {g | the promoter of g contains potential cis element z}, the set of genes whose promoters have at least one copy of the potential cis element (motif) z. Then, the composite expression for potential cis element z at time t is: W_zt = Σ_gεGz E_gt. Similarly, let F_xt be the expression of some transcription factor x at time t. We then calculate the simple linear correlation (Pearson product moment) between composite expression based on a potential cis element, W_zt1, W_zt2…W_ztn and the expression of a transcription factor, F_xt1,F_xt2…F_xtn, where n is the number of different time points or experiments. The program calculates correlations between all transcription factors and all potential cis elements. The output lists each transcription factor and the potential cis elements to which it binds ranked by the highest correlation coefficients. For most of the analysis, we examined the 10 cis elements with the highest correlation for each transcription factor.

Significance of Correlation

We tested whether each correlation was significantly different from zero using the following formulas: first, the standard error of the correlation coefficient was computed as follows: s_r = ([1 − r²]/[n − 2])^1/2, where r is the Pearson correlation coefficient and n is the number of experimental points in the correlation. The probability of the null hypotheses was then computed using a student's t test, t = r/s_r (Sokol and Rohlf 1995).