Active multistage coarsening of actin networks driven by myosin motors

Abstract

In cells, many vital processes involve myosin-driven motility that actively remodels the actin cytoskeleton and changes cell shape. Here we study how the collective action of myosin motors organizes actin filaments into contractile structures in a simplified model system devoid of biochemical regulation. We show that this self-organization occurs through an active multistage coarsening process. First, motors form dense foci by moving along the actin network structure followed by coalescence. Then the foci accumulate actin filaments in a shell around them. These actomyosin condensates eventually cluster due to motor-driven coalescence. We propose that the physical origin of this multistage aggregation is the highly asymmetric load response of actin filaments: they can support large tensions but buckle easily under piconewton compressive loads. Because the motor-generated forces well exceed this threshold, buckling is induced on the connected actin network that resists motor-driven filament sliding. We show how this buckling can give rise to the accumulation of actin shells around myosin foci and subsequent coalescence of foci into superaggregates. This new physical mechanism provides an explanation for the formation and contractile dynamics of disordered condensed actomyosin states observed in vivo.

Cells undergo dramatic changes in shape and internal organization during vital processes such as migration and division. These changes involve remodeling of the cytoskeleton partly driven by collective physical interactions between molecular motors and cytoskeletal filaments. The motors use adenosine triphosphate (ATP) as fuel and hydrolyze it to actively generate forces and move along filaments (1). Multiheaded motors or complexes of motors may cross-link neighboring filaments and generate relative motion between them. Kinesin and dynein motors interact with microtubules to form the mitotic spindle, which is responsible for chromosome segregation (2). Myosin motors interact with filamentous actin (F-actin) to form complex arrays such as the contractile ring driving cell division (3, 4) and contractile networks that drive cell migration (4) and polarizing cortical flows (5, 6).

To identify the biophysical processes underlying cytoskeletal organization, many in vitro model systems of purified motors and filaments that lack biochemical regulation have been recently developed. It is known that kinesins can organize microtubules into polarity sorted asters, as well as vortex or bundle states (7–10). These structures resemble physiological arrays such as the mitotic spindle (11). In contrast to microtubules, purified F-actin does not form well-defined structures when motors are added. Actin-myosin II solutions remain disordered at high levels of ATP (12–14) and generate dense condensates that appear internally unstructured if the ATP level is lowered or when the actin filaments are cross-linked (15–18). Interestingly, similar dense condensates appear in cells during myosin-driven shape changes of the actin cytoskeleton. Formation of the contractile ring in dividing fibroblasts (19) and Caenorhabditis elegans embryos (20) both involve large-scale flows and coalescence of dense actomyosin condensates. Similarly, the lamellipodium of migrating cells displays dense myosin aggregates (21, 22). Wounded cells display similar phenomena, with accumulation of myosin foci at the wound border and fusion of these foci into a tight ring capable of constriction (23). Collective shape changes in epithelial cell layers also seem to be driven by the transient formation of myosin spots that subsequently fuse (24–27).

The physical mechanism of self-organization in the actin-myosin cytoskeleton remains unknown. There are several theoretical models describing pattern formation in motor-filament systems (7, 28). These models predict the emergence of ordered aster, vortex, and bundle architectures due to polarity sorting that relies on unidirectional motion of motors along the filaments they connect. Such patterns are also predicted from symmetry considerations, resulting in general hydrodynamic theories of active polar gels (29–31). These patterns are consistent with experimental observations in microtubule-kinesin mixtures (7, 8), but are different from the disordered condensed states seen in actin-myosin mixtures. Microscopic theories model the filaments as rigid and the motors as small, highly processive clusters. Microtubules are indeed rigid and nearly rodlike (32), and their associated motors tend to be highly processive (1), explaining the success of the proposed models in elucidating experimental observations. Unlike kinesins, most myosins are not processive and must act together in large macromolecular assemblies of several tens to hundreds of molecules (33). In addition to the difference in motor processivity, F-actin is 1,000-fold less rigid than microtubules and is known to buckle under compressive loads of fractions of a piconewton (32, 34). In densely cross-linked networks, these microscopic features suggest that the collective organization of myosin and actin into force-generating cellular machines is not driven by polarity sorting but by a different organizing mechanism.

Here we use a model system of purified actin and myosin to uncover the physical mechanism by which myosin motors organize F-actin into contractile structures. We demonstrate that myosin actively drives a multistage coarsening process that brings actin filaments into disorganized condensates that resemble structures seen in vivo. We suggest a microscopic mechanism that can explain this multistage process in terms of buckling of the actin network under the random internal forces generated by motors in such an isotropic structure. This mechanism is fundamentally different from polarity sorting mechanisms operating in microtubule/kinesin systems (7, 8). Furthermore, this mechanism depends crucially on the open meshwork structure of actin networks, which is not well captured by continuum mechanical modeling that is frequently applied in active gel theories at larger scales (35–37).

Results

To examine how actin filament reorganization emerges from the collective activity of molecular motors, we reconstituted a minimal model system from purified proteins. F-actin was polymerized from monomers at a 1 mg/mL concentration to form homogeneous networks with no preferred filament orientation or polarity. To generate active internal stresses, we added skeletal muscle myosin II. Myosin II has two identical head domains with binding sites for actin filaments and ATP, and a coiled-coil tail domain (1). Individual myosin motors are nonprocessive: they release immediately after taking one step toward the plus end of an actin filament. However, multiple myosins can assemble tail-to-tail into bipolar filaments with motor heads at each end (in green, Fig. 1D) (38). Such assemblies have an increased collective duty cycle, allowing them to transiently cross-link actin filaments (in red, Fig. 1D). Moreover, their bipolar geometry enables myosin heads to pull actin filaments of opposite orientations toward each other, as shown by the arrows. We used myosin filaments with an average length of 0.69 μm (Fig. 1E) or approximately 100 myosin motors (39). This size is larger than the size of myosin minifilaments in nonmuscle cells, which have 10–30 motors (21, 22). A test with minifilaments of approximately 16 skeletal muscle myosins showed little effect on actin filament reorganization (Fig. S1 A–C). However, we expect that minifilaments of nonmuscle myosin, in particular myosin IIB, will be more processive because this myosin has a higher duty ratio than its muscle counterpart (Table S1).

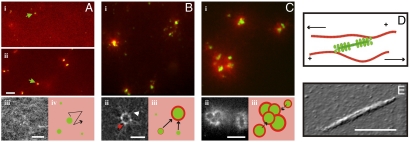
Fig. 1.

Actin-myosin networks self-organize through a three-stage coalescence process. (A) (i) Fluorescence micrograph of an active network, taken 2 min after initiating actin polymerization in the presence of myosin bipolar filaments (1∶200 myosin∶actin). The actin network is homogenous and isotropic (red) and randomly cross-linked by active motors (green). (ii) After 6 min, the motors accumulate in larger structures (scale bar 10 μm). (iii) The actin network is still homogeneous in this stage. Scale bar 5 μm. (iv) In Stage 1 the actin network is homogeneous (pink) and contains small myosin foci (green) that move along the actin network (black arrow). (B) (i) After 30 min, the actin network is organized in thin shells (red) around myosin foci (green). (ii) High-resolution image of an actomyosin condensate shows that actin filaments form a ring-like set of patches (red arrow) with actin filaments radiating out (white arrow). Scale bar 5 μm. (iii) In Stage 2, myosin foci are surrounded by thin actin shells and small foci move toward larger immobile foci (arrows). (C) (i) After 45 min, actomyosin condensates are packed in large superstructures. (ii) High-resolution image of a superstructure, showing merged actin ring-like structures. Scale bar 10 μm. (iii) In Stage 3, superaggregates form by contractile coarsening (black arrows). (D) Network activity results from bipolar myosin filaments (green) sliding actin filaments (red) of opposite orientation toward one another (arrows). (E) AFM image of a myosin filament. Scale bar 0.5 μm.

Active self-organization was initiated by polymerizing actin in the presence of preformed myosin filaments and 100 μM ATP. Motor activity was kept constant by an enzymatic ATP regeneration system (16). To enable observation of the network structure by microscopy, we fluorescently labeled actin and myosin. Within 2 min after mixing, actin was polymerized into a homogeneous network (red in Fig. 1A i). The myosin filaments were initially homogeneously dispersed in the network (green dots indicated by arrow). However, after about 5 min, the myosin was redistributed into bright foci (green in Fig. 1A ii). The F-actin network was still homogeneous (Fig. 1A iii). After about 30 min, the myosin foci were surrounded by actin rings (red in Fig. 1B i). These rings are reminiscent of actin rings observed in the presence of skeletal myosin minifilaments and the actin bundler fascin (40). However, high-resolution images of the rings with only actin fluorescently labeled (to avoid spectral crosstalk with myosin) revealed that they were not composed of a continuous band of actin filaments, but rather of a collection of compact actin aggregates with a size below 1 μm (Fig. 1B ii, red arrow). The rings were surrounded by a diffuse halo of actin filaments that radiated outward (Fig. 1B ii, white arrow). Three-dimensional image stacks further revealed that, rather than forming flat rings, actin deposited in a shell all around the myosin foci (Movie S1 and Fig. S2A). These actin-myosin condensates were initially isolated structures within the actin network, but after 30–45 min we observed larger structures that appeared to be aggregates of actomyosin condensates (Fig. 1C i). High-resolution images showed that each aggregate consisted of a few hollow actin rings stuck together (Fig. 1C ii). Three-dimensional image stacks showed that these actin rings were again not flat, but that actin formed shells around the myosin foci (Movie S2). Each aggregate contained several myosin foci with actin intercalated between them (Fig. S2B), suggesting that they result from coalescence of multiple actomyosin condensates.

These observations suggest that myosin motors drive coalescence of actin into disordered aggregates through a multistage process. To elucidate the transition pathway between these stages, we studied the dynamics of the myosin motors and the actin network in each stage by time-lapse imaging.

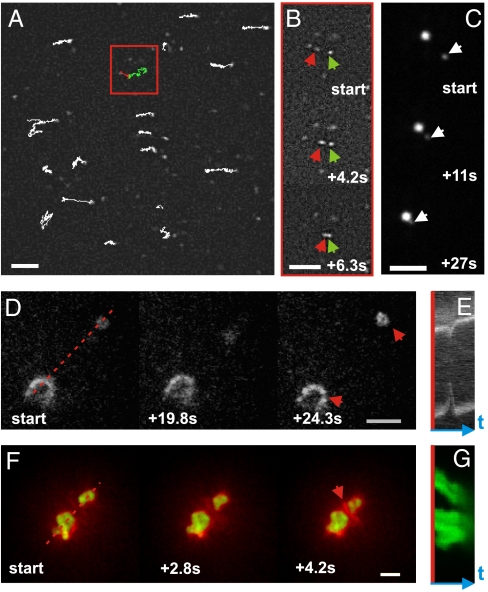
In the first stage, the myosin filaments were homogeneously distributed in the network. We tracked the filaments over time and found that they were strikingly mobile (Fig. 2A and Movie S3). Many filaments moved by a sequence of straight runs, punctuated by abrupt changes in direction. The long run lengths indicate the motors were not simply diffusing in solution, but moved on the F-actin network. Occasionally, two neighboring myosin filaments came together and fused into a small myosin focus (Fig. 2B and Movie S4). Upon meeting, small foci sometimes coalesced further into larger myosin foci (Fig. 2C and Movie S5). Once the myosin foci reached a size similar to the average pore size (300 nm), they no longer moved because their motion was presumably hindered by the actin mesh. Nonetheless, they could still grow by coalescence with smaller mobile aggregates.

Fig. 2.

Dynamics of actin/myosin coalescence. (A) Trajectories of myosin filaments moving on an actin network (1∶200 myosin∶actin; 3 min after sample preparation). Red and green traces represent two filaments that coalesce after an active walk. Scale bar 5 μm. (B) Time-lapse image sequence of coalescing myosin filaments corresponding to the green and red traces (see arrows). (C) Time-lapse image sequence of two fusing myosin foci. (D) Time-lapse image sequence of two actomyosin condensates (red arrows, actin labeled) undergoing a contractile fluctuation (1∶200 motors). Scale bar, 10 μm. (E) Kymograph constructed along red dashed line in (D). (F) Time-lapse image sequence of two actomyosin aggregates that coalesce and accumulate actin between them (red arrow, 1∶50 myosin∶actin). Scale bar, 10 μm. (G) Kymograph constructed along red dashed line in (F).

Initially, myosin foci formation did not drastically reshape the actin network (sketched in Fig. 1A iv). However, once myosin foci became immobile, they were able to capture actin from the surrounding network (Movies S6 and S7). Such events account for the deposition of dense actin patches on the surface of the myosin foci (Fig. 1B iii).

The condensation of actin into shells around myosin foci was typically complete within 30 min. Yet, the networks continued to display striking manifestations of contractile activity. Often, two neighboring actomyosin condensates were suddenly pulled toward one another and then recoiled. An example of such a contractile fluctuation event is displayed in Fig. 2D (see Movie S8 and Fig. S3A, Upper). Usually we observed only one recoil, but sometimes recoils occurred twice (Movie S9 and Fig. S3A, Lower) or even three times (Movie S10 and Fig. S3B). Kymographs show that the actin condensates approach and recoil at velocities of approximately 0.3 μm/s (Fig. 2E). The myosin foci apparently build up tension over a processivity time window of several tens of seconds, until they unbind from the F-actin leading to an abrupt release of the built-up elastic stress. These observations are consistent with prior indirect observations of contractile network fluctuations based on motions of embedded probe particles (16, 41). Especially at larger motor densities, contraction often resulted in permanent coalescence, likely reflecting the dissipation of elastic stresses before the motors disengage. An example of such a coalescence event is displayed in Fig. 2F, where two myosin foci (green) approach each other (Fig. 2G) and compact the actin (red) between them (Movie S11). Surprisingly, myosin foci were able to attract each other over distances of up to 25 μm, about five times the average length of the actin filaments. This observation suggests that the actin network between myosin foci is sufficiently connected by myosin cross-links to mediate long-range force transmission. Because the network is disordered on this scale (tens to hundreds of mesh sizes), it is unlikely that filament polarity is the main origin of the directed motion. In a few cases, we observed cable-like actin structures between actomyosin foci that shortened over time (see Movie S12). Contractile coalescence continued until the resulting clusters were too far apart to interact (Fig. 1C iii). This final state was typically reached within 100 min.

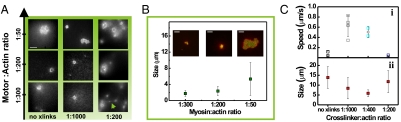
The extent of aggregation strongly depended on motor density. Higher motor densities increased the probability of irreversible coalescence. At a myosin∶actin ratio of 1∶200, only half of the contractile events (N = 55) resulted in permanent coalescence, whereas at a myosin∶actin ratio of 1∶50 most events (N = 29) resulted in permanent coalescence (Fig. S3C). Accordingly, the final steady state at low motor density showed small isolated foci (1∶300 and 1∶200 in Fig. 3A), whereas high motor densities resulted in large superaggregates (1∶50 in Fig. 3A). To quantify this enhanced tendency for coalescence at high motor densities, we measured the overall size of actin aggregates in steady state. The average size increased from 1.8 μm at low (1∶300) myosin∶actin ratio to 5.3 μm at high (1∶50) myosin∶actin ratio (Fig. 3B and Table S2). As shown in the insets, this larger size was caused by an increased number of myosin foci at the aggregate core, whereas the thickness of the actin shell remained constant.

Fig. 3.

Active coarsening is promoted by increased motor and cross-link density. (A) Steady-state actin patterns observed in active networks containing varying concentrations of myosin motors and biotin-streptavidin cross-links. Scale bar, 10 μm. (B) The average size of actomyosin condensates increases with increasing motor density (1∶400 biotin∶actin). (Inset) Confocal images show that this size increase results from an increased degree of coalescence. Scale bars 5 μm. (C) (i) The average speed of foci movement depends nonmonotonically on cross-link density (actin∶myosin ratio 1∶50). Open squares represent individual data points; open diamonds represent the average speed for each cross-linker density. (ii) The cross-linker density-dependence of the size of actomyosin condensates mirrors that of the contraction speed. All error bars represent SD.

The increasing tendency for coarsening with rising motor density is probably the combined outcome of a larger contractile driving force and larger connectivity due to motor cross-linking. We assessed the effect of network connectivity on contractility by adding passive cross-linkers. F-actin was doped with varying amounts of biotin-actin and cross-linked with streptavidin at a fixed streptavidin∶actin ratio (1∶25). Biotin-streptavidin cross-links are near-permanent, generating elastic behavior on time scales that are long compared to the lifetime of myosin-actin attachments. We used low cross-link densities to ensure a homogeneous actin network structure (Fig. S4A) and prevent macroscopic contraction (15, 17). In the presence of cross-linkers, actin again formed patches around myosin foci, and the resulting actomyosin condensates coalesced. However, coalescence occurred at much lower motor density (myosin∶actin ratio 1∶200) than in the absence of cross-linkers (1∶50) (Fig. 3A). This confirms our hypothesis that increased network connectivity promotes contractile coarsening. Interestingly, adding cross-links also influenced the coalescence dynamics. In the absence of cross-links, merging foci had velocities of approximately 0.10 μm/s (Fig. 3C i and Table S2). Cross-linking substantially increased the velocity, to a maximum of approximately 0.6 μm/s at a biotin∶actin ratio of 1∶1000. However, at high cross-linker densities (1∶200) the velocity fell back to 0.03 μm/s. The size of the actomyosin condensates showed a reverse dependence on cross-linking, with smallest sizes where the coalescence speed was highest (Fig. 3C ii and Table S2). We expect that increasing network connectivity leads to a trade-off between a higher velocity as a greater fraction of filaments is connected to others, and a decreased velocity as the passive stress opposing the active contraction increases. In the most cross-linked networks, the foci were connected by bundle-like actin structures (green arrow in last panel of Fig. 3A). Whereas these structures probably facilitate contraction, they are likely connected to the background actin network, thus impeding coalescence.

Discussion

Based upon fluorescence microscopy of active actin/myosin networks, we conclude that myosin drives the formation of disordered actomyosin condensates through a multistage coarsening process. Actin filaments are compacted into dense clouds around large myosin foci and these actomyosin condensates then contract into larger superaggregates. The resulting structures are intrinsically three-dimensional (3D), in strong contrast to the more two-dimensional (2D) aggregates reported previously, such as rings formed in fascin-bundled actomyosin systems (40) and vortices formed in actomyosin networks on surfaces (42). Although planar ring structures might relate to the vortex-like states predicted by active gel theories (29, 31, 43), such features are intrinsically 2D patterns and are topologically not possible in 3D (44). Thus, the nonplanar, shell-like structures we observe must form by another mechanism.

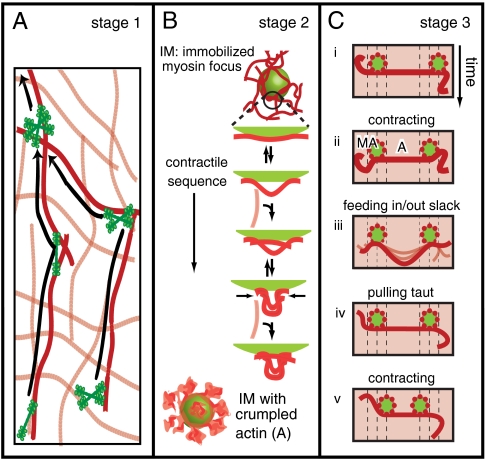
In most active gel theories, the driving force for self-organization comes from small, processive motors or motor clusters. By contrast, we find that large motor assemblies drive the active remodeling in this actin/myosin system. Myosin motor filaments spontaneously form foci, beginning from a uniform distribution in an isotropic actin network. Motors and small motor foci perform random walks on the network: they bind to actin filaments, move along and switch between them, coalescing as they meet (Stage 1, Fig. 4A). The apparent, large-scale diffusion constant of this process should be D ≈ vl ≈ 1 μm²/s. Here v ≈ 1 μm/s is the typical speed of myosin aggregates and ℓ ≈ 1 μm is the typical run length between direction changes, set to be somewhat larger than the mesh size. Because we expect the internal dynamics of the myosin load cycle to be rate limiting, D should be insensitive to aggregate size. As the foci grow to a size comparable to the mesh size of the network, however, their motion will be impeded by elastic interactions with the network. The accumulation of motor filaments into foci occurs without significant concurrent F-actin transport. This differs from self-organization in mixtures of microtubules and kinesin oligomers, where the motors accumulate into foci as they focus microtubules into radial arrays (8, 9).

Fig. 4.

Proposed multistage mechanism of myosin-driven self-organization of actin networks. (A) Stage 1: Myosin filaments or aggregates thereof, move actively on the actin network and coalesce upon meeting. (B) Stage 2: An immobilized myosin focus (IM) accumulates a cloud of actin patches in a stochastic sequence of expansive steps (resulting in marginal extension) and contractile steps (resulting in buckling, made permanent by subsequent bridging). The myosin foci have a large interaction surface with the surrounding actin via the protruding myosin heads. Compressive forces exerted by the focus cause the actin to buckle at the surface and form a crumpled actin structure (A). (C) Stage 3: Two actomyosin aggregates (MA, in green) interact isotropically with the background actin network (shaded red) and will move together by interacting via a connected cluster of actin filaments (represented by a red line). This contraction involves net extension of the connecting actin structure, which brings the foci together, followed by net contraction, which pushes in slack due to buckling. Slack needs to be pulled out before the foci can move closer together.

Once the myosin foci reach a certain size, they initiate Stage 2 of the assembly process by drawing actin in. Due to the random directions of actin filaments in an isotropic network, the net force exerted by a myosin focus [Fig. 4B, immobilized myosin focus (IM)] should grow as N^1/2, where N is the number of actin filaments it interacts with. Eventually, the net force should be sufficient to overcome elastic constraints and perform dissipative work remodelling the local network structure. Collectively, the myosin heads projecting from each focus can exert either an expansive or a compressive force on the surrounding network of actin filaments. We propose that stochastic alternations between expansion and compression will have the net effect of pulling in actin toward a myosin focus (Fig. 4B). The physical argument is that actin filaments have a highly asymmetric response to axial loading: They strongly resist stretching but not compression. Under compression, an actin segment of length L readily buckles at a critical force f_c ∼ π²k_BTℓ_p/L², where the persistence length ℓ_p ∼ 17 μm (32). For a segment of micrometer length or longer, this force is less than 1 pN (34). The internal forces generated by a single myosin filament already well exceed this buckling threshold (16, 35). Thus, a net expansive force over a patch of actin connected to a myosin focus will be strongly opposed by the high stretch modulus of the actin filaments within the patch. By contrast, a net compressive force will buckle the actin filaments, drawing actin in. This mechanical asymmetry is necessary and sufficient for actin to accumulate, as detailed in SI Text, Contractility from Asymmetric Load Response. Bridging of buckled structures by (transient) myosin cross-linking to other actin filaments will further enhance this accumulation [Fig. 4B, IM surrounded by crumpled actin (A)].

In the final stage of the coalescence process (Stage 3), actomyosin condensates coalesce into large superaggregates. We propose that if two myosin foci happen to exert forces on the same connected cluster of actin filaments, they will eventually coalesce, again due to the asymmetric load response of actin filaments. If the net forces of the two foci happen to stretch the connecting actin structure, its resistance to extension will force the foci together (Fig. 4C ii). If the net forces of the two foci instead happen to compress the connecting actin structure, it will buckle and push in slack between the two foci rather than bearing the load and pushing them apart (Fig. 4C iii). Before the random forces can pull the aggregates together again (Fig. 4C v), any material buckled during prior compressive loads must be pulled out (Fig. 4C iv). Only when the connecting structure is taut can it exert significant forces on the foci. Then the myosin foci will tend to be driven toward each other. Instead of the coherent, unidirectional motion normally associated with motor transport, this model predicts that foci will move in an incoherent, intermittent fashion (SI Text and Movie S13). The time-dependent motion of coalescing foci is consistent with this prediction (Fig. S5E).

The physical mechanism for actomyosin self-organization outlined above differs substantially from prior models of self-organization in active gels. The nonlinear buckling events that are crucial in our mechanism cannot be captured by linear hydrodynamic theories (29–31, 43) and hitherto have not been part of microscopic theories (36, 45) or simulations (7, 28, 43). Both hydrodynamic and microscopic theories were inspired by experiments in microtubule/kinesin systems (7, 8, 10). These systems differ from actin/myosin systems in at least two aspects. First, microtubules have a persistence length of several millimeters (32) and are therefore not buckled by motor-driven forces. We expect that bundling F-actin should bring the system closer to microtubule systems. Indeed some experimental work points to this: In actomyosin systems bundled by fascin, the final steady states are networks of asters reminiscent of microtubules organized by kinesins (40). In vivo, actin asters with dense clusters of myosin at their center were observed in fibroblasts stimulated to contract with cytochalasin D (46). Such asters had a uniform polarity with actin plus-ends pointing inward, as expected in case of polarity sorting by plus-end directed motors. Second, force centers in active microtubule gels were small, processive motor clusters interacting mostly with microtubule pairs, whereas the force centers in active actin gels are large myosin aggregates interacting with many actin filaments. At a large scale, these force centers can be modeled as force dipoles in a continuum (visco)elastic background. However, on the micrometer scale on which actin reorganizes in our experiments, it is unlikely that continuum elasticity represents a realistic description, especially in view of the asymmetric, nonlinear response of the individual filaments. Thus, a more microscopic model is needed (SI Text).

Our work suggests that mechanisms of self-organization in motor-filament systems are not strictly universal, but depend on the biophysical characteristics of both filaments and motors. This nonuniversality is biologically relevant: the physiological function of microtubule arrays differs from that of actin arrays. Microtubules form well-focused mitotic spindle poles, to accomplish high-fidelity separation of the duplicated chromosomes (2). In contrast, actomyosin aggregates appear in cells from diverse tissues and organisms as transient structures that coalesce into larger arrays that exert contractile forces. Examples include the formation of contractile rings driving cytokinesis (3, 4) and wound healing (23), and the formation of contractile networks driving deformation of epithelial cell layers in developing embryos (24–26) and polarizing cortical flows (5, 6). Our findings suggest that the formation and subsequent coalescence of myosin foci in vivo can emerge spontaneously from physical interactions between actin filaments and motors. However, Rho-mediated signaling events certainly contribute to the localized assembly and activation of myosin alongside with purely biophysical effects by changing myosin’s phosphorylation state (47). Localized Rho zones for instance lead to localized assembly of active myosin foci in the cleavage furrow (20, 48) and in wound borders (23). Interestingly, the size of the actomyosin condensates in vitro is comparable to the size of condensates observed in vivo (Table S3). It will be interesting to test the activity of purified nonmuscle myosins in our assay. Muscle and nonmuscle myosins differ in duty ratio, sliding velocity, and filament size (Table S1). Nonmuscle myosin IIB is substantially more processive than muscle myosin II, which should suppress the dissolution of actomyosin condensates and enhance the late stages of coalescence. Nonmuscle myosins also have a substantially smaller sliding velocity than muscle myosin II, which should reduce the coalescence rate.

Even though our reconstituted assay mimics self-organized structures and dynamics of actomyosin in cells, there is an important difference. Our in vitro structures are irreversible once assembled, whereas cellular structures dissolve and reform on time scales of minutes. The low (0.1 mM) ATP level in the in vitro assay compared to the typical mM ATP level in nonmuscle cells may contribute to the enhanced stability of the structures. This low level was a prerequisite for active coarsening by skeletal muscle myosin II. At mM ATP concentrations, we did not observe active contractility (Fig. S1D) in line with prior studies (12, 13). We attribute this ATP dependence to the low duty ratio of skeletal muscle myosin II. With excess ATP, the duty ratio is only 4%, but lowering the ATP concentration to 100 μM increases the duty ratio about fourfold (12, 13, 49). In addition to the different ATP level, multiple factors that cause dynamic remodeling in cells are absent in our assay. Disassembly will likely require actin depolymerization and monomer recycling. The actin filaments in our experiments were not stabilized and were, thus, in a state of constant treadmilling. Nonetheless, this treadmilling process is very slow (50) and stabilization of actin with phalloidin indeed did not change the self-organization process (Fig. S6A). However, cells contain protein factors that accelerate depolymerization or sever F-actin. It will be interesting to incorporate some of these regulators in our assay (51). Another contribution to fast pattern renewal in cells may be the transient nature of physiological actin-cross-linking proteins. Notably, a recent in vitro study of actin networks bundled with fascin showed that myosin could spontaneously disassemble contractile structures (40). There may be an interplay between myosin force production and force-induced dissociation of cross-link proteins that controls the lifetime of cellular contractile structures (52, 53). Finally, assembly of cellular actomyosin condensates into ordered structures such as contractile rings depends not only on myosin contractility but also on forces produced by actin disassembly (23, 54).

Conclusion

We have shown that myosin motors organize actin filaments into contracted states through a multistage aggregation process. We propose a physical mechanism that can account for this process based on motor-induced buckling in connected actin structures. The fact that the reconstituted system is able to mimic cellular self-organized states and their contractile dynamics suggests that physical interactions contribute to the regulation of cell and tissue morphogenesis.

Material and Methods

Preparation of Actomyosin Networks.

Myosin synthetic filaments were formed at room temperature by dilution of myosin II in 25 mM imidazole buffer (pH 7.4) with 300 mM KCl to 70 mM KCl. Actomyosin network formation was initiated by adding monomeric G-actin and transferring the samples to glass flow cells (25 μm depth) at room temperature. The assembly buffer had final concentrations of 25 mM Imidazole-HCl (pH 7.4), 50 mM KCl, 2 mM MgCl₂, 1 mM DTT, and contained 0.1 mM MgATP. An enzymatic ATP regeneration system was included and 2 mM Trolox was added to prevent photobleaching. The average length of the actin filaments measured by fluorescence microscopy was 6 μm (N = 3711). The actin network was fluorescently labeled with AlexaFluor488-actin, and myosin was labeled with DyLight 488 or 594. Cross-links were created by copolymerizing actin with Biotin-G-actin and adding streptavidin. Details on protein purification and labeling, network reconstitution, and atomic force microscopy (AFM) imaging of myosin filaments are given in the SI Text, Materials and Methods.

Fluorescence Microscopy.

Samples were imaged within 5 min after mixing with a spinning disk confocal microscope (CSU22, Yokogawa Electric Corp.) on a DMIRB Leica inverted microscope. The sample was excited with 561 nm laser light (Melles Griot) or 488 nm laser light (Coherent Inc.). Images were recorded with a cooled EM-CCD camera (C9100, Hamamatsu Photonics) using an exposure time of 50–100 ms. Image stacks were obtained by scanning through the z-direction in steps of 100 nm with a piezo-driven 100× (1.3 NA) oil immersion objective (PL Fluotar Leica).

Image Analysis.

To determine the size of actin condensates, we binarized 8-bit images in Image J (http://rsbweb.nih.gov/ij/) and measured the major radius of each feature using the “Measure” command. Data are shown as averages ± S.D. Kymographs were made with the Kymograph plugin for Image J by J. Rietdorf (Friedrich Miescher Institute Basel, Switzerland) and A. Seitz (European Molecular Biology Laboratory, Heidelberg, Germany).