Abstract
Haplotype analysis of disease chromosomes can help identify probable historical recombination events and localize disease mutations. Most available analyses use only marginal and pairwise allele frequency information. We have developed a Bayesian framework that utilizes full haplotype information to overcome various complications such as multiple founders, unphased chromosomes, data contamination, and incomplete marker data. A stochastic model is used to describe the dependence structure among several variables characterizing the observed haplotypes, for example, the ancestral haplotypes and their ages, mutation rate, recombination events, and the location of the disease mutation. An efficient Markov chain Monte Carlo algorithm was developed for computing the estimates of the quantities of interest. The method is shown to perform well in both real data sets (cystic fibrosis data and Friedreich ataxia data) and simulated data sets. The program that implements the proposed method, BLADE, as well as the two real datasets, can be obtained from http://www.fas.harvard.edu/∼junliu/TechRept/01folder/diseq_prog.tar.gz.
In the quest to identify genes responsible for specific illnesses, it has been observed in many cases that a large portion of the carriers of the disease gene in the current population are descendant from a small number of “founders” in whose genomes the deleterious mutation appeared some generations ago. This translates into inhomogeneity between the allele frequencies in the general population and those with the disease for genetic markers close to the location of the disease gene(s). The reason is that the allele frequencies of these markers in the disease population still reflect those originally carried by the founder chromosome(s), with modifications introduced by recombinations and mutations. This phenomenon, known as linkage disequilibrium (LD), can be exploited to identify the location of a disease gene by measuring the dependence between disease status and allele distributions among a set of markers.
Simply looking at the marginal dependency between each marker and disease status in a case/control sample of chromosomes is clearly inefficient. For an LD mapping strategy to be optimal in fine mapping, it is essential to consider the information observed in a set of contiguous markers (i.e., haplotypes). The primary goal of our Bayesian analysis is the localization of a gene responsible for the disease within the considered set of markers. Secondary goals are the determination of ancestral haplotypes, the separation of distinct founders of the disease, the construction of haplotypes from unphased chromosomes, and inference on the ages of the mutations causing the disease. Our method, like any others based on LD, is appropriate when there are reasons to assume the existence of a founder effect in at least a significant proportion of the diseased individuals. We note that several attempts along the lines of our approach have been discussed in the literature, and we compare these methods with our approach herein.
By employing a Bayesian approach, we explicitly model positions of the historical recombinations and mutation events that produced the observed haplotypes from an initial set of founders. As a result, our Bayesian LinkAge DisEquilibrium mapping (BLADE) algorithm produces the posterior distribution of the location of the disease mutation by accounting for all sources of uncertainties. A major advantage of our approach is its flexibility in treating various complications such as missing marker data, multiple founders, and unphased chromosomes. For example, the algorithm provides not only the estimation of the mutation location but also the haplotype construction in the case when part or all of the disease chromosomes are unphased. Our methodology is well suited for the fine mapping of a disease gene within a previously identified linked region. The main idea presented here can also be extended to LD genome screens and single nucleotide polymorphism (SNP) studies.
RESULTS
The BLADE algorithm can be regarded as a specialized expert system: It takes as input the prior knowledge such as mutation rate, the range of founders' ages, etc., and produces the posterior distributions of the location of the disease mutation(s), ancestral haplotypes, founder ages, cluster indicators, and haplotypes of unphased chromosomes. All of these output components can be inspected directly by the researcher for further validation.
The centerpiece of the BLADE algorithm is an explicit stochastic model describing the dependence structure among the many variables related to the generation of the observed disease haplotypes. This model is closely related to the hidden Markov model employed by McPeek and Strahs (1999) and Morris et al. (2000) but appears to be simpler and more transparent. Our model assumes that the disease haplotypes can be grouped into k+1 clusters, corresponding to k founder chromosomes in the current disease population and 1 “null” cluster for all other disease chromosomes. Each non-null cluster is characterized by an ancestral haplotype associated with a single disease-causing mutation coalescing to a single time point (age). These k ancestral mutations are assumed to be at the same (or very close) location. Although BLADE relies on the simplifying assumption that the disease haplotypes of the current generation within each cluster are mutually independent given the ancestral haplotype, allowing for multiple clusters and for different founder ages alleviates the need for a faithful (and very complex) model of the underlying genealogy. A Markov chain Monte Carlo strategy was developed to facilitate the computation needed for a proper inference on the parameters of interest (i.e., integrating out all of the nuisance parameters and the missing data). Our method also allows for modeling the control haplotypes as an inhomogeneous Markov chain, which is useful when studying closely spaced markers.
We applied the BLADE algorithm to two real datasets and conducted a simulation study to test its performance and robustness. These results show that our method performed markedly better than pairwise methods and can make correct predictions even when the data show a substantial departure from some key assumptions.
Cystic Fibrosis
This well-known dataset was reported in Kerem et al. (1989) and used to fine-map the location of the gene for cystic fibrosis. The haplotypes in consideration have 23 RFLP markers. The control group has 92 haplotypes and the disease group has 94. Many disease haplotypes (39%) have missing observations at certain markers. It is known in this dataset that one founder mutation, ΔF508, located between markers 17 and 18, ∼0.88 cM away from the leftmost marker, accounts for the majority (67%) of disease chromosomes.
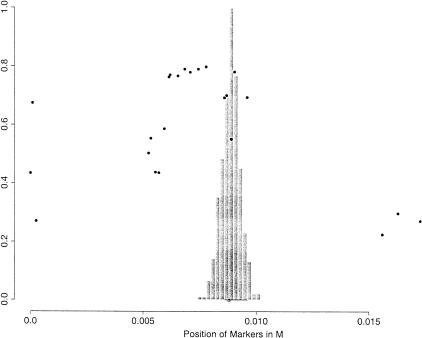
We decided to first model the data with a single founder cluster (the null cluster for phenocopies is always present). Because some markers in the region are very tightly spaced, the haplotypes in the control group strongly violate the linkage equilibrium assumption. Consequently, a first-order Markov model was used for the markers in the control haplotypes (see the Methods section). Monte Carlo draws from the posterior distribution of the disease location τ are shown in Figure 1, with [0.82, 0.93] cM as its 95% probability interval (PI). The algorithm also found that 71% of the disease haplotypes belong to the founder cluster, with remaining ones being phenocopies. To better illustrate our results, we also plot in Figure 1 a single marker measure of disequilibrium, which is defined as
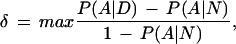 |
where A ranges over all of the possible alleles, D indicates the disease population, and N the normal population. To test the robustness of the BLADE's missing data strategy, we also applied BLADE to the set of 57 completely observed disease haplotypes. The posterior mean of τ was essentially unchanged but the posterior variance increased, with a 95% PI of [0.79,0.94] cM. Using a Markov model for the control haplotypes is important. If an equilibrium model is used, the 95% PI would not cover the true location.
Figure 1.
Histogram of a posterior sample for the location of the disease locus for cystic fibrosis. At the bottom of the figure, the true position of the disease-causing mutation is indicated by a small triangle, and the gene that contains it is indicated with a segment. The dots on the graph represent the δ-values for each marker in the dataset.
The good result shown in Figure 1 is somewhat surprising and counterintuitive because all but one of the disease haplotypes with the ΔF508 mutation have the identical configuration “0 0 1 1 0 1 0 1 0 0 1 0” for markers from 9 to 20. Indeed, if it were known that no crossovers had occurred in this region, the posterior distribution for τ would have been flat from 0.62cM to 0.96cM. However, the crossover events are unobservable and there is a substantial uncertainty in inferring their true locations. For example, a number of control haplotypes (23%) have the configuration “0 0 1 1 0 1 0” for markers from 9 to 15, of which four haplotypes also have alleles “1” and “0” at markers 16 and 17. Thus, for some disease haplotypes, the chance that the left crossover point occurred somewhere between markers 15 and 18 is nonnegligible. Another reason for BLADE to put the posterior mode between markers 16 and 19 is that the interval lengths between markers 15–16 and 19–20 are much greater than the interval lengths between markers 16–17, 17–18, and 18–19. By comparing the disease haplotypes with the control ones under a coherent probabilistic framework, BLADE incorporates relevant information and provides a posterior distribution of τ resulting from a weighted average over all of the possible ways of imputing the crossover points. To confirm our analysis, we applied BLADE to the 63 haplotypes with an identified ΔF508 mutation. A result similar to that of Figure 1 was obtained, although the last haplotype (the one in Group IIIa of Kerem et al.) was singled out as belonging to the null cluster by the algorithm. We also did the same analysis assuming that the distances between adjacent markers are all equal to 0.02cM (other values were also tested) and found that the posterior mode was shifted leftward to between markers 15 and 17. From this analysis we noted that BLADE performed robustly if the ratio of physical to genetic distance is constant in the region (we assumed that 1cM ≈ 1MB), whereas the result can be misleading if this uniformity does not hold.
We re-ran the algorithm with k = 2 (i.e., two founder clusters and one null cluster), which required slightly greater CPU time but gave a posterior distribution of τ almost identical to that in Figure 1 for the location of the disease mutation (the same mean, variance, median, etc.). The algorithm singled out from the previous null cluster an additional group consisting of two haplotypes:
0 0 0 0 1 0 0 0 1 1 0 0 1 0 1 0 1 0 0 1 1 0 0
0 0 0 0 1 0 0 2 1 1 0 0 1 0 1 0 1 0 0 1 1 1 1
Here “2” denotes that the marker information is missing at that locus. When we let k = 3, the algorithm pulled out a small group of about 8∼15 haplotypes (with some uncertainty), mostly from the previous main founder cluster. The central segment of the new ancestral haplotype was the same as that of the main cluster, indicating that the new group might be pulled out because of the genealogy. The posterior mean of τ moved slightly to the left, and its 95% PI was increased to [0.76, 0.94] cM.
To partially account for the correlations among the disease haplotypes, we implemented a heuristic purging strategy. That is, if the dataset contains ni copies of a haplotype, we retain only ƒ(ni) of them, where f() is given by the user. For example, we tested both ƒ(n) = n/[1 + (n − 1)cn, where cn is the coalescence factor proposed by McPeek and Strahs (1999), and the simple one ƒ(n) = √n. BLADE performed robustly, giving 95% PIs of [0.83,0.96] cM and [0.82, 1.0] cM, respectively, corresponding to the reduced disease datasets of sizes 78 and 58 for the two purging functions.
A number of LD methods have been applied to this dataset with satisfactory results (Xiong and Guo 1997; Lazzeroni 1998; McPeek and Strahs 1999; Morris et al. 2000). McPeek and Strahs used a maximum likelihood method based on a model similar to ours. They gave a confidence interval of τ with other parameters fixed. Their interval is somewhat larger than the one we obtained, even without the coalescence correction. The length of the PI obtained by Morris et al. is consistent with ours, although their interval was not able to cover the true location before the coalescence correction.
Friedreich Ataxia
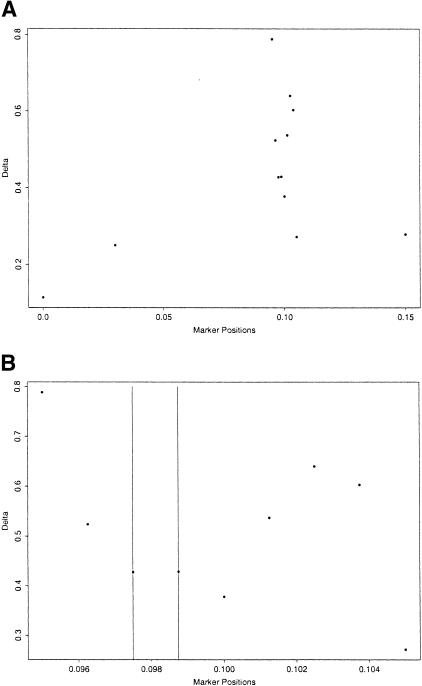
Our second LD analysis is based on previously unpublished data concerning the localization of the gene for Friedreich ataxia (FA), an autosomal recessive degenerative disease that involves the central and peripheral nervous system and the heart. The data came from the Acadian population of Louisiana (Sirugo et al. 1992). Campuzano et al. (1996) identified the gene responsible for FA and discovered that the disease is caused by a trinucleotide repeat expansion. Our data consist of haplotypes of 58 disease haplotypes, 69 control haplotypes, and one pair of unphased disease chromosomes, all from the Acadian population. There are 12 microsatellite markers spanning a region of 15 cM with intermarker distances of 3, 6.5, 0.125, 0.125, 0.125, 0.125, 0.125, 0.125, 0.125, 0.125, and 4.5 cM, respectively. The gene is located between the fifth and sixth markers. In Figure 2, we again plot the single-marker LD parameter δ for the 12 markers for comparison.
Figure 2.
(A) δ values for all of the markers in the Friedreich ataxia dataset. (B) δ values for the markers with distances from the disease locus less than 1 cM. The vertical lines indicate the two marker positions flanking the disease gene.
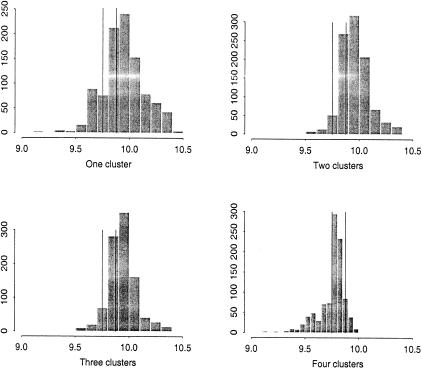
We first assumed that there is only one founder responsible for the disease mutation (k = 1). The program identified an ancestral haplotype of “2 7 8 2 5 9 2 2 2 2 6 3,” and 33 disease chromosomes including one of the unphased chromosomes are likely to belong this cluster. The posterior distribution of the disease gene location is given in the upper left panel of Figure 3; it is quite flat and not clearly pointing to the true disease location.
Figure 3.
Histograms of the posterior samples for the location of the Friedreich ataxia gene mutation under the assumption of one to four clusters, respectively. The X-axis is the distance between the first marker and the disease locus (in cM). The vertical lines indicate the two marker positions flanking the disease gene.
To explore whether there are any other ancestral mutations, we re-ran the program assuming that k = 2. Since we identified one ancestral haplotype in the first step, we used it as the initial value for one of the two founder haplotypes. The program identified another ancestral haplotype of “? ? 8 5 6 (2/3) 3 2 2 2 1 9,” and 7 disease chromosomes were found to conform to this ancestral type. To find other possible founder mutations, we ran the program with the assumption of more ancestral mutations. The program found two more distinct ancestral haplotypes, “? ? 7 7 3 3 3 4 2 2 7 5” and “? ? 8 7 6 3 3 2 3 3 5 ?”', respectively, each corresponding to six disease chromosomes. As we increased k from 1 to 4, the posterior distribution of the disease gene location as shown in Figure 3 concentrated more and more on the true mutation location. This was particularly the case when the fourth cluster was included, as it was in this group that a likely nearby flanking crossover event occurred. Analysis of just the major haplotype group (cluster 1) dominates most single-marker methods and leads to a misleading result.
When we ran the program with k = 5, the program picked out “? ? 8 5 6 2 3 2 2 2 ? ?” as the fifth ancestral haplotype, which is almost identical to the second most prominent ancestral haplotype we found earlier, with a minor difference only at the sixth marker. These two likely represent the same original mutation, but possibly reflect the fact that there is a mutation hotspot at marker 6 or that there was a mutation at an early stage at that marker. In summary, our analysis shows that these data consist of one principal mutation, present in 55% of the disease chromosomes, and three minor mutations, present in about 10% of the disease chromosomes each.
A Simulation Study
We simulated 50 populations of disease haplotypes originating from a single ancestor 200 generations earlier (control haplotypes are assumed in equilibrium). The growth rate of the population was 1.031, except for the first eight generations where the expansion rate was doubled. These parameters were chosen to mimic the history of the European population and to ensure the survival of the mutation. Each chromosome had a negative binomial number of descendants. We considered 10 microsatellite-like markers, each 0.2 cM apart and with 16 possible alleles. We set the mutation rate for each marker to be 0.001 per generation, which is high and can cause difficulties for some established LD mapping methods. When recombination occurs, a disease haplotype recombines with a random one in equilibrium. The ancestral haplotype consists of alleles with the following population frequencies: (0.0625, 0.4, 0.7, 0.0625, 0.4, 0.7, 0.4, 0.0625, 0.7, 0.0625). For each marker, the alleles not on the ancestral haplotype have equal probabilities. The disease location is between the fifth and sixth markers.
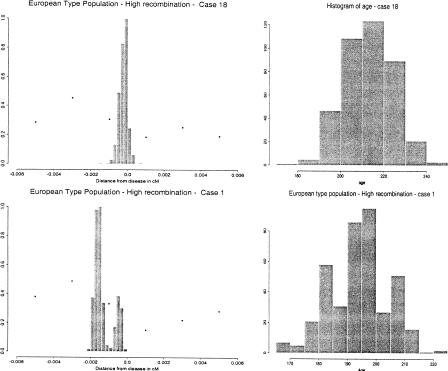
For each of the 50 simulated populations, we produced a set of 200 disease haplotypes by sampling at random from the final generation, and then we generated independently a control set of 200 normal haplotypes. We then ran our algorithm and compared its performance with the single marker method based on the δ-value defined earlier. The single marker method can serve as an index of the difficulty of the problem. More precisely, the δ-values for all of the markers are computed, and these values are interpolated by a smoothing spline. The point where the smoothed curve reaches its maximum is taken as a point estimate of the location of the disease mutation. Age is estimated by an average of the method-of-moments (MOM) estimates obtainable by each δ-value. Figure 4 illustrates a success and a failure of our procedure. The results may be summarized as follows: (a) the estimated location for the disease locus was between the two markers flanking the true disease location in 43 cases out of 50 (compared to 26/50 with a simple use of pairwise disequilibrium); (b) the posterior probability of the interval flanking the disease locus was greater than 0.9 in 33 cases out of 50; (c) the root mean square error of the location estimate was 0.0629 cM (compared to 0.1534); and (d) the posterior mean of age was 233.06 (compared to 402.19 with a simple use of pairwise disequilibrium). When we assume that there are two clusters (k = 2) in the disease population, the mutation location was estimated correctly 47 times out of 50, showing that allowing for multiple founder clusters can improve the performance of the algorithm even when only a single founder event occurred.
Figure 4.
Examples of outcomes of the first simulation. Left panels: Histograms of samples from the posterior distribution of the disease gene for two cases of our simulation (the true location is at position 0 and the distances are in Morgans). Superimposed are the values of δ corresponding to the markers whose position is within the limits of the picture. Right panels: Histograms of samples from the posterior distribution of the age in the same two cases.
DISCUSSION
Since linkage disequilibrium was rediscovered as a tool for mapping disease genes, various statistical techniques have been developed for this purpose. Early success in utilizing LD information has been achieved by examining the pattern of pairwise disequilibrium between the disease gene and a set of markers (Kerem et al. 1989; Hastbacka et al. 1992; Ozelius et al. 1992). This simple approach can be very effective, but suffers from limitations that become evident when the information content of the data is low, for example, when missing data, multiple founders, and unphased chromosomes, are present. Additionally, pairwise disequilibrium measures are not robust to (a) variation in marker allele frequencies, (b) multiple founder mutations, and (c) varying mutation rates at markers. Likelihood methods address some of these problems by making specific assumptions on the evolutionary history of the disease haplotypes and using the statistical framework of likelihood inference (see, for example, Kaplan et al. 1995; Xiong and Guo 1997; Graham and Thompson 1998; Rannala and Slatkin 1998). Two drawbacks of these methods are that they require assumptions on many exogenous parameters whose value is in fact unknown, and the likelihood functions on which they are based are prohibitively complex. As a consequence, one is effectively limited to consider pairwise disequilibrium.
It is evident, however, that considering the entire haplotype leads to more robust estimates. Indeed, there have been numerous cases in which the entire haplotype information was utilized through an ad hoc “imputation” of the recombination locations done by well-trained experts (Feder et al. 1996). The literature also documents various multilocus methods that allow the consideration of a group of markers at the same time without, however, exploiting the complete haplotype structure (Terwilliger 1995; Devlin et al. 1996; Lazzeroni 1998).
True haplotype methods have been proposed only recently by Service et al. (1999), McPeek and Strahs (1999), Lam et al. (2000), Morris et al. (2000), and us. Except for ours, no method allows for multiple ancestral haplotypes, although the methods of both McPeek and Strahs (1999) and Morris et al. (2000) can handle phenocopies. Because of computational limitations, Service et al.'s method is applicable only to haplotypes of small size (they have implemented it for the case of three markers). The method proposed by Lam et al. is based on a partial Bayesian analysis, which is conducted by first estimating a genealogical tree for the disease haplotypes and then deriving posterior distributions for quantities of interest based on a certain marginal likelihood. The hidden Markov model used by McPeek and Strahs and that used by Morris et al. are very similar to our model, depicted in Figure 5. A further simplification we made is to ignore the probability that a current disease haplotype may have more than one chromosomal piece in the region of consideration that is identical by descent (IBD) with the founder. This strategy seems to give us some computational advantages without sacrificing much in terms of sensitivity. A limitation of McPeek and Strahs' approach is that their inference on τ has to be made conditional on a set of nuisance parameters fixed at their maximum likelihood estimates (MLEs). Morris et al. used a Bayesian method that properly handles the nuisance parameters. Unfortunately, they did not allow for the flexibility in modeling the control haplotypes, which is perhaps a reason why they failed to cover the true location of ΔF508 mutation for the CF data (their Fig. 2).
Figure 5.
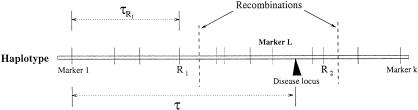
A graphical representation of the haplotype model. There are a total of k markers. Parameter τ is the “recombination distance” from the disease locus to the leftmost marker (which is equal to −log{(1+e−2d)/2}, where d is the genetic distance). The recombination event closest to the disease locus from the left arm occurred between markers R1 and R1+1 and that from the right arm occurred between markers R2 and R2+1.
Many previous authors have discussed the issue of dependent disease haplotypes due to the underlying genealogy. Because of the very high chance of including more than a single cluster in the real dataset, estimating a genealogical tree before the elimination of unrelated haplotypes is inappropriate. As stated in Rannala and Slatkin (2000), the use of a star genealogy “undoubtedly involves a tradeoff of statistical accuracy and efficiency for mathematical simplicity and rapid computability.” McPeek and Strahs propose to address the problem by “powering down” the likelihood function derived from the star genealogy, and Morris et al. follow the same strategy. Their correction factor, however, is computed independent of the observed haplotypes. Although this strategy helps one make more a conservative confidence statement by enlarging the confidence interval of τ, it does not address the more serious bias problem caused by the overrepresentation of certain closely related haplotypes. In comparison, we treat the deficiency of the star genealogy by allowing for multiple ancestral clusters and by haplotype purging (as implemented in the CF example). Haplotype-specific weighting schemes similar to the one used for protein sequence analysis could be another promising route.
We have assumed that all mutations occur in the same location of the disease gene. This assumption appeared robust in the two examples we considered. However, in the case where disease mutations occur in different parts of a gene separated by one or more markers, our analysis (or any similar analysis with the same assumption) would likely lead to a broader confidence interval, including multiple markers. From a positional cloning perspective, however, this should not be a serious limitation.
In summary, the BLADE algorithm can handle various data complications, and its output components can be directly inspected and interpreted by the researcher. The algorithm reports the posterior clustering information on each disease haplotype by providing a vector of probabilities of it belonging to different ancestral groups. Every haplotype is also associated with a Monte Carlo sample drawn from the posterior distribution of the proximal recombination events. In a way, our method mimics the “empirical process” followed by many experienced practitioners. For these researchers, BLADE can help quantify their intuitions and strengthen their insights. The main limitation of our method is that it uses a collection of star-trees, each characterized by an ancestral haplotype, to approximate the true genealogy of the disease haplotypes. This strategy may still be insufficient to remove all the bias and undercoverage problems caused by the correlations among the disease haplotypes and may also lead to a decrease in efficiency. However, our experience has shown that from a practical perspective, the greater flexibility inherent in our approach compared to other methods more than compensates for this loss in efficiency.
METHODS
Data Structure and Model Specifications
Data
Our data consist of a collection of haplotypes Ht of marker loci (1,2, … , m). They are divided into the control group and the disease group. The latter, corresponding to t = 1, 2, … , N, is denoted by H. A chromosome is classified as a “disease” or a “control” chromosome according to whether or not it segregates with disease status. The genetic distance di(in unit of Morgan) between markers M1 and Mi is assumed known. The recombination probability, which can be obtained as θi = (1 − e−2di)/2 by inverting Haldane's map function, is known as well. We further define τi = −log(1 − θi) so that e−τi is the probability that there is no recombination between markers M1 and Mi. If we assume that recombinations occur as a homogeneous Poisson process in the region under study, the probability of having no recombination between markers Mi and Mj can be computed as e−τj−τi. Clearly, τi ≈ di when di is small, say, less than 5 cM. For simplicity, in the later text we refer to τi as the genetic distance between markers, assuming implicitly that τi ≈ di holds true; this does not result in any loss of generality since τi can always be calculated from the true genetic distance as illustrated above. Although we assume a no-interference model for simplicity, it is unlikely to have much influence on the analysis, especially over short genetic distances, because the multiple crossovers that have occurred on a current chromosome are most likely the result of distinct independent meioses.
Each haplotype Ht is a vector; that is, Ht = (H , … , H
, … , H ), where Htj is the allele at marker locus Mj. We assume that there are nj different possible alleles at marker locus j, labeled as {1, 2, … , nj} and associated with allele frequencies pj1, pj2, … , pjnj. These frequencies can be estimated from the control group.
), where Htj is the allele at marker locus Mj. We assume that there are nj different possible alleles at marker locus j, labeled as {1, 2, … , nj} and associated with allele frequencies pj1, pj2, … , pjnj. These frequencies can be estimated from the control group.
Model Parameters
Throughout the article, the age of a mutation refers to the number of generations for the current sample to coalesce (their most recent common ancestor) rather than the historical time of occurrence. Suppose k disease-predisposing mutations at the disease locus have occurred in the past and survived in the current population. These mutations were most likely located on different ancestral chromosomes and may have occurred at different times. In our notation, A = (Aij)k×m are the ancestral haplotypes on which the original mutations occurred; G = (G1, G2, … ,Gk) are the ages of different mutations; τ is the genetic distance between the disease mutation and the marker locus 1; and L is equal to max{i : τi ≤ τ}, that is, the disease locus is between marker L and L+1 (where τ0and τm+1 = +∞). We assume that τ is the same for all disease mutations in the sample (except for phenocopies).
Disease chromosomes in the present day could carry either one or none of these mutations at the disease locus. In our model, to account for locus heterogeneity, we allow for a “null” cluster of haplotypes that doesn't share any ancestral mutation. Accordingly, the disease chromosomes can be subdivided into k+1 clusters based on the types of ancestral mutations they carry. A disease chromosome is put into the null cluster “0” if it carries none of the ancestral mutations (i.e., it is a phenocopy).
Haplotype Generation
For each disease haplotype Ht, we introduce a cluster indicator variable Ct, indicating to which mutation cluster Ht belongs. We assume a priori that P(Ct = 0) = αc, where αc can be input by the user. A default value of α0 = 0.5 was used in all the analyses. Generally, we let α0 = β0 and αc ∝ β1rc, c > 1, for some r < 1. If Ct = 0, then Ht is regarded as a random draw from the normal population (with parameters estimated from the control group); whereas Ct = c ≠ 0 implies that the disease locus is inherited from the founder haplotype c, and it is likely that neighboring marker loci also inherited the alleles on the same ancestral haplotype. The founder haplotype, however, would have been eroded by recombinations and mutations.
In order to simplify the specification of the likelihood, it is useful to introduce a pair of variables, R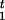 and R
and R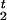 , that identify positions of the recombination events nearest to the disease locus. In our notation, moving away from the disease locus towards marker 1, the nearest recombination event took place between markers R1+1 and R1; in the opposite direction, the nearest recombination event took place between markers R2 and R2+1. The probability distributions of R1 and R2 are simple functions of the age of the mutation and the transformed distances between markers. This model is shown as in Figure 5.
, that identify positions of the recombination events nearest to the disease locus. In our notation, moving away from the disease locus towards marker 1, the nearest recombination event took place between markers R1+1 and R1; in the opposite direction, the nearest recombination event took place between markers R2 and R2+1. The probability distributions of R1 and R2 are simple functions of the age of the mutation and the transformed distances between markers. This model is shown as in Figure 5.
During each meiosis, there is a small probability r for each locus Mi to mutate. In what follows, we assume that it has equal probability to mutate to any other allele. Although not very accurate, this assumption is not crucial for our analysis and can be easily changed to accommodate any desired transition rule. Furthermore, we assume a priori that r follows a distribution π0(r) defined on a given interval, say, [10−4, 10−3]. We discretized the interval so that r only takes on a finite number of values. The simplest special case is that r is fixed at a given value. Let r(i,G,j1,j2) be the probability of a mutation from j1 to j2 in G generations at locus i. Then, ignoring the small probabilities of recurrent mutations, we have
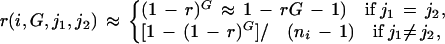 |
where the approximation holds when rG is small.
Likelihood Function For a Single Haplotype
Suppose there is no interference for crossovers in the region under investigation. Given A, G, and τ, the joint probability of (Ht, Ct, 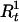 ,
, 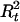 ) is
) is
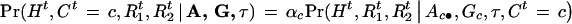 |
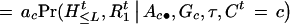 |
1 |
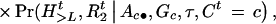 |
for c ≠ 0, where Ac• = (Ac,1, … , Ac,m) denote the ancestral haplotype for cluster c, H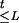 is the left haplotype segment, (
is the left haplotype segment, (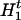 ,
,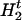 , … ,
, … ,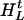 ), and H
), and H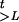 is (HtL+1, … , Htm). Note that the αc represent the a priori specification of the cluster frequencies and that the algorithm will produce a posteriori estimates of the same parameters. Since the probability of having at least one recombination in G generations between two markers Ma and Mb is 1 − e−| τb−τa|G; we have
is (HtL+1, … , Htm). Note that the αc represent the a priori specification of the cluster frequencies and that the algorithm will produce a posteriori estimates of the same parameters. Since the probability of having at least one recombination in G generations between two markers Ma and Mb is 1 − e−| τb−τa|G; we have
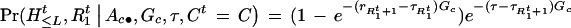 |
2 |
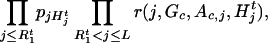 |
and
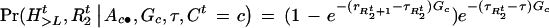 |
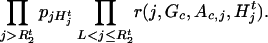 |
When Ct = 0, we have P(Ht, Ct = 0| A, G, τ) = α0∏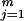 pjHtj (a Markov model can be used when the control haplotypes are not in equilibrium). If we think of Ct,
pjHtj (a Markov model can be used when the control haplotypes are not in equilibrium). If we think of Ct, 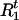 , and
, and 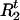 as missing data, then the foregoing expressions represent the “complete-data likelihood“ of a single disease haplotype. Marginalizing out
as missing data, then the foregoing expressions represent the “complete-data likelihood“ of a single disease haplotype. Marginalizing out 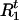 and
and 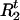 , we have
, we have
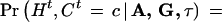 |
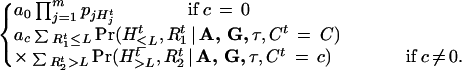 |
3 |
Hence,
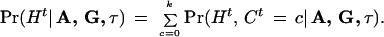 |
Likelihood of the Observed Data
At this point we assume that the coalescence process that generates the observed disease haplotypes within each cluster can be approximated by a star genealogy; that is, the haplotypes in cluster c are mutually independent conditional on the ancestral haplotype. This assumption represents a great simplification of the actual genealogy structure and is desirable because it allows us to construct a procedure that deals with a variety of other complications such as the missing marker data, unknown phases, multiple disease predisposing mutations, and locus heterogeneity. The correlations among the disease haplotypes are partially accounted for by allowing for multiple founder haplotypes with different ages. For example, if a few closely related haplotypes are present in the disease sample, our method automatically clusters them, treating them as if they had a founder haplotype independent of all others. Additionally, for the founder mutations in our study, the initial generations are likely to be characterized by rapid growth conditional on the survival of the mutation. This scenario, where a substantial amount of diversity is introduced early on, can be approximated by a collection of star trees reasonably well.
Under the conditional independence assumption, the likelihood of the observed disease haplotypes can be obtained by the multiplication of the single-observation likelihood:
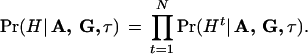 |
4 |
Although the explicit form of the observed-data likelihood is not very difficult to write down as in (4), finding the MLE of A, G, and τ from it presents a challenge. Additionally, the information on G from the haplotype data is usually very limited, and very strong prior knowledge regarding it is often available. Equipped with Markov chain Monte Carlo (MCMC) computational tools, a Bayesian estimation method seems to be a more reasonable choice for this problem than the maximum likelihood approach.
Prior Distributions
A Bayesian procedure requires us to specify prior distributions for all of the parameters. For the ease of interpretation and justification, we limit ourselves to very simple choices. Firstly, τ is uniformly distributed in the region (τ1,τm) a priori. Similarly, Gc takes values x,x+d, … ,x+nd with equal probability for c from 1 to k. We assume that the ancestral haplotype Ac< for cluster c is a random draw from the normal population whose parameters can be estimated by the control group. For example, if the linkage equilibrium is assumed, then
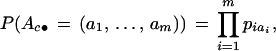 |
where pij is the allele frequency of marker Mi in the control group. The mutation rate for each marker is assumed to be identical and is uniformly distributed on finite possible values. Note that this assumption is purely for simplicity of presentation and is not essential. All the parameters are independent a priori.
There are several complications that can cause difficulties for our basic model. The first complication is the missing data problem. Part of the marker information may be missing for some individuals, or, only the marker genotypes are observed, whereas the phases of the two chromosomes are unknown. The second problem is that sometimes the genetic markers are so close to each other that linkage equilibrium cannot be assumed even for the control chromosomes. Hence, treating the marker data in the control group as if they were in linkage equilibrium (i.e., independent) can give misleading results. A Markov model for the control group is often helpful. The third problem regards our assumption that the subjects in our study are mutually independent (or unrelated) once their common ancestral haplotype is given. Although we can alleviate the dependence problem of the disease haplotypes by using multiple clusters, it is of interest to quantify the information loss due to our approximation. A related problem is the determination of k, the number of clusters. These issues will be addressed in the last part of this section.
The Basic Algorithm
Based on the probabilistic model described in the previous section, inferences on the unknowns are based on the posterior distribution Pr(A, G, τ|H). However, it is much easier to work with its augmented version Pr(A, G, τ, R1, R2, C|H), which is proportional to the product of the complete-data likelihood and prior distributions, that is, Pr(A, G, τ, R1, R2, C|H) ∝ Pr(H, R1, R2|C, A, G, τ) Pr(C, A, G, τ). Since the distribution Pr(A, G, τ, R1, R2, C|H) is a high-dimensional and nonstandard function, we use an MCMC algorithm to sample from it and base our inference on the obtained Monte Carlo samples.
The BLADE algorithm is a combination of the Metropolis algorithm (Metropolis et al. 1953) and the conditional sampling method. Because of the special structures of the variables in our problem (e.g., a high correlation between the recombination locations and the disease locus), special care is needed for speeding up the convergence of the sampler. For a simple presentation, in the following text we use [X|Y, … , Z] to denote the conditional distribution of X given Y, … , Z under the target posterior distribution. Since our Bayesian analysis is always conditional on the observations, the notation H is omitted in the conditioning in all of the following formulas. The algorithm iterates through the following Monte Carlo sampling steps.
- 1.
- Draw G from [G|A, τ, C, R1 ,R2 ]. Given A, τ, C, R1, R2 , we are able to compute the posterior probability of Gc, which is of the form
We draw a new g from this distribution to replace the previous Gc.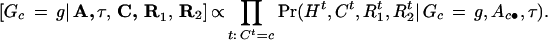
- 2.
- Draw disease locus τ from [τ|A, G]. Since the value of τ is highly correlated with the recombination positions R
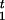 and R
and R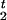 , we need to sum out all the R's and c's in order to speed up the algorithm. Hence, we draw τ from [τ|A, G] via a Metropolis-Hastings step (Metropolis et al. 1953; Hastings 1970) rather than from the more convenient one, [τ|A, G, C, R1, R2 ], as in the usual Gibbs sampling. More precisely, a candidate τ‘ is first generated from the distribution:
, we need to sum out all the R's and c's in order to speed up the algorithm. Hence, we draw τ from [τ|A, G] via a Metropolis-Hastings step (Metropolis et al. 1953; Hastings 1970) rather than from the more convenient one, [τ|A, G, C, R1, R2 ], as in the usual Gibbs sampling. More precisely, a candidate τ‘ is first generated from the distribution:
This candidate is accepted with probability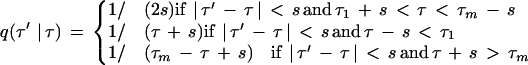
where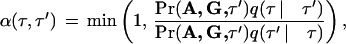
is computed from (3).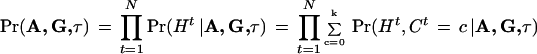
- 3.
Draw Ct from [C|A,G,τ] for t = 1,…,N. Given A,G, and τ, it is simple to compute and to sample from the posterior distribution of
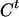 according to (3).
according to (3).- 4.
Draw
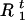 and
and 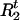 from [
from [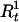 ,
,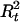 | A,G,τ,Ct] for t = 1,…,N. Given A,G, τ, and Ct ≠ 0, we compute Pr(
| A,G,τ,Ct] for t = 1,…,N. Given A,G, τ, and Ct ≠ 0, we compute Pr(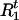 | A,G,τ,Ct,Ht) and Pr(
| A,G,τ,Ct,Ht) and Pr(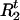 |A,G,τ,Ct,Ht) from (1). Then
|A,G,τ,Ct,Ht) from (1). Then 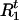 and
and 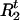 are updated by sampling from these two distributions, respectively.
are updated by sampling from these two distributions, respectively.- 5.
- For c = 1,…,k, we update the ancestral haplotype Ac• = (Ac,1,…,Ac,m) one locus at a time. That is, we draw from [Ac,i| A[c,i],G,τ,C] for i = 1,…,m and c = 1,…,k, where A[c,i] consists of all of A but Aci. Given A[c,i],G,H,C, and τ, the posterior probability of Ac,i = j is proportional to
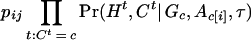
where Ac,[i] = Ac•\ Ac,i. We update all Ac,i where c and i are chosen in a specified order, by sampling from the above distribution.
- 6.
- Draw a new mutation rate r from [r| G,R1, R2, A, C]. Based on formulas in (1), we see that the likelihood of r given all the rest of the variables can be written as
where mc is the total number of mutations in cluster group c, M = Σcmc, and nc = Σ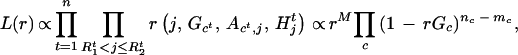
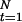 I[Ct=c](
I[Ct=c](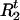 − R
− R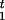 ) is the total number of “original alleles” in cluster c. Thus, when combined with the prior distribution π0(r), we sample r from π(r) ∝ π0(r)L(r). In practice, we assume a priori that r is equally likely to take one of a few possible values.
) is the total number of “original alleles” in cluster c. Thus, when combined with the prior distribution π0(r), we sample r from π(r) ∝ π0(r)L(r). In practice, we assume a priori that r is equally likely to take one of a few possible values.
- 7.
The algorithm terminates when the likelihood value does not improve after k0 steps.
Handling Practical Complications
Phase Unknown and Other Missing Data
For some chromosomes, the phase may be unknown. The data are of the form
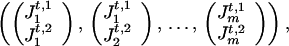 |
from which we can form 2m−1 possible haplotypes. Let (Ht,1, Ht,2) be a consistent pair of these haplotypes, which is unobservable and is imputed by the algorithm. More precisely, we update (Ht,1, Ht,2) iteratively in the following manner. Each marker locus Mi is visited in some specified order. Conditioned on the realized phase of other marker loci, there are two possible haplotypes, (Ht,1, Ht,2) and (H̃t,1,H̃t,2), determined by the two possible phases of Mi, where (Ht,1, Ht,2) and (H̃t,1, H̃t,2) differ only at locus Mi by a switch between 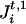 and
and 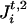 . Then, given A, G, τ, and Ct,1, Ct,2, we can compute, assuming random mating,
. Then, given A, G, τ, and Ct,1, Ct,2, we can compute, assuming random mating,
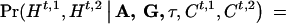 |
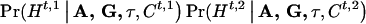 |
and
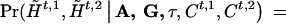 |
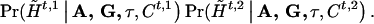 |
So a Metropolis step (Metropolis et al. 1953) can be implemented for updating the haplotype.
Another type of missing information results from a few untyped or mistyped markers for some haplotypes in the disease population. We can practically ignore these missing data and use recombination distances based on the actual observed markers. More precisely, in evaluating quantities
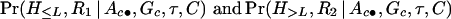 |
for formula (1), we only need to consider the observed markers. For example, the quantity
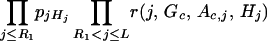 |
involves only the product over the observed marker loci Mj.
Control Data Not in Linkage Equilibrium
When the markers on control chromosomes are not in linkage equilibrium, a simple solution is to use a first-order Markov model to describe haplotype frequencies. Thus, formula (1) has to be modified. For example, (2) is changed to
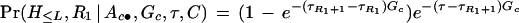 |
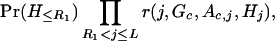 |
where Pr(H≤R1) is computed based on a Markov model. This modification of the algorithm handles the Cystic fibrosis data (see the Results section) very well. An intrinsic difficulty with this approach is that there are usually too many parameters to estimate when the number of alleles at each locus is large. So far the Markov approach is most appropriate for haplotypes with biallelic markers. Alternatively, haplotype frequencies in the control population can be estimated prior to analyzing disease chromosomes. Further studies on more delicate modeling of marker correlations are needed (see Lam et al. 2000 for another approach).
Determining the Number of Clusters
Using a number k slightly greater than the actual number of clusters is often a good strategy since it helps alleviate the bias and under-coverage problem caused by the correlations among the disease haplotypes. Operationally, we can start with k = 1 and repeat the computation with k = 2, 3 and so on. The best result is selected according to the maximum a posteriori (MAP) criterion; that is, we choose k that maximizes
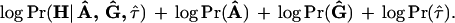 |
In most cases, however, one can easily tell what might be a correct number for k by examining the output files: When k is greater than needed, some of the ancestral haplotypes would look very similar to each other and the estimated location of the disease mutation does not change much. It is also observed that increasing the number of clusters sequentially and using the result for k clusters as the starting point for k+1 clusters speeds the convergence of the algorithm.
Acknowledgments
We thank Saunak Sen for helpful discussion. J.S.L. was supported in part by NSF grants DMS-9803649 and DMS-0094613, and N.R. was supported in part by NIH grant GM057672. Part of the manuscript was prepared while J.S.L. and J.T. were on the faculty of the Statistics Department of Stanford University. The collection of the Friedreich Ataxia data was supported by the Muscular Dystrophy Association and the National Ataxia Foundation.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Footnotes
E-MAIL jliu@stat.harvard.edu; FAX (617) 496-8057.
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.194801.
REFERENCES
- Campuzano V, Montermini L, Molto MD, Pianese L, Cossee M, Cavalcanti F, Monros E, Rodius F, Duclos F, Monticelli A, et al. Friedreich’s ataxia: Autosomal recessive disease caused by an intronic GAA triplet repeat expansion. Science. 1996;271:1423–1427. doi: 10.1126/science.271.5254.1423. [DOI] [PubMed] [Google Scholar]
- Devlin B, Risch N, Roeder K. Disequilibrium mapping: Composite likelihood for pairwise disequilibrium. Genomics. 1996;29:311–316. doi: 10.1006/geno.1996.0419. [DOI] [PubMed] [Google Scholar]
- Feder JN, Gnirke A, Thomas W, Tsuchihashi Z, Ruddy DA, Basava A, Dormishian F, Domingo R, Jr, Ellis MC, Fullan A, et al. A novel MHC class I-like gene is mutated in patients with hereditary haemochromatosis. Nat Genet. 1996;13:399–408. doi: 10.1038/ng0896-399. [DOI] [PubMed] [Google Scholar]
- Graham J, Thompson E. Disequilibrium likelihoods for fine-scale mapping of a rare allele. Am J Hum Genet. 1998;63:1517–1530. doi: 10.1086/302102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hastbacka J, et al. Linkage disequilibrium mapping in isolated founder populations: Diastrophic dysplasia in Finland. Nat Genet. 1992;2:204–211. doi: 10.1038/ng1192-204. [DOI] [PubMed] [Google Scholar]
- Hastings WK. Monte Carlo sampling methods using Markov chains and their applications. Biometrika. 1970;57:97–109. [Google Scholar]
- Kaplan N, Hill W, Weir B. Likelihood methods for locating disease genes in nonequilibrium populations. Am J Hum Genet. 1995;56:18–32. [PMC free article] [PubMed] [Google Scholar]
- Kerem B, Rommens JM, Buchanan JA, Markiewicz D, Cox TK, Chakravarti A, Buchwald M, Tsui LC. Identification of the cystic fibrosis gene: Genetic analysis. Science. 1989;245:1073–1080. doi: 10.1126/science.2570460. [DOI] [PubMed] [Google Scholar]
- Lam J, Roeder K, Devlin B. Haplotype fine mapping by evolutionary trees. Am J Hum Genet. 2000;66:659–673. doi: 10.1086/302756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazzeroni L. Linkage disequilibrium and gene mapping: An empirical least-squares approach. Am J Hum Genet. 1998;62:159–170. doi: 10.1086/301678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McPeek M, Strahs A. Assessment of linkage disequilibrium by the decay of haplotype sharing, with application to fine-scale genetic mapping. Am J Hum Genet. 1999;65:858–875. doi: 10.1086/302537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E. Equations of state Calculations by fast computing machines. J Chem Phys. 1953;21:1087–1091. [Google Scholar]
- Morris AP, Whittaker JC, Balding DJ. Bayesian fine-scale mapping of disease loci, by hidden Markov Models. Am J Hum Genet. 2000;67:155–169. doi: 10.1086/302956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ozelius LJ, Kramer PL, de Leon D, Risch N, Bressman SB, Schuback DE, Brin MF, Kwiatkowski DJ, Burke RE, Gusella JF, et al. Strong allelic association between the torsion dystonia gene (DYT1) and loci on chromosome 9q34 in Ashkenazi Jews. Am J Hum Genet. 1992;50:619–628. [PMC free article] [PubMed] [Google Scholar]
- Rannala B, Slatkin M. Likelihood analysis of disequilibrium mapping, and related problems. Am J Hum Genet. 1998;62:459–473. doi: 10.1086/301709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rannala B, Slatkin M. Methods for multipoint disease mapping using linkage disequilibrium. Genet Epidemiol Supp. 2000;19:S71–S77. doi: 10.1002/1098-2272(2000)19:1+<::AID-GEPI11>3.0.CO;2-D. [DOI] [PubMed] [Google Scholar]
- Service S, Temple Lang D, Freimer N, Sandkuijl L. Linkage-disequilibrium mapping of disease genes by reconstruction of ancestral haplotypes in founder populations. Am J Hum Genet. 1999;64:1728–1738. doi: 10.1086/302398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sirugo G, Keats B, Fujita R, Duclos F, Purohit K, Koenig M, Mandel JL. Friedreich ataxia in Louisiana Acadians: Demonstration of a founder effect by analysis of microsatellite-generated extended haplotypes. Am J Hum Genet. 1992;50:559–566. [PMC free article] [PubMed] [Google Scholar]
- Terwilliger J. A powerful likelihood method for the analysis of linkage disequilibrium between trait loci and one or more polymorphic marker loci. Am J Hum Genet. 1995;56:777–787. [PMC free article] [PubMed] [Google Scholar]
- Xiong M, Guo S. Fine-scale genetic mapping based on linkage disequilibrium: Theory and application. Am J Hum Genet. 1997;60:1513–1531. doi: 10.1086/515475. [DOI] [PMC free article] [PubMed] [Google Scholar]