Relating domain size distribution to line tension and molecular dipole density in model cytoplasmic myelin lipid monolayers

Abstract

We fit the size distribution of liquid-ordered (L_o) domains measured from fluorescence images of model cytoplasmic myelin monolayers with an equilibrium thermodynamic expression that includes the competing effects of line tension, λ, dipole density difference, Δm, and the mixing entropy. From these fits, we extract the line tension, λ, and dipole density difference, Δm, between the L_o and liquid-disordered (L_d) phases. Both λ and Δm decrease with increasing surface pressure, , although λ/Δm² remains roughly constant as the monolayer approaches the miscibility surface pressure. As a result, the mean domain size changed little with surface pressure, although the polydispersity increased significantly. The most probable domain radius was significantly smaller than that predicted by the energy alone, showing that the mixing entropy promotes a greater number of smaller domains. Our results also explain why domain shapes are stable; at equilibrium, only a small fraction of the domains are large enough to undergo theoretically predicted shape fluctuations. Monolayers based on the composition of myelin from animals with experimental allergic encephalomyelitis had slightly lower values of λ and Δm, and a higher area fraction of domains, than control monolayers at all . While it is premature to generalize these results to myelin bilayers, our results show that the domain distribution in myelin may be an equilibrium effect and that subtle changes in surface pressure and composition can alter the distribution of material in the monolayer, which will likely also alter the interactions between monolayers important to the adhesion of the myelin sheath.

The compact multilamellar structure of the myelin sheath forms a capacitor surrounding the nerve axons, which allows for faster and more efficient transmission of electric impulses than unmyelinated nerves (1–3). To take full advantage of the low dielectric constant of the lipid bilayer (ϵ_l ∼ 2), the myelin sheath must be impervious to water (ϵ_w ∼ 80) and ions and remain tightly wrapped (4, 5). Defects or disruptions in the myelin bilayers increase the capacitance, which could lead to changes in nerve signal conduction, resulting in sensory and motor disabilities. Multiple Sclerosis (MS) is the most common progressive neurological disorder in young adults and is characterized by the appearance of lesions in the myelin, reflecting loss of bilayer adhesion, swelling across the water gaps, vacuolization, vesiculation, and eventual disintegration of the myelin sheath (6–8).

One feature of experimental allergic encephalomyelitis (EAE) in the common marmoset, an accepted animal model for MS (6, 9), is a change in the overall myelin lipid composition (10) (Table 1). Changes in lipid composition may lead to changes in the lateral distribution, extent, and stability of phase-separated domains within the myelin bilayer (5). The domain distribution and the line tension between domains couples strongly to membrane curvature and can lead to budding and vesiculation from phase-separated bilayers (11, 12). Domain formation and its effects on line tension and membrane curvature can also influence the distribution of proteins within the membrane (5). Hence, understanding the relationship between monolayer composition and the factors that govern the domain size distribution, such as the line tension, λ, and dipole density difference, Δm, in healthy and EAE monolayers and bilayers may lead to a better understanding of the events leading to demyelination in MS.

Table 1.

Lipid compositions used for the cytoplasmic (CYT) myelin monolayers

Lipid Class	Mole% lipid
	Control	EAE
Cholesterol (CHOL)	31.6	37.4
Phosphatidylserine (PS−)	7.3	7.4
Sphingomyelin (SM + /−)	6.2	2.2
Phosphatidylcholine (PC + /−)	25.9	20.1
Phosphatidylethanolamine (PE + /−)	29.0	32.9

In any biomembrane, lateral compositional fluctuations, even in otherwise homogeneous monolayers and bilayers, can stabilize nanometer scale “rafts” enriched in cholesterol, saturated, long-chain lipids, and certain proteins (13–15). Coupling between lipids and proteins can either stabilize domain formation or conversely, promote lipid miscibility (5). The size and lifetime of rafts depends on the energy costs of forming phase-separated lipid domains, and hence on the line tension, λ, and dipole density difference, Δm. To date, λ and Δm have been measured for a limited number of monolayer compositions by analyzing the relaxation of deformed, individual domains (16) and by analysis of the fluctuations of the domain boundaries of individual large domains (14, 17, 18). Here we present a unique way of measuring λ and Δm from the entire distribution of domain sizes in lipid monolayers assuming this distribution is at equilibrium (or at least metastable equilibrium). This approach is a necessary first step in understanding the physical phenomena that determine if micron and submicron domains can exist to form rafts, and how changes in lipid composition associated with MS might alter domain, and hence raft organization in the myelin sheath. Rafts may also play important roles in adhesion (19), intermembrane spacing (20), permeability (21), intracellular transport of proteins and lipids (22), electrical properties such as signal transduction (23), and localization (24) and regulation (25) of ion channels. Several studies have shown that domains also act as a gateway for and preferential location for binding of various pathological infections including Alzheimer’s disease (26) and human immunodeficiency virus 1 (26).

Experimental Results

Fig. 1 shows fluorescence images of monolayers based on the estimated lipid composition of the normal (left) and EAE (right) cytoplasmic (CYT) leaflet of myelin [Table 1; (4, 5, 10)]. 1 wt% of the fluorescent lipid Texas-Red 1,2-dihexadecanoyl-sn-glycero-3-phophoethanolamine and triethylammonium salt (DHPE) (Invitrogen), was added to provide contrast in the images (5) (for additional details see SI Text). The dark, circular domains are, by analogy to similar systems (27), likely liquid-ordered (L_o) phase, which excludes the fluorescent lipid and is richer in cholesterol and saturated lipids than the surrounding bright, continuous, liquid-disordered (L_d) phase (5, 27). As the surface pressure (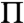) was increased (Fig. 1), the same pattern of dark domains in a bright, continuous background persisted until the two phases mixed to form a single, homogeneous phase at ∼30 mN/m for the control and ∼20 mN/m for the EAE monolayer at room temperature (5). From the images, we measured the sizes of the L_o domains using ImageJ [National Institute of Health (NIH)] and plotted the results as histograms showing the relative fraction of domains within a certain size range (Figs. 2 and 3). The number of bins in each histogram was set equal to 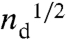, in which n_d is the number of domains counted. The bins were distributed uniformly from 0.5 μm (the minimum optically resolved radius) to the maximum domain radius observed in the image, which defined the width of each bin. The total area under the histogram was thus set to 1, making the histogram a probability distribution.

Fig. 1.

Fluorescence images of (A)–(D) control and (E)–(H) EAE CYT myelin monolayers containing 1 wt% TR-DHPE on a MOPS [3-(N-morpholino)propanesulfonic acid] buffer subphase at T ≈ 22 °C and pH ≈ 7.2 as a function of surface pressure. Also shown an enlarged view of domains obtained at 11 mN/m in the control monolayer.

Fig. 2.

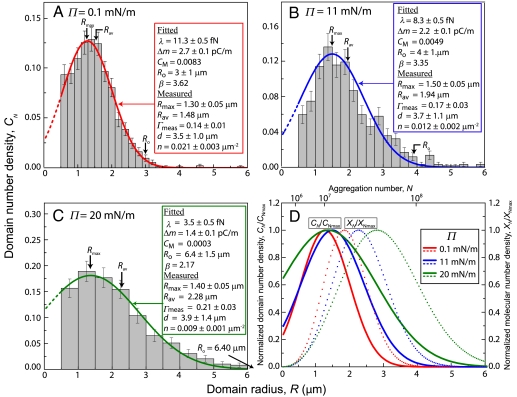
Experimentally determined fraction of domains of a given radius, C_N, as a function of domain radius, R, of control CYT myelin monolayers at three different surface pressures, 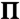: (A) 0.1 mN/m, (B) 11 mN/m, and (C) 20 mN/m determined from the fluorescence images in Fig. 1 A–D displayed as histograms. The solid curves are the theoretical distributions (Eq. 8) fit to the histograms. The fitting parameters R_o, C_M, and β are listed in the inset. From R_o and β, both Δm = (4ϵϵ_ok_BTβ/R_o)^1/2 and λ = (k_BTβ/πR_o)· ln[4R_o/e³δ] were evaluated. The mean domain radius, R_av, the measured area fraction of domains, , the mean distance between neighboring domains, d, and the number density of domains, n, taken directly from the images are listed along with R_max, the maximum in the fitted theoretical size distribution. (D) Comparison of the three fitted curves in (A)–(C) plotted both in terms of the normalized domain concentrations C_N/C_N max (solid curves, A–C), as well as in terms of the molecular number densities X_N/X_N max (dotted curves), where X_N = NC_N.

Fig. 3.

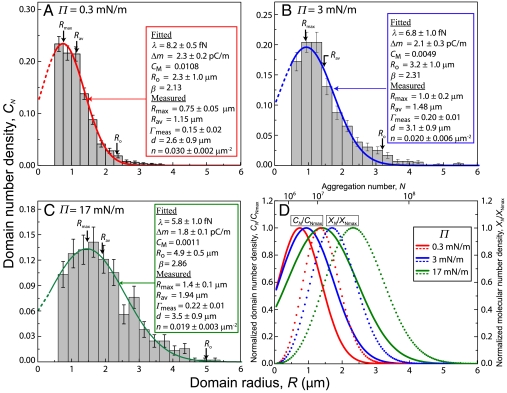
As in Fig. 2 but for EAE CYT myelin monolayers at 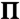: (A) 0.3 mN/m, (B) 3 mN/m, and (C) 17 mN/m. (D) Same as (D) in Fig. 2.

Theory

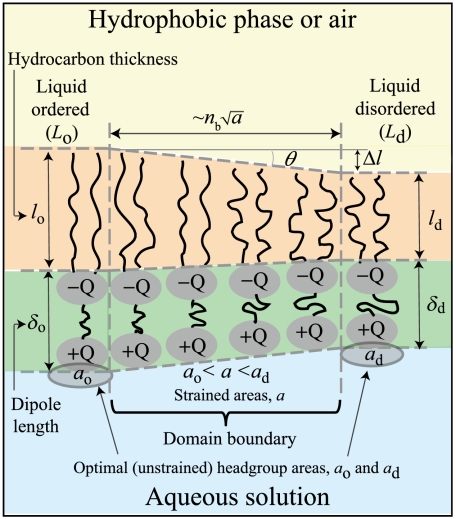
The size distribution of domains at equilibrium is set by a balance between the line tension, λ, between domains, the dipole density difference, Δm, between phases, and the entropy of distributing the molecules between the different domains. The energy per molecule, E/N, in an isolated circular domain of radius R(N = πR²/a_o) is (see Figs. 1B and 6):

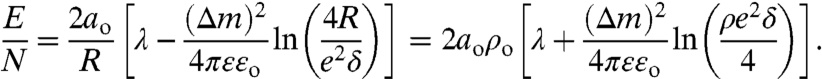[1]

In Eq. 1, ρ = 1/R, ϵ is the dielectric constant of interfacial water (ϵ ∼ 40–80), ϵ_o = 8.854 × 10^-12 C²/J·m is the permittivity of free space, δ is a molecular cut-off distance, ∼0.5 nm, and e is the exponential, 2.714 (27, 28). The minimum energy domain radius, R_o = 1/ρ_o is given by ∂(E/N)/∂ρ = 0:

[2]

While Eq. 2 shows that the radius of an isolated, noninteracting domain increases with λ, and decreases with Δm (27), it is impossible to separate the two parameters.

Fig. 6.

Schematic of lipid domain in a monolayer at the air-water interface.

However, as shown in the fluorescence images in Fig. 1, the L_o domains are polydisperse; there is no obvious R_o in the images that reflects the energy minima in Eq. 2. This broad size distribution may be due to a lack of equilibration between domains, although molecular diffusivities in these liquid-liquid mixtures are high [1–20 μm²/s (27)] and the size distribution remains stable, albeit polydisperse, for hours (29, 30). The large difference between R_o and the most probable domain size R_max shows that entropy of mixing can play a significant role in determining domain size distribution, as it does for spontaneous micelles and vesicles (31–33).

At equilibrium, the chemical potential of a molecule of area a_o in a L_o domain of M molecules, corresponding to 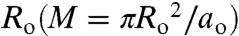, is equal to that of a molecule in a L_o domain of N molecules of radius R(N = πR²/a_o):

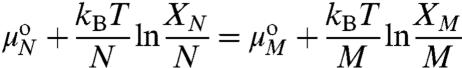[3]

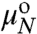, X_N and 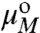, X_M are the standard state chemical potentials and mole fractions of molecules in domains of size N and M, respectively; k_B is the Boltzmann constant (1.38 × 10^-23 J·K^-1), and T is the temperature (K). This ideal entropy of mixing assumes no interactions between domains (30), which is true if the domains are sufficiently dilute (in these experiments, the area fraction of L_o domains is < 20% ). Eq. 3 can be rearranged to give the equilibrium size distribution of domains:

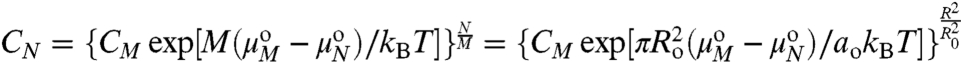[4]

C_N = X_N/N and C_M = X_M/M are the number fractions of domains of radius R containing N molecules, as a function of the number of domains of radius R_o containing M molecules. 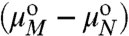is the difference in standard state chemical potential between a domain with M and N molecules (see SI Text). To evaluate 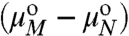, we expand Eq. 1 in a Taylor series around ρ = ρ_o:

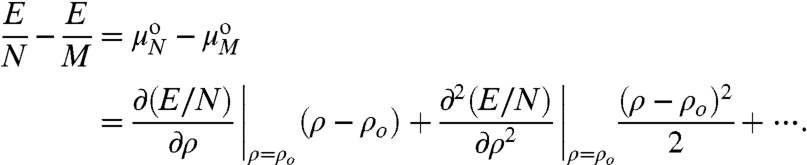[5]

At ρ = ρ_o, the first derivative is zero (Eq. 2), so to quadratic order:

[6]

and Eq. 4 becomes:

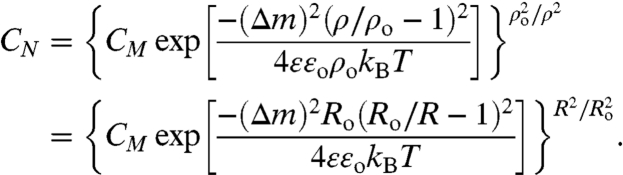[7]

Eq. 7 can be simplified to give three adjustable parameters R_o, β, and C_M, to fit histograms of the domain size distributions (Figs. 2 and 3):

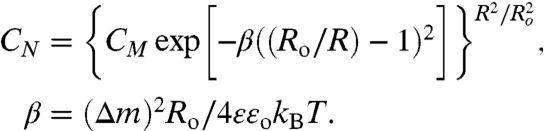[8]

C_M is the value of the distribution at R_o; β is related to the width of the distribution, but the three parameters are not independent and are adjusted to best fit the data as well as to normalize the probability distribution. The form of Eq. 8 is identical to the form of the size distributions used to fit spontaneous vesicle size distributions (31, 32) although the physics that determines domain energy is quite different from the physics that determines vesicle curvature or micelle packing number.

R_o, β, and C_M were used as parameters to fit the histograms in Figs. 2 and 3 to Eq. 8 using OriginPro 8: From R_o and β, both (Δm) = (4ϵϵ_ok_BTβ/R_o)^1/2 and λ = (k_BTβ/πR_o)· ln[4R_o/e³δ] were evaluated. The magnitude of λ depends on the value chosen for the cut-off parameter, δ, in Eq. 2, which is taken here to be 0.5 nm (34). The theoretical size distribution (Eq. 8) is an excellent representation of the measured size distributions for both control (Fig. 2 ) and EAE (Fig. 3) myelin monolayers at all surface pressures examined. The parameters extracted from the fits are shown in each box.

For the control monolayers, λ decreases from 11 fN (femto-Newton) at liftoff (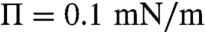) to 3.5 fN (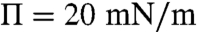) with increasing surface pressure; Δm decreases from 2.7 to 1.4 pC/m, which corresponds to 0.85–0.45 D/nm²; this is consistent with the size distribution growing more polydisperse and shifting to larger mean domain sizes with increasing surface pressure. This trend of decreasing line tension and dipole density difference with surface pressure is consistent with previous measurements for binary dimyristoylphophatidylcholine (DMPC)-cholesterol (CHOL) monolayers, particularly when a miscibility transition is approached (5, 16–18). However, while the measured dipole density difference for the control CYT monolayers is in the same range as the simple DMPC-CHOL mixtures (18, 35), the line tensions we find are about two orders of magnitude less than for the binary mixtures, which range from (100–1,000 fN). In bilayer vesicles, line tensions as low as 10–20 fN have been found for ternary mixtures near the miscibility transition (14). For the EAE monolayers, we find less variation with surface pressure, λ decreases from 8.2 fN at liftoff (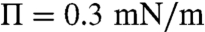) to 5.8 fN (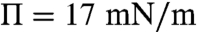) with increasing surface pressure; Δm decreases from 2.3 to 1.8 pC/m, which corresponds to 0.72–0.56 D/nm².

By evaluating ∂C_N/∂R = 0 from Eq. 8, we can determine the most probable domain size R_max = R_o/(1 - (ln(C_M)/β)). As can be seen from Figs. 2 and 3, R_max ranges from 0.8–1.5 μm, which is much less than R_o, which ranges from 2.3-6.4 μm. The mixing entropy decreases the most probable size considerably from the optimal size predicted by considering the energy alone (Eq. 2); in fact, there are very few domains with radii equal to or larger than R_o. This entropic effect on domain size has important implications for the shape stability of monolayer domains. The radius R_n at which isolated circular shapes become unstable with respect to a shape with n-fold symmetry is predicted to be R_n = e^(Z_n-3)·R_o (28). For the transition to elliptical domains of 2-fold (n = 2) symmetry, Z_n = 10/3, or R₂ ≈ 1.4R_o. From the histograms, essentially all the domains are smaller than R₂, and so are stable against elliptical distortions, which is why we see only circular domains in Fig. 1, even though the measured line tensions are quite small.

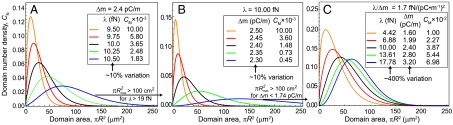
Fig. 4A shows the theoretical distributions in which λ was varied at constant Δm; Fig. 4B shows the distribution in which Δm was varied at constant λ (C_M was adjusted to normalize the area under the curves). Small increases in the line tension at constant dipole density greatly increase both the polydispersity and the average size of the domains. Conversely, small changes in the dipole density difference decrease both the polydispersity and average size of the domains at constant line tension. However, if both λ and Δm are increased at constant λ/Δm² (constant R_o) as shown in Fig. 4C, the polydispersity and average size also increase, but much less than varying either parameter independently.

Fig. 4.

Theoretical domain size distribution curves at 25 °C generated using Eqs. 7, 8. showing trends on (A) Varying λ at fixed Δm.(B) Varying Δm at fixed λ. (C) Varying both λ and Δm at constant λ/Δm².

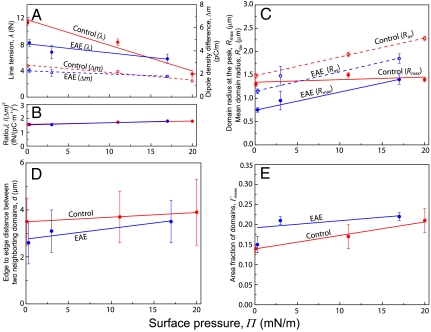
Fig. 5A summarizes the measured values of λ and Δm for the control and EAE monolayers as a function of surface pressure; Fig. 5B shows that the ratio, λ/Δm², increases slowly with surface pressure even though the two parameters change significantly. As a result, the most probable domain size changes little with surface pressure, the major change is in the polydispersity of the domains (Fig. 5C). The small differences in λ and Δm between control and EAE monolayers are magnified in their effect on the area fraction of L_o domains. EAE domains have a higher measured area fraction 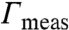(Fig. 5E), although R_max, the most probable domain radius is larger for the control monolayers than the EAE monolayers (Fig. 5C). However, the control domains are, on the average, farther apart from each other (Fig. 5D).

Fig. 5.

(A) Measured values of λ (solid lines) and Δm (dotted lines) for the control (red) and EAE (blue) monolayers as a function of surface pressure. (B) The ratio, λ/Δm², is roughly constant over the range of surface pressure. (C) R_max (solid lines), the most probable domain radius and R_av (dotted lines), the average domain radius as a function of surface pressure. Control domains are larger than the EAE domains at all surface pressures. (D) The average distance between domains is greater in control than EAE monolayers. (E) EAE domains have higher measured area fraction 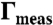than the control monolayers.

Discussion and Conclusions

A yet unanswered question in monolayer morphology is if the distribution of domains at phase coexistence is at equilibrium or determined by the nucleation and growth kinetics; which in turn depend on the values of λ and Δm. In myelin and simple monolayers that contain cholesterol, saturated and unsaturated phospholipids, an important driving force for phase separation is the preference for cholesterol to intercalate into all trans saturated lipid alkyl chains, as opposed to saturated chains with gauche conformers or kinked unsaturated chains. In the L_o phase, the reduced molecular tilt and gauche conformer fraction lead to an increase in monolayer thickness relative to the L_d phase. The resulting hydrophobic mismatch at L_o-L_d domain borders leads to a line tension, λ (see Fig. 6).

An approximate equation for λ at a domain boundary separating two fluid regions of equilibrium thickness l_o and l_d and molecular headgroup area a_opt (a_o and a_d) (Fig. 6) may be obtained in terms of the hydrophobic mismatch Δl ≈ (l_o - l_d), the strained area a, and corresponding energy needed to deform the lipids in the boundary region, γ(a - a_opt)²/a (33). Allowing a smooth transition in thickness at the domain boundary, the line tension is given by the following (See SI Text for derivation):

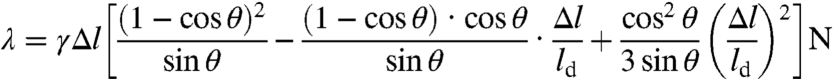[9]

in which γ( ≈ 25 mJ/m²) is the interfacial tension of the hydrocarbon-air interface, and θ is the slope of the boundary (see Fig. 6). For reasonable values of Δl, λ can vary from pN (pico-Newton) for θ = π/2 (step interfaces) to fN for the optimal θ [See SI Text; a similar derivation is presented in (36)]. In addition to variations in the molecular conformations, certain lipids in multicomponent mixtures can act as line-active components to reduce the line tension by adsorbing at the domain boundaries and bridging the differences in thickness (37, 38). Hence, it may be that for the DMPC-CHOL mixture, the domain boundaries are sharp and the line tension is of order pN, while for the more complex myelin mixtures with large fractions of unsaturated lipids of varied chain length and composition, the domain boundaries go smoothly from one phase to the other while being decorated with the appropriate line-active molecules, thereby reducing the line tension to fN.

The difference in composition and packing density between the two phases also causes a difference in the average dipole density, Δm, which leads to an electrostatic repulsion within the domains and between domains (27). The average areas per molecule in the ordered or disordered phases are a_o or a_d (of order 50 Å²), with (zwitterionic) charges ± Q separated by a distance δ_o or δ_d (of order 0.5 nm), which leads to a dipole density difference (see Fig. 6). The effects of surface pressure on λ and Δm can be rationalized as follows: λ is proportional to the difference in the hydrophobic mismatch as given by Eq. 9, and Δm is proportional to the difference in the hydrophilic (headgroup) lengths, and inversely to their areas. Because the L_o monolayer is more ordered than the more fluid L_d monolayer, lateral compression is expected to have a larger impact on the L_d monolayer. Therefore, increasing the pressure should result in a larger decrease in a_d, and larger increases in δ_d and l_d, making both λ and Δm smaller, which explain the observed trends shown in Fig. 5A. Interestingly, the ratios λ/Δm² remained essentially constant with increasing surface pressure, and are almost the same for both the control and EAE monolayers (see Fig. 5B).

As mentioned in the introduction, domains in membranes are known to play crucial roles in many aspects and most of these properties feature in demyelinating diseases (4, 5, 10). Our results show that the domain size distribution in model myelin cytoplamsic monolayers suggests that the domains are in equilibrium with values of line tension considerably smaller than simple binary mixtures. While it is too early to generalize these results to in vivo conditions (only monolayers rather than bilayers were studied, and no proteins such as the peripheral cytoplasmic myelin basic protein, MBP, were involved), the existence of domains in myelin membranes that are highly sensitive to pressure, composition, and—from our theoretical analysis—lipid chain length, fluidity, and headgroup charge or dipole moment suggests a new paradigm linking subtle changes in the molecular-level organization/structure of membranes to overall structure (for example, the swelling of the cytoplasmic and/or extracellular spacings/gaps in myelin leading to vacuolization and vesiculation), and biological performance (for example, as effective transmitters of electric nerve signals, which is the main function of the myelin sheath).