SSAHA: A Fast Search Method for Large DNA Databases

Abstract

We describe an algorithm, SSAHA (Sequence Search and Alignment by Hashing Algorithm), for performing fast searches on databases containing multiple gigabases of DNA. Sequences in the database are preprocessed by breaking them into consecutive k-tuples of k contiguous bases and then using a hash table to store the position of each occurrence of each k-tuple. Searching for a query sequence in the database is done by obtaining from the hash table the “hits” for each k-tuple in the query sequence and then performing a sort on the results. We discuss the effect of the tuple length k on the search speed, memory usage, and sensitivity of the algorithm and present the results of computational experiments which show that SSAHA can be three to four orders of magnitude faster than BLAST or FASTA, while requiring less memory than suffix tree methods. The SSAHA algorithm is used for high-throughput single nucleotide polymorphism (SNP) detection and very large scale sequence assembly. Also, it provides Web-based sequence search facilities for Ensembl projects.

There is an extensive literature on the topic of DNA and protein sequence search and alignment, but as the quantity of available sequence information continues to multiply the problem remains very much relevant today. The pre-eminent class of methods for aligning two sequences are those based on dynamic programming, a technique first brought to bear on the problem by Needleman and Wunsch (1970) and subject to many later refinements, most notably by Smith and Waterman (1981).

The need for greater speed, especially when searching for matches within a large database of subject sequences, has led to the development of other software tools such as FASTA (Lipman and Pearson 1985; Pearson and Lipman 1988), BLAST (Altschul et al. 1990, 1997) and Cross_match (P. Green, unpubl.; see http://www.phrap.com). In each case a preliminary word-based search stage identifies likely candidate matches, which are then extended to full alignments.

In recent years, suffix tree algorithms have been gaining favor as methods for sequence search; an extensive treatment of the subject is given by Gusfield (1997). Delcher and co-workers (1999) describe a suffix-tree-based tool that is capable of aligning genome length sequences and also locating SNPs, large inserts, significant repeats, tandem repeats, and reversals. Suffix tree methods are attractive because of their potentially fast search speed, but they can devour a large amount of memory: Delcher et al. quote an upper bound of 37 bytes per base of the subject sequence for their suffix tree implementation. For a sequence comparable in size to the human genome (around three gigabases), one would require a machine with an exceptionally large amount of memory (at least by current standards) to fit the associated suffix tree entirely into RAM.

In this paper we describe a DNA sequence search algorithm that is based on organizing the DNA database into a hash table data structure. Other hash table based search methods have been described by Waterman (1995, Chapter 8) and by Miller et al. (1999), while Benson (1999) has developed a tool that uses hashing to detect tandem repeats in sequences. Our algorithm, which we have called SSAHA (Sequence Search and Alignment by Hashing Algorithm), exploits the fact that machines are now available with sufficient RAM to allow us to store a hash table that can describe a database containing multiple gigabases of DNA. This enables us to perform very rapid searches on databases the size of the human genome and larger.

We analyze the performance of the SSAHA algorithm with respect to search speed, memory usage, and sensitivity, and give the results of computational experiments that show that our algorithm can be three to four orders of magnitude faster than BLAST and FASTA.

METHODS

Definitions and Notation

We consider the problem of searching for exact or partial occurrences of a query sequence Q within a database of subject sequences D = {S₁, S₂, … ,S_d}. Each sequence in D is labeled with an integer i, to which we refer as its index. We use the term k-tuple to denote a contiguous sequence of DNA bases that is k bases long. A sequence S of DNA that is n bases long will contain (n−k+1) overlapping k-tuples. The offset of a k-tuple within S is the position of its first base with respect to the first base of S. We use the letter j to denote offsets and use the notation w_j(S) to denote the k-tuple of S that has offset j. Thus, it is clear that the position within D of each occurrence of each k-tuple may be described by an (i, j) pair. Each of the four possible nucleotides are encoded as two binary digits as follows:

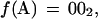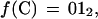1

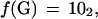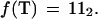Using this encoding, any k-tuple w = b₁b₂ … b_k may be represented uniquely by a 2k bit integer

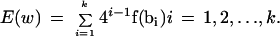2

Constructing the Hash Table

The first stage of our algorithm is to convert D into a hash table. The hash table is stored in memory as two data structures, a list of positions L and an array A of pointers into L. There are 4^k pointers in A, one for each of the 4^k possible k-tuples. The pointer at position E(w) of A points to the entry of L that describes the position of the first occurrence of the k-tuple w in the subject database D. We can obtain the positions of all occurrences of w in D by traversing L from that point until we reach the location pointed to by the pointer that is at position E(w)+1 of A.

The hash table is constructed by making two passes through the subject data. On each pass, we consider only non-overlapping k-tuples in the subject sequences; that is, for the subject sequence S_i we consider the k-tuples w₀(S_i), w_k(S_i), w_2k(S_i), and so on. On the first pass we count all non-overlapping occurrences in D of each of the 4^k possible k-tuples. From this, we can calculate the pointer positions for A and allocate the correct amount of memory for L. At this point, we may decide to ignore all words that have a frequency of occurrence that exceeds a cutoff threshold N; as well as reducing the size of the hash table, this acts as an effective filter for spurious matches attributable to repetitive DNA (see below). Excluding these words from the hash table is a suitable approach when the hash table is created for a one-off search. However, for many applications (such as the Ensembl SSAHA server) it is more flexible to retain all occurrences of all words and implement the cutoff threshold N in software. It is simple to do this by returning only the hits for words for which the difference between E(w) and E(w)+1 does not exceed N. Finally, once we have constructed A, we make a second pass through the data, using A to place the position information into L at the correct positions.

The two-bits-per-base representation we are using is compact and efficient to process, but has the disadvantage that there is no way to encode any characters apart from the four valid bases. Therefore, during the process of creating a hash table from a data source (such as an ASCII file in FASTA format), we are faced with choosing between ignoring any unrecognized characters completely and translating them to one of the four valid bases. The latter option has the advantage that the positions of matches found correspond exactly to positions in the original sequence data. We choose to treat unrecognized characters as if they were “A”s, which has the further advantage that any long stretches of unrecognized characters will be translated to the k-tuple containing all As. Often, this is already the commonest word in the database and so will be excluded from matching by the cutoff threshold N.

We illustrate the method with a simple example. Suppose k = 2 and our database D contains just the following three sequences:

  S₁ = GTGACGTCACTCTGAGGATCCCCTGGGTGTGG, S₂ = GTCAACTGCAACATGAGGAACATCGACAGGCCCAAGGTCTTCCT,S₃ = GGATCCCCTGTCCTCTCTGTCACATA.

The rows of Table 1 contain the lists of positions for each of the 16 possible 2-tuples. Taken together, moving from left to right and then from top to bottom in the table, the concatenation of these lists forms L.

Table 1.

A 2-tuple Hash Table for S1, S2, and S3

w	E(w)	Positions
AA	0	(2, 19)
AC	1	(1, 9)	(2, 5)	(2, 11)
AG	2	(1, 15)	(2, 35)
AT	3	(2, 13)	(3, 3)
CA	4	(2, 3)	(2, 9)	(2, 21)	(2, 27)	(2, 33)	(3, 21)	(3, 23)
CC	5	(1, 21)	(2, 31)	(3, 5)	(3, 7)
CG	6	(1, 5)
CT	7	(1, 23)	(2, 39)	(2, 43)	(3, 13)	(3, 15)	(3, 17)
GA	8	(1, 3)	(1, 17)	(2, 15)	(2, 25)
GC	9
GG	10	(1, 25)	(1, 31)	(2, 17)	(2, 29)	(3, 1)
GT	11	(1, 1)	(1, 27)	(1, 29)	(2, 1)	(2, 37)	(3, 19)
TA	12	(3, 25)
TC	13	(1, 7)	(1, 11)	(1, 19)	(2, 23)	(2, 41)	(3, 11)
TG	14	(1, 13)	(2, 7)	(3, 9)
TT	15

Sequence Search

Now we describe how to use the hash table to search for occurrences of a query sequence Q within the subject database. We proceed base-by-base along Q from base 0 to base n−k, in which n is the length of Q.

At base t, we obtain the list of r positions of the occurrences of the k-tuple w_t(Q). These are pointed to by entry E(w_t(Q)) of A. We take this list of positions

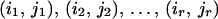and from this we compute a list of hits

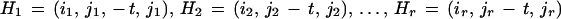which are added to a master list M of hits that we accumulate as t runs from 0 to n−k. From leftmost to rightmost, the elements of a hit are referred to as the index, shift, and offset.

Once M has been completed it is sorted, first by index and then by shift. The final part of the search process is scanning through M looking for “runs” of hits for which the index and shift are identical. Each such hit represents a run of k bases that are consistent with a particular alignment between the query sequence and a particular subject sequence. We can make some allowance for insertions/deletions by permitting the shift between consecutive hits in a run to differ by a small number of bases. If we sort the run of hits by offset, we can determine regions of exact match between the two sequences and we can create gapped matches from these by joining together exact matching regions that are sufficiently close to one another.

As an example, we search for the query sequence Q = TGCAACAT within the sequences that we used to form Table 1. In Table 2, Column 3 shows the positions of occurrence in D for each 2-tuple in Q; the corresponding hits are shown in Column 4. After sorting, we obtain the list M shown on the right. The run of four hits highlighted in bold shows that there is a match between Q and S₂, starting at the seventh base of S₂ and continuing for eight bases.

Table 2.

List of Matches for the Query Sequence

t	wt(Q)	Positions	H	M
0	TG	(1, 13)	(1, 13, 13)	(1, 5, 9)
		(2, 7)	(2, 7, 7)	(1, 13, 13)
		(3, 9)	(3, 9, 9)	(2, −2, 3)
1	GC			(2, 1, 3)
2	CA	(2, 3)	(2, 1, 3)	(2, 1, 5)
		(2, 9)	(2, 7, 9)	(2, 4, 9)
		(2, 21)	(2, 19, 21)	(2, 7, 7)
		(2, 27)	(2, 25, 27)	(2, 7, 9)
		(2, 33)	(2, 31, 33)	(2, 7, 11)
		(3, 21)	(3, 19, 21)	(2, 7, 13)
		(3, 23)	(3, 21, 23)	(2, 16, 19)
3	AA	(2, 19)	(2, 16, 19)	(2, 16, 21)
4	AC	(1, 9)	(1, 5, 9)	(2, 19, 21)
		(2, 5)	(2, 1, 5)	(2, 22, 27)
		(2, 11)	(2, 7, 11)	(2, 25, 27)
5	CA	(2, 3)	(2, −2, 3)	(2, 28, 33)
		(2, 9)	(2, 4, 9)	(2, 31, 33)
		(2, 21)	(2, 16, 21)	(3, −3, 3)
		(2, 27)	(2, 22, 27)	(3, 9, 9)
		(2, 33)	(2, 28, 33)	(3, 16, 21)
		(3, 21)	(3, 16, 21)	(3, 18, 23)
		(3, 23)	(3, 18, 23)	(3, 19, 21)
6	AT	(2, 13)	(2, 7, 13)	(3, 21, 23)
		(3, 3)	(3, −3, 3)

Finally, we note that the method described here will find matches only in the forward direction. To find matches in the reverse direction, we simply take the reverse complement of Q and repeat the procedure.

RESULTS AND DISCUSSION

We have produced a software implementation of the SSAHA algorithm; all the computational results described in this section were obtained by running this software on a 500 MHz Compaq EV6 processor with 16 Gb of RAM. As subject data we used the GoldenPath final draft assembly of the July 17, 2000 freeze of the human genome data (International Human Genome Sequencing Consortium 2001; data downloadable from http://www.genome.ucsc.edu), comprising ∼2.7 gigabases of DNA split into 292,016 sequences. For query sequences, we used a set of 177 sequences containing 104,755 bases in total.

Storage Requirements

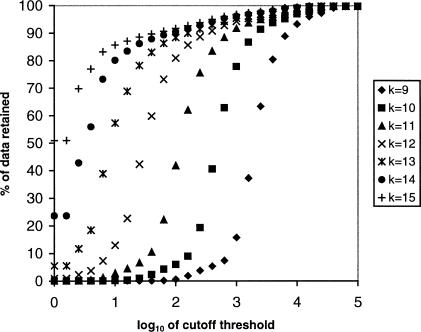
Storage of the hash table requires 4^k+1+8W bytes of RAM in all, in which the first and second terms account for the memory requirements of A and L, respectively, and W is the number of k-tuples in the database. Conceptually, the elements of A are pointers, but our implementation uses 32-bit unsigned integers for this purpose because, for a 64-bit architecture such as the one we are using, this halves the size of A while retaining the ability to handle a subject database of up to k2³² bases in size, more than enough for our present purposes. W will at most be equal to the total number of bases in the subject database divided by k. We can cause W to be considerably less than this if we choose not to store words whose frequency of occurrence exceeds the cutoff threshold N. Figure 1 shows the percentage of k-tuples retained when a hash table is created from our test database using different values of k and N. However, we note that retaining all occurrences of all k-tuples gives us the potential to query the same data multiple times, using different values of N to adjust the sensitivity.

Figure 1.

Percentage of data remaining as the cutoff threshold N is varied, for different values of the word size k.

Clearly, we also require storage for the query sequences, although this can be kept to a minimum by loading in query sequences from disk in batches and using 2-bits-per-base encoding. In practice, we have found housekeeping functions, temporary storage, and the like add ∼10%–20% to the total RAM usage.

Search Speed

The CPU time required for a search may be divided into two portions, the time T_hash required to generate the hash table and the time T_search required for the search itself. Table 3 shows T_hash and T_search for the data described at the beginning of this section, in which k varies from 10 to 15 and the cutoff threshold N is set so that either 90, 95, or 100% of the k-tuples are retained. T_search is the time taken to search for all occurrences of each of the 177 query sequences in both the forward and reverse directions.

Table 3.

SSAHA Searches for Different Values of k

k	90%		95%		100%
Thash	Tsearch	Thash	Tsearch	Thash	Tsearch
10	824.0s	102.5s	842.4s	128.8s	868.5s	389.5s
11	798.3s	26.3s	810.5s	36.1s	808.8s	199.1s
12	952.2s	7.3s	969.9s	11.0s	961.2s	119.0s
13	850.8s	2.2s	859.1s	4.5s	851.4s	78.7s
14	914.1s	0.9s	932.0s	2.5s	927.1s	51.6s
15	996.0s	0.1s	1015.5s	1.7s	999.2s	35.4s

The first thing to note is that the value of T_hash actually is not that important, because for a given set of subject data the hash table needs to be generated only once. After creation, it can be saved to disk for future use or just retained in RAM for server applications. Having said this, even in the worst case T_hash is never more than twice the time required to format the same data for BLAST searches.

For the search itself, the CPU time is dominated by the sorting of the list of matches M. If we make the simplistic assumption that each of the four possible nucleotides has an equal probability of occurrence at each base of D, then the expected number of occurrences of each k-tuple is given by W/4^k (for m = 3 Gb and k = 12, this evaluates to just under 15). Hence, for a query sequence of length n we would expect M to contain nW/4^k entries. A comparison sort algorithm such as Quicksort can, on average, sort a list of this length in O((nW/4^k)log(nW/4^k)) time. We refer the reader to Knuth's (1998) definitive treatise on sorting algorithms. Thus, for a given hash table (that is, for given values of W and k), we might expect T_search to be O(nlog(n)) with respect to the query length n. We tested this by extracting from the subject database a contig of around 40 kb, then truncating this contig to various lengths and measuring the time taken to run the resulting sequences as queries. Using Quicksort, the variation in search speed was found to be closer to linear than to O(nlog(n)). We speculate that this pleasing behavior is because the algorithm is such that the hits happen to come out of the hash table in an order that ensures Quicksort's worst-case behavior is unlikely to occur. Algorithms such as radix sort (Knuth 1998, Sec. 5.2.5) perform a guaranteed linear time sort on a collection of integers having a finite number of digits (basically by carrying out one pass per digit). We experimented briefly with such methods, but did not find that they conferred a significant improvement in the search speed.

Now we consider how we might optimize the speed of the algorithm by varying k and W. Note that W must be altered indirectly by varying the cutoff threshold N. When generating the hash table, it is convenient to compute a series of values for N that cause different percentages of the k-tuples to be retained. From our formula for the expected size of M, we might expect T_search to be roughly proportional to W and to drop off rapidly with increasing k. The latter effect is observed readily in Table 3, but we also see that decreasing W has a far greater effect on the search speed than might be expected from the simple analysis we gave above; at k = 15 a 10% reduction in W causes the search speed to increase by a factor of >100! This is because the human genome is, of course, far from random; in particular, it contains large stretches of repetitive DNA. In our test data set, some k-tuples occur hundreds of thousands of times more frequently than others and so excluding highly repetitive k-tuples has a disproportionate effect on the size of M and hence on T_search. In the first instance, typically we would search a database of human DNA using a value of N that caused 10% of the k-tuples to be ignored in the search process. Empirically, we have found this level of rejection improves the search speed greatly without noticeable detriment to the sensitivity. However, the search time is sufficiently small that it is not too inconvenient to re-run the search with a larger value of N if we wish to verify that our chosen level of rejection has not caused us to miss anything.

Table 3 shows that, for the parameters we tried, optimum search speed was achieved when k was set to 14 or 15 and N was set to retain 90–95% of the k-tuples; the query was processed in around 2 sec, or less. By way of comparison, BLAST took >10000 CPU sec on the same machine to carry out the same search and FASTA3 took >8700 CPU sec. For a fairer comparison, BLAST was run with the “-b 0” option enabled, which suppresses the output of full alignments. Similarly, FASTA3 was run with the “-H” option enabled, suppressing the output of histograms. For BLAST and MegaBLAST, pre-computed formatted databases were used. We also tried MegaBLAST (Zhang et al. 2000), which took between 600 and 900 sec, depending on the level of output data specified on the command line.

SSAHA is fast for large databases because the database is hashed; thus, search time is independent of the database size as long as k is selected to keep W/4^k small. Both FASTA and BLAST hash the query and scan the database; therefore, the search time is related directly to the database size. The tradeoff, of course, is that SSAHA requires large amounts of RAM to keep A and L in memory.

Search Sensitivity

It is easy to see that the SSAHA algorithm will under no circumstances detect a match of less than k consecutive matching base pairs between query and subject, and almost as easy to see that, in fact, we require 2k−1 consecutive matching bases to guarantee that the algorithm will register a hit at some point in the matching region. In comparison, with their default settings FASTA, BLAST, and MegaBLAST require at least 6, 12, and 30 base pairs, respectively, to register a match.

However, there are various modifications that can be made to SSAHA to increase sensitivity. The search code can be adapted to allow one substitution between k-tuples at the expense of a roughly 10-fold increase in the CPU time required for a search. By modifying the hash table generation code so that k-tuples are hashed base-by-base, we can ensure that any run of k consecutive matching bases will be picked up by the algorithm, at a cost of a k-fold increase in CPU time and in the size of the hit list L for a given k.

Software Implementation and Applications

The software used to obtain the results in this paper takes the form of a library that forms a “core” around which applications can be built. Because the algorithm works by concatenating exact matches between k-tuples, it is clear that for the software to register a match between two regions we must be reasonably certain that stretches of k or more consecutive matching bases will occur at regular intervals. This makes the software better suited to applications requiring “almost exact” matches than to situations that demand the detection of more distant homology. However, there are many useful applications that meet this criteria. Applications currently under development from the SSAHA library include the detection of overlapping reads as part of shotgun sequence assembly and the determination of contig order and orientation. The Ensembl project (see http://www.ensembl.org) features a Web server that allows users to conduct SSAHA searches of both the latest GoldenPath assembly of the human genome and the Ensembl Trace Repository (see http://trace.ensembl.org). At the time of writing, these datasets contain ∼3.2 gigabases and 11 gigabases of sequence data, respectively.

In addition, an earlier implementation of the SSAHA algorithm has been adapted successfully to the detection of single nucleotide polymorphisms; in fact, this tool was used to detect over one million of the SNPs now registered at the dbSNP database (International SNP Map Working Group, 2001; see http://www.ncbi.nlm.nih.gov/SNP/). Two types of SNPs were detected using ssahaSNP: (1) SNPs detected from random human genomic reads, as was the case for The SNP Consortium (TSC) project (http://snp.cshl.org/), and (2) genomic clone overlap SNPs registered at the dbSNP Web site (query by submitter SC_JCM).

To detect SNPs, ssahaSNP builds a SSAHA hash table of the human genome using k = 14 and a cutoff threshold of 7, which causes ∼2% of the genome to be excluded from matching. For random human genomic reads, the high quality region of the base sequence from each read is used as the query. If an SSAHA match is found which extends over nearly the full length of the high quality region, and if the read does not match to more than ten other places in the genome, then a full base-by-base alignment is made between the read and the localized genomic sequence(s). High quality base discrepancies using the Neighborhood Quality Standard (Altshuler et al. 2000; International SNP Map Working Group 2001) are reported as SNPs. This program can process reads at a rate of ∼200 per second against the human genome. For genomic overlap SNPs, the program generates pseudo-reads from the human genomic sequence by chopping up the genome into 500 bp pieces every 250 bp. These pseudo-reads are processed exactly like the random sequencing reads described above, except we ignore the alignment of the read back to the location from which it was derived. The latest run of this program on a 16-May-2001 freeze of the human genomic clone sequence (4.9Gbp) took 26 h to run (on one EV6 CPU and 15Gb of memory of a Compaq Alpha ES40) and detected about one million SNPs.

The SSAHA library was developed for Compaq DEC Alphas, but has been ported successfully to several other platforms (see http://www.sanger.ac.uk/Software/analysis/SSAHA/ for the latest information).