Setting priors and enforcing constraints on matches for nonlinear registration of meshes

Abstract

We show that a simple probabilistic modelling of the registration problem for surfaces allows to solve it by using standard clustering techniques. In this framework, point-to-point correspondences are hypothesized between the two free-form surfaces, and we show how to specify priors and to enforce global constraints on these matches with only minor changes to the optimisation algorithm. The purpose of these two modifications is to increase its capture range and to obtain more realistic geometrical transformations between the surfaces. We conclude with some validation experiments and results on synthetic and real data.

1. Introduction

In medical image analysis, nonlinear registration is a key tool to study the normal and abnormal anatomy of body structures. It allows to spatially normalise different subjects in a common template, to build the average anatomy in a population and to assess the variance about this average, and ultimately to perform group studies via statistical analyses. Many methods have been dedicated to deal with grey level volumes directly, while others have been devised to tackle surfaces representing anatomical structures (e.g. after segmentation from MRI or CT) [1]. The last approach allows a more focused analysis of structures of interest, and is the topic of our paper. In Section 2 we show that a simple probabilistic modelling of the registration problem allows to solve it by using standard clustering techniques. In this framework, point-to-point correspondences are hypothesized between the two free-form surfaces, and we show how to specify priors (Section 3) and to enforce global constraints (Section 4) on these matches with only minor changes to the optimisation algorithm. This extends our previous work on the same problem [2]. The purpose of these two modifications is to increase its capture range and to obtain more realistic geometrical transformations between the surfaces. We conclude with some validation experiments and results on synthetic and real data (Section 5).

2. Surface Registration as a Clustering Problem

The problem of interest in this paper is to find the transformation T best superposing two free-form surfaces X and Y (represented by point clouds or meshes). A convenient probabilistic viewpoint on this classical problem is to consider the surface Y as a noised version of T (X). If we note Y = (y_j)_{j=1… card(Y)} and X = (x_k)_{k=1… card(X)}, and if we hypothesize an isotropic Gaussian noise, a simple way to formulate this viewpoint is to assume that each sample y_j has been drawn independently from any one of card (X) possible 3-variate normal distributions with means T (x_k) and covariance matrices σ²I (with σ unknown).

This way, the registration problem becomes a clustering problem, whose challenge is i) to find the label of each point y_j, i.e. the one out of card(X) possible distributions from which y_j has been drawn, and ii) to estimate the parameters of these card(X) distributions. The connection between registration and clustering becomes clear when one realises that i) actually amounts to match each point y_j in Y with a point x_k in X, while ii) simply consists in computing T given these matches. This viewpoint is extremely fruitful, as it allows one to refer to classical clustering techniques and especially the maximum likelihood principle to solve the registration problem. Two different paradigms have been especially followed in this context [3]. Let us introduce some notations first:

$$\begin{array}{l}\forall k\in 1\dots \text{card}(X),p_k(.;T)=\mathcal{N}(T(x_k),{\sigma }^{2}I)\\ \forall j\in 1\dots \text{card}(Y),\forall k\in 1\dots \text{card}(X),z_{jk}=1\text{if}{y}_j\text{comes}\text{from}{p}_k(.;T),0\text{else}\end{array}$$

In the Classification ML (CML) approach, one tries to find the indicator variables z_jk and the parameter T so as to maximise the criterion CL [4]:

$$CL=\prod _{y_j\in Y}\prod _{x_k\in X}{[p_k(y_j;T)]}^{z_{jk}}$$ (1)

The problem is typically solved by the Classification EM (CEM) algorithm [5], which can be shown to find an at least local maximum of the criterion CL and proceeds as follows, in an iterative way, starting from an initial value T̃:

$$\begin{array}{l}\mathbf{EC}-\mathbf{step}:\forall j,{\stackrel{\sim }{z}}_{jk}=1\text{if}k\text{maximises}{p}_k(y_j;\stackrel{\sim }{T}),0\text{else}\\ \mathbf{M}-\mathbf{step}:\stackrel{\sim }{T}=arg{min}_T{\sum }_{jk}{\stackrel{\sim }{z}}_{jk}{\left|\right|y_j-T(x_k)\left|\right|}^2\end{array}$$

In other words, the Expectation-Classification (EC) step consists in matching each point y_j of Y with the closest point in T̃(X), while the Maximisation (M) step consists in computing the transformation best superposing these pairs of matched points. In case T is a rigid-body transformation, this is nothing else than the popular ICP algorithm [6].

In the ML approach, the indicator values z_jk are no longer considered as unknown quantities to estimate, but rather as hidden/unobservable variables of the problem. This is actually a drastic and fundamental change of viewpoint, as the focus is no longer on assigning each y_j to one of the distributions p_k but rather on estimating the parameters of the Gaussian mixture made of these distributions. If we involve priors π_jk on the indicator variables (∀j, k, 0 < π_jk < 1, and ∀j, Σ_k π_jk = 1), the likelihood then simply writes [7]:

$$L=\prod _{y_j\in Y}\sum _{x_k\in X}{\pi }_{jk}{p}_k(y_j;T)$$ (2)

In essence, the prior π_jk conveys the probability that the point y_j comes from the distribution p_k without knowing anything else. The criterion L can be maximised by using the popular EM algorithm, which converges to an at least local maximum of the likelihood [8]. If we consider the priors π_jk as known beforehand and if we introduce the notation γ_jk as the posterior probability of the hidden indicator variable z_jk to be equal to 1, the EM algorithm writes:

$$\begin{array}{l}\mathbf{E}-\mathbf{step}:{\stackrel{\sim }{\gamma }}_{jk}=\frac{{\pi }_{jk}exp[-{\left|\right|y_j-\stackrel{\sim }{T}(x_k)\left|\right|}^2/(2{\sigma }^2)]}{{\sum }_i{\pi }_{ji}exp[-{\left|\right|y_j-\stackrel{\sim }{T}(x_i)\left|\right|}^2/(2{\sigma }^2)]}\\ \mathbf{M}-\mathbf{step}:\stackrel{\sim }{T}=arg{min}_T{\sum }_{jk}{\stackrel{\sim }{\gamma }}_{jk}{\left|\right|y_j-T(x_k)\left|\right|}^2\end{array}$$

To our knowledge, Granger & Pennec [9] were the first to formulate the problem this way, and they proposed the so-called EM-ICP as a simplified version of the previous algorithm for rigid-body registration, where the priors π_jk were considered as uniform. They noted that the parameter σ, which is not estimated in this framework, acts as a scale parameter, and that it can be given an initial value and decreased throughout the iterations for improved performances.

Interpretation & Extensions

Intuitively, the EM approach is a fuzzy version of the CEM. It appears clearly from the iterative formulas of both algorithms that the classification likelihood is an “all-or-nothing” version of the likelihood, leading to a “bumpier” and harder-to-maximise criterion, something that is well known by those who are familiar with the ICP algorithm. Note that the ML formulation and the EM algorithm lead to the same iterative formulas that would have resulted from the addition of a barrier function on the indicator variables in the ICP criterion [10]. This formalism is not limited to rigid-body transformations, and can be easily used for any T, the challenge being to choose T such that the M-step remains tractable. In particular, the ML estimation can be easily turned into a MAP problem with only slight modifications to the optimisation scheme, as shown by Green [11]. This allows to view T as a random variable, on which priors (acting as regularisers on T) can be easily specified. Different choices have been proposed for T and associated priors in this context, such as the thin plate splines [10] or locally affine transformations [12]. If p(T) is a prior of the form p(T) ∝ exp(−αR(T)) then the optimal transformation can be found using the MAP principle (also termed penalised ML) and the EM algorithm with only a slight modification to the M-step (addition of αR(T)).

3. Setting Priors on Matches

3.1. Why Using Priors on Matches?

Most works in this context have been focused on designing transformations and related priors allowing to i) compute realistic deformations between the two surfaces and ii) keep the M-step tractable. Much little has been done to enforce similar constraints on the matches (E-step). Dropping the priors π_jk, as done in the ICP of Besl & McKay or the EM-ICP of Granger & Pennec amounts to say that the posteriors γ_jk are only estimated using the spatial distance between the points y_j and T (x_k) (E-step). This is unsatisfactory, for two reasons. First, this distance is highly conditioned by the previous estimation of T, which in turn depends on the previous estimation of γ_jk and so on. This chicken-and-egg problem limits the capture range of the algorithm, which is likely to converge to a bad solution if no good initial T is given. Second, in medical imaging it is difficult to design a physical model T capturing the expected deformation between two structures. Thus the global maximiser of the ML criterion is likely not to be realistic. By specifying relevant priors π_jk, we provide a way to partially alleviate these two limitations. First, it allows to introduce additional information on matches independent of the transformation and thus to compute reliable posteriors even for a bad initial estimate of T. Second, it allows to modify the criterion in a way that its global maximiser is a more realistic transformation.

3.2. Building Priors on Matches

In this section we show how to design the priors π_jk to encode very heterogeneous types of a priori knowledge on the matches, such as “two points with similar curvatures are more likely to be matched than others” as well as knowledge of the labels of structures in the objects to be matched (e.g. gyri/sulci in cortical registration). In practice, we choose to design π = (π_jk) such that π_jk ∝ exp(−βc(y_j, x_k)) where c: X × Y → IR⁺ conveys the cost of matching points y_j and x_k, independently of T. The parameter β > 0 weighs the influence of π_jk over ||y_j − T (x_k)|| during the E-step. Depending on the information to encode (continuous value or label), we propose two approaches to build c.

Using descriptors

c can be computed via the comparison between continuous values (or vectors) d(x) describing the surface around the considered points. To account for potential inaccuracies on d(.), we define the measure as: c^d(y_j, x_k) = 0 if ||d(y_j) − d(x_k)|| < τ; = penalty > 0 else. To the best of our knowledge, there exists no descriptor invariant to any nonlinear transformation. However, one can use some descriptors invariant to more constrained transformations (Fig. 1, left):

Fig. 1.

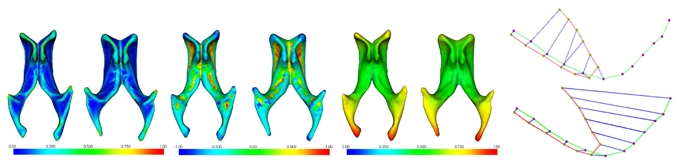
Left: Mapping of descriptor values: From left to right: curvedness, shape index and total geodesic distance on two lateral ventricles. Homologous anatomical landmarks yield qualitatively the same descriptor values. Right: point-based matching (top) vs line-based matching performed by our algorithm (bottom).

• the shape index sh(x) [13] that describes the local shape irrespective of the scale and that is invariant to similarities

• the curvedness cu(x) [13] that specifies the amount of curvature and that is invariant to rigid-body transformations

• the (normalised) total geodesic distance tgd(x) [14] that is invariant to isometries in the shape space (including non-elastic deformations).

Using labels

c can be computed via the comparison between labels on points (cortical sulci/gyri). We define: c(y_j, x_k) = 0 if points j and k have compatible labels; = penalty > 0 else. In practice, we extract the crest lines from both meshes as they constitute salient features. Each point is given a label depending on whether it belongs to a crest line or not. Then, we define c_crest(y_j, x_k) = 0 if y_j and x_k have the same label and c(y_j, x_k) = penalty else.

Mixing the two approaches

In practice, we choose to mix the previous four sources of information to build the function c: c(y_j, x_k) = a₁c^sh(y_j, x_k) + a₂c^cu(y_j, x_k)+a₃c^tgd(y_j, x_k)+a₄c_crest(y_j, x_k) with a₁+a₂+a₃+a₄ = 1. Parameters a_i allow to weigh the different terms. Their values is application-dependent and will not be studied in this paper, in which we set them to 0.25.

3.3. Efficient Implementation

In practice, we do not consider all points during the computation of γ_jk (E-step). For that, we consider p_k(.; T) as a truncated Gaussian pdf with cut-off distance δ. This allows to reduce the computational burden (by the use of a kd-tree) and increase robustness. It can be shown that our algorithm still converges to an at least local maximum of the new (truncated) criterion. The E-Step becomes:

$$\begin{array}{l}\text{initialise}\gamma =({\gamma }_{jk})\text{to}\text{the}\text{null}\text{matrix}\\ \forall x_k\in X\\ \mathcal{S}=\{y_j\in Y\text{such}\text{that}{\left|\right|y_j-\stackrel{\sim }{T}(x_k)\left|\right|}^2<\delta \}(\text{using}\text{a}k\text{d}-\text{tree})\\ \forall y_j\in S\\ {\gamma }_{jk}=exp(-({\left|\right|y_j-\stackrel{\sim }{T}(x_k)\left|\right|}^2/(2{\sigma }^2)+\beta c(y_j,x_k)))\\ \forall j,\forall k,{\stackrel{\sim }{\gamma }}_{jk}={\gamma }_{jk}/{\sum }_l{\gamma }_{jl}(\text{normalisation})\end{array}$$

Moreover, we choose to initialise α (regularisation weight), σ (scale parameter) and β (prior weight) with high values and reduce them throughout iterations.

4. Enforcing Global Constraints on Matches

In the formalism presented so far, the matches in the E-step are performed on an individual basis without any global constraint such as one-to-one matches for instance. Another desirable global constraint is that some geometrical relationships between points in Y should be preserved between their correspondences in X. Thus if we consider each crest line in Y as a set of ordered points, then their correspondences must i) lie on the same crest line in X and ii) be ordered in the same way (up to the orientation of the line) (Fig. 1 right). To enforce these two constraints, let us introduce some notations first. Let L and M be the sets of crest lines of Y and X, each crest line being defined as a set of ordered points. Let u = (u^lm) be a block matrix whose lines (resp. columns) correspond to the concatenated crest lines of Y (resp. X). Then $u_{jk}^{lm}$ is the indicator variable $u_{jk}^{lm}=1$ iff y_j in crest line l corresponds to the point x_k in crest line m. The two constraints i) and ii) are specified as follows: the submatrix u^lm is either null (the line l does not match with the line m) or contains one 1 per line, with the 1s drawing a “staircase” going to the left or to the right, all “steps” of the staircase having potentially different widths and different heights. Then we propose to maximise the following criterion over T and u having this staircase structure:

$$L-CL=\left[\prod _{y_j\in Y\backslash L}\sum _{x_k\in X\backslash M}{\pi }_{jk}{p}_k(y_j\mid T)\times \prod _{l\in L}\prod _{y_j\in l}\sum _{x_k\in m}{[p_k(y_j\mid T)]}^{u_{jk}^{lm}}\right]\times p(T)$$ (3)

This criterion is an hybrid between the classification likelihood and the likelihood approaches. Introducing u only modifies the E-step of the algorithm, in which u and γ can be estimated independently. The algorithm becomes:

$$\begin{array}{l}\mathbf{E}-\mathbf{Step}:\text{compute}\stackrel{\sim }{\gamma }\text{as}\text{before}\\ \forall l,\text{compute}{\stackrel{\sim }{u}}^{lm}\text{respecting}\text{the}\text{staircase}\text{structure}\\ \text{and}\text{maximising}{\prod }_{y_j\in l}{\sum }_{x_k\in m}[p_k{(y_j\mid \stackrel{\sim }{T})}^{{\stackrel{\sim }{u}}_{jk}^{lm}}]\\ \mathbf{M}-\mathbf{Step}:\stackrel{\sim }{T}=arg{min}_T{\sum }_{y_j\in Y\backslash L,x_k\in X\backslash M}{\stackrel{\sim }{\gamma }}_{jk}{\left|\right|y_j-T(x_k)\left|\right|}^2\\ +{\sum }_{l\in L}{\sum }_{y_j\in l,x_k\in m}{\stackrel{\sim }{u}}_{jk}^{lm}{\left|\right|y_j-T(x_k)\left|\right|}^2+\alpha R(T)\end{array}$$

To our knowledge, an exhaustive search is the only way to maximise the proposed criterion over u. Instead, we propose to design an heuristic algorithm to do so, that extends the one proposed by Subsol [15] and consists of two steps: i) finding the crest line m ∈ M that corresponds to each l ∈ L and ii) starting from different initial potential matches and assigning iteratively each point y_j ∈ l to a point x_k ∈ m by keeping the staircase structure of the submatrix u^lm.

5. Experiments & Results

In the following we choose to adopt a locally affine regularisation [12] (with only the translational part) because of its ability to perform efficiently (~ 7min) on large datasets (~ 50K points).

5.1. Experiments on Synthetic Data

Generation of ground truth data

We first segment a structure X (typically, a pair of lateral ventricles or caudate nuclei, giving surfaces of about 10K points, itksnap.org) from a 3T T1-weighted brain MRI of a healthy subject. Then Y is generated from X by applying a random thin plate spline transformation [2]. Then, we add a uniform Gaussian noise of std 0.5 mm on each point of the deformed surface and remove groups of adjacent vertices to generate holes. This way we generate ground truth pairs of 100 ventricles and 100 caudate nuclei.

Evaluation

We evaluate the error by computing the mean distance between homologous points after registration using different strategies. The results are reported in Tab. 1 and an example is displayed in Fig. 2. They show the strong added value of using priors. The error is further reduced when using constraints, which ensure that the ordering of the points on the lines is kept unchanged, and thus help the algorithm to obtain anatomically coherent matches elsewhere.

Table 1. Experiments on synthetic data (stats).

Mean and std (mm) of the registration error for the 100 ventricles and 100 caudate nuclei by varying the parameters.

	no prior/no constraint	prior/no constraint	prior/constraint
ventricle	2.19 ± 0.82	1.43 ± 0.91	1.39 ± 0.93
caudate nuclei	1.54 ± 0.43	1.04 ± 0.57	0.98 ± 0.56

Fig. 2. Experiments on synthetic data.

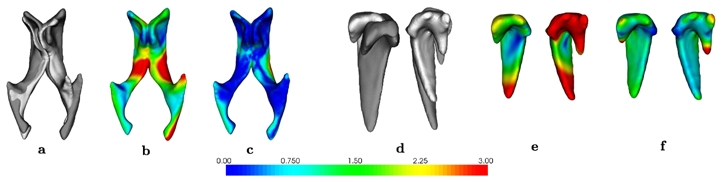
From left to right: Experiments on two different structures: ventricles and caudate nuclei. a) and d) original and deformed; b) and e) mapping of registration error (mm) without using prior/constraint; c) and f) mapping of registration error using prior/constraint.

5.2. Experiments on Real Data

In a first experiment, we choose X and Y as two different lateral ventricles and manually extract a set of 8 anatomical landmarks common to X and Y. We then apply a random affine transformation A to Y, register A(Y) to X with and without using priors/constraints, and evaluate the registration error on landmarks. We perform this experiment 100 times (but we display only 10 on Fig. 3 for better clarity). We observe a mean error of 1.73 ± 1.24mm with the priors/constraints and 2.55 ± 2.46mm without (Fig. 3, left). In a second experiment, we segment the brain from T1-weighted MRI data of two healthy subjects (300,000 points, brainvisa.info), and we extract four sulcal fundus beds (using our algorithm for crest lines) and label them manually for each subject. Then we register the two surfaces with and without using priors/constraints. The distance between the homologous sulci after registration is used as a quality metric. It is evaluated to be 3.3mm in the first case and 6.8mm in the second (Fig. 3, right).

Fig. 3. Experiments on real data. Ventricles.

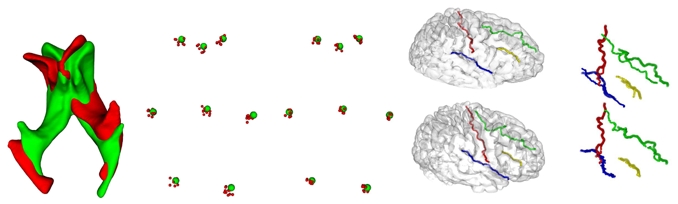
From left to right: X (green) and A(Y) (red) before registration, position of the 8 anatomical landmarks of the 10 random experiments after registration without priors/constraints and with priors/constraints. Brain: From left to right and top to bottom: 1) brain 1 (top) and brain 2 (bottom); 2) brain 2 (with sulci shown in transparency) towards brain 1 without (top) and with (bottom) using priors/constraints. The four sulci are the central (red), lateral (blue), superior frontal (green) and inferior frontal (yellow) sulci.

6. Conclusion and Perspectives

We proposed techniques to set priors and enforce some global geometrical constraints on matches for ML-based nonlinear registration of surfaces. The priors on matches give a flexible way to devise structure-specific registration algorithms. They ideally complement the global, generic, prior on the transformation and thus help to obtain a result coherent with the application of interest. In addition, they provide a convenient framework to include additional knowledge (segmentation, landmarks, etc.) provided by experts when available. In the future, comparisons with other recent methods, especially landmark-free approaches [16] and others that do not resort to point-to-point correspondences [17] will be led.