Abstract
We investigated numerical discrimination and numerical rule-learning in ring-tailed lemurs (Lemur catta). Two ring-tailed lemurs were trained to respond to two visual arrays, each of which contained between one and four elements, in numerically ascending order. In Experiment 1, lemurs were trained with 36 exemplars of each of the numerosities 1–4 and then showed positive transfer to trial-unique novel exemplars of the values 1–4. In Experiments 2A and 2B, lemurs were tested on their ability to transfer an ascending numerical rule from the values 1–4 to novel values 5–9. Both lemurs successfully ordered the novel values with above chance accuracy. Accuracy was modulated by the ratio between the two numerical values suggesting that lemurs accessed the approximate number system when performing the task.
Keywords: numerical cognition, ratio effects, distance effects, ordinal rule
Introduction
Over the last 100 years, a great many studies have investigated the numerical abilities of non-human animals and have suggested that a broad range of species are capable of attending to the numerical attributes of the world around them (for reviews, see Brannon and Cantlon, 2009; Merritt et al., in press). For example, monkeys and apes can learn numerical rules (Brannon and Terrace, 1998, 2000), match numerical values across sensory modalities (Jordan et al., 2005, 2008), and even make simple arithmetic calculations (e.g., Rumbaugh et al., 1987; Boysen and Berntson, 1989; Olthof et al., 1997; Beran, 2004; Anderson et al., 2005, 2007; Addessi et al., 2007; Cantlon and Brannon, 2007a; Evans et al., 2009).
While food reinforcers are frequently used in studies of quantity discrimination in primates and other animals, food presents difficulties in controlling for alternative cues such as hedonic value or total surface area. Brannon and Terrace (1998, 2000) used a touch-screen procedure with rhesus monkeys to carefully control for alternative stimulus dimensions and to test whether monkeys were capable of abstract numerical rule-learning. Rhesus monkeys were first trained to respond to specific exemplars of the numerosities 1–4 in ascending numerical order. By varying the size and shape of the elements across stimulus sets and testing the monkeys with trial-unique stimuli, Brannon and Terrace showed that the monkeys could order the values based on numerosity alone. To test whether the monkeys had learned something specific about the values 1–4 or a more abstract numerical rule, monkeys were then tested with novel values 5–9. Both monkeys successfully transferred the ordinal rule they learned with the values 1–4 to the novel values 5–9 (see also, Brannon et al., 2006; Cantlon and Brannon, 2006a).
Although no study has examined whether a non-primate species can form numerical rules, other studies, replicating the procedure used by Brannon and Terrace, have shown that squirrel monkeys, baboons, cebus monkeys, and humans also successfully order the values 5–9 following training on values 1–4 (Smith et al., 2002; Judge et al., 2005; Cantlon and Brannon, 2006b). In all cases, performance showed ratio dependence, with accuracy increasing and reaction-time decreasing as the ratio between the two numerosities approached one.
The shared behavioral signatures shown by humans and monkeys suggest that both tap a common approximate number system – and that the acquisition of numerical abilities was not a recent development in the course of human cognitive evolution. But how ancient are these abilities? How far back do they go in the primate lineage? One group of primates that has been neglected in most cognitive research is lemurs. Lemurs are potentially interesting and informative because they diverged from the lineage leading to monkeys, apes, and humans 75 million years ago (Horvath et al., 2008). Therefore, studying numerical abilities in lemurs provides a unique opportunity to understand the ancient cognitive antecedents that underlie numerical thinking in modern humans. Do lemurs have the ability to represent numerical values? If so, can they learn a numerical rule and extrapolate that rule to novel values?
A handful of studies suggest that lemurs can represent approximate numerical values. In one study, Lewis et al. (2005) placed a set of grapes into a bucket, one by one, while mongoose lemurs watched. When the experimenter finished, the lemurs were allowed to reach inside the bucket to retrieve the grapes. On half of the trials, the experimenter secretly placed some of the grapes into a hidden compartment. The critical question was how long would lemurs continue to search the empty pail after they had retrieved the available grapes. Lewis et al. found that lemurs searched longer when grapes should have been present in the bucket, but only when the number of retrieved to total grapes was a 1:2 ratio or greater. This shows that lemurs formed expectations about how many grapes were in the bucket.
Santos et al. (2005) used a modified version of the Wynn (1992) violation of expectancy paradigm to assess numerical abilities in four different lemur species. Lemurs watched as a screen was raised in front of a lemon placed on a small stage. Next, the experimenter placed an additional lemon behind the occluding screen. The screen was then lowered to reveal either a possible outcome (e.g., two lemons), or an impossible outcome (e.g., one lemon). Regardless of species, lemurs looked longer at the impossible outcome than at the possible outcome. This suggested that lemurs were able to represent the number of lemons behind the screen, and form expectations about how many lemons should be present when the screen was lowered.
Here we used a modified version of the Brannon and Terrace (1998, 2000) task to test whether ring-tailed lemurs could extrapolate a numerical rule learned with the values 1–4 to the values 5–9. The main departure from the Brannon and Terrace procedure was that lemurs were trained with pairs of the values 1–4 rather than four-item sequences. By using trial-unique test stimuli and controlling for surface area we provide the most stringent test to date of a lemur's numerical ability.
Experiment 1
Method
Subjects
Two male ring-tailed lemurs (Lemur catta), Teres and Aristides, aged 10 and 12 years participated. Both lemurs were housed in indoor enclosures at the Duke University Lemur Center and had approximately 1 year of prior experience in a touchscreen serial ordering task which did not involve numerical discriminations (Merritt et al., 2007)1. Water access was unlimited and fresh fruit and Purina monkey chow was provided daily. The experimental protocols were evaluated and approved by the Institutional Animal Care and Use Committee at Duke University.
Apparatus
Lemurs were tested in their home enclosures. All equipment for stimulus presentation, data acquisition, and reward delivery was housed in a custom-built, stainless steel, portable testing station (86 cm × 43 cm × 35 cm). Stimuli were displayed on a 15-inch touch-sensitive computer monitor. Custom-built Java™ and REALbasic® programs presented the stimuli and recorded responses. Correct responses were rewarded with 190-mg fruit punch-flavored sucrose reward pellets.
Stimuli
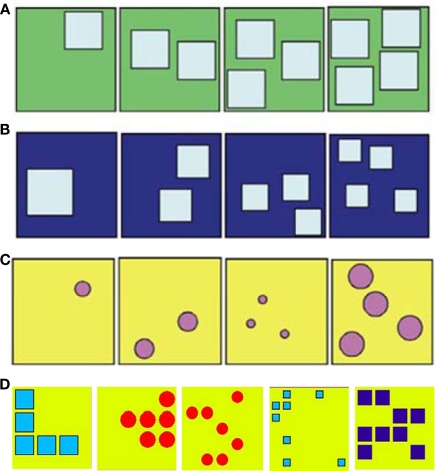
Subjects were trained to select the numerically smaller exemplar from pairs of stimulus sets containing between one and four elements. The stimulus sets were modeled after those used by Brannon and Terrace (2000), however, stimuli were presented in pairs rather than as sets of four. Each stimulus was an array of circles or squares positioned randomly on a 3 cm × 3 cm backdrop (Figure 1). To control for non-numerical stimulus attributes that typically covary with number, we generated stimuli that conformed to three different control classes: equal element size, random element size, and equal cumulative area (Figure 1). Each stimulus set contained one exemplar of a numerosity ranging in value from 1 to 4. For equal element size sets, the elements in each pair of exemplars were the same size regardless of the array's numerosity. For random element size sets, the elements in each pair of exemplars varied such that element size and overall cumulative surface area did not increase or decrease monotonically with number. For equal cumulative area sets, the cumulative surface area of the elements in each pair of exemplars was constant regardless of the array's numerosity. Collectively, these controls prevented a subject from using individual element size or overall surface area as a basis for ordering stimuli.
Figure 1.
Examples of stimuli used in Experiment 1 (A–C) and Experiments 2A and 2B (D). Stimuli in Experiment 1: (A) element size-constant, (B) overall surface area-constant, and c) random element size groups of stimuli. Stimuli in Experiments 2A and 2B: (D) an example of the computer generated stimuli for numerosities 5–9.
Procedure
A trial began when the subject touched a small rectangular start stimulus at the bottom left corner of the screen. Following this response, both stimuli appeared simultaneously, positioned randomly within a 3 × 3 matrix. A response to the numerically smaller value delivered a 190-mg sucrose reward tablet as well as positive auditory and visual feedback. A response to the numerically larger value yielded negative auditory feedback and a 3-s timeout during which the screen was black. Subjects were tested 5 days per week and performed 72 trials per training session.
The experiment was conducted in three phases modeled after Brannon and Terrace (2000): training, multiset training, and transfer. In the training phase, subjects were trained with 36 different stimulus sets. Each stimulus set consisted of four stimuli (one-, two-, three- and four-element arrays) and thus allowed for six possible numerosity pairs, each of which was presented with equal frequency. Subjects were trained with each stimulus set for 3 days, or until they scored 75% correct in a single session, whichever came first. Stimulus sets from the three stimulus control categories were presented pseudo-randomly such that each control category was presented with equal frequency and evenly distributed across training.
In multiset training the lemurs were trained in sessions that incorporated a diverse mix of the stimuli from their initial training. The 36 stimulus sets were divided into three groups of 12 stimulus sets, with one 12-set group presented per session. The 12 sets each contained four sets from each of the three control categories. Since there were 6 possible pairs derived from each of the 12 stimulus sets, this resulted in 72 unique trials per session. The three multiset groups were rotated across days such that each of the three multiset groups was tested once every 3 days. A multiset group was removed from the rotation once a subject scored 75% correct in a single session with that group of stimuli. Subjects continued training with the remaining group(s) until they reached the accuracy criterion for each of the three multiset groups.
In transfer, lemurs were tested on their ability to order novel exemplars of the numerosities 1–4. Subjects were tested in 10 sessions, each of which contained 12 previously untrained novel stimulus sets (four from each control category). Given that there were 6 possible pairs within each of the 12 sets, this resulted in 72 unique trials per session. Each numerosity comparison was presented 12 times per session, resulting in 120 data points for each numerosity comparison over the 10 sessions.
Results
Training
Analysis of the 36 training sessions showed that both subjects learned to choose the smaller numerical stimulus at levels exceeding chance expectation (one-sample t-test: Aristides: M = 66%, t(35) = 10.93, p < 0.01; Teres: M = 67%, t(35) = 8.9, p < 0.01). In order to determine whether lemurs were using non-numerical cues to order the stimuli, we conducted separate analyses on trials when (1) cumulative surface area was held constant for both stimuli, (2) element size was held constant for both stimuli, and (3) element size and cumulative surface area varied randomly from trial to trial. Overall, we found that accuracy was above chance regardless of whether the cumulative surface area of the stimuli was equated, when the size of the elements in each stimulus was equated, and when there was no systematic relationship between the element size or cumulative surface area and numerosity (see Table 1).
Table 1.
Accuracy during three stimulus control conditions in Experiment 1.
| Condition | Subject | Training | Transfer |
|---|---|---|---|
| Surface area equated | Aristides | M = 64%, t(34) = 12.37, | M = 70%, t(5) = 4.15, |
| p < 0.01 | p < 0.01 | ||
| Teres | M = 63%, t(29) = 8.01, | M = 71%, t(5) = 9.89, | |
| p < 0.01 | p < 0.01 | ||
| Element size equated | Aristides | M = 71%, t(24) = 15.48, | M = 74%, t(5) = 6.05, |
| p < 0.01 | p < 0.01 | ||
| Teres | M = 68%, t(25) = 9.04, | M = 67%, t(5) = 2.80, | |
| p < 0.01 | p < 0.05 | ||
| Random | Aristides | M = 67%, t(27) = 9.62, | M = 66%, t(5) = 5.38, |
| p < 0.01 | p < 0.01 | ||
| Teres | M = 61%, t(27) = 4.31, | M = 68%, t(5) = 3.72, | |
| p < 0.01 | p < 0.05 |
To examine whether performance in the first session with each stimulus set increased across training, we conducted a linear regression on the accuracy of the first session for each new stimulus set. Because Teres received some pre-training (in a pilot study) that did not follow the strict three session criterion implemented during the training phase, we also included the first session accuracies for this period in order to measure changes in accuracy with experience to each new set of stimuli. Only Teres showed consistent increases in accuracy across training (Aristides: R2 = 0.01, F(1,34) = 0.50, p = 0.50; Teres: R2 = 0.34, F(1,46) = 23.98, p < 0.05). Aristides’ lack of improvement across training sessions is likely a result of the fact that he began two-item training at a relatively high accuracy after a brief pilot attempt to train him with three and four-item number sequences.
Multiset training
Analysis of overall accuracy (one sample t-tests) for each of the six possible numerical pairs revealed that both lemurs continued to order numerical stimuli in the 1–4 range at above chance levels when each session contained stimuli from 12 different stimulus sets (Aristides: M = 69%; t(5) = 4.49, p < 0.01; Teres: M = 68%, t(5) = 4.17, p < 0.01). Again, as shown in Table 1, performance was above chance when the cumulative area in each stimulus was equated, when the size the elements was the same in both stimuli, and when there was no systematic relationship between cumulative surface area or element size and numerosity. The number of sessions required to reach criterion in multiset training was 31 and 25 for Aristides and Teres respectively.
Transfer
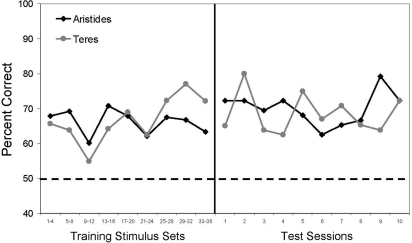
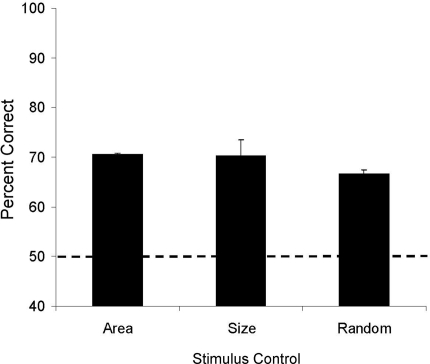
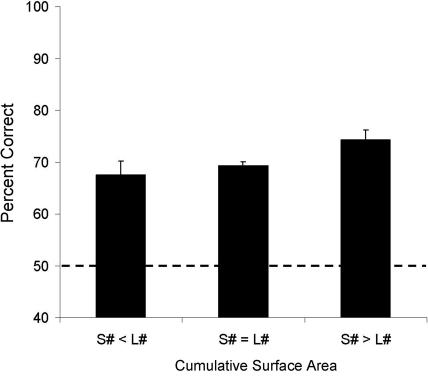
Both lemurs correctly ordered trial-unique numerical stimuli across the 10 transfer sessions (Aristides: M = 70%, one-sample t(9) = 13.5, p < 0.01; Teres: M = 68%, t(9) = 10.21, p < 0.01). To examine performance during transfer relative to performance during training, stimulus sets given during training were combined into blocks of four (see Figure 2). We then calculated the mean accuracy for the first session of each stimulus set within each block, and then compared these accuracies to those obtained during the 10 transfer sessions (Figure 2). Accuracy for training and test did not differ significantly for Teres [t(17) = −0.61, p = 0.55], but there was a trend toward higher performance during transfer testing compared to training for Aristides [t(17) = −1.99, p = 0.06]. Analysis of the stimulus control conditions (Figure 3) revealed that performance was above chance when the cumulative area in each stimulus was equated (Aristides: M = 70%, t(5) = 4.15, p < 0.01; Teres: M = 71%, t(5) = 9.89, p < 0.01), when the size of the elements was the same in both stimuli (Aristides: M = 74%, t(5) = 6.05, p < 0.01; Teres: M = 67%, t(5) = 2.80, p < 0.05), and when there was no systematic relationship between cumulative surface area or element size and numerosity (Aristides: M = 66%, t(5) = 5.38, p < 0.01; Teres: M = 68%, t(5) = 3.72, p < 0.05).
Figure 2.
Average first session accuracy during training in blocks of four stimulus sets and performance during the 10 transfer sessions. The dotted line indicates chance for the task.
Figure 3.
Average accuracy during Experiment 1 transfer for each of the three stimulus control classes. Error bars reflect the standard error of the mean and the dotted line indicates chance for the task.
In order to examine the effects of ratio on accuracy, a linear regression was conducted on the overall mean for each ratio. For both subjects, we found that accuracy was modulated by the ratio of the numerical values being compared. Specifically, accuracy decreased as the ratio of the values being compared approached one (Aristides: R2 = 0.93, F(1,3) = 40.74, p < 0.01; Teres: R2 = 0.96, F(1,3) = 66.44, p < 0.01). There was no relationship between reaction-time and ratio for either lemur (Aristides: R2 = 0.71, F(1,3) = 7.27, p = 0.07; Teres: R2 = 0.02, F(1,3) = 0.08, p = 0.80).
Experiment 2A
Experiment 1 demonstrated that lemurs could discriminate numerical order independent of non-numerical features such as surface area and element size. One possibility is that lemurs used an ordinal rule such as choose the numerically smaller value, that allowed them to order the six possible numerical pairs. An alternative possibility is that lemurs learned a set of numerical categories for the values 1–4, and through training, learned which numerical category to select first for each of the six numerical pairs. Under this scenario the lemurs would have had to learn to respond to 1 before 2, 3 or 4, 2 before 3 or 4, and 3 before 4. The purpose of Experiment 2A was to disentangle these two possibilities by testing the lemurs with the novel numerical values 5–9.
Method
Subjects and apparatus
The subjects and apparatus were the same as in Experiment 1.
Stimuli
Stimuli in Experiment 2 were generated on a trial-unique basis by the experimental software. The controls for non-numerical stimulus properties differed slightly from those in Experiment 1. On 1/3 of all trials, the program generated stimuli for which the cumulative area of the smaller numerical stimulus was larger than that of the larger numerical stimulus. On another 1/3 of trials the cumulative surface area of the two numerical stimuli was equated. On the last 1/3 of trials, the cumulative surface area of the smaller numerical stimulus was smaller than that of the larger numerical stimulus. The order in which these controls were implemented was random within a session.
Procedure
Training sessions were identical to those in Experiment 1. Lemurs were re-trained with the numerosities 1–4 until meeting an accuracy criterion of two consecutive sessions at or above 80% correct2. Lemurs were then tested on their ability to order the 36 possible pairs constructed from the numerosities 1–9. As in Brannon and Terrace (1998, 2000), we only provided differential reinforcement when testing the six pairs comprised of the familiar numerosities 1–4 (familiar–familiar). However, when testing pairs with one familiar (1–4) and one novel (5–9) numerosity, or pairs with two novel numerosities, we provided non-differential reinforcement. This was different from Brannon and Terrace (1998, 2000) in that we provided positive auditory and visual feedback and a food pellet regardless of whether the lemur chose the smaller or larger numerosity whereas Brannon and Terrace provided no positive or negative feedback on these trials. The 30 pairs that comprised two novel values (novel–novel, NN) or one familiar and one novel value (familiar–novel, FN) were each presented once per session. The six familiar–familiar (FF) pairs were presented at a higher frequency than all other pairs (7 trials each for a total of 42 trials). Twenty 72-trial test sessions were conducted.
Results
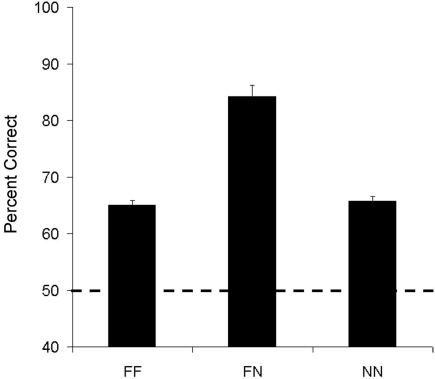
Figure 4 shows performance for each lemur for the three types of pairs: (FF, FN, and NN). Not surprisingly, as shown in Table 2, both lemurs successfully ordered the new exemplars of the pairs composed of two familiar values with above chance accuracy (Aristides: M = 66%, t(5) = 4.34, p < 0.01; Teres: M = 64%, t(5) = 4.63, p < 0.01)3. Both lemurs were also highly accurate at ordering pairs with one familiar and one novel value. The main finding however, was that both lemurs were above chance on the critical NN pairs.
Figure 4.
Average accuracy for familiar–familiar (FF), familiar–novel (FN), and novel–novel (NN) number pairs in Experiment 2A.
Table 2.
Accuracy during three different familiarity conditions during Experiments 2A and 2B.
| Condition | Subject | Experiment 2A | Experiment 2B |
|---|---|---|---|
| Familiar–Familiar | Aristides | M = 66%, t(5) = 4.34, | M = 69%, t(5) = 3.87, |
| p < 0.01 | p < 0.01 | ||
| Teres | M = 64%, t(5) = 4.63, | M = 66%, t(5) = 5.11, | |
| p < 0.01 | p < 0.01 | ||
| Familiar–Novel | Aristides | M = 82%, t(19) = 10.92, | M = 84%, t(19) = 14.27, |
| p < 0.01 | p < 0.01 | ||
| Teres | M = 86%, t(19) = 17.42 | M = 75%, t(19) = 11.60 | |
| p < 0.01 | p < 0.01 | ||
| Novel–Novel | Aristides | M = 67%, t(9) = 3.91, | M = 66%, t(9) = 4.03, |
| p < 0.01 | p < 0.01 | ||
| Teres | M = 65%, t(9) = 4.12, | M = 65%, t(9) = 4.69, | |
| p < 0.01 | p < 0.01 |
Figure 5 shows overall performance across the three different stimulus control classes. One sample t-tests on means for the 36 numerical pairs revealed that both subjects scored above chance when the cumulative surface area was greatest for the smaller numerosity, when the cumulative surface area was equal for both stimuli, and when the cumulative surface area was greatest for the larger numerosity (see Table 3). A similar analysis on only the NN pairs indicated that both subjects scored above chance when the overall surface area was equal for both stimuli (Aristides: M = 62%, t(9) = 2.30, p < 0.05; Teres: M = 75%, t(9) = 3.37, p < 0.01) and when the smaller numerosity had a greater cumulative surface area (Aristides: M = 73%, t(9) = 4.55, p < 0.01; Teres: M = 70%, t(9) = 3.41, p < 0.01). Aristides showed a trend toward above chance performance when the area of the larger numerosity was greater than that of the smaller numerosity, but Teres accuracy did not exceed chance levels (Aristides: M = 62%, t(9) = 1.65, p = 0.07; Teres: M = 51%, t(9) = −0.57, p = 0.29).
Figure 5.
Average accuracy for Experiment 2A across each of the three stimulus control classes. Error bars reflect the SEM and the dotted line indicates chance for the task.
Table 3.
Transfer accuracy during three surface area control conditions in Experiments 2A and 2B.
| Surface area | Subject | Experiment 2A | Experiment 2B |
|---|---|---|---|
| Small # > Large # | Aristides | M = 72%, t(35) = 10.46, | M = 79%, t(35) = 12.21, |
| p < 0.01 | p < 0.01 | ||
| Teres | M = 76%, t(35) = 11.87, | M = 76%, t(35) = 11.32, | |
| p < 0.01 | p < 0.01 | ||
| Small # = Large # | Aristides | M = 69%, t(35) = 5.71, | M = 77%, t(35) = 9.23, |
| p < 0.01 | p < 0.01 | ||
| Teres | M = 70%, t(35) = 9.18, | M = 70%, t(35) = 8.39, | |
| p < 0.01 | p < 0.01 | ||
| Small # < Large # | Aristides | M = 70%, t(35) = 10.46, | M = 72%, t(35) = 6.88, |
| p < 0.01 | p < 0.01 | ||
| Teres | M = 65%, t(35) = 11.87, | M = 67%, t(35) = 5.85, | |
| p < 0.01 | p < 0.01 |
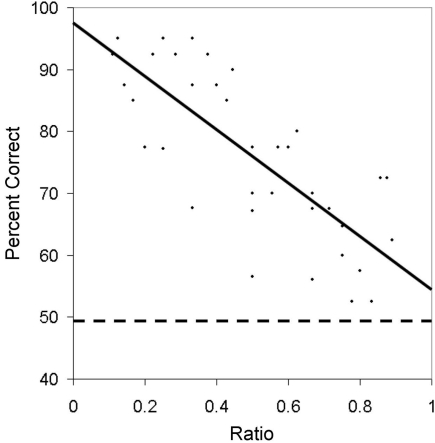
As shown in Figure 6, accuracy was modulated by the ratio of numerical values being compared. A linear regression on accuracy as a function of ratio revealed that accuracy decreased for both lemurs as the ratio between the numerical stimuli approached 1 (Aristides: R2 = 0.52, F(1,25) = 27.29, p < 0.01; Teres: R2 = 0.61, F(1,25) = 39.09, p < 0.01). Mean response time however, was not related to the ratio of the values being compared for either subject (Aristides: R2 = 0.05, F(1,25) = 1.30, p = 0.27; Teres: R2 = 0.10, F(1,25) = 2.81, p = 0.11).
Figure 6.
Average accuracy for Experiment 2A as a function of the ratio of the numerical values being compared. The dotted line indicates chance for the task.
Experiment 2B
Experiment 2A demonstrated that, like other primates, lemurs could learn a numerical rule and transfer that rule to order novel numerical values. However, the limited number of data points (20 trials for each FN and NN pair) made it difficult to analyze reaction-time data, and to compare overall accuracy patterns with published data on monkeys. Therefore, in Experiment 2B, we tested the lemurs with an additional 20 sessions and equally weighted the 36 pairs composed of the values 1–9. This provided a total of 40 trials for each numerical pair.
Method
The subjects and apparatus were the same as in Experiment 2A. The stimuli were constructed according to the same parameters as Experiment 2A and were trial-unique images generated by the Real Basic program. The task was identical to Experiment 2A with the following exceptions. There were 36 possible pair combinations that could be derived from the numerosities 1–9, and each pair was presented twice per session to produce 72 trials. All trials were differentially reinforced regardless of the numerosities being tested.
Results
As shown in Table 2, accuracy was significantly above chance for both lemurs in the FF condition. Both lemurs were also highly accurate at ordering pairs with one familiar and one novel value, and they were also above chance on the NN pairs.
One sample t-tests on means for the 36 numerical pairs revealed that both subjects scored above chance when the cumulative surface area was greatest for the smaller numerosity, when the cumulative surface area was equal for both numerosities, and when the cumulative surface area was greatest for the larger numerosity (see Table 3).
When the NN pairs were analyzed separately, both subjects scored above chance when the overall surface area was equal (Aristides: M = 69%, t(9) = 3.28, p < 0.01; Teres: M = 64%, t(9) = 2.49, p < 0.05) and when the smaller numerosity had a greater cumulative surface area (Aristides: M = 72%, t(9) = 4.13, p < 0.01; Teres: M = 69%, t(9) = 6.41, p < 0.01). Teres showed a trend toward above chance performance when the area of the larger numerosity was greater than that of the smaller numerosity, but Aristides accuracy did not exceed chance levels (Aristides: M = 54%, t(9) = 0.89, p = 0.20; Teres: M = 62%, t(9) = 1.71, p = 0.06).
It is important to note that NN pairs in this experimental design present more difficult ratios than the pairs that comprise FF and FN conditions, thus confounding numerical difficulty with numerical familiarity. Prior work has shown that macaques trained to order the values 4–5–6 and then tested with novel values that have favorable ratios such as 2 versus 8 show superior performance on NN compared to FF pairs (Brannon et al., 2006). Thus, when familiarity and numerical ratio are pitted against each other, it seems clear that ratio drives performance and not the relative familiarity or novelty of the individual values.
The fact that performance was relatively poor on NN pairs in both Experiment 2A and Experiment 2B when the larger numerosity had the larger cumulative surface area suggests that lemurs may have used a non-numerical strategy when numerical discrimination was difficult. It is interesting to note that if lemurs did use a non-numerical rule, it led them to make choices that were incongruent with both surface area and numerosity. Previous research has shown that lemurs have difficulty when the ratio between two values is greater than 1:2 (Lewis et al., 2005), and in the NN condition, all pairs had a ratio greater than 1:2, and 7 of the 10 pairs were greater than a 2:3 ratio. In similar tasks, rhesus monkeys have shown that they rely on non-numerical cues when the ratio between the two numerosities approaches one (Cantlon and Brannon, 2007b), but they use numerical features when ratios are large. Would this also be true of lemurs in the NN task when surface area was congruent with numerical value? To test this we examined the difficult stimulus control condition (larger numerosity has a larger cumulative surface area) for NN pairs that had a ratio of 2:3 or lower. Both lemurs showed above chance performance for the problematic stimulus control condition for these NN pairs that were more discriminable (Aristides: M = 69%, t(2) = 3.14, p < 0.05; Teres: M = 70%, t(2) = 11.13, p < 0.01) suggesting that the lemurs may have only relied on an alternative inverse cumulative surface area rule when numerical discriminations were particularly difficult.
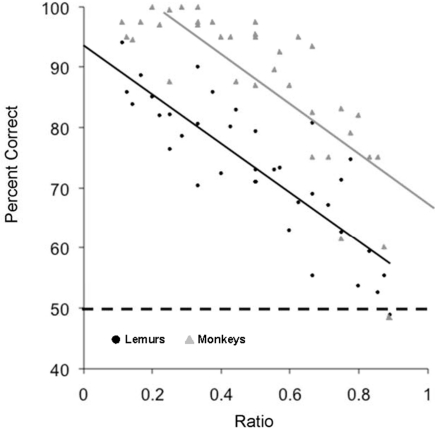
As in Experiment 2A, lemurs showed ratio effects, with accuracy decreasing as the ratio of the two values approached one (Aristides: R2 = 0.82, F(1,25) = 116.89, p < 0.01; Teres: R2 = 0.68, F(1,25) = 52.68, p < 0.01). Notably, performance for the lemurs closely resembled the performance shown by rhesus monkeys that performed the same task (Brannon and Terrace, 2000). As shown in Figure 7, monkeys were generally more accurate than lemurs, but the slopes of the regression lines were remarkably similar (lemurs: y = −40.57x + 93.69; monkeys: y = −41.31x + 108.6). This suggests that lemurs were ordering numerical values using processes that were similar to those used by monkeys.
Figure 7.
Lemur accuracy (black circles) for Experiment 2B as a function of the numerical ratio between the values being compared. Monkey data (gray triangles) from Brannon and Terrace (2000) is plotted for comparison. The regression slopes for the two species are highly similar (lemurs: y = −40.57x + 93.69; monkeys: y = −41.31x + 108.6). The dotted line indicates chance for the task.
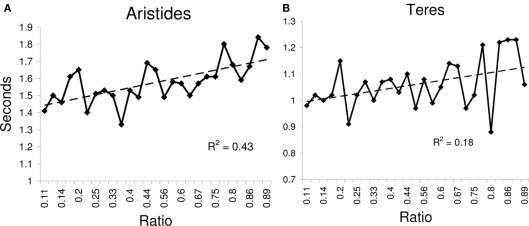
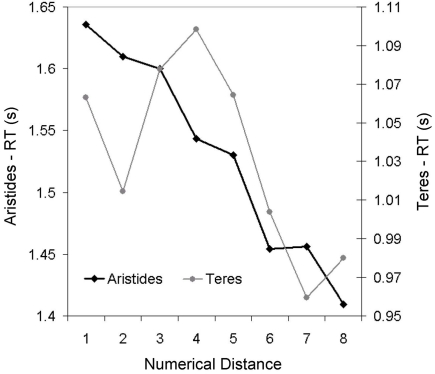
A regression of RT on ratio showed that RT increased as the ratio of the values being compared approached one (Figure 9; Aristides: R2 = 0.43, F(1,25) = 18.73, p < 0.05; Teres: R2 = 0.18, F(1,25) = 5.56, p < 0.05). Lemurs also showed distance effects, with reaction-time decreasing with increasing numerical distance; this pattern was statistically significant for Aristides, but only approached statistical significance for Teres (Figure 8; Aristides: R2 = 0.97, F(1,6) = 174.27, p < 0.01; Teres: R2 = 0.42, F(1,6) = 4.33, p = 0.08).
Figure 9.
Response time for Experiment 2B as a function of the numerical ratio between the values being compared for (A) Aristides, and for (B) Teres.
Figure 8.
Response time for Experiment 2B as a function of the numerical distance between the values being compared.
General Discussion
In recent years, several studies have shown that various primate species are capable of forming and applying an abstract numerical ascending rule to novel sets of numerosities. This suggests that some of our more complex numerical abilities may be rooted in our ancient evolutionary past. Here we ask whether the ability to learn abstract numerical rules is also present in lemurs and thus likely to be shared by all primates. Although some research has examined basic numerical abilities in lemurs (Lewis et al., 2005; Santos et al., 2005), prior studies have not carefully controlled non-numerical features, or assessed whether lemurs are capable of abstracting a numerical rule.
The present set of experiments had two main objectives: The first was to determine whether lemurs were capable of representing number independent of co-varying stimulus factors such as surface area and element size. The studies presented here represent the first attempt to systematically control for these features, and to determine whether lemurs can make discriminations using only numerical information. The second objective was to determine whether lemurs were capable of learning an ordinal numerical rule. Could lemurs generalize a numerical rule from one set of values, to a completely new set of values that they had never seen before?
In Experiment 1, lemurs were trained to order the numerical values 1–4, and subsequently, they ordered novel exemplars of the same numerical values. Analyses of perceptual features revealed that numerical value predicted performance independent of cumulative surface area and element size. Although Experiment 1 showed that lemurs could transfer to exemplars of the same value, it was possible that the lemurs did not learn a numerical rule per se, but instead, learned to identify and order a set of trained numerical categories. Experiments 2A and 2B addressed this question by examining whether lemurs could extend an ordinal rule they learned with the values 1–4 to values outside that range. Lemurs showed that once they had learned to properly order the values 1–4, that they could spontaneously order novel values 5–9. This suggests that the lemurs were not simply ordering on the basis of trained numerical categories, but rather, they had learned an ascending numerical rule during training, and applied that rule to the novel numerosities 5–9.
These results are roughly similar to those of previous studies examining numerical rules in other primates (Brannon and Terrace, 1998, 2000; Smith et al., 2002; Judge et al., 2005). However, as shown in Figure 7 monkeys were generally more accurate than lemurs in ordering pairs of the values 1–9. Given the small number of lemurs tested here and monkeys tested in previous studies, it is difficult to draw conclusions about potential species differences in numerical acuity. Even if larger sample sizes conformed an overall species difference in accuracy in our task there are alternative potential explanations. For example, it is possible that lemurs’ relatively poor visual acuity and color discrimination place them at a disadvantage in a visually oriented numerical task. Another possibility is that differences in the training procedure used for monkeys and lemurs placed the lemurs at a disadvantage. Monkeys were trained to order the values 1–4 in ascending order whereas the lemurs were trained to make pairwise numerical discriminations. The lemurs were also given different numerical stimuli than the monkeys. These procedural differences may account for the overall accuracy differences between species. At present, we are uncertain whether the species differences found here represent true species differences, or whether they can be accounted for by individual within-species differences. In order to address this question more effectively, we are currently in the process of testing multiple individuals from several lemur species and testing numerically naïve macaques with the identical stimuli and procedure.
Nevertheless these results strongly suggest that lemurs share a common numerical processing mechanism with other primates. Accuracy followed Weber's Law and the overall pattern of results was markedly similar for rhesus monkeys and lemurs. Although non-primate species have shown the same ratio-dependent behavioral signature for numerical discrimination, to date no study has investigated abstract ordinal rule-learning in a non-primate. Whether this ability is primate-unique, or more broadly shared by other species remains an interesting question for future research. At a minimum our results suggest that within the primate lineage, the ability to form ordinal numerical rules is an evolutionarily ancient ability that emerged prior to the divergence of Strepsirrhine (e.g., lemurs, lorises, and galagos) and Haplorrhine (e.g., apes and monkeys) primates 75 million years ago.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank the Duke Lemur Center and the many Duke University undergraduates who assisted with this research. We thank members of the Brannon laboratory for their helpful discussion of these data. This work was supported by a National Science Foundation CAREER award (no. 0448250), National Institute of Child Health and Human Development Grant R01 (HD49912) and a John Merck Fund fellowship to Elizabeth M. Brannon. DLC # 1197, and also the National Institutes of Health under Ruth L. Kirschstein National Research Service Award No. F32MH082623 to Dustin J. Merritt.
Footnotes
1In addition to memorizing sequences of photographs we initially attempted to train Aristides to execute four- and then three-item numerical sequences. However we were concerned with his relatively poor performance and decided to switch to a simpler two-item numerical ordering task. This early training on the sequence 1–2–4 likely explains his high performance at the outset of pairwise numerical training in Experiment 1.
2This was done because we switched from a Java-based to a Real Basic-based program and wanted to make sure that there was no reduction in performance due to slight differences in appearance or timing of the trial structure before conducting the experiment.
3We calculated the mean accuracy for each pair, and then conducted one-sample t-tests on these means for each of the three categories (FF, FN, and NN).
References
- Addessi E., Crescimbene L., Visalberghi E. (2007). Do capuchin monkeys (Cebus apella) use tokens as symbols? Proc. Biol. Sci. 274, 2579–2585 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson U. S., Stoinski T. S., Bloomsmith M. A., Maple T. L. (2007). Relative numerousness judgment and summation in young, middle-aged, and older adult orangutans (Pongo pygmaeus abelii and Pongo pygmaeus pygmaeus). J. Comp. Psychol. 121, 1–11 [DOI] [PubMed] [Google Scholar]
- Anderson U. S., Stoinski T. S., Bloomsmith M. A., Marr M. J., Smith A. D., Maple T. L. (2005). Relative numerousness judgment and summation in young and old Western lowland gorillas. J. Comp. Psychol. 119, 285–295 [DOI] [PubMed] [Google Scholar]
- Beran M. J. (2004). Chimpanzees (Pan troglodytes) respond to nonvisible sets after one-by-one addition and removal of items. J. Comp. Psychol. 118, 25–36 [DOI] [PubMed] [Google Scholar]
- Boysen S. T., Berntson G. G. (1989). Numerical competence in a Chimpanzee (Pan troglodytes). J. Comp. Psychol. 103, 23–31 [DOI] [PubMed] [Google Scholar]
- Brannon E. M., Cantlon J. F. (2009). “A comparative perspective on the origin of numerical thinking,” in Cognitive biology: Evolutionary and developmental perspectives on mind, brain, and behavior, eds Tomasi L., Peterson M. A., Nadel L. (Cambridge: MIT Press; ), 191–220 [Google Scholar]
- Brannon E. M., Cantlon J. F., Terrace H. S. (2006). The role of reference points in ordinal numerical comparisons by rhesus macaques (Macaca mulatta). J. Exp. Psychol. Anim. Behav. Process 32, 120–134 [DOI] [PubMed] [Google Scholar]
- Brannon E. M., Terrace H. S. (1998). Ordering of the numerosities 1 to 9 by monkeys. Science 282, 746–749 10.1126/science.282.5389.746 [DOI] [PubMed] [Google Scholar]
- Brannon E. M., Terrace H. S. (2000). Representation of the numerosities 1-9 by rhesus macaques (Macaca mulatta). J. Exp. Psychol. Anim. Behav. Process. 26, 31–49 [DOI] [PubMed] [Google Scholar]
- Cantlon J. F., Brannon E. M. (2006a). The effect of heterogeneity on numerical ordering in rhesus monkeys. Infancy 9, 173–189 10.1207/s15327078in0902_5 [DOI] [Google Scholar]
- Cantlon J. F., Brannon E. M. (2006b). Shared system for ordering small and large numbers in monkeys and humans. Psychol. Sci. 17, 402–407 10.1111/j.1467-9280.2006.01719.x [DOI] [PubMed] [Google Scholar]
- Cantlon J. F., Brannon E. M. (2007a). Basic math in monkeys and college students. PLoS Biol. 5(12), e328. 10.1371/journal.pbio.0050328 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cantlon J. F., Brannon E. M. (2007b). How much does number matter to a monkey (Macaca mulatta)? J. Exp. Psychol. Anim. Behav. Process. 33, 32–41 10.1037/0097-7403.33.1.32 [DOI] [PubMed] [Google Scholar]
- Evans T. A., Beran M. J., Harris E. H., Rice D. F. (2009). Quantity judgments of sequentially presented food items by capuchin monkeys (Cebus apella). Anim. Cogn. 12, 97–105 [DOI] [PubMed] [Google Scholar]
- Horvath J. E., Weisrock D. W., Embry S. L., Fiorentino I., Balhoff J. P., Kappeler P., Wray G. A., Willard H. F., Yoder A. D. (2008). Development and application of a phylogenomic toolkit: resolving the evolutionary history of Madagascar's lemurs. Genome Res. 18, 489–499 10.1101/gr.7265208 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jordan K. E., Brannon E. M., Logothetis N. K., Ghazanfar A. A. (2005). Monkeys match the number of voices they hear to the number of faces they see. Curr. Biol. 15, 1–5 [DOI] [PubMed] [Google Scholar]
- Jordan K. E., Maclean E. L., Brannon E. M. (2008). Monkeys match and tally quantities across senses. Cognition 108, 617–625 10.1016/j.cognition.2008.05.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Judge P. G., Evans T. A., Vyas D. K. (2005). Ordinal representation of numeric quantities by brown Capuchin monkeys (Cebus apella). J. Exp. Psychol. Anim. Behav. Process. 31, 79–94 [DOI] [PubMed] [Google Scholar]
- Lewis K. P., Jaffe S., Brannon E. M. (2005). Analog number representations in mongoose lemurs (Eulemur mongoz): evidence from a search task. Anim. Cogn. 8, 247–252 [DOI] [PubMed] [Google Scholar]
- Merritt D., Maclean E. L., Jaffe S., Brannon E. M. (2007). A comparative analysis of serial ordering in ring-tailed lemurs (Lemur catta). J. Comp. Psychol. 121, 363–371 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merritt D. J., DeWind N., Brannon E. M. (in press). “The comparative cognition of number representation,” in Handbook of comparative cognition, eds Zentall T., Wasserman E. (Oxford: Oxford University Press; ). [Google Scholar]
- Olthof A., Iden C. M., Roberts W. A. (1997). Judgments of ordinality and summation of number symbols by squirrel monkeys (Saimiri sciureus). J. Exp. Psychol. Anim. Behav. Process. 23, 325–339 [DOI] [PubMed] [Google Scholar]
- Rumbaugh D. M., Savage-Rumbaugh S., Hegel M. T. (1987). Summation in the Chimpanzee (Pan Troglodytes). J. Exp. Psychol. Anim. Behav. Process. 13, 107–115 [PubMed] [Google Scholar]
- Santos L. R., Barnes J. L., Mahajan N. (2005). Expectations about numerical events in four lemur species (Eulemur fulvus, Eulemur mongoz, Lemur catta and Varecia rubra). Anim. Cogn. 8, 253–262 [DOI] [PubMed] [Google Scholar]
- Smith B. R., Piel A.K., Candland D. K. (2002). The numerical abilities of a socially-housed Hamadrayas Baboon (Papio hamadrays) and Squirrel Monkey (Saimiri sciureaus). Abstr. Psychon. Soc. 545, 81. [DOI] [PubMed] [Google Scholar]
- Wynn K. (1992). Childrens acquisition of the number words and the counting system. Cogn. Psychol. 24, 220–251 [Google Scholar]