DASH: A Method for Identical-by-Descent Haplotype Mapping Uncovers Association with Recent Variation

Abstract

Rare variants affecting phenotype pose a unique challenge for human genetics. Although genome-wide association studies have successfully detected many common causal variants, they are underpowered in identifying disease variants that are too rare or population-specific to be imputed from a general reference panel and thus are poorly represented on commercial SNP arrays. We set out to overcome these challenges and detect association between disease and rare alleles using SNP arrays by relying on long stretches of genomic sharing that are identical by descent. We have developed an algorithm, DASH, which builds upon pairwise identical-by-descent shared segments to infer clusters of individuals likely to be sharing a single haplotype. DASH constructs a graph with nodes representing individuals and links on the basis of such segments spanning a locus and uses an iterative minimum cut algorithm to identify densely connected components. We have applied DASH to simulated data and diverse GWAS data sets by constructing haplotype clusters and testing them for association. In simulations we show this approach to be significantly more powerful than single-marker testing in an isolated population that is from Kosrae, Federated States of Micronesia and has abundant IBD, and we provide orthogonal information for rare, recent variants in the outbred Wellcome Trust Case-Control Consortium (WTCCC) data. In both cohorts, we identified a number of haplotype associations, five such loci in the WTCCC data and ten in the isolated, that were conditionally significant beyond any individual nearby markers. We have replicated one of these loci in an independent European cohort and identified putative structural changes in low-pass whole-genome sequence of the cluster carriers.

Introduction

Recent advances in whole-genome sequence analysis have led to the discovery of many directly causal variants in small cohorts with highly penetrant diseases and stirred an interest in understanding the links between rare variation and phenotype. In complex diseases, however, independent testing of single rare variants could still be underpowered for statistically unequivocal genetic mapping. However, strategies that examine multiple common markers simultaneously can leverage combinations of co-occurring proximate alleles, or haplotypes, in much larger and readily available sets of samples and precisely infer rare variation. A haplotype consisting of common alleles would differ in frequency between cases and controls at causal loci whenever it co-occurs with a causal allele and serves as its tag. Approaches that exhaustively test such haplotypes,^1,2 or a local spectrum of haplotypes,^3–5 have been devised and tend to focus on relatively short haplotypes (below 20 SNPs) of high frequency that can be identified confidently. Methods that focus on haplotypes known to tag previously observed variants culminate in imputation of the untyped polymorphism on the basis of a densely typed reference panel.^6–8 This approach has been widely successful, particularly with the availability of the HapMap Project as a reference panel for common variants. However, imputation inherently depends on a reference panel that has haplotypes in common with the study samples as well as deeply typed markers that are good tags for the underlying causal variant. This has proven a hurdle for imputation in outlier populations⁹ and in recovering low-frequency alleles.¹⁰

Alternatively, current work focusing on cryptic relatedness has resulted in accurate methods for discovery of long genomic regions recently coinherited by pairs of individuals. These methods look for a nonrandom increase of alleles identical by state that indicates that the region is identical by descent from a recent common ancestor and identify these shared segments using a hidden Markov model (HMM)^11–13 or haplotype sampling.^14,15 Although the HMM schemes offer high resolution of detection (segments 1 centimorgan [cM] and longer), the implementations require examining all pairs of samples and are intractable for GWAS-sized cohorts. The latter technique, implemented in the GERMLINE algorithm¹⁴ (used here) and recently in the fastIBD algorithm,¹⁵ is computationally efficient enough to handle populations in the tens of thousands with trillions of putative identical-by-descent segments. In aggregate, these identical-by-descent segments can represent the totality of detectable recent haplotype sharing and could thus serve as refined proxies for recent variants that are generally rare and difficult to detect otherwise. Here, we propose a method that efficiently constructs pairwise identical-by-descent segments into multisample haplotype clusters that are oriented toward rare and uncommon variants and can be directly tested for association with phenotype without dependence on a reference panel.

We test our method with power simulations as well as genome-wide association with quantitative traits on a population isolated from the island of Kosrae, Federated States of Micronesia, where identical-by-descent sharing is pervasive and an ancestrally-close, densely typed reference panel is unavailable. We also analyze association with common diseases in the Wellcome Trust Case-Control Consortium (WTCCC), a large, well-studied cohort of individuals of European origin. The WTCCC data has previously been analyzed in several haplotype association studies with a localized haplotype-clustering method implemented in BEAGLE¹⁶ as well as a window- or gene-based search for short haplotypes.^17–19 Although we cannot compare our results directly to those findings without conditional analysis of the underlying markers detected by each method, we examine regions of association found by our method for loci identified in previous work and report putative candidate genes.

Material and Methods

We defined haplotypes as contiguous blocks of genomic material free of recent recombination and shared haplotypes as those haplotypes which have been coinherited by multiple individuals from a common ancestor. We distinguish these from haploid copies of the genome, which are phased genome-wide. We first formulated the problem of recovering shared haplotypes from pairwise identity by descent at a single locus and then extended this methodology for multiple loci. Note that because the construction of haplotype clusters is fundamentally dependent on the presence of identical-by-descent segments, we could partition individuals into different haplotype clusters even though their local marker alleles were identical by state because the larger region was not identified as being shared IBD. This is an important conceptual difference between our method and the resultant haplotype clusters and traditional identity by state (IBS) clustering techniques.

Formally, we considered N haploid copies of the genome numbered 1, …, N, along a genome with coordinates 1, …, M. We assumed a previously identified collection S = s₁, …, s_k of identical-by-descent segments in this phased data set, where each s_k is a quartet (h_k,h'_k,l_k,r_k) specifying a segment shared between haploid copies h_k, h'_k ∈ {1, …, N} along the genomic interval [l_k,r_k] ⊆ [1,M]. We observed that the set of interval boundaries B = {l_k} U {r_k} includes the only sites where identical-by-descent status changes in this cohort. We therefore denoted the unique elements of B = b₁ ≤ b₂ ≤ … b_|B| and partition the genome by these boundaries to the intervals {(b_i,b_i+1)} from i = 1 to |B|−1 where identical-by-descent status is fixed for the entire cohort.

Single-Locus Analysis

Within a given fixed identical-by-descent region (b_i,b_i+1) along the genome, we define a weighted undirected graph Gⁱ = (V, Eⁱ, Wⁱ) to capture known relatedness. The presence of a segment shared between two individuals who are identical by descent across this locus is represented as an edge between their respective vertices, with the weight of the edge corresponding to the total genetic length of the shared segment. Formally, V = {1 … N}, Eⁱ = { (h_k, h′_k) | l_k ≤ b_i, b_i+1 ≤ r_k} and for the edge eⁱ_k = (h_k, h′_k) ∈ Eⁱ, we set Wⁱ(eⁱ_k) equal to the genetic distance, in cM, from r_k to l_k. Assuming error-free data, a complete subgraph of Gⁱ would be indicative of a region commonly coinherited by all vertices in this subgraph and thereby represent a haplotype cluster shared by all individuals carrying the respective haploid copies. Furthermore, we would expect all connected components of Gⁱ to be such fully connected graphs because sharing a detectable identical-by-descent segment is transitive with regards to haploid copies. Under these assumptions, finding all shared haplotype clusters involves a simple search that identifies the set of all connected components, which would also be maximal cliques in Gⁱ.

In the presence of error, where identical-by-descent segments are incorrectly detected or undetected, we would expect to see false or missing edges in the graph. In particular, when the errors are not pervasive enough to generate an entire false haplotype cluster, we expect to observe partially-complete subgraphs similar to the error-free ideal. Practically, such error is typical around the boundaries of a true segment, where low marker density or insufficient detection specificity could result in shared segments that are called as extended to loci beyond the region that is genuinely shared or fall below the detectable segment length and be missed. Our goal is then to systematically identify a set of subgraphs that most likely represent shared haplotypes. In calculating this likelihood, we assume known rates of false-positive, true-positive, false-negative segments given a corresponding edge, e, as ϕ_FP(e), ϕ_TP(e), and ϕ_FN(e), respectively. We can then compute a likelihood-ratio for any subgraph g induced by Gⁱ as

$$L\left(g\right)=\frac{\prod _{e\in g}{\varphi }_{TP}\left(e\right)\prod _{e\in \overline{g}}{\varphi }_{FN}\left(e\right)}{\prod _{e\in g}{\varphi }_{FP}\left(e\right)},$$

where $e\in g$ and $e\in \overline{g}$are edges in g and edges in the complement of g (with respect to the complete graph induced by g only), respectively. This effectively calculates the probability that the graph is a clique with erroneous edges over the probability that the graph is entirely false, assuming edges are independent. We note that this formulation can easily incorporate error rates that vary with segment length by parameterizing the ϕ values according to the edge weight Wⁱ(eⁱ_k) for each examined edge, and we have shown in previous work that error is indeed directly correlated to segment length.¹⁴ In practice, we expect type I error measures to be segment-specific, and type II error to be specific to the population and the expected number of generations to the common ancestor.

In searching for the maximum likelihood subgraphs, we observe that the likelihood ratio is correlated to the density of that subgraph. Specifically, when the error rates are constant, the ratio is a function of the density d and the size of the graph:

$$L_{\text{fixed}}\left(g\right)=\frac{{\varphi }_{TP}^{\left|E\left(g\right)\right|}{\varphi }_{FN}^{\left|E\left(\overline{g}\right)\right|}}{{\varphi }_{FP}^{\left|E\left(g\right)\right|}}$$

$$\left|E\left(g\right)\right|=\frac{1}{2}\left|\mathrm{V}\left(g\right)\right|\left(\left|\mathrm{V}\left(g\right)\right|-1\right)d$$

$$\left|E\left(\overline{g}\right)\right|=\frac{1}{2}\left|\mathrm{V}\left(g\right)\right|\left(\left|\mathrm{V}\left(g\right)\right|-1\right)\left(1-d\right)$$

In light of this, we borrow a highly connected subgraphs (HCS) algorithm from the systems biology domain.²⁰ HCS relies on iteratively identifying the minimum cut in a graph, that is, the minimal set of edges whose removal divides the graph into two subgraphs with disjoint vertices and edges. The algorithm performs this min-cut recursively until it identifies a subgraph of desired density or a trivial subgraph that contains no edges to be cut. The algorithm provably identifies dense subgraphs with minimum diameter of two and, in practice, is fast when the underlying subgraphs have relatively few sparsely connected outlier vertices. This gives us an efficient starting point of dense subgraphs likely to be representing haplotypes. We make amendments to the algorithm specifically to encourage the largest likely haplotype cluster (Appendix A, Algorithm 1: Hierarchical Haplotype Clustering). In our case, we use a weighted min-cut so that our desired cut set is minimal in total weight rather than size.²¹ For each identified subgraph, we also perform a two-part postprocessing step to encourage homogenously connected graphs: (1) during clustering any vertex whose removal would increase the likelihood of the graph is excluded from it (Appendix A, Algorithm 1: Hierarchical Haplotype Clustering, lines 7–10) and (2) after clustering any vertex not in a subgraph but incident to a subgraph for which adding the vertex would increase its likelihood is incorporated into it (Appendix A, Algorithm 2, lines 5–9). The latter step is performed in a greedy fashion such that vertices are incorporated into larger subgraphs first, in accordance with our desire to identify the largest likely subgraphs. This procedure accounts for instances where the HCS threshold is not aggressive enough in removing the few outliers that do not majorly impact the overall density of a very dense subgraph. As computed in Algorithm 2 (Appendix A), our final output is then π_i, a set of subgraphs representing the largest likely haplotype clusters within the region (b_i,b_i+1), where each node is present in at most one subgraph.

Multilocus Analysis

We implement multilocus clustering as an extension to the single-locus method by scanning across consecutive fixed identical-by-descent regions (Appendix A, Algorithm 3). The first region (b₀,b₁) is analyzed with the single-locus algorithm and produces an initial set of haplotype clusters π₀. Subsequently, within a given fixed identical-by-descent region (b_i,b_i+1) we now have the set of subgraphs π_i−1 from the previous region as well as the graph Gⁱ representing identical-by-descent segments overlapping (b_i,b_i+1). Because the subgraphs in π_i−1 have already passed the likelihood ratio test at least once, we give them precedence in constructing π_i; this strategy also offers the benefit of tracking a single haplotype cluster as it evolves across multiple regions to minimize redundancy. For each subgraph in π_i−1, we generate a new subgraph g′ with an identical set of vertices as well all incident edges and additional incident vertices observed in Gⁱ and cluster g′ (Appendix A, Algorithm 3, lines 3–9). Whereas in the single-locus analysis we primarily used this procedure to clean established subgraphs of outliers, here it also removes or adopts any vertices that are newly incident on a previously established subgraph or have lost edges and should be disconnected from a previously established subgraph. In practice, the scan for removal or adoption can be made much faster by examining only those members of π_i−1 that were modified from (b_i−1,b_i) to (b_i,b_i+1). The resultant set of haplotype clusters from g′ is then incorporated into π_i and removed from Gⁱ (Appendix A, Algorithm 3, lines 10–11). Subsequently, the remaining graph can also be clustered in accordance with the single-locus approach and incorporated into π_i. In this way, multilocus subgraphs will tend to grow and shrink as the focus moves through consecutive fixed identical-by-descent regions and their respective graphs (Figure 1).

Figure 1.

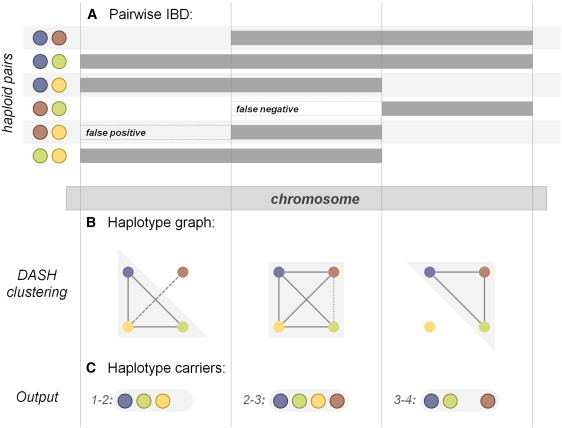
Method Workflow

A generalized representation of the DASH clustering algorithm across three windows (vertical lines) of a single chromosome.

(A) Pairs of haploid individuals (left, colored circles) and their respective identical-by-descent segments, if any. True segments are represented by a thick gray bar spanning at least one window; false positive and negative regions are labeled and unfilled.

(B) The corresponding haplotype graph for each respective window; the haploid individuals are represented as nodes (circles) (the color is consistent with that in A) and identical-by-descent sharing at the locus represented as edges (lines); false positive and false negative segments are dashed and dotted lines, respectively. Gray fill shows the most likely dense cluster detected by DASH.

(C) The final haplotypes determined by the algorithm for each window; color is consistent with that in (A) and (B).

Software Implementation

The method has been implemented in C++ and is freely available.

Data

Isolated Population from the Island of Kosrae, Federated States of Micronesia

A full description of the screening and genotyping of the Kosraen cohort was provided elsewhere.²² In brief, 3148 highly-related individuals, who represent >75% of the adult population on the island, were surveyed from the Pacific island of Kosrae in three separate screenings carried out in 1994, 2001, and 2003. Of these study participants, 2906 were successfully genotyped on the Affymetrix 500k array; data were generated at Affymetrix. Genotypes were called with the BRLMM algorithm and a minimum call rate of 95% was achieved, with a final set of 398,876 polymorphic autosomal markers. Twenty-six traits relating to metabolic syndrome were ascertained and are detailed in Table S6, available online. Phenotypes were adjusted for age and gender, transformed to approximate a normal distribution, and recalculated to Z scores. Previously, 17 of these traits were tested with the PLINK/QFAM-total framework,^22,23 and all have been tested with the EMMAX variance components model.^24,25 We compare our data to the EMMAX model results when referencing single-marker analysis in study participants from Kosrae. Analysis was determined as exempt from institutional review board approval at Columbia University.

Data from the WTCCC

Data ascertainment and cleaning for the WTCCC cohort have been described in detail previously.²⁶ The WTCCC data we used consist of genotypes ascertained in 2000 cases for each of seven common disease and 3,000 shared controls from the 1958 Birth Cohort (58C) and National Blood Services (NBS). Genotyping was performed on the Affymetrix 500k array and called using the Chiamo algorithm. After excluding the 30,956 SNPs and 815 individuals that did not pass the WTCCC's quality thresholds, our final data set consisted of 16,179 individuals and 455,566 autosomal markers. The traits studied and their respective sample sizes are listed in Table S7. We tested this final set of markers for association by splitting up the cohort in two ways: by using only the 58C and NBS samples as controls (controls only) and by using all other samples—58C and NBS and cases for traits other than the one tested—as controls (pooled controls).

Simulation of Rare Causal Variants

We sought to measure the performance of our algorithm within a realistic simulation of rare causal variants with few nearby low-frequency proxy SNPs. In particular, we designed our simulation to require as few assumptions as possible about the underlying haplotype space to maintain an unbiased analysis. Using a typical framework for testing variant imputation,^6,27 we randomly selected rare alleles to be our simulated causal mutations. For each such causal allele, we simulated a dichotomous trait from existing genotype data by randomly assigning case or control labels to respective individuals such that the causal allele has a prescribed effect size. We then hid all rare variants from the analysis and measured the power of various methods to recover their association signal at a fixed level of statistical significance.

In each population we randomly selected 500 variants for each of 23 designated minor allele frequencies (MAFs) from 0.5% to 4.9% (in steps of 0.2%). To obtain variants that are likely independent, we divided the genome into 1 Mb blocks and for each designated frequency selected a single variant closest in frequency; we then randomly selected a subset of 500 such variants. In both cohorts, the chosen variants were within 0.1% of the designated frequency, and the root sum of squared differences around each designated frequency had been <0.05%. For each selected variant, we constructed a dichotomous phenotype with fixed direct allelic p value cutoff under an additive disease model. Specifically, the cutoff was set to 2.5 × 10⁻²⁰ = 0.5 × 0.05 × (10⁻⁹)² to detect a two-sided, genome-wide significant result with 0.5-fold reduction of significance between the selected causal variant and any nearby genotyped marker. We considered the one-degree-of-freedom χ² statistic Z² = 85 required for this significance level while fixing the frequency, p, of the risk allele in the entire cohort, the fraction, f, of cases and the total sample size, N, of cases and controls. We then solved for the necessary observed deviation, Δ, of case allele frequency from its expected value,$\Delta =\text{z}/\sqrt{2Nf\left(1-f\right)p\left(1-p\right)}$, so that a Z score of Z is attained.

In Kosrae, where we fixed the number of cases and total samples at 500 and 2,906, respectively, the resultant causal variants range in relative risk from 4.89 (at 0.4% MAF) to 2.44 (at 4.8% MAF). In the WTCCC cohort, we kept the 500:2,906 ratio of cases to total samples with 2,783 assigned cases and 13,396 assigned controls to each simulated phenotype. The relative risks ranged from 2.62 to 1.56. We then removed all markers below 5% MAF, including those marked as directly causal in our analysis. Removing all markers in this manner forces incomplete tagging between the direct causal variant and remaining SNPs, simulating our desired scenario where the untyped variant might not be well represented in the study set. The final test set consisted of 11,500 individually simulated phenotypes for each population; 277,243 SNPs remained in the Kosrae data and 357,594 SNPs in the entire WTCCC data (Table S1). After hiding low-frequency SNPs, we phased both data sets by using the BEAGLE software package with default parameters.

Methods Compared

Identical-by-Descent Detection and Haplotype Clustering

We used the GERMLINE algorithm for all estimates of identical-by-descent segments in our analysis.¹⁴ We ran GERMLINE with parameters tuned to identify short identical-by-descent segments of 1 cM or greater; genetic distances were taken from the fine-scale recombination map estimated by the HapMap project.²⁸ We also set a window size of 32 sites and one allowed mismatching site (command-line flags: ‘-haploid -min_m 1 -bits 32 -err_hom 1 -err_het 1’). These parameters are much less restrictive than is typical because we wanted to enrich for relatively short haplotypes. To minimize the overall number of parameters and potential biases, we executed DASH on the identical-by-descent segments as if we had no prior information on identical-by-descent error, and all segments reported as identical by descent were assumed truly so (ϕ_FP = 0, ϕ_TP = 1, ϕ_FN = 1; 1 SNP minimum window size), which effectively reports all connected components of any size as haplotype clusters. Overall, the DASH analysis identified 330,189 and 787,046 haplotype clusters with a frequency greater than 0.1% in the Kosrae and the WTCCC data, respectively.

The analysis was run in parallel batches, and 10% of the genome required approximately 14 hr to phase with BEAGLE, 29 hr for the GERMLINE identical-by-descent discovery, and 64 hr for the DASH haplotype clustering on a single 3 GHz Intel Xeon node with 16 Gb of RAM.

Imputation of Untyped Variants from HapMap Reference

We compared DASH directly to the SNP array SNPs as well as to imputed variants from a corresponding HapMap reference panel. For consistency with the phasing used for GERMLINE, we also performed the imputation with the BEAGLE software package in the final pruned test set. Because of restrictions on available computation power, we performed the imputation in batches of 500 randomly chosen individuals with default parameters and kept all imputed calls that had a minimum estimated r² of 0.9. As a reference panel, we used 1,387,466 phased markers from the HapMap phase 3 panels of 113 European ancestry (CEU) samples and 170 East Asian ancestry (JPTCHB) samples for imputation to the WTCCC and Kosrae samples, respectively. In both cohorts, the imputation roughly doubled the number of variants, resulting in 606,051 total markers in the Kosrae data and 706,312 total markers in the WTCCC data. We observe that over 80% of the hidden variants in each cohort are typed in the reference panel; this provides the opportunity for many of the causal variants to be imputed directly. This effectively implies a lower bound of 80% on association power given perfect imputation and reference. Although an optimal strategy would incorporate imputation uncertainty directly into the association test, this would require evaluating and comparing a variety of proposed testing models¹⁰ that are outside the scope of our analysis. In light of this, we stress that our threshold-based analysis strictly measures the power of high-quality imputed variants rather than that of an ideal imputation-based association study.

Assessing Significance

To establish significance for each method and cohort, we performed 1000 genome-wide permutations of an allelic χ² association test¹³ and identified an empirical genome-wide significance threshold at a family-wise error rate of 0.05 (Table S1). We note that although there are many fewer haplotype clusters than single markers, the empirical threshold p value for genome-wide haplotype clusters was consistently lower than that of SNPs (Table S1). This suggests the redundancy is higher among the SNP tests as a whole than among the haplotype clusters. Standard Bonferroni correction that takes into account only the sizes of these sets can thus be an inconsistent measure of the testing burden they incur. For each method and frequency window of 500 markers, we then measured association with the respective simulated phenotype of any markers within a 1 Mb region of the true causal variant. The percentage of such regions that contained an association beyond genome-wide significance was then taken as the estimate of power for that frequency.

Real-Data Association Analysis

Variance Components-Based Association in Kosrae

Because of the significant degree of relatedness between individuals on Kosrae, we used the EMMAX program²⁴ to perform the association testing in real data. EMMAX uses a pairwise relatedness matrix to incorporate random effects into the association test. This approach has been shown to be very effective in general populations²⁹ and specifically in Kosrae.²⁵ We used a relatedness matrix constructed from pairwise genome-wide identical-by-state scores and ran EMMAX with default parameters for all analysis.

Conditional Analysis of Haplotype Clusters

In instances where multiple significant haplotype clusters overlapped a single locus, we performed a step-wise conditional analysis to identify independent haplotype clusters. Iterating in order of decreasing significance, we introduced each cluster as a covariate for all remaining clusters within a logistic regression test in PLINK or directly as a fixed effect in EMMAX for the WTCCC and Kosrae data, respectively. Any haplotype clusters that remained genome-wide significant after conditioning were reported as independent.

To identify whether a cluster association was more significant than typed markers, particularly in regions with multiple independent association signals, we performed two types of conditional analysis. First, we iteratively conditioned the cluster of interest on each SNP within 1 Mb of either physical cluster boundary (or from chromosome 6:20–40 Mbp for any cluster within the MHC) and reported the association that minimizes conditional significance. This measure represents the residual haplotype cluster signal given any single nearby marker, and we refer to it as the conditioned p value. Separately, we performed a step-wise logistic regression where all genome-wide significant SNPs were iteratively added as additional covariates until no such SNPs were present and reported the final residual haplotype cluster association. This measure represents the residual haplotype cluster signal given all independently genome-wide significant markers, and we refer to it as the stepwise conditioned p value.

Fine-Mapping of Nominal Haplotype Clusters

We assess the utility of very short haplotype clusters that cannot be efficiently detected on a genome-scale by performing a second-stage short haplotype association analysis in regions of nominal significance. We identified any haplotype associations at most two orders of magnitude less significant than the genome-wide threshold and established nonoverlapping regions of interest within 500 kb of the haplotype boundaries. We then reran GERMLINE identical-by-descent detection with no minimum length threshold and a window size of 10 markers with no allowed mismatches (command-line flags: ‘-min_m 0 -bits 10 -err_hom 0 -err_het 0′), effectively looking for ten SNP haplotypes with complete IBS. We then ran the DASH haplotype clustering and association in the same way as described above (including testing for independence) and retained only those clusters that had surpassed the significance threshold established in genome-wide analysis and were conditionally independent of any previously identified clusters in the region.

Follow-Up in Low-Pass Sequencing Pilot

Seven Kosraen individuals were lightly sequenced using the SOLiD System with 50 bp and 35 bp mate-paired reads for an average of 3×–6× sequence coverage of nonredundant, uniquely placed pairs for each individual.³⁰ Calling and variant quality filtering was done in all samples together using the Genome Analysis Toolkit³¹ following the best practices of the 1,000 Genomes Project.

Results

Estimated Association Power

We performed the causal variant simulation in both cohorts and report average power to recover the planted variant using four association techniques in Figure 2. Figure 2A shows power in the Kosraen cohort to be significantly higher for either of the DASH-based techniques at all risk-allele frequencies, particularly at the low end of the spectrum where testing DASH and SNPs together has a 40×, 5×, and 2× increase in power over SNPs alone for the risk-allele frequencies of 0%–1%, 1%–2%, and 2%–3%, respectively. We caution that although the relative power increase is high, the absolute power for rare variants below 1% MAF is still in the low range of 0%–11%. High-quality imputed variants from the HapMap East Asian panel offer greater power over the SNP-based association but still underperform when compared to DASH and SNPs and, likewise, when compared to DASH and imputed variants together. Looking at the detailed power distribution (Figure S5A), we see that the power of DASH alone converges with imputation and single-marker power at 4.5% MAF and becomes less powerful subsequently. However, testing DASH in conjunction with the other methods always offers more power than testing the methods separately, and DASH and imputation exhibit approximately 20% more power across the entire risk-allele-frequency spectrum.

Figure 2.

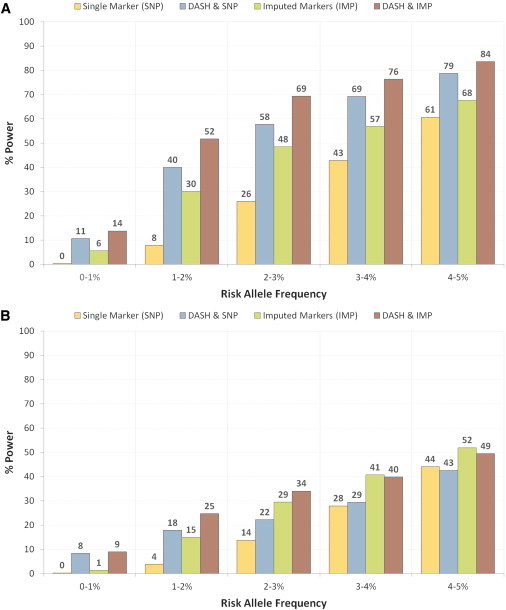
Method Comparison of Rare-Variant Association Power in One Isolated and One Outbred Cohort

Power to detect a single rare variant was estimated by simulating causal sites at risk-allele frequency range of 0%–5% with fixed direct allelic significance of 2.5 × 10⁻²⁰. All variants below 5% MAF were subsequently hidden from analysis, and power to detect association with remaining proxy markers was measured. Tested separately were single markers (yellow, SNP), high-quality imputed markers from HapMap reference and single markers (green, IMP), DASH haplotypes and single markers (blue DASH and SNP), and DASH haplotypes and high-quality imputed markers (DASH and IMP). For each method, power was measured as a percentage of variants for which a genome-wide significant proxy was identified (see Material and Methods).

(A) Results in isolated cohort from Kosrae, Federated States of Micronesia (imputed from JPTCHB reference).

(B) Results in European cohort from WTCCC data (imputed from CEU reference).

Figure 2B shows the power distribution in the WTCCC cohort and relatively decreased power across all methodologies. As in the Kosrae analysis, though, we again see that using DASH in conjunction with the other methods increases power within the low-frequency range (allele frequencies of 0%–4% in comparison to using single markers and 0%–3% comparison to using imputation). However, if we examine the detailed distribution in Figure S5B, we see a conspicuous decrease in power when testing DASH alone beyond 1.5% MAF, and the power level eventually intersects with single-marker tests at 3%. This is primarily an artifact of the minimum identical-by-descent-length length threshold we place on GERMLINE; this threshold de facto restricts the potential for DASH to capture shorter, more ancient haplotypes. Because higher-frequency variants tend to be older³² and therefore lie on the background of more ancient haplotypes, this thresholding effect will decrease the power of DASH to capture such alleles and result in the decreasing power curve. Nevertheless, testing the DASH haplotype clusters together with imputed variants maintains power gains over imputed markers of 8×–1.5× in the MAF range of 0%–1.5% and decreased power in the MAF range of 3.5%–5%; the average decrease is 0.95×.

Robustness to Missing Genotypes and Haplotype Phasing Error

We sought to examine the effect that missing genotypes and phasing error can have on the power of the association methodologies. We focused on the 2% risk-allele frequency in Kosrae; at this frequency all methods had appreciable power to detect the planted variants and again performed the power simulation (including phasing, identical-by-descent detection, haplotype clustering, and imputation) while introducing increasing rates of missing genotypes. Figure 3A shows the effects on power caused by randomly marking increasing subsets of SNPs as missing without changing the multiple-testing burden. When SNPs were randomly labeled as missing (solid line), we see little effect on power in any of the methods. Even when 20% of the SNPs are excluded, power dropped by a factor of 0.85, 0.91, and 0.97 for SNPs, tests with imputed markers, and DASH, respectively, in comparison to the same tests with no missing markers. This limited decline demonstrates the high degree of correlation between the ascertained SNPs that allows for such robustness to missing genotypes. On the other hand, when we labeled the SNPs missing in increasing order of allele frequency (Figure 3A, dashed line) to simulate incomplete ascertainment of low-frequency variants, we see a significant decrease in the power of association from SNPs and imputed markers but we do not see this in the DASH analysis. When comparing simulated data sets with no missing markers to those in which 20% of the SNPs were excluded, the most extreme scenario, we see power drop by a factor of 22.3, 1.4, and 1.1 for SNPs, imputed markers, and DASH, respectively. This is consistent with the general trend of an increased association power of DASH haplotype clusters for tagging low-frequency variants.

Figure 3.

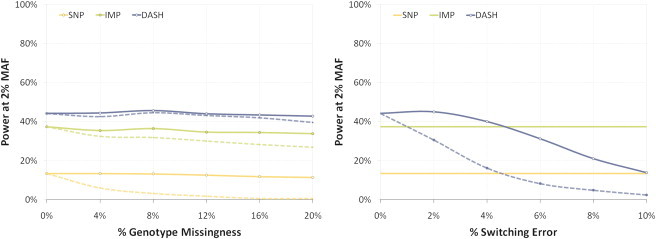
Method Comparison of Association Power in the Presence of Missing Genotypes and Phasing Error

Power estimates (as in Figure 2) for causal variant at 2% risk-allele frequency are plotted with increasing levels of missing genotypes and phasing error. For both fault types, three methods are compared: single marker (yellow, SNP), imputation from HapMap JPTCHB (green, IMP), and DASH haplotypes (blue, DASH).

Left: power as a function of percentage of variants excluded at random (filled line) and in increasing order of minor allele frequency (dashed line).

Right: power as a function of probability that a heterozygous site will be switched (filled line) and probability a heterozygous site will switch the subsequent haplotype (dashed line); SNP and IMP methods unaffected by haplotype structure are shown for comparison.

Because the GERMLINE algorithm works explicitly on phased data, the presence of phasing errors could significantly impact the sensitivity of identical-by-descent detection and subsequently introduce noise into the DASH clusters. To measure this impact, we introduced a random chance of phasing error into the input haplotypes for GERMLINE and, as we did in the previous analysis, examined the effect on power at a 2% risk-allele frequency in the Kosrae data. Figure 3B shows power measured across increasing rates of two types of error. The solid line represents data where heterozygous sites were flipped without effecting adjacent haplotypes, and the dashed line represents the traditional scenario of a flip also inducing a phase switch in all subsequent markers. Because the other two methods are not affected by phasing error, they are plotted unchanged for reference. We see that both types of phasing error have an effect on the power of DASH, and power decreases by a factor of 0.69 for a 2% haplotype switch rate and slightly for a 4% single-point flip rate. We stress that this demonstrates the decrease in power is an effect of phasing error in excess of what is already inherent in the data.

Haplotype Cluster Associations to Real Phenotypes

We identified a number of loci with haplotype-based associations to real phenotypes in the two data sets and explore these in more detail here. Table 1 details all of the haplotype cluster associations identified in either data set that had genome-wide significance and had strong residual signal when conditioned on single markers overlapping the region. Specifically, we compared p values of the DASH clusters at each such locus to the localized DASH analysis, listing the cluster which is most significantly associated from either analysis of that locus. We further list the most significant association with a single marker from the original GWAS within 1 Mb of the physical haplotype boundaries (or chromosome 6:20–40 Mbp for clusters in the MHC) as well as the conditional p value, representing the residual association signal of the cluster given any individual markers in the region (see Material and Methods). For the WTCCC data (Table 1), all p values shown are from the pooled controls analysis which used cases for alternative traits as controls. We detail the DASH clusters that are significant but partially explained by single-marker association in Tables S2–S5. Overall, association results across the entire genome (Figures S3 and S4) demonstrate a distribution with low genomic inflation (Figures S1 and S2).

Table 1.

Conditionally Significant Haplotype Associations Identified in WTCCC and Kosraen Cohorts

Trait	Locus	f	OR	P DASHa	P GWASb	Conditional P DASHc	Published Relevant Associations
WTCCC Cohort
CD	16q12	7.2%	1.80	1.7 × 10−24	7.5 × 10−19	3.0 × 10−10	NKD1
T1D	6p21	0.6%	3.94	4.2 × 10−24	4.9 × 10−175	2.7−13	MHC
RA	6p21	2.4%	2.35	1.0 × 10−23	9.4 × 10−64	1.8 × 10−16	MHC
CAD	6q26	1.7%	2.17	4.1 × 10−14	5.9 × 10−5	2.6 × 10−9	SLC22A3, LPAL2, LPA
T2D	11p14	0.3%	3.79	1.9 × 10−10	3.1 × 10−3	4.3 × 10−8
Kosraen Cohort
uric acid	11q13	1.8%	0.13	6.6 × 10−49	9.6 × 10−35	2.9 × 10−17	SLC22A11, SLC22A12
HBA1C	16q24	9.9%	0.47	2.5 × 10−24	6.3 × 10−8	2.1 × 10−17
triglycerides	11q23	27.4%	1.31	2.2 × 10−15	3.0 × 10−12	6.8 × 10−5	APOA1, APOA5
total cholesterol	6q26	13.4%	1.33	6.9 × 10−11	2.5 × 10−6	4.9 × 10−6	LPA
total cholesterol	12q23	2.7%	0.54	9.1 × 10−11	5.9 × 10−4	1.6 × 10−8
LDL	12q23	2.8%	0.59	1.0 × 10−8	1.0 × 10−4	2.5 × 10−6
LDL	19q13	1.0%	0.45	2.1 × 10−8	1.7 × 10−6	1.0 × 10−3
folate	19p13	3.2%	1.68	6.4 × 10−8	6.7 × 10−5	5.1 × 10−5	LDLR; TYK2
total cholesterol	11q23	23.5%	1.21	8.5 × 10−8	2.0 × 10−5	9.1 × 10−4	APOA1, APOA5
uric acid	19q13	1.6%	0.46	9.3 × 10−8	3.4 × 10−3	9.5 × 10−6

^aMost significant association in locus, conditionally independent of all genome-wide significant and local haplotypes on chromosome.

^bMost significant nearby single-marker association (see Table S2 for breakdown by type of controls).

^cLeast significant haplotype association after conditioning on all nearby single markers.

In the Kosrae data, DASH identified eight association loci, with the localized test strengthening three of these and uncovering two additional genome-wide significant regions for a total of ten unique regions. The strongest association we identified was a cluster at 11q13 for uric acid (p value = 5.5 × 10⁻⁴⁸) that we have refined in a separate work and found to be four-fold more significant than any previously associated SNP at that locus.²⁵ We also identified regions with no significant single-marker associations and describe these in detail. A region at 12q23 containing a single cluster was strongly associated with both total cholesterol (p value = 9.1 × 10⁻¹¹) and low density lipoprotein (LDL) cholesterol (1.0 × 10⁻⁸). This cluster overlaps the Farnesoid X-activated receptor NR1H4 (MIM 603826), which regulates the catabolism of cholesterol into bile acid and is a likely candidate gene. Two clusters at 16q24 associated with hemoglobin levels (HBA1c) were localized into a single core cluster that was strongly significant with a p value of 2.5 × 10⁻²⁴. This cluster lies nearby the interleukin-17 receptor IL17C (MIM 604628), which is involved in the TnF pathway and has been linked with autoimmune diseases in lower organisms.

In the WTCCC data, we identified twelve unique associations of which five were conditionally more significant than any nearby single markers. Two such associations, for rheumatoid arthritis (MIM 180300) and T1D (MIM 222100), were identified in the MHC region significantly independent of any individual SNP (conditional P DASH column) or combination of genome-wide significant SNPs (Tables S2–S3). The presence of multiple causal signals is not unexpected in this region because it exhibits complexity in linkage disequilibrium (LD) structure and enrichment for disease associations. Three other haplotype clusters were identified outside this region; one refined a well-known association of Crohn disease (MIM 266600) to NKD1 (MIM 607851) and another was intergenic at 11p14 with no significant nearby single-marker tags. Lastly, we found a genome-wide significant cluster associated with Coronary Artery Disease (MIM 607339) at 6q26 with a p value of 8.2 × 10⁻¹⁵, much stronger than the most significant single-marker variant (associated at 5.9 × 10⁻⁵). Indeed, this region has recently been mapped to the SLC22A3-LPAL2-LPA gene cluster (MIM 604842, 611682, and 152200, respectively) in a genome-wide haplotype association study that focused on short 10 SNP haplotypes,¹⁷ although it found much lower significance (4.34 × 10⁻⁸ with 6-degrees-of-freedom test) than we find here.

Figures S6 and S7 show the region of association signal at each of the detected loci in detail. In most instances, the haplotype clusters are bounded by recombination hot spots as would be expected; however, some can span multiple such hot spots, particularly in the Kosraen population, for which haplotypes tend to be longer and decay more slowly (e.g., T2D (MIM 125853) at 11p14, uric acid at 11q13, folate at 19p13). We also note that a number of the clusters do not overlap any markers of nominal significance. In particular, two of the five significant clusters identified in the WTCCC data do not overlap nominally significant markers (CAD at 6q26 and T2D at 11p14), as well as four of the ten significant clusters identified in the Kosrae data (total cholesterol at 12q23, LDL at 12q23, folate at 19p13, and uric acid at 19q13). These regions generally have several nominal clusters surrounding those that are significant at a genome-wide level but do not appear to have any overlapping single-marker tags.

Potential Effects of Genotyping Error

Previous analysis of the WTCCC data identified a number of spurious associations that were a result of genotyping error,^16,33 and such sites even introduce false short-haplotype associations in some instances. Identifying such sites conclusively has necessitated reanalyzing the genotype call intensity plots by hand or recalling the genotypes with diverse methods. Qualitatively, the fact that significant associations identified by DASH are almost all in regions implicated by independent studies suggests that the method is robust to false-positive associations. However, because we only filtered out those markers that failed standard metrics, this possibility of confounding genotyping error is still a serious concern. To estimate the potential effects of such error, we retested all regions harboring genome-wide significant haplotype clusters on subsets of markers with much more stringent filtering criteria. If the original signal is robust and not the result of calling error, we expect strong correlation between the cluster identified in the original and filtered data. Specifically, we established two minimum call-confidence thresholds (0.95 and 0.98) and designated any markers with fewer than 98% of individuals called below the respective thresholds as entirely missing (excluding 12.6% and 17.0% of markers, respectively). For each region, we then reran the GERMLINE and DASH analysis on this filtered data and reported the strongest r² correlation between any resultant clusters and the original associated clusters. For the genome-wide analysis (Table S2), we find that three out of 11 haplotype clusters are significantly disrupted (r² < 0.8) by the 0.95 call-confidence threshold, and an additional cluster is disrupted by the 0.98 threshold. This lack of correlation implies that low-confidence calls that might have been poorly genotyped are contributing to some of the original haplotype cluster associations. However, in the localized analysis (Table S3), where the underlying identical-by-descent segments are very short and exact, none of the identified clusters were significantly affected by strict filtering. Overall, none of the conditionally significant associations we report in Table 1 fall below an r² of 0.98 under either filtering scenario, suggesting that the underlying haplotypes are not the spurious result of low-confidence genotype calls.

Replication of Associated Kosraen Locus in a European Cohort

We have sought replication of the independent haplotype cluster associations from the Kosraen data set in an independent European cohort from the Diabetes Genetics Initiative (DGI).³⁴ The cohort consists of 3,142 Scandinavian samples genotyped on the Affymetrix 500k platform and phenotyped for 18 clinical traits. In particular, 480 of the DGI samples were phenotyped for HBa1c, for which we identified a highly significant cluster in the Kosrae data at 16q24 (Table 1 and Table S8). We performed a standard DASH analysis on the DGI samples according to the previously described phasing and haplotype construction protocol. Looking within 1 Mb of the boundaries of the Kosraen haplotype cluster, we identified a nominally significant overlapping cluster spanning 16 SNPs from 87,404,625 to 87,560,132. Though it is significantly less frequent at 0.64%, the cluster is associated with an allelic p value of 0.015 (after Bonferroni correction) and stronger effect size in the same direction (Table S8). Additionally, a Kolmogorov-Smirnov-like analysis³⁵ across the entire chromosome tested sets of replication clusters that lie increasingly further away from the initial association for enrichment of significant associations and showed that haplotype clusters at this locus in the DGI were generally of elevated significance compared to the null hypothesis. We did not observe any single-marker associations that surpassed their respective multiple-testing burden in the region.

Putative Causal Mutation and Structural Variation

To assess the utility of these haplotype cluster associations in the context of whole-genome sequence data, we analyzed seven Kosraen genomes that had been lightly sequenced (unpublished data), three of which were carriers for the HBA1c associated cluster. We identified seven nonsynonymous single-nucleotide variants (SNVs) present only in carriers of the haplotype cluster, four of which were not in dbSNP (Table S9), and classified these according to their effect using the SiFT tool.³⁶ We used the Sequenom iPLEX genotyping platform to assay these sites in 90 islanders that were selected to be a mix of haplotype cluster carriers at the extreme end of the respective phenotype distribution and noncarriers near the phenotype mean. Of the four sites that were typed as polymorphic, none showed strong correlation to cluster status or significant residual association (Table S9). Because of the low sensitivity of variant detection in the sequencing pilot, these findings are still inconclusive.

Focusing on copy number variant (CNV) analysis in the associated region, we find a number of long heterozygous deletions contained within the HBA1c associated haplotype that are not present at such length in the noncarriers. Figure S8 shows the CNV calls within 500 kbp of the haplotype region and normalized coverage as well as the algorithmic segmentation of the region into discrete heterozygous deletion calls (p < 0.05). Overall, we see that the cluster carriers have three times more deleted content per sample overlapping the associated region and that there are a number of regions present in two or more carriers explicitly (Figure S9B). For comparison, only 3.3% of the mapped autosomal genome contains a CNV overlapping in at least two of samples, and 0.2% contains a CNV explicitly in two or more of these carriers. The presence of these carrier-specific subregions is highly unusual, and they harbor a number of candidate gene targets for this trait (Figure S9G).

Discussion

Haplotypes can provide insights into underlying LD structure at a locus of interest and help map rare causal loci that are not well tagged by a single common marker. With high-density array data, using identical-by-descent segments as building blocks we can base haplotype identification in recent sharing that is likely to be accurately detected. We have presented here a method that uses graph techniques to rapidly construct haplotype clusters out of segments shared IBD between pairs of individuals.

We have explored the power of this method through simulations in two very different data sets: one isolated (Kosrae data set) with an abundance of long identical-by-descent segments and one large and outbred European cohort (WTCCC data set). In the isolated population, we have demonstrated haplotype cluster association to be much more powerful than direct or imputed association for all variants below 5% risk-allele frequency. In the European samples, where identical-by-descent segments are likely to be much less recent and therefore harder to detect, we see that haplotype association is still powerful for tagging rare variants. Additionally, haplotype association provides orthogonal information to directly typed or imputed markers and testing both is the most powerful strategy for risk alleles up to 4% in frequency.

Lastly, we have shown this approach to be effective at uncovering regions of association in real data. In the Kosrae data, we identified ten independent loci with haplotype cluster associations that were more significant than any surrounding individual markers. Half of these loci were in regions harboring no significantly associated SNPs, and one of these loci replicated in an independent European cohort. In the WTCCC data, we identify five conditionally independent haplotype clusters; two of the clusters were in regions not implicated in the original study and one of these was recently identified in a separate multimarker analysis with additional samples.¹⁷ The identified clusters provide us with the boundaries of the associated region as well as the expected carrier individuals. Researchers can use such information in conjunction with LD structure and SNP tagging to select samples and define region boundaries when they use fine-mapping techniques in follow-up studies.³⁷ Indeed, whole-genome sequencing of carriers of one cluster revealed a significant enrichment in low copy number that identified candidate genes for additional follow-up.

Overall, the haplotype-based approach provides a bridge between the availability of tens of thousands of samples with densely-typed genotypes and the emerging sequence-based studies that attempt to capture rare causal variants. For the former, our algorithm dramatically increases power to discover putative associations with rare underlying variants. For the latter, haplotypes emphasize features of the data that are practically useful in study design. Looking forward, when thousands of fully sequenced genomes are readily available an emphasis on transmitted regions rather than individual markers can inform us of other potential underlying causes, such as structural variants, that are not yet straightforward to identify or test.

Appendix A

Algorithm 1: Hierarchical Haplotype Clustering

clusterGraph:

 Input: a subgraph g induced by Gⁱ

 if |V(g)| < 2 or E(g) = {} then

 return {}

 else if L(g) ≤ 1 then

 { g^a, g^b } ← subgraphs of g after single weighted minimum cut

 return { clusterGraph(g^a), clusterGraph(g^b) }

else

 for each vertex v in g do

 if L(g \ {v}) > L(g) then mark v as removable end if

 end for

 remove all marked v from g

 return { g }

end if

Algorithm 2

DASH-singleLocus:

 Input: relatedness graph Gⁱ for fixed identical-by-descent region i.

 for each connected component g in Gⁱ do

 π_i′← clusterGraph(g)

 for each subgraph c in π_i′ in decreasing order of size do

 for each vertex v incident on c and not in a subgraph, in decreasing order of degree do

 if L(c U {v}) > L(c) then c ← c U {v} end if

 end for

 done for

 π_i ← { π_i, π_i′ }

 done for

 return π_i

Algorithm 3

DASH-multiLocus:

 Input: set of relatedness graphs { G⁰ … Gⁿ } for all identical-by-descent regions 0 to n

 π₀ ← DASH-singleLocus(G⁰)

 for i ← 1 to n do

 for each g in π_i−1 do

 Create new empty subgraph g′

 for each vertex v in V(g) do

 V(g′) ← { V(g′), v }

 add all edges and vertices incident on v in Gⁱ to g′

 done for

 g′ ← clusterGraph(g′)

 π_i ← { π_i, g′ }

 Gⁱ ← Gⁱ / g′

 done for

 π_i ← { π_i, DASH-singleLocus(Gⁱ) }

 done for

Web Resources

The URLs for data presented herein are as follows:

• 1,000 Genomes Project, http://www.1000genomes.org/

• Best Practice Variant Detection, http://www.broadinstitute.org/gsa/wiki/index.php/Best_Practice_Variant_Detection_with_the_GATK_v2

• DASH, http://www.cs.columbia.edu/∼gusev/dash/

• GERMLINE, http://www.cs.columbia.edu/∼gusev/germline/

• Online Mendelian Inheritance in Man, http://www.omim.org/

• PLINK, http://pngu.mgh.harvard.edu/∼purcell/plink/

• Wellcome Trust Case Control Consortium, http://www.wtccc.org.uk