Thermodynamic and kinetic basis for recognition and repair of 8-oxoguanine in DNA by human 8-oxoguanine-DNA glycosylase

Abstract

We have used a stepwise increase in ligand complexity approach to estimate the relative contributions of the nucleotide units of DNA containing 7,8-dihydro-8-oxoguanine (oxoG) to its total affinity for human 8-oxoguanine DNA glycosylase (OGG1) and construct thermodynamic models of the enzyme interaction with cognate and non-cognate DNA. Non-specific OGG1 interactions with 10–13 nt pairs within its DNA-binding cleft provides approximately 5 orders of magnitude of its affinity for DNA (ΔG° approximately −6.7 kcal/mol). The relative contribution of the oxoG unit of DNA (ΔG° approximately −3.3 kcal/mol) together with other specific interactions (ΔG° approximately −0.7 kcal/mol) provide approximately 3 orders of magnitude of the affinity. Formation of the Michaelis complex of OGG1 with the cognate DNA cannot account for the major part of the enzyme specificity, which lies in the k_cat term instead; the rate increases by 6–7 orders of magnitude for cognate DNA as compared with non-cognate one. The k_cat values for substrates of different sequences correlate with the DNA twist, while the K_M values correlate with ΔG° of the DNA fragments surrounding the lesion (position from −6 to +6). The functions for predicting the K_M and k_cat values for different sequences containing oxoG were found.

INTRODUCTION

A great wealth of structural data on the proteins that interact with DNA or RNA is currently available. It is now clear that both the structures of free proteins and nucleic acids and their conformational changes upon binding play important roles in the recognition of specific DNA and RNA sequences by proteins [(1–4) and references therein). However, X-ray structural analysis of protein–nucleic acid interactions does not provide quantitative estimates of the relative contribution of individual contacts or different types of contact to the total affinity of an enzyme for its nucleic acid target. To carry out a detailed quantitative analysis of energy of protein–nucleic acid interactions we have developed an approach of stepwise increase in ligand complexity (SILC), which provides information on the relative contributions of each nucleotide and its structural elements to the total enzyme affinity for DNA ligands [reviewed in refs (3,5)]. These ligands can be either cognate (i.e. containing specific features recognized by the particular protein, such as a recognition sequence of a restriction endonuclease, or a DNA lesion for DNA repair proteins) or non-cognate (general DNA containing no such specific features). Using the SILC approach, we have studied a number of DNA-dependent enzymes including those not specific for DNA structure or sequence such as Escherichia coli RecA (6), specific for DNA structure but not for sequence such as DNA polymerases of prokaryotes, eukaryotes, viruses, and archaea (3,7,8) and human DNA ligase I (3), specific for DNA damage such as human uracil DNA glycosylase (UNG) (9,10), E. coli 8-oxoguanine DNA glycosylase (Fpg) (11,12), and human apurinic/apyrimidinic (AP) endonuclease (APEX1) (13), and specific for DNA sequence such as EcoRI restriction endonuclease (14), human topoisomerase I (15,16), and HIV integrase (17). We have shown that all these enzymes recognize DNA by forming multiple additive contacts with all DNA units covered by the protein globule (7–20 depending on the enzyme), and that the total interaction is a combination of weak electrostatic and hydrophobic and/or van der Waals interactions of the enzyme with the individual structural elements of DNA, which can be described by the following equation:

where K_d[(P_i)] is the dissociation constant (K_d) for the minimal orthophosphate ligand, e is the electrostatic factor reflecting the increase in enzyme affinity due to the interaction with one internucleoside phosphate group, h are hydrophobic factors for A, C, G and T nucleotide bases, the numbers of which in d(pN)_n are a, c, g and t, respectively. This equation describes the interaction of non-cognate single-stranded (ss) and double-stranded (ds) DNA with any enzyme. Only the values of e and h factors and K_d for ortho-phosphate change from one enzyme to another [reviewed in ref. (3,5)].

The high affinity of the enzymes for DNA is mainly (5–8 orders of magnitude) provided by multiple weak, additive interactions they form with various structural elements of the nucleotides under the footprint (3,5). The relative contribution of specific interactions to the total affinity of the enzymes for DNA is rather small, not exceeding 1–2 orders of magnitude. The specificity of the enzyme is provided by the enzyme-dependent stages of adjustment of DNA conformation to one optimal for catalysis and by the chemical step of catalysis: k_cat is higher by 4–8 orders of magnitude for cognate DNA than for non-cognate DNA.

Oxidized DNA bases are an important source of mutations, playing a crucial role in human mutagenesis, carcinogenesis and aging (18). Mutagenic 7,8-dihydro-8-oxoguanine (oxoG) is easily generated in human cells. In human cells, oxoG is removed from DNA by oxoguanine-DNA glycosylase (OGG1). The enzyme has two catalytic activities, acting as a DNA glycosylase excising oxoG and as a lyase eliminating the 3′-phosphate at the resulting abasic site (19). The substrate specificity of OGG1 has been described (19,20), and the enzyme’s mechanism has been analyzed using the stopped-flow approach (21,22). The kinetic scheme for OGG1 processing an oxoG:C-containing substrate was found to include at least three fast equilibrium steps followed by two slow, irreversible steps and then another equilibrium step. OGG1 is not homologous to Fpg, the bacterial oxoguanine-DNA glycosylase, and belongs to the endonuclease III superfamily (23,24). X-ray structure of OGG1 and its complexes with DNA also lacks any similarity with Fpg (25–28). Thus, it is of interest to study the thermodynamic aspects of oxoG recognition by OGG1 and to compare it with the data available for Fpg.

To dissect the mechanisms of substrate specificity of OGG1, we used the SILC approach to probe the interaction of the enzyme with a series of ss and ds non-cognate and cognate oligodeoxyribonucleotides (ODNs), and analyzed the results using a thermodynamic model of non-specific and specific DNA recognition. Since the rate of the reactions catalyzed by OGG1 can depend on the DNA sequence, we have also addressed a possible effect of different conformational and physicochemical properties of cognate DNAs on the K_M and k_cat parameters of the reaction.

MATERIALS AND METHODS

Enzymes and oligonucleotides

Isolation of the recombinant OGG1 from the E. coli BL21(DE3) overproducing strain was described previously (21). The concentration of the active form of the enzyme was determined in burst-phase kinetic experiments as in (29). Sequences of the ODNs used in this work are given in Tables 1 and 2. The ODNs were prepared from commercially available phosphoramidites (Glen Research, Sterling, VA, USA) on an ASM-700 synthesizer (BIOSSET, Novosibirsk, Russia). All ODNs were homogeneous as judged by ion-exchange and reversed-phase chromatography and electrophoresis in 20% polyacrylamide gel (PAGE) containing 89 mM Tris–borate (pH 8.3), 2 mM EDTA and 8 M urea. ODNs used as substrates were 5′-labeled using γ[³²P]ATP (Radioisotope, Moscow, Russia) and phage T4 polynucleotide kinase (New England Biolabs, Beverly, MA, USA) according to the manufacturer’s protocol and annealed to the appropriate complementary strand.

Table 1.

Affinity of OGG1 for minimal ligands, single- and double-stranded homo-ODNs and mixed-sequence ODNs

Liganda	Ki, Mb	Ligand	Ki, M	Ligand	Ki, M	Ligand	Ki, M	Ligand	Ki, M
Pi	68.0 × 10−3	dGMP	6.5 × 10−3	oxo-dGMP	1.6 × 10−3	T6:A6	3.9 × 10−4	T14:A14	1.0 × 10−5
dAMP	1.5 × 10−3	dTMP	2.0 × 10−3	dCMP	9.4 × 10−3	T8:A8	5.7 × 10−5	T16:A16	1.0 × 10−5
A2	4.4 × 10−3	T2	4.8 × 10−3	C2	9.0 × 10−3	T10:A10	6.8 × 10−5	T20:A20	9.0 × 10−6
–	–	T4	7.3 × 10−4	C4	1.5 × 10−3	T12:A12	3.7 × 10−5	T23:A23	1.0 × 10−5
A6	3.7 × 10−4	T6	3.7 × 10−4	C6	6.0 × 10−4	OG11:comp11	KM = 1.1 × 10−8	G11:comp11	8.7 × 10−6
A8	9.0 × 10−5	T8	1.1 × 10−4	C8	1.3 × 10−4	–	–	–	–
A9	7.0 × 10−5	T10	7.7 × 10−5	C10	6.7 × 10−5	–	–	–	–
A10	9.3 × 10−5	T11	5.3 × 10−5	C12	3.3 × 10−5	–	–	–	–
–	–	T12	3.0 × 10−5	C14	3.7 × 10−5	–	–	–	–
A14	3.7 × 10−5	T14	5.7 × 10−5	G11c	2.0 × 10−5	–	–	–	–
A16	2.0 × 10−5	T16	4.0 × 10−5	OG11c	8.0 × 10−8	–	–	–	–
A20	4.3 × 10−5	T20	2.3 × 10−5			–	–	–	–
A23	2.0 × 10−5	T23	1.7 × 10−5			–	–	–	–

^aThe K_i values estimated from the Lineweaver–Burk plot are given in bold, all other K_i were calculated from I₅₀ values.

^bMean of three independent experiments; the error did not exceed 15%.

^cThe sequence of G11 and OG11 is CTCTCCCTTCXCTCCTTTCCTCT, where X = G or oxoG, respectively. The sequence of comp11 is AGAGGAAAGGAGCGAAGGGAGAG.

Table 2.

Kinetic parameters of 8-oxoG excision from DNA substrates of different sequence

ds ODN ID	ss ODNs ID	Structure and numbering of ds ODNsa	Number of mis-matches	KM (nM)b	kcat (min−1)
		+100-12
ODN1c	OG11	5′-CTCTCCCTTCXCTCCTTTCCTCT-3′	0	11 ± 3	1.0 ± 0.1
	comp11	3′-GAGAGGGAAGCGAGGAAAGGAGA-5′
ODN2	2	5′-CTCTCCCTTCXCTCCTCTCCTCT-3′	0	23 ± 4	1.4 ± 0.1
	2c	3′-GAGAGGGAAGCGAGGAGAGGAGA-5′
ODN3	3	5′-CTCTCCCCTCXCTCCTCTCCTCT-3′	0	21 ± 5	1.1 ± 0.1
	3c	3′-GAGAGGGGAGCGAGGAGAGGAGA-5′
ODN4	4	5′-CTCTCCCCTCXCTCCTTTCCTCT-3′	0	20 ± 4	0.9 ± 0.1
	4c	3′-GAGAGGGGAGCGAGGAAAGGAGA-5′
ODN5	5	5′-CTCTCCTTTCXCTCCTTTCCTCT-3′	0	16 ± 4	1.1 ± 0.1
	5c	3′-GAGAGGAAAGCGAGGAAAGGAGA-5′
ODN6	6	5′-AAAAAAAAACXCGCCCGCCCGCG-3′	0	26 ± 5	1.2 ± 0.1
	6c	3′-TTTTTTTTTGCGCGGGCGGGCGC-5′
ODN7	7	5′-TTTTTTTTTCXCTTTTTTTTTTT-3′	0	11 ± 3	1.3 ± 0.1
	7c	3′-AAAAAAAAAGCGAAAAAAAAAAA-5′
ODN8	8	5′-TTTTTTTTTTXTTTTTTTTTTTT-3′	0	29 ± 6	0.96 ± 0.07
	8c	3′-AAAAAAAAAACAAAAAAAAAAAA-5′
ODN9	9	5′-CCGCCCGCGCXCAAAAAAAAAAA-3′	0	64 ± 8	2.9 ± 0.2
	9c	3′-GGCGGGCGCGCGTTTTTTTTTTT-5′
ODN10	10	5′-TTTTTTTGGGXGGGTTTTTTTTT-3′	0	66 ± 12	1.0 ± 0.1
	10c	3′-AAAAAAACCCCCCCAAAAAAAAA-5′
ODN11	11	5′-GAGCGAGCGCXCGCGAGCGAGCG-3′	0	78 ± 8	2.4 ± 0.1
	11c	3′-CTCGCTCGCGCGCGCTCGCTCGC-5′
ODN12	12	5′-CTCTCCCTTCXATCCTTTCCTCT-3′	0	41 ± 11	1.2 ± 0.1
	12c	3′-GAGAGGGAAGCTAGGAAAGGAGA-5′
ODN13	OG11	5′-CTCTCCCTTCXCTCCTTTCCTCT-3′	1	22 ± 2	0.94 ± 0.10
	12c	3′-GAGAGGGAAGCTAGGAAAGGAGA-5′
ODN14	7	5′-TTTTTTTTTCXCTTTTTTTTTTT-3′	2	390 ± 20	1.3 ± 0.4
	8c	3′-AAAAAAAAAACAAAAAAAAAAAA-5′
ODN15	8	5′-TTTTTTTTTTXTTTTTTTTTTTT-3′	6	400 ± 50	0.40 ± 0.02
	10c	3′-AAAAAAACCCCCCCAAAAAAAAA-5′
ODN16	7	5′-TTTTTTTTTCXCTTTTTTTTTTT-3′	6	310 ± 50	0.48 ± 0.07
	10c	3′-AAAAAAACCCCCCCAAAAAAAAA-5′
ODN17	8	5′-TTTTTTTTTTXTTTTTTTTTTTT-3′	2	70 ± 10	1.7 ± 0.05
	7c	3′-AAAAAAAAAGCGAAAAAAAAAAA-5′
ODN18	OG11	5′-CTCTCCCTTCXCTCCTTTCCTCT-3′	1	16 ± 7	0.80 ± 0.10
	7c	3′-GAGAGGGAAGCGAGGAGAGGAGA-5′
ODN19	OG11	5′-CTCTCCCTTCXCTCCTTTCCTCT-3′	2	59 ± 14	1.9 ± 0.1
	3c	3′-GAGAGGGGAGCGAGGAGAGGAGA-5′
ODN20	OG11	5′-CTCTCCCTTCXCTCCTTTCCTCT-3′	1	22 ± 6	1.4 ± 0.1
	4c	3′-GAGAGGGGAGCGAGGAAAGGAGA-5′
ODN21	OG11	5′-CTCTCCCTTCXCTCCTTTCCTCT-3′	1	8.0 ± 4.0	1.4 ± 0.1
	5c	3′-GAGAGGAAAGCGAGGAAAGGAGA-5′

^aX = oxoG. Mismatched nucleotides are underlined. The 21-nt stretches shown in capital letters without two nucleotides that are italicized were used for correlating physicochemical properties of the ODNs with K_M and k_cat.

^bK_M and k_cat values are given as mean ± SEM of 3–5 independent experiments.

^cds ODN1 is identical to OG11:comp11.

Enzyme kinetics

The reaction mixtures (10–20 µl) contained 50 mM Tris–HCl (pH 7.5), 100 mM NaCl, 1 mM EDTA, and 1 mM dithiothreitol; the concentrations of ODN substrates were varied. In the inhibition experiments, the standard substrate was used in a fixed concentration (22 nM, 2 × K_M, see below), and ODN inhibitors were used at various concentrations depending on their affinity for the enzyme. All measurements were performed in the linear regions of the time courses and enzyme concentration dependences of the reaction rate. The reactions were initiated by adding OGG1 (0.5 nM), incubated at 37°C, and quenched after 2–10 min by addition of NaOH (final concentration, 100 mM). These conditions correspond to the linear part of the rate dependences on the enzyme concentration, and the time of incubation was in the linear range of the time courses. The mixtures were heated for 2 min at 95°C, supplemented with an equimolar amount of HCl and 0.5 volumes of loading dye (0.25% xylene cyanol, 0.25% bromphenol blue, 20 mM EDTA in formamide). Reaction products were separated by PAGE and quantified by phosphorimaging (Molecular Imager FX system, Bio-Rad Laboratories, Hercules, CA, USA).

The K_M and V_max (k_cat) values were calculated by least-squares nonlinear regression fitting using SigmaPlot v8.0 software (SPSS, Chicago, IL, USA). The type of inhibition and the inhibition constants (K_i) for a subset of ODN inhibitors were obtained using different concentrations of the ODNs from the Lineweaver–Burk plot (30). I₅₀ values were determined from a range of inhibitor concentrations (0.1–10 × I₅₀) at the concentration of the standard substrate equal to 2 × K_M. Errors in the I₅₀ values were within 20%. K_i values were estimated from the equation for competitive inhibition, v = V_max × [S]/[[S] + K_M × (1 + [I]/K_i)]; it is easy to see that I₅₀ = 3 × K_i at [S] = 2 × K_M.

ΔG° values for contribution of various DNA elements into binding energy and ΔΔG° values for differences between the energy contributions in different substrates were calculated from the equation ΔG° = –RT × ln K_d (30) for T = 310 K.

Correlation analysis of the kinetic data

To reveal possible correlations between ODN sequences and kinetic parameters, we have used ACTIVITY software specifically designed for analysis and prediction of conformational and physicochemical properties of various DNA sequences (31). We have customized this program, which was originally used for fully dsDNA, to predict the properties of DNA containing mismatches. To do this, it was necessary first to analyze independently each of two strands of fully dsDNA. The analysis was restricted to the string {e_–10…e₀…e₊₁₀} (written simply as {e_–10…e₊₁₀} for fully complementary ODNs) corresponding to a 21-mer ds fragment of the ODNs (Table 2, see below), where e₀ is G instead of oxoG in the modified strand, or e₀ is C opposite oxoG in the complementary strand (henceforth, the upper index 0 will be used to describe the modified strand, and the upper index ‘#’ will be used for the complementary strand). Due to the presence of mismatches in some ds ODNs, {e⁰_–10…G…e⁰₊₁₀/e^#_–10…C…e^#₊₁₀}, the predictions for a ds ODN based on individually treated strains can be different. Therefore, to match these interim predictions we have used a heuristic approximation of the ‘limiting stage’ using the equations:

(1)

(2)

To maximize the diversity of the analyzed sequences, we have used a learning set encompassing ds ODN1–ODN6, the strands of which contain all variants of CT and AG permutations and A_n, T_n, and (C/G)_n runs encountered in the complete set of substrates (Table 2). At the final stage of the analysis, the partially mismatched ds ODN13–ODN15 were used as typical examples of ODNs containing mismatches. Fully complementary ODN7–ODN12 and mismatched ODN16–ODN21 were used as an independent control set to test the predictions made from the learning set.

Finally, we have searched for possible correlations between the experimentally determined K_M or k_cat values with P_q;[a;b] indexes of average conformational and physicochemical properties (1 ≤ q ≤ 38) of a DNA helix from the ACTIVITY database (freely available at: http://srs6.bionet.nsc.ru/srs6bin/cgi-bin/wgetz?-page+LibInfo+-lib+PROPERTY, the PROPERTY table) (32) between positions a and b of the ds ODNs (−10 ≤ a < b ≤ +10):

(3)

Table 3 shows two examples of conformational and physicochemical properties of a B-DNA helix in the ACTIVITY database, which includes a total of 38 different properties such as size (step, width, groove depth, etc.), angles (twist, opening, tilt, etc.); melting point, flexibility, entropy, enthalpy, Gibbs free energy and other (32). Altogether there are 38 × 21 × 20 / 2 = 7980 variants of P_q;[a;b] for ds DNA containing 21 bp.

Table 3.

Examples of conformational and physicochemical properties of all sixteen possible dinucleotide steps of a DNA helix in the ACTIVITY database (32)

MI P0000011a		MI P0000038
MN Conformational		MN Physicochemical
ML dinucleotide step		ML Dinucleotide step
RN Suzuki et al. (52)		RN Sugimoto et al. (53)
PN Twist angle		PN Free energy change
PM Average from X-ray structures		PM Calculated
PU Degree		PU kcal/mol
AA 35.3	GA 40.3	AA −1.2	GA −1.5
AT 31.2	GT 32.6	AT −0.9	GT −1.2
AG 31.2	GG 33.3	AG −1.5	GG −2.1
AC 32.6	GC 37.3	AC −1.5	GC −2.3
TA 40.5	CA 39.2	TA −0.9	CA −1.7
TT 35.3	CT 31.2	TT −1.2	CT −1.5
TG 39.2	CG 36.6	TG −1.7	CG −2.8
TC 40.3	CC 33.3	TC −1.5	CC −2.1

^aMI, number of entry in the database; MN, type of the property (conformational or physicochemical); ML, elementary unit for the entry (a nucleotide or a dinucleotide step); RN, reference to the source of the data; PN, property name; PM, type of primary data; PU, units of measurements for the given property. Examples of a conformational property (twist angle, left column) and a physicochemical property (ΔG°, right column) of dinucleotide steps are given.

We have correlated every P_q;[a;b] with K_M and k_cat using bootstrapping (33) on seven sets using 6 of 12 chains of ds ODN1–ODN6 (Table 2): (i) minimal P_q;[a;b]; (ii) maximal P_q;[a;b]; (iii) the P_q;[a;b] value nearest to the mean for ds ODN1–ODN6; (iv) minimal K_M or k_cat values; (v) maximal K_M or k_cat values; (vi) the K_M or k_cat values nearest to the mean for ds ODN1–ODN6; (vii) minimal, maximal, and nearest to the mean values of P_q;[a;b] and K_M or k_cat for ds ODN1–ODN6. For each of these seven sets of P_q;[a;b] and K_M or k_cat pairs, 11 statistical criteria were checked: (i) linear correlation; (ii) Spearman’s rank correlation coefficient, (iii) Kendall τ rank correlation coefficient; (iv) Pearson’s χ² and (v) Fisher’s exact tests for 2 × 2 contingency tables; (vi) and (vii) uniformity of distribution of P_q;[a;b] and K_M or k_cat; (viii) and (ix), normality of distribution of the residuals of K_M or k_cat after a direct regression K_M = κ × [P_q;[a;b] − ρ] (or k_cat = κ × [P_q;[a;b] − ρ]) or of P_q;[a;b] after the inverse regression P_q;[a;b] = ρ × [K_M − κ] (or P_q;[a;b] = ρ × [k_cat − κ]); (x) and (xi); sign test for Δ = P_q;[a;b] − ρ × [K_M − κ] (or Δ = P_q;[a;b] − ρ × [k_cat − κ]) and Δ′ = K_M − κ ×[P_q;[a;b] − ρ] (or Δ′ = k_cat − κ ×[P_q;[a;b] − ρ]). The analysis of each of the eleven criteria (m) using each of these seven sets of data (n) produces 11 × 7 = 77 levels of statistical significance (α_m,n) of paired conformity between the context-dependent calculated parameters P_q;[a;b] for the strands of ds ODN1–ODN6 (Table 2) and the experimentally determined K_M or k_cat values for these ODNs. The levels of significance α_m,n were analyzed using Zadeh’s fuzzy logic (34) by their representation on a scale of ‘fuzzy decision’ from −1 to +1 on the basis of a heuristic rule: significant positive decision (α_m,n < 0.05), insignificant or negative decision (α_m,n > 0.05); detection threshold α_m,n = 0.05. Thus, the decision scale q_m,n(P_q;[a;b]) was assigned the constant value of 1 in the case of α_m,n(P_q;[a;b]) ≤ 0.01, the opposite constant value −1 in the case of α_m,n(P_q;[a;b]) ≥ 0.1 and between them, 0.01 ≤ α_m,n(P_q;[a;b]) ≤ 0.1, by the square approximation:

(4)

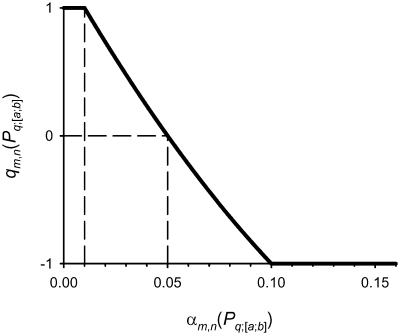
The decision scale described by Equation (4) is shown in Figure 1. As one can see, this dependence is a parabola defined by three points: the common decision threshold (α_m,n = 0.05; q_m,n = 0) and two points of continuity: (α_m,n = 0.01; q_m,n = 1) and (α_m,n = 0.1; q_m,n = −1). Every evaluation of P_q;[a;b] properties of ds ODN1–ODN6 (Table 2) generates 77 fuzzy decisions q_m,n(P_q;[a;b]) on the significance of their correlation with K_M or k_cat values for these ODNs. All 77 fuzzy decisions were finally averaged according to the theory of additive decision making (35):

(5)

Equation (5) gives the final decision Q(P_q;[a;b]) about the correspondence between the given property of ds DNA helix and the experimentally measured values of K_M or k_cat for this DNA. Maximal positive Q(P_q;[a;b]) indicates which property P_q over the [a;b] stretch of DNA helix, of all 7980 variants produced by Equation (3), best correlates with the measured K_M or k_cat.

Figure 1.

The scale of ‘fuzzy decision’ of Zadeh fuzzy logic (34) given by projection of the output of the mth statistical test on the nth data set (the level of statistical significance α_m,n) onto an interval [−1, 1] with the fuzzy decision threshold q_m,n = 0, assigned to the statistical threshold α_m,n = 0.05, separating the positive fuzzy decision q_m,n >0 in the case of a statistically significant result (α_m,n <0.05) from the negative fuzzy decision q_m,n <0 in the case of an insignificant result (α_m,n ≥0.05).

RESULTS

Inhibition of OGG1 by various ligands

In order to estimate the contribution of various elements of DNA structure into the total affinity of OGG1 for non-cognate and cognate DNA, we have determined the affinity of this enzyme for several ligands of increasing complexity, including orthophosphate, dNMPs, ss homooligomeric ODNs, ss ODNs of mixed sequence, ds homooligomeric ODNs and ds ODNs of mixed sequence (Table 1 and Supplementary Table). The binding affinities were determined from competition experiments using the ligands as competitors in the OGG1-catalyzed reaction of cleavage of an oxoG-containing substrate, ds ODN OG11:comp11 (Table 1 and Supplementary Table). Since undamaged ss or ds DNA, as well as oxo-dGMP and oxoG-containing ODN OG11 in an ss form, are not cleaved by OGG1 (19), the inhibition constant may be equated with the binding affinity of these ligands for OGG1.

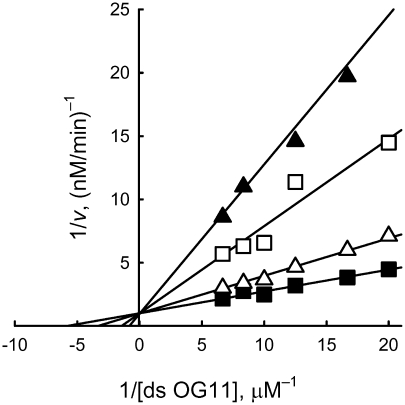
All tested short cognate and non-cognate ss or ds ODNs inhibited the reaction of cleavage of oxoG catalyzed by OGG1. Using ds OG11 as a substrate, several other ODN substrates and inhibitors were shown to be competitive inhibitors towards it (Figure 2, Table 1). Therefore, K_i gives an estimate of binding affinity (K_d = K_i) of ODNs for the DNA-binding site of OGG1. In the absence of the inhibitor, the reaction was characterized by K_M = 11 nM. Since most of the short ODNs had relatively low affinities for OGG1, the K_i values were calculated from the IC₅₀ values using the equation corresponding to competitive inhibition, IC₅₀ = 3K_i at S = 2K_M (Table 1).

Figure 2.

Analysis of the inhibition type and estimation of K_i for d(pT)₁₀:d(pA)₁₀ in the reaction of oxoG excision from ds OG11 catalyzed by OGG1, using a Lineweaver–Burk plot. The inhibitor was used at 0 (line 1), 0.15 (line 2), 0.30 (line 3) and 0.45 mM (line 4).

The minimal inhibiting ligands of OGG1 were orthophosphate (P_i; K_i = 68 mM) and different dNMPs, which demonstrated affinities (K_i = 1.5–9.4 mM) comparable with that for oxo-dGMP (K_i = 1.7 mM, Table 1). Consequently, the DNA-binding groove of OGG1 recognizes all free dNMPs.

Additive interactions of OGG1 with nucleotide units of ss oligonucleotides

The underlying assumption of SILC analysis is that the Gibbs free energy for complex formation can be expressed as a sum of the ΔG° values for individual contacts: ΔG° = ΔG°₁ + ΔG°₂ + … +ΔG°_n, with ΔG°_i = −RT × ln K_di, where K_di characterizes the contribution of an individual contact (30). Hence, the overall K_d value for the formation of an enzyme:DNA complex is the product of the K_d values for the individual contacts: ΔG° = −RT × ln K_d = −RT × ln(K_d1 × K_d2 × … × K_dn).

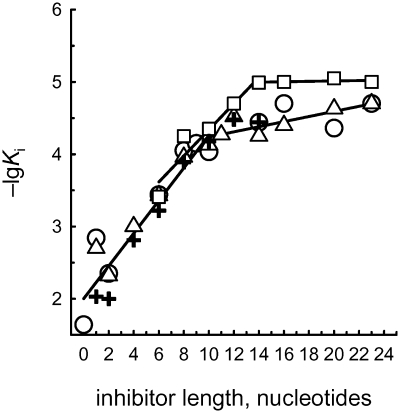
To assess whether the energy of interactions of OGG1 with ODNs is indeed additive in this manner, the data (Table 1) were analyzed as log dependences of K_i (directly proportional to ΔG°) for d(pN)_n versus the number of mononucleotide units (n; Figure 3). The linear log dependences for ss d(pN)_n (for 0 ≤ n ≤ 10; n = 0 corresponds to P_i) provide the evidence for the additivity of ΔG° values for the interaction of ten individual d(pN)_n units with OGG1, consistent with our earlier observations that the protein globules of all relatively small DNA-dependent enzymes (30–40 kDa; the molecular mass of OGG1 is 39 kDa) interact with 9–11 nt units of DNA [reviewed in ref. (5)].

Figure 3.

Dependencies of log K_i on the length (n) of ss (solid line) and ds (dashed line) d(pN)_n inhibitors of oxoG excision from ds OG11 by OGG1. Triangles, d(pT)_n; circles, d(pA)_n; crosses, d(pC)_n; squares, d(pT)_n:d(pA)_n.

Values of the f factor (1.78 ± 0.05) reflecting the increase in the affinity of OGG1 for various d(pN)_n per a unit increase in length, were evaluated from the slopes of the linear parts of these curves (Figure 3). The uniform increases in K_i, corresponding to the interaction between the enzyme and one unit of ss DNA, are equal to the reciprocals of these factors (K_i = 1/f = 0.56 ± 0.02 M). An extrapolation of all dependences to n = 1 gives K_i = 12 mM; this value characterizes the interactions of the active center of OGG1 DNA-binding groove with one position standing out among the 10 nt of any ss DNA bound by the enzyme. Notably, the K_i values experimentally determined for free dNMPs (1.5–9.4 mM, Table 1) are 1.3- to 8.0-fold lower. Such a situation was observed earlier for other enzymes (5) and is thought to reflect a greater conformational freedom of free nucleotides as compared with dNMPs in DNA constrained by its 3′- and 5′-linkages, especially if the enzyme’s action involves a specific conformational adjustment of the target dNMP in the natural substrate, such as flipping of the damaged dNMP out of the DNA helix into the active site of OGG1 (25). Thus, one distinguished position in the DNA-binding groove of OGG1, presumably the active site of the enzyme, is characterized by the affinity for non-cognate d(pN) within ss DNA (K_i = 12 mM) that is ∼47-fold stronger than the interaction of OGG1 with any other nucleotide unit of long ss DNA in the groove (K_i = 0.56 M).

The interaction of OGG1 with all units of d(pN)_1–10 is additive, and the K_d (K_i) values for any ODN can be obtained by multiplying K_d for the minimal ligand (P_i) by K_d = 1/f = 0.56 M for each mononucleotide unit:

(6)

In contrast to DNA polymerases, human uracil–DNA glycosylase (UNG), AP endonuclease (APEX1), and topoisomerase I (3,7,8,10,13,15,16) but similarly to E. coli Fpg and EcoRI endonuclease (11,12,14), the affinity of OGG1 for non-cognate d(pC)_n, d(pT)_n and d(pA)_n did not depend on the relative hydrophobicity of their bases (Figure 3). The affinity of a 23-mer mixed-sequence ODN G11 (20 µM) was the same as that for all homo-d(pN)₂₃ (17–20 µM; Table 1). This means that the enzyme essentially does not contact nine of the ten DNA bases, but mainly interacts with the sugar-phosphate backbone of these units. To confirm this and to assess the contribution of the sugar-phosphate backbone structural units to the formation of the weak additive contacts between OGG1 and ODNs, we synthesized an abasic oligomer, (pF)₉pT, where F is an analog of deoxyribose resistant to cleavage by OGG1 because its hydroxyl moiety at C1′ has been replaced by a hydrogen atom. The affinity of (pF)₉pT for OGG1 (K_i = 70 ± 14 µM) was not different from that of regular d(pN)₁₀ (67–93 µM; Table 1). In addition, r(pA)₁₀ and r(pC)₁₀ demonstrated the affinity only 1.5- to 1.9-fold lower (140 µM and 130 µM, respectively) than the corresponding d(pN)₁₀.

A ∼1.78-fold change in the affinity with d(pN)_n elongation by 1 nt unit (ΔG° approximately −0.34 kcal/mol) is lower than would be expected for strong electrostatic contacts (up to −1.0 kcal/mol) or hydrogen bonds (from −2 to −6 kcal/mol), but comparable to the values characterizing weak ion–dipole and dipole–dipole interactions (30). According to the crystal structure, OGG1 possesses a large positively charged groove (25–27). Thus, the interactions of the negatively charged internucleotide groups of non-cognate ODNs with the DNA-binding groove of OGG1 may use electrostatic interaction of dipoles rather than point charges and resemble the interface between oppositely charged surfaces.

Affinity of OGG1 for non-cognate and cognate DNA duplexes

As the next step in our analysis of OGG1 specificity, we have compared the affinities of this enzyme for ds ODN of different composition and length. Figure 3 and Table 1 show that the minimal ligand exhibiting duplex properties for OGG1 (i.e. bound by the enzyme differently from binding its two strands independently) is d(pT)₈:d(pA)₈, for which the value of T_m (21°C) (36) is lower than the temperature at which the reaction was performed (37°C). Thus, OGG1 can stabilize short ODN duplexes. A similar phenomenon of duplex ‘assembly’ and stabilization has been observed for topoisomerase I and DNA polymerases (3,7,8,15,16). In contrast to ss ODNs, the increase in log(K_i) for ODN duplexes was linear up to n = 13–14. The affinity of OGG1 for non-cognate homo-ODN and mixed-sequence ODN duplexes was ∼1.5- to 3.3-fold higher than for the corresponding ss ODNs (Table 1). The affinities of d(pT)_n:d(pA)_n duplexes (n ≥ 8) could be formally described by the same Equation (6) as for ss ODN, the f factor having decreased from 1.78 ± 0.05 to 1.60 ± 0.05. Thus, the second strand contributes to the affinity of OGG1 for DNA much less than the first one. The continued increase in the affinity for ds d(pN)_n between n = 10 and 13–14 may be caused by additional contacts of the second strand with the enzyme and complementary interactions between the strands.

The affinity of the enzyme for mixed-sequence ss and ds G11 (20 ± 2 and 8.7 ± 0.9 µM, respectively) is comparable with that for ss and ds homo-d(pN)_n (34 ± 13 and 9.8 ± 0.5 µM, respectively, averaged over all sequences with n ≥11 and ≥14, respectively; Table 1). The substitution of cognate ss OG11 (K_i = 0.080 µM) for non-cognate ss G11 (20 µM) leads to a 250-fold increase in the affinity for OGG1. Finally, the affinity of OGG1 for cognate ds ODN OG11 was estimated from K_M of oxoG excision; since k_cat of this reaction is quite low, on the order of 1 min⁻¹ [(19) and see below], the Michaelis complex is in a rapid equilibrium with the substrate and K_M ≈ K_d. The affinity of OGG1 for cognate ds OG11 (0.011 µM) was higher than for d(pT)_14–23:d(pA)_14–23 and ds G11 by a factor of ∼790 (Table 1). Interestingly, the active site of OGG1 binds free oxo-dGMP ∼7.5-fold more tightly than one non-cognate d(pN)_n unit within DNA only 4.1-fold more tightly than free dGMP (Table 1). Thus, the relative contribution of specific interactions of the active center of OGG1 with oxoG is higher for oxo-dGMP units within cognate DNA than for free oxo-dGMP.

Thermodynamic models of OGG1 interaction with cognate and non-cognate DNA

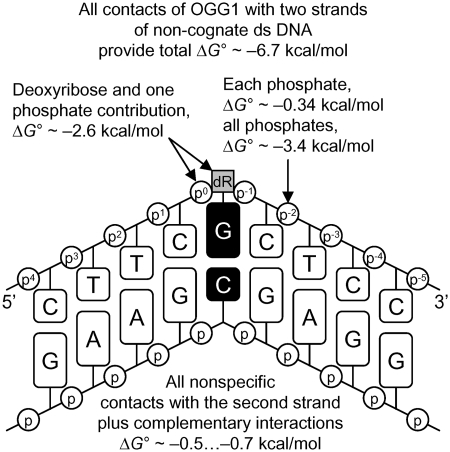
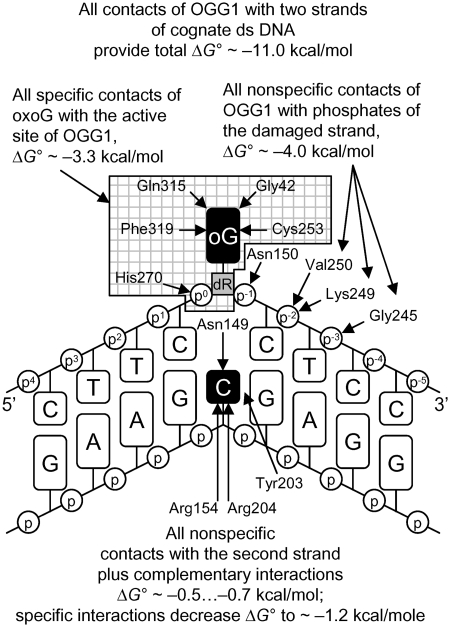
Based on the measurements of binding affinity of OGG1 for various ligands, we have constructed a model summarizing the contribution of different interactions to DNA binding by OGG1. As mentioned above, extrapolation of the log(K_i) dependencies to n = 1 gives a K_i value of 12 mM, which characterizes the interaction of the active site of OGG1 with one of the nucleotides of d(pN)_n bound to the protein. From this, the ΔG° of one non-specific dNMP interaction with the active site of OGG1 can be estimated as −2.6 kcal/mol. Since 12 phosphate groups of one strand of ds d(pN)₁₃ interact with OGG1 through weak, additive contacts, (ΔG° approximately −0.34 kcal/mol each, as calculated from the f factor), the summarized relative contribution of these internucleotide phosphates is ΔG° approximately −4.1 ± 0.2 kcal/mol. A comparable value of ΔΔG° approximately −3.9 ± 0.2 kcal/mol may be calculated from the ratio of the K_i values for dTMP and d(pT)_13–23 (average ΔG° = −4.0 ± 0.2 kcal/mol for n = 13–23). Thus, all contacts of OGG1 with 10–14 nt (including the dNMP unit with the higher affinity) of one strand of DNA provide ΔG° of −6.7 ± 0.3 kcal/mol at most. From the ratio of the average K_i values for ss and ds d(pN)_13–23 including G11 (2.3- to 3.3-fold) characterizing the difference in the affinity of OGG1 for ds ODNs compared to ss ODNs, the contribution of the second strand to the affinity are only ΔG° approximately −0.5 … −0.7 kcal/mol. The X-ray structure of cognate and non-cognate OGG1:DNA complexes and stopped-flow data indicate that the enzyme distorts any DNA, creating a sharp kink, but fails to insert the non-damaged base into the active site pocket (21,22,25,27). Therefore, the active site of OGG1, as defined using the thermodynamic SILC approach, probably mostly interacts with the sugar-phosphate backbone of a dNMP unit within non-cognate DNA, which explains why the affinity of the enzyme for free dNMPs is greater than the affinity of its active site for dNMP units within long ODNs. Overall, the types of OGG1 interaction with non-cognate DNA can be summarized by the thermodynamic model shown in Figure 4.

Figure 4.

Thermodynamic model of the interaction of OGG1 with non-cognate DNA. ΔG° values characterizing various contacts between the enzyme and DNA containing a G base are shown. All types of non-specific additive interactions of the enzyme and two strands of non-specific DNA provide ΔG° = −6.7 kcal/mol of total binding energy.

The issue how much binding energy is contributed by the lesion itself is less straightforward. In the bacterial Fpg protein, which recognizes oxoG but is not related to OGG1 by sequence or structure, the relative contribution (approximately −0.8 kcal/mol) of the specific interactions of with oxoG unit is nearly comparable at the level of minimal dNMP ligands, cognate ss d(pN)_n, and ds ODNs (11). The same situation was observed for two other repair enzymes, UNG and APEX1 (9,13). This means that the contribution of specific and non-specific interactions of the damaged nucleotides of cognate DNA to its total affinity for these enzymes is close to additive. On the other hand, since the difference in the affinity of OGG1 for non-cognate and oxoG-containing ligands increases significantly from free dNMP (4.1-fold) to ss (250-fold) and finally to ds DNA (790-fold, see the values for the corresponding pair of cognate and non-cognate ligands in Table 1), the ratio of the K_i values for dGMP and oxo-dGMP (4.1, corresponding to ΔΔG° = −0.8 kcal/mol) may provide only a lower estimate of the true contribution of a oxoG unit to the affinity of OGG1 for cognate DNA. The upper limit of this contribution is given by the 250-fold difference (−3.3 kcal/mol) for ss DNA and the 790-fold difference (−4.0 kcal/mol) for ds DNA. However, at least some of this additional binding energy is most likely provided by strengthening of the non-specific contacts between the enzyme and the undamaged part of damaged DNA in the catalytically competent complex. As OGG1 was totally deficient in the removal of oxoG from ss DNA (data not shown), one can reason that no conformational adjustment takes place in OGG1 complexes with cognate ss DNA, and therefore the additional binding energy of −3.3 kcal/mol most closely reflects the contribution of an oxoG unit when incorporated in the DNA strand (Figure 5).

Figure 5.

Thermodynamic model of the interaction of OGG1 with cognate DNA with an oxoG base. Strengthening of the enzyme contacts with the damaged and complementary strands of the cognate DNA is indicated. The estimated ΔΔG° value characterizing the net change in the interactions of all types between non-cognate and cognate DNA complexed with OGG1 is −4.3 ± 0.2 kcal/mol. The amino acid residues of OGG1 interacting with specific DNA are shown after (25).

In contrast to OGG1, at least some cleavage of ss cognate DNA was reported for Fpg (37) and APEX1 (13), whereas UNG actually prefers ss over ds substrates (38). Taking into account the 790-fold (ΔΔG° = −4.0 kcal/mol) increase in the affinity of OGG1 for ds oxoG11 as compared with ds G11, it is likely that the second strand of the cognate ds DNA is more important for ‘orbital steering’ by OGG1 than by Fpg, UNG, or APEX1. Since the ratio of K_i values for cognate ss and ds OG11 (∼7.3-fold; ΔΔG° = −1.2 kcal/mol) is higher than that for non-cognate ss and ds ODNs (2.3- to 3.3-fold), the contribution of the undamaged strand to the affinity of the enzyme for cognate DNA is greater than for non-cognate DNA.

In principle, the 790-fold increase in the affinity may be caused by several factors, including strengthening of the contacts formed between OGG1 and ss OG11 after the addition of the second strand, a change in conformation of both strands, or even formation of additional contacts of the enzyme with both strands of ds DNA; these possibilities cannot be distinguished from the present data. However, all non-specific interactions contribute approximately ΔG° = −6.7 kcal/mol, the approximate contribution of the oxoG estimated from the increase in the affinity from ss G11 to ss OG11 (see above) is −3.3 kcal/mol, while the increase in the affinity due to specific interactions of the enzyme with both strands of ds OG11, calculated from the difference in the affinity of OGG1 for ss and ds cognate and non-cognate ODNs, is ΔΔG° = (−1.2 kcal/mol) − (− 0.5 kcal/mol) = (−0.7 kcal/mol). The sum of these energies, −10.7 kcal/mol, is close to ΔG° = −11.0 kcal/mol, the value characterizing binding of OGG1 to ds OG11. Overall, the interaction of OGG1 with cognate ds OG11 may be approximately described by the thermodynamic model in Figure 5.

Obviously, formation of a complex between OGG1 and cognate DNA cannot explain the in vivo high enzyme specificity. At the same time, canonical bases are not removed from DNA by OGG1 even at very high enzyme concentrations and long incubation times, putting the estimate of the preference for the damaged base at >10⁶- to 10⁷-fold (considering the detection limits of a phosphorimaging-based assay). Therefore, k_cat for oxoG exceeds that for normal bases by approximately 6–7 orders of magnitude, suggesting that, similar to other investigated enzymes, the adjustment and catalytic stages appear significantly more sensitive to the DNA structure than the stage of complex formation between OGG1 and DNA. Yet, even in the case of completely sequence- and structure-independent enzymes, like canonical DNases, the rate of the catalysis varies significantly with the structure of cleaved sites (39). Therefore, as the next step of our analysis, we inquired how local conformational and thermodynamic parameters of cognate DNA may influence the removal of oxoG by OGG1.

Effect of substrate DNA structure on the reaction kinetics

The footprint of OGG1 defined by its X-ray structure covers 10–11 bp of DNA around oxoG, with the enzyme sharply kinking DNA and flipping the damaged deoxynucleotide out of the double helix (25,27). The extensive enzyme–DNA interactions suggest that the affinity of OGG1 for cognate ds DNAs of different sequences and the rate of oxoG removal from them may significantly depend on the structural features of the substrate. We have constructed 21 ds ODNs (ODN1–ODN21) using 12 ss ODNs containing oxoG (strands 1–12) and 12 completely or partially complementary ss ODNs (strands 1c–12c, resulting in 0–6 mismatches after the annealing) containing a C base opposite oxoG and determined the K_M and k_cat values for them (Table 2). The maximal affinity (in terms of K_M), 11 nM, and a high k_cat value (1.3 min⁻¹) was observed for a completely complementary ds ODN7 (T₉CXCT₁₁, here and below X = oxoG), and variation of the sequences flanking the central CXC trinucleotide (ODN1–ODN6) produced only a 1.0- to 2.6-fold increase in the K_M values and even smaller changes in the k_cat values (0.9–1.4 min⁻¹). Only for two ds substrates containing a CXC trinucleotide, ODN9 and ODN11, the changes in K_M and k_cat were higher, 5.8- to 7.1-fold and 1.8- to 2.2-fold, respectively. A replacement of the central CXC of ODN7 with a TXT trinucleotide in ODN8 slightly increased the K_M (2.6-fold) and decreased the k_cat (1.3-fold) values (Table 2). A stronger decrease in the affinity (3.7- to 8.0-fold) was observed for ODN10 and ODN12 containing oxoG in the GXG and CXA context, but the decrease in k_cat values for these ODNs was relatively small, 1.1- to 1.3-fold as compared with ODN7. The ds ODNs used in these experiments contained different AA-, TT-, CC-, AT- and GT-rich sequences, different in their rigidity and local conformational parameters (40–42). The observed moderate changes in the kinetic parameters for ds ODN1–ODN7 indicate that the conformation of these ODN in solution exerts little influence on the reaction efficiency after their binding to the enzyme.

Mismatches in DNA facilitate its structural deformation that can either assist or interfere with its adjustment in the enzyme’s DNA-binding groove (43). A replacement of the complementary T:A pair in ds ODN1 in the position +3 with a T:G mismatch (ds ODN20, see Figures 4 and 5 for the numeration of the positions) increased the K_M value twofold, while a replacement of the C:G pair with a C:A mismatch in the position +4 (ODN21) led to an 1.4-fold increase in K_M (Table 2); in both cases the k_cat value became 1.4-fold higher. Introduction of a T:G mismatch in the position −6 (ds ODN18) decreased the affinity and the rate constant relative to ds ODN1 1.5- and 1.3-fold, respectively. The maximal 5.4-fold decrease in the affinity and 1.9-fold increase in the k_cat value relative to ODN1 was observed for ODN19 containing two T:G mismatches in positions +3 and −6.

At the next step, we introduced mismatches in the immediate vicinity of the lesion where they could affect both the local deformability of DNA and the easiness of eversion of the damaged base. Interestingly, a replacement of two complementary C:G pairs of ODN7 in the positions +1 and −1 with two T:G mismatches resulted in a smaller 6.4-fold decrease in the affinity (ds ODN17) than the 35-fold decrease in the affinity observed for ds ODN14 containing two C:A mismatches in the same positions (Table 2). This observation may reflect the tendency of T:G mispairs to form rather stable wobble pairs. Despite the higher K_M values, the reaction rate was hardly affected: relative to ds ODN7, the k_cat value for ds ODN17 was increased 1.3-fold, while ODN7 and ODN14 demonstrated the same catalytic rate. Only in the case of ODN15 an ODN16 containing six mismatches flanking the lesion (from +1 to +3 and from −1 to −3), the coincidental and maximal decrease in the affinity (28- to 36-fold) and in the reaction rate (2.7- to 3.3-fold) in comparison with ODN7 was observed (Table 2).

It can be seen that various modifications of the structure of ds ODNs can produce different effects on the affinity and reaction rate. The introduction of mismatches 3–6 nt away from oxoG can either improve or impair the catalysis by OGG1 in terms of K_M and k_cat, whereas the mismatches flanking the lesion always decrease the affinity of the enzyme for such substrates but only a stretch of flanking mismatches can significantly decrease both the affinity and the rate of catalysis. Taking this into account, it was interesting to analyze what properties of ds ODN substrates in solution may be the most important for their effective use by the enzyme.

Analysis of correlation between OGG1 kinetics and DNA structure parameters

The adjustment of DNA and enzyme conformation in the case of nonspecific and specific repair enzymes includes many changes of their initial structure: change of conformation of sugar–phosphate backbone, partial or complete melting of DNA, destruction of staking interactions, formation of kinked conformation, etc. (3). Only in the case of cognate DNA having specific structural parameters there may be perfect adaptation of enzyme and DNA. In order to analyze possible relationships between properties of DNA and kinetic constants of the OGG1-catalyzed reaction, we have used the ACTIVITY software (31) to correlate these constants with 38 conformational (twist, propeller, bend toward major or minor groove, width of major or minor groove, etc.) or physicochemical (changes in enthalpy, entropy, Gibbs free energy, etc.) parameters of the ds ODN used in our experiments.

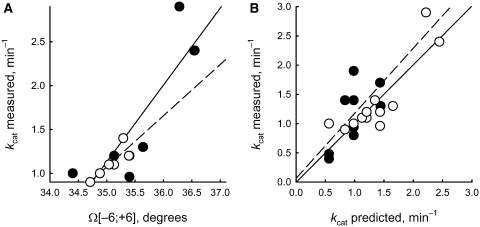
The maximal positive decision parameter Q = 0.389 [Equation (5)] was found for k_cat in the case of P_11;[–6;+6] representing the average twist (Ω angle) of the 21 bp of the ds ODN helix (Table 3) between the positions −6 and +6 (the position of the oxoG residue is defined as position 0). The second value, Q(P_11;[–8;+8]) = 0.065 indicates a lower but significant correlation of the twist for a longer stretch of the ds ODN helix between the positions −8 and +8. The P_11;[–6;+6] estimates calculated for each chain of all ds ODNs are given in Fig. 6A. The correlations between P_11;[–6;+6] and k_cat values for each strand of ds ODN1–ODN6 (r = 0.862, α < 0.0005) and for the independent control set, each strand of ds ODN7–ODN12 (r = 0.835, α < 0.001) were statistically significant (Figure 6B), producing the following linear regression after pooling the data for fully complementary ds ODN1–ODN12 (r = 0.869, α < 0.00025):

(7)

To analyze correlation of k_cat with the twist angle for partially mismatched duplexes, for which no experimentally determined structural parameters is available, we used a ‘limiting stage’ approach. Briefly, the twist angle (or any other parameter that may be included in the analysis) is calculated for two fully complementary duplexes, each corresponding to one strand of the mismatched duplex. The value of k_cat is then calculated for both duplexes using the regression obtained above for fully complementary duplexes, and the worst value of the two (i.e. lower k_cat) is kept for the correlation analysis. The k_cat values calculated using Equations (1) and (7) for partially mismatched ds ODN13–ODN21 correlate statistically significantly (Figure 6B; r = 0.667, α < 0.05) with the experimental k_cat values. Overall, Δk_cat reflecting the difference between the experimental and predicted k_cat values [Equations (1) and (7); Δk_cat = k_cat – k_cat{e⁰_–10…G…e⁰₊₁₀/e^#_–10…C…e^#₊₁₀}] varied from −0.47 to 0.92 for all 21 ds ODNs. These values showed no correlation with the number of mismatches (r = −0.021, α > 0.925, data not shown), indicating that the ‘limiting stage’ approximation [Equations (1) and (7)] fully describes the linearly additive contribution of DNA sequence to the reaction rate for both completely and partially mismatched duplexes and does not introduce a systematic bias in the predicted k_cat values.

Figure 6.

Linear correlations between the experimentally measured k_cat values and either (A) the twist angle averaged over −6 to +6 position of the ODNs [Equation (3)] as calculated by the ACTIVITY software or (B) the k_cat values predicted by Equations (1), (3) and (7). Open circle and dashed line, learning set: (A) each strand of ds ODN1–ODN6 (r = 0.862, α <0.0005); (B) ds ODN1–ODN12 (r = 0.869, α <0.00025). Closed circle and straight line, control set: (A) each strand of ds ODN7–ODN12 (r = 0.835, α <0.001); (B) mismatched ds ODN13–ODN21 (r = 0.667, α <0.05).

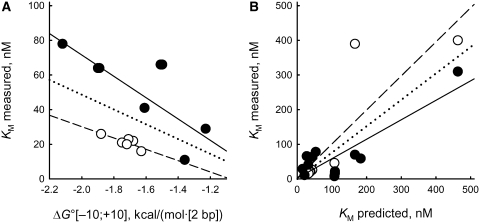
For K_M values, the maximal positive Q = 0.083 [Equation (5)] was found for the negative correlation with the average ΔG° (P_{38;[–10;+10]}) of the analyzed DNA sequences (Figure 7A). The correlation was significant for both the learning set, each strand of ds ODN1–ODN6 (r = −0.832, α < 0.001), and the control set, ODN7–ODN12 (r = −0.806, α < 0.0025) (see ‘Materials and Methods’ section for a description of learning and control sets). For the pooled set of completely complementary ds ODN1–ODN12, the following linear regression was found (r = −0.462, α < 0.025):

(8)

The deviation of the experimental K_M values from the values calculated using the ‘limiting stage’ approximation (Equations (2) and (7); ΔK_M = K_M – K_M{e⁰_–10…G…e⁰₊₁₀/e^#_–10…C…e^#₊₁₀}) varied from −10.3 to 38.3 nM for ODN1–ODN12 and from −27 to 373 nM for partially mismatched ODN13–ODN21. Unlike in the case of k_cat, a statistically significant correlation was found between these values and the number of mismatches for the set of all 21 ds ODNs (r = 0.814, α < 0.00001, data not shown). Therefore, a linearly additive contribution of disturbance of strand complementarity to the K_M value exists. Using the data for ODN1–ODN6 and ODN13–ODN15, we have introduced a regression correcting Equation (2) for the number of mismatches (N_≠):

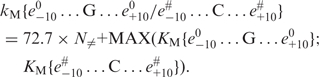(9)

The predicted K_M values calculated using Equation (9) for all 21 ds ODNs are shown in Figure 7B. They are statistically significant both for the learning set combining ODN1–ODN6 and ODN13–ODN15 (r = 0.850, α < 0.005) and for the control set combining ODN7–ODN12 and ODN16–ODN21 (r = 0.862, α < 0.0005).

Figure 7.

Linear correlations between the experimentally measured K_M values and either (A) the Gibbs free energy averaged over −10 to +10 position of the ODNs [Equation (3)] as calculated by the ACTIVITY software or (B) the K_M values predicted by Equations (3), (8) and (9). Open circle and dashed line, learning set: (A) each strand of ds ODN1–ODN6 (r = –0.832, α <0.001); (B) ds ODN1–ODN6 and ODN13–ODN15 (r = 0.850, α <0.005). Closed circle and straight line, control set: (A) each strand of ds ODN7–ODN12 (r = −0.806, α <0.00025); (B) ds ODN7–ODN12 and ODN16–ODN21 (r = 0.862, α <0.0005). Dotted line, all data combined: (A) each strand of ds ODN1–ODN12 [r = −0.457, α <0.025; Equation (8)]; (B) ds ODN1–ODN21 (r = 0.806, α < 0.00001).

As an independent test of validity of the ‘limiting stage’ approximation, we have applied it to predict specific ΔG° for one step of DNA helix, δG°:

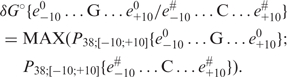(10)

The value of δG° for all ds ODNs calculated using Equation 10 (Table 4) statistically significantly correlated (r = 0.813, α < 0.00001) with ΔG° but not with enthalpy (ΔH°; r = 0.027, α > 0.9) or entropy (ΔS°; r = 0.270, α > 0.2). Earlier, we have found correlation of melting temperature of fully dsDNA with the frequency of mutations induced by 2-aminopurine (44). Here we have calculated the melting point of ds ODNs and have found its correlation with δG° (Table 4; r = −0.880, α <10⁻⁶). These data indicate that the use of the ‘limiting stage’ approximation [Equations (1), (2) and (9)] is appropriate.

Table 4.

Comparison of specific δG° (ΔG° for one step of DNA helix) predicted from the K_M and the energy parameters of ds ODNs

ds ODN ID	Predicted	Calculated or measureda					Predicted
	δG°b (kcal/mol/step)	ΔG° (kcal/mol)	ΔH° (kcal/mol)	ΔS° [cal/(mol × K)]	Tm (°C)	kcata (min−1)	Δkcatc (min−1)
ODN1	−1.68	−19.6	−138.47	383	64.0	1.00	0.02
ODN2	−1.71	−18.4	−113.59	307	66.7	1.40	0.06
ODN3	−1.75	−20.7	−129.05	349	69.3	1.10	−0.10
ODN4	−1.72	−21.2	−139.77	382	67.9	0.90	0.07
ODN5	−1.63	−19.4	−139.68	388	63.1	1.10	−0.02
ODN6	−1.88	−20.7	−121.12	324	71.8	1.20	−0.23
ODN7	−1.36	−14.6	−146.86	426	50.5	1.30	−0.35
ODN8	−1.23	−11.6	−108.02	311	46.0	0.96	−0.47
ODN9	−1.89	−21.1	−137.78	376	68.2	2.90	0.68
ODN10	−1.50	−16.7	−136.68	387	56.7	1.00	0.44
ODN11	−2.12	−19.9	−91.50	231	81.3	2.40	−0.05
ODN12	−1.61	−17.9	−123.44	340	62.5	1.20	0.00
ODN13	−1.61	−16.0	−129.44	366	56.0	0.94	−0.04
ODN14	−1.23	−7.6	−106.92	320	34.2	1.30	−0.13
ODN15	−1.23	−3.7	−102.34	318	23.1	0.40	−0.16
ODN16	−1.36	−2.2	−101.60	320	18.9	0.48	−0.08
ODN17	−1.23	−8.7	−137.07	414	37.5	1.70	0.27
ODN18	−1.68	−16.8	−120.95	336	59.9	0.80	−0.18
ODN19	−1.68	−14.6	−109.83	307	55.2	1.90	0.92
ODN20	−1.68	−18.6	−140.74	394	61.0	1.40	0.57
ODN21	−1.63	−13.8	−94.70	261	55.3	1.40	0.42
R		0.813d	0.027	0.270	0.880	−0.517	−0.282
P		<10−5	>0.9	>0.2	<10−6	<0.025	>0.2

^ak_cat from Table 2, other parameters calculated using the ACTIVITY software.

^bFrom Equation (10).

^cΔk_cat = k_cat – k_cat{e⁰–₁₀…G…e⁰+₁₀/e^#_–10…C…e^#₊₁₀}.

^dR, correlation coefficient; P, level of significance.

Finally, Table 4 gives a comparison of predicted δG° (10) with the experimental k_cat values and their deviations (Δk_cat) from the values predicted from DNA twist [Equations (1) and (7)]. One can see that δG° correlates with k_cat (r = −0.517, α < 0.025) but not with Δk_cat (r = −0.282, α > 0.2). Therefore, the linearly additive contribution of δG° to the k_cat value is limited to the internal energy of DNA helix twisting, which is a part of δG°. Thus, we have found the equations that use DNA sequence and helix structural properties to predict the k_cat and K_M values characterizing interaction of OGG1 with ds cognate 21-mer ODNs.

DISCUSSION

The present study shows that the recognition of non-cognate DNA by OGG1 is similar to its recognition by DNA polymerases (7,8,45), UNG and Fpg DNA glycosylases (10–12), APEX1 (13), topoisomerase I (15,16), EcoRI (14), HIV integrase (17), RecA protein (6), DNA ligase I and RNA helicase p68 (DDX5) (3) in terms of additivity of Gibbs free energies. Usually, the footprint of 30–40 kDa enzymes, including OGG1, covers one helix turn or 10 base pairs of DNA, and their active sites bind one singled out cognate or non-cognate nucleotide unit with a relatively high affinity. In contrast to many enzymes but similarly to UNG and EcoRI (10,14), OGG1 forms efficient contacts only with the internucleotide phosphate groups of non-cognate ds DNA. The f factor (1.78) for OGG1, reflecting its interaction with one internucleotide phosphate (K_d characterizing the enzyme interaction with one nucleotide unit is 1/f = 1/1.78 = 0.56 M), is comparable with f factors for other enzymes: 1.35 for human UNG; 1.45 for human APEX1; 1.52 for Klenow fragment of DNA polymerase I from E. coli; 1.54 for E. coli Fpg; 1.61 for human RNA helicase p68; 1.3–2.0 for HIV-1 integrase; 2.0 for EcoRI, and 2.14 for human DNA ligase I. Similarly to all these enzymes, the second strand contributes to the affinity of OGG1 for ds DNA much less than the first strand.

The affinity of OGG1 for ds OG11 (11 nM) is only 1.8-fold lower than that found for Fpg (6 nM) (11). Interestingly, the high and comparable affinity of these enzymes for ds OG11 is achieved by different means. Non-specific interactions with ds G11 contribute to the total affinity of Fpg for cognate ds DNA (K_i = 67 nM) (11) 130-fold more than do the non-specific interactions of OGG1 (8.7 µM, Table 1), while the efficiency of non-specific interactions of Fpg with internucleotide phosphate groups of one strand of ss G11 (K_i = 10 µM) is only 2-fold better that that for OGG1 (K_i = 20 µM) (Table 1). Thus, the second strand (complementary to G11) contributes to the increased efficiency of non-specific interaction of Fpg with ds OG11 to a much greater extent than in the case of OGG1. In addition, Fpg does not rely on cooperative interactions with the substrate to any extent. The contribution of specific interactions of a oxo-d(pG) unit and non-specific contacts with other units ds OG11 to the total affinity are close to additive; the affinity of Fpg protein for an oxo-d(pG) unit (∼0.1 M) is comparable for oxo-dGMP, ss OG11 and ds OG11 (11). Like Fpg, other enzymes studied by SILC usually do not show more than 1–2 orders of the increase in affinity for cognate ds ODNs compared with non-cognate ones; there is only a 2- to 5-fold difference for APEX1, 7- to 10-fold for UNG, 50- to 70-fold for HIV integrase, 50- to 100-fold for EcoRI, and 200- to 250-fold for topoisomerase I (10,13–17).

In contrast to Fpg (11), the transition from ss to ds non-cognate G11 led to only a 2.3- to 3.3-fold increase in the affinity. At the same time, cognate ss OG11 is bound 250-fold stronger than non-cognate ss G11 (Table 1). Thus, the formation of specific contacts between the oxoG unit and the active site of OGG1 has a cooperative effect on the DNA-binding groove of the enzyme. Some non-specific, previously weak interactions with non-cognate ODNs may greatly strengthen when cognate DNA is bound; for example, in the complex of DNA with topoisomerase I they attain the character of specific interactions (15,16). A very pronounced strengthening of non-specific electrostatic interactions of HIV integrase is observed even for non-cognate ss d(pC)_n, which is more flexible structure than ss d(pT)_n (17). The highest, 790-fold increase in the affinity was observed for ds OG11 as compared with ds G11 (Table 1). Therefore, in contrast to Fpg, the specific structure of the oxoG unit is very important for the productive cooperative changes during mutual adjustment of conformations of OGG1 and cognate DNA. In conclusion, OGG1 is the first example of a DNA-dependent enzyme for which the contribution of the specific interactions with DNA is close to three orders of magnitude.

All DNA-dependent enzymes studied by the SILC approach are highly specific, converting their cognate DNA 4–8 orders of magnitude more efficiently than non-cognate DNA [reviewed in refs (3,5)]. Formation of the enzyme–substrate complex cannot alone explain this specificity. For instance, all these enzymes, including OGG1, interact with non-cognate RNA–RNA and RNA–DNA duplexes with affinities comparable to those for DNA–DNA duplexes with the affinity that is only 1–2 orders of magnitude lower than their affinity for cognate DNA–DNA duplexes. Yet these enzymes do not process RNA–RNA and RNA–DNA duplexes even at saturating concentrations of these ligands. Many data indicate that all enzymes acting on long DNA first bind to DNA of any sequence in and then slide to the site containing a specific sequence or a lesion [reviewed in refs (3,5,46)]. There they stop due to increase in the affinity for DNA (estimated 5- to 790-fold for different enzymes) and can change the conformation of the DNA sugar–phosphate backbone in multiple ways. Formation of hydrogen bonds between the enzymes and the bases of their cognate sites identified by X-ray analysis is most probably one of the final stages in the selection of the cognate DNA substrates. However, only the formation of these bonds can promote the proper fit of specific bases into recognition pockets of the enzymes, accelerating the reactions by 4–8 orders of magnitude. Thus, it is not the stage of complex formation, but rather the second (DNA adjustment to the optimal conformation) and third stages (the irreversible catalytic step), which provide most of the specificity for the enzymes involved in DNA replication, DNA repair and other processes of DNA metabolism.

The affinity and rate constant for enzymes recognizing specific features in DNA can be influenced by the conformational flexibility, and dynamic behavior of the enzyme and DNA, and their capability for specific mutual conformational adjustment. Therefore, it was interesting to find out which conformational and structural properties of cognate DNA can affect the K_M and k_cat values of OGG1. Using the ACTIVITY software, we have shown that the k_cat values are correlated with the twist of DNA between the positions −6 and +6. Lower but still significant correlation existed with the twist over a longer [−8;+8] stretch, consistent with the importance of the twist parameter for the k_cat, but the lower Q value in this case may indicate that the twist is less relevant outside of the enzyme’s footprint. OGG1 kinks and partially unwinds DNA to evert the oxoG deoxynucleoside into the active site (25), and the increased twist may assist the enzyme in these acts. Another possibility is that some optimal twist angle is required for the most favorable positioning of DNA phosphates for interactions with the DNA-binding groove of OGG1. Some other DNA-binding proteins are also sensitive to the twist angle of B-DNA. For example, higher twist is associated with increased efficiency of transcription initiation from E. coli promoters by RNA polymerase (47,48) and with preferred places of nucleosome assembly (49). Characteristic twist angle patterns are observed for binding sites of Sp1 and p53 transcriptional regulators (50) and for eukaryotic ribosomal promoters (51).

For K_M values, a negative correlation was observed with the average ΔG° characterizing the stretch of DNA between the positions −10 and +10. The most likely explanation is that the lower values of ΔG° are associated with a more stable DNA duplex, more resistant to the disruption of base pairing effected by OGG1. This enzyme is known to search for oxoG lesions flipping out normal bases from DNA (27), a process that overall would be more efficient in less stable duplexes. Additionally, the ‘limiting stage’ approximation was applied for prediction of specific ΔG° for one step of DNA helix, δG°. The calculated δG° for all ds ODNs correlated with the changes in ΔG° but neither with enthalpy nor entropy (Table 4). Therefore, using correlation of the kinetic parameters with conformational and physicochemical DNA properties, we have found empirical dependencies for estimating the K_M and k_cat values for various ds ODNs containing an oxoG nucleotide on the basis of theoretically calculated twist, ΔG°, or δG°.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Presidium of the Russian Academy of Sciences (grants 6.7, 6.14); Russian Foundation for Basic Research (10-04-91058, 11-04-00807); Russian Ministry of Science and Education (02.740.11.0079, NSh-3185.2010.4); National Cancer Institute (CA017395-33); Siberian Branch of the Russian Academy of Sciences. Funding for open access charge: Russian Foundation for Basic Research.

Conflict of interest statement. None declared.