Measuring directionality of the retinal reflection with a Shack-Hartmann wavefront sensor

Abstract

The directional sensitivity of the retina, known as the Stiles-Crawford effect (SCE), originates from the waveguide property of photoreceptors. This effect has been extensively studied in normal and pathologic eyes using highly customized optical instrumentation. Here we investigate a new approach based on a Shack-Hartmann wavefront sensor (SHWS), a technology that has been traditionally employed for measuring wave aberrations (phase) of the eye and is available in clinics. Using a modified research-grade SHWS, we demonstrate in five healthy subjects and at four retinal eccentricities that intensity information can be readily extracted from the SHWS measurement and the spatial distribution of which is consistent with that produced by the optical SCE. The technique is found sufficiently sensitive even at near-infrared wavelengths where the optical SCE is faint. We demonstrate that the optical SCE signal is confined to the core of the SHWS spots with the tails being diffuse and non-directional, suggesting cones fail to recapture light that is multiply scattered in the retina. The high sensitivity of the SHWS to the optical SCE raises concern as to how this effect, intrinsic to the retina, may impact the SHWS measurement of ocular aberrations.

1. Introduction

As first reported by Stiles and Crawford in 1933 [1], the human visual system is more sensitive to light rays that enter near the center of the pupil compared to at the edge. This phenomenon is referred to as the psychophysical Stiles-Crawford effect (SCE) and originates from the waveguide properties of photoreceptors. Based in part on the principle of optical reciprocity, a similar effect is present in the retinal reflection that exits the eye and is generally referred to as the optical SCE. The spatial distribution of the light exiting the eye is composed of a Gaussian-shaped bright core (directional contribution from the photoreceptors) and a uniform veil (broadly scattered contribution from the other parts of the retina). The bright core is of significant clinical interest since normal morphology of the photoreceptors and extracellular spacing is required for normal directionality.

The SCE has been extensively studied in normal and pathologic eyes using a wide range of novel instruments that deliver light to the retina and capture the returning faint reflection [2–5]. While successful, the high degree of customization and dedication to a specific measurement have largely confined these instruments to the research laboratory with slow progress towards commercial use in the clinic. Counter to this trend, optical coherence tomography (OCT) – a technology that is commercially available and used in clinics – has been demonstrated recently for measuring the optical SCE [6]. Another commercial technology that might hold promise for measuring the optical SCE is wavefront sensing. Wavefront sensing also delivers light to the retina, and captures and analyzes the retinal reflection, but the analysis is entirely for measuring ocular wave aberrations (phase information) rather than amplitude information.

Numerous commercial wavefront sensing instruments for the eye are available with most based on Shack-Hartmann wavefront sensor (SHWS) technology. The key components of a SHWS are a light source that forms a focused beacon on the retina, a 2D lenslet array that samples the reflected wavefront at the eye's pupil, and an areal CCD – positioned at the back focal plane of the array – that records the array of focused intensity spots. Displacement of the spots relative to a set of reference locations provides local wavefront slope spatially resolved across the pupil and from which the aberrated wavefront is reconstructed.

While the SHWS is routinely used for measuring ocular aberrations (wavefront phase), the complementary wavefront amplitude information, which should be intrinsically encoded in the raw SHWS data, is discarded. Using a modified research-grade SHWS, we investigate the utility of this extra information for characterizing the directional property of the retina. While seemingly straightforward, several key technical concerns are apparent: (1) the optical SCE is faint at near infrared wavelengths, which is the spectral range of commercial SHWS instruments, (2) post processing algorithms must effectively extract the encoded directional information, and (3) SHWS beam entry (XY pupil location) must be controlled to maximize the strength of the optical SCE. Here we show that the SHWS technique is sufficiently sensitive for measuring the optical SCE at near-infrared wavelengths when the beam entry point is coarsely positioned near the peak of the optical SCE. Sensitivity of the instrument was found highly dependent on the post processing to separate the core from the tail of each raw SHWS spot. Early accounts of this work were presented at the 2008 SPIE [7] and ARVO meetings [8]. Independent of the work presented here, a laser ray tracing technique – which shares some attributes with the SHWS - has been reported recently for measuring cone directionality at 532 nm [9].

2. Methods

2.1 SHWS Apparatus

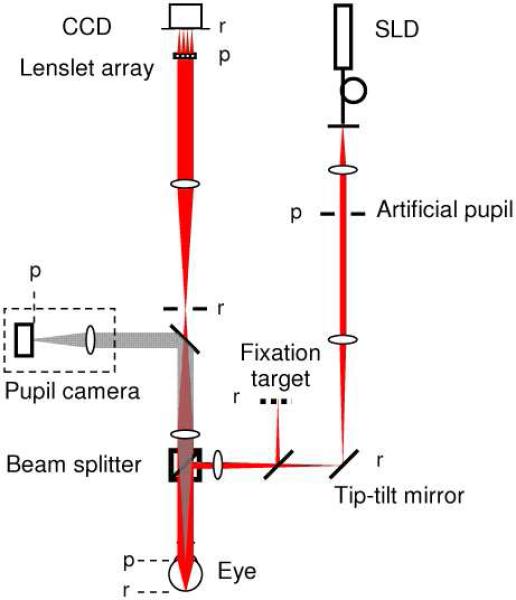
An existing laboratory SHWS was modified for use in this study (Fig. 1). The system is composed of four channels: illumination, detection, fixation, and pupil alignment. The illumination channel employs a superluminescent diode (SLD) ($\stackrel{‒}{\lambda }=788\mathrm{nm}$; Δλ = 20 nm) that generates a 2 mm beam that enters the subject's eye. The beam focuses onto a small patch of retina that is nominally 23 μm in diameter, defined as 2.44 λ f/d, where λ is the wavelength of light (788 nm), f the focal length of the eye, and d the beam diameter entering the eye. To control pupil entry position in X and Y while keeping the retinal spot fixed, a planar mirror with tip/tilt controls was positioned conjugate to the retina in the illumination channel (bottom right mirror in Fig. 1). The tip/tilt provided sufficient range to cover a large (~7 mm) pupil. The beamsplitter cube shown in Fig. 1 was non-polarizing with transmission and reflection of s and p polarization approximately equal at the wavelength of the SHWS. The SLD delivered 3 μw to the eye, more than 100 times below the ANSI guideline [10]. The detection channel consists of a Shack-Hartmann wavefront sensor (SHWS) that contains a cooled, 12-bit CCD camera (Ropier Scientific, Inc.) and 17 by 17 lenslet array (400 μm pitch) that samples a 6.8 mm pupil at the eye. A 2 mm pinhole was inserted upstream of the SHWS and was large enough to allow the SHWS beacon to pass unobstructed, yet small enough to block much of the bright corneal reflex. The 2 mm diameter corresponded to approximately 1 degree at the retina, more than an order magnitude larger than the 23 μm beacon diameter at the retina. Camera read noise is 11.9 electrons root mean square (RMS) with an exposure time of 50 ms. The acquisition rate (20 Hz) was realized with 4×4 binning of the 6.5μm pixels, giving an effective pixel size of 26 μm.

Fig. 1.

Layout of the laboratory SHWS for measuring the optical SCE. The beam of a 788 nm pigtailed SLD (linearly polarized) passes through an artificial pupil, limiting the beam size to 2 mm at the eye's pupil. The XY position of the beam at the eye's pupil is controlled via a tip-tilt mirror that is conjugate to the retina. After entering the eye, the beam focuses to a small spot on the retina. The fixation target and pupil camera are used to align the eye to the system. The camera also confirms location of the beam entry position. Light reflected from the retina, exits the eye and after a relay telescope is sampled by a lenslet array and captured by a CCD camera. ‘p’ refers to planes conjugate to the pupil; ‘r’ refers to planes conjugate to the retina. The system contains no polarization controlling components. See text for additional system details.

The fixation and pupil camera channels aided alignment of the subject's eye during SHWS data collection. The fixation target consisted of a grid of high-contrast cross hairs regularly spaced at 1 degree intervals and back illuminated with diffuse green light. The subject was instructed to fixate at selected cross hairs depending on the retinal eccentricity at which SHWS measurements were to be taken. The pupil camera, sensitive in the near infrared, was inserted downstream of the eye using a motor-controlled flip mirror that temporarily redirected light exiting the eye to a video camera. The retroillumination view at 788 nm coupled with the corneal reflex provided real-time confirmation of the beam entry location in the subject's pupil. The flip mirror was retracted prior to SHWS measurements.

2.2 Experimental protocol and data processing

Five subjects were recruited for optical SCE measurements using the SHWS system in Fig. 1. The subjects ranged in age from 31 to 39 years. All were free of ocular disease and had normal corrected vision. Refractive error ranged from −2.75 to −4.5 diopters sphere and 0 to −1.5 diopters cylinder. Measurements were acquired at the fovea and 1, 2, and 3 degree eccentricity in the superior retinal field.

Prior to SHWS measurements, one drop of 1% Tropicamide was applied topically to the subject's eye for pupil dilation and paralysis of accommodation. A bite bar mount and forehead rest attached to an XYZ positioning stage stabilized the subject's head. The subject was instructed to fixate at a specific target location during which the subject was aligned to the SHWS system. Alignment entailed centering the subject's pupil on the optical axis of the SHWS and axially positioning the subject's pupil to coincide with the SHWS entrance pupil. Both were accomplished with the XYZ positioning stage and pupil camera for monitoring. Next the general location of the optical SCE peak was found by systematically moving the position of the 788 nm beam in the pupil using the tip-tilt mirror (see Fig. 1). Determination of the peak location was based on the raw SHWS output (displayed on a video monitor, an example of which is shown in Fig. 2 (left)) and to a lesser extent the pupil camera (displayed on a second video monitor). The optical SCE often appeared faint or not at all with the pupil camera and difficult to observe in the raw SHWS spots, requiring SHWS measurements to be acquired and processed at several different pupil entry locations. In hindsight, this step could be optimized by incorporating a real time display of the SHWS amplitude to provide much better visual indication of the optical SCE location. For each selected pupil entry location, approximately 60 SHWS images were acquired and averaged. Substantial averaging coupled with involuntary eye motion assured that many cone photoreceptors contributed to the optical SCE signal, not just the handful that occupied the 23 μm illuminated patch at any instant. Averaging also improved the signal to noise by reducing the impact of speckle noise and structured reflections from other retinal layers such as the retinal vasculature.

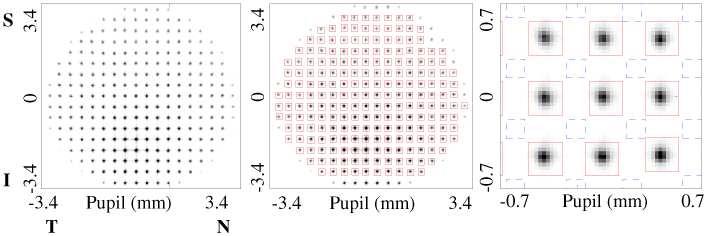
Fig. 2.

(left) Raw SHWS image acquired on one subject using the Fig. 1 system. Colored boxes are superimposed across (middle) the entire spot array and (right) an enlarged subsection. Red and blue boxes are positioned to sample the core and tail portions of the spots, respectively, and are the regions used for data analysis in this study. The raw image is displayed using an inverted grayscale. T, N, S and I represent temporal, nasal, superior and inferior sides of the pupil, respectively.

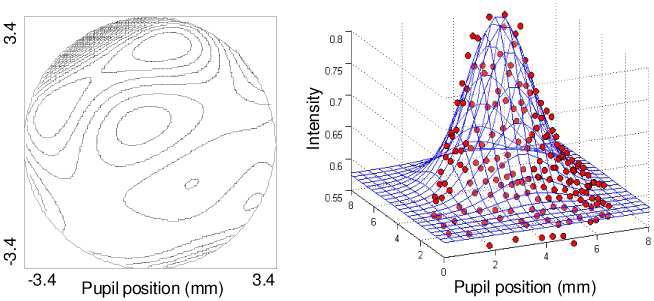
Reconstruction of the wavefront aberrations (phase) and wavefront amplitude from the same raw SHWS data (Fig. 2(left)) follows two distinctly different processes. Reconstruction of the wavefront aberrations requires centroiding of the SHWS spots, determining spot displacement relative to a calibrated reference, converting to local wavefront slopes, fitting to Zernike modes, and finally summing of the modes to obtain the wavefront aberrations. Details of these steps can be found elsewhere [11]. Figure 3(a) shows a representative wavefront aberration reconstructed from an averaged SHWS image acquired on one of the subjects following our experimental protocol.

Fig. 3.

Wavefront (a) aberration and (b) amplitude maps reconstructed from the same raw SHWS data on one subject. The wavefront aberration map is composed of 18 Zernike modes (3rd through 6th order). The contour interval is 0.2 μm, and the peak-to-valley across the 6.8 mm pupil is 3.56 m. Data points in the amplitude map correspond to intensity measurements, one per lenslet (red boxes in Fig. 2). The superimposed surface is a least-squares fit of Eq. (1) to the data points.

From the same averaged SHWS image, the wavefront amplitude was reconstructed using the following sequence of steps, implemented in Matlab (MathWorks, Inc.) and customized for extracting the optical SCE signal. First, summation boxes were superimposed on the raw SHWS image, each nominally centered on the centroid of a given spot (see Fig. 2(middle)). The spots had a typical diameter of about 80 μm at the SHWS CCD and were spaced 400 μm (pitch of lenslet array). Empirically we found a summation box size of 260 μm by 260 μm was adequate for capturing essentially all of the intensity in the spot core, while reducing the impact of the spot tails (see Fig. 2 (right)) spot tails. We wanted to avoid the spot tails as we hypothesized that the SHWS lenslets spatially separate the retinal reflection into two principle parts: a spot core that is composed of both a directional component (optical SCE) and a non-directional component (light multiply scattered in the retina [12]), and a spot tail that is composed almost entirely of the non-direction component. The underlying rationale is that the multiply scattered light generated in the tail is not recaptured by cone photoreceptors and thus the tails should exhibit minimal waveguiding. Conversely, a large proportion of the light in the spot core is captured by the cone photoreceptors being illuminated and thus the core should exhibit strong waveguiding [6]. To test this hypothesis a second set of summation boxes were superimposed on the raw SHWS image, but repositioned so as to be centered between four adjacent centroid locations (see Fig. 2(right)). Care was taken to avoid the rectilinear diffraction pattern that represents an extension of the spot core and reflects the square geometry of the lenslets. Second, for both sets of boxes, the total light intensity was summed over each box and from which a spatial distribution map of the retinal reflectance (wavefront amplitude) in the pupil plane of the eye was reconstructed. A representative example is shown in Fig. 3(b) for the boxes centered on the spot core. The number of summation boxes equaled the number of lenslets (221) that filled a 6.8 mm pupil.

Finally, the wavefront amplitude map for both scenarios (core and tail boxes) was fit using a non-linear least square algorithm (function “lsqcurvefit” in Matlab, Mathworks, Inc.) to a five-parameter model composed of a constant bias and a Gaussian:

$$R\left(x\right)=B+I^{\ast }{10}^{-\rho \left[{(x-x_0)}^2+{(y-y_0)}^2\right]}$$ (1)

Equation (1) is well established for modeling the pupil intensity distribution of the optical SCE [3]. B represents a uniform illumination of the pupil generated by non-directional scatter in the retina. I, ρ, and x_o and y_o define the optical SCE contribution and represent the peak intensity, directionality, and lateral displacement, respectively. Displacement of the peak position is relative to the geometric center of the eye's pupil.

As a practical problem, the corneal reflex contaminated a small fraction of the SHWS spots. A pinhole (closed iris diaphragm) inserted in the detection channel and conjugate to the retina (Fig. 1) greatly reduced the corneal reflex during SHWS measurements. The remaining reflex was removed in post processing using a maximum threshold that discarded lenslet spots contaminated by the reflex. In the same manner, a minimum threshold was set to discard spots formed by lenslets partially occluded by the pupil edge.

2.3 Calibration of SHWS system

Performance of the modified SHWS system (Fig. 1) was validated in two steps. First, we measured the transmission errors (spatial non-uniformities in intensity) generated by propagating the beam from a model eye to the SHWS lenslet array. The beam profile was measured and compared before and after propagation. Second, we measured errors generated by propagating the beam through the lenslet array to the CCD, acquiring raw SHWS images, and reconstructing the intensity distribution with the custom software. All images collected for the validation and subsequent subject experiments were background subtracted prior to processing.

The model eye consisted of a pigtailed 780 nm laser diode and 30 mm achromat lens with the tip of the pigtail placed at the front focal plane of the lens. The collimated Gaussian beam that exited the model eye was directed through the SHWS system. Special care was taken to assure the beam followed essentially the same path as that with real eyes. A beam profiler (BP109-VIS, Thorlabs) measured successively the cross-sectional intensity distribution of the beam along the horizontal and vertical meridians. Profiler measurements were collected at the normal position occupied by the pupil of a real eye (i.e., immediately downstream of the model eye) and at the position of the SHWS lenslet array, the latter realized by temporarily inserting a planar mirror immediately in front of the lenslet array to redirect the beam to the profiler. Difference in beam uniformity between the two locations was evaluated by directly comparing the measured intensity profiles. The profiles were found to be within 5% of each other with most of the differences appearing as random, local fluctuations, as opposed to large, gradual changes that would be more characteristic of a systematic error such as vignetting. This calibration experiment indicates that transmission errors generated by beam propagation through the SHWS system are sufficiently small to be inconsequential for optical SCE measurements.

For the second validation step, a beam of uniform intensity was directed onto the SHWS lenslet array and the corresponding spot array captured and processed (including the fit to Eq. (1)). Total light captured by the SHWS CCD was comparable to that used for the subjects, and the CCD gain and number of pixels binned were unchanged. The uniform profile made it readily straightforward to assess the extent of errors generated between the lenslet array and the fit to the processed intensity profile. The uniform profile at the lenslet array was generated by positioning the same 780 nm laser source 10 meters from the lenslet array, realized by reflecting the beam off of multiple planar mirrors in the laboratory. Based on this separation and the 0.12 numerical aperture of the fiber, a variation in intensity across the central 6.8 mm portion of the lenslet array is predicted to be less than 0.1%. 60 SHWS images were acquired, averaged, processed, and then fit to Eq. (1). For these images, the ratio of I/(I+B) was found to be just 0.065, indicating exceedingly little overall energy in the Gaussian term of Eq. (1) and consistent with the predicted uniform beam profile incident on the lenslet array. We interpreted I/(I+B) = 0.065 as the sensitivity of the combined SHWS sensor and post processing. Based on this definition, values above 0.065 exceed the SHWS's noise floor and therefore should be detectable by the instrument.

3. Results

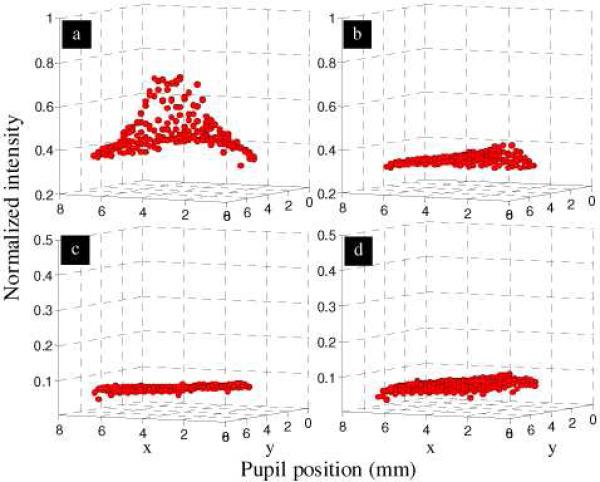
SHWS measurements on all five subjects show the same general reflectance pattern in the pupil with the total reflectance and distribution of reflectance sensitive to the entry beam location. As a representative example, Fig. 4(a) shows the measured pupil reflectance with entry on the subject's optical SCE peak. The total reflectance is large and the distribution highly arched (directional), both general characteristics of the optical SCE as observed with conventional reflectometric techniques. In contrast, entry displaced from the optical SCE peak results in a broad veil of reduced reflectance, an example of which is shown in Fig. 4(b) for the same eye. The total reflectance and distribution of reflectance also depend on which portion of the SHWS raw image is used for analysis. For example, use of the spot tails as defined by the blue boxes (as opposed to the spot cores as defined by the red boxes – see Fig. 2) results in a uniform reflectance that is insensitive to the entry position. An example of this case is shown in Fig. 4(c and d) using the same SHWS data set as in Fig. 4(a and b).

Fig. 4.

Wavefront amplitude reconstructed from SHWS images acquired at 2 degree retinal eccentricity on the same subject. The four plots represent the four possible combinations of pupil entry position (on and off the optical SCE peak) and summation box location (core and tail of SHWS spots): (a) on SCE peak and core, (b) off SCE peak and core, (c) on SCE peak and tail, and (d) off SCE peak and tail. Beam entry positions differed by 2 mm. Data points correspond to intensity measurements, one per lenslet.

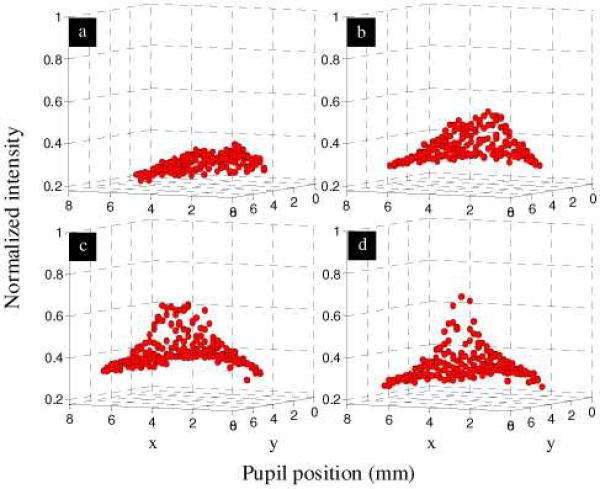
With beam entry on the optical SCE peak, additional SHWS measurements were acquired at each of four retinal eccentricities (fovea, 1, 2, and 3 degrees) in the superior retinal field. We confirmed that the reflex of the inner limiting membrane [13] did not contribute to the peak as the position of the peak was observed insensitive to the entry beam location. Unlike the optical SCE, the direction of the ILM reflection is strongly dependent on beam entry. As a representative example on one eye, Fig. 5 shows surface plots of the reconstructed pupil intensity at the four eccentricities examined. The figure reveals noticeable steepening of the central reflectance with eccentricity. For these reconstructions, the summation boxes were centered on the core of SHWS spots.

Fig. 5.

Pupil intensity (wavefront amplitude) reconstructed from raw SHWS images for (a) fovea, (b) 1 degree, (c) 2 degree, and (d) 3 degree retinal eccentricity of the superior retinal field. Data points correspond to intensity measurements, one per lenslet, with corneal reflex removed.

To quantify the relative magnitude and shape of the reflectance maps, the intensity data for both summation box locations was fit to Eq. (1), the five-parameter model. Figure 6 (left) shows the fitted directionality values (ρ_core and ρ_tail), averaged across the five subjects and plotted against retinal eccentricity. ρ_core is seen to be sensitive to retinal eccentricity, increasing monotonically (0.0607 mm⁻², 0.1258 mm⁻², 0.1732 mm⁻², and 0.2039 mm⁻²) with an overall increase of almost three times. ρ_tail, on the other hand, is insensitive, remaining flat with values of about 0.04 mm⁻² (0.0358 mm⁻², 0.0451 mm⁻², 0.0448 mm⁻², and 0.0333 mm⁻²).

Fig. 6.

Fit of the SHWS measurements on five subjects to the five-parameter model (Eq. (1). (left) Average directionality is plotted as a function of retinal eccentricity and summation box location (core, tail). Error bars represent +/− one standard deviation. (right) A simplified Eq. (1) (defined in text) is plotted as a function of pupil position. The simplified equation captures the relative contribution (I/(I + B)) and the directional strength ρ_core of the Gaussian portion.

Figure 6 (right) captures the impact of the three principle parameters (B, I, and ρ_core) that define the relative magnitude and shape of the Gaussian portion of Eq. (1). Curves are restricted to the summation boxes centered on the SHWS spots. Specifically, I/(I + B) 10^{- ρcore×2} is plotted as a function of position in the pupil for the four retinal eccentricities. As shown in the figure, the Gaussian amplitude (I) varies from 28% to 46% of the total amplitude (B + I), thus representing a significant fraction of the returning light at the peak of the optical SCE. At the pupil edge, however, the Gaussian contribution is greatly reduced and contributes little to the total amplitude (B + I). Note the steepness of the Gaussian for 2 and 3 degree retinal eccentricities compared to that at the fovea. While not plotted, the summation boxes in the tails yielded noticeably broader Gaussian curves (smaller ρ). The relative amplitude, I/(I+B), was somewhat smaller (20-25%) for 1, 2, and 3 deg, though higher for the fovea (37%). Note that these relative amplitudes lie well above the 0.065 noise floor measured in the calibration of the SHWS system.

4. Discussion

4.1 Comparison of directionality with conventional reflectrometric measurements

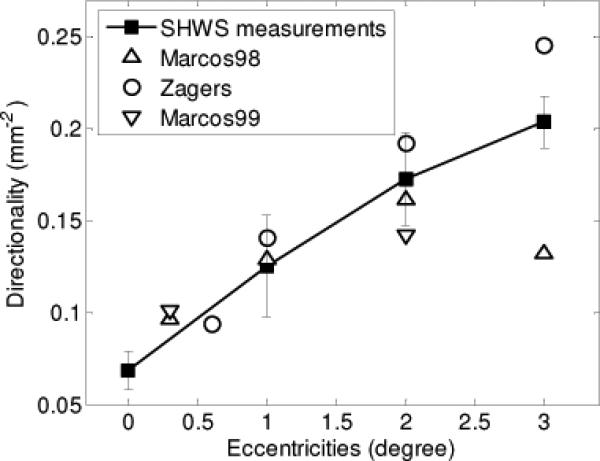
Figure 7 compares our measurements of directionality (Fig. 6) to that obtained with conventional reflectometers. The analysis that underlies the comparison, however, is not straightforward as directionality depends on the illumination and detection configuration of the techniques (e.g., configuration of entrance and exit pupils at the eye), illumination wavelength, and retinal eccentricity. Meaningful comparison of our ρ_SHWS measurements to that in the literature must therefore account for these differences. To do this we employed the model developed by Marcos et al. [14], which directionality is a function of two independent retinal components: waveguiding by cone photoreceptors (ρwg) and scatter by the optically rough retina (ρscatter), which is driven by the topography of the cone mosaic [14,15]. To first order, ρwg has been shown to be independent of the wavelength of light (λ) and row-to-row cone spacing (s), while ρscatter scales as 1/λ² and s² [16]. For comparison, we selected the studies by Marcos et al. [14], Marcos and Burns [15], and Zagers et al. [16], based partially on simplicity in that directionality for these is the sum of ρwg and ρscatter, the same relation as expected for ρSHWS. In this way, conversion of the directionality measurements (ρ_Marcos1, ρ_Marcos2, and ρ_Zagers) reported in these studies to an equivalent ρ_SHWS (defined here as, ρ_{Marcos1_equiv}, ρ_{Marcos2_equiv}, and ρ_{Zagers_equiv}) requires taking into account only differences in wavelength and cone spacing, factors that are confined to the ρscatter term. Described below is this conversion for each study with the most pertinent methodological parameters summarized in Table 1 for reference.

Fig. 7.

The filled squares are the measurements from the SHWS. Error bars represent the +/−1 standard deviation. The open circles, upward-pointing triangles and downward-pointing triangles stand for equivalent measurements from Zagers et al. (2003), Marcos et al. (1998) and Marcos and Burns (1999), respectively.

Table 1.

Relevant parameters of the different reflectometric techniques.

Study	Wavelength	Retinal ecc.	Field diameter
1. Marcos and Burns (1999)	543, 632 nm	0, 2°	1°
2 Marcos et al. (1998)	543 nm	0, 1, 2, 3°	1°
3. Zagers et al. (2003)	480-720 nm	0	1.9°
4. Current study	788 nm	0, 1, 2, 3°	23 μm spot coupled with eye motion

Before describing this conversion, however, it should be noted that a more recent study by van de Kraats and van Norren [17] could have been included in our comparison. While appropriate, we chose not to largely because their technique and results are very similar to that reported by Zagers et al. [16]. Also, it is important to mention that while our comparison utilizes published directionality measurements and models that have undergone significant scrutiny, the extension of these to near infrared wavelengths (788 nm) and retinal eccentricities outside the fovea (3°) introduce some degree of uncertainty. Previous measurements in the near infrared have demonstrated substantial loss in signal to noise, making measurements in this spectral band less reliable. Measurements outside the fovea are increasingly complicated by the contribution of rods and the extended spacing of the cones. Additionally, the model developed by Marcos et al., which our comparison relies heavily on, is based on a limited number of subjects. Nevertheless even with these limitations, the absence of more appropriate data to compare our results to – in particular at near-infrared wavelengths and outside the fovea - motivated the comparison that we have developed here.

Based on the Marcos model, ρ_Marcos1 [15] and ρ_SHWS differ only in wavelength used (543 nm versus 788 nm). ρ_SHWS is defined as single pass through the pupil of the eye and thus mathematically is expected to equal ρ_wg + ρ_scatter(λ,s). Here we provisionally assume there are sufficient cones illuminated by the SHWS beacon for ρ_scatter(λ,s) to be applicable. While conservatively only tens of cones are illuminated at any instant of time by the 23 μm diameter beacon, the long exposure (50 ms) coupled with the many images averaged easily increases that to thousands of cones. To convert ρ_Marcos1 to an equivalent ρ_SHWS (i.e., ρ_{Marcos1_equiv}) requires separately determining ρ_wg and ρ_scatter(λ=543 nm,s), converting ρ_scatter(λ=543 nm,s) to ρ_scatter(λ=788 nm,s), and then recombining using ρ_{Marcos1_equiv} = ρ_wg + ρ_scatter(λ=788 nm, s). In Marcos and Burns [15], ρ_scatter(λ=543nm) = 0.016 and 0.089 at 0 and 2 degree eccentricity, respectively, obtained by taking the difference between directionality from single (0.110 and 0.189) and multiple (0.094 and 0.1) entry measurements. Single and multiple entry measurements are defined in the citation. ρ_scatter(λ=788nm) is obtained by applying the relationship, 1/λ² and yields (543nm/788nm)²*0.016 = 0.0076 for 0 degree eccentricity and (543nm/788nm)²*0.089 = 0.042 for 2 degree eccentricity. In effect, the directional component due to scatter reduces by more than ½ at the longer wavelength of 788 nm. The corresponding ρ_wg is equal to the directionality of the multiple-entry measurement (which is independent of wavelength) and is 0.094 and 0.1 at 0 and 2 deg eccentricity, respectively, in the paper. Thus ρ_{Marcos1_equiv} = 0.094 + 0.0076 = 0.10 at 0 degree eccentricity and 0.1 + 0.037 = 0.137 at 2 deg eccentricity. Both values of ρ_{Marcos1_equiv} (0 and 2 degree eccentricity) are plotted in Fig. 7. Note, however, that for the 0 degree measurement, the contributing cone density is not that of the foveal center but rather an average across the entire 1.0 degree field. Using the anatomical cone density distribution reported by Curcio et al. [18], average spacing is predicted to be 2.73 μm, which corresponds to a retinal eccentricity of 0.3 degrees. Thus the 0 degree measurement is shifted to 0.3 degree in the Fig. 7. For the 2 degree eccentricity, variation across the 1.0 degree field was negligible.

To convert ρ_Marcos2 to an equivalent ρ_SHWS (i.e., ρ_{Marcos2_equiv}), we follow the same methodology used above for ρ_{Marcos1_equiv}: determine the separate contributions of ρ_wg and ρ_scatter(λ=543 nm,s), convert ρ_scatter(λ=543 nm,s) to ρ_scatter(λ=788 nm,s), and finally recombine using ρ_{Marcos2_equiv} = ρ_wg + ρ_scatter(λ=788 nm, s). ρ_Marcos2 was measured at four retinal eccentricities (0, 1, 2, and 3 degrees), as opposed to the two (0 and 2 degrees) for ρ_Marcos1. One caveat, however, is that only single entry measurements were taken and therefore there is insufficient information to separate ρ_wg and ρ_scatter(λ=543 nm,s). To resolve this, we took advantage of the fact that the same subjects were measured for both ρ_Marcos1 and ρ_Marcos2. In this way, we used the above estimates of ρ_wg (0.094 and 0.1) for the retinal eccentricities of 0 and 2 degrees and linearly interpolated these estimates for values at 1 and 3 degree eccentricity. Combining ρ_wg with ρ_scatter(λ=788 nm,s) yields ρ_{Marcos2_equiv}, which is plotted in Fig. 7, again taking into account the 0.3 degree shift at 0 degrees.

Lastly, we convert ρ_Zagers to an equivalent ρ_SHWS (i.e., ρ_{Zagers_equiv}). Zagers et al. collected directionality measurements as a function of wavelength (480-720 nm) for a 1.9 degree field centered on the fovea. A least-squares fit of the form ρ_Zagers = ρ_wg + α(s)/λ² was applied to the measurements with the result that ρ_wg = 0.085 mm⁻², and s = 3.38 μm. To convert ρ_Zagers to ρ_{Zagers_equiv}, requires setting λ equal to 788 nm and s to the cone spacing predicted by Curcio et al. [18] for the additional retinal eccentricities 1, 2, and 3 degrees. Note that for the 0 degree measurement, average cone spacing in the 1.9 degree field is predicted to be 3.3 μm based on Curcio et al. [18]. Thus the 3.3 μm corresponds to a retinal eccentricity of 0.6 degrees, not 0 degrees, which is correctly shown in Fig. 7. For the other eccentricities, cone variation was negligible.

As a check of our conversion procedure (e.g., convert ρ_Zagers to ρ_{Zagers_equiv}), we used the same procedure to extrapolate our foveal SHWS results to 1, 2, and 3 degrees and then compared these to our actual measurements at the same retinal locations. The extrapolated ρ_SHWS estimates differed by 14.4%, 8.5% and 3.9% from the SHWS measurements of 0.126, 0.173 and 0.204 at 1, 2, and 3 degrees, respectively. This strong agreement (between extrapolation and experiment) supports the use of our conversion procedure on the Zagers et al. and Marcos et al. data.

Figure 7 shows that the SHWS measurements are indeed consistent with directionality reported by the other methods: ρ_{Marcos1_equiv}, ρ_{Marcos2_equiv}, and ρ_{Zagers_equiv}. ρ_SHWS shows a general increase with retinal eccentricity with values that fall well within the variability between the other methods. Interestingly, the small SHWS beacon size at the retina, even with the effect of eye motion, should in principle allow highly localized measurements. This may be advantageous as for example at the fovea where the density of cones varies rapidly. In comparison the large 1 and 1.9 degree diameter illumination used by Marcos [14, 15] and Zagers [16], respectively, make assessing directionality in such areas like the fovea difficult. The fact that ρ_{Marcos1_equiv}, ρ_{Marcos2_equiv}, and ρ_{Zagers_equiv} straddle the ρ_SHWS curve at 0.3 and 0.6 degree suggests the ρ_SHWS value at the nominal 0 degree location is indeed quite close to the foveal center.

We were somewhat surprised that ρ_SHWS did not decrease at 3 degree eccentricity as did ρ_{Marcos2_equiv}. While Fig. 7 shows that ρ_SHWS is straddled by ρ_{Marcos2_equiv} and ρ_{Zagers_equiv}, ρ_{Marcos2_equiv} is possibly a more reliable estimate since it is based on actual measurements at this eccentricity. The authors purport that the ρ_{Marcos2_equiv} decrease might result from the increased presence of rods and the decrease of cone aperture size relative to their row-to-row spacing at this eccentricity. Neither of these effects is fully accounted for by the extrapolation approach we employed to estimate ρ_{Zagers_equiv}. For the SHWS method, we see no fundamental reason as to why it should not be sensitive to these effects. This inconsistency will require future investigation.

4.2 Directionality of core and tail of SHWS spots

We hypothesize that the SHWS lenslets spatially confine the directional component (optical SCE) of the retinal reflection to the spot core. In contrast, the non-directional component (light multiply scattered in the retina) is not confined, instead extending across both core and tail. We tested this hypothesis by reconstructing reflectance distribution maps from SHWS data sets using two different sets of summation boxes, one that sampled the SHWS spot core and the other that sampled the spot tail (Fig. 2(right)). The resulting maps (e.g., Fig. 4), and corresponding directionality (Fig. 6(left)) and relative contribution (Fig. 6(right)) strongly support the hypothesis. The optical SCE was clearly confined to the spot core. For the core, strength of the directionality and its dependence on retinal eccentricity are consistent with optical SCE measurements reported in the literature using conventional methods (Fig. 7). For the tail, directionality was weak (ρ ~0.04 mm⁻²) and insensitive to retinal eccentricity, both indicate that the cones fail to recapture light that is scattered in the retina. Figure 6(right) reveals that a large portion of the core energy is non-directional even at the radial pupil position of 0 mm (>50%). At the edges of a large pupil (>6 mm), the non-directional component accounts for essentially all of the energy (>90%) in the spot core.

While the non-directional portion is large in the core, it should be emphasized that the directional proportion is not insignificant and in fact appreciable compared to that reported with other techniques at near infrared wavelengths. As an example, van de Kraats and van Norren [17] report an I/(I+B) value of 0.10 at 788 nm at the fovea. This value was obtained by converting their Fig. 10 I/B value of 0.11 to I/(I+B), using the expression I/(I+B) = (I/B) / ((I/B)+1). In comparison our foveal measurement with the SHWS gives an I/(I+B) of ~0.3, three times higher than that of van de Kraats and van Norren, suggesting the SHWS is a more sensitive method. Perhaps more revealing, Fig. 10 in van de Kraats and van Norren shows I/(I+B) values in the central portion of the visible spectrum (500 to 600 nm) that are comparable to our 0.3 in the near infrared, i.e., approximately 0.33 for an I/B of 0.5. Thus it appears the fundamental operation of the SHWS with spatial sampling of the pupil with lenslets and detection in the image plane enables effective spatial filtering (reduction) of non-directional reflections. The end result is a near-infrared signal with the SHWS that is comparable in strength (relative to the diffuse background) to that at visible wavelengths with traditional optical SCE techniques.

4.3 Influence of optical SCE on SHWS measurements of ocular aberrations

This paper focuses on the extent to which the SHWS can measure the optical SCE. Our finding that it is indeed sensitive to this effect raises a potential concern as to the impact this effect may have on the SHWS accuracy for measuring ocular aberrations. To our knowledge, current research and commercial SHWS instruments do not account for the optical SCE or for that matter any other optical property of the retina that deviates from the assumption of a thin uniformly scattering layer. The plot in Fig. 6(right) shows that the optical SCE represents a significant (28% to 46%) portion of the light exiting through the center of the pupil and an almost negligible portion near the pupil edge for pupils larger than 5 mm. Since centroiding algorithms rely almost exclusively on the spot core (i.e., tails are removed by thresholding or subtracting), the algorithms must be exposed to the optical SCE, which could in principle generate virtual aberrations (errors in the aberration content) depending on how the optical SCE is handled [19]. Of course there is a wide range of centroiding algorithms and so the actual impact of the effect will likely be algorithm dependent. This would be of interest to investigate and, if necessary, potential algorithmic adjustments to reduce the generation of virtual aberrations. Any effective solution, however, must account for other variables that influence the optical SCE such as the beam entry location (Fig. 4), polarization control of the SHWS system (polarizing beam splitter), and polarization properties of the eye [20–22].

5. Conclusion

The Shack-Hartmann wavefront sensor has been traditionally employed for measuring phase in the eye (ocular aberrations). Here we demonstrate that intensity information can also be retrieved from the same measurements and the spatial distribution of which is consistent with that produced by the optical SCE. The measured intensity distributions, obtained at four different retinal eccentricities over five subjects, showed two distinguishable components: a diffused retinal reflection that extends across both spot core and tail and a guided component that is confined to the spot core and presumably originates from the photoreceptors. The directionality of the tail was found weak and insensitive to retinal eccentricity. In contrast, directionality of the core was strong and highly sensitive to eccentricity.

The SHWS represents an attractive alternative to the conventional, customized instruments that have been used for measuring the optical SCE and can provide a more complete description of the wavefront than in its current implementation.