Synaptic Scaling Stabilizes Persistent Activity Driven by Asynchronous Neurotransmitter Release

Abstract

Small networks of cultured hippocampal neurons respond to transient stimulation with rhythmic network activity (reverberation) that persists for several seconds, constituting an in vitro model of synchrony, working memory, and seizure. This mode of activity has been shown theoretically and experimentally to depend on asynchronous neurotransmitter release (an essential feature of the developing hippocampus) and is supported by a variety of developing neuronal networks despite variability in the size of populations (10–200 neurons) and in patterns of synaptic connectivity. It has previously been reported in computational models that “small-world” connection topology is ideal for the propagation of similar modes of network activity, although this has been shown only for neurons utilizing synchronous (phasic) synaptic transmission. We investigated how topological constraints on synaptic connectivity could shape the stability of reverberations in small networks that also use asynchronous synaptic transmission. We found that reverberation duration in such networks was resistant to changes in topology and scaled poorly with network size. However, normalization of synaptic drive, by reducing the variance of synaptic input across neurons, stabilized reverberation in such networks. Our results thus suggest that the stability of both normal and pathological states in developing networks might be shaped by variance-normalizing constraints on synaptic drive. We offer an experimental prediction for the consequences of such regulation on the behavior of small networks.

1 Introduction

Persistent rhythmic network activity is observed in a wide variety of experimental preparations (O’Donovan, Chub, & Wenner, 1999; Segev, Shapira, Benveniste, & Ben-Jacob, 2001; Beggs & Plenz, 2004; Lau & Bi, 2005), suggesting that it may represent a ubiquitous motif to store and transmit information in the nervous system (Sejnowski & Paulsen, 2006). A variety of models have described the initiation and sustenance of persistent activity (Tabak, Senn, O’Donovan, & Rinzel, 2000; Tsodyks, Uziel, & Markram, 2000; Tegner, Compte, & Wang, 2002; Volman, Baruchi, Persi, & Ben-Jacob, 2004), however, most of these models operate under the assumption that the underlying pattern of synaptic connectivity is randomly uniform. However, experimental data suggest that neuronal networks possess ultrastructural organizational motifs (Shefi, Golding, Segev, Ben-Jacob, & Ayali, 2002; Segev, Baruchi, Hulata, Shapira, & Ben-Jacob, 2004; Song, Sjostrom, Reigl, Nelson, & Chklovskii, 2005) in which the probability or strength of synaptic connections exhibits a highly nonrandom correlation structure. Because such topological structure influences dynamics (Sporns, Tononi, & Edelman, 2000; Wang, Poe, & Zochowski, 2008; Baruchi, Volman, Shein, Raichman, & Ben-Jacob, 2008; Raichman & Ben-Jacob, 2008), the dependence of emergent persistent activity patterns on the topology of synaptic connectivity requires investigation (Pham, Pakdaman, Champagnat, & Vibert, 1998; Izhikevich, Gally, & Edelman, 2004; Volman, Baruchi, & Ben-Jacob, 2005).

One model for persistent network activity is reverberation—the capacity of activity in a neuronal network to transiently store information about preceding sensory stimuli (de No, 1933; Hebb, 1949). In small networks of cultured hippocampal neurons, transient electrical stimulation of a single neuron can lead to correlated activity across the entire network lasting for seconds (Lau & Bi, 2005), whereas spontaneous network activity is exceedingly rare. Such evoked activity patterns are reminiscent of the canonical cell assembly proposed to underlie working memory (Hebb, 1949), but it also bears resemblance to experimental models of electrographic seizure (Traub, Borck, Colling, & Jefferys, 1996). In either case, hypotheses concerning the relationship between synaptic connectivity and population activity can be tested in spontaneously organizing biological networks.

In contrast to some working memory models in cortical networks (Wang, 1999; Buzsaki, 2006), reverberations are oscillatory, reflecting an alternation between synchronous firing and quiescence (see Figures 1A and 1B), and do not require the activation of inhibitory interneurons. However, for the reverberatory oscillation to be sustained across cycles without terminating, asynchronous release (AR) of neurotransmitter from presynaptic terminals is required (Lau & Bi, 2005). AR is abundant at developing synapses in the hippocampus and other brain areas (Goda & Stevens, 1994; Atluri & Regehr, 1998; Lu & Trussell, 2003; Hagler & Goda, 2001; Otsu et al., 2004; Hefft & Jonas, 2005) and may act as a form of synaptic noise. In contrast to synchronous or phasic release, which occurs shortly after the action potential invades the presynaptic terminal, asynchronous release persists for hundreds of milliseconds following synaptic stimulation. These two forms of neurotransmitter release differ in timescale (phasic release ≪ AR) (Goda & Stevens, 1994), presynaptic free calcium affinity (phasic release ≫ AR) (Ravin, Spira, Parnas, & Parnas, 1997) and molecular mechanisms (Saraswati, Adolfsen, & Littleton, 2007; Sun et al., 2007; Nishiki & Augustine, 2004). Previous investigations of topology-dependent persistent network activity utilizing only phasic neurotransmission (Wang, 1999; Izhikevich et al., 2004; Netoff, Clewley, Arno, Keck, & White, 2004; Roxin, Riecke, & Solla, 2004; Volman et al., 2005) are unlikely to capture the dependence of reverberation on synaptic parameters, primarily because AR can delay and decorrelate the excitation of postsynaptic partners from presynaptic spikes.

Figure 1.

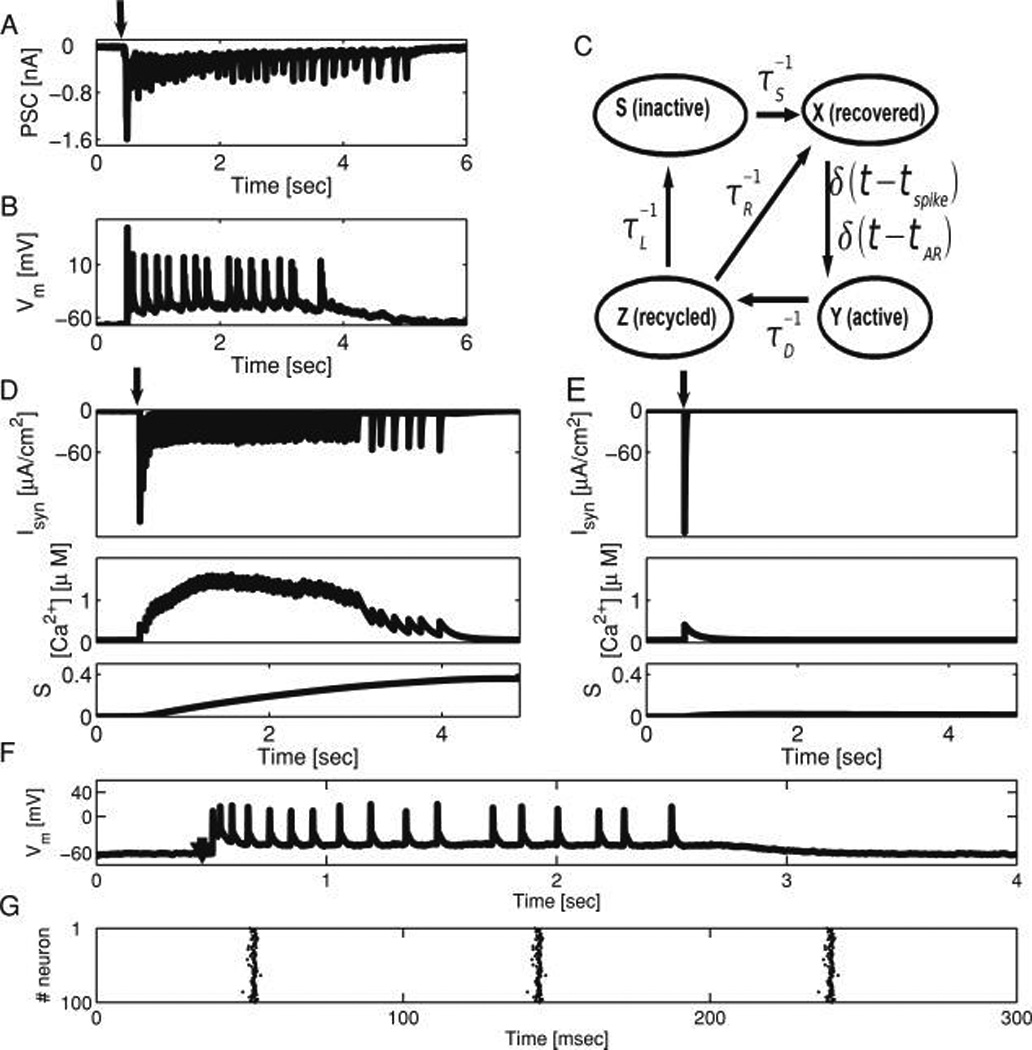
Presynaptic calcium-driven asynchronous neurotransmitter release and short-term depression underlie network reverberations. (A) Postsynaptic current recorded from a cultured hippocampal neuron in a small (≈100 neurons) network in response to a transient (2 msec) suprathreshold input delivered to another neuron (stimulation time marked with arrow). Recurrent synaptic activity can be observed in the recorded neuron at increasing intervals, lasting for seconds. (B) Membrane voltage dynamics of simultaneously recorded neuron in the same network. (C) Schematic presentation of the synaptic dynamics model used in this work, elaborated from Tsodyks et al. (2000) and described in Volman et al. (2007). Synaptic resource (excitatory neurotransmitter) traffics between four states in an activity-dependent manner: X (recovered, ready for release), Y (active, bound to postsynaptic receptors), Z (recycled, unbound or uptaken), and S (inactive, a longer route to recovery). Postsynaptic currents are generated at times t_SP and t_AR that describe the occurrence of action potential–driven (phasic) and asynchronous release (AR) events, correspondingly. (D, E) The rate of AR depends on presynaptic calcium concentration, which is a function of previous action potential times. The calcium dependence of the rate of AR determines whether a model network will respond to a brief stimulation with persistent reverberatory activity lasting for seconds, composed of dozens of approximately 50 ms polysynaptic current (PSC) clusters (D, upper panel, η_max = 0.3), or a single PSC cluster with no further network activity, as in E, upper panel, η_max = 0. Stimulation times marked with an arrow. Compare to Lau and Bi (2005) for experimental analogs of each scenario. The dynamics of presynaptic calcium (middle panels) and the slow synaptic depression variable S (lower panels) at model synaptic terminals are shown. In the case of a reverberatory response (D), recurrent network activity is terminated when a critical fraction of synaptic resource has accumulated in the inactive state (S), acting as a sink to deprive synapses of sufficient efficacy to drive the next PSC cluster. (F) In the course of model network reverberation, the neuronal membrane remains depolarized, and eachmodel neuron generates 0–1 spikes per PSC cluster, as in the experimental analog (B; Lau and Bi, 2005). (G) Raster plot of model network activity, showing that during the PSC clusters, most of the model neurons are engaged in collective, highly correlated activity, ruling out the possibility that the reverberatory response is due to the circulation of activity in the network with a return time ≈ 1/rate. Only AR, not spike-locked phasic release, can bridge the gap between PSC clusters. In all model cases shown, the probability of establishing a unidirectional connection between a pair of model neurons was p = 0.1.

The experimentally observed abundance and diversity of networks that both reliably exhibit long-lasting reverberations evoked by a single action potential and do not exhibit spontaneous activity suggest that some biological constraint leads developing networks to a regime in which reverberation is nearly bistable: hard to trigger but easy to maintain. Previously we constructed a biophysical model to describe reverberation (Lau & Bi, 2005; Volman, Gerkin, Lau, Ben-Jacob, & Bi, 2007). In this model, we showed how it is sustained by the activity-dependent elevation of AR and both oscillates and terminates due to synaptic depression. We also showed that in random networks, stimulus-specific, AR-mediated reverberation could be sustained only under conditions of proper balance between the strengths of AR and phasic release. However, such fine-tuning is incompatible with the observation of reverberation in a diversity of networks, and so we ask whether a topological constraint on synaptic connection probabilities might serve to explain the observed robustness of AR-mediated reverberation. It has been reported that specific topologies, such as the small-world network architecture thought to be efficient for the propagation of network activity (Netoff et al., 2004; Roxin et al., 2004), might be important in this regard. However, we find that reverberation is largely invariant to such constraints on synaptic connection probabilities. In contrast, a constraint on the strength of input to each neuron, reflecting synaptic homeostasis, provides a robust mechanism to guarantee stimulus-evoked reverberation and abolish spontaneous reverberation across a range of networks. This results from the suppression of statistical fluctuations in synaptic connectivity, suggesting that the effects of synaptic scaling on small networks may be realized not through control over the mean value of synaptic input, as typically assumed, but over its variance.

2 Methods

2.1 Synaptic Kinetics and Asynchronous Transmitter Release

As in our previous report (Volman et al., 2007), we adapted and expanded a canonical model of the vesicle cycle (Tsodyks et al., 2000) and assumed that synaptic resources are trafficked among four states: X (available), Y (active), Z (recycled), and S (inactive) at each model presynaptic terminal. The equations that govern the exchange of resource between these states are:

$$\begin{array}{c}\frac{\mathit{\text{dX}}}{\mathit{\text{dt}}}=\frac{S}{{\tau }_S}+\frac{Z}{{\tau }_R}-\mathit{\text{uX}}\delta (t-t_{\mathit{\text{SP}}})-\xi X\delta (t-t_{\mathit{\text{AR}}})\hfill \\ \frac{\mathit{\text{dY}}}{\mathit{\text{dt}}}=-\frac{Y}{{\tau }_D}+\mathit{\text{uX}}\delta (t-t_{\mathit{\text{SP}}})+\xi X\delta (t-t_{\mathit{\text{AR}}})\hfill \\ \frac{\mathit{\text{dZ}}}{\mathit{\text{dt}}}=\frac{Y}{{\tau }_D}-\frac{Z}{{\tau }_R}-\frac{Z}{{\tau }_L}\hfill \\ \frac{\mathit{\text{dS}}}{\mathit{\text{dt}}}=\frac{Z}{{\tau }_L}-\frac{S}{{\tau }_S}.\hfill \end{array}$$ (2.1)

As each action potential invades the presynaptic terminal (at time t_SP), a fraction 1 − exp(−u) of available synaptic resource is transferred from the available X-state to the active Y-state (corresponding to release and subsequent binding to postsynaptic receptors), from where it rapidly decays to the recycled Z-state (corresponding to uptake). Once in the Z-state, synaptic resource can directly recover to the X-state on a relatively fast (hundreds of milliseconds) timescale τ_R. A small fraction of resource leaks from the Z-state to the inactive S-state (which models slow synaptic depression) from where it recovers slowly (τ_S = 8 s). Thus, the Z → X and the S → X transitions jointly model the observed multiple timescale recovery from synaptic depression (Ghandi & Stevens, 2003). Transitions of synaptic resource between different functional states are shown schematically in Figure 1C. Note that the postsynaptic currents due to either phasic or asynchronous release decay with the same timescale (τ_D = 5 ms).

In addition to phasic transmission, neurotransmitter is also released from biological synapses in a manner that is more weakly correlated with the time of the presynaptic action potential—the so-called asynchronous release (AR) (Goda & Stevens, 1994; Ravin et al., 1997; Lu & Trussell, 2003; Kirischuk & Grantyn, 2003). In our model, we assume that such spontaneous events of stochastic normally distributed amplitude ξ are generated at times t_AR with the calcium-dependent rate η([Ca²⁺]_r):

$$\eta ({[{\mathit{\text{Ca}}}^{2+}]}_r)={\eta }_{\text{max}}\frac{{({[{\mathit{\text{Ca}}}^{2+}]}_r)}^m}{k_a^m+{({[{\mathit{\text{Ca}}}^{2+}]}_r)}^m}.$$ (2.2)

In equation 2.2, η_max is the maximal rate of asynchronous synaptic transmission, and so η([Ca²⁺]_r)dt is the probability that AR will occur in the time interval [t, t + dt]. This empirical relationship between the concentration of residual presynaptic calcium, [Ca²⁺]_r, and the rate of AR has been measured for large presynaptic terminals (Ravin et al., 1997; Kirischuk & Grantyn, 2003), but evidence from detailed computational studies of synaptic microphysiology indicates that it may also hold for central synapses with a small active zone (Nadkarni, Bartol, Sejnowski, & Levine, 2010).

To complete the specification of the synaptic model, we provide the equation that handles the presynaptic residual calcium:

$$\frac{d{[{\mathit{\text{Ca}}}^{2+}]}_r}{\mathit{\text{dt}}}=\frac{-\beta {({[{\mathit{\text{Ca}}}^{2+}]}_r)}^n}{K_p^n+{({[{\mathit{\text{Ca}}}^{2+}]}_r)}^n}+\gamma \mathit{\text{log}}\left(\frac{{[{\mathit{\text{Ca}}}^{2+}]}_{\mathit{\text{out}}}}{{[{\mathit{\text{Ca}}}^{2+}]}_r}\right)\delta (t-t_{\mathit{\text{SP}}})+I_p.$$ (2.3)

In equation 2.3, the first term represents the extrusion of residual presynaptic calcium by an active pump. The amount of calcium that is deposited at the model presynaptic terminal following action potentials is approximated to be proportional to the calcium reversal potential across the synaptic membrane, with a proportionality constant γ (see the appendix for an explanation of this approximation). The extracellular calcium concentration, [Ca²⁺]_out, is taken equal to 2 mM. The term I_p is added in order to provide a biophysically plausible steady-state calcium concentration (50 nM) in the absence of any action-potential related activity.

2.2 Stimulus-Induced Network Reverberations

In previous experiments with cultured hippocampal neurons (Lau & Bi, 2005; Lau & Bi, unpublished observations, 2010), a transient suprathreshold stimulus was delivered intracellularly to a single neuron. The resulting spike times across the network ensemble were determined with low-affinity calcium dyes, and recurrent synaptic activity was simultaneously measured in two intracellularly recorded neurons. Both measurements indicated that recurrent activity typically lasted for either a short period of time (≈ 100 ms) or for several seconds after the transient stimulus. In the latter case, it exhibited a characteristic decaying oscillation that self-extinguished when it fell below a critical amplitude. Reverberation was defined to be an episode of this recurrent activity lasting for more than 500 ms and terminating when either population spiking or synaptic current fell below half of its peak value during the episode (Lau & Bi, 2005). Critically, during each reverberation, the overwhelming majority of synaptic transmission events recorded in the trough of the oscillation (assessed electrically) were not cotemporal with spikes in other neurons (assessed optically), despite negligible levels of (spontaneous) synaptic activity prior to the stimulus. Consequently, AR was responsible for this synaptic activity that bridged the oscillation cycles. We developed a model (Volman et al., 2007) of randomly connected neurons with synaptic and excitability parameters calibrated against these experimental data (Lau & Bi, 2005), and other sources as cited below, and as given in the appendix (see Table 1). Delays in synaptic conduction for this small, spatially compact circuit were negligible (R.C.G., unpublished observations) and thus were not taken into account. Also, because experimental reverberations did not require inhibitory neurotransmission (Lau & Bi, 2005), we studied networks composed of only excitatory neurons.

Table 1.

Parameters Used to Model Neuronal Dynamics and Synaptic Transmission.

Parameter	Parameter Value	Parameter	Parameter Value
gNa	10 mS/cm2	Ka	0.1 µM
gK	10 mS/cm2	m	4
gleak	1.3 mS/cm2	β	2 µM/s
ENa	50 mV	Kc	0.4 µM
EK	−100 mV	n	2
Eleak	−65 mV	γ	80 nM/ms
V1	−1.2 mV	c0	2 mM
V2	23 mV	Ip	0.11 µM/s
V3	−2 mV	ξ	10−3
V4	21 mV	τR	0.3s
ϕ	0.15	τD	10 ms
C	1 µF/cm2	τS	8 s
ES	0 mV	τL	5 s

In model simulations, a brief (5 ms) and strong (50 µA·cm⁻²) stimulus was delivered to one neuron. The response of the model network depends on the level of AR at its synapses. For sufficiently high levels of AR (see Figure 1D, upper panel, η_max = 0.3), the network can sustain reverberation; this ability is lost when asynchronous release is blocked (see Figure 1E, upper panel, η_max = 0), as observed experimentally (Lau & Bi, 2005). In turn, as Figures 1D and 1E (middle panels) show, activation of AR is caused by sustained elevation of presynaptic free calcium concentration. After fast synaptic depression terminates a single cycle of recurrent synaptic activity (see Figure 1D, upper panel, each sharp vertical transient = one cycle, ≈ 100 ms width), there is no subsequent suprathreshold depolarization, and thus no spikes in the network, for hundreds of milliseconds (see Figure 1G), as in experiment (Lau & Bi, 2010). Since there are no spikes, and thus no evoked neurotransmitter release to sustain network activation, only AR can sustain synaptic current in the network until the recovery from synaptic depression spawns the next cycle (intercycle interval: 100–500 ms = 2–10 Hz), thus bridging the gap that fast, evoked synaptic transmission alone cannot (Wang, 1999). Eventually reverberations in model networks terminate when the slow accumulation of synaptic depression (increase in S) reaches a critical value, leaving insufficient synaptic resource to drive another cycle of the reverberation (see Figures 1D, 1E, lower panels). Thus, in randomly connected networks of excitatory neurons with synaptic depression, AR critically determines the potential for and form of persistent activity. In model and experiment with sufficient AR, it takes the form of reverberation.

2.3 Construction of Network Topology

2.3.1 Networks with Random Synaptic Connectivity

Unless otherwise indicated, we assume a random-graph-like topology. That is, the probability that p_ij will establish a unidirectional contact between a pair of neurons i and j (i ≠ j) is constant p_ij = p₀. Then the probability that a neuron in a network containing N neurons has k incoming contacts is described by a binomial distribution: $P(k,N,p_0)=\frac{N!}{(N-k)!k!}{p}_0^k{(1-p_0)}^{N-k-1}$ if p₀ is independent of N. Given this, the expected number of synaptic contacts per neuron is 〈k〉 = p₀N, such that the overall mean synaptic drive (overall synaptic conductance) per neuron is higher for larger networks. To focus on the variability in the number of presynaptic partners rather than variability of individual synaptic weights, we drew the maximal synaptic conductances for each synapse from a normal distribution truncated at ±20% around its mean (Tsodyks et al., 2000; Volman et al., 2007). Values of parameters for this distribution are given in the appendix.

2.3.2 Networks with Correlated Connectivity

Networks of neurons connected by unidirectional synapses can be approximated as directed graphs (Boccaletti, Latora, Moreno, Chavez, & Hwang, 2006). To capture the effect of a graph’s structure on the dynamics of a graph’s vertices (neurons), one can use topological correlation as the measure of similarity in connectivity between neurons. In general, the information about topological correlations between the vertices (neurons) of a directed graph can be captured by the network-averaged clustering coefficient, C, defined as $\frac{1}{N}{\mathrm{\Sigma }}_i\frac{\tilde{P}\{e_{\mathit{\text{ij}}},e_{\mathit{\text{il}}},e_{\mathit{\text{jl}}}\}}{k_i(k_i-1)}$, where k_i is the in-degree, or number of (synaptic) inputs, for the ith neuron; P̃{e_ij, e_il, e_jl} is the number of all connected pairs of neurons e_jl that are also inputs to the ith neuron; and averaging is performed over all neurons of a network. It is possible to show analytically that in the limit of a very large random graph, in which connections are chosen independently and the averaged number of inputs per neuron is kept constant, C → 0 (Dorogovtsev & Mendes, 2002). Furthermore, the network-averaged minimal path length between a pair of neurons L, representing the ability of two neurons to communicate with low latency, is small for random graphs. By contrast, in a regular lattice where neurons connect only to their nearest neighbors, C is large, representing a highly clustered network, but L is large as well, indicating that signaling between any two neurons may require a large number of steps. Small world networks (Watts & Strogatz, 1998; Dorogovtsev & Mendes, 2002; Roxin et al., 2004) represent a compromise between random and regular graphs. In small-world networks, C is high (compared with random graphs) but L is low (compared with regular graphs) (see Figures 3A and 3B), and this combination is believed to play an important role in the regulation of signal propagation (Dorogovtsev & Mendes, 2002; Boccaletti et al., 2006). For example, it has been suggested (Buzsaki, Geisler, Hense, & Wang, 2004; Buzsaki, 2006) that in networks of hippocampal neurons, the small-world features in the connectivity of inhibitory neurons might enable fast and efficient control of pathological hyperexcitation associated with epileptic-like dynamics. On the other hand, small-world connectivity facilitates seizing in a model of hippocampal networks (Netoff et al., 2004) and in epidemic networks can underlie the fast spread of disease and massive contamination (Dorogovtsev & Mendes, 2002).

Figure 3.

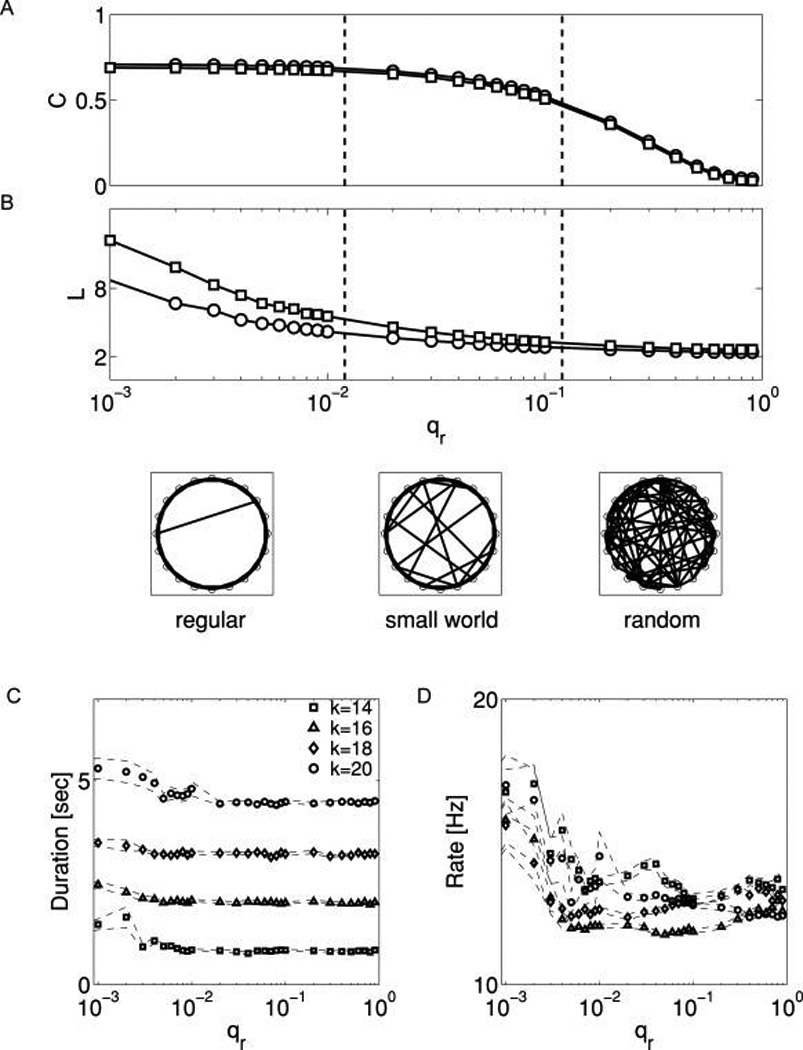
Reverberation is insensitive to connection topology. (A, B) As the value of synaptic rewiring (shuffling) parameter, q_r, is increased, both the network clustering coefficient C (A) and mean minimal path length L (B), decrease. Top: These topology changes are shown for networks with N = 500; circles: number of inputs per neuron k = 20; squares: k = 14. Bottom: The same changes are illustrated with three selected values of q_r in N = 20 networks (for clarity), showing the transition from regular graph (left), to small-world network (middle), to random graph (right) as q_r increases. (C) Duration of evoked reverberation depends on k, not q_r. Squares, k = 14; triangles, k = 16; diamonds, k = 18; circles, k = 20. (D) The frequency of PSC clusters is also insensitive to q_r over a wide range of values through the space of possible network topologies. All data points are averages over 20 independent realizations for networks with N = 500.

Various methods exist to construct a small-world network starting from a completely regular graph (Watts & Strogatz, 1998; Dorogovtsev & Mendes, 2002; Roxin et al., 2004; Netoff et al., 2004). Here, we have chosen to manipulate topology in a way that leaves 〈k〉 unchanged, to avoid conflating the effects of changes in mean synaptic drive with changes in topology. We start from a k-regular graph in which model neurons are arranged on a ring, and each neuron is bidirectionally connected to its k nearest neighbors on the ring (k ≥ 2 and even). Next, all synaptic connections are subject to random rewiring with the probability q_r. The extent of a network being “small world” depends on the value of rewiring probability. In the limit of q_r → 1, the rewiring procedure is analogous to a complete reshuffling of the initial set of links, and it transforms the highly correlated k-regular graph into a random graph with the same average number 〈k〉 of synaptic inputs to each model neuron but a very low clustering coefficient (Watts & Strogatz, 1998). Networks with a small-world structure are obtained for intermediate values of q_r (see Figures 3A and 3B).

2.3.3 Homeostatic Regulation of Neuronal Firing Rate

In order to generate a plausible synaptic scaling rule, we performed network simulations with synaptic modifications determined by a simple realization of homeostasis, according to which the synaptic input weights to each neuron were periodically adjusted to bring that neuron closer to a target firing rate, ν₀. Since homeostatic processes may operate on a very slow (hours to days) timescale, it is not computationally tractable to model the actual timescale in network models across a range of parameters. Therefore, we approximated the dynamic action of homeostatic constraints in the following way: at time T = 0, one of the network’s neurons was given a brief stimulus (50 µA·cm⁻² for 5 milliseconds), and the response of all neurons was monitored for a period of time (T = 15 s). The values of synaptic conductances were then adjusted according to the following equation:

$$w_{\mathit{\text{ij}}}=w_{\mathit{\text{ij}}}+{\alpha }_H({\nu }_0-\langle {\nu }_i\rangle )w_{\mathit{\text{ij}}},$$ (2.4)

where 〈ν_i〉 is the averaged firing rate of a postsynaptic neuron i during the time window of 15 second and α_H(= 10⁻³) is the rate of adjustment. The stimulation, monitoring, and adjustment of weights operationally defined one epoch of homeostasis and were repeated, with one stimulus per epoch, until the network reached its target firing rate ν₀ over one epoch. By performing these simulations, we verified that, starting from randomly distributed subthreshold weights, homeostatic regulation of the firing rate led model networks to exhibit reverberations (see Figure 6). This homeostatic rule scaled initially random synaptic weights according to postsynaptic firing rates. Since initial postsynaptic firing rates are highly correlated with the summed synaptic input, we made the assumption that directly scaling synaptic weights according to summed synaptic input could approximate the results of a dynamic homeostatic process.

Figure 6.

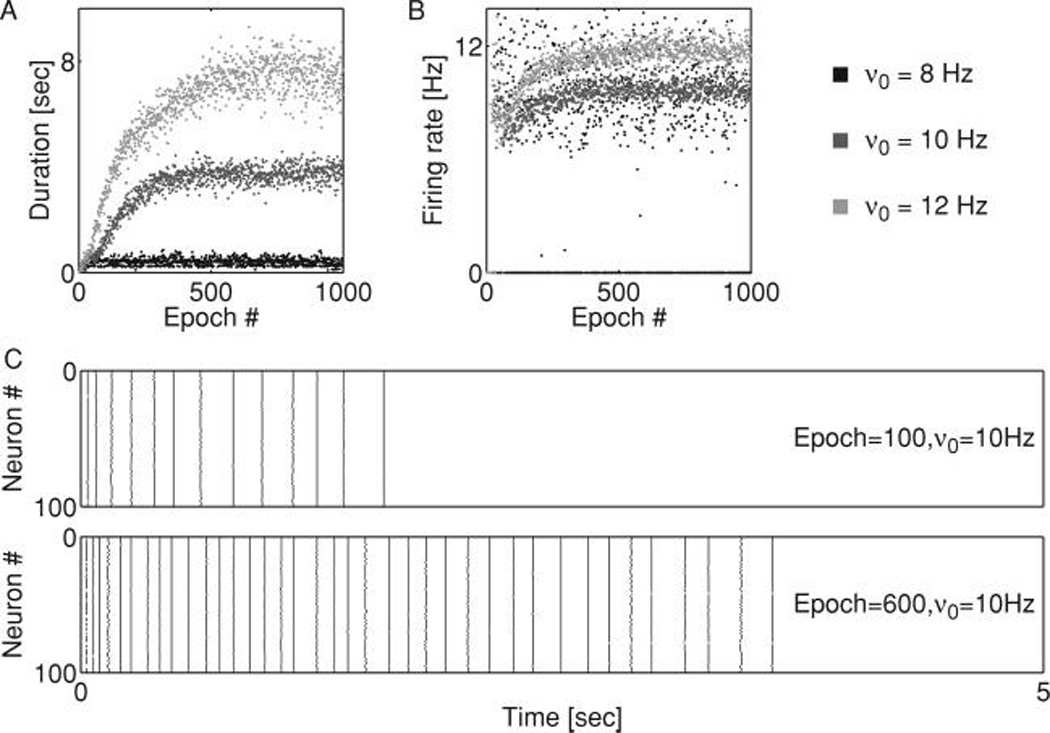
Homeostatic regulation of firing rate leads to network reverberations. (A) Duration of the network response to a brief stimulus delivered to one of the neurons (as described in text) plotted versus the epoch of homeostatic conductance update for different target rates, as shown in the accompanying legend. (B) Firing rate (averaged over all neurons) versus the epoch of homeostatic conductance update for different target rates, as shown in the accompanying legend. Reverberation emerged for a finite range of target firing rates. (C) Sample raster plots of the network response at different epochs for the target firing rate of ν₀ = 10 Hz. Top: epoch 100. Bottom: epoch 600. The studied networks had N = 100, and p = 0.1.

2.3.4 Networks with Scaled Synaptic Drive

In this set of simulations, we scaled synaptic drive according to one of two rules. In the first scenario, we set the probability of a synaptic connection to be inversely related to network size, p₀ ∝ N⁻¹, such that the mean input number, 〈k〉, was constant for all sizes (see Figure 4); we refer to this scheme as network scaling. The alternative scenario, cell-specific scaling, is identical with the exception of a constraint: the total synaptic input strength per neuron is forced to be constant (see Figure 6). Denoting by W_i the overall synaptic strength as seen by the ith postsynaptic neuron due to its k_i presynaptic partners, the constraint is

$$W_i=\mathit{\text{constant}}={\displaystyle \sum _j^{k_i}}{w}_{\mathit{\text{ij}}},$$ (2.5)

in which w_ij is the maximal conductance, or strength, of a synaptic connection between i and j. The scaling was implemented by multiplicative scaling each w_ij to achieve constant W_i. For constant p₀, this would imply N⁻¹ weakening of average synaptic strength, 〈w_ij〉. Because 〈w_ij〉 is observed experimentally to scale as N^−a, with a > 0 (Wilson, Ty, Ingber, Sur, & Liu, 2007), this scenario represents an example of network size–dependent scaling of synaptic weights.

Figure 4.

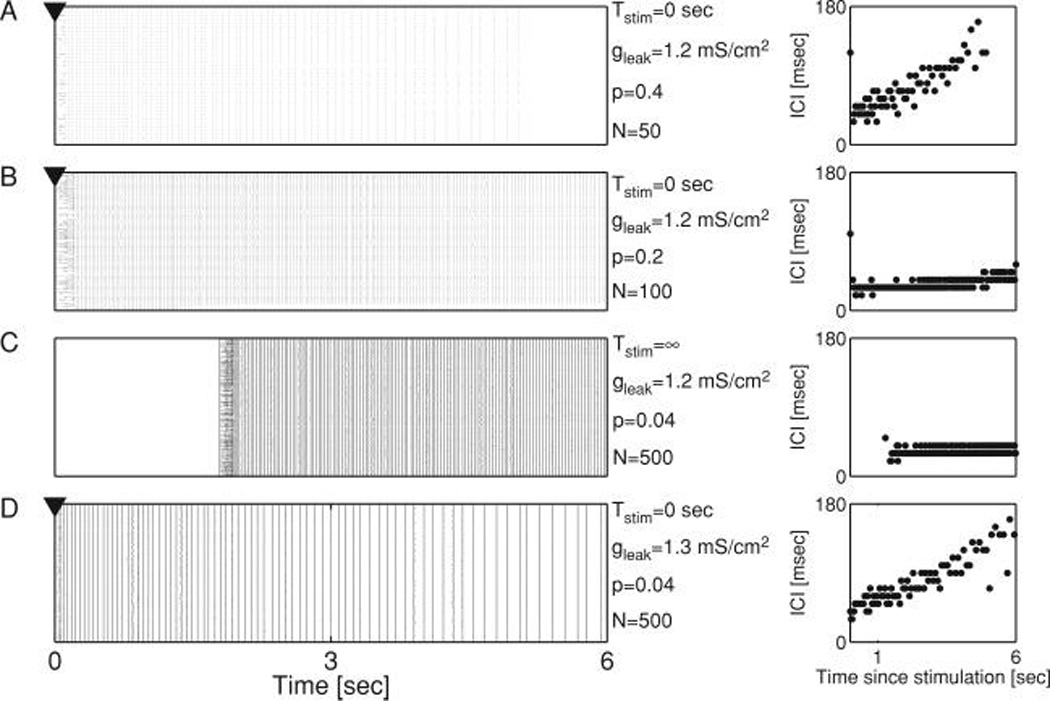
Connectivity fluctuations destabilize networks with fixed input number. (A) Raster plot of evoked activity (stimulus applied at T_stim = 0 sec) for a small network (N = 50). The reverberatory response to the stimulus is characterized by rhythmic activity with clearly separated epochs of spikes. In A–D, right panel shows the interval between spike clusters. (B) Raster plot of evoked activity for a larger network (N = 100), with connection probability p reduced to preserve the same mean input synapse count as in (A). This network sustains evoked reverberations with a much lower oscillation period. (C) For still larger networks (N = 500), a spontaneous outbreak of activity is observed even though p has been further reduced to ensure a constant mean synaptic input count. (D) Increasing the neuronal membrane leak conductance, g_leak, reduces the sensitivity of model neurons to the statistical fluctuations in synaptic drive, and restores rhythmic reverberations. In all simulations, the averaged number of inputs per neuron is 〈k〉 = N_p = 20. In panels A, B, and D, the stimulation time is marked with arrowhead.

To generate the actual synaptic connectivity and weight patterns for model networks, we considered a variety of distributions for p_ij. The first case, p_ij = p, represents random connectivity and a binomial distribution for the number of presynaptic partners, k, for each neuron. A binomial distribution characterized by (N, p) has standard deviation ${\sigma }_k=\sqrt{N_p(1-p)}$ and as N → ∞ follows a gaussian distribution according to the de Moivre-Laplace theorem. To deviate from random connectivity and account for additional inhomogeneity in synaptic targeting (e.g., variations in the elaboration of dendritic trees), we also considered distributions more variable than a binomial. We implemented this by drawing the number of inputs k_i from gaussian distributions (truncated to obtain integer values for actual k_i) with values of σ_k greater than that observed in the binomial distribution, but still restricted to the range [1, N − 1], the minimum and maximum number of possible presynaptic partners. With this restriction, the limit of σ_k → ∞ corresponds to a uniform distribution for k. For each of these possible distributions, we enforced the same scaling rule as above.

Greater values of σ_k imply broader distributions of k and more hub neurons with many inputs; however, the scaling rule causes each synaptic input to a hub to be relatively weak. By the same token, for large values of σ_k, some neurons receive a small number of relatively strong connections (see Figure 5A). The efficacy of these two kinds of input (numerous and weak versus scarce and strong) in evoking postsynaptic spikes will depend on the total magnitude and distribution of these inputs (Brunel, 2000), the spike thresholds, and the instantaneous activity of presynaptic neurons. The last of these can be expected to vary during the course of a reverberation as the number of neurons participating quickly increases and then slowly declines (on a timescale of seconds) and as the dominant mode of synaptic transmission switches between phasic release and AR (on a timescale of hundred of milliseconds). For a scaled postsynaptic neuron that receives c 〈k〉 afferents of weight 〈w〉/c each, firing at the Poisson rate ν, the standard deviation of the postsynaptic current in a fixed time interval [t, t + Δt] is given by ${\sigma }_I(c)=\langle w\rangle c^{-1/2}\sqrt{\langle k\rangle \nu \mathrm{\Delta }t(1-\nu \mathrm{\Delta }t)}$. Since we here consider networks composed of only excitatory neurons, a smaller value of σ_I(c) implies less frequent crossing of a threshold for spike generation. Thus, counterintuitively, neurons receiving relatively numerous inputs (c > 1) may, by virtue of the scaling rule, spike less reliably during a noise-driven spiking regime (see Figures 5E–5I). Consequently, the connectivity scheme described offers a tool for investigating differences in phasic release and AR in determining network dynamics.

Figure 5.

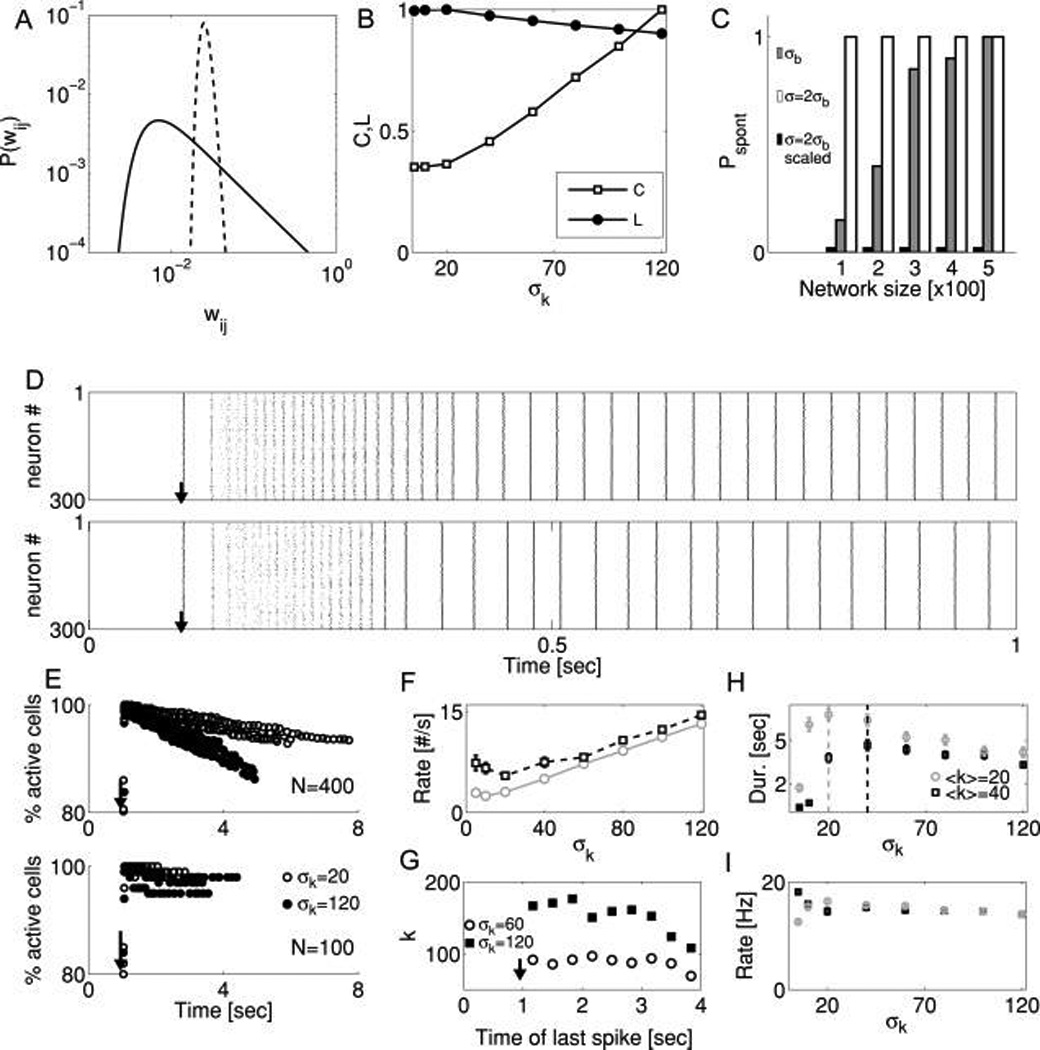
Synaptic scaling regularizes and stabilizes reverberation. (A) Probability distribution P(w) of synaptic weights for two model networks (N = 500). Each network was generated such that each neuron received a number of inputs determined by a mean 〈k〉 = 40 with standard deviation σ_k. The amplitude of all inputs was then scaled such that the summed input to each neuron in the network had constant amplitude. Dashed line: σ_k = 5; solid line: σ_k = 120. (B) Incidental changes in topological measures (clustering coefficient, C, and path length, L, both scaled relative to their maximal values for clarity of presentation) accompanying changes in σ_k. (C) Probability of observing a spontaneous outbreak of activity from a resting network during a 10 second time window, for different scenarios of network size and connectivity. For networks whose connections were determined only by network size p = 〈k〉/N, the variability in input number is given by a binomial distribution ${\sigma }_k={\sigma }_b=\sqrt{N_p(1-p)}$. Without synaptic scaling, such networks were vulnerable to spontaneous activity (gray bars) due to variability in input number across neurons: some neurons receive many inputs, and spontaneously fire, triggering the network. When neurons receive synapses with different probabilities, the distribution is broader (2σ_b) and spontaneous activity is guaranteed (white bars). However, spontaneous activity was abolished in all networks when synaptic inputs were scaled according to the summed input onto each neuron (black bars). For all cases shown, 〈k〉 = 22. (D) Sample raster plots of evoked network activity (N = 300, 〈k〉 = 22). Upper panel: Unscaled network that did not exhibit spontaneous activity in 10 sec observation window. Lower panel: Same network with synaptic strengths scaled. Arrow indicates stimulation time. Note that scaling has very little effect on the structure of a normal reverberation. (E) The number of active neurons per PSC cluster declines during the reverberation, prior to sudden termination, for networks of different sizes (upper panel, N = 400; lower panel, N = 100). Open circles: σ_k = 20. Closed circles: σ_k = 120. Data points are pooled results from five independent realizations. Reverberation was initiated with a brief stimulus at T = 1 second. (F)Quantification of (E). The rate of change in the number of active neurons during the reverberation is nearly linear in the variability of synaptic input number σ_k. N = 500. Gray circles: 〈k〉 = 20; black squares: 〈k〉 = 40. (G) Due to scaling, the number of synaptic inputs received by a neuron predicts when that neuron will drop out of the reverberation. Neurons with numerous but small-amplitude inputs will drop out earlier. Black squares: σ_k = 120; open circles: σ_k = 60. N = 500. Stimulus at T = 1 second. (H, I) For a wide range of heterogeneities in synaptic input number, both the duration of reverberation (H) and the rate of PSC cluster appearance (I) are nearly constant. Keys are the same as in (F). For (F–I), all data points are averages over 20 realizations. Data points are mean ± S.E.M.

3 Results

The core model was presented in Volman et al. (2007). There, we investigated the dependence of reverberation characteristics on biophysical parameters related to presynaptic dynamics and calcium handling. In the study reported in this article, motivated by literature suggesting that network topology dictates network activity patterns, we asked whether the topology of model networks had a role in the generation or sustenance of reverberation.

3.1 Duration and Frequency of Evoked Reverberations Depend on the Mean Number of Synaptic Inputs per Neuron

In small, cultured hippocampal networks (Lau & Bi, 2005), neurons are confined to a fixed area (≈1 mm diameter) on a glass coverslip. The number of neurons in these small networks varies with each coverslip and each culture (see Figure 2A), as do the characteristics of reverberation. Thus, our first hypothesis was that the size of the population was the primary determinant of reverberation characteristics. To test this hypothesis, we constructed networks of various sizes but with a fixed value of the synaptic connection probability p_ij = p₀, that is, a random network.

Figure 2.

Duration of evoked reverberations in small networks with random synaptic connectivity. (A) Distribution of neuron counts in small networks of cultured neurons in which reverberation experiments were typically performed. (B) Duration of evoked reverberatory activity in cultured networks increases with increasing network size (p < 0.1). However, duration varies greatly even for networks of similar size (r² < 0.1). (C) Duration of reverberatory activity in model networks versus network size for a simple binomial connectivity rule with constant connection probability p. Scatter plot shows outcomes of several independent realizations, and solid line is the average over 20 realizations. Duration depends more strongly on network size in simulation (C) than in cultured networks (B) and is more variable, suggesting that this simple connectivity model cannot account for the data. (D) Rate of PSC cluster generation in cultured networks versus the network size. (E) Rate of PSC cluster generation in model networks versus the network size.

We observed that in both cultured and model networks, reverberation duration was positively correlated with the population of the network (see Figures 2B and 2C, respectively). The naive assumption of constant p implies a greater number of synaptic inputs per neuron in larger networks and a greater recurrent drive at all time points. We previously showed that reverberation terminates when slow synaptic depression (see Figure 1: Z → S) exceeds the capacity of recurrent synaptic activity to generate the next oscillation cycle (Volman et al., 2007). With stronger recurrent drive, it follows that a deeper depression is required for this to occur, which takes longer to accumulate. Thus, under constant p, larger networks should have longer reverberations. Furthermore, while the constant p assumption implies greater phasic release and greater AR in larger networks, these are not matched in time. In between cycles of recurrent activity, phasic release is nearly zero while AR is high. The higher the strength of AR, the less time must pass before synapses are sufficiently recovered from fast synaptic depression (see Figure 1: Z → X) for AR to trigger the next cycle of recurrent activity. Thus, in larger networks where AR is stronger, one might expect reverberations to occur at higher oscillation frequency. While this trend was observed in the model (see Figure 2E), the data exhibited no such relationship (see Figure 2D). Thus, the constant p assumption failed to explain the relatively invariant character of reverberation as a function of population size.

3.2 Duration of Persistent Activity Is Not Affected by Network Topological Correlation

Furthermore, the diversity of durations and rates, even around a given population size, was substantially greater in experimental networks than in model networks. What could account for this diversity? The level of development of experimental networks was very similar (± 1 day), so it seemed unlikely that fundamental biophysical parameters would vary across these networks. We hypothesized that the variability in synaptic connection topology from network to network might account for the variability in reverberation characteristics. For example, networks with well-placed hubs that coordinate long-lasting activity might be expected to exhibit reverberations of greater duration. Furthermore, it has been shown in networks with purely phasic release that the topology of connectivity is a primary determinant of the exhibited modes of network activity (Netoff et al., 2004; Roxin et al., 2004; Volman et al., 2005). However, since the AR of the neurotransmitter evidently changes the rules for the propagation of activity, it is unclear whether the same topological considerations should hold in circuits where AR is a central feature.

We analyzed the dynamics of networks with fixed population size but connectivity architecture ranging from purely regular lattices, through small-world topologies, to randomized graphs that do not exhibit topological correlations. The transition between different architectures is controlled by varying the value of a hypothetical rewiring probability for synaptic connections, q_r, which indicates the degree to which links have been shuffled from a perfectly regular lattice (see section 2). This rewiring is not a proposed mechanism for the construction of real networks, but rather a tool to achieve a wide range of network topologies by varying a single parameter. For low values of q_r, both the correlation between edges (the tendency to form connectivity triangles; Dorogovtsev & Mendes, 2002, as captured by clustering coefficient C) and the minimal synaptic path length L between a pair of neurons are high. For high values of q_r, connectivity is nearly random, so the network has a short minimal path length but also a low edge correlation. Intermediate values of q_r result in small-world networks, with a large number of connectivity triangles but short minimal path lengths, in principle enabling efficient spread of activity.

To assess whether any particular network topology (such as small-world architecture) facilitated reverberation, we initialized networks with a fixed number of inputs 〈k〉 per neuron and randomly rewired synaptic connections to obtain each topology. Figure 3 shows the dependence of evoked reverberatory activity on the rewiring probability q_r. For graphs ranging from almost regular (left) through small-world (middle), to nearly random (right), we found that neither the duration of reverberation nor the rate of PSC clusters (i.e. oscillation frequency) within a reverberation showed any indications of strong dependence on the value of q_r (see Figures 3C and 3D). Instead, the duration of rhythmic network activity was strongly dependent on the mean number of synaptic inputs 〈k〉 = np₀, while the rate showed no clear dependence on 〈k〉. Thus, the experimentally observed diversity in reverberation durations and rates could not be ascribed to the variation in the topological organization of cultured networks. Instead, this suggested that in these networks, the overall synaptic drive, rather than topological correlations, was the primary determinant of reverberation characteristics.

3.3 Synaptic Connectivity Scaled by Network Size

Increases in network size may increase the number of distinct synaptic partners per neuron, thus enhancing the frequency and duration of reverberation. As network size increases, it is not uncommon in experiments to observe both stimulus-evoked reverberation that transforms into chaotic activity that never terminates, spontaneous reverberation, or other modes of network activity (Eytan & Marom, 2006; Gerkin, Lau, & Bi, 2010). The likelihood of observing such behavior is increased by manipulations that augment the strength of synaptic connections. In fact, such behavior is a hallmark of the hippocampal culture model of seizure (Furshpan, 1991). Thus, our next goal was to identify the origins of such dynamical instabilities in both the quiescent and the reverberatory states in larger model networks. In other words, why do spontaneous reverberations start, why do stimulus-evoked reverberations end, and why do these phenomena depend on network size? In the constant p case, neurons in larger networks receive more synaptic input than neurons in smaller networks. This offers a trivial explanation of the instability of the quiescent state: the probability of spontaneous activation of a fraction of the neurons, triggering network activity, would scale with network size. However, experimental evidence suggests that the synaptic connection probability between any two neurons may decrease as population size is increased (Wilson et al., 2007). Thus, we examined model networks in which the mean number of incoming synaptic connections per neuron, 〈k〉, was held constant. For a network of N neurons, we assumed that the probability of establishing a unidirectional connection between a pair of neurons is p₀ = 〈k〉N⁻¹. While the mean number of inputs per neuron remains constant as network size increases, each neuron still receives a variable number of inputs.

With such a constraint, small networks reliably generate reverberations that persist for several seconds (see Figure 4A), which then decay due to the accumulation of slow, synaptic depression. As network size increases, with 〈k〉 held constant and p₀ ∝ N⁻¹, more prolonged reverberations with a higher rate of PSC cluster appearance are exhibited, as in the constant p case (see Figure 4B). Despite the constraint of constant 〈k〉, for sufficiently large networks, spontaneous activity emerges in the absence of stimulation (see Figure 4C). Because the distribution of afferents per neuron has a mean p₀N = 〈k〉 and a variance p₀N(1 − p₀) = 〈k〉 (1 − 〈k〉N⁻¹), the statistics of all networks with identical 〈k〉 and for which N ≫ 〈k〉 would appear to be similar. However, as network size increases, there is an increasing probability that at least one or a few postsynaptic neurons will have a sufficient number of presynaptic partners releasing neurotransmitter to exceed a firing threshold. This results in an increase in the probability that one or a small number of action potentials can recruit activity throughout the network, resulting in shorter waiting times between PSC clusters, and thus a higher reverberation frequency. This also results in an increased probability that the first PSC cluster can be generated from rest due to the spontaneous release of neurotransmitter (see Figure 5C, gray bars). In support of this explanation, both spontaneous reverberation and nonreverberatory activity disappeared when membrane conductance was increased (see Figure 4D for an arbitrarily long monitoring time before stimulation at T_stim = 0 s), or when the fluctuations in the connectivity pattern were eliminated by forcing each neuron to receive exactly 〈k〉 afferents (results not shown). Thus, in a network tuned to respond to a stimulus by reverberating, random fluctuations in synaptic connectivity resulting from binomial statistics can have a large effect on reverberation frequency, bringing the activity to the point of dynamical instability as the network size increases, even when the mean synaptic input is made invariant to network size.

3.4 Synaptic Connectivity Scaled by Synaptic Input

How can the reverberatory dynamical response of a large network be ensured, and spontaneous activity be avoided, in the face of statistical fluctuations in the number of inputs per cell? It has been established that individual neurons employ homeostatic regulatory processes on multiple timescales that enable them to constrain synaptic input and output firing rates within reasonable limits (Turrigiano, 1999, 2008). Indeed, a cell-specific form of synaptic homeostasis, synaptic scaling has been widely reported (Turrigiano, 1999, 2008). It is hypothesized to stabilize weight-independent Hebbian learning rules that otherwise suffer from unbalanced positive feedback (van Rossum, Bi, & Turrigiano, 2000; Rubin, Lee, & Sompolinsky, 2001; Watt & Desai, 2010) and can lead to synaptic competition and activity-dependent redistribution of synaptic strength (Song, Miller, & Abbott, 2000; van Rossum et al., 2000). A comprehensive study of the effects of a homeostatic regulatory process necessitates the inclusion of spike-timing-dependent plasticity and synaptic competition, as well as sufficient simulation time to achieve equilibrium, and is thus a problem of significant computational complexity. In order to show that a homeostatic process was consistent with the emergence of reverberation, we applied a simple negative feedback rule to model networks (see section 2). Briefly, synaptic weights were modified after each epoch of time according to whether the postsynaptic neurons had firing rates which were above (resulting synaptic depression) or below (resulting synaptic potentiation) average firing rates. This homeostatic process brought the network to a steady state during which the activity was characterized by reverberation occurring at the firing rate set point (see the appendix). We observed that starting from random networks, neurons with a greater number of presynaptic partners tended to spike more frequently; however, ultimately the weights of synaptic inputs to these neurons were scaled down by the feedback rule, while the weights of inputs to neurons with few presynaptic partners were scaled up.

To overcome the difficulty associated with the computational demand of simulations of a dynamic synaptic homeostasis process, in the subsequent simulations, we introduced a simple hard scaling rule for synaptic conductances: the sum of the strength of synaptic inputs to each neuron was set to a constant. For neurons with a large number of synaptic inputs, each input was scaled down, and for neurons with a small number of inputs, the input was scaled up. In all cases, the initial weights are drawn from a single distribution and then scaled. This implies that as σ_k increases (i.e., as the distribution of number of inputs per neuron broadens), the scaling rule will cause the distribution of synaptic weights to broaden, as we show in Figure 5A. Even with the scaling constraint, for network size N and mean input number 〈k〉 = Np₀, a wide variety of networks is still possible, each corresponding to different standard deviations of the number of presynaptic partner neurons, σ_k. Larger values of σ_k would correspond to greater heterogeneity in the number of presynaptic partners made by each neuron, and various values of σ_k could each reflect different rules for synaptic connectivity in developing networks. For random connectivity where the connection probability between any two neurons is a constant p₀, the distribution of synaptic inputs derives from a binomial distribution, and ${\sigma }_k=\sqrt{N_{p_0}(1-p_0)}$. For connectivity with variable p, σ_k will have a greater value. However, because the scaling we consider here is cell specific, in all cases the variance in total input strength is zero: Var(∑_j w_ij) = 0 for each neuron i.

We analyzed reverberations as a function of changes in the population size N as before, only now we applied the scaling rule and examined the stability of reverberation for different values of σ_k. Increasing σ_k increases the heterogeneity of connectivity; however, in scaled networks, the total maximal synaptic input conductance per neuron is a constant. The standard deviation σ_k also incidentally influences the topology of the network (see Figure 5B): for larger variance in synaptic input number, more neurons receive a large number of inputs, serving as hubs. Such hubs tend to decrease the mean path length L between neurons in a network, although because the weights of inputs to these hubs are scaled to be small, it is unclear whether path length remains a meaningful metric.

We showed earlier (see Figure 4) that the variance ${\sigma }_k=\sqrt{N_p(1-p)}$ introduced by random connectivity predisposes some neurons to be highly sensitive to spontaneous synaptic input. The probability that such randomly connected but unscaled networks exhibited spontaneous activity within a 10 second period is shown in Figure 5C. Intuitively, as the population size N increases, the probability of one or a few highly connected neurons triggering spontaneous network activity must increase (see Figure 5C, gray bars). The probability that at least one neuron in a randomly connected network receives at least k^* inputs can be derived from the cumulative distribution function for a binomial distribution and is given by

$$p(\{k_i\ge k^{*}\}\ne \varnothing )=I_{1-p}(n-k^{*},1+k^{*}),$$ (3.1)

where I_x(a, b) is the regularized incomplete beta function. However, when synaptic weights in such networks are scaled to a constant, such that the mean total synaptic input remains the same but the variance becomes zero, spontaneous activity disappears completely (see Figure 5C, black bars versus white bars). Even in networks with large values of σ_k, where spontaneous activity is guaranteed to occur in unscaled networks (see Figure 5C, white bars), applying a scaling rule completely abolishes spontaneous activity (see Figure 5C, black bars). This occurs because while the distribution of k across the neuronal population is unchanged by scaling, the distribution of summed synaptic input strength collapses to a delta function.

However, scaled networks are far from homogeneous; some neurons may still be strategically connected to receive important inputs. Thus, in spite of the changes in spontaneous activity, the population raster during stimulus-evoked reverberation remains relatively invariant to such scaling (see Figure 5D), indicating that the stability of the quiescent state can be guaranteed without significantly altering the stimulus response. However, in scaled networks, the participation of neurons in the reverberation over time depends critically on the value of σ_k. This is because as σ_k increases, a larger fraction of neurons will have a large number of weak inputs compared to the median neuron. Because these inputs will not always be sufficiently coordinated to drive the postsynaptic neuron to threshold during a PSC cluster (as explained in section 2), these neurons will tend to drop out of the reverberation over time. The reverberation is thus characterized, counterintuitively, by gradually decreasing participation of the most densely connected neurons. We demonstrated this by computing the number of neurons active over the course of the reverberation, where “active” was defined as firing at least one spike during the time interval [T_PSC − 20 ms,T_PSC + 20 ms] and T_PSC is the time of PSC cluster generation, defined as the local maximum of neuronal population activity (see Figure 5E).

This “dropout” behavior, in which the number of neurons participating in the reverberation decreases over time (see Figures 5E and 5F), is not observed in networks with random connectivity and unscaled synaptic strength (not shown), and is less prominent in smaller networks even with scaling (see Figure 5E, lower panel), suggesting that it results from the action of scaled synaptic connectivity in networks where the range of possible presynaptic partners is large. Finally, we confirmed the hypothesis that the neurons dropping out first are those with large numbers of small-amplitude inputs by plotting the number of synaptic inputs k_i received by a neuron versus the time t of its last spike (see Figure 5G).

The reduced recruitment of such neurons during the PSC cluster further acts to decrease the overall AR drive onto their postsynaptic partners. This in turn reduces the probability that the next PSC cluster will be generated, contributing to an earlier termination of reverberatory activity (see Figure 5H). On the other extreme, networks with low σ_k will have few neurons with many inputs and few neurons with strong inputs, thus reducing the probability that reverberation can even begin. Consequently, there is a value of σ_k, that is, heterogeneity of synaptic input number, that is optimal for producing the longest-lasting reverberation (see Figure 5H).

4 Discussion and Outlook

Sustained reverberation of activity in neuronal assemblies could represent a holding mechanism, allowing long intervals of time to elapse between stimulus and response and enable working memory (WM) (Hebb, 1949). Under this hypothesis, reverberations should be more prolonged in larger assemblies (Hebb, 1949). However, as developing brains grow, imbalances in patterns of synaptic connectivity can result in seizures. Experimental observations of cultured hippocampal networks (Lau & Bi, 2005; Gerkin et al., 2010), and our computational modeling results also suggest that the size of a neuronal network and the pattern of synaptic inputs can determine the duration and stability of both a stimulus-evoked reverberatory response and the quiescent period between such responses in the absence of a stimulus. This makes it difficult to explain how modes of network activity can persist across networks of different sizes (e.g., homologous brain regions in different species) or different instances of the same circuit (e.g., homologous bran regions across individuals within a species). However, we posit that rather than simply increasing the mean number of inputs (for constant p) or the likelihood of finding highly connected cells (for p = kN⁻¹) as the population becomes larger, developmental rules might act to impose topological, size-invariant homeostatic constraints on synaptic strength and connectivity, which could become crucial for the generation and sustenance of reverberations without the emergence of coordinated, stimulus-independent activity.

This could be important for maintaining stimulus discriminability in the face of development. Networks that are activated just as easily by spontaneous- as by stimulus-evoked synaptic activation will be unable to effectively communicate the timing or identity of a stimulus to downstream targets. And if the timing of activation of the neurons carries information about the stimulus or some other state variable, then it is important for reverberation to remain coherent while it is engaged; spontaneous input cannot drive neurons to begin firing out of turn (Abeles, 1991). These observations indicate that constraints on synaptic drive might play a crucial role in determining the ability of diverse networks to retain these characteristics.

Previous studies (van Vreeswijk & Sompolinsky, 1998) have stressed that neuronal networks with random connectivity have significant variability in the actual number of synaptic inputs per cell. In our studies, we found that variability in synaptic connectivity, even if generated entirely by binomial statistics, might become sufficient in large networks to result in a dynamical instability of an evoked reverberatory response. Thus, since biological networks do exhibit reverberation and other modes of stimulus-evoked rhythmic persistent activity, this suggests the existence of organizational motifs in the architecture of synaptic connectivity (Sporns et al., 2000; Segev, Benveniste, Shapira, & Ben-Jacob, 2003; Song et al., 2005). We propose that synaptic homeostasis may be such an organizing force. In model networks with a variable number of inputs per neuron, the destabilizing effects on reverberation of random variability in synaptic connectivity were suppressed by imposing a simple normalization constraint on synaptic drive. By making this constraint cell specific (see Figure 5; Turrigiano, 2008) and not simply a population statistic (see Figure 4; Wilson et al., 2007), we illustrated that the destabilizing effects of changes in neuron number or heterogeneity of connectivity could be easily corrected. This reveals a potentially important role for synaptic scaling that has been overlooked: rather than simply preserving the mean value of synaptic input and potentially preserving mean firing rates, normalization of synaptic drive can also suppress the variance of synaptic input, thus regularizing and stabilizing patterns of activity. By suppressing the variance, cell-specific scaling permits stimulus-evoked modes of network activity to be exhibited faithfully in the face of variability in network size or intrinsic neuronal properties rather than permitting these modes to collapse when statistical fluctuations in synaptic connectivity become significant. Thus, synaptic homeostasis may not only normalize firing rates (by normalizing mean synaptic input per neuron) but also regularize activity patterns (by reducing the variance in synaptic input per neuron). Experiments that measure the rate of network activity, but not its temporal structure, are likely to miss this distinction. Additional experiments may aim to validate this hypothesis.

Earlier modeling work suggested that small-world connectivity might support self-sustained population activity (Roxin et al., 2004) but could also be at the origin of epileptic-like seizures (Netoff et al., 2004). Thus, we expected that such a topological constraint might be essential to preserving reverberations across a range of population sizes and a range of realizations of model networks. However, neither the duration nor the frequency of reverberation in model networks was enhanced in the small-world regime; instead, introducing a synaptic scaling constraint imparted networks with robust reverberatory dynamics. Because neither of the earlier models (Roxin et al., 2004; Netoff et al., 2004) included features of short-term synaptic depression or AR, this may explain why, in those models, such a dependence on topology was observed. Interestingly, both topological and homeostatic constraints govern the correlation structure of synaptic connectivity. In the former, the probability of a connection is related to the number of connections to the jth neuron. By contrast, in the latter, the amplitude of a connection is related to the number of connections to the jth neuron. Together, these complementary principles could work to provide rich network dynamics that operate within predetermined boundaries.

Our numerical results for networks employing synaptic scaling lead to an experimental prediction in systems where AR represents a significant fraction of total synaptic transmission. Under a synaptic scaling rule, the rate, duration, and form of reverberation are only weakly affected by increasing the heterogeneity of synaptic input number, indicating that the capacity to reverberate normally under such a constraint is preserved for a wide range of connectivity patterns (many values of σ_k). However, only networks whose synapses are scaled should show drop out dynamics, such that the number of participating neurons decreases over the course of a reverberation. Nonscaled networks should exhibit no such dynamics, although the population activity inferred from measuring recurrent synaptic input onto a single neuron may be indistinguishable in the two cases. Furthermore, the rate at which neurons drop out from the reverberation should be related to σ_k, such that networks with greater variance in synaptic input number exhibit faster dropout (see Figures 5E and 5F). Finally, those neurons receiving the greatest number of synaptic inputs should drop out the earliest (see Figure 5G). These predictions should be testable with calcium- or voltage-sensitive dye imaging, which should in principle be able to track the activity in individual cells over the course of seconds. Unfortunately, in the face of spike rates ≫ 1 Hz, calcium dyes can quickly saturate, and it can be impossible to detect single spikes once this occurs. Perhaps more sophisticated imaging techniques can be used to test this model prediction.

Appendix: Equations of the Neuronal Model

We model the neurons as one-compartment, two-variable entities with dynamics described by a slightly revised version of a Morris-Lecar model (Morris & Lecar, 1981). This version has been recently developed (Prescott, Ratte, de Koninck, & Sejnowski, 2006) to account for spike shape and values of biophysical parameters that are consistent with the data for hippocampal pyramidal neurons. We chose the Morris-Lecar model because it is computationally less expensive than the full Hodgkin-Huxley model yet allows us to retain some biological plausibility regarding the mechanism of spike generation and neuronal excitability. For each of our model neurons, the dynamics of membrane potential are given by the following equation:

$$C\frac{\mathit{\text{dV}}}{\mathit{\text{dt}}}=-I_{\mathit{\text{ion}}}(t)-I_{\mathit{\text{syn}}}(t).$$ (A.1)

In equation A.1, the quantity I_ion(t) is an ionic current that sums contributions from different ion channels; here, it is given as the sum of a fast, noninactivating sodium channel, a noninactivating potassium channel, and a current due to the leak conductance:

$$I_{\mathit{\text{ion}}}(t)=g_{\mathit{\text{Na}}}{m}_{\mathrm{\infty }}(V)(V-E_{\mathit{\text{Na}}})+g_{K}w(V)(V-E_K)+g_{\mathit{\text{leak}}}(V-E_{\mathit{\text{leak}}}).$$ (A.2)

The dynamics of the activation variable for the potassium conductance are

$$\frac{\mathit{\text{dw}}}{\mathit{\text{dt}}}=\varphi \frac{w_{\mathrm{\infty }}(V)-w(V)}{{\tau }_w(V)}.$$ (A.3)

And the relaxation curves of sodium and potassium conductance activation are

$$m_{\mathrm{\infty }}(V)=0.5(1+\text{tan}h(\frac{V-V_1}{V_2}\left)\right)$$ (A.4)

$$w_{\mathrm{\infty }}(V)=0.5(1+\text{tan}h(\frac{V-V_3}{V_4}\left)\right).$$ (A.5)

The relaxation time of w(V) is voltage dependent and is given by

$${\tau }_w(V)={\left(\text{cos}h\right(\frac{V-V_3}{2V_4}\left)\right)}^{-1}.$$ (A.6)

The quantity I_syn(t) represents a summation over all incoming synapses to a given neuron. For the synaptic current to ith model neuron, it is described by

$$I_{\mathit{\text{syn}}}(t)=-(V_i-E_S){\displaystyle \sum _j}{g}_{\mathit{\text{ij}}}{Y}_{\mathit{\text{ij}}}(t),$$ (A.7)

with Y reflecting the fraction of neurotransmitter in the active state in equation 1 and the sum running over the set of all presynaptic partners j of that neuron. We study the dynamics of networks composed solely of excitatory neurons, and therefore the synaptic reversal potential is set to E_S = 0 mV. The value of the maximal synaptic conductance, g_ij, is picked up from truncated (±20% around the mean) gaussian distribution with 〈g_ij〉 = 3 mS/cm², σ = 1.5 mS/cm².

The parameters of neuronal and synaptic dynamics that were used in the model are given in Table 1.

A.1 Modeling the Dynamics of Presynaptic Residual Calcium

It is often assumed in modeling studies that ionic current is linearly related to the transmembrane voltage. However, this relation does not hold for ions for which a steep concentration gradient exists between the extra- and intracellular sides of the membrane. For example, for calcium, the Goldman-Hodgkin-Katz equation is used to describe the flux of these ions through the membrane:

$${\mathrm{\Phi }}_{\mathit{\text{Ca}}}=4_{\mathit{\text{PCa}}}\frac{V_s{F}^2}{\mathit{\text{RT}}}\frac{{[{\mathit{\text{Ca}}}^{2+}]}_{\mathit{\text{in}}}-{[{\mathit{\text{Ca}}}^{2+}]}_{\mathit{\text{out}}}\text{exp}(-4V_{s}F/\mathit{\text{RT}})}{1-\text{exp}(-4V_{s}F/\mathit{\text{RT}})}.$$ (A.8)

In this equation A.8, Φ_Ca is the flux of calcium ions, p_Ca is the permeability of Ca²⁺ ions, F is the Faraday constant, R is the gas constant, and T is the temperature (in Kelvins). The flux of calcium ions depends on the extra-synaptic concentration [Ca²⁺]_out as well as on the intrasynaptic concentration, [Ca²⁺]_in. In addition, Φ_Ca depends on the transmembrane potential, V_s.

The dependence of calcium flux on transmembrane voltagemakes long-term network simulations computationally demanding, as it requires us to model the dynamics of voltage in presynaptic terminals. To overcome this difficulty, we make an educated guess here by assuming that the per spike amount of residual synaptic calcium is proportional to the reversal potential of synaptic calcium channels, $E_{\mathit{\text{Ca}}}=(13.32\text{mV})\text{log}(\frac{{[{\mathit{\text{Ca}}}_{2+}]}_{\mathit{\text{out}}}}{{[{\mathit{\text{Ca}}}^{2+}]}_r})$ (a substitution [Ca²⁺]_in = [Ca²⁺]_r was made). The spike-triggered increase in residual calcium is thus modeled as $\gamma \text{log}(\frac{{[{\mathit{\text{Ca}}}^{2+}]}_{\mathit{\text{out}}}}{{[{\mathit{\text{Ca}}}^{2+}]}_r})\delta (t-t_{\mathit{\text{SP}}})$, where γ captures the density of synaptic calcium channels, the permeability to calcium ions, and the conversion factor (from voltage to a change in concentration). Consistent with experimental observations (Majewska, Brown, Ross, & Yuste, 2000; Sabatini, Oertner, & Svoboda, 2002), we tuned the parameter γ to result in ≈0.1 µM increase in residual calcium after each synaptic spike (see Table 1).

A.2 Homeostatic Regulation of Synaptic Conductance Leads to the Emergence of Network Reverberations

In a separate set of simulations, we modeled homeostatic regulation of synaptic conductances. Starting from a network with subthreshold synaptic conductances (a spike generated by any one of the model neurons failed to cause a spike in any of its postsynaptic targets), homeostasis adjusted synaptic weights to bring the averaged firing rate to the preset target rate ν₀. The increase in the firing rate was accompanied by an increase in the duration of the response (see Figure 6). Thus, the homeostatic adjustment of synaptic conductance explained the emergence of reverberations in initially quiescent networks and also shows the positive relationship between reverberation duration and equilibrium network firing rates.