Laser speckle imaging in the spatial frequency domain

Abstract

Laser Speckle Imaging (LSI) images interference patterns produced by coherent addition of scattered laser light to map subsurface tissue perfusion. However, the effect of longer path length photons is typically unknown and poses a limitation towards absolute quantification. In this work, LSI is integrated with spatial frequency domain imaging (SFDI) to suppress multiple scattering and absorption effects. First, depth sensitive speckle contrast is shown in phantoms by separating a deep source (4 mm) from a shallow source (2 mm) of speckle contrast by using a high spatial frequency of illumination (0.24 mm⁻¹). We develop an SFD adapted correlation diffusion model and show that with high frequency (0.24 mm⁻¹) illumination, doubling of absorption contrast results in only a 1% change in speckle contrast versus 25% change using a planar unmodulated (0 mm⁻¹) illumination. Similar absorption change is mimicked in vivo imaging a finger occlusion and the relative speckle contrast change from baseline is 10% at 0.26 mm⁻¹ versus 60% at 0 mm⁻¹ during a finger occlusion. These results underscore the importance of path length and optical properties in determining speckle contrast. They provide an integrated approach for simultaneous mapping of blood flow (speckle contrast) and oxygenation (optical properties) which can be used to inform tissue metabolism.

1. Introduction

Laser Speckle Imaging (LSI) is a wide-field imaging method used for mapping blood flow and mechanical properties in tissue [1,2]. LSI typically uses a CCD camera to image the interference (i.e., speckle) patterns produced by the coherent addition of scattered laser light propagating with varying path lengths. The motion of scattering particles causes intensity fluctuations in the speckle pattern that can be analyzed with temporal, spatial, or combined spatiotemporal algorithms [3]. For example, laser Doppler flowmetry (LDF) and diffuse correlation spectroscopy (DCS) analyze fluctuations at a single point in space over time. The LSI technique has been used to track relative changes in blood flow in tissues such as skin and brain over a specified time [4,5].

Fercher and Briers introduced the LSI method using spatial statistics to characterize the fluctuations at the surface [6]. This method enables imaging of two-dimensional structure and flow. A single snapshot taken at an exposure time on the order of the speckle correlation time is analyzed using spatial statistics. The local speckle contrast, K, is calculated from a reflectance image as:

$$K=\frac{{\sigma }_s}{\langle I\rangle }$$ (1)

where σ_s and <I> represent the spatial standard deviation and mean pixel intensity in a region of interest. In practice, a speckle contrast image is calculated with use of a sliding window operator moved across the entire image. In principle, regions with increased flow result in rapid intensity fluctuations. During a single camera exposure (typically on the order of 1-20ms), these fluctuations will reduce speckle visibility as compared with regions with relatively less motion. Thus, speckle contrast is inversely proportional to motion in a sample.

Several methods have been suggested to convert speckle contrast to a measure of flow in tissue [7]. Assumptions must be made to describe the nature of the motion. Methods using Gaussian, Lorentzian, hybrid, random, and calibration models of perfusion have been described but absolute flow quantification remains difficult [7,8]. In general, the speckle contrast value is inversely related to blood flow and a metric such as the Speckle Flow Index (SFI) can be defined to assess relative flow in an image [9]. Regardless of the model used, the calculation of an accurate speckle contrast value is crucial. This manuscript describes factors that affect the measured speckle contrast value and assumes random Brownian motion for all samples.

Measurement and model considerations for accurate measurement of speckle contrast depend on many factors. These include the ratio of speckle size to pixel size [10], speckle window size, choice of dynamic model, noise [11], and effects of static scattering [12–14]. Comprehensive reviews of image processing algorithms and applications have covered many of these studies [15,16].

LSI is used to measure many types of tissue such as brain and skin with a large span of optical properties and optical path length. In addition, optical path length can change for a given tissue during dynamic physiological measurements. Thus, absolute quantification of speckle contrast remains a significant challenge due to modulation of the speckle pattern resulting from multiple light scattering and variation in optical path length. We systematically evaluate the impact of path length for LSI by introducing an approach for modulating LSI in the spatial frequency domain. Spatial frequency domain imaging (SFDI) is used to quantify absorption and scattering properties of turbid media by employing multi-frequency structured light illumination scheme and model based reconstruction [17]. Specifically, the sample is illuminated with a periodic illumination pattern with various frequencies of the form:

$$S\left(x,y\right)=\frac{S_0\left(x,y\right)}{2}[1+M_0\cos (2\pi f_x+\alpha )]$$ (2)

where S₀, M₀, f_x, and α are the source intensity distribution, modulation depth of the periodic pattern, spatial frequency, and spatial phase respectively. The diffuse reflectance imaged with a CCD camera, is composed of AC and DC components:

$$I=I_{AC}+I_{DC}$$ (3)

Assuming that the pattern does not vary in the y-direction (i.e., sinusoidal pattern with amplitude variation only in the x-direction), the measured AC component of the reflected intensity, I_AC, can be characterized as:

$$I_{AC}=M_{AC}(x,f_x)\ast \cos (2\pi f_x+\alpha )$$ (4)

where M_AC(x,f_x) represents the modulation of reflected photon density wave. M_AC depends on the optical properties of the tissue and can be estimated with diffusion-based light transport algorithms. To extract M_AC(x,_fx) from measurements of I_AC, a signal demodulation algorithm is employed. The tissue is illuminated with a sinusoidal pattern at a specific f_x with three relative spatial phases α = 0, 2π/3, and 4π/3 radians. M_AC(x,f_x) is then calculated with the following demodulation equation:

$$M_{AC}(x,f_x)=\frac{\sqrt{2}}{3}{[{(I_1-I_2)}^2+{(I_2-I_3)}^2+{(I_3-I_2)}^2]}^{1/2}$$ (5)

In practice, M_AC(x,f_x) is determined from images collected at multiple f_x. As f_x increases, the contribution of longer path length photons to the measured reflectance is reduced. There are two major implications due to this phenomenon. First, since absorption lengths in the near infrared (NIR) are much greater than the transport scattering length (>10-fold), an increase in f_x means that M_AC(x,f_x) is progressively insensitive to absorption. Thus, measurements at multiple f_x values enables quantitation of both absorption and scattering properties [17,18]. To estimate local tissue optical properties, we fit M_AC(x,f_x) to predictions of M_AC calculated with a forward diffusion or Monte Carlo light transport model. Second, multiply scattering photons can be suppressed by increasing f_x, resulting in improved axial/lateral resolution and higher contrast of superficial structures [18,19].

In this work, we integrate LSI and SFDI in order to understand the impact of path length and optical properties on speckle contrast. First, a model framework for calculation of speckle contrast in the spatial frequency domain is presented. Second, initial phantom experiments show that suppression of long path length photons in the SFD result in speckle contrast measurements that are (1) depth sensitive and (2) closer to unity. Third, the impact of static optical properties is discussed in the context of measured speckle contrast. Finally, a method is presented to calculate optical properties and speckle contrast in a single measurement. This method is used to calculate bulk optical properties and speckle contrast simultaneously in phantoms and a dynamic in vivo skin perfusion measurement.

2. Correlation diffusion equation

Although intensity fluctuations are quantified in LSI measurements (Eq. (1)), the speckle contrast can also be written as a function of the electric field temporal autocorrelation function, $G_1\left(\tau \right)$, and camera exposure time, T, as derived in previous literature [3,8,14]:

$$K^2=\frac{\frac{2}{T}{\displaystyle {\int }_0^T\beta G_1^2\left(\tau \right)\left(1-\tau /T\right)d\tau }}{G_1^2\left(\tau =0\right)}$$ (6)

$G_1\left(\tau \right)$ is related to the intensity autocorrelation function, $G_2\left(\tau \right)$, via the Siegert relationship. The factor β accounts for polarization and coherence effects of the system. Theoretically, β = 1, but in practice it will be smaller. For simplicity, we proceed with β = 1. It has also been shown that the correlation diffusion equation can be used to model $G_1\left(\tau \right)$ in a turbid media [20]:

$${\nabla }^2{G}_1\left(\tau \right)-{\mu }_{eff}{G}_1\left(\tau \right)=q$$ (7)

In these equations, q is the source, µ_tr = (µ_a + µ_s') the transport or total attenuation coefficient, µ_a the absorption coefficient, µ_s', the reduced scattering coefficient, µ_a,dyn is the dynamic absorption term, and µ_eff = [3µ_a,dynµ_tr]^1/2. The µ_a,dyn term is unique to this framework as it incorporates the motion in the turbid system:

$${\mu }_{a,dyn}\to {\mu }_a+\frac{1}{3}{\mu }_s\text{'}{k}_o^2\langle \Delta r^2\left(\tau \right)\rangle$$ (8)

Here $k_o=\frac{2\pi n}{\lambda }$ is the wave number of the propagating photons, and $\langle \Delta r^2\left(\tau \right)\rangle$ is the mean square displacement of the dynamic scattering particles. Note that for Brownian motion $\langle \Delta r^2\left(\tau \right)\rangle =6D_B\tau$, where D_B is the Brownian diffusion coefficient. The solution for Eq. (7) is in the same form as the photon fluence equation in the diffuse regime, except that the absorption term is modified [20]. If we apply the solution for the photon diffusion equation in the spatial frequency domain for a sinusoidally modulated light source [17], $G_1\left(\tau \right)$ in the SFD becomes

$$G_1\left(\tau \right)=\frac{3P_{0}A\frac{{\mu }_s\text{'}}{{\mu }_{tr}}}{\left(\frac{{\mu }_{eff}\text{'}}{{\mu }_{tr}}+1\right)\left(\frac{{\mu }_{eff}\text{'}}{{\mu }_{tr}}+3A\right)}$$ (9)

In this equation, µ_eff ’ = (µ_eff² + k²)^1/2, where k is the spatial frequency of the illumination pattern (2πf_x), P_o is incident optical power, and A is a constant that depends on choice of boundary conditions [17]. In this work, a partial current boundary condition is used, and A becomes

$$A=\frac{1-R_{eff}}{2(1+R_{eff})};R_{eff}\approx 0.0636n+0.668+\frac{0.710}{n}-\frac{1.440}{n^2}$$ (10)

where n is the index of refraction of the turbid media. Based on these derivations, a model has been established to characterize the speckle contrast in the spatial frequency domain using a diffusion approximation to correlation transport.

3. Materials and methods

3.1 Instrumentation

LSI instruments consist of two major components: a coherent light source and a CCD camera. SFDI instruments require a light source, a spatial light modulator (SLM), and a CCD camera. The similarity in the required instrumentation for the two methods allows for their integration into a single-platform system using a 785nm, long-coherence-length source (CrystaLaser, Reno, NV) to illuminate a reflective liquid crystal-on-silicon (LCOS) SLM (1080 L-RC Holoeye, Lake Forest, CA) (Fig. 1 ). Linearly polarized light was used to illuminate to the LCOS micro display in conjunction with a beam splitter. A diffusing glass was used to expand the light prior to reaching the SLM. The molecules in the liquid crystal layer change orientation based on the applied voltage, which controls the amplitude and the polarization of the light at each pixel. Light whose polarization state was fully rotated, was reflected back through the beam splitter, resulting in projection of spatially-modulated, coherent light patterns onto the sample. Three spatial phases (α = 0, 2π/3, and 4π/3 radians) were used. A 12-bit, cooled CCD camera (Retiga EXi, Q-Imaging, Surrey, Canada) was used to capture the reflectance pattern. The camera exposure time was set to 15 ms unless noted otherwise. SLM pattern projection and image acquisition were controlled with software written in C# and data reduction performed with software written in MATLAB (The Mathworks, Natick, MA).

Fig. 1.

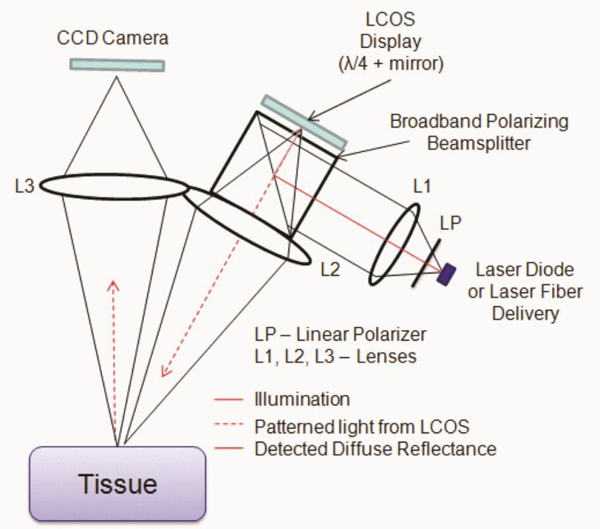
System diagram.

3.2 Phantom experiments

Tissue-like polydimethysiloxane (PDMS) phantoms were fabricated using the method described by Ayers et al. [21]. The phantom was fabricated with tissue-like µ_a and µ_s’ values of 0.01 mm⁻¹and 0.8 mm⁻¹, respectively at 785 nm. Two 2 mm diameter tubes were placed at depths of 2 mm and 4 mm, respectively, and a syringe pump was used to induce flow of a scattering liquid through the tubes at a speed of 6 mm/s (Fig. 2(a) ). The optical properties of the liquid were matched to the PDMS phantoms. f_x values between 0 mm⁻¹ and 0.25 mm⁻¹ were used, in intervals of 0.01mm⁻¹.

Fig. 2.

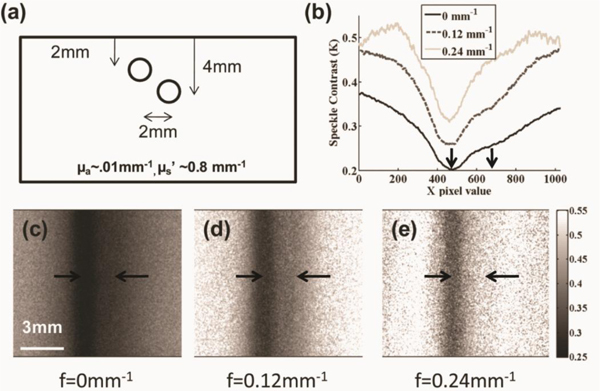
Spatial frequency depth speckle contrast maps. (a) A PDMS phantom with two tubes separated by 2 mm and buried 2 mm and 4 mm below the surface was fabricated, (b) Horizontal line profiles of (c-e) demodulated maps at three spatial frequencies shows increased sensitivity to 2 mm superficial tube flow (centered at left arrow) compared to 4 mm deep flow (centered at right arrow) as spatial frequency increases.

For each reflectance image captured at a specific spatial frequency (f_x) and α, a 7x7 sliding window was applied to generate maps of local mean pixel intensity and local standard deviation. For each f_x, the demodulation algorithm (Eq. (5)) was applied to calculate separately a demodulated mean intensity image and a demodulated standard deviation image. To compute local speckle contrast for a given spatial frequency (f_x), the quotient image of the demodulated mean and standard deviation images was calculated, resulting in a spatial frequency dependent speckle contrast image.

The distribution of photon path lengths is an important consideration for understanding speckle contrast. Multiple scattering and absorption events affect the photon path length distribution. An increase in reduced scattering has been shown to reduce speckle contrast due to longer photon path lengths [14]. Similarly, an increase in absorption suppresses the contribution of long path length photons and results in an increase in speckle contrast [20,22]. To demonstrate this experimentally, a titration of scattering (0.5 mm⁻¹ < µ_s’ < 4 mm⁻¹) and absorption (0.0025 mm⁻¹ < µ_a < 0.08 mm⁻¹) coefficients was performed at multiple exposure times. Liquid phantoms were used for this portion of this study with Intralipid (Baxter Healthcare, Deerfield, IL) used as primary scattering agent and water soluble nigrosin (Sigma-Aldrich, St. Louis, MO) was used as the absorbing agent.

3.3 In vivo experiments

An occlusion measurement was performed in vivo to determine the impact of our findings in tissue. A tourniquet was applied to the finger of a volunteer for 10 minutes and released after baseline data were collected over two minutes. The tourniquet was designed to occlude arterial and venous flow. Time-resolved optical properties and the spatial-frequency dependent speckle contrast were calculated for the occluded region.

For this experiment, a 633 nm HeNe laser was used to image the occlusion instead of a 785 nm laser. This wavelength was chosen to highlight the impact of changes in optical properties during a hemodynamic measurement. In an arterial/venous occlusion, oxy-hemoglobin (ctO₂Hb) is converted to deoxy-hemoglobin (ctHHb) as the blood supply is shut down and tissue metabolic demand persists. At 633 nm, the molar extinction coefficient of ctHHb is approximately ten times larger than ctO₂Hb. Thus, the conversion of hemoglobin changes the absorption at 633 nm even if total blood volume remains the same.

4. Results

4.1 Depth-sensitive speckle characterization

With increasing f_x, the contribution of the scattering liquid in the deeper tube to the overall local speckle contrast map decreased (Fig. 2(b)). At f_x = 0 mm⁻¹, which is identical to the uniform illumination used typically in LSI, contributions to speckle contrast from scattering liquid in both tubes, was apparent (Fig. 2(c)). Although an identical flow rate of 6 mm/s was achieved within both tubes, the speckle contrast associated with flow in the deeper tube was higher due to the relatively larger contribution of light scattering from the overlying unmoving (i.e., “static”) PDMS phantom. With increasing f_x, the sensitivity of LSI to flow in the shallower tube is improved (Figs. 2(d) and 2(e)). Furthermore, at higher f_x, the full width-at-half maximum (FWHM) of line profiles taken orthogonal to the tube length decreased. Due to suppression of longer path length photons, the speckle contrast images at higher f_x contains information primarily from superficial scatterer motion.

4.2 Optical properties and speckle contrast

Our scattering titration data (Fig. 3(a) ) demonstrate that an increase in reduced scattering coefficient results in a decrease in speckle contrast. Our absorption titration data (Fig. 3(b)) demonstrate that an increase in absorption coefficient results in an increase in speckle contrast. For each experiment, the experimental values were fit with the correlation diffusion equation at multiple exposure times. A β value was calculated for each titration curve to correct for any systematic offset due to the system setup. A value of 10⁻⁶ cm²/s was used for the Brownian diffusion coefficient of Intralipid.

Fig. 3.

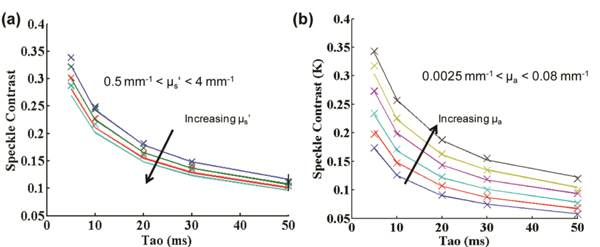
Optical property effect on speckle contrast for intralipid phantoms. (a) Scattering titration shows that as µ_s’ is increased, the speckle contrast decreases and (b) absorption titration shows that as µ_a is increased, the speckle contrast increases.

The values of absorption and scattering shown in the titration experiment are in the range expected for skin perfusion imaging. In skin, the absorption mean free path (~10-100mm) is ten to one hundred times longer than the transport (scattering) mean free path (~1mm), for a light skinned individual. The speckle contrast value for absorption (Fig. 4(a) ) and reduced scattering (Fig. 4(b)) titrations are plotted for multiple spatial frequencies of illumination using the spatial frequency domain correlation diffusion equation. As expected, at high spatial frequencies (> 0.2 mm⁻¹) the calculated speckle contrast value is insensitive to long path length interactions (i.e. absorption). In contrast, the sensitivity to shorter interaction events such as scattering is maintained at high spatial frequencies.

Fig. 4.

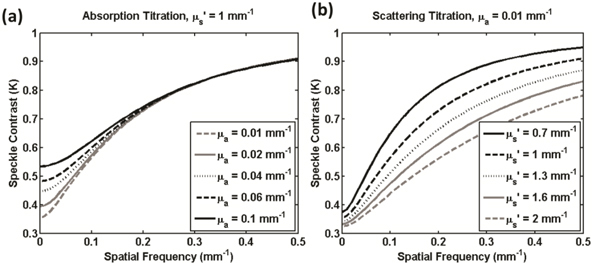
Correlation Diffusion Equation in the Spatial Frequency Domain. (a) Speckle contrast has reduced sensitivity to absorption at high spatial frequencies. (b) Speckle contrast retains sensitivity to reduced scattering at high spatial frequencies.

4.3 Dynamic in vivo measurement

This method is also capable of simultaneous measurement of optical properties (Fig. 5 ). To extract tissue optical properties, the SFDI analysis method described above, was applied to the demodulated mean intensity image at each f_x. In other words, the same spatially-modulated coherent illumination data set was used to calculate both optical properties and speckle contrast (Fig. 5).

Fig. 5.

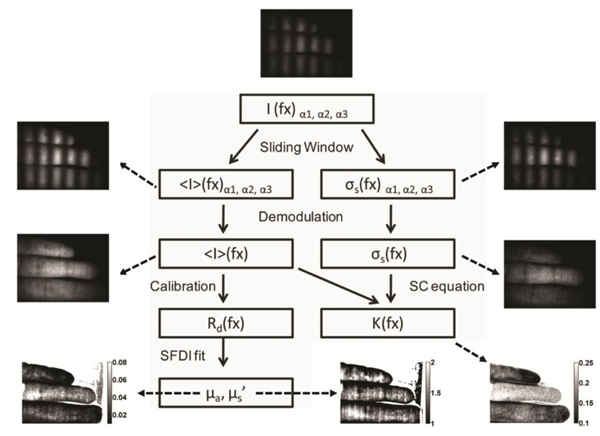
Data flow for modulated speckle. Sample images are from a hand with an occluded middle finger.

According to extracted SFDI data, an 80% increase in absorption was observed during the occlusion as ctO₂Hb was consumed (Fig. 6(a) ). The scattering value decreased slightly, most likely due to some cellular swelling, but the percentage change is less than 3% (Fig. 6(b)). A multiple frequency measurement of speckle contrast demonstrated the presence of spatial frequency-dependent flow dynamics in the tissue (Fig. 6(c)). During occlusion, the maximum change in speckle contrast at a high frequency (0.26 mm⁻¹), was much less (10% vs. 75%) than that observed with planar speckle illumination during occlusion. Following release, the peak absolute magnitude of the change again was lower (30% vs. 40%) with data collected at the higher spatial frequency.

Fig. 6.

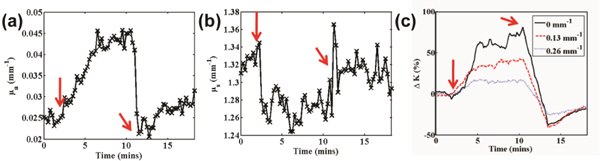
In vivo demonstration of spatial frequency dependent speckle contrast. (a) Absorption time trace, (b) reduced scattering time trace, and (c) spatial frequency dependent speckle contrast time trace. Red arrows indicate start and end of occlusion.

5. Discussion

Previous research has shown that tissue acts as a low-pass filter for an incoherent light source [18]. In this work, the same principle has been used for coherent illumination in order to separate superficial sources of speckle contrast from deep sources of speckle contrast. This observation suggests that sources of speckle contrast can be resolved in depth, although methods for quantitative reconstruction require further investigation. Recent work on laser Doppler flowmetry showed that optical path length is an important consideration during measurement [23,24]. Laser Doppler spectra have also been shown to be similar to laser speckle analysis for tissue perfusion measurements [25]. In this paper, the effect of optical path length on speckle contrast was modeled and demonstrated in phantoms for cases that satisfy the correlation diffusion regime. Thus, it is important to note that for many applications, these findings explain a trend: an increase in µ_a increases speckle contrast and an increase in µ_s’ decreases speckle contrast when measured in a reflectance geometry. In our model, the dynamic scattering term (Eq. (8)) increases the effective absorption which we refer to as dynamic absorption. Typically, the dynamic absorption needs to be an order of magnitude lower than reduced scattering for the model to be absolutely valid. This criterion may not be satisfied in tissue at longer exposure times (~10 ms) and for cases with rapid or highly ordered flow. Thus, the diffusion approximation may not be applicable and Monte Carlo modeling of correlation transport is needed to understand this system.

These studies have used a single platform that is able to image both optical properties (absorption and reduced scattering) and speckle contrast. An occlusion measurement (Fig. 6) shows concurrent changes in absorption, scattering and spatial-frequency dependent speckle contrast. The variation in spatial-frequency dependent speckle contrast shown in the arm occlusion could be due to two effects that currently cannot be decoupled. First, at higher spatial frequencies, the sampling volume is more superficial. The majority of blood vessels are located in the dermis, which may not be adequately sampled at high f_x. Second, the higher frequencies diminish the impact of long path photons. This could suppress the effects of absorption changes at 633 nm during occlusion and represent a more accurate change in contrast. Trends suggest both effects and thus the full impact of optical properties on speckle contrast in vivo is unclear. The dynamics need to be modeled for tissue and may vary based on applications (i.e. skin perfusion vs. vessel imaging).

In the results discussed so far, imaging has been limited to perfusion applications with low spatial frequency content. Samples with high spatial frequency content may not be a suitable subject for this simultaneous measurement. The smoothing used to calculate optical properties of samples with a coherent light source will affect the resolution of the final image. Further work is needed to understand these phenomena.

6. Conclusions

The introduction of multiple-frequency spatially modulated light for laser speckle imaging enables gating of long path length interactions. First, qualitative suppression of deeper sources of speckle contrast modulation in phantoms occurs with higher spatial frequencies. Second, our data suggest that longer path length interactions are suppressed at higher spatial frequencies. Based on this, a change in optical properties is shown to affect the speckle contrast value in an Intralipid titration experiment. Specifically, a two-fold increase in absorption translates to a 25% increase in speckle contrast value for Intralipid phantoms. This magnitude of change in absorption is observed in skin perfusion imaging during an occlusion measurement at 633 nm. A multi-frequency illumination scheme shows spatial-frequency dependent effects, including speckle contrast for a dynamic measurement. This dependence is due to a combination of differential partial volume sampling and suppression of absorption. Further work using Monte Carlo based correlation transport in the spatial frequency domain will help understand this problem.

In this work, a platform has been developed to simultaneously image optical properties and speckle contrast. This is the frequency domain analog of the fiber-probe based geometry developed by Boas et al. to extract optical properties in DCS [26,27]. Optical properties have also been calculated using a source with coherence length that is comparable to the optical path length [28]. Multi-spectral imaging has already been performed with planar LSI in the brain in order to calculate relative metabolic rate of oxygen consumption [29]. A multi-spectral embodiment of this platform would allow calculation of metabolic extraction rate with simultaneous measurement of path length corrected oxygen utilization and hemodynamics. Finally, SFDI methods have shown utility in tomography applications suggesting that further model development for speckle contrast in the spatial frequency domain could help quantify flow speed and correct for partial volume effects [30,31].