Abstract
This paper describes a fast and scalable strategy for constructing a radiation hybrid (RH) map from data on different RH panels. The maps on each panel are then integrated to produce a single RH map for the genome. Recurring problems in using maps from several sources are that the maps use different markers, the maps do not place the overlapping markers in same order, and the objective functions for map quality are incomparable. We use methods from combinatorial optimization to develop a strategy that addresses these issues. We show that by the standard objective functions of obligate chromosome breaks and maximum likelihood, software for the traveling salesman problem produces RH maps with better quality much more quickly than using software specifically tailored for RH mapping. We use known algorithms for the longest common subsequence problem as part of our map integration strategy. We demonstrate our methods by reconstructing and integrating maps for markers typed on the Genebridge 4 (GB4) and the Stanford G3 panels publicly available from the RH database. We compare map quality of our integrated map with published maps for GB4 panel and G3 panel by considering whether markers occur in the same order on a map and in DNA sequence contigs submitted to GenBank. We find that all of the maps are inconsistent with the sequence data for at least 50% of the contigs, but our integrated maps are more consistent. The map integration strategy not only scales to multiple RH maps but also to any maps that have comparable criteria for measuring map quality. Our software improves on current technology for doing RH mapping in areas of computation time and algorithms for considering a large number of markers for mapping. The essential impediments to producing dense high-quality RH maps are data quality and panel size, not computation.
Many genome-wide maps have been constructed as part of the Human Genome Project. A current widely used technique is radiation hybrid (RH) mapping (Goss and Harris 1975; Cox et al. 1990; Walter et al. 1994). One purpose of constructing maps is to provide landmarks along each chromosome to guide sequencing of the DNA. To date, most of the mapping effort has been put into iteratively constructing denser and denser maps rather than integrating new maps with old maps. Recurring problems in using maps from several sources are that the maps use different markers, the maps do not place the overlapping markers in same order, and the objective functions for map quality are incomparable. Because many large contigs of human DNA sequence are now finished and submitted to GenBank, it would be desirable to integrate maps of markers with the DNA sequence so that the maps can continue to be used to fill in the rest of the sequence and to identify genes in regions bounded by well-mapped markers.
In this paper we propose and evaluate new strategies for reconstructing RH maps and integrating those maps as well as others that have comparable objective functions for map quality. We also evaluate whether the current maps and the new maps we compute are consistent with human DNA sequence contigs in GenBank.
It is possible to reconstruct maps of previously mapped markers because the RH database (RHdb, http://www.ebi.ac.uk/RHdb/index.html) contains publicly submitted RH vectors (rhvectors) for sequence-tagged site (STS) markers. An rhvector for an STS x is a vector (x1, x2, … , xn), where n is the number of hybrids (or cell lines) in the RH panel and each xi = 0, 1, 2, depending on whether hybrid i is typed and retains x, typed and does not retain x, or not typed and/or ambiguous, respectively (Cox et al. 1990; Boehnke et al. 1991; Matise et al. 1998).
The rhvectors in RHdb are generated from multiple mapping panels; those reviewed in this paper are from the Genebridge 4 (GB4) panel (Gyapay et al. 1996) and the Stanford G3 panel (Stewart et al. 1997). Previously published maps used the GB4 and G3 panels independently and used independent resources such as YAC contig data to build their maps (Hudson et al. 1995; Deloukas et al. 1998). We decided to reconstruct the RH maps to take advantage of the fact that some markers were typed on both panels. The concatenation of rhvectors for the same marker from both panels makes the resulting rhvectors longer, which Ben-Dor and Chor (1997) showed is essential to compute more accurate RH maps.
RH mapping is based on the hypothesis that the closer the loci are on a chromosome, the more likely they are to be retained or lost together in a hybrid. That is, their rhvectors will have few differences. The two criteria typically used for assessing the closeness of rhvectors are the number of obligate chromosome breaks (OCB) and maximum likelihood estimate (MLE). Other criteria like Bayesian posterior probabilities involve more modeling assumptions (Lange et al. 1995) and have not been used in developing software for computing RH maps. It is known that OCB and MLE are not identical, but to our knowledge, Ben-Dor and Chor (1997) are the first to show that OCB and MLE are equivalent under conditions of equally spaced markers and 50% retention of markers on hybrids. However, these conditions are not satisfied by data on current panels. We verify the incomparability of the two objective functions.
The number of OCB for a marker order on a RH map with markers typed on the same panel is the number of times a 1 is followed by a 0 or vice versa, ignoring intervening 2s (unknown), between consecutive markers at all vector positions. The OCB objective for creating a map from rhvectors, then, is to find the marker order that implies the minimum number of OCB among all possible marker orders. For the MLE objective, the breakage probability and retention probability are calculated from rhvectors that are then used for estimating the distance between markers and the likelihood of a map. The order of the markers that maximizes the likelihood of the map is considered the true order of markers on the map.
Current RH maps are produced with specially tailored software packages such as RHMAP (Boehnke et al. 1991), RHMAPPER (Slonim et al. 1997), and MultiMap (Matise and Chakravarti 1995). The packages currently in use choose either OCB or MLE as the objective function and use statistical parameters and/or heuristics to produce a map. When using MLE, Lange et al. (1995) proposed a way of constructing a model that specifically incorporates the possibility of typing error and presence of unknowns, and Lunetta et al. (1996) specifically allowed for multiple panels. We propose extensions to the OCB and MLE objective functions, different from those in previous papers such as (Lange et al. 1995), to incorporate the presence of unknowns and present a strategy that identifies markers with the same map order independent of which extended version of objective functions is used.
We borrow several tools and techniques from domains of computer science and combinatorial optimization (Papadimitriou and Steiglitz 1982) to design and implement our strategy. It has been known for several years that for haploid error-free data, the problem of computing a RH map for either the OCB or MLE criterion can be mathematically transformed into an instance of a much studied optimization problem called the traveling salesman problem (TSP; Karp et al. 1996; Ben-Dor and Chor 1997). The transformation employs an approach using multiple pairwise comparisons between markers rather than the more commonly used multipoint comparisons. The transformation is exact when there are no unknown entries in the data and approximate otherwise. The TSP has been the subject of intense research for decades (Papadimitriou and Steiglitz 1982; Lawler et al. 1985; Reinelt 1994), and there is now a superb software package called CONCORDE (combinatorial optimization and networked combinatorial optimization research and development environment; Applegate et al. 1998) for solving large instances. We decided to test CONCORDE for RH mapping as part of our effort to reconstruct maps. An unintended result of our experiments is that CONCORDE consistently computes maps with lower OCB and higher MLE than those computed by RHMAPPER. Moreover, CONCORDE is much faster on large data sets than RHMAPPER when RHMAPPER is required to compute its initial framework internally de novo. In the past, the users of RHMAPPER have constructed an initial framework map, in part, by relying on information from other sources such as genetic map and YAC contig data (Slonim et al. 1997).
Ben-Dor and Chor (1997) showed that with the current number of hybrids, the probability of getting “the correct order” for all the markers is very low (<0.01). Even for only 20 markers, the success probability is <0.5, so any strategy that is pinned to framework maps of >20 markers is likely to produce maps with serious large-scale errors. The attempts made to model errors in data by hidden Markov models (Heath 1997; Slonim et al. 1997) have been successful in placing a few hundred markers but cannot be used for placing the thousands of markers that are becoming available without starting from a fairly dense initial framework map.
For consistency, we compare previous maps and our integrated map with large sequence contigs submitted to GenBank. The maps are consistent with the sequence if markers are placed in the correct sequence order on the map. We choose this objective function for map quality because there is currently no good way to assess how much better one map is compared with another one in terms of the number of markers actually ordered correctly except for chromosome 22 for which the completed sequence is available. We find that all of the maps are inconsistent with the sequence data for at least 50% of the contigs, but our integrated maps are more consistent. We provide some evidence that the inconsistencies are in large part due to data quality or panel sizes and not as much due to mapping strategy. We also list the number of markers in the same order between every pair of Généthon (Dib et al. 1996), RH Consortium (Deloukas et al. 1998), Stanford (Stewart et al. 1997), and our integrated map.
The next section of this paper presents definitions and theoretical background on RH mapping and its relationship to problems in combinatorial optimization. (More background material that is relevant to the rest of the paper, but less essential, can be found in the Appendix.) This is followed by a section in Results describing our map reconstruction strategy, our map integration strategy, and our computational experiments with these strategies. We conclude with a short Discussion and a short section on Methods summarizing availability of our software and data.
Definitions and Theoretical Background
Our methods rely on known algorithms for two problems widely studied in computer science and combinatorial optimization: the longest common subsequence problem (LCSP, sometimes also called the longest common substring problem) and the TSP. Both LCSP and TSP have many applications to problems in computational biology (Gusfield 1997) but may be unfamiliar to practitioners of RH mapping. Therefore, we summarize the most essential background material in this section. More background material including a brief history of the TSP can be found in the Appendix.
LCSP
Given two sequences A = a1, a2, … , an and B = b1, b2, … , bm, find a longest sequence C = c1, c2, … , ck such that C is a subsequence of both A and B. For example, if A = a, l, g, o, r, i, t, h, m and B = l, o, g, a, r, i, t, h, m, then longest common subsequences (LCS) are l, g, r, i, t, h, m and l, o, r, i, t, h, m, both of length 7. In the weighted version of the problem, we look for common subsequence that has maximum weight. In the previous example, if the weights are a = 3 and for other letters 1, then the weighted common subsequence for A and B is a, r, i, t, h, m that has weight 8 and not l, g, r, i, t, h, m or l, o, r, i, t, h, m that have weight 7.
The LCSP and its weighted version can both be solved using dynamic programming (Gusfield 1997). The length of the LCS is often used to measure the similarity of two strings. We shall use it to quantify the consistency between a pair of maps where two or more markers are said to be consistent with a pair of maps if their partial order on both maps is the same; that is, if for every pair of markers x, y, either x < y in both maps, x > y in both maps, or the relative positions of x, y are not specified in both maps.
Maximum Likelihood Computation
The steps for doing data analysis using maximum likelihood are as follows (Boehnke et al. 1991; Lange et al. 1995):
The retention probability p of the data set is estimated by the ratio of the total number of 1s to the total number of 1s and 0s.
-
The likelihood of observing rhvector (x1, x2, … , xn) for a single marker x is
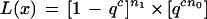
1 where c is 1 for haploid, 2 for diploid, q = 1 − p, and nj is the number of positions i such that xi = j.
-
The likelihood of observing rhvectors for a pair of markers x and y is
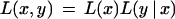
2 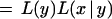
3 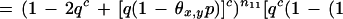
4 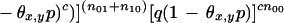
where θx,y is the breakage probability between markers x and y, and nij is the number of positions r such that xr = i and yr = j.
-
L(x,y) is maximized when θx,y is the smaller root of the equation obtained by setting the derivative of L(x,y) with respect to θx,y to 0. For the diploid case, the equation to be solved is a degree five polynomial, and for the haploid case, we get a degree two polynomial whose solution gives the following:
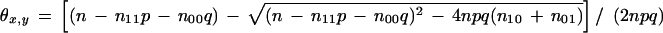
5 The root of the quadratic equation chosen for θ is the smaller root to satisfy the constraint that θx,y = 0 when n10 + n01 = 0.
-
The maximum likelihood ℒ(M) of marker order x1, x2, … , xm on a map M, also known as likelihood of M, is
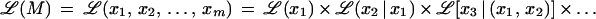
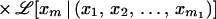 We use ℒ to denote multipoint likelihood and L to denote two-point likelihood. By considering conditioning events as independent and removing the conditioning on independent events, the multipoint maximum likelihood of map x1, x2, … , xm is approximated by several two-point likelihood estimates as
We use ℒ to denote multipoint likelihood and L to denote two-point likelihood. By considering conditioning events as independent and removing the conditioning on independent events, the multipoint maximum likelihood of map x1, x2, … , xm is approximated by several two-point likelihood estimates as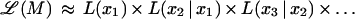
6
When there are many errors in the data, two-point likelihood estimates are preferred over multipoint likelihood estimates because the errors should not propagate as badly. Our evaluation of rhvector data, as summarized in Table 4, below, suggests that the error rate is high.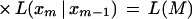
Table 4.
Number of Markers Pairs that Are Consecutive on a Contig But Have Rhvectors at OCB Distance
| OCB | GB4 rhvectors | G3 rhvectors |
|---|---|---|
| 0 | 595 (15) | 0 (0) |
| 1 | 764 (19) | 33 (34) |
| 2 | 674 (17) | 19 (19) |
| 3 | 567 (14) | 27 (28) |
| 4 | 409 (10) | 10 (10) |
| 5 | 311 (8) | 5 (5) |
| 6 | 209 (5) | 1 (1) |
| 7 | 162 (4) | 1 (1) |
| 8 | 123 (3) | 1 (1) |
| 9 | 74 (2) | 0 (0) |
| 10 | 58 (1) | 0 (0) |
| 11 | 34 (1) | 1 (1) |
| 12 | 28 (1) | 0 (0) |
| 13 | 25 (1) | 0 (0) |
| 14 | 13 (0) | 0 (0) |
| 15–24 | 18 (0) | 0 (0) |
| 25–34 | 4 (0) | 0 (0) |
| 35–44 | 3 (0) | 0 (0) |
| >44 | 0 (0) | 0 (0) |
Percentages are in parentheses.
TSP
Given a finite number of cities and the cost of travel between each pair of them, find the cheapest way of visiting all of the cities and returning to the starting point. As explained in the Appendix, the TSP is intractable in a formal sense, but much research has gone into methods for solving specific instances either approximately or optimally. A well-known software package for the TSP, namely CONCORDE (Applegate et al. 1998), has been shown to do fairly well even on huge data sets and has set several world records for the largest instances solved to optimality.
In RH mapping, markers correspond to cities with a dummy marker as the start and end city, and the cost of travel corresponds to the measures of similarity of rhvectors. For haploid error-free data, the objective functions for RH mapping can be translated into distance functions for TSP (Karp et al. 1996). We then briefly state the reductions described in the reference.
Reducing OCB to a Distance Measure for TSP
The distance between two rhvectors (x1, x2, … , xn) and (y1, y2, … , yn) is the number of positions at which xi = 1 and yi = 0 or vice versa with distance from dummy marker to any other marker being any constant. If there are no unknowns in the given RH data, then the marker order produced by TSP achieves minimum OCB.
Reducing MLE to a Distance Measure for TSP
Define the transition probability for marker x as
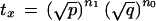 |
7 |
and the transition probability between markers x and y as
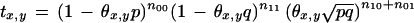 |
8 |
tx is also referred to as the transition probability between dummy marker and x. The transition probability of a map x1, x2, … , xm is given by
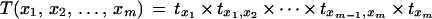 |
9 |
Karp et al. (1996) left it as an exercise to show that for haploid error-free data
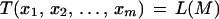 |
10 |
(See Appendix for a proof of equation 10.) The objective in TSP is to minimize a sum of distances. To convert the objective from maximizing a product to minimizing a sum, suitable for TSP, set the distance dx,y as −log(tx,y).
Computing retention frequency and breakage probabilities for diploid data with errors results in Markov and hidden Markov models that can be used for estimating the likelihoods by techniques such as the estimation-maximization (EM) algorithm. These methods are thus limited in the number of markers they can map reliably and are not suitable for translation to TSP. Ben-Dor and Chor (1997) used the approach of first estimating the breakage probability between every pair of markers, taking into account whether the data are haploid/diploid and contain laboratory errors instead of assuming that data are haploid and error free, and then reduced the MLE problem to TSP as above. They remark that using the breakage probability derived from the (degree five) polynomial for diploid data did not always improve the results compared with using the (degree two) polynomial for haploid data. Because the reduction for haploid error-free data can be used to approximate the likelihoods for diploid data, we chose to compute the breakage probabilities assuming the data to be haploid and error free. We note that the ideas presented below can be extended to the case where breakage probabilities are derived from the polynomial for diploid data but the transformations to TSP are valid only for haploid error-free data.
The reductions from OCB and MLE to TSP achieve the corresponding objective function when the data does not have unknowns and is relatively error free. Recent advances in software for TSP, namely CONCORDE, make it appealing to extend the above reductions to incorporate unknowns to reduce the effect of unknowns on the quality of map produced using TSP. We then present five such extensions for the two reductions. Note that the reductions are a method for assigning edge weights in the TSP instance, not the method for evaluating the marker order on a map. The OCB and MLE objective functions are applied in the same way to a marker order, regardless of how the marker order was obtained. To indicate which of the reductions from OCB or MLE to TSP is being extended, we tag each name by TSP+OCB or TSP+MLE. We present them in terms of distances between a marker pair x = (x1, x2, … , xn) and y = (y1, y2, … , yn). We use p and nij as before.
Normalized TSP+OCB
The distance (n10 + n01) as computed in the reduction of OCB to TSP is normalized by n/(n00 + n01 + n10 + n11) under the assumption that the positions with unknowns in them have the same distribution of differences as the positions in which both xi and yi are known. The distance according to this objective function is, then,
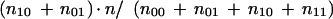 |
11 |
Weighted TSP+OCB
In this objective function, all six combinations for a pair from {0, 1, 2} are assigned a weight. We did several experiments with different weighting schemes. Each experiment has three steps: (1) compute edge weights between every pair of markers, including the dummy marker, according to the weighting scheme, (2) solve TSP by using the part of CONCORDE that guarantees an optimal order for given distances (see Appendix for details), and (3) compute OCB for the marker order M obtained by TSP; compute the sum of (n10 + n01) for consecutive markers on map M. Among the edge weights that we tested, the scheme that results in a map with lowest OCB is
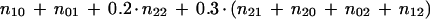 |
12 |
The schemes we tried were tested on the data we have for GB4 and G3 panels. As the above scheme gave lower OCB and higher MLE for virtually all chromosomes and for both GB4 and G3 panel data, we believe that the scheme should be generalizable to all human radiation hybrid data. For example, consider the unweighted scheme of (n10 + n01). The average number of breaks between consecutive markers for the marker orders using the weighting scheme in equation 12 was 2.70 as against the unweighted scheme that had the average of 2.79. The only case in which the unweighted scheme did better was for GB4 panel data for chromosome 21 where the weighting scheme in equation 12 needed 2.36 average number of breaks and unweighted scheme needed 2.35.
Base TSP+MLE
Same as reduction from MLE to TSP.
Extended TSP+MLE
Same as reduction from MLE to TSP except that in equation 5, n is replaced by (n00 + n01 + n10 + n11).
Normalized TSP+MLE
The breakage probabilities are computed as in Extended TSP+MLE. The transition probabilities are normalized to reflect that compution of breakage probabilities ignores positions contributing to n22. The distance between x and y resulting from this normalization is
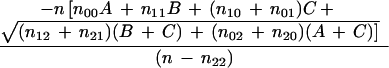 |
where A = log(1 − θx,yp), B = log(1 − θx,yq), and C = log(θx,y√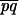 ). The distance between dummy marker and x is given by
). The distance between dummy marker and x is given by
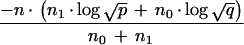 |
When the data does not have unknowns, the above five extensions simplify to the two reductions mentioned earlier in this section.
When OCB and MLE are incomparable, as in GB4 and G3 panel data, we should not expect solutions of TSP for each of the above five theoretically meaningful and robust reductions to result in the same map. We find the subset of markers for which order is not affected by the criteria used for placing them on a map. Because each TSP+OCB [TSP+MLE] weighting scheme is a minor variation of OCB [MLE] objective function, we attribute the differences in marker order on maps to limitations of the data vectors and panels for the markers. The markers whose order is sensitive to the choice of reduction are removed in favor of constructing a reliable map at the cost of not placing every marker. In the next section we present how we can extract the pieces of the map that are consistent among all maps to produce a single RH map for each panel and then use the same idea to integrate the map for each panel.
RESULTS
We first present a RH map construction strategy with the goal of producing maps that can be integrated. The emphasis is on striking a balance between the reliability of the map produced and the number of markers that get placed on the map. Second, we present a map integration strategy. The map integration procedure is not specific to RH maps and can be used for any maps that have the same objective criteria. Third, we present comparisons of our new maps with previously published maps, maps reconstructed with RHMAPPER, and sequence data submitted to GenBank.
Map Construction
The steps are as follows:
Step 1: Compute Framework Markers
The candidates C for framework markers are the markers typed on all panels. For each candidate framework marker in C, its rhvectors from different panels are concatenated to produce a virtual rhvector for the marker. The set of framework markers F is a subset of framework candidate markers C such that no marker pair in F is “very close” or “too ambiguous” to another marker in F where closeness and ambiguity are determined by cutoffs for break count B, negative logarithm of transition probability LL, and percentage of unknowns U. If a marker x∈C has more unknowns with respect to the length of its rhvector than U, then x is not present in F. If a pair of markers x,y∈C have a break count <B or have −log(tx,y)>LL, at least one of x,y is not present in F. The breakage probability for tx,y was computed as in Extended TSP+MLE. The cutoffs are determined experimentally and necessarily depend on the data. We look for cutoffs that give a non-negligible set F of framework markers such that the maps for markers in F computed in step 2 and step 3 are mostly consistent. For all maps described here, we used B = LL = 3 but did not use any cutoff for percentage of unknowns.
Step 2: Compute Maps
Reduce the problem of computing a map to that of TSP using each of the five reductions described in the previous section. Use CONCORDE to solve each instance of TSP and transform the solution to a map. This results in five maps for framework markers corresponding to five reductions.
Step 3: Compute a Framework Map
We compute a framework map as the map with only those framework markers whose order is consistent with all the maps computed in step 2. In practice, we find that in step 1, deleting markers that have rhvectors with more unknowns than those conflicting with them is effective.
Step 4: Compute Maps for Each Panel
Same as step 2 but with all markers for the panel and not just the framework markers.
Step 5: Reorder Maps
If there are m markers on the framework map, say f1, f2, …, fm, and two terminals (f0 for p-terminal and fm+1 for q-terminal), then there are m + 1 intervals on the framework map into which each remaining marker on the panel can be placed. For each marker x, we find the interval fi, fi+1 such that the likelihood of fi, x, fi+1 is the maximum among all the intervals. We compute the lod score of placing x as the logarithm of the likelihood ratios of placing x in the best interval to placing x in the next best interval. Then, each map computed in step 4 is globally reordered as follows:
For each fi, find the consecutive set of markers on map M including fi that have the interval i, i − 1 or i + 1 assigned to them. This piece of the map is called an extendible piece of M for fi.
Consider f0, … , fm+1 in order of their increasing index. For each fi, find the set of markers X in the extendible piece for fi such that each marker in X is also present in a previously considered extendible piece for f0, f1, … , fi−1. Delete markers in X from the extendible piece for fi. In practice, we do not see markers in extendible pieces overlapping with markers in extendible pieces of more than one or two previous framework markers.
Determine if the assignment of interval i − 1 or i + 1 orients the piece with respect to the framework map. If the interval assigned to the first marker of an extendible piece is less (greater) than the interval to the last marker of the extendible piece, then the piece is oriented from p-terminal to q-terminal (q-terminal to p-terminal). If the first and last markers are assigned to the same interval, then the piece is unoriented.
If an extendible piece of M for fi can be oriented, the piece replaces fi, and relative ordering of markers in the piece is preserved; otherwise, all the markers in the piece are collapsed at the position for fi.
The global reordering of extendible pieces allows for framework markers to be reordered locally on the map when the extendible piece of M for fi contains the extendible pieces of M for fi+1, fi+2, … , fi+k (resulting in empty extendible pieces of M for fi+1, fi+2, … , fi+k) and the extendible piece of M for fi is oriented in the direction that puts fi+1 before fi. Thus, we are not treating the framework map as absolutely rigid.
We illustrate step 5 with the following example: Let p-terminal, a3, a11, a8, a14, q-terminal be the framework map computed in step 3 and let p-terminal, a1, a2, … , a14, q-terminal be a map computed in step 4. Suppose we assign the following: interval 0 to marker p-terminal, a1; interval 1 to markers a2, a3, a4; interval 2 to marker a5; interval 5 to marker a6; interval 3 to markers a7, a8, a9; interval 2 to markers a10, a11, a12; interval 4 to markers a13, a14; and interval 5 to marker q-terminal. Then, the extendible piece for p-terminal is p-terminal, a1, a2, a3, a4 ordered from p-terminal to a4; for a3 gets reduced from p-terminal, a1, a2, a3, a4, a5 to just a5; for a11 is a7, a8, a9, a10, a11, a12 ordered from a12 to a7; for a8 gets reduced from a7, a8, a9, a10, a11, a12 to empty; for a14 is a13, a14 unordered; and for q-terminal is q-terminal. Note that a6 does not get assigned to any extendible piece. The map computed in step 4 gets reordered in step 5 to p-terminal, a1, a2, a3, a4, a5, a12, a11, a10, a9, a8, a7, a13, a14, q-terminal with a6 getting dropped and a13, a14 collapsing to same position as that of framework marker a14.
The concatenation of rhvectors for the same marker but different panels produces a longer virtual rhvector. This gives us a better chance of obtaining a reliable map for the common markers as we have more data to decipher their order on the map. If there is only one panel for which we have to compute a RH map, we do step 2 and step 3 described above using all markers available for the panel. However, when maps are to be constructed for more than one panel and these maps are to be integrated, we devise our map construction strategy to take advantage of the fact that we have some markers that are present in all panels. The reordering of the map in step 5 results in some markers not getting placed on the map. These markers are discarded because their vectors were not consistent with the piece of the map that they were close to.
Map Integration
In this subsection we describe how to integrate two or more maps that have the same criteria for measuring the score of placing a marker on a map. The core of the integration strategy is to use the algorithm for the weighted LCSP for finding a set of markers that are common and have same relative order in a pair of maps.
Merging Maps
To merge two maps, we first compute their weighted LCS. The markers common in both maps but not present in the LCS are deleted from both maps. The markers that are not common between the two maps are interleaved by interpolation between markers that are in the LCS. For more than two maps, the number of common markers among all of them may be considerably less than the number of common markers for any pair of maps. Our algorithm for merging more than two maps is to first merge maps for all pairs and then iteratively merge the results of those pairwise merged maps. There is no fixed order in which pairwise maps are merged.
For RH maps produced using the strategy in the previous subsection, the weight of a marker is its lod score that is computed in step 5. The steps for producing an integrated RH map use the merge procedure described in the previous paragraph. The steps are as follows:
Step 6
Merge reordered maps to produce one map per panel.
Step 7
Merge maps for each panel to produce an integrated map.
New Maps and Quality Assessment
We have presented a method of constructing RH maps from data on various panels with the aim of integrating them to produce a single RH map. We use our algorithm on G3 panel and GB4 panel data downloaded from RHdb to construct an integrated G3/GB4 panel RH map. We seek to balance the quality of the map and the number of markers that get placed on the map. Because the objective functions for RH mapping cannot be directly used to evaluate the quality of the maps, we check our maps using segments of contiguous genomic sequence (contigs) reconstructed from individual clone sequences (Jang et al. 1999), from chromosome 22 sequence (Dunham et al. 1999), and with already published maps. We compare our software with RHMAPPER.
New Maps
We obtained the rhvector inputs for our experiments from the RH database (RHdb, http://www.ebi.ac.uk/RHdb/index.html). Before using the data from RHdb, we first assign a unique identifier to each pair of forward and reverse primers for STS markers. Two markers with identical primer sequences are, in reality, the same STS marker and are assigned the same identifier. If an identifier has more than one rhvector, we pick an rhvector with the fewest unknowns.
We reconstructed maps for the GB4 and G3 panel data using CONCORDE and the five transformations to TSP (two variants of OCB and three variants of MLE) described earlier. These maps were then integrated to produce a single RH map. We have used the chained Lin–Kernighan (Lin and Kernighan 1973) heuristic from CONCORDE and the module that finds an optimal solution. Our experience is that the chained Lin–Kernighan heuristic from CONCORDE performs very well for RH data sets. For our data set, the running time for the number of iterations (250,000 kicks, two runs) for which we ran chained Lin–Kernighan heuristic is comparable with the running time of the module that finds an optimal solution. The module that finds an optimal solution requires a license for a software library that is not free. To make the comparisons fair and to make our software free to all, the results shown here use only the free parts of CONCORDE.
The numbers of unique identifiers in the GB4 panel and G3 panel data downloaded from RHdb are 40,898 and 7011, respectively. Each unique identifier corresponds to a marker in our analysis. The number of markers common to both panels is 2087. Of these 2087 markers, 1330 are candidates for the framework map as the rest are too close to another candidate framework marker. The number of markers placed on the framework map is 1084 with a maximum of 103 markers on the framework for chromosome 4 and a minimum of 17 markers on the framework of chromosome 21. The total number of markers placed on the integrated map is 23,723 out of 45,822 unique identifiers assigned to the panel data.
Software Quality
As described above, we have constructed an integrated G3/GB4 RH map. We also attempted to produce maps with RHMAPPER using the same data on both panels, to compare RHMAPPER with our software that uses CONCORDE. We chose RHMAPPER because it was used to construct the Whitehead Institute map (Hudson et al. 1995). We did not constrain RHMAPPER to any initial framework or to any set of markers for the initial framework. We computed an initial framework using the options available in RHMAPPER on the panel data because we did not want to constrain RHMAPPER to a possibly erroneous initial framework not of its own choosing.
Running Time
To compute all the single-chromosome maps described above with CONCORDE took <2 weeks total on a Sun Ultra10 workstation. We even tested CONCORDE with input consisting of all the markers on all the chromosomes together, and that computation took 3 days. Because we used the chained Lin–Kernighan heuristic from CONCORDE whose running time is dependent on the number of iterations as well as the size of data, computing a map of all the markers together with (500,000 kicks, two runs) takes less time than the computation of chromosome-specific map where each map is run for (250,000 kicks, two runs). In contrast, RHMAPPER could not finish a chromosome 1 map within 3 weeks, and took >2 months to compute all the remaining single-chromosome maps. Constraining to an initial framework would reduce the running time for RHMAPPER considerably but may impact the quality of the map and make the quality comparison done below invalid as the errors in maps computed by RHMAPPER may be attributed to the initial framework.
Map Comparison in Terms of OCB and MLE
We consider Whitehead Institute map, maps computed by us using RHMAPPER for both G3 and GB4 panel data, and maps computed using CONCORDE for both G3 and GB4 panel data. For each map and each chromosome, we compute the average number of chromosome breaks observed between consecutive markers and the average of the logarithm of two-point likelihood for the maps with breakage probabilities computed as in Extended TSP+MLE. We could not use RHMAPPER for evaluating the multipoint likelihood of the maps because RHMAPPER suffers from underflow for the number of markers we have on our maps. We compared maps computed using CONCORDE for both G3 and GB4 panel data and not our integrated map because we cannot compute OCB or MLE when consecutive markers on a map are from different panels. Furthermore, the maps produced by RHMAPPER are for one panel. The results are summarized in Tables 1 and 2. RHMAPPER runs for chromosome 1 were aborted after 3 weeks of computation and is reflected by a “?” in Tables 1 and 2. There, we have not attempted to produce an “optimal” order for the markers that are binned to the same position on the maps because the rhvectors for markers binned to the same position, in principle, should be similar.
Table 1.
Average Number of Chromosome Breaks Between Consecutive Markers and the Average of the Logarithm of Two-Point Likelihood for the Maps with Breakage Probabilities Computed as in Extended TSP + MLE
| Chr | OCB/no. of markers | Log [L(M)]/no. of markers | ||||
|---|---|---|---|---|---|---|
| Whitehead | RHMAPPER | CONCORDE | Whitehead | RHMAPPER | CONCORDE | |
| 1 | 3.70 | ? | 1.66 | −5.74 | ? | −2.28 |
| 2 | 4.18 | 3.80 | 2.12 | −6.37 | −5.47 | −3.02 |
| 3 | 3.92 | 2.71 | 1.97 | −6.17 | −4.22 | −2.82 |
| 4 | 3.84 | 3.75 | 2.15 | −5.97 | −5.37 | −3.01 |
| 5 | 3.66 | 3.37 | 1.99 | −5.72 | −4.98 | −2.73 |
| 6 | 3.59 | 2.60 | 1.70 | −5.73 | −4.07 | −2.44 |
| 7 | 4.00 | 2.86 | 1.92 | −6.20 | −4.41 | −2.79 |
| 8 | 3.64 | 3.64 | 2.09 | −5.88 | −5.39 | −2.97 |
| 9 | 3.56 | 2.86 | 1.85 | −5.59 | −4.28 | −2.55 |
| 10 | 3.76 | 3.55 | 2.04 | −5.95 | −5.24 | −2.91 |
| 11 | 3.35 | 2.53 | 1.86 | −5.26 | −3.87 | −2.42 |
| 12 | 3.67 | 3.87 | 1.98 | −5.86 | −5.66 | −2.81 |
| 13 | 3.58 | 2.92 | 2.01 | −5.72 | −4.50 | −2.89 |
| 14 | 3.43 | 2.43 | 1.79 | −5.52 | −3.78 | −2.53 |
| 15 | 4.28 | 4.16 | 2.25 | −6.64 | −5.99 | −3.19 |
| 16 | 4.43 | 3.18 | 2.32 | −6.70 | −4.87 | −3.30 |
| 17 | 4.27 | 2.74 | 2.03 | −6.71 | −4.29 | −2.83 |
| 18 | 4.22 | 3.07 | 2.47 | −6.48 | −4.76 | −3.63 |
| 19 | 4.40 | 2.78 | 1.99 | −6.74 | −4.26 | −2.67 |
| 20 | 3.76 | 2.41 | 1.74 | −6.10 | −3.83 | −2.45 |
| 21 | 3.99 | 2.64 | 2.19 | −6.65 | −4.40 | −3.35 |
| 22 | 4.12 | 2.87 | 2.17 | −6.62 | −4.53 | −3.09 |
| X | 3.37 | 2.36 | 1.70 | −5.22 | −3.61 | −2.32 |
(Chr) Chromosome number; (Whitehead) Whitehead Institute map (Hudson et al., 1995); (RHMAPPER) maps computed by us using RHMAPPER for GB4 panel data; (CONCORDE) maps computed using CONCORDE for GB4 panel data.
Table 2.
Average Number of Chromosome Breaks Between Consecutive Markers and the Average of the Logarithm of Two-Point Likelihood for the Maps with Breakage Probabilities Computed as in Extended TSP + MLE
| Chr | OCB/no. of markers | Log [L(M)]/no. markers | ||
|---|---|---|---|---|
| RHMAPPER | CONCORDE | RHMAPPER | CONCORDE | |
| 1 | ? | 2.91 | ? | −4.41 |
| 2 | 4.96 | 2.88 | −6.24 | −4.40 |
| 3 | 5.18 | 3.13 | −6.55 | −4.73 |
| 4 | 5.52 | 2.96 | −6.77 | −4.59 |
| 5 | 5.17 | 3.09 | −6.67 | −4.69 |
| 6 | 4.76 | 3.11 | −6.28 | −4.72 |
| 7 | 5.91 | 3.69 | −7.16 | −5.29 |
| 8 | 5.34 | 3.09 | −6.73 | −4.70 |
| 9 | 4.73 | 3.16 | −6.21 | −4.79 |
| 10 | 5.35 | 3.47 | −6.73 | −5.08 |
| 11 | 5.79 | 3.24 | −7.00 | −4.84 |
| 12 | 5.31 | 3.32 | −6.86 | −5.05 |
| 13 | 4.58 | 3.17 | −5.96 | −4.79 |
| 14 | 4.04 | 2.93 | −5.69 | −4.57 |
| 15 | 4.70 | 3.76 | −6.36 | −5.39 |
| 16 | 5.04 | 3.49 | −6.47 | −5.12 |
| 17 | 4.39 | 3.69 | −6.07 | −5.50 |
| 18 | 6.10 | 3.88 | −7.52 | −5.54 |
| 19 | 4.95 | 3.23 | −6.59 | −4.88 |
| 20 | 4.87 | 3.70 | −6.43 | −5.53 |
| 21 | 3.79 | 3.36 | −5.73 | −5.16 |
| 22 | 4.21 | 3.41 | −6.24 | −5.20 |
| X | 4.35 | 2.80 | −5.52 | −4.22 |
(Chr) chromosome number; (RHMAPPER) maps computed by us using RHMAPPER for G3 panel data; (CONCORDE) maps computed using CONCORDE for G3 panel data.
Because the maps produced using RHMAPPER by us (columns 2, 3, 5, and 6 of Table 1) have lower average OCB and higher average logarithm of likelihood than the Whitehead Institute map, we feel that our strategy of not constraining RHMAPPER by an initial framework does not degrade the quality of maps produced. Therefore, it is fair to compare the maps produced by us using RHMAPPER with the maps produced using CONCORDE. Some of the differences in results for GB4 panel between the map of Whitehead Institute and the one produced by us using RHMAPPER on GB4 panel can be attributed to the fact that we are using markers that became available since their map was published. It is also possible that the currently available data have been cleaned since earlier versions that may have been used for previous maps or that the genetic map and YAC contig data used by the Whitehead Institute to build the initial framework was erroneous.
CONCORDE consistently produces maps that have lower average OCB and higher average logarithm of likelihood than those constructed with RHMAPPER. Because computation of maps using RHMAPPER and our software started with the same data and RHMAPPER was not constrained by an initial (possibly erroneous) framework map, Tables 1 and 2 suggest that our strategy is able to do a better job than RHMAPPER. Based on work for TSP, there is some intuitive justification for why this should be so. First, orders of magnitude more person years have been spent developing algorithms and software for TSP than for RH mapping. Second, the approach taken by RHMAPPER is to consider triples of markers and to do local extensions. For the initial framework map, RHMAPPER does local extensions several times with random permutations of the file containing information for triples. For growing the map by a marker, RHMAPPER considers only the triples created by consecutive markers on the initial framework map and the marker. There is an analogous method for TSP called 2-opt (in general k-opt) that considers changing only two edges of the traveling salesman tour at a time and continues doing so until no further improvement can be found. It is established that for typical large TSP problems, the chained Lin–Kernighan method in CONCORDE finds lower cost tours than 2-opt (e.g., see Johnson and McGeoch 1997). This is because the Lin–Kernighan heuristic does more large-scale rearrangements and looks at a much larger neighborhood of solutions than 2-opt to try to improve the current solution. We see no reason why this general difference in performance should be different for RH mapping problems. RHMAPPER does not formally treat the problem as an instance of TSP, but the heuristic used by RHMAPPER suffers from the same weakness that 2-opt has for TSP. It is an open research problem to design and implement good software for finding best global order when information given is for only triples.
Quality of Integrated Map
We compare the quality of our integrated map with that of previously published maps by looking at consistency with sequence data and by looking at the maximum number of markers placed in same relative order between pairs of maps.
Consistency with Sequence Contigs
To test the correctness of a map, we can check the order of markers that are on the contigs that have been sequenced. We place markers on contigs using the e-PCR program (Schuler 1997). On October 27, 1999, there were 1807 human DNA contigs in GenBank on which we placed at least one marker. The position of a marker on a contig was determined by the physical base pair position of the left end of the marker from one end of the contig. The number of pairs of markers that were consecutive on a contig and typed on GB4 and/or G3 panels were 4071 and 98, respectively. We say that a contig is consistent with the map if there are at least three markers that are both on the map and on the contig under consideration and the order of these markers is the same. Our analysis considers all the markers on the map and is not restricted to the markers that are placed with significant statistical support. We also consider the case when one marker is allowed to be misplaced on the contig. The number of consistent contigs are 159 of 799 (19.90%) for GB4 map of RH Consortium (Deloukas et al. 1998), 97 of 291 (33.33%) for GB4 map of Whitehead (Hudson et al. 1995), 27 of 84 (32.14%) for G3 map of Stanford (Stewart et al. 1997), and 199 of 496 (40.12%) for the integrated map we produced. The number of contigs that become consistent when one marker is allowed to be misplaced are 318 of 799 (39.80%) for GB4 map of RH Consortium (Deloukas et al. 1998), 162 of 291 (55.67%) for GB4 map of Whitehead (Hudson et al. 1995), 46 of 84 (54.76%) for G3 map of Stanford (Stewart et al. 1997), and 309 of 496 (62.30%) for the integrated map we produced. By each measure, our map is better than the other three maps. The number of contigs that could be considered is lower for the integrated map than for the RH Consortium map because the number of markers on the integrated map is lower. Furthermore, the number of consistent contigs is higher, which can be viewed as evidence that we are not deleting too many markers and we are deleting markers with problematic data. However, the contig data and maps produced are still very inconsistent. Inconsistencies can arise either because (1) the contig data have many errors, (2) the mapping procedure is incorrect, or (3) the RH data have many errors. Evidence that either the contig or RH data are incorrect, and not the mapping strategy, comes from looking at the rhvectors of the markers that are placed consecutively on a contig. We check whether the contig data are consistent with the RH data by looking at the OCB distance (rhvector differences) between rhvectors for the markers consecutively placed on a contig. Table 4, below, summarizes the OCB distance observed between markers that were placed consecutively on a contig. For a RH mapping strategy to place markers consecutively, the rhvectors of these markers should be close to each other. Therefore, no plausible RH mapping strategy should place markers consecutively if they have more than two or three differences. We found many cases where two markers that are consecutive on sequence contigs have many differences in their rhvectors. Consider, for example, markers on GenBank entry AC004231 shown in Table 5, below. The physical base pair positions on the sequence suggest that marker 55194 is contained in marker 77310, which is clearly disputed by the rhvectors for two markers as they differ in 41 positions. For such extreme discrepancies, the RH mapping strategy is clearly not the cause of the inconsistency, and there is some experimental error. We believe, and analysis of Ben-Dor and Chor (1997) suggests, that smaller discrepancies like those in Table 4, below, are unavoidable and affect the map computation because of the small size of RH panels currently in use. We cannot rule out some other types of errors in conducting the RH experiments or in depositing the data in RHdb, but the error rates would have to be extremely high to account for the inconsistencies between rhvectors and contigs.
Table 5.
Data for Markers on Sequence AC004231
| Marker identifier | Radiation hybrid name | bp | Distance | |
|---|---|---|---|---|
| bp | OCB | |||
| 61868 | RH55030 | 124404..124553 | — | — |
| 72154 | RH39412 | 127258..127493 | 2854 | 4 |
| 77310 | RH13349 | 149852..150089 | 22594 | 42 |
| 55194 | RH55082 | 149856..150027 | 4 | 41 |
| 52532 | RH18130 | 173790..174030 | 23934 | 2 |
| 19032 | RH55096 | 173894..174232 | 104 | 0 |
| 64513 | RH46938 | 188674..188820 | 14780 | 0 |
| 62207 | RH28210 | 211868..212062 | 23194 | 0 |
| 80183 | RH47583 | 214891..215050 | 3023 | 10 |
| 21845 | RH55137 | 215148..215274 | 257 | 4 |
| 12533 | RH46475 | 220582..220701 | 5434 | 3 |
Base pair difference is taken from left end. Distances are shown with respect to the previous marker.
Consistency with Chromosome 22 Sequence
The completed sequence for chromosome 22 is available from http://www.sanger.ac.uk/HGP/Chr22/ (Dunham et al. 1999). It consists of 12 contiguous segments covering 33.4 million bp separated by 11 gaps of known size. The availability of chromosome 22 sequence allows us to consider only the markers that are placed reliably on a chromosome 22 map and to find out the percentage of these markers that are in the same order as the chromosome 22 sequence. Table 3 summarizes the results for the RH Consortium, Whitehead, Stanford, and our integrated maps. It is shown that the integrated map consistently does better than the RH Consortium and Whitehead maps. In places where the integrated map does not do as well in percent of markers correct as the Stanford map, we are considering almost three times as many markers as the Stanford map. The Généthon map could not be considered for Table 3 as it does not assign reliability to placement of markers.
Table 3.
Number of Markers that Are in Same Order on the Map as Chromosome 22 Sequence Out of the Top K% of Markers on the Map
| Top K% | RH Consortium | Integrated | Whitehead | Stanford |
|---|---|---|---|---|
| 5 | 14/23 (61) | 11/12 (92) | 8/10 (80) | 4/4 (100) |
| 10 | 29/46 (63) | 19/25 (76) | 15/20 (75) | 6/8 (75) |
| 15 | 45/70 (64) | 28/38 (74) | 20/30 (67) | 10/13 (77) |
| 20 | 57/93 (61) | 37/51 (73) | 27/40 (68) | 12/17 (71) |
| 25 | 74/117 (63) | 47/64 (73) | 33/50 (66) | 16/22 (73) |
| 50 | 107/234 (46) | 84/129 (65) | 60/100 (60) | 30/44 (68) |
| 75 | 145/351 (41) | 111/194 (57) | 78/150 (52) | 49/66 (74) |
| 100 | 183/469 (39) | 151/259 (58) | 100/201 (50) | 66/89 (74) |
The markers are sorted by lod score and the top-most marker has the best lod score. Percentages are given in parentheses.
Map Comparison in Terms of LCS
We consider every pair of Généthon, RH Consortium, Stanford, and our integrated map. Table 6 lists the number of markers that are common between a pair of maps and the number of markers in their LCS. A LCS between a pair of maps gives the largest subset of markers whose relative order on both maps is the same. As expected, the number of markers common between the integrated map and G3/GB4 is more than the number of markers common between G3 and GB4 maps. The integrated map looks more consistent with the G3 map than with the GB4 map, when consistency is measured in terms of the length of the LCS of markers. It is interesting to note that 82.42% of markers are in LCS between our integrated map and Généthon's genetic map that was not constrained by any initial framework map as against 95.76% and 90.49% of markers for GB4 and G3 maps, respectively, which used information from Généthon's genetic map for constructing their initial framework map.
Table 6.
Number of Markers that Are in the Same Order Between a Pair of Maps Out of the Number of Markers that Are Common Between Them
| Chr | Gnt vs. Int | Gnt vs. GB4 | Gnt vs. G3 | G3 vs. GB4 | Int. vs. GB4 | Int vs. G3 |
|---|---|---|---|---|---|---|
| 1 | 106/141 | 121/133 | 53/61 | 150/199 | 1149/2074 | 338/428 |
| 2 | 65/83 | 55/58 | 64/75 | 98/136 | 817/1223 | 287/355 |
| 3 | 90/106 | 65/66 | 68/81 | 96/132 | 815/1172 | 324/410 |
| 4 | 43/52 | 67/68 | 22/22 | 74/99 | 549/877 | 444/517 |
| 5 | 41/47 | 34/34 | 24/26 | 46/53 | 733/900 | 181/220 |
| 6 | 79/98 | 123/127 | 29/33 | 72/89 | 825/1268 | 260/295 |
| 7 | 62/78 | 49/49 | 53/63 | 78/102 | 530/803 | 236/295 |
| 8 | 32/37 | 27/27 | 24/24 | 56/65 | 421/734 | 193/227 |
| 9 | 34/38 | 24/25 | 27/28 | 57/77 | 444/640 | 161/210 |
| 10 | 57/65 | 54/59 | 33/37 | 73/96 | 649/925 | 219/268 |
| 11 | 49/58 | 41/41 | 42/45 | 79/102 | 788/1037 | 275/305 |
| 12 | 51/57 | 57/60 | 32/33 | 49/67 | 680/1038 | 213/236 |
| 13 | 26/33 | 35/35 | 18/19 | 33/34 | 247/436 | 119/141 |
| 14 | 29/35 | 30/30 | 23/23 | 54/66 | 463/707 | 185/211 |
| 15 | 22/31 | 29/30 | 16/17 | 37/53 | 378/639 | 108/159 |
| 16 | 34/40 | 34/35 | 28/28 | 32/38 | 370/519 | 137/150 |
| 17 | 25/29 | 26/26 | 14/14 | 46/62 | 487/782 | 139/153 |
| 18 | 26/28 | 26/27 | 16/16 | 31/43 | 184/326 | 109/140 |
| 19 | 19/24 | 25/25 | 12/12 | 25/43 | 381/591 | 136/147 |
| 20 | 46/55 | 44/50 | 19/20 | 41/46 | 378/582 | 123/133 |
| 21 | 17/22 | 17/18 | 11/13 | 16/20 | 156/228 | 99/113 |
| 22 | 9/12 | 15/17 | 7/9 | 16/20 | 147/251 | 78/82 |
| 23 | 32/37 | 42/46 | 12/16 | 22/28 | 383/528 | 68/112 |
| Total | 994/1206 | 1040/1086 | 647/715 | 1281/1670 | 11974/18280 | 4432/5307 |
| (82.42%) | (95.76%) | (90.49%) | (76.71%) | (65.50%) | (83.51%) |
(Chr) Chromosome number; (Gnt) Généthon map (Dib et al. 1996); (Int) our integrated map; (GB4) RH Consortium map (Deloukas et al. 1998); (G3) Stanford map (Stewart et al. 1997).
DISCUSSION
We presented a method for producing RH maps that robustly treats the data currently available. Some steps in the process can be further optimized. In particular, one would like to have a mechanism in which vectors with errors can be detected before the TSP is used to construct a map. This would decrease the number of markers that are thrown out in step 5 of our algorithm.
We demonstrated with markers from the two largest human RH maps currently available (Stewart et al. 1997; Deloukas et al. 1998) that our map integration strategy produces maps that are more consistent with sequence data in GenBank than either map alone. This validates the hypothesis that integrated maps can add value over nonintegrated maps. However, our integrated map is still quite inconsistent with sequence data, and we showed that this is largely due to poor data quality that cannot be easily overcome by better mapping algorithms. The inconsistency between rhvectors and DNA sequence contigs casts doubt on the hypothesis that adding more markers to current RH maps can guide future DNA sequencing effectively.
To compute our integrated chromosome maps, we found it necessary to first recompute maps based on the previously used markers, so as to take advantage of some markers that were typed on multiple panels. Recomputing the initial maps was practical only because the genomics research community has had the foresight to insist on making sequence, marker, and rhvector data freely available. The recomputation process confirmed serious concerns raised by Ben-Dor and Chor (1997) about how RH mapping is being performed in practice.
Ben-Dor and Chor (1997) presented both theoretical and practical assessments of RH mapping methods. On the practical side they tested the usage of TSP to construct maps. They suggested that computing RH maps via the reduction to TSP could produce maps of comparable quality to RHMAPPER. However, they used smaller data sets than ours, and used only three simple heuristics for TSP. We pushed their suggestion much further by using much larger data sets and using the CONCORDE software package for TSP. The results both in terms of map quality (Tables 1 and 2), and running time are striking. CONCORDE consistently produces maps that have fewer OCB and higher maximum likelihood than published maps and maps recomputed with RHMAPPER. Moreover, CONCORDE could easily handle all the data for each chromosome, computed all our single chromosome maps in under 2 weeks, and was even able to compute a map using all markers from all chromosomes together in 3 days. In contrast, RHMAPPER without a precomputed initial framework did not finish the chromosome 1 map within 3 weeks. Thus, our map construction strategy is the first one than can be scaled up to handle many more markers than are currently available without being pinned to a possibly erroneous framework. We show that RH mapping can be done efficiently by taking advantage of the theoretical work and software package developed for solving a general combinatorial optimization problem.
On the theoretical side, Ben-Dor and Chor (1997) raised serious doubts about the ability of the RH approach to produce good maps with current panel sizes. We rewrite theorem 3 of Ben-Dor and Chor (1997) as follows:
Theorem
The success probability s of correctly ordering n uniformly distributed markers is bounded by
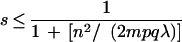 |
13 |
where m is the number of hybrids, p is the retention probability, q = 1 − p, and λ is the intensity of the breakage process.
Using the parameter values of n = 200, m = 83 (for G3 panel), p = 0.3, λ = 10 (Ben-Dor and Chor 1997), the above inequality shows one has a <1% chance of finding the correct marker order. The maximum and minimum number of markers on our framework maps are 103 for chromosome 4 and 17 for chromosome 21, respectively. Using the larger m = 93 (GB4 panel) and 103 and 17 markers, the chance of ordering 103 and 17 randomly chosen markers correctly is <3.6% and 58%, respectively. Although the theorem as stated does not apply when one selects a subset of markers, which may be easier to order correctly, it does suggest that sticking to a rigid framework is unlikely to work well. Stringham et al. (1999) propose a way of not relying completely on a fixed framework map but do not produce a whole genome map based on that method. To avoid the Ben-Dor and Chor lower bound, one should choose the framework markers carefully and allow for the possibility of rearranging or changing the framework markers in light of the other data. Our method is not pinned to a framework map and allows for the possibility of framework markers to be rearranged locally in step 5 followed by possible removal of framework markers during merge in step 6 and step 7.
Moreover, from inequality 13, it follows that panel sizes must be 2 orders of magnitude larger than currently used to boost the success probability significantly. It is not the case that using too small panel sizes simply causes local rearrangements that can be ignored by the commonly used practice of binning nearby markers. Rather, we find that marker pairs that belong close together according to the DNA sequence often have a very large number of OCB in their rhvectors. This indicates that either the data quality is poor or the panel sizes are too small, so that the essential assumption that nearby markers have nearby rhvectors does not hold with high enough probability. Furthermore, at present there is no good way to assess the fraction of markers correctly ordered on a map. This confirms the theoretical evidence by Ben-Dor and Chor (1997) that adding more markers without increasing the panel size is not a fruitful strategy to obtain maps with better quality.
In sum, there is a map integration and reconstruction strategy that can produce maps with better quality. Our software improves current technology for doing the RH mapping in areas of computation time and algorithms for considering large number of markers for mapping. The essential impediments to producing dense high-quality RH maps are data quality and panel size, not computation.
METHODS
The maps are stored in SQL Server Release 11.0.x of the Sybase database management software. The functions are implemented using Transact-SQL and C version of Open Client DB-Library. The algorithm was developed on Unix System V release 4.0 running under SunOS 5.5.1 using Sun WorkShop Compiler C 4.2, but it is compatible with other Unix computers. The mapping software and a copy of this paper are available via an electronic mail request to richa@helix.nih.gov. The integrated G3/GB4 marker map is available at http://www.ncbi.nlm.nih.gov/genome/rhmap. For each chromosome, the recomputed integrated map has columns for (1) marker name, (2) position (cR) on recomputed GB4 map, (3) odds on recomputed GB4 map, (4) position (cR) on recomputed G3 map, and (5) odds on recomputed G3 map. In our computation, we assigned a unique identifier to each marker. For each marker its unique identifier and the following information, when available, can be obtained by clicking on the marker name: (1) primer information, (2) aliases for marker name, (3) mapping information with respect to GeneMap'99, and (4) e-PCR results on genomic contigs and cDNAs as appropriate. Information on CONCORDE is available at http://www.caam.rice.edu/keck/concorde.html. Finished sequences of individual clones produced by the Human Genome Project have been merged into contiguous sequence segments (contigs) as previously described (Jang et al. 1999). The positions of markers within these sequences were determined by the e-PCR program (Schuler 1997), using a word size of six (W = 6), a variability of up to 10 bases in the PCR product size (M = 10), and up to 1 mismatching base allowed (N = 1).
Acknowledgments
We thank David Lipman and James Ostell for helpful discussions. We are indebted to the reviewers of this manuscript for carefully reading it and making several extremely useful suggestions that have improved the exposition of our work.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Appendix
TSP
If a salesman, starting from his home city, is to visit exactly once each city on a given list and then return home, he could select the order in which cities are visited in such a way that the total distances traveled is as small as possible. Even when he knows the distance between every pair of cities, it is not at all clear how the data should be used to get the tour of minimum distance efficiently. This is called the TSP.
Mathematically, an instance of TSP is composed of a number n of cities and an n × n distance matrix D = [dij], where each dij is a non-negative integer and the question asked by the TSP is, “What is the shortest tour for the n cities?” It is well known that TSP belongs to a class of problems called NP-Complete problems (Garey and Johnson 1979). Loosely speaking, this is a class of problems for which there is no known polynomial time algorithm, and also for any pair of problems belonging to this class, one can be reduced to the other in polynomial time. So, if any problem that belongs to this class can be solved in polynomial time, all of them will become solvable in polynomial time. This suggests that a fast algorithm for the TSP is unlikely to exist.
Work in complexity theory (Karp 1972) indicates that problems like TSP are probably inherently exponential, that is, the computing time grows exponentially with the number of cities. In view of the computational difficulties in obtaining optimal tours, a number of algorithms have been developed that run faster but do not necessarily produce an optimal tour (Lawler et al. 1985; Reinelt 1994).
However, even though the TSP is hard in general, in practice the situation is not hopeless. The software package CONCORDE (Applegate et al. 1998) provides two primary tools for solving TSPs. The first is a chained Lin–Kernighan heuristic (Lin and Kernighan 1973; Martin et al. 1991). Any two cities are connected by an edge whose cost is the distance between the two cities. The Lin–Kernighan heuristic is a local improvement heuristic that starts with an initial tour (e.g., a “nearest-neighbor” tour that at each step goes to the nearest city not already in the tour) and then repeatedly searches for a set of edges in the current tour that can be exchanged with a set of edges not in the current tour, shortening the length of the tour. Lin–Kernighan generalizes the 2-Opt and 3-Opt heuristics, which only consider exchanges of sets of edges of size 2 and 3, respectively. Chained Lin–Kernighan uses the Lin–Kernighan heuristic, but when Lin–Kernighan fails to find an improving exchange, it repeatedly applies a random “kick” (a four-edge exchange that is not easily made by Lin–Kernighan) to the tour, reruns the Lin–Kernighan heuristic, and keeps the new tour if the kick plus Lin–Kernighan resulted in an improvement. Because the kick is a relatively small disruption to the tour, the Lin–Kernighan process after a kick is much faster than the first Lin–Kernighan process from the initial tour.
The second tool provides a lower bound on all tours. This lower bound is used to prove that a tour is optimal or to obtain a quality guarantee for a tour. The approach CONCORDE uses to establish a lower bound, introduced by Dantzig et al. (1954), is to consider a linear relaxation of the TSP. Linear relaxation means that the problem is reformulated as minimizing a linear objective function subject to a set of linear inequalities. The linear relaxation is different from the TSP because in TSP some variables must have integer values, but the linear relaxation drops the constraint that variables must take on integer values.
The linear relaxation is solved using the simplex method (Papadimitriou and Steiglitz 1982). To work back from the solution of the linear relaxation to a solution for the TSP instance, the solution is refined by adding “cutting planes,” linear inequalities that are true for every tour, but violated by the solution of the current linear relaxation. Because at each step we are considering a relaxation of the TSP, the solution of the relaxation provides a lower bound on the solution of the TSP. If CONCORDE is unable to find any cutting planes for the current solution or if the lower bound has ceased improving over a series of cutting planes CONCORDE resorts to branching. Because for any nonempty proper subset of the cities a tour must enter or leave the subset a positive even number of times, CONCORDE branches by selecting a nonempty proper subset of the cities, splitting the problem into two subproblems, one in which the solution is permitted to enter or leave the subset only twice and the other in which the solution is required to enter or leave the subset at least four times. CONCORDE then recursively applies the same procedure to each subproblem. Once branching has begun, the weakest lower bound from the subproblems provides a lower bound for the TSP. Of course, if the lower bound in any subproblem exceeds the length of the best known tour, that subproblem can be pruned. As a result, when solving a TSP, the chained Lin–Kernighan heuristic is applied to obtain a very good tour prior to branching, so that subproblems may be pruned more readily.
These two tools are very effective at handling even moderately large TSPs. TSPLIB (Reinelt 1991), available at http://www.iwr.uni-heidelberg.de/iwr/comopt/soft/TSPLIB95/TSPLIB.html, is a library of TSP and related variants that provides a benchmark of the state of the art in solving TSPs. CONCORDE has been used to solve every TSP problem from TSPLIB with up to 13,509 cities and has obtained tours provably within 0.11% of optimal for the five remaining problems (with 14,051–85,900 cities). On a modern workstation, the chained Lin–Kernighan heuristic obtains a tour provably with 1.0% of optimal within 1 min for every TSP problem in TSPLIB.
Equivalence of Likelihood and Transition Probabilities for Haploid Error-Free Data
For haploid error-free data, equation 1 gives
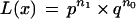 |
14 |
and equation 2 gives
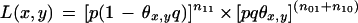 |
15 |
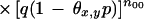 |
We prove equation 10 by the induction on length of map.
Base Case
(m = 1 ). From equation 1
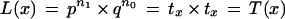 |
Induction Hypothesis
Suppose the claim holds for all maps of length k < m.
Induction Step
Assume k = m. From equation 6, we want to show that
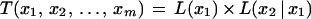 |
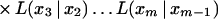 |
Substituting for T(x1, x2, … , xm) from equation 9 and using induction hypothesis, we get
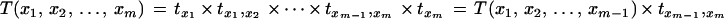 |
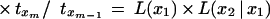 |
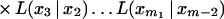 |
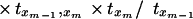 |
Therefore, to prove the claim, it is sufficient to prove that
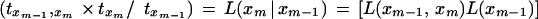 |
Rewriting the above equation and using notation x = xm-1, y = xm, and nji is the number of times i occurs in rhvector for marker j, it is sufficient to prove that
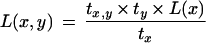 |
We first use equation 15 after substituting nx1 = (n10 + n11), nx0 = (n01 + n00), ny1 = (n01 + n11), and ny0 = (n10 + n00).
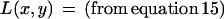 |
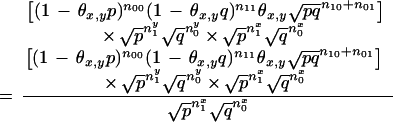 |
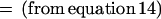 |
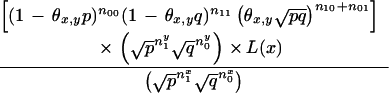 |
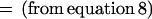 |
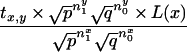 |
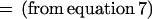 |
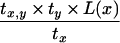 |
Footnotes
E-MAIL schaffer@helix.nih.gov; FAX (301) 480-9241.
REFERENCES
- Applegate, D., R. Bixby, V. Chvátal, and W. Cook. 1998. On the solution of traveling salesman problems. Documenta Math.III, (http://www.mathematik.uni-bielefeld.de/documenta/Welcome-eng.html) International Congress of Mathematics III: 645–656.
- Ben-Dor A, Chor B. On constructing radiation hybrid maps. J Comp Biol. 1997;4:517–533. doi: 10.1089/cmb.1997.4.517. [DOI] [PubMed] [Google Scholar]
- Boehnke M, Lange K, Cox DR. Statistical methods for multipoint radiation hybrid mapping. Am J Hum Genet. 1991;49:1174–1188. [PMC free article] [PubMed] [Google Scholar]
- Cox DR, Burmeister M, Price ER, Kim S, Myers RM. Radiation hybrid mapping: A somatic cell genetic method for constructing high-resolution maps of mammalian chromosomes. Science. 1990;250:245–250. doi: 10.1126/science.2218528. [DOI] [PubMed] [Google Scholar]
- Dantzig GB, Rulkerson R, Johnson SM. Solution of a large-scale traveling salesman problem. Operations Res. 1954;2:393–410. [Google Scholar]
- Deloukas P, Schuler GD, Gyapay G, Beasley EM, Soderlund C, Rodriguez-Tomé P, Hui L, Matise TC, McKusick KB, Beckmann JS, et al. A physical map of 30,000 human genes. Science. 1998;282:744–746. doi: 10.1126/science.282.5389.744. [DOI] [PubMed] [Google Scholar]
- Dib C, Faure S, Fizames C, Samson D, Drouot N, Vignal A, Millasseau P, Marc S, Hazan J, Seboun E, Lathrop M, Gyapay G, Morissette J, Weissenbach J. A comprehensive genetic map of the human genome based on 5,264 microsatellites. Nature. 1996;380:152–154. doi: 10.1038/380152a0. [DOI] [PubMed] [Google Scholar]
- Dunham I, Shimizu N, Roe BA, Chissoe S, Dunham I, Hunt AR, Collins JE, Bruskiewich R, Beare DM, Clamp M, et al. The DNA sequence of human chromosome 22. Nature. 1999;402:489–495. doi: 10.1038/990031. [DOI] [PubMed] [Google Scholar]
- Garey MR, Johnson DS. Computers and intractability: A guide to the theory of NP-Completeness. San Francisco, CA: Freeman; 1979. [Google Scholar]
- Goss SJ, Harris H. New method for mapping genes in human chromosomes. Nature. 1975;255:680–684. doi: 10.1038/255680a0. [DOI] [PubMed] [Google Scholar]
- Gusfield D. Algorithms on strings, trees, and sequences. Cambridge, UK: Cambridge University Press; 1997. [Google Scholar]
- Gyapay G, Schmitt K, Fizames C, Jones H, Vega-Czarny N, Spillett D, Muselet D, Prud'Homme J-F, Dib C, Auffray C, Morissette J, Weissenbach J, Goodfellow PN. A radiation hybrid map of the human genome. Hum Mol Genet. 1996;5:339–346. doi: 10.1093/hmg/5.3.339. [DOI] [PubMed] [Google Scholar]
- Heath SC. Markov chain monte carlo methods for radiation hybrid mapping. J Comp Biol. 1997;4:505–517. doi: 10.1089/cmb.1997.4.505. [DOI] [PubMed] [Google Scholar]
- Hudson TJ, Stein LD, Gerety SS, Ma J, Castle AB, Silva J, Slonim DK, Baptista R, Kruglyak L, Xu S-H, et al. An STS-based map of the human genome. Science. 1995;270:1945–1954. doi: 10.1126/science.270.5244.1945. [DOI] [PubMed] [Google Scholar]
- Jang W, Chen HC, Sicotte H, Schuler GD. Making effective use of human genomic sequence data. Trends Genet. 1999;15:284–286. doi: 10.1016/s0168-9525(99)01762-x. [DOI] [PubMed] [Google Scholar]
- Johnson DS, McGeoch LA. The traveling salesman problem: A case study in local optimization. In: Aarts EHL, Lenstra JK, editors. Local search in combinatorial optimization. London, UK: John Wiley and Sons; 1997. pp. 215–310. [Google Scholar]
- Karp RM. Reducibility among combinatorial problems. In: Miller RE, Thatcher JW, editors. Complexity of computer computations. New York, NY: Plenum Press; 1972. pp. 85–103. [Google Scholar]
- Karp RM, Ruzzo WL, Tompa M. “Algorithms in molecular biology—Lecture notes”. 1996. , Department of Computer Science and Engineering, University of Washington, Seattle, WA. [Google Scholar]
- Lange K, Boehnke M, Cox DR, Lunetta KL. Statistical methods for polyploid radiation hybrid mapping. Genome Res. 1995;5:136–150. doi: 10.1101/gr.5.2.136. [DOI] [PubMed] [Google Scholar]
- Lawler EL, Lenstra JK, Rinnooy Kan AHG, Shmoys DB. The traveling salesman problem: A guided tour of combinatorial optimization. Wiley-Interscience Series in Discrete Mathematics. New York, NY: John Wiley & Sons; 1985. [Google Scholar]
- Lin S, Kernighan BW. An effective heuristic for the traveling salesman problem. Operations Res. 1973;21:498–516. [Google Scholar]
- Lunetta KL, Boehnke M, Lange L, Cox DR. Selected locus and multiple panel models for radiation hybrid mapping. Am J Hum Genet. 1996;59:717–725. [PMC free article] [PubMed] [Google Scholar]
- Martin O, Otto SW, Felten EW. Large-step Markov chains for the traveling salesman problem. Complex Syst. 1991;5:299–326. [Google Scholar]
- Matise TC, Chakravarti A. Automated construction of radiation hybrid maps using MultiMap. Am J Hum Genet. 1995;57:A15. , meeting abstract. [Google Scholar]
- Matise TC, Wasmuth JJ, Myers RM, McPherson JD. Genome analysis: A laboratory manual. Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press; 1998. Somatic cell genetics and radiation hybrid mapping; pp. 259–302. [Google Scholar]
- Papadimitriou CH, Steiglitz K. Combinatorial optimization: Algorithms and complexity. EngleWood Cliffs, NJ: Prentice-Hall; 1982. [Google Scholar]
- Reinelt G. TSPLIB—A traveling salesman problem library. ORSA J Comput. 1991;3:376–384. [Google Scholar]
- ————— . The traveling salesman: Computational solutions for TSP applications. Lecture Notes in Computer Science. Vol. 840. Berlin, Germany: Springer Verlag; 1994. [Google Scholar]
- Schuler GD. Sequence mapping by electronic PCR. Genome Res. 1997;7:541–550. doi: 10.1101/gr.7.5.541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slonim D, Kruglyak L, Stein L, Lander E. Building human genome maps with radiation hybrids. J Comp Biol. 1997;4:487–504. doi: 10.1089/cmb.1997.4.487. [DOI] [PubMed] [Google Scholar]
- Stewart EA, McKusick KB, Aggarwal A, Bajorek E, Brady S, Chu A, Fang N, Hadley D, Harris M, Hussain S, et al. An STS-based radiation hybrid map of the human genome. Genome Res. 1997;7:422–433. doi: 10.1101/gr.7.5.422. [DOI] [PubMed] [Google Scholar]
- Stringham HM, Boehnke M, Lange K. Point and interval estimates of marker location in radiation hybrid mapping. Am J Hum Genet. 1999;65:545–553. doi: 10.1086/302496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walter MA, Spillett DJ, Thomas P, Weissenbach J, Goodfellow PN. A method for constructing radiation hybrid maps of whole genomes. Nat Genet. 1994;7:22–28. doi: 10.1038/ng0594-22. [DOI] [PubMed] [Google Scholar]


