Random walk with barriers

Abstract

Restrictions to molecular motion by barriers (membranes) are ubiquitous in porous media, composite materials and biological tissues. A major challenge is to characterize the microstructure of a material or an organism nondestructively using a bulk transport measurement. Here we demonstrate how the long-range structural correlations introduced by permeable membranes give rise to distinct features of transport. We consider Brownian motion restricted by randomly placed and oriented membranes (d − 1 dimensional planes in d dimensions) and focus on the disorder-averaged diffusion propagator using a scattering approach. The renormalization group solution reveals a scaling behavior of the diffusion coefficient for large times, with a characteristically slow inverse square root time dependence for any d. Its origin lies in the strong structural fluctuations introduced by the spatially extended random restrictions, representing a novel universality class of the structural disorder. Our results agree well with Monte Carlo simulations in two dimensions. They can be used to identify permeable barriers as restrictions to transport, and to quantify their permeability and surface area.

Brownian motion in a uniform medium is characterized by a single parameter, the diffusion coefficent D, which is a measure of mean square molecular displacement. A packet of random walkers spreads with time t according to a Gaussian distribution with variance 〈x²〉 = 2Dt. Complexity in the microscopic structure of a sample, such as heterogeneity in diffusive properties and restrictions to molecular motion, results in non-Gaussian evolution^1,2. In particular, diffusion becomes dispersive, leading to the time-dependence of the diffusion coefficient D(t).

A fundamental question is how specific complexity features manifest themselves in the dispersive dynamics. Random drifts are known to drastically slow the dynamics down to 〈x²〉 ~ ln⁴ t, thereby suppressing the diffusion, D|_t→∞ = 0, in one dimension^3,4. Their effect in higher dimensions is less profound^5–9. Short-range disorder in local diffusion coefficient preserves Gaussian diffusion for t → ∞, resulting in the finite macroscopic diffusion constant D_∞ ≡ D(t)|_t→∞. However, it causes a long-time tail^10,11 in the velocity autocorrelator 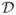(t) = 〈v(t)v(0)〉 ~ t^−(d+2)/2, with the power-law exponent depending on the spatial dimensionality d. Equivalently, the diffusivity $\mathcal{D}(\omega )={\int }_0^{\infty }\text{d}t{e}^{i\omega t}\mathcal{D}(t)\simeq D_{\infty }+\text{const}·{\omega }^{d/2}$ acquires non-analytic dispersion at low frequencies^10,11. Studying dispersive diffusion, therefore, is a way to characterize the type of disorder and of restrictions to molecular motion in a complex sample.

Here we consider a novel class of restrictions to diffusion, represented by extended barriers (membranes). Practically, membranes regulate the transport of ions¹², water molecules^13–16 and gases¹⁷ in biological tissues¹⁸. Permeable barriers may partition cell membranes, modulating phospholipid motion^19–21. Barriers also restrict molecular motion in porous and composite materials^22–27. On a fundamental level, extended barriers may introduce significant long-range correlations into the sample structure. We show that these correlations give rise to distinct transport features, qualitatively different from those due to short-range disorder which is a default assumption in the models of transport^10,11,28.

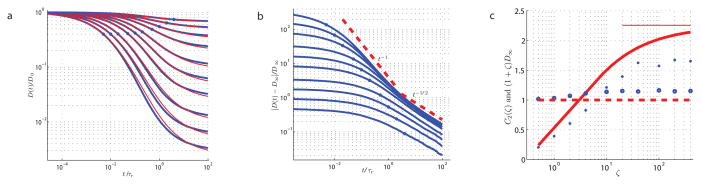
We develop a minimal model of a d-dimensional medium with spatially extended disorder, assuming that diffusion is restricted by randomly placed and oriented infinite flat membranes with a given permeability, such as in the d = 2 example of Fig. 1. Based on the renormalization group analysis, we find an accurate approximation for the diffusion coefficient as a function of time or frequency, for all membrane concentrations and permeabilities, as confirmed numerically for d = 2 in Fig. 2.

FIG. 1.

A fragment of a two-dimensional patch with randomly placed and oriented membranes (one of the disorder realizations used in the simulations).

FIG. 2.

Time-dependent diffusion coefficient D(t) for the two-dimensional random medium of Fig. 1. a, Comparison of the RG solution (6), red, with the Monte Carlo simulations, blue, for the set of decreasing permeabilities, corresponding to ζ = 0.5, 1, 2, 4, 10, 20, 40, 100, 200, 400 (top to bottom). The diffusion time τ_D is marked by blue circles. b, Scaling behavior of D(t). As the strength ζ of the restrictions increases from bottom to top, the numerical curves begin to collapse as a signature of the universal behavior (10). Dashed lines show the ζ → ∞ limits from our RG solution: the “impermeable” limit D(t)/D_∞ = 2d τ_r/t and the scaling limit (10) with $C_2(\infty )=4/\sqrt{\pi }$. c, Parameters of the scaling limit (10), C₂(ζ) (filled circles) and D_∞(ζ) (open circles), determined from the fit of the simulations in b to equation (10), compared with the RG predictions (solid and dashed red lines). Thin solid line is the RG limit $C_2(\infty )=4/\sqrt{\pi }$.

Remarkably, the spatially extended disorder introduced by the membranes in any d results in a long-term memory, that manifests itself in the long-time tail 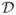(t) ~ t^−3/2 in the velocity autocorrelator (Fig. 3); in a non-analytic dispersive diffusivity 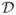(ω) ≃ D_∞ + const · ω^1/2 at low frequencies; and in a characteristically slow decrease of the diffusion coefficient, D(t) = D_∞ + const · t^−1/2 as t → ∞, Fig. 2, causing the mean square displacement to increase as 〈x²〉 ≃ 2D_∞t + const · t^1/2. The ω^1/2 ~ t^−1/2 dispersive diffusion is shown to be a consequence of anomalously strong structural fluctuations in a sample with spatially extended barriers. For membranes with finite extent or correlation length r_c, the signature ω^1/2 dispersion will switch to its short-ranged counterpart ω^d/2 after the diffusion length exceeds r_c.

FIG. 3.

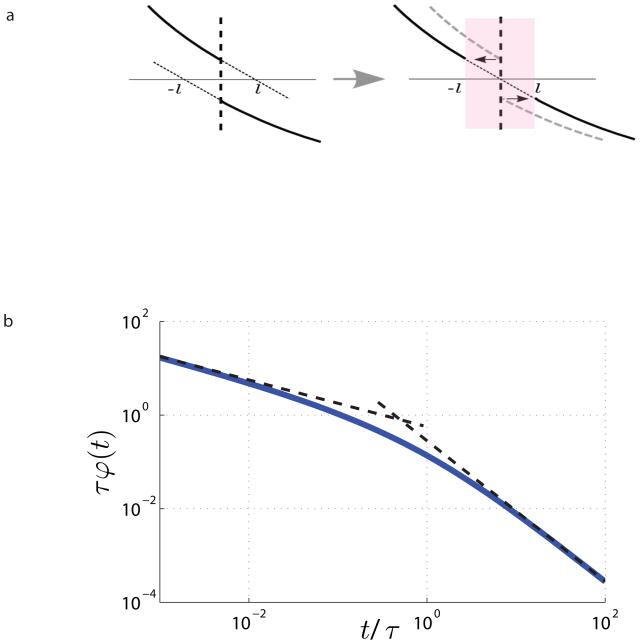
Effect of a single membrane. a, Meaning of effective membrane thickness: 2ℓ = D₀/κ is the distance by which one should shift the density profile ψ(x) on each side of membrane if one were to heal p the jump discontinuity (1). b, The memory kernel ϕ(t), equation (5), together with its limits $\varphi \simeq 1/\sqrt{\pi \tau t}$ for t ≪ τ, and $\varphi \simeq \sqrt{\tau /4\pi }{t}^{-3/2}$ for t ≫ τ.

Our model represents a novel universality class of the structural disorder in classical random media. An essential feature of the ω^1/2 ~ t^−1/2 dispersion is that, at sufficiently long times, it dominates the short-range disorder contribution for d > 1. Hence, if observed, this dispersion can serve as a “fingerprint” of spatially extended restrictions within the complexity of heterogeneous samples. Practically, such a dependence can manifest itself in a variety of transport measurements, such as the electrical²⁹ or heat conduction, or the diffusion-weighted NMR¹⁵.

Model

A membrane is an idealization of a thin slice of a poorly diffusive material, as long as its thickness is negligible compared to the shortest observable diffusion length. In the limit when both the diffusion coefficient D_m of the membrane material and its thickness l_m vanish, the ratio κ ≡ D_m/l_m is by definition the permeability. The effect of a membrane is described by the boundary condition^18,30

$$-\mathbf{nJ}{\mid }_{{\mathbf{r}}_m}=D_0\mathbf{n}{\partial }_{\mathbf{r}}\psi {\mid }_{\mathbf{r}={\mathbf{r}}_m}=\kappa [{\psi }_{{\mathbf{r}}_m+\mathbf{n}0}-{\psi }_{{\mathbf{r}}_m-\mathbf{n}0}].$$ (1)

Here D₀ is the unrestricted diffusion coefficient. The condition (1) means that, at each point r_m of the membrane, the density ψ of random walkers experiences a jump proportional to the component of the current J along the normal n to the membrane surface.

The permeability has the dimensions of velocity. In what follows, we find it useful to associate an effective thickness, 2ℓ = D₀/κ, with a membrane. This length scale is defined relative to the free diffusion coefficient D₀. Its physical meaning is derived from the condition (1) and is illustrated in Fig. 3a; the membrane indeed appears D₀/D_m ≫ 1 times thicker than its “nominal” vanishing thickness l_m.

Consider now diffusion in a macroscopic sample embedded with multiple membranes, each one imposing the condition (1). The diffusion propagator depends on their number, shape, and spatial distribution. The number of membranes is characterized by the ratio S/V of their total surface area to the sample volume. Here we adopt the convention from the porous media literature^16,24: as the random walkers can approach a membrane from both faces, the membrane’s surface area is counted twice in S. The shape and the spatial distribution of the membranes vary greatly depending on the physical context. The distinct dispersive features of transport due to spatially extended restrictions can be captured by making the simplest assumption which also allows us to keep the number of parameters to a minimum. Namely, below we consider the membranes as infinite d − 1 dimensional planes placed and oriented in a completely random (uncorrelated) way, dividing the sample into pores with random shapes, as shown in Fig. 1 for d = 2. In this case, the ratio S/V is all that is needed to characterize the geometry.

In what follows, we first outline our main results for the model medium. Next, we derive them, compare with numerical simulations, discuss and generalize.

Results for randomly oriented flat membranes

In the t → ∞ limit, the diffusion becomes Gaussian with the reduced diffusion coefficient

$$D_{\infty }\simeq \frac{D_0}{1+\zeta },\zeta =\frac{S\ell }{Vd}.$$ (2)

Here the dimensionless parameter ζ quantifies the ability of membranes to hinder the diffusion. It is the “volume fraction” occupied by the membranes based on the effective thickness ℓ defined above. The result for D_∞ is exact in d = 1, ref. 31. As follows from Fig. 2, it is a good approximation for d > 1, with 1/d in equation (2) arising from the mean-field orientational averaging, cf. Methods section. Strong restrictions correspond to ζ > 1, when the domains of thickness ~ ℓ associated with each membrane overlap, such that transport across a membrane is affected by its neighbors.

For finite t, we shift to the frequency representation since the restrictions are stationary. Technically, we focus on the diffusion propagator G averaged over the disorder in positions and orientations of the random membranes. After disorder averaging, the propagator becomes translation invariant. Its pole in the frequency – wave vector representation, $G_{\omega ,\mathbf{q}}^{-1}=-i\omega +\mathcal{D}(\omega )q^2+\mathcal{O}(q^4)$, defines the dispersive diffusion coefficient (diffusivity) 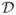(ω) which is a retarded response function that relates the disorder-averaged particle current J_ω,r = −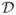(ω)∂_rψ_ω,r to the density gradient³².

The corresponding time-dependent diffusion coefficient

$$D(t)\equiv \frac{\langle x^2(t)\rangle }{2t}=-\frac{1}{t}\int \frac{d\omega }{2\pi }{e}^{-i\omega t}\frac{\mathcal{D}(\omega )}{{(\omega +i0)}^2}$$ (3)

is given³² by a contour integration along the real axis with all the singularities in the lower half-plane of complex ω.

We find 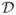(ω) in three steps. First, we develop a scattering approach for the transmission events described by the boundary conditions (1) at each membrane. Second, we solve the problem perturbatively in the volume fraction ζ at the mean-field level, starting from infinitely permeable limit 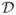(ω) ≡ D₀. These two steps are done in the Methods section. The resulting diffusivity

$$\mathcal{D}(\omega )=D_0[1-\zeta \stackrel{\sim }{\varphi }(\omega )],\stackrel{\sim }{\varphi }(\omega )=\frac{1}{1-z_{\omega }},$$ (4)

with $z_{\omega }=i\sqrt{i\omega \tau }$ and τ = ℓ²/D₀ = D₀/(2κ)², is exact in the limit when the correction ζ|ϕ̃(ω)| ≪ 1 is small. This condition holds either for sufficiently permeable membranes, ζ ≪ 1, or at short times $\sqrt{D_{0}t}S/V\ll 1$ for arbitrary permeability. The corresponding velocity autocorrelator 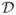(t) = D₀ [δ(t) − ζϕ(t)] contains a nonlocal in time memory kernel

$$\varphi (t)=\int \frac{\text{d}\omega }{2\pi }{e}^{-i\omega t}\stackrel{\sim }{\varphi }=\frac{1}{\sqrt{\pi \tau t}}-\frac{1}{\tau }{e}^{t/\tau }\text{erfc}\sqrt{t/\tau },$$ (5)

Fig. 3b, which will be discussed in detail below.

At the third step, we extend equation (4) onto the non-perturbative domain ζ ≫ 1 using the real-space renormalization group to account for the multiple transmission events self-consistently, as described below. Thereby we obtain our main result for all ζ,

$$\frac{D_0}{\mathcal{D}(\omega )}=1+\zeta +2z_{\omega }(1-z_{\omega })\left[\sqrt{1+\zeta /{(1-z_{\omega })}^2}-1\right].$$ (6)

Effective circuit

Before deriving our main result (6), we note that the perturbative limit (4) can be represented as a simple effective circuit. As the random walkers are uncharged, the current J has only the diffusive component, and the diffusivity 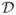(ω) defines its response to a density gradient ∂_rψ rather than to a potential bias. With this important distinction²⁹, the 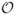(ζ) result (4) can be viewed as an “impedance” Z(ω) of a hypercube L^d, L^d−2Z(ω) ≡ 1/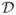(ω) ≈ 1/D₀ + nZ_m(ω), which acts as a one-dimensional disordered transmission line of length L with point impedances Z_m = ϕ̃(ω)/κ placed at random positions in series, with density n = S/(2V d). Adding independent contributions Z_m is tied to the Poissonian statistics in the positions of the barriers (see the sections on the origin of the $\sqrt{\omega }$ dispersion, and Methods).

In the dc limit, a membrane acts as a resistor with the “resistance” 1/κ ≡ Z_m(0); as ζ = 2ℓn, each membrane effectively adds the length 2ℓ to the original clean wire L if its dc resistance were to match Z(0) ∝ 1/D_∞. At finite frequencies the resistor is shunted by the Warburg element³³ with the “conductance” $g_W(\omega )=-\kappa z_{\omega }=\sqrt{i\omega D_0}/2i$ independent of the permeability. The Warburg impedance ~ 1/g_W, first observed at a flat metal electrode in an electrolyte by Kohlrausch³⁴ and Wien³⁵ in the 19th century, is associated with the diffusion-limited response³³. Incidentally, the impedance Z(ω) matches the empirical Cole form^36,37 with power law exponent $\frac{1}{2}$.

Renormalization group

To calculate the response 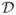(ω) of the disordered transmission line for finite ζ, we employ the following scaling argument, which we first develop for d = 1. Consider a slab of length L with the diffusivity 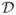(ω)|_L. Let us extend the slab to the length L′ = bL, b > 1, and rescale; now the slab’s length L′ in new units is back to L, while the original, shorter slab has length L → L/b. The rescaled slab conductance decreases due to adding extra N′ − N = Nδb membranes, δb = b − 1. The diffusivity is then reduced as

$$\mathcal{D}(\omega ){\mid }_{L^{\prime }}=\mathcal{D}(\omega ){\mid }_L\left[1-\delta n\frac{\mathcal{D}(\omega ){\mid }_L}{\kappa -\frac{i}{2}\sqrt{i\omega \mathcal{D}(\omega ){\mid }_L}}\right]$$ (7)

according to equation (4), as long as the added membrane density δn = (N/L)δb is small, δb ≪ 1. Since we assumed from the beginning that the membrane positions are uncorrelated, adding a small number of membranes in an uncorrelated way at each step is consistent. Choosing an infinitesimal dn ∝ db, we represent equation (7) in the differential form, obtaining the real-space renormalization group (RG) equation

$$\frac{\text{d}\mathcal{D}(\omega )}{\text{d}n}=-\frac{{\mathcal{D}}^2(\omega )}{\kappa -\frac{i}{2}\sqrt{i\omega \mathcal{D}(\omega )}}.$$ (8)

This is a telegraph equation for a disordered transmission line. Equivalently, it can be obtained by adding membranes in small increments δn in a macroscopic sample of a fixed length with bare diffusivity D₀, and applying the relation (4), treating all previously added membranes in the effective-medium fashion^38–40 at each RG step. The diffusivity thus decreases as long as κ < ∞. In d dimensions, rescaling a hypercube L^d as in ref. 41 is equivalent to rescaling a d = 1 slab in which the effective one-dimensional membrane concentration n = S/(2V d). At the mean-field level, the problem is always one-dimensional, with the fraction 1/d of membranes exerting full resistance.

Integrating equation (8) yields our main result (6). In the dc limit 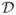(0) ≡ D_∞, the RG flow 1/D_∞|_L′ = 1/D_∞|_L + (N′ − N)/(κLd) recovers the above exact result (2) for d = 1, if one identifies L with the microscopic scale such that D_∞|_L ≡ D₀ (the bare diffusivity) and (N′ − N)/Ld → n, the final membrane density. Written as RG flow, however, the evolution of the diffusivity is not tied to a particular microscopic cutoff; indeed, the diffusivity D_∞|_L can itself originate from “more microscopic” membranes on the scale finer than L, and so forth.

We also note an interesting equivalent way of looking at the RG flow: Formally identifying the particle number density ψ entering the diffusion equation with an electrostatic potential, the dc limit corresponds to the electrostatic screening of the one-dimensional electric field (the slope ∂_xψ) by the dipoles (membranes acting as double layers). Coarse-graining corresponds to more dipoles contributing to the screening⁴², which renormalizes the effective dielectric constant, 1 → 1 + ζ.

Regimes for D(t) and numerical simulations

Consider first the most general case, which corresponds to the strong disorder, ζ ≫ 1. In this case, there are three distinct regimes in D(t), Fig. 2, separated by the two time scales, τ_r ≫ τ_D, defined below.

The initial decrease of the diffusion coefficient

$$D(t)\simeq D_0\left[1-\frac{S}{Vd}\left(\frac{4\sqrt{D_{0}t}}{3\sqrt{\pi }}-\kappa t\right)\right]$$ (9)

exactly reproduces the well-known universal short-time $\sqrt{t}$-expansion²⁴. The correction to free diffusion arises from the random walkers within the diffusion length $\sim \sqrt{D_{0}t}$ from the barriers; the term ∝ t is the permeability effect²⁷ of flat pore walls. The limit (9) is valid as long as only a small fraction of random walkers has encountered the barriers, i.e. for t ≪ τ_D, where τ_D = ā²/2D₀ is the diffusion time across the typical pore size ā ≃ 1/n = 2V d/S. Equation (9) follows already from the perturbative limit (4) universally valid for high frequencies, ωτ_D ≫ 1. It corresponds to the t ≪ τ limit of the memory kernel (5), Fig. 3b, exemplifying negative velocity autocorrelation near a wall⁴³, which diverges as t^−1/2 at short t. There is a perfect agreement between theory and simulations in this regime for all ζ.

Highly restrictive membranes look completely impermeable for t ≪ τ_r, where τ_r = V/(κS) is the residence time¹⁸ within a typical pore; in our notation, τ_r = (ζ/d)τ_D. As a result, the mean square displacement 〈x²〉 is bounded by ~ ā², and D(t)/D₀ ~ τ_D/t. For our RG result (6), the “impermeable” behavior occurs for $1\ll \sqrt{\zeta }\ll \mid z_{\omega }\mid \ll \zeta$, and yields the purely imaginary ζ-independent limit 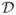(ω) ≃ −iωā² (similar to the purely reactive electrical conductivity), corresponding to D(t)/D₀ ≃ 2τ_D/t, or, equivalently, to D(t)/D_∞ ≃ 2d τ_r/t, Fig. 2b. Both our result (6) and the simulations display the 1/t dependence for ζ ≳ 100, with the theory somewhat overestimating the D(t) obtained from the numerics for very large ζ (as discussed in the Methods section).

For times longer than τ_r, the system becomes aware of the finite leakage across the membranes, with D(t) approaching the limit (2) which can be qualitatively estimated as hopping on a d-dimensional lattice with a step ā over the time τ_r, D_∞ ~ ā²/(τ_rd).

Remarkably, the way D(t) approaches D_∞ slows down from 1/t to $1/\sqrt{t}$-decrease in any dimensionality d, defining the novel disorder universality class:

$$D(t)\simeq D_{\infty }\left(1+C_d(\zeta )\sqrt{\frac{{\tau }_r}{t}}\right),t\gtrsim {\tau }_r.$$ (10)

This follows in our model (6) from $D(\omega )\simeq D_{\infty }[1-C_d(\zeta )·i\sqrt{i\pi \omega {\tau }_r}/2]$ in the $\text{limit}\mid z_{\omega }\mid \ll \sqrt{\zeta }$, with $C_d(\zeta )=C_d(\infty )\sqrt{\zeta }(\sqrt{1+\zeta }-1)/(1+\zeta )$ and $C_d(\infty )=\sqrt{8d/\pi }$. The regime (10) can be clearly seen from the simulation results of Fig. 2b where time is in the units of τ_r for a set of permeabilities. In this limit, the relative deviation [D(t) − D_∞]/D_∞ ≲ 1. We emphasize that for ζ → ∞, the dependence (10) approaches a universal scaling law with a fixed C_d = C_d(∞), which can be represented only in terms of the effective parameters D_∞ and τ_r, independent of the original microscopic parameters D₀, κ and S/V. Approaching this law corresponds to the collapse of the simulation curves in Fig. 2b onto one universal curve for ζ ≳ 100 and t ≳ τ_r. Our RG approximation (6) overestimates the C₂(∞) obtained from the fit of the numerical curves to equation (10), as illustrated in Fig. 2c. For finite ζ, the parameters C_d(ζ) and D_∞ [equation (2)] agree with the simulations within about 15% and 30% correspondingly, even in the strongly non-perturbative regime of ζ ≳ 100. For the moderate disorder, ζ ~ 1, the agreement between theory and simulations is very good.

The fact that the RG solution works fairly well even when the “small parameter” ζ ≫ 1 can be understood in terms of the flow to the moderately disordered limit with strongly renormalized parameters, D₀ → D_∞ and τ → τ_r. Indeed, for t ≫ τ_r, the medium effectively looks as if it had a decreased diffusion coefficient D_∞. This, in turn, reduces the contrast between the diffusion coefficient inside the membrane and of its surroundings, effectively changing D₀ → D_∞ in the boundary condition (1), thereby reducing the effective thickness ℓ → ℓ̃ = D_∞/(2κ) ≃ ℓ/ζ ~ ā down to the mean distance between membranes. Hence, the renormalized disorder strength is reduced, ζ → ζ̃ ≡ Sℓ̃/Vd ~ 1. Likewise, the renormalized time scale τ → τ̃ ≡ ℓ̃²/D₀ ~ τ_r matches the residence time. At this point the perturbative limit (4) is matched.

Conversely, when the membranes are highly permeable, ζ ≪ 1, the residence time in a pore is of the order of τ_D, and the time scale τ_r defined above becomes obsolete. In this limit, our result (4) becomes exact, the intermediate 1/t regime does not appear, and the short-time behavior (9) directly crosses over to the nonanalytic dispersion of the form (10),

$$D(t){\mid }_{t\gg \tau }\simeq D_{\infty }\left(1+\frac{2\zeta }{\sqrt{\pi }}\sqrt{\frac{\tau }{t}}\right),\zeta \ll 1,$$ (11)

which follows from the expansion of C_d(ζ) using τ = ζ(d/2)τ_r, and corresponds to the t ≫ τ limit of the kernel (5), Fig. 3b.

Origin of the $\sqrt{\omega }\sim 1/\sqrt{t}$ dispersion

Consider first the perturbative ζ ≪ 1 limit, which already contains the necessary physics. Here the two important time scales are τ_D and $\tau =\frac{1}{2}{\zeta }^2{\tau }_D$. We first focus on the case t ≪ τ_D, where adding independent contributions, as done in the Effective circuit and Methods sections, is justified since multiple scatterings off different membranes are not yet important. In this case, the dispersive behavior (11) for τ ≪ t ≪ τ_D is a result of scattering off individual barriers. As described in the Methods section, it represents slow density equilibration across a barrier, following the t^−1/2 decrease of the probability of a random walker to never return to the origin.

For longer times t ≫ τ_D, multi-barrier scatterings determine the time dependence of D(t) which becomes sensitive to spatial correlations between membranes. Indeed, by the time t, the medium is effectively coarse-grained into domains of the size $\sim L(t)=\sqrt{2Dt}\gg \overline{a}$. These domains have slightly different diffusion coefficients D_j due to a different amount of restrictions falling into them as a result of the disorder. The net diffusion coefficient D(t) ≡ 〈D_j〉 is the ensemble average over the domains; in d dimensions, D(t) ≃ D_∞ + 〈(δD_j)²〉/dD_∞, where δD_j = D_j − 〈D_j〉. The distribution variance 〈(δD_j)²〉 ~ 1/L^d(t) scales inversely with the domain volume for the short-range disorder due to the Poissonian statistics, yielding the ω^d/2 ~ t^−d/2 dispersion^{10,11,44–46}. This disorder effect should be contrasted with the much faster decrease of D(t) and 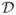(t) in the absence of spatial fluctuations, both for the strictly periodic barriers in d = 1,^47,48 and for the single-scale dominated disorder in any d, ref. 32.

Remarkably, the spatially extended disorder introduced in this work produces qualitatively stronger fluctuations in the coarse-grained distribution of {D_j}, with the variance 〈(δD_j)²〉 ~ 1/L(t) decreasing much slower than 1/L^d(t) in d > 1. This signature scaling in fact holds for any ζ, resulting in the ω^1/2 ~ t^−1/2 dispersion as long as L(t) ≫ ā, both for t ≫ τ_D (when ζ ≪ 1) and for t ≫ τ_r (when ζ ≳ 1). To see this, one can first assume the membranes oriented normal to the orthogonal basis vectors (with otherwise random positions). In this basis, the eigenvalues of the isotropic diffusion tensor correspond to the d = 1 disorder, with the scaling 〈(δD_j)²〉 ~ 1/L(t) due to the Poissonian disorder along each basis direction, effectively bringing us back to the d = 1 case^{10,11,44–46}. The observed ω^1/2 ~ t^−1/2 dispersion attests to the fact that tilting each membrane in a random direction (Fig. 1) does not qualitatively alter this scaling.

Finally, we note that the above single-barrier and coarse-graining pictures are equivalent for our model, i.e. the connection with the return-to-origin probability can be formally extended onto t ≫ τ_D or t ≫ τ_r, by substituting the rest of the system via a “featureless” effective medium with diffusivity D_∞. Indeed, by adopting the lattice calculation⁴⁴ to barriers randomly placed on a line, we observe that the prefactor C₁(ζ) for ζ ≪ 1, and, with it, equation (11), is exact in d = 1. This means that, for ζ ≪ 1, adding independent barrier contributions in a mean-field way (4) is fully compatible with the Poissonian statistics of the disorder for L(t) ≫ ā. For finite ζ, the equivalence between the Poissonian disorder in barrier positions and the return-to-origin probability persists in the RG solution, as it is utilized at every RG step (7). As a result, these two pictures remain equivalent even in the ζ ≫ 1 limit, after the effective-medium substitution τ → τ_r, yielding the scaling behavior (10) for all ζ and t.

Outlook

In this work we have introduced a novel disorder class, the extended disorder, represented by straight permeable membranes which are randomly placed and oriented. A random medium of this type has dispersive diffusion 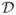(ω) = D_∞ + const · ω^1/2 in any dimensionality d as a result of anomalously strong structural fluctuations. According to the coarse-graining argument, any medium with extended structural blocks (e.g. infinite membranes with finite thickness) falls into this class.

The ω^1/2 dispersion for d > 1 is notably more singular than its well studied ω^d/2 counterparts arising due to short-range disorder^10,11. As the ω^1/2 singularity originates from long-range spatial correlations introduced by the membranes, the dispersive behavior of the form (10) will persist in a variety of samples with random extended restrictions, and will become increasingly important for longer diffusion times when the contributions from short-range disorder components vanish. However, the behavior (10) will eventually terminate if the membranes cease to be extended past their intrinsic correlation radius r_c, i.e. for $t>t_c\sim r_c^2/D(t_c)$, when the structural memory is forgotten, and the short-range dispersion ω^d/2 of a coarse-grained random medium sets in.

Methods

A single barrier in one dimension

The boundary condition (1) can be represented as a local scattering term in the diffusion equation

$${\partial }_t\psi =D_0{\partial }_x^2\psi +{\widehat{V}}_x\psi ,{\widehat{V}}_x\psi \equiv -2D_0\ell {\delta }^{\prime }(x){[{\partial }_x\psi ]}_{x=0}.$$ (12)

Here δ′(x) is the derivative of the Dirac delta-function at the position x = 0 of the membrane.

We focus on the Green’s function 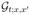of the problem (12), defined by the initial condition 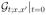= δ(x − x′). As the problem is stationary, we shift to the frequency domain, ∂_t → −iω. In this representation, the Green’s function 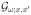is formally an operator inverse

$${\mathcal{G}}_{\omega }={\left[G_{\omega }^{{(0)}^{-1}}-\widehat{V}\right]}^{-1}$$ (13)

where the coordinates x play a role of indices in infinite-dimensional matrices, and the free propagator

$$G_{\omega ,q}^{(0)}=\frac{1}{-i\omega +D_0{q}^2}.$$ (14)

The result of inversion (13) is the Born series

$${\mathcal{G}}_{\omega ;x,x^{\prime }}=G_{\omega ;x-x^{\prime }}^{(0)}+\int {\text{d}x}_1{G}_{\omega ;x-x_1}^{(0)}{\mathbf{V}}_{\omega ;x_1}{G}_{\omega ;x_1-x^{\prime }}^{(0)}$$ (15)

where the exact vertex V (the T-matrix) satisfies the Dyson’s equation, which in the Fourier representation reads

$${\mathbf{V}}_{\omega ;k,k^{\prime }}=V_{k,k^{\prime }}+\int \frac{\text{d}q}{2\pi }{V}_{k,q}{G}_{\omega ,q}^{(0)}{\mathbf{V}}_{\omega ;q,k^{\prime }}.$$ (16)

In our case, the bare vertex is separable,

$$\widehat{V}\to V_{k,k^{\prime }}=2D_0\ell k{k}^{\prime }.$$ (17)

The solution of equation (16), the exact vertex

$${\mathbf{V}}_{\omega ;k,k^{\prime }}=\stackrel{\sim }{\varphi }(\omega )V_{k,k^{\prime }}.$$ (18)

Throughout this work, ω is understood as having an infinitesimal positive imaginary part +i0 due to causality; this way the retarded response functions are analytic in the upper-half-plane of the complex variable ω.

The ω^1/2 singularity in ϕ̃(ω) parallels that of the energy-dependent quantum scattering off a localized potential λδ(x) in one dimension, identifying iω → ε + i0. In the quantum problem, however, energy comes with a negative power ε^−1/2 in the denominator of the corresponding exact vertex λ̃(ε), so that the high-energy scattering corresponds to the Born limit λ̃ → λ, whereas the low-energy amplitude $\stackrel{\sim }{\lambda }\sim \lambda \sqrt{\epsilon }$. For the diffusion, the Born approximation V_ω;k,k′ → V_k,k′ corresponds to the dc limit, whereas at high frequencies ${\mathbf{V}}_{\omega ;k,k^{\prime }}\sim V_{k,k^{\prime }}/\sqrt{\omega }$, as the scope of the p barrier is reduced down to the particles within the diffusion length $\sim \sqrt{D_0/\omega }$.

Return to origin probability and impedance

The Green’s function 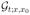describes the density equilibration after injecting a unit packet of random walkers at the point x₀ at t = 0. For x₀ > 0, the excess number of walkers $Q_{x_0}(t)\equiv {\int }_0^{\infty }\text{d}x{\mathcal{G}}_{t;x,x_0}-\frac{1}{2}\simeq \frac{1}{2}{P}_{\text{surv}}(t;x_0+\ell )$ that has not yet leaked out across the barrier, asymptotically follows the survival probability $P_{\text{surv}}(t;{\stackrel{\sim }{x}}_0)\simeq {\stackrel{\sim }{x}}_0/\sqrt{\pi D_{0}t}$ of a particle released at a distance x̃₀ = x₀ + ℓ, to never return to the origin. This relation is valid for $t\gg {\stackrel{\sim }{x}}_0^2/D_0$, such that the resulting density gradient is uniform on either side of the barrier, and relaxes as t^−1/2, following the fraction P_surv(t, x̃₀) of the walkers who have managed to wander around the “biased” side (x > 0) and have not yet encountered the barrier. The finite permeability κ in this picture is substituted by the minimal effective distance $\ell =\sqrt{D_0\tau }$ to the origin, and perfect transmission. The leakage current $-{\stackrel{.}{Q}}_{x_0}\simeq \frac{1}{2}p(t)$, where p(t) = −Ṗ_surv(t; x₀ + ℓ) is the probability density for time intervals t between successive returns to the origin. For x₀ ≪ ℓ, $p(t)\simeq \varphi (t)\simeq \sqrt{\tau /4\pi }{t}^{-3/2}$ (Fig. 3b).

In general, driving the current J₀(ω), e.g. by the source J₀(ω) [δ(x − x₀) − δ(x + x₀)], results in the current J(ω) = ϕ̃(ω) J₀(ω) across the barrier for $\omega \ll D_0/x_0^2$. The “potential drop” −Δψ(ω) ≡ J(ω)/κ = Z_m(ω)J₀(ω) across the barrier is then related to J₀(ω) via the “impedance” Z_m(ω) = ϕ̃(ω)/κ. The excess current in the previous example is equivalent to $J_0(\omega )=\frac{1}{2}$, yielding $J(t)=\frac{1}{2}p(t)$.

Multiple barriers

Averaging over positions of randomly placed barriers with concentration n is done in a standard way^{1,2,10,11,28,32}, by introducing the self-energy part Σ_ω,q,

$$G_{\omega ,q}^{-1}=G_{\omega ,q}^{{(0)}^{-1}}-{\mathrm{\sum }}_{\omega ,q}.$$ (19)

On the mean-field level, we keep in Σ_ω,q only the exact interaction vertex with a single barrier,

$${\mathrm{\sum }}_{\omega ,q}\simeq n{\mathbf{V}}_{\omega ;q,q}.$$ (20)

The mean-field approximation is correct in the first order in barrier concentration n = S/2V for all frequencies, as justified in the section on the origin of the $\sqrt{\omega }$ dispersion.

The self-energy shifts the pole of the propagator G_ω,q, thereby changing the diffusive dynamics due to disorder-averaged interaction with random membranes. Remarkably, on this level there are no higher-order terms in powers of q². This allows us to represent interaction with membranes solely as renormalization of the effective diffusivity D₀ → 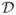(ω), equation (4), which acquires frequency dependence ϕ̃(ω) dictated by that of the vertex (18). The role of 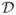(ω) is similar to that played by the dispersive refraction index. Indeed, the relation (20) is analogous to the mean-field relation between the refraction index and the forward scattering amplitude⁴⁹. In our case, the presence of “scatterers” (barriers) introduces the memory kernel (5) into the current-density response.

In higher dimensions d > 1, averaging is performed both over positions of the barrier in the direction n normal to its surface, and over its orientations. This amounts to a frequency shift $i\omega \to i\omega (\mathbf{q})=i\omega -D_0{\mathbf{q}}_{\left|\right|}^2$, Σ_ω,q;n = (S/2V)V_ω(q);qn,qn, with q_|| = q − (qn)n the conserved momentum parallel to the barrier, and subsequent orientational average Σ_ω,q ≡ 〈Σ_ω,q;n〉_n. Substituting the latter self-energy part in equation (19), obtain the result (4) for any d.

Effective medium picture

The RG approach assumes that the boundary condition (1) is adjusted accordingly, D₀ → 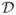(ω)|_L at each RG scale L. Strictly speaking, this is valid only for sufficiently small frequencies $\sqrt{\mathcal{D}(\omega )/\omega }\gg 1/n$, corresponding to diffusing past many membranes, when the system can be treated as a uniform effective medium at each RG step. Luckily, for the opposite case of large frequencies the full result (6) matches the exact $\sqrt{\omega \tau }\gg \zeta$ limit (4), corresponding to the original boundary condition (1). This allows us to keep the frequency simply as a parameter in equation (8).

From this discussion one expects that the agreement of the RG result (6) with the simulations to be the worst in the intermediate regime, when $\sqrt{\mathcal{D}/\omega }\sim 1/n$, equivalent to t ~ τ_r. Fig. 2a shows that the discrepancy between the RG result and the simulations is indeed highest around t ~ τ_r and remains under 25%. The agreement improves for t ≫ τ_r to within 10% even for the largest ζ.

We note that in d = 1, the RG limit C₁(∞) overestimates the exact result for the one-dimensional lattice model^11,44–46, $\sqrt{2/\pi }$, by the factor of two. We also observe this in the one-dimensional simulations (not shown). There are no exact results for this problem for d > 1. As it is often true with mean-field-like description, the accuracy of our solution is likely to improve for increasing d. This is consistent with the notably better agreement (Fig. 2c) of the theoretically obtained coefficient C₂(ζ) with that determined from the d = 2 simulations.

Monte Carlo dynamics was realized on a square patch with periodic boundary conditions, embedded with randomly placed and oriented membranes, cf. Fig. 1, of nearly identical S/V in each disorder realization. For every ζ value in Fig. 2, the diffusion coefficient D(t) was calculated by averaging the displacement variance 〈x²〉, cf. equation (3), over a total of 4 × 10⁵ random walkers evenly split between 40 disorder realizations, with an average of 385 membranes per patch. The trajectory of each random walker was a sequence of moves in a randomly chosen direction over a distance $\text{d}r=\sqrt{4D_0\text{d}t}$ during a time step dt, with the total diffusion time t up to 100 τ_r, corresponding to a maximum of 4 × 10⁶ time steps per walker. Transmission across a membrane occurred with probability P ∝ κdr/D₀ ≪ 1, cf. refs. ^30,50. The disorder strength ζ was varied by changing κ. The time step dt for each ζ was chosen so that P < 0.007, and the ratio dr/ā = Sdr/4V < 0.1. We calibrated our results for a quasi-one-dimensional disorder (random parallel membranes), which reproduced the exact limit (2) with about 1% accuracy. The random walk simulator was developed in C++. Simulations were performed on the NYU General Cluster. With an average of 200 CPU cores used simultaneously, all simulations took a total of about 100 hours.