Abstract
The ultimate goal of quantitative ultrasound (QUS) imaging methods based on backscatter coefficient (BSC) estimates is to obtain system-independent structural information about samples. In the current study, three BSC estimation methods were compared and evaluated using the same backscattered pressure datasets in order to assess their consistency. BSC estimates were obtained from two phantoms with embedded glass spheres and compared to theoretical BSCs calculated using size distributions estimated using optical microscopy. Effective scatterer diameter and concentration estimates of the glass spheres were also obtained from the estimated BSCs. One estimation method needed to be compensated by more than an order of magnitude in amplitude in order to produce BSCs comparable to the other two methods. All calibration methods introduced different frequency-dependent effects, which could have noticeable effects on the bias of QUS estimates derived from experimental BSCs. Although in most cases the experimental QUS estimates obtained with all three methods were observed to differ by less than 10%, larger differences are expected depending on both the pressure focusing gain of the transducer (proportional to the ratio of the square of the aperture radius to the product of the wavelength and focal length) and ka range used in the estimation.
INTRODUCTION
The backscatter coefficient (BSC) is a fundamental quantity that contains information about material microstructure. Extraction of microstructural properties through analysis of BSCs has been extensively studied in the past for tissue characterization applications in biomedical ultrasound.1, 2, 3, 4 The ultimate goal of quantitative ultrasound (QUS) imaging methods based on BSC estimates is to obtain meaningful, system-independent information about the analyzed tissues. Therefore, ideally any instrumentation dependence should be removed when estimating BSCs.
Many practical implementation aspects, however, may have an impact on the estimation of BSCs from tissues. Several transducer geometries have been studied in the past including unfocused5 and focused6, 7 single-element transducers, as well as array systems.8, 9 Even for a fixed experimental system, several spectrum calibration methods have been proposed resulting in several methodologies for BSC estimation. Two of the most common ways of compensating for system-dependent effects are the substitution10, 11, 12 and reference phantom13, 14, 15 methods. Finally, several methods for compensating attenuation effects have also been proposed.16, 17
Given the availability of several methods for BSC estimation, it becomes of high importance to evaluate the feasibility of obtaining accurate and consistent BSC estimates. To that effect, inter-laboratory comparisons of ultrasonic BSC estimates have been performed in the past18, 19 but only a limited agreement among BSC estimates obtained at different laboratories was observed. The goal of the current study is to evaluate three different BSC estimation methods using the same experimental datasets. This approach allows eliminating experimental discrepancies in order to assess the consistency of these BSC estimation methods and determine under what conditions a particular method may be preferred. The three approaches for obtaining BSC estimates are representative of the methods commonly used in the literature. All measurements were obtained using focused transducers having different center frequencies and focal numbers for the analysis of two well-characterized physical phantoms. Estimated BSCs were compared to the theoretical BSCs obtained given the knowledge of the scatterer distributions in both phantoms.
METHODS
BSC estimation methods
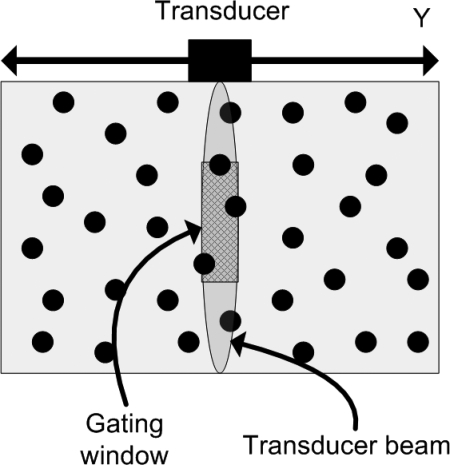
In this section, details of BSC estimation using a planar reflector to compensate for the imaging transducer characteristics will be provided. BSCs are estimated from pulse-echo data corresponding to regions of interest (ROIs) within the sample under study. An acoustic aperture receives pulse-echo pressure waveforms sm(t) when located at several positions along the Y axis, as shown in Fig. 1. The backscattered data is gated between depths (F − Δz/2) and (F + Δz/2) using a rectangular window, where F is the transducer focal length and Δz is the gate length. BSC estimates from a ROI require the calculation of the normalized power spectrum defined as
| (1) |
where 〈|Sm(k)|2〉 is the average of the power spectra of several adjacent, gated scan lines sm(t), H(k) is a function that compensates for attenuation effects, and S0(k) is the Fourier transform of a reference waveform. The normalized power spectrum can be related to BSCs after properly compensating for the transducer geometry.
Figure 1.
(Color online) Schematic of the configuration for backscatter measurements from a phantom with randomly positioned scatterers.
Three different estimation methods have been studied in this work and are summarized below for completion. All methods assume S0(k) is obtained by measuring the reflection of ultrasound from a planar reflector located at the center of the ROI and perpendicular to the transducer axis. Furthermore, the methods assume that circular, single-element focused transducers are used to perform the measurements with the center of the ROI located at the acoustic focus of the transducer.
Estimation method 1
The first estimation method used in this study was derived by Insana et al.11 The volumetric integral wave equation derived under the first order Born approximation was used to estimate the power spectrum of both weakly scattering random media (Ref. 11, Secs. 2A, 2B) and the planar reflector (Ref. 11, Sec. 2 C). BSC estimates can be estimated using [Ref. 11, Eqs. (34), (35), and (41)]
| (2) |
where A0 = πR2 is the aperture area of the transducer of radius R and γ is the pressure reflection coefficient of the planar reflector. The expressions in Ref. 11 were derived assuming a Hanning window to gate the radiofrequency data. Different windows can be used by updating the value of Bg(0) in Ref. 11, Eq. (40) which is equal to 0.375Δz and Δz for Hanning and rectangular windows, respectively. Therefore, BSCs can be estimated using a rectangular window as
| (3) |
A notation inconsistency in the development of can be tracked back to Ref. 11, Sec. 2 C, where the corresponding equations for spectral calibration were derived. In particular, the source function corresponding to a planar reflector was defined as γ(r0) = γ′h(z0 – zc) [Ref. 11, Eq. (32)] with h(z0 – zc) a step function located at the center of the gate and γ′ defined to be the planar reflection coefficient by the authors. However, if κ′ = κ0(l + δκ) and ρ′ = ρ′(1 + δρ) and under the weak scattering assumption (i.e., δκ, δρ ≪ 1) used by the authors
| (4) |
where Z0 and Z = (Z0 + ΔZ) are the characteristic acoustic impedances of the background and planar reflector, respectively. Therefore, γ′ is equal to four times the pressure reflection coefficient γ of the planar reflector and not to γ as stated in Ref. 11. As a result, the expression in Eq. 3 is off by a factor of 16. A corrected version of the BSC estimation method is given by
| (5) |
where Gp = (kR2/2F) is the pressure focusing gain of the transducer20, 21 and D1(·) = 1 has been defined for convenience when comparing the studied BSC estimation methods. It must be stressed that Eq. 5 is not equal to the final expression given in Ref. 11, but rather an updated expression that corrects a magnitude inconsistency in the BSC estimation derivation.
Estimation method 2
The second estimation method was derived by Chen et al.12 The authors determined the theoretical reference power spectrum using the mirror image method assuming a perfectly reflecting plate.22 The resulting expression for |S0(k)|2 was scaled by the power reflection coefficient of the plate to account for its finite reflectivity. BSCs can be estimated as [Ref. 12, Eqs. (31), (54), and (57)]
| (6) |
where Jm(·) is the mth order Bessel function.
Estimation method 3
The third estimation method was developed by Ueda and Ozawa.10 The reference power spectrum was derived in Ref. 10, Sec. VI using the boundary integral wave equation under the first order Born approximation [Ref. 10, Eq. 4]. An approximate closed form solution for estimating BSCs assuming a Gaussian profile for the transducer radiation pattern was proposed and developed by the authors and is given by [Ref. 10, Eq. (73)]
| (7) |
| (8) |
The BSC for a circular focused transducer can be calculated as [Ref. 10, Eq. (74)]
| (9) |
where L(kR, kF) is a frequency-dependent correction factor and . The procedure for numerically calculating L(kR, kF) was outlined in Ref. 10, Sec. IV.
Experimental methods
Experimental setup
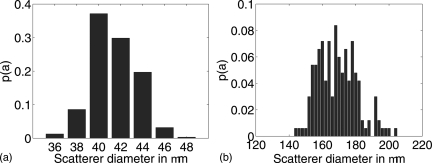
In order to evaluate the reported estimation methods, experimental BSC estimates were obtained from two agar phantoms with glass bead inclusions.23 The first phantom, labeled “41 μm phantom,” contained 47 glass spheres∕mm3 ranging in diameter from 36 to 48 μm. The second phantom, labeled “150–180 μm phantom,” contained 20 g∕l of glass spheres (approximately 3.2 glass spheres∕mm3) ranging in diameter from 144 to 204 μm. The scatterer size distributions of the glass spheres for both phantoms were estimated from optical microscopy images, and the estimated scatterer size probability distribution functions (PDFs) p(a), i.e., the probability that the spherical inclusion radius takes the value a, for both phantoms are reported in Fig. 2. The corresponding attenuation coefficients were estimated with through-transmission techniques and approximated with a third- and fifth-order polynomial for the 41 μm and 150–180 μm phantoms, respectively. Ultrasound was transmitted into the phantoms through a layer of thin plastic film. The transmission coefficient through the film was compensated using the method outlined in Ref. 19.
Figure 2.
(Color online) Estimated scatterer size probability distribution functions for the 41 μm (left) and 150–180 μm (right) phantoms.
It has been previously reported in the literature24 that using a reference from a planar reflector at a single location to estimate S0(k) may affect the estimated BSCs especially when using tightly focused transducers and long gate lengths. To reduce these effects, in this work the reference spectrum S0(k) was estimated by averaging the power spectra obtained at several depths between (F − Δz/2) and (F + Δz/2) from a planar Plexiglas® reflector (γ ≈ 0.37).
BSC estimates were obtained using all three estimation methods described in Sec. 2A. The phantoms were raster scanned in one plane over a 4 cm by 4 cm area at 2 mm steps for a total of 441 scan locations. Attenuation compensation was performed using Ref. 17, Eq. 16. The properties of the transducers used for the experiments are listed in Table TABLE I.. For all transducers, the radio frequency data was gated using a gate length Δz of 18 wavelengths at the nominal center frequency of the transducer.
Table 1.
Properties of the transducers used for the experimental BSC measurements. In the first column, f0 represents nominal center frequency of the transducer. Gp was calculated using the experimentally estimated focal distance F.
| f0 (MHz) | f# | Diameter | Analysis bandwidth (MHz) | Gp range |
|---|---|---|---|---|
| 2.25 | 2.7 | 0.75 in. (19.05 mm) | [1.2–3.4] | [3.6–9.9] |
| 5 | 3 | 0.75 in. (19.05 mm) | [2.3–7.3] | [7.7–24.5] |
| 7.5 | 4 | 0.75 in. (19.05 mm) | [3.1–11.5] | [8.0–29.4] |
| 10 | 4 | 0.5 in. (12.7 mm) | [5.7–16.1] | [8.9–25.3] |
| 10 | 2 | 1 in. (25.4 mm) | [4.3–14.4] | [28.2–95.0] |
| 13 | 3 | 0.5 in. (12.7 mm) | [7.0–19.1] | [15.8–43.2] |
| 15 | 2 | 0.5 in. (12.7 mm) | [7.1–20.1] | [23.4–66.9] |
| 20 | 4 | 0.25 in. (6.35 mm) | [8.6–27.0] | [6.9–21.9] |
| 20 | 3 | 0.25 in. (6.35 mm) | [8.9–28.6] | [8.9–28.6] |
The theoretical BSC corresponding to the experimental phantoms were calculated assuming the analyzed media consisted of randomly located spherical scatterers embedded in an otherwise homogeneous background at a concentration of β scatterers per unit of volume. Neglecting coherent and multiple scattering effects, the theoretical BSC η(k)th can be expressed as
| (10) |
where σ(k, a) is the backscattering cross-section of an individual scatterer. In this work, σ(k, a) was calculated using the analytic solution of the scattering of a plane wave by a solid sphere.25, 26 The values of density, longitudinal sound speed, and Poisson’s ratio of the glass spheres were assumed to be equal to 2.38 g∕ml, 5.57 mm∕μs, and 0.21, respectively.11
Performance assessment
In order to experimentally assess the performance of the different BSC estimation methods, QUS estimates were obtained from the estimated BSCs. Effective scatterer diameter (ESD) estimates were obtained by solving the optimization problem11, 27
| (11) |
| (12) |
where is the mean value of X(k, a) within the analysis wave number bandwidth ki ∈ [kmin, kmax]. Other methods for ESD estimation such as least mean squares (LMS)15 have also been studied in the literature. However, no significant difference was observed when using LMS to obtain ESD estimates (results not shown in this manuscript). Once an estimate of the ESD has been obtained, the effective scatterer concentration (ESC) can be estimated as
| (13) |
The fit between the estimated η(k) and theoretical ηth(k) BSCs corresponding to both phantoms was also quantified. For consistency, the fit was quantified using the first- and second-order moments of the error function in Eq. 12, i.e.,
| (14) |
| (15) |
The quantities Errμ and Errσ are measures of the amplitude and frequency dependence agreements, respectively, between the estimated η(k) and theoretical ηth(k) BSCs.
RESULTS
Frequency-dependent effects of the estimation methods
For all three BSC estimation methods, it was independently demonstrated that only the amplitude, and not the frequency dependence, of 〈|Sm(k)|2〉 depended on the transducer geometry when measurements were conducted near the transducer focus.10, 11, 12 However, the frequency dependence of |S0(k)|2 varies depending on which estimation method is used. Further, it follows from Eqs. 5, 6, 7, and 9 that the studied BSC estimation methods can be related to each other using the relationships
| (16) |
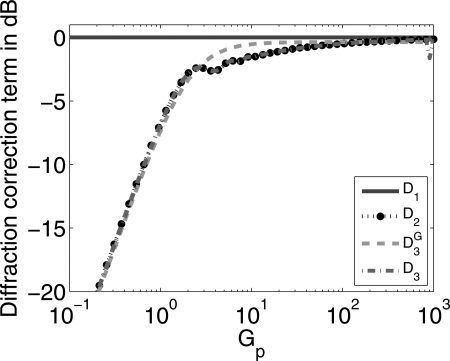
All BSC estimation methods were compared by plotting the diffraction correction factors D1(Gp), D2(GP), D3(kR, kF), and , which relate the estimated BSCs as given by Eq. 16. Both D2(GP) and depend exclusively on the pressure focal gain Gp. In contrast, D3(kR, kF) does not depend on Gp but rather on kR and kF separately. Therefore, nine different D3(kR, kF) curves were computed and plotted, each one corresponding to the geometry of all nine transducers listed in Table TABLE I.. The results are shown in Fig. 3 for Gpvalues between 10−1 and 103.
Figure 3.
(Color online) Comparison of the frequency-dependent calibration terms in the denominator of Eq. 16. The curves correspond to η1 (solid line), η2 (dotted line), (dashed line), η3 and (nine dash-dotted lines).
Observation of Fig. 3 indicates that all nine D3(kR, kF) curves were almost perfectly overlapping and virtually indistinguishable from each other, which suggests L(kR, kF) is mainly dependent on Gp for moderate to large kR values. This observation is consistent with numerical evaluations presented by Ueda and Ozawa in Ref. 10, Fig. 5. Further, all D3(GP) curves were in excellent agreement with the curve corresponding to for all Gp values. The curve corresponding to had good agreement with D2(GP) and D3(kR, kF) for low Gp values and with D1(Gp) for large Gp values. The curves corresponding to D2(GP), D3(kR, kF), and agreed with G1(Gp) to within 1 dB for Gp > 25, Gp > 25, and Gp > 5, respectively.
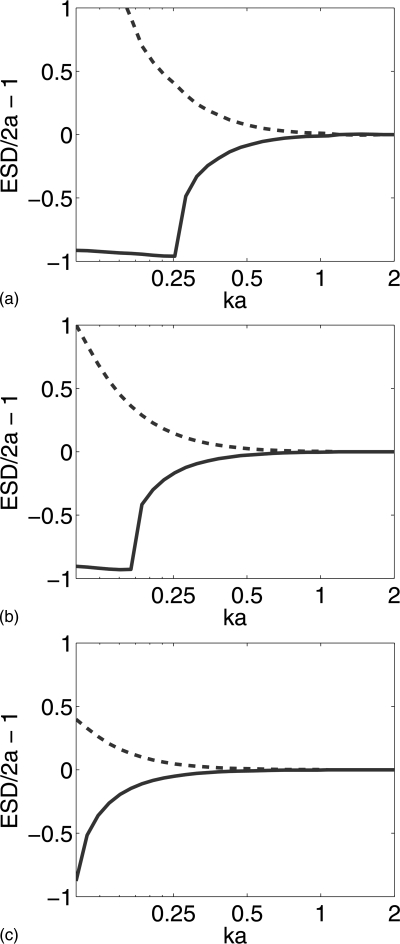
Figure 5.
(Color online) Fractional error (ESD/2a – 1) when estimating ESDs as a function of ka when the input η to the estimator is set proportional to ηth × D2(GP) (solid lines) and ηth/D2(Gp) (dashed lines). The Gp/ka ratio was set to 50 (top), 500 (center), and 5000 (bottom).
BSC and QUS estimates
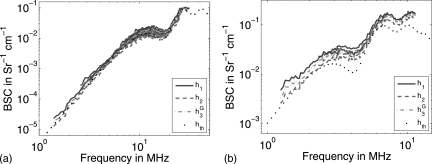
A total of 21 experimental BSC estimates per transducer per phantom were obtained using all estimation methods by using backscattered data from 21 independent scan lines per BSC estimate. The average BSCs obtained using the estimation methods from Eqs. 5, 6, and 7 together with the theoretical BSC curves expected from using Eq. 10 are shown in Fig. 4 for both experimental phantoms. The BSCs estimated using Eq. 9 were not plotted because of their high correlation with the BSCs obtained using η2.
Figure 4.
(Color online) BSC estimates from the 41 μm (left) and 150–180 μm (right) phantoms estimated using methods 1 (solid lines), 2 (dashed lines), and 3 (dash-dotted lines) together with the theoretical BSC derived from the scatterer size PDFs reported in Fig. 2 (dotted lines).
All methods produced BSC estimates that had similar agreement with the theoretical BSCs (also plotted). The errors between the experimentally estimated and theoretical BSCs are reported in Tables TABLE II. and TABLE III. for the 41 μm and 150–180 μm phantoms, respectively. As expected from the results in Sec. 3A, the Errμ values corresponding to different methods are close to each other, i.e., less than 2 dB error difference among all estimation methods for a fixed phantom and transducer combination. Further, the difference in Errμ values for a fixed phantom and transducer combination is reduced when using transducers with higher Gp values.
Table 2.
Experimental BSC estimation errors when analyzing the 41 μm phantom.
| Transducer | Errσ | Errμ | ||||||
|---|---|---|---|---|---|---|---|---|
| η1 | η2 | η3 | η1 | η2 | η3 | |||
| 2.25 MHz, f∕2.7 | 1.34 ± 0.16 | −0.51 ± 0.16 | 0.59 ± 0.16 | −0.50 ± 0.16 | 1.04 ± 0.09 | 1.04 ± 0.09 | 1.04 ± 0.09 | 1.05 ± 0.09 |
| 5 MHz, f∕3 | 0.60 ± 0.16 | −0.66 ± 0.16 | 0.15 ± 0.16 | −0.65 ± 0.16 | 1.05 ± 0.12 | 1.07 ± 0.11 | 1.05 ± 0.12 | 1.07 ± 0.11 |
| 7.5 MHz, f∕4 | 0.84 ± 0.20 | −0.35 ± 0.20 | 0.40 ± 0.20 | −0.34 ± 0.20 | 0.95 ± 0.08 | 0.97 ± 0.07 | 0.95 ± 0.07 | 0.97 ± 0.07 |
| 10 MHz, f∕4 | 0.18 ± 0.17 | −1.04 ± 0.17 | −0.26 ± 0.17 | −1.04 ± 0.17 | 0.97 ± 0.11 | 0.97 ± 0.11 | 0.97 ± 0.11 | 0.97 ± 0.11 |
| 10 MHz, f∕2 | −0.06 ± 0.27 | −0.71 ± 0.27 | −0.43 ± 0.27 | −0.71 ± 0.27 | 1.10 ± 0.11 | 1.05 ± 0.11 | 1.10 ± 0.11 | 1.05 ± 0.11 |
| 13 MHz, f∕3 | 1.17 ± 0.25 | 0.25 ± 0.25 | 0.79 ± 0.25 | 0.26 ± 0.25 | 0.98 ± 0.09 | 0.98 ± 0.09 | 0.97 ± 0.09 | 0.98 ± 0.09 |
| 15 MHz, f∕2 | 1.37 ± 0.34 | 0.60 ± 0.34 | 0.99 ± 0.34 | 0.61 ± 0.34 | 1.05 ± 0.14 | 1.01 ± 0.14 | 1.05 ± 0.14 | 1.01 ± 0.14 |
| 20 MHz, f∕4 | 1.53 ± 0.28 | 0.13 ± 0.28 | 1.02 ± 0.28 | 0.14 ± 0.28 | 1.30 ± 0.22 | 1.28 ± 0.20 | 1.30 ± 0.22 | 1.28 ± 0.20 |
| 20 MHz, f∕3 | 0.62 ± 0.58 | −0.41 ± 0.58 | 0.22 ± 0.58 | −0.41 ± 0.58 | 1.54 ± 0.22 | 1.47 ± 0.21 | 1.53 ± 0.22 | 1.47 ± 0.21 |
Table 3.
Experimental BSC estimation errors when analyzing the 150–180 μm phantom.
| Transducer | Errμ | Errσ | ||||||
|---|---|---|---|---|---|---|---|---|
| η1 | η2 | η3 | η1 | η2 | η3 | |||
| 2.25 MHz, f∕2.7 | 2.54 ± 0.19 | 0.63 ± 0.19 | 1.74 ± 0.19 | 0.63 ± 0.19 | 1.13 ± 0.14 | 1.13 ± 0.14 | 1.12 ± 0.14 | 1.13 ± 0.14 |
| 5 MHz, f∕3 | 2.24 ± 0.28 | 0.96 ± 0.28 | 1.79 ± 0.28 | 0.99 ± 0.28 | 1.31 ± 0.17 | 1.26 ± 0.16 | 1.30 ± 0.17 | 1.26 ± 0.16 |
| 7.5 MHz, f∕4 | 2.71 ± 0.31 | 1.53 ± 0.31 | 2.27 ± 0.31 | 1.53 ± 0.20 | 1.27 ± 0.16 | 1.20 ± 0.14 | 1.24 ± 0.15 | 1.20 ± 0.14 |
Mean and standard deviations of ESD and ESC estimates obtained from all 21 estimated BSCs per transducer are reported in Table TABLE IV. for the 41 μm phantom and Table TABLE V. for the 150–180 μm phantom. In general, a larger difference in mean QUS values corresponding to different estimation methods was observed for transducer and phantom combinations with lower ka values. The most dramatic difference was observed when analyzing the 41 μm phantom with the 2.25, f∕2.7 transducer.
Table 4.
ESD and ESC estimates derived from experimental data corresponding to the 41 μm glass bead phantom, ka and Gp were calculated using the transducer nominal center frequency, with ka corresponding to a scatterer diameter of 41 μm.
| Transducer | ka | Gp | ESD (μm) | ESC (scatt./mm3) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| η1 | η2 | η3 | η1 | η2 | η3 | |||||
| 2.25 MHz, f∕2.7 | 0.19 | 6.6 | 49.1 ± 19.1 | 15.6 ± 19.8 | 21.2 ± 22.81 | 15.4 ± 19.6 | (2.4 ± 10.7) × l08 | (1.3 ± 1.5) × l09 | (7.2 ± 12.2) × l08 | (1.3 ± 1.5) × l09 |
| 5 MHz, f∕3 | 0.43 | 16.8 | 54.8 ± 3.6 | 50.7 ± 4.0 | 53.8 ± 3.7 | 50.8 ± 4.0 | 16.7 ± 5.7 | 19.3 ± 8.1 | 16.7 ± 6.1 | 19.3 ± 8.2 |
| 7.5 MHz, f∕4 | 0.64 | 19.2 | 42.6 ± 1.4 | 40.4 ± 1.5 | 42.1 ± 1.5 | 40.4 ± 1.5 | 52.4 ± 7.7 | 51.3 ± 8.8 | 50.1 ± 7.6 | 51.3 ± 8.8 |
| 10 MHz, f∕4 | 0.86 | 15.7 | 41.6 ± 0.8 | 40.8 ± 0.8 | 41.4 ± 0.8 | 40.8 ± 0.8 | 48.5 ± 3.6 | 39.0 ± 3.0 | 44.5 ± 3.3 | 39.0 ± 3.0 |
| 10 MHz, f∕2 | 0.86 | 65.9 | 44.9 ± 1.0 | 44.4 ± 1.0 | 44.9 ± 1.1 | 44.4 ± 1.0 | 36.2 ± 3.9 | 32.5 ± 3.6 | 33.3 ± 3.6 | 32.6 ± 3.6 |
| 13 MHz, f∕3 | 1.12 | 29.4 | 41.7 ± 0.9 | 41.4 ± 1.3 | 41.7 ± 1.0 | 41.4 ± 1.3 | 61.9 ± 5.7 | 51.2 ± 5.4 | 56.8 ± 5.3 | 51.2 ± 5.4 |
| 15 MHz, f∕2 | 1.29 | 49.8 | 41.4 ± 0.6 | 41.4 ± 0.6 | 41.4 ± 0.6 | 41.4 ± 0.6 | 66.9 ± 6.0 | 56.4 ± 5.1 | 61.4 ± 5.5 | 56.4 ± 5.1 |
| 20 MHz, f∕4 | 1.71 | 16.2 | 39.2 ± 0.9 | 39.6 ± 0.9 | 39.3 ± 0.9 | 39.6 ± 0.9 | 79.4 ± 8.1 | 57.5 ± 5.9 | 70.9 ± 7.2 | 57.5 ± 5.9 |
| 20 MHz, f∕3 | 1.71 | 20.0 | 38.0 ± 1.0 | 38.3 ± 1.0 | 38.0 ± 1.0 | 38.3 ± 1.0 | 76.1 ± 9.8 | 58.8 ± 7.7 | 69.1 ± 8.8 | 58.9 ± 7.7 |
Table 5.
ESD and ESC estimates derived from experimental data corresponding to the 150–180 μm glass bead phantom. ka and Gp were calculated using the transducer nominal center frequency, with ka corresponding to a scatterer diameter of 165 μm.
| Transducer | ka | Gp | ESD (μm) | ESC (scatt./mm3) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| η1 | η2 | η3 | η1 | η2 | η3 | |||||
| 2.25 MHz, f∕2.7 | 0.78 | 6.6 | 169.4 ± 4.4 | 161.2 ± 4.8 | 163.3 ± 4.7 | 161.1 ± 4.8 | 5.9 ± 0.6 | 4.6 ± 0.6 | 5.7 ± 0.7 | 4.6 ± 0.6 |
| 5 MHz, f∕3 | 1.73 | 16.8 | 163.5 ± 5.9 | 165.3 ± 5.5 | 164.0 ± 5.9 | 165.3 ± 5.5 | 5.4 ± 0.8 | 4.0 ± 0.6 | 4.8 ± 0.7 | 4.0 ± 0.6 |
| 7.5 MHz, f∕4 | 2.59 | 19.2 | 131.8 ± 49.9 | 135.8 ± 48.9 | 131.1 ± 50.7 | 135.8 ± 48.9 | 88.7 ± 121.3 | 63.8 ± 94.7 | 84.8 ± 114.2 | 63.9 ± 94.9 |
DISCUSSION
Three representative methods for BSC estimation have been studied in this work. It should be mentioned that other approaches presented in the literature can be related to the methods evaluated here. For example, D’Astous and Foster28 presented a estimation method based on geometrical considerations that resulted in expressions similar to those provided by Insana et al. in Ref. 11. Another study in BSC estimation was presented by Madsen et al.29 Analytic expressions for BSC calculation were provided, but such expressions depended on integrals that required numerical evaluation. The formulation by Madsen et al. was shown to be equivalent to η2 by Chen et al.12 The advantage of using the results from Ref. 12 is the availability of explicit expressions for normalizing BSC estimates.
All studied estimation methods have an effect on the magnitude and frequency dependence of the estimated BSCs. Both effects are discussed below.
BSC amplitude effects
All estimation methods studied in this work can be compared in the large Gp limit, for which it holds that
The first limit can be derived by using the approximate expression D2(k) → exp[−(2∕π)(Gp∕π)−1∕2] valid for large Gp values given in Ref. 12, Eq. (58). The second limit follows directly from the expression in Eq. 8. The third limit was validated through numerical simulations. Therefore, the asymptotic values of the relationships in Eq. 16 are given by
| (17) |
The expressions given in Eq. 17 indicate an excellent agreement in BSC amplitude for all studied BSC estimation methods. Methods η1, η2, and η3 have a perfect agreement in the Gp → ∞ limit, and in the asymptotically large Gp limit these methods differ from by less than 10%. This analysis is consistent with the experimental values of Errμ reported in Tables 2, TABLE III. where differences of less than 2 dB in Errμ among different estimation methods were observed. Further, the Errμ absolute values were less than 1.6 and 2.8 dB for the 41 μm and 150–180 μm phantoms, respectively. The small error indicates a very good correspondence between the estimated and expected BSC magnitudes. The slightly larger magnitude disagreement for the 150–180 μm phantom may be due to a less accurate assumed value for the scatterer concentration.
It should be noted that η1 agreed with the other BSC estimation methods and experimental measurements only after the magnitude correction described in Sec. 2A1 was applied. Therefore, the use of the expressions provided in Ref. 11 is expected to result in a BSC magnitude underestimation by slightly more than an order of magnitude.
As for the validity of the η1 magnitude correction presented in Sec. 2A1, it should be acknowledged that the approximations in Eq. 4 only hold for weakly scattering media and may appear inappropriate to characterize the reflection off a planar reflector with high impedance mismatch from water, e.g., a Plexiglas reflector. However, the scattering by a planar reflector in the original work presented in Ref. 11, Sec. 2 C was derived under the first order Born approximation for which weakly scattering media is assumed, and therefore the correction factor is self-consistent. Further, excellent agreement was found between methods η2 and η3 although expressions for the reflection off a planar reflector were derived by Chen et al. in Ref. 12 by assuming the plate to be a perfect acoustic reflector and Ueda and Ozawa in Ref. 10 by invoking first order Born scattering. Therefore, it appears reasonable to assume expressions for reflection off a plate derived under limiting scattering conditions (such as weak scattering conditions) can be generalized to materials of finite reflectivity by scaling the resulting expressions by the reflectivity γ at the plate surface.
Finally, other estimation methods available in the literature also suffer from discrepancies in BSC magnitude. For example, D’Astous and Foster proposed in Ref. 28, Eq. 6 to estimate BSCs as
| (18) |
where θt is the half angle of the transducer subtended at its focus. If a small angle approximation is performed, and therefore
| (19) |
Therefore, this estimation method has the same frequency dependence of η1, but its amplitude for large Gp is off by roughly a factor of 2.2 when compared to methods η1, η2, and η3.
Frequency-dependent effects
The diffraction correction curves presented in Fig. 3 illustrate the different frequency dependencies of all studied estimation methods, which arise from the different assumptions involved in the derivation of the corresponding BSC estimation expressions.
When deriving η2, and following the seminal formulation by O’Neil,30 the incident field was assumed proportional to ∫∫Sexp(−jks)/s dS, where s is the distance between a surface element dS on the surface S of the transducer and the observation point. When deriving η3 the incident field was assumed to be proportional to jinc(kR sin θ)exp(−jkr), where jinc(x) = 2J1(x)/x with J1(·) the first order Bessel function, and r is the radial coordinate of the observation point. As shown by O’Neil in Ref. 30 both expressions are in good agreement in the focal plane of the transducer. Therefore, the use of almost equivalent models for both amplitude and phase of the incident field resulted in very good agreement between η2 and η3.
Although Insana et al. used the same incident field model as Ueda and Osawa, the phase front was assumed to be plane instead of spherical in the evaluation of |S0(k)|2 (see Ref. 11, Sec. 2 C). The use of a different expression for the incident field phase caused frequency-dependent discrepancies between η1 and η2, η3. For large Gp values, however, these three methods become essentially equivalent, i.e., frequency-dependent effects in η2, η3 become weak. For a focused transducer, the −6-dB angular beamwidth at the transducer focus can be approximated as Δθ ≈ arctan(λf#/F) = arctan(π/4Gp), where f# is the transducer focal number. Therefore, the incident field can be safely approximated as a local plane wave as Gp → ∞, which is the cause for the asymptotic agreement among η1, η2, and η3.
As for , although it was derived assuming a spherical wave front the use of a different amplitude function (i.e., a Gaussian function instead of a jinc function) resulted in frequency-dependent discrepancies with η2 and η3. Therefore, both the amplitude and phase modeling of the assumed incident field have an effect on the frequency-dependent behavior of BSC estimation methods.
The results presented in this work suggest η1 is significantly different than η2, η3, and at very low Gp values, i.e., Gp < 1. This is due to the fact that the local plane wave approximation used in η1 breaks down in the low Gp limit. In practice, however, these effects may not be observed. It has already been discussed in the literature that energy focusing cannot occur in the far field of the equivalent flat transducer, i.e, for R2/λF < 1 or equivalently Gp/π < 1.31 Therefore, transducers with Gp < π (the region where most of the significant differences in the curves presented in Fig. 3 were observed) will most likely not be used in experimental practice.
The experimental results suggest all methods are capable of producing similar frequency dependencies of BSC estimates, as suggested by the Errσ values in Tables 2, TABLE III.. The experimental Errσ corresponding to different estimation methods had mean absolute and relative values that differed among each other in all cases by less that 0.1 dB and 6%, respectively.
Implications for QUS estimation
Both amplitude and frequency-dependent effects introduced by BSC estimation methods will affect QUS estimates. Amplitude differences will only change estimates of ESC. It was observed in this study that η1, η2, η3, and were successful in approximately reproducing the expected BSC magnitude from two well-characterized experimental phantoms. Other methods reported in the literature such as in Eq. 3 and ηDaf in Eq. 19 had amplitude disagreements that would result in BSC amplitude under-determination factors of 12 and 3.4 dB, respectively. Therefore, different estimation methods reported in the literature can potentially introduce significant BSC amplitude variations.
Frequency-dependent effects are expected to affect primarily ESD estimates, although it is worth remarking that errors in ESD will ultimately propagate to ESC estimates through the use of Eq. 13. Two adimensional, frequency-dependent parameters are expected to affect the mean ESD estimate values.
-
(1)
Gp: Because different BSC estimation methods introduce different frequency-dependent corrections which depend on Gp, mean ESD estimates are expected in principle to change depending on the chosen BSC estimation method. However, the Gp range of the transducers should determine the extent of the spread of mean ESD estimates. This is expected because the results in Sec. 3A suggest all estimation methods become nearly equivalent when Gp → ∞ but are significantly different when Gp < π.
-
(2)
ka: The accuracy and precision of ESD estimates can be compromised depending on the ka range used for BSC analysis. In particular, for low ka values the dependence of BSC on the actual scatterer size becomes weak which degrades the precision of ESD estimates.32 On the other hand, for large ka values the scattering model becomes too complex which may cause convergence of the ESD estimator to inaccurate solutions due to convergence to local minima.6 It has been proposed that ka values satisfying 0.5 < ka < 1.2 provide good ESD estimates when analyzing glass bead phantoms.11
Therefore, all estimation methods are only expected to provide similar QUS estimates under certain circumstances. Simulations were conducted to explore the dependence of ESD estimates on ka and Gp values. The theoretical BSC, ηth, corresponding to a single glass sphere was calculated for 0.1 < ka < 2. Two modified BSCs were set proportional to ηth × D2(GP) and ηth/D2(Gp). These two curves represent the hypothesis that η1 is the correct estimation method but either η2 or η3 [because D2(GP) is almost equivalent to D3(kR, kF)] are used to estimate BSCs and vice versa. Portions of these modified BSCs with different center frequencies and 100% fractional bandwidths were used as input for the estimator in Sec. 2B2. The fractional error (ESD/2a – 1) when obtaining ESD estimates using the modified BSCs are shown in Fig. 5 for the cases where Gp/ka = 50, Gp/ka = 500, and Gp/ka = 5000. It can be observed that the ESD estimation error spread was indeed dependent on both ka and Gp. The variation induced by the ka range was the most significant, but the results predict the ESD estimation error spread should be significant only when approaching Rayleigh scattering, i.e., ka < 0.5. Although the results also confirm the spread is reduced for increasing Gp, reducing the ESD estimation error spread below ±16% for ka > 0.25 required significantly large Gp values (i.e., Gp/ka ratios of around 500).
The experimental results validated the dependence of the spread of ESD mean estimates on ka range. The results from Table TABLE IV. obtained from the 41 μm phantom suggest that the differences in ESD mean values introduced by the choice of estimation method became significant when low ka values (i.e., ka < 0.5) were used. For example, the absolute spread was 33.7 μm (15.4 μm for η3 vs 49.1 μm for η1) when using the 2.25 MHz, f∕2.7 transducer. This corresponds to a relative spread of 82% when compared to the assumed mean particle diameter of 41 μm. Similarly, for the 5 MHz, f∕3 transducer the absolute and relative maximum spreads were 4.1 μm and 10%, respectively. In contrast, for the 20 MHz, f∕4 transducer the absolute and relative spreads of ESD mean values were 0.3 μm and 0.7%, respectively, even though the spread of Errσ for this transducer was larger than those of the 2.25 MHz, f∕2.7 and 5 MHz, f∕3 transducers. However, in all cases the spread of ESD mean values was comparable to the standard deviation of the ESD estimates. The results presented in Table TABLE V. obtained from the 150–180 μm phantom further supports the dependence of the spread of mean ESD values on ka range. With the same 2.25 MHz, f∕2.7 transducer used when analyzing the 41 μm phantom the absolute and relative (considering a mean diameter size of 165 μm) spreads of mean ESD estimates were 8.3 μm and 5%, respectively. It can also be observed that the spread of mean ESD values increased for the 7.5 MHz transducer. For this transducer, the estimates followed a binomial distribution due to high ka convergence problems discussed above.
The dependence of the QUS estimates on Gp was also supported by the experimental results. As discussed in Sec. 3A, all estimation methods agree within less than 1 dB for Gp > 25. Two transducer pairs covered very similar frequency ranges with different Gp ranges and at least one of them satisfying Gp > 25 for most of the analysis bandwidth. The first pair was the 10 MHz, f∕4 (Gp ∈ [8.9,25.3]) and 10 MHz, f∕2 (Gp ∈ [28.2,95.0]) transducers for which the spreads of mean ESD values were 0.8 and 0.5 μm, respectively, when analyzing the 41 μm phantom. The second pair was the 13 MHz, f∕3 (Gp ∈ [15.8,43.2]) and 15 MHz, f∕2 (Gp ∈ [23.4,66.9]) transducers for which the spreads of mean ESD values were 0.3 and 0 μm, respectively, when analyzing the 41 μm phantom. Therefore, the limited experimental data in this study supports the fact that the use of sufficiently large Gp values helps reduce the dependence of mean ESD estimates on the method used for normalizing BSC estimates. However, it should be noted that the spread of mean ESD estimates for the discussed cases corresponded at most to 2% of the actual mean scatterer size present in the phantom. Therefore, and as the results from Fig. 5 suggest, the spread of mean ESD estimates was not significant when ka > 0.5 even for moderate (i.e., Gp < 100) Gp values.
Although all estimation methods provided similar experimental BSCs in this work with good fits to the theoretical BSCs as evidenced by the results in Tables 2, TABLE III., the subtle frequency-dependent effects of each method had in some cases noticeable effects on the bias of QUS estimates. These differences in mean QUS estimates can be reduced by proper choice of ka and Gp ranges. Given that Gp only depends on transducer properties whereas ka depends on properties of the imaging target, in practice it should be easier to control the Gp rather than the ka range. If Gp is made sufficiently large, the spread of mean estimation values introduced by the different estimation methods would be reduced and relatively good BSC estimation consistency would also imply relatively good QUS estimation consistency. However, in this work it was found that for the Gp values encountered in practice the frequency-dependent effects of the studied BSC estimation methods did not have a significant effect on the spread of mean QUS estimates, and any of them can be safely used for BSC estimation.
Finally, significant deviations in mean ESD values from the actual mean glass bead diameter introduced by estimation methods were noticeable for low ka values. This observation is important because it has been commonly understood that the precision and not the accuracy of ESD estimates should suffer at low ka.32 Furthermore, it has been demonstrated that methods such as spatial compounding can be used to effectively reduce the standard deviation without affecting the mean of ESD estimates.33 However, the ill-conditioning of ESD estimation in the low ka regime may cause the ESD estimates to be too sensitive to even slight experimental errors due to compensating for the transmission through the plastic film, nonlinear behavior of the amplifiers used to measure the data, attenuation compensation, measurement noise, and improper modeling of the transducer radiation pattern. Therefore, it was not possible to determine which BSC estimation method may be preferred when analyzing near Rayleigh (ka < 0.5) data. This may be yet another reason to advocate for large Gp values in order to reduce frequency-dependent effects on BSC estimates.
ACKNOWLEDGMENTS
The authors want to thank Aiguo Han for technical assistance and Dr. Ernest Madsen for providing the experimental phantoms used in this study. This work was supported by National of Institute of Health Grants R21-CA139095, R01-EB008992, and R01-CA111289.
References
- Lizzi F. L., Greenebaum M., Feleppa E. J., Elbaurn M., and Coleman D. J., “Theoretical framework for spectrum analysis in ultrasonic tissue characterization,” J. Acoust. Soc. Am. 73, 1366–1373 (1983). [DOI] [PubMed] [Google Scholar]
- Campbell J. A. and Waag R. C., “Ultrasonic scattering properties of three random media with implications for tissue characterization,” J. Acoust. Soc. Am. 75, 1879–1886 (1984). [DOI] [PubMed] [Google Scholar]
- Feleppa E. J., Lizzi F. L., Coleman D. J., and Yaremko M. M., “Diagnostic spectrum analysis in ophthalmology: A physical perspective,” Ultrasound Med. Biol. 12, 621–631 (1986). [DOI] [PubMed] [Google Scholar]
- Lizzi F. L., Ostromogilsky M., Feleppa E. J., Rorke M. C., and Yaremko M. M., “Relationship of ultrasonic spectral parameters to features of tissue microstructure,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 34, 319–329 (1986). [DOI] [PubMed] [Google Scholar]
- Sigelmann R. A. and Reid J. M., “Analysis and measurement of ultrasound backscattering from an ensemble of scatterers excited by sine-wave bursts,” J. Acoust. Soc. Am. 53, 1351–1355 (1973). [Google Scholar]
- Insana M. F. and Hall T. J., “Parametric ultrasound imaging from backscatter coefficient measurements: Image formation and interpretation,” Ultrason. Imaging 12, 245–267 (1990). [DOI] [PubMed] [Google Scholar]
- Lizzi F. L., Astor M., Liu T., Deng C., Coleman D. J., and Silverman R. H., “Ultrasonic spectrum analysis for tissue assays and therapy evaluation,” Int. J. Imaging Syst. Technol. 8, 3–10 (1997). [Google Scholar]
- Insana M. F., Hall T. J., and Cook L. T., “Backscatter coefficient estimation using array transducers,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 41, 714–723 (1994). [DOI] [PubMed] [Google Scholar]
- Gerig A., Zagzebski J., and Varghese T., “Statistics of ultrasonic scatterer size estimation with a reference phantom,” J. Acoust. Soc. Am. 113, 3430–3437 (2003). [DOI] [PubMed] [Google Scholar]
- Ueda M. and Ozawa Y., “Spectral analysis of echoes for backscattering coefficient measurement,” J. Acoust. Soc. Am. 77, 38–47 (1985). [Google Scholar]
- Insana M. F., Wagner R. F., Brown D. G., and Hall T. J., “Describing small-scale structure in random media using pulse-echo ultrasound,” J. Acoust. Soc. Am. 87, 179–192 (1990). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X., Phillips D., Schwarz K. Q., Mottley J. G., and Parker K. J., “The measurement of backscatter coefficient from a broadband pulse-echo system: a new formulation,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 44, 515–525 (1997). [DOI] [PubMed] [Google Scholar]
- Peters K. J. and Waag R. C., “Compensation for receiver bandpass effects on ultrasonic backscatter power spectra using a random medium reference,” J. Acoust. Soc. Am. 84, 392–399 (1988). [DOI] [PubMed] [Google Scholar]
- Chen J.-F., Zagzebski J. A., Dong F., and Madsen E. L., “Estimating the spatial autocorrelation function for ultrasound scatterers in isotropic media,” Med. Phys. 25, 648–655 (1998). [DOI] [PubMed] [Google Scholar]
- Franceschini E., Yu F. T. H., Destrempes F., and Cloutier G., “Ultrasound characterization of red blood cell aggregation with intervening attenuating tissue-mimicking phantoms,” J. Acoust. Soc. Am. 127, 1104–1115 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Donnell M. and Miller J. G., “Quantitative broadband ultrasonic backscatter: An approach to nondestructive evaluation in acoustically inhomogeneous materials,” J. Appl. Phys. 52, 1056–1065 (1981). [Google Scholar]
- Oelze M. L. and W. D.O’Brien, Jr., “Frequency-dependent attenuation-compensation functions for ultrasonic signals backscattered from random media,” J. Acoust. Soc. Am. 111, 2308–2319 (2002). [DOI] [PubMed] [Google Scholar]
- Madsen E. L., Dong F., Frank G. R., Gara B. S., Wear K. A., Wilson T., Zagzebski J. A., Miller H. L., Shung K. K., Wang S. H., Feleppa E. J., Liu T., W. D.O’Brien, Jr., Topp K. A., Sanghvi N. T., Zaitsen A. V., Hall T. J., Fowlkes J. B., Kripfgans O. D., and Miller J. G., “Interlaboratory comparison of ultrasonic backscatter, attenuation, and speed measurements,” J. Ultrasound Med. 18, 615–631 (1999). [DOI] [PubMed] [Google Scholar]
- Wear K. A., Stiles T. A., Frank G. R., Madsen E. L., Cheng F., Feleppa E. J., Hall C. S., Kim B. S., Lee P., W. D.O’Brien, Jr., Oelze M. L., Raju B. I., Shung K. K., Wilson T. A., and Yuan J. R., “Interlaboratory comparison of ultrasonic backscatter coefficient measurements from 2 to 9 MHz,” J. Ultrasound Med. 24, 1235–1250 (2005). [DOI] [PubMed] [Google Scholar]
- Lucas B. G. and Muir T. G., “The field of a focusing source,” J. Acoust. Soc. Am. 72, 1289–1296 (1982). [Google Scholar]
- Chen X., Schwarz K. Q., and Parker K. J., “Radiation pattern of a focused transducer: A numerically convergent solution,” J. Acoust. Soc. Am. 94, 2979–2991 (1993). [DOI] [PubMed] [Google Scholar]
- Chen X., Schwarz K. Q., and Parker K. J., “Acoustic coupling from a focused transducer to a flat plate and back to the transducer,” J. Acoust. Soc. Am. 95, 3049–3054 (1994). [DOI] [PubMed] [Google Scholar]
- Anderson J. J., Herd M.-T., King M. R., Haak A., Hafez Z. T., Song J., Oelze M. L., Madsen E. L., Zagzebski J. A., W. D.O’Brien, Jr., and Hall T. J., “Interlaboratory comparison of backscatter coefficient estimates for tissue-mimicking phantoms,” Ultrason. Imaging 32, 48–64 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall T. J. and Insana M. F., “High speed quantitative imaging over extended fields of view,” Proc.-IEEE Ultrason. Symp. 2, 1037–1041 (1989).
- J. J.Faran, Jr., “Sound scattering by solid cylinders and spheres,” J. Acoust. Soc. Am. 23, 405–418 (1951). [Google Scholar]
- Peters K. J. and Waag R. C., “Analysis of echoes from a solid elastic sphere in water,” J. Acoust. Soc. Am. 34, 1582–1592 (1962). [Google Scholar]
- Oelze M. L., Zachary J. F., and W. D.O’Brien, Jr., “Characterization of tissue microstructure using ultrasonic backscatter: Theory and technique for optimization using a Gaussian form factor,” J. Acoust. Soc. Am. 112, 1202–1211 (2002). [DOI] [PubMed] [Google Scholar]
- D’Astous F. T. and Foster F. S., “Frequency dependence of ultrasound attenuation and backscatter in breast tissue,” Ultrasound Med. Biol. 12, 795–808 (1986). [DOI] [PubMed] [Google Scholar]
- Madsen E. L., Insana M. F., and Zagzebski J. A., “Method of data reduction for accurate determination of acoustic backscatter coefficients,” J. Acoust. Soc. Am. 76, 913–923 (1984). [DOI] [PubMed] [Google Scholar]
- O’Neil H. T., “Theory of focusing radiators,” J. Acoust. Soc. Am. 21, 516–526 (1949). [Google Scholar]
- Kossoff G., “Analysis of focusing action of spherically curved transducers,” Ultrasound Med. Biol. 5, 359–365 (1979). [DOI] [PubMed] [Google Scholar]
- Chaturvedi P. and Insana M. F., “Error bounds on ultrasonic scatterer size estimates,” J. Acoust. Soc. Am. 100, 392–399 (1996). [DOI] [PubMed] [Google Scholar]
- Gerig A., Chen Q., Zagzebski J. A., and Varghese T., “Correlation of ultrasonic scatterer size estimates for the statistical analysis and optimization of angular compounding,” J. Acoust. Soc. Am. 116, 1832–1841 (2004). [DOI] [PubMed] [Google Scholar]