Abstract
This paper investigates the opening and closing mechanism for the Venus flytrap (Dionaea muscipula). A mathematical model has been proposed to explain how the flytrap transitions between open, semi-closed and closed states. The model accounts for the charge accumulation of action potentials, which generated by mechanical stimulation of the sensitive trigger hairs on the lobes of the flytrap. Though many studies have been reported for the Venus flytrap opening and closing mechanism, this paper attempts to explain the mechanism from nonlinear dynamics and control perspective.
Key words: Venus flytrap, modelling, kinetics
Introduction
The complex process of trap closing in the Venus flytrap (Dionaea muscipula) has long been recognized as one of the most interesting examples of plant movements in nature. Researchers have studied both the signaling and mechanics of trap closure since 1875, when Darwin first noted that the closure mechanism was “one of the most wonderful in the world.”1 The Venus flytrap is a small plant consisting of 5–7 leaves, each of which is divided further into an upper leaf and a lower leaf. The upper leaf, or trap, has two trapezoidal lobes that are held together by a midrib at the base. Each lobe of the leaf contains 3–5 trigger hairs, arranged in a triangular pattern, which are sensitive to mechanical stimuli. On the edge of each trap are fingerlike projections known as cilia, which interlock when the trap closes to keep prey from escaping.
The motion of the Venus flytrap can be divided into three distinct states:2–4 (1) The fully open state (Fig. 1A), which occurs in the absence of prey, and which is characterized by a convex curvature of the trap lobes. (2) The semi-closed state (Fig. 1B and D), which occurs immediately after the trap is triggered, and which is characterized by interlocking cilia that restrict large prey but allow small prey to escape. (3) The fully closed state (Fig. 1C and E), which occurs after prolonged stimulation, and which is characterized by a tight appression and recurved bending of the trap-margins. The semi-closed state of the Venus flytrap is of particular interest, as it represents an intermediate step which has been neglected in most previous models of the trap closing mechanism. When a trap is in the semi-closed state, two different outcomes are possible. If the prey escapes or other non-nutritive material is captured, then the semi-closed state will return to the fully open state. If, however, there is a constant stimulus in the semi-closed state, such as the prey struggling and bending the trigger hairs, then the trap will proceed to the fully closed state. It usually takes 5–7 days to complete the digestion process through an array of digestive glands, and it is only after digestion is complete that trap can begin to open again.
Figure 1.
Closing states of the Venus flytrap (Dionaea muscipula). (A) The open state of the trap characterized by the separation of the 2 lobes, (B) The semi-closed transition state, lobes brought together, but not tightly closed, (C) Tightly closed state, trap appearance changes and buckling occurs around outer edges of trap, lobes in direct contact. (D and E) Higher magnification of the trap lobes in the transition and tightly closed states respectively. Images captured using a Sony HDR-HC9 Handycam attached to a Meiji EMZ-13TR Stereoscope. Images were processed using Pinnacle Studio™ Ultimate.
The mechanical stimulation of the trigger hairs generates a receptor potential (RP) followed by an action potential (AP) leading to an electrochemical signal for trap closure.5,6 This process is similar to the AP found in mammalian muscle contraction and nerve impulses. Further experimentation confirmed that an AP or electrical charges can precede trap closure, and that consecutive injections of smaller electrical charges can also lead to closure when a total of 14 µC charge is reached.7 In addition, the APs generated from different cell types within the trap do not vary.8 Furthermore, it was demonstrated that two mechanical stimuli, within 20–30 s, were required for trap closure at temperatures ranging from 15–25°C.9,10 At temperatures between 35–40°C only one stimulation is required for trap closure.9
With the knowledge of how to initiate trap closure, the next obstacle to researchers was to determine the biological mechanisms underlying the swift closure of the trap. It was known by early researchers that the flytrap actively employs turgor pressure and hydrodynamic flow to initiate closure. Once the accumulated charge reaches the trigger threshold, ATP hydrolysis11 and fast proton transport begin,4,12 which create a gradient that initiates the opening of aquaporin channels. The movement of water causes a shape change in the leaf leading to the rapid closing of the trap. However, these cellular mechanisms alone cannot explain the rapid motion on a macroscopic scale.13 The mechanism of how water flow can mechanically cause trap closure is not well established, and several mathematical models have been proposed to explain this process. Forterre et al. suggested that elastic deformation (snap-buckling theory) plays a role in generating the force required to close the trap.14 Transitioning from the open to the closed state, the lobes of the leaf pass through a region of bistability and quickly convert its potential energy into the kinetic energy required for closure. Bobji considered the Venus flytrap as a bistable vibrator, which is stable in both the open and closed states.15 Volkov et al. combined the snap-buckling theory and turgor pressure theory, and put forth a hydroelastic curvature model stating that the lobes possess curvature elasticity and have inner and outer hydraulic layers with different hydraulic pressures.16 The open state has high elastic energy and a stimulus induces fast water transport resulting in a mono-stable closed state. The hydroelastic curvature model is also based on the anatomical observation that the cell walls of the upper and lower epidermis and adjacent mesophyll feature a preferential microfibril orientation in the direction of the applied stress.13,16
These models describe only the post-stimulation closure stage, and neglect the triggering process, reopening process, and the intermediate semi-closed transition state (Fig. 1). As suggested above, the semi-closed state of the trap is of particular interest, since it represents an intermediate state from which both the fully open and fully closed states are accessible. Experiments on Venus flytraps suggest that within 0.1–0.3 s of receiving enough stimulation, the trap will snap to a semi-closed transition state. In this state the cilia overlap, but there is still a visible gap between two lobes. If there is no further stimulation, then the trap will reopen within 1–2 days; however, if constant stimulation of the trap takes place, the trap will proceed to a sealed state and will remain closed for up to 2 weeks. By possessing this intermediate signaling point,17,18 the plant is able to “make a decision” to reopen if the prey escapes, which is adaptively advantageous. More specifically, studies conducted on flytraps fed ants, concluded that constant mechanical stimulation of the trigger hair causes the trap to fully close, leading to secretion of digestive enzymes.3 It is energetically costly for the plant to secrete digestive enzymes into an empty trap. A holistic model of trap opening and closing, including the semi-closed state, has not been explored up to this point.
In this paper, we propose a mathematical model to explain (1) why the Venus flytrap requires two mechanical stimuli in 20–30 s for closure; (2) why the Venus flytrap does not close from rain drops, or blasts of air; (3) how the Venus flytrap snaps in 0.3 s; (4) why trap closure results in a “decision-making” semi-closed state; (5) how the Venus flytrap seals and kills the struggling prey; and (6) how the Venus flytrap slowly reopens.
Model Development
Mathematical modeling.
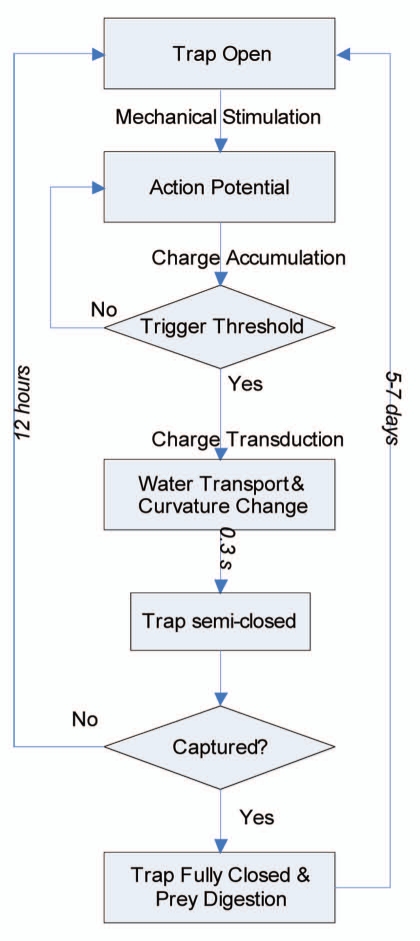
The motion of the flytrap has three distinct states: open, semi-closed and closed (Fig. 2). When trigger hairs in the open trap receive mechanical stimulation, an action potential is generated and an electrical charge is accumulated. Once the charge has acquired enough energy to exceed a threshold value, ATP hydrolysis11 and fast proton transport start,4,12 which create an ion gradient that initiates the opening of aquaporin channels. Water driven by fast proton transport rushes from the outer to the inner layer of the lobes and, in combination with the high elastic energy of the lobes themselves, causes the trap to transition to the semi-closed state within 0.3 seconds.16 If no further stimulation occurs, the lobes will slowly return to an open position within 12–24 hours. However, if further stimulation does occur, the trap transitions to the fully closed state, which takes more than 5–7 days to reopen.
Figure 2.
The conceptual diagram of the opening/closing mechanism of the Venus flytrap. The open trap is triggered by mechanical stimulation of the trigger hairs. The resulting action potentials are accumulated in the leaves. Once the charge accumulates above the trigger threshold, water rushes through open aquaporin channels and the trap is semi-closed in 0.3 s. If no further stimuli occur, then the trap reopens in 12 hours; if prey struggles and triggers more stimuli, then trap becomes fully closed. It requires 5–7 days to reopen after digestion of prey.
Although the molecular and cellular mechanisms involved in water movement remain poorly understood, we agree that the macroscopic mechanism is based on the hydroelastic curvature theory proposed by Volkov et al.16 However, we consider both the open state and closed state as two stable equilibria, similar to Bobji's bistable vibrator theory.15
Trigger process.
The trigger process results from mechanical stimulation of the trigger hairs. The open state is indeed very stable, and does not spontaneously close, even with rain drops and gusts of wind. Using a steady stream of water or a gust of air directed at a trigger hair, it is possible to flex the trigger hair and initiate trap closure (see experimental data); however this only occurs when the force of the air or water is strong enough to cause the trigger hair to flex twice in 30 seconds.
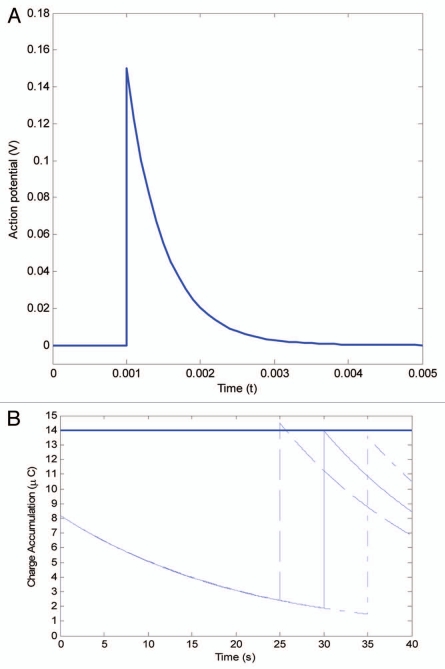
The mechanical stimulation of the trigger hair generates a receptor potential (RP) followed by an action potential (AP) leading to an electrochemical signal for trap closure.5,6 The most recent experiments using an ultrafast data acquisition system, measured that the action potential is 150 mV with a duration time of 1–1.4 ms. The velocity of the action potential is 10 m/s,19 and it has been proven that the trap can accumulate electrical charges. Researchers have delivered multiple small charges, via electrodes attached to the trap lobes, and discovered that a total charge of 14 µC is necessary to initiate closure. Volkov et al. recorded the dynamics of the action potential induced by a piece of gelatin stimulating a trigger hair. The action potential jumped to 0.15 V at 0.001 s and rapidly dissipated to zero after 0.003 s.20 As illustrated in Figure 3A, the action potential ut evoked by bending the trigger hair can be described as an exponential function by recent measurements (Fig. 2).19
Figure 3.
The ‘memory’ of Venus flytrap. (A) The action potential is evoked by mechanical stimuli of the trigger hair. (B) The first action potential can not accumulate enough charge accumulation, however, if the second action potential occurs within 30 s (dashed line), then the charge grows above the activation threshold 14 µC and leads to a trigger impulse. If two action potentials occur over 30 s, the trigger threshold cannot be reached (dot-dashed line). The 30 s time-point is the critical value in reaching the threshold (solid line).
| (1) |
Ueda et al. suggested that the charge accumulation may relate to the stepwise accumulation of a bioactive substance, resulting in ion channel activation by the action potential.20 The charge accumulation can be described by the following linear dynamic system,
| (2) |
where C (unit: µC) stands for the accumulated charge in the lobes, kc (s−1) stands for the charge dissipation rate, and ka (µC/V·s) stands for the charge accumulation rate. Initial charge accumulation is small and negligible.10
Figure 3B shows how action potentials lead to a stepwise response of charge accumulation in the lobes. If two stimuli occur within 30 seconds (dashed line), the charge build-up will exceed the threshold value of 14 µC and trap closure will be triggered. If, however, there is only one stimulus within 30 seconds, then the charge build-up will not reach the threshold value, and the trap will remain open (dot-dashed line). 30 seconds is the critical time period to reach the threshold (solid line). The values used in the model are typical values measured in the experiments. The threshold value and the peak of the action potential may vary in different settings, thus the trigger interval ranges from 20 to 30 s.
It was demonstrated that two mechanical stimuli were required for trap closure at temperatures ranging from 15–25°C.9,10 In contrast, at temperatures between 35–40°C only one stimulation was required for trap closure.9 The temperature effect on the action potential has been investigated previously in plants such as Chara coralline.21 There it was found that the peak potential was largely independent of temperature, and that the duration of the action potential decreased with increasing temperature.21 Since the higher temperature does not imply a larger action potential, it is most likely that the decline of the threshold value causes the reduction of stimuli at higher temperature. In Figure 3B, we show that if the threshold value decreases from 14 µC to 8 µC the first action potential can trigger the closure.
This model can also explain why heavy rain or blasts of wind could not initiate trap closure. This was proven in our experiments (see experimental data) that a strong stream that bends the trigger hairs can initiate the trap closure. In nature, there is only a small chance that, rain or wind would occur with such a focused stream directed right on the trigger hair twice in 30 seconds. As a result, the stimulus provided by either rain or wind will typically be below the trigger threshold value. It thus leads to Darwin's observation that rain is not able to initiate trap closure.1
Water kinetics.
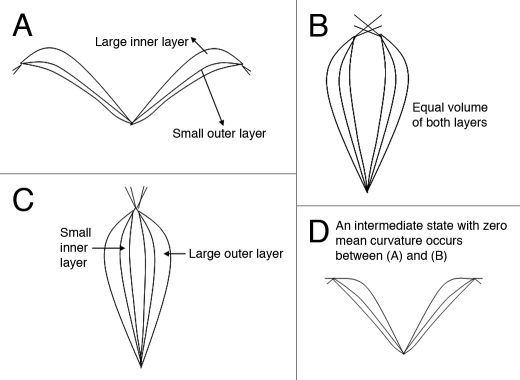
The mathematical model for the opening and closing mechanism of the Venus flytrap is based on the water movement between the outer and inner hydraulic layers of the lobes. As illustrated in Figure 4, the open state of the Venus flytrap corresponds to a maximum/minimum water volume in the inner/outer layer (Fig. 4A). The closed state happens in a minimum/maximum water volume in the outer/inner layer (Fig. 4C). The semi-closed state has equal water volume in both layers (Fig. 4B). This state is an intermediate state, which can move to either the fully closed or open state.
Figure 4.
Water volume in the outer and inner layers in the open, semi-closed, and closed states. (a) The open state has large inner layer and small outer layer. (b) The semi-closed state has equal volume in both layers. (c) The closed state has large outer layer and small inner layer, in contrast to the open state. (d) An intermediate state has zero mean curvature. It happens between the open and the semi-closed state.
A large number of aquaporin channels exist between two layers of the lobes to facilitate transcellular water transport.7,17 At the open state, no significant gradient exists between the inside of the cell and the outer environment, thus aquaporins remain closed to stop water from flowing through the pores of the cells from the outer to inner layer. An AP opens voltage-gated channels that connects the layers, and creates a gradient that allows water to flow through aquaporin channels from the outer to the inner layer. The importance of water flow on the closing process of the Venus flytrap has been illustrated in experiments with ion and water channel blockers and uncouplers. Treatment with both uncouplers of ion transport, and blockers of aquaporin-based water channels resulted in a slow closing upon stimulation of the trigger hairs.7 The fast water movement releases high elastic energy and causes a rapid change in curvature of the lobes. The amazing closing speed is thus essentially caused by the rapid water transport. It has been shown that water transport through one aquaporin channel can proceed as quickly as 106 molecules per second.22
The motion process can be modeled on a macroscopic level as follows,
| (3) |
The water volumes in the outer and inner layer of the lobes are denoted by XO and XI, respectively. Many plants have the ability to control transpiration rates by controlling the opening of stomatal pores. This ability to maintain relatively constant water tissue concentrations is termed ‘isohydric’.23 Thus we assumed that the total water volume of the lobe tissue is a constant and can be normalized to 1, that is,
| (4) |
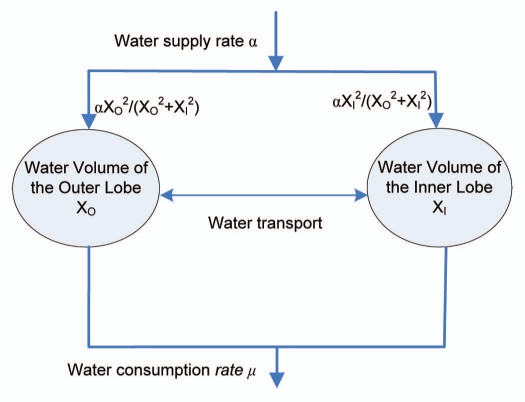
As illustrated in the conceptual diagram in Figure 5, volume kinetics implies that fluid is supplied at rate and fluid evaporates at the rate µ. Thus, without water transport between the two layers, the water kinetics can be described using a two-dimension system of ordinary differential equations as follows,
| (5) |
| (6) |
where the coefficient is the water supply rate from the roots, while and are the water supply rates distributed to both layers depending on the volume of the layer with a cooperative coefficient p > 1. If the coefficient p = 1, then the water dynamics can be balanced at any point in the line XO + XI = 1. However, in the case of the Venus flytrap, much more water is directed towards the larger layer initially allowing the cells in this layer to grow, elongate, and result in the hydroelastic curvature.17,25,26 In fact, the system dynamics has no significant difference for any p > 1. In this paper, we choose p = 2, that is, the flow rates to the outer/inner layers has a ratio of .
Figure 5.
A bistable model of the Venus flytrap opening/closing mechanism. The model is constructed based on water kinetics between the outer and inner layers of the lobes. Water supply is distributed to both layers depending on the layer volume, while water is consumed by transpiration and chemical reactions. Voltage-gated channels block water flow to the inner layer by maintaining a H+ gradient, which leads to high elastic energy in the open state of the trap. In an energy consuming step, the AP triggers an ATP-dependant H+ pump that rapidly pumps H+ against the gradient. APs open the voltage gated channels for a short time, water rushes into the inner layer, and the trap relaxes to semi-closed state. More APs can open the voltage gated channels again, and push a small amount of water to the inner layer. The reopening signal can transport the water back to the outer layer.
The water consumption rate µ describes the water loss due to plant transpiration and chemical synthesis. Because of relatively constant water volume in the lobes, the water supply rate α must be the same as the water consumption rate µ.23 A rapidly transpiring sunflower leaf loses the equivalent of the entire leaf water content every 20 minutes.27 Since the leaf of the Venus flytrap is smaller than the sunflower leaf, we assume that the Venus flytrap consumes the entire of leaf water every hour, i.e., µ = 1. The smaller value of µ is, the longer time it takes to reopen the trap.
As illustrated in Figure 6, there are three steady states for the above system. Two stable equilibria, (0, 1) and (1, 0) (circles in Fig. 6), are in symmetric positions corresponding to the open and closed states. The unstable equilibrium (0.5, 0.5) (square in Fig. 6) is the semi-closed state with equal volumes of both layers. This is a transient state between two attractor states. Without water transport, the Flytrap will eventually stay in one of the stable states. Water transport can drive the dynamics away from stable states. If the dynamics do not move across the transient state, then the dynamics will return to the original stable state. However, once the dynamics run across the semi-closed state, then the dynamics will flip to another stable state.
Figure 6.
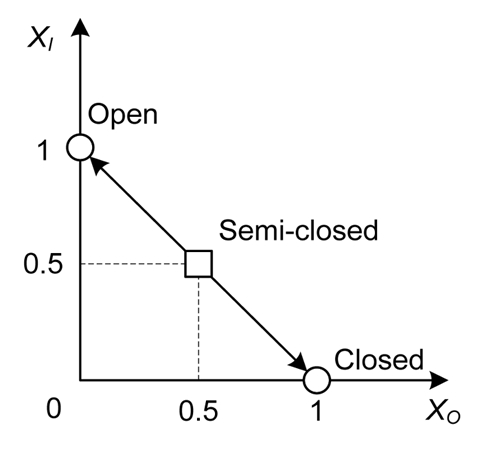
The nonlinear dynamics of Venus flytrap model [Equation (4–6)]. The total water volume has been normalized to one. The open state corresponds to (XI, XO) = (1, 0) (circle on the left), the semi-closed state is (XI, XO) = (0.5, 0.5) (square) and the closed state (XI, XO) = (0, 1) (circle on the right). The open/closed states are two attractors and semi-closed state is a saddle. The water dynamics moves along the line XO + XI = 1. It tends to the open state when XO > 0.5, and converges to the closed state when XO < 0.5.
The opening and closing mechanism of the flytrap is essentially based on the water transport between the two layers. In the open state, voltage-gated channels block water flow to the inner layer by maintaining a stable H+ gradient, which leads to high elastic energy in the open state of the trap. In an energy consuming step, an AP triggers an ATP-dependant H+ pump that rapidly pumps H+ against the gradient.4 This ATP consumption step consumes most of the cell's ATP storage, and thus if subsequent APs are generated, the flow of water is not as great.28 It is believed that aquaporin channels are the main driving force behind water transport in the Venus flytrap, and these channels are dependent on an osmotic gradient for flow.7 If prey stimulates an AP, then the voltage gated channels open for a short time creating a gradient, which allows the aquaporin channels to open. Water then rushes into the inner → outer layer, and the trap relaxes to semiclosed state. Our model is based on experimental evidence for a H+ gradient, however, other ionic pumps exist and function in a similar manner.13,28 More APs can open the voltage gated channels again, and push a small amount of water to the inner → outer layer. The flow would not be as great, however, due to depleted ATP stores. This process leads to the fully closed state. Although water could theoretically then diffuse back to the outer → inner layer at this stage, we assume that the diffusion rate is very small and can thus be neglected. Once digestion is finished, however, the water flow will be transported back to the outer → inner layer, causing a slow reopening of the trap. The experimental data on water flow in the reopening step is highly lacking, and thus we will assume that the mechanism involves a similar pathway to the closing process, although without the speed of the reaction. We assume there exists a chemical signal driving the water transport in the reopening process.
Mathematical model.
The mathematical model of the flytrap opening/closing mechanism can be described as follows,
| (7) |
| (8) |
| (9) |
where uh, ua and uc are the water transport rates driven by a hydraulic gradient, osmotic gradient and chemical signals in different processes. The system parameters are summarized in Table 1.
Table 1.
Parameters of the Venus flytrap model
| Symbol | Description | Value |
| kc (s−1) | dissipation rate of charge accumulation | 0.012 |
| ka (µC/V·s) | accumulation rate of charge | 0.11 |
| CT (µC) | trigger threshold | 14 |
| α (hour−1) | water supply rate | 1 |
| µ (hour−1) | water consumption rate | 1 |
| kt (s−1) | transport parameter from the inner to the outer layer according to hydraulic pressure | 10 |
| kf (s−1) | transport parameter from the inner to the outer layer according to osmotic gradient | 2 |
| kd (s−1) | diffusion coefficient from the inner to the outer layer according to electrochemical energy | 0.000045 |
| T0 (s) | the time of water channel opens | 0.3 |
| TD (hour) | the time of reopening chemical signal occurs | 15 |
(1) Capture process: From open to semi-closed.
The closing process is characterized by fast water transport. Every time the charge accumulation is above the trigger threshold, the voltage gate will be opened for a short time (a few seconds). If we denote the opening period of the voltage gated channels by T0 seconds, then the voltage gate opening can be looked at as an impulse:
| (10) |
where ts is the trigger time when the charge accumulation reaches the trigger threshold.
This impulse triggers fast water transport driven by the hydraulic pressure. The hydraulic transport rate uh is proportional to the hydraulic pressure induced by the volume difference.29 Moreover, aquaporin channels allow water to flow only from the inner layer to the outer layer. Hence, the hydraulic transport rate can be written as follows,
| (11) |
where the coefficient kt is a flow rate coefficient describing the capacity allowing flow moving through the channels.
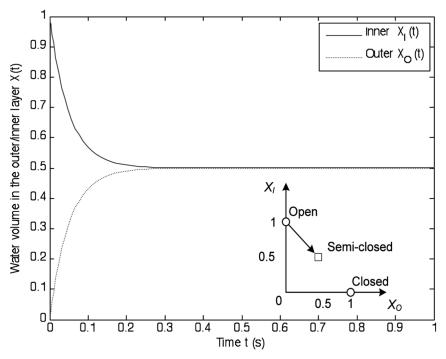
The water transport driven by osmotic gradient [Eq. (12)] and chemical signals [Eq. (14)] does not occur in the capture process, i.e., ua = 0, and uc = 0. As shown in Figure 7, the outer volume rapidly decreases and the outer volume increases. The water dynamics approaches an equal volume position in 0.3 s. This implies that the lobes transition from the open state to the semi-closed state.
Figure 7.
Illustration of the capture process. The water rapidly flows into the outer layer, and the open trap (XI, XO) = (1, 0) moves to the semi-closed state [(XI, XO) = (0.5, 0.5)] in 0.3 s.
Markin et al. also linked the pressure difference to the mean curvature.31 The curvature changes from convex to concave in this stage. It is notable that there exists an intermediate state that the mean curvature is zero.31 But this intermediate state (Fig. 4D) is not the semi-closed state. It is a state between the open and the semi-closed states.
(2) Release process: From semi-closed to open.
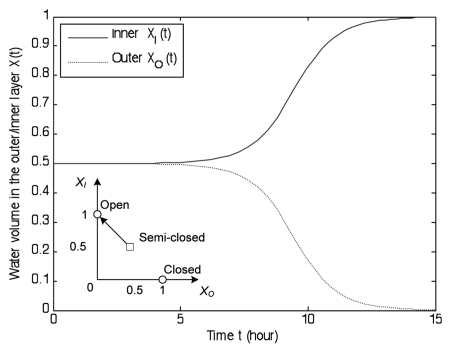
The release process has no water transport between two layers, i.e., uh = 0, ua = 0 and uc = 0. The water dynamics tend to the semi-closed state (XO, XI) = (0.5, 0.5) during the capture process, but the inner layer is still slightly larger than the inner layer. However, without further water transport between the two layers, the water dynamics will return to the closest equilibrium, i.e., open state (XI, XO) = (1, 0). That is because the water supply rate favors the larger layer, the inner layer thus becomes larger and larger. Figure 8 illustrates the reopening process; the inner volume is gradually refilled, while the outer volume slowly returns to the minimal level. It takes 14 hours to transition from the semi-closed state to the open state. The opening speed significantly decreases in the final 2 hours. Since the water change directly leads to a curvature change, the water kinetics can be translated to kinetics of the distance between the two lobes, as in Stuhlman's paper.30
Figure 8.
Illustration of the release process. It takes 14 hours to transition from the semi-closed state (XI, XO) = (0.5, 0.5) to the open state (XI, XO) = (1, 0). The opening speed significantly decreases in the final 2 hours.
(3) Sealing process: From semi-closed to fully closed.
The sealing process requires further stimulation. We found that if the prey is not moving, the plant will proceed to release process and expel the prey. To start the digestion of the unmoving prey, touch of the hairs or rub the surface is necessary. If the prey struggles inside the lobes, more trigger impulses will be evoked until the prey is killed by acid fluid (pH 2–3) secreted by the trap.3 More APs can open the voltage gated channels again, and push a small amount of water to the outer layer. The flow would not be as great, however, due to depleted ATP stores. The hydraulic pressure is no longer a major factor, because the pressure between the inner and outer layer becomes negative and the backward transport is blocked by the osmotic gradient. This electrochemical energy can only result in a small flux of water transport. As more action potentials occur; more water will be pushed into the outer layer. This leads to the fully closed state.
The water transport rate ua driven by osmotic gradient depends on the remaining volume in the inner layer. It can be written as follows,
| (12) |
where kf is the transport parameter from the outer to the inner layer according to osmotic gradient. The hydraulic pressure uh is in a direction opposite to osmotic gradient to impede the water transport. The chemical reopening signal has not been released, and thus uc = 0. n is the number of triggering after capture process, and N is the maximal number of triggers after the capture process that leads to ATP depletion. In this paper, we assume N is a large number.
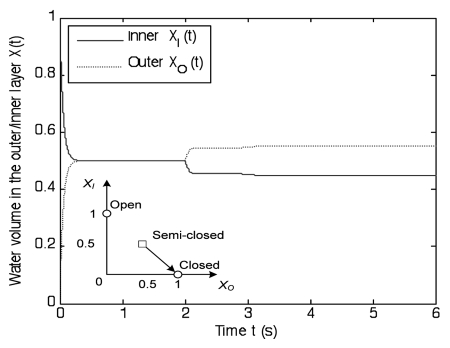
As illustrated in Figure 9, the sealing process requires multiple bursts of water transport triggered by APs. Each small burst of water transport leads to a stepwise response to accelerate the closing. The prey in the trap can struggle for a long time until killed by an acidic fluid. The complete sealing can take hours, and has been reported in some experiments that the trap can be sealed in 1 hour post-stimulation using a 5-sec period of stimulation.25
Figure 9.
Illustration of the sealing process. Stepwise stimuli accelerate the flytrap transition from the semi-closed state (XI, XO) = (0.5, 0.5) to the closed state (XI, XO) = (0, 1). Two trigger impulses occur at 2 and 3 seconds, respectively. They can help the dynamics move across the semi-closed state. The cell growth becomes the main driving force later. It may take more than 1 hour to complete the whole process.
(4) Reopening process: (from fully closed to open).
The trap reopening requires a stimulus to initiate opening. Our experiment confirmed that the flytrap can identify whether the prey has nutrient value, if not, the trap proceeded to the open state within 1–2 days (see experimental data). The reopening signal can interrupt the sealing process. Lysophosphatidic acid compounds have been suggested for such a reopening signal.18 These compounds increased in the closing process and returned to a normal concentration in 24 hours post-stimulation, which is consistent with the reopening process. In another paper, leaf growth was suggested to be the major factor in the reopening process.30 No matter what the driving force is, the fact is that the trap does slowly and reversely repeat the closing process. Thus, there exists a force slowly directing water transport to the inner layer, and across the water-balanced semi-closed state. Let us assume this force is a chemical signal, which is an impulse with duration TD hours as follows,
| (13) |
The water flow from the outer to inner layer is a very slow process. The chemical signal continues pushing water at a small constant rate. Thus, the water flow rate uc due to the chemical signal can be approximated as follows,
| (14) |
where kd is the water flow coefficient according to chemical energy.
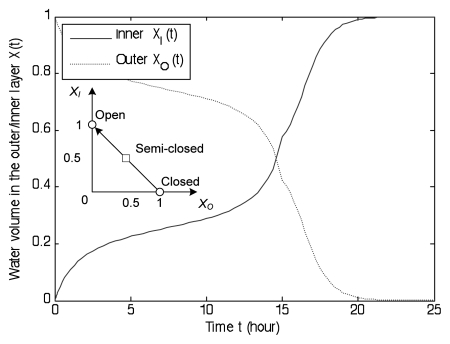
As illustrated in Figure 10, without mechanical stimuli, the dynamics move across the semi-closed state in 15 hours driven by chemical energy and gradually move to the fully open state in 23 hours. The maximum opening speed occurs near the position of the semi-closed state. The opening speed significantly decreases in the final 2 hours. This result is consistent with the observation by Stuhlman.30 If any AP is evoked to open the aquaporin channels, the water transport, driven by a hydraulic or osmotic gradient, takes effect, i.e., uh ≠ 0 or ua ≠ 0, and the reopening process will be interrupted, while the capture or sealing process starts again.
Figure 10.
Illustration of the reopening process. Electrochemical force drives the water dynamics across the semi-closed state (XI, XO) = (0.5, 0.5) in 15 hours. Then the Flytrap transits from semi-closed state (XI, XO) = (0.5, 0.5) to open state (XI, XO) = (1, 0) in 8 hours. The maximum opening speed occurs in the neighborhood of the semi-closed state. The opening speed significantly decreases in the final 2 hours.
Results
(A) Forced water and air stimulation.
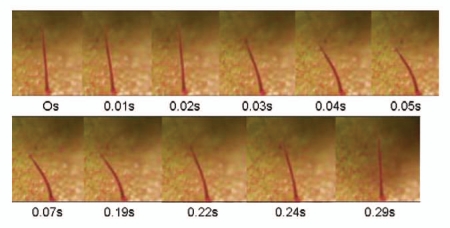
Results from the forced water experiment confirmed the results of Brown and Sharp's 1910 experiment that indicated that water was capable of causing trap closure. Using a syringe with a 22 g needle it was possible to achieve bending of the trigger hair for 0.03 s initially and then again for another 0.03 s to initiate trap closure (Fig. 11). The trigger hair was minimally flexed by each jet of water, but still able to cause trap closure. The initial test distance of 5 mm was the most effective at initiating closure because more force was applied directly to the trigger hair, and caused the hair to bend the most. At distances greater than 15 mm it was difficult to consistently apply enough force to the hair to consistently initiate closure. Similarly, the greatest stimulation of the trigger hair was achieved using the highest amount of pressure applied to the syringe. At low levels of pressure, the trigger hair did not bend and trap closure was not initiated (See Suppl. Material, Movie 1).
Figure 11.
Steady streams of water can bend the trigger hair, and thus lead to trap closure. The trigger hair was slightly bent twice, which initiated the closure.
Similar to the forced water experiments, forced air was able to initiate trap closure through bending of the trigger hair. Since the pressure of the air was much greater than that of the water, trap closure was initiated at every distance. The bending of the trigger hair due to the air experiments was much greater than water experiments, and often led to the hair bending near the trap surface (Fig. 12). It is thus possible that a strong gust of wind could initiate trap closure if the trigger hair was flexed to a great enough degree (See Suppl. Material, Movie 2).
Figure 12.
Strong jets of air can bend the trigger hair, and thus lead to trap closure. The trigger hair was significantly bent twice, which initiated the closure.
(B) Semi-closed state.
In order to characterize the semi-closed state for the purpose of model integration it was necessary to measure the amount of time that the trap remained at this state. It was determined that after the initial process of closing to the semi-closed state, without further stimulation, the trap would minimally begin to proceed to the open state within 8 hours. By the end of 12–36 hours the trap would return to the fully open state. If, however, the trap was further stimulated while at the semi-closed state, then it would rapidly proceed to the fully closed state. It would often take between 1–2 weeks for the trap to open from the fully closed state, and varied greatly on the individual specimen. Similar results were obtained from dropping small pieces of plastic into the trap. This initiated trap closure to the semi-closed state, even close to closed state, but without further stimulation, the trap proceeded to the open state within 1–2 days.
Materials and Methods
(A) Plants.
Healthy adult Venus flytraps were purchased from a local nursery and used for these experiments. The flytraps were grown in well-drained peat moss in 250 ml plastic pots at 27°C. Flytraps were maintained in a 12 hour light/dark cycle and placed in indirect sunlight. Throughout the course of experimentation, the flytraps were pruned, and dead traps were removed.
(B) Forced water stimulation.
To experimentally test if a stream of water was capable of initiating trap closure, a Becton-Dickinson 5-ml syringe with attached 22 gauge needle was used to directly force water onto the trigger hair. The distance between the needle and the trigger hair varied from 5–30 mm, and the stream was always directed onto one trigger hair. In addition, to varying the distance between the needle and hair, the strength of the stream was varied by applying differing forces to the syringe (high, low, intermediate). Hyclone® cell culture grade water (Thermo Scientific), pH 7, was used to ensure that closure was not the result of an ionic imbalance. To record mechanical stimulation of the trigger hair, experiments were conducted under a Meiji EMZ-13TR stereoscope with an attached Sony HDR-HD9 video camera and recorded using the Pinnacle® Studio™ Ultimate (Avid) software.
(C) Forced air stimulation.
Forced air stimulation was achieved with a Fisherbrand Air'IT™ compressed air canister with attached straw. This system allowed air to be directed onto a specific trigger hair. The same experimental apparatus described above was used to visualize the specimen. Again the distance between the straw and trigger hair was varied, but the stream of air was directed at one trigger hair. The same setup as above was used to visualize the bending of the trigger hair.
(D) Semi-closed transition state.
It was important to characterize the semi-closed transition state for the purposes of the model described above. Briefly, one trigger hair of a trap was mechanically stimulated several times with a fiber held by a hemostat. This triggered the rapid closing of the trap to the semi-closed state. This state was always characterized by a loose association between the cilia, and a gap between the trap lobes (Fig. 1B and D). An experimental group was established, in which the trigger hair was constantly stimulated while at the semi-closed state. A control group was also established that had no stimulation after reaching this state. Similarly, small pieces of plastic were dropped into the trap to initiate closure, and then the Flytrap was monitored to determine if they would proceed to the fully closed state without further stimulation.
Conclusions
The goal of this study was to generate a mathematical model to explain the complex stages involved in trap opening and closing, and to model the transition state between these two states. Our model comprehensively accounts for the effects of temperature, electrical charge accumulation, multiple mechanical stimuli, and the slow opening and fast closing states. Most models generated thus far have ignored the semi-closed transition state; however, biologically this is one of the most important stages involved in trap closure. This “decision-making” state allows the plant to select whether to fully close and secrete digestive enzymes, or to reopen in the event of a “false” closure. The secretion of digestive enzymes and the biological consequences of the fully closed state are energetically costly. If the plant were to proceed to the fully closed state with any kind of mechanical stimulation of the trigger hair, without secondary signaling, then a lot of energy would be consumed and not regained. In addition, the opening process has been hypothesized to also require energy and thus be a costly movement. In the case of a trapped insect, the energy gained from digestion of the insect will more than compensate for the energy lost in trap closure, which can be seen as growth of the trap upon digestion. Without the increased nutrients gained from digestion, traps often remain small. It is this type of biological redundancy systems that leads to “bio-inspired” applications in the engineering fields.
Experimental data for the semi-closed transition state was able to more accurately explain some of the conditions important for design of the model. It was observed that without further stimulation, the semi-closed state returned to the open state within 12–24 hours. If further mechanical stimulation was applied, by cotton fibers brushing the trigger hair in our experiments, then the trap would proceed to the fully closed state within 30–45 min. Once at this fully closed state, it took 1–2 weeks for the plant to return to the open state. Similar studies have been conducted by feeding insects to the flytrap. If the insects were small, then they were able to escape through the gaps in the cilia. However, if the insect was large, then the insect would constantly apply pressure to the trigger hairs, until death, and the trap would proceed to the fully closed state.3 In this way the flytrap is able to select the size of its prey. It can be assumed that the energy gained from digestion of an insect small enough to escape the trap does not replenish the energy expended in closure of the trap. Hypothetically, the trap will only allow insects large enough to give the plant an overall energy gain to remain in the trap. This complex sensing and trapping system is an example of what is commonly termed “smart biology.”
The other “decision-making” step in trap closure has been widely studied since the discovery of this plant. The requirement for two mechanical stimuli within 20–30 s to allow trap closure can also be explained in terms of the plant “making a decision” on whether or not to close. As explained earlier, trap closure is an energetically costly process. Early researchers were stunned to learn that a memory function existed in these plants and that multiple stimuli were required to initiate closure. However, biologically this evolved system is a way of preventing closure of the trap to rain, wind, and other environmental conditions. If the trap closed every time that it rained, and then took 1–2 weeks for the trap to reopen, the plant would spend most of its life in the closed state. Additionally, if the trap closed with rain, then less surface area would be available for the plant to obtain sunlight and water from the environment. By requiring multiple signals, the plant can try to ensure that the signals for closure are from a prey item and not the environment. Our experiments were aimed at proving that a stream of water or a jet of air directed at the trigger hair would cause the trigger hair to bend, and the trap to close. This was proven in our experiments; however, it is unlikely that such a situation would occur in nature with such a focused stream directed right on the trigger hair. When conducting the same experiments with drops of water, we observed that the drop of water did not bend the trigger hair due to the angle from which the drop encountered the hair. The drops tended to fall directly on the tip of the trigger hair, and thus did not bend the hair. This is no doubt what led to (1)'s observation that rain was not able to initiate trap closure. A similar concept can be illustrated with the gusts of wind observed by (1). The gusts are not focused or strong enough to cause the trigger hair to bend, artificially this force can be generated from compressed air, but this is unlikely in nature.
Studies of complex biological systems such as these are of significant interest to engineers, and more recently this discipline is lending itself to the idea of “bio-inspired” technology. By mathematically modeling the processes involved in trap closure, and the sensing system used in the Venus flytrap we can begin to apply this model as a control component in a large number of engineering applications. Another avenue to explore is the potential to derive a kind of robotics approach based on the movements of the flytrap. The rapid speed of closure has long been of interest to engineers wishing to develop a simple, high-speed switching mechanism. Through more thorough models of the mechanism of closure and the signaling components used by this plant it can be imagined that this system could one day be integrated into a “smart robot.”
Acknowledgements
We thank Dr. Sharon Bewick and Dr. Ruobo Zhou for helpful suggestions.
Footnotes
Previously published online: www.landesbioscience.com/journals/psb/article/12136
Supplementary Material
References
- 1.Darwin C. Insectivorous Plants. London: Murray; 1875. [Google Scholar]
- 2.Ashida J. Studies on the leaf movement of Aldrovanda vesiculosa. Mem Coll Sci Kyoto Imp Univ Ser B. 1934;9:141–244. [Google Scholar]
- 3.Lichtner FT, Williams SE. Prey capture and factors controlling trap narrowing in dionaea (Droseraceae) Am J Bot. 1977;64:881–886. [Google Scholar]
- 4.Willams SE, Bennett AB. Leaf Closure in the Venus flytrap: An Acid Growth Response. Science. 1982;218:1120–1122. doi: 10.1126/science.218.4577.1120. [DOI] [PubMed] [Google Scholar]
- 5.Burden-Sanderson J. On the electromotive properties of the leaf of Dionaea in the excited and unexcited states. Philos Trans R Soc Lond B Biol Sci. 1882;173:1–55. [Google Scholar]
- 6.Stuhlman O, Jr, Darder E. The action potentials obtained from Venus's-flytrap. Science. 1950;111:491–492. doi: 10.1126/science.111.2888.491. [DOI] [PubMed] [Google Scholar]
- 7.Volkov AG, Coopwood KJ, Markin VS. Inhibition of the Dionaea muscipula Ellis trap closure by ion and water channels blockers and uncouplers. Plant Sci. 2008;175:642–649. [Google Scholar]
- 8.Hodick D, Sievers A. The action potential of Dionaea muscipula Ellis. Planta. 1988;174:8–18. doi: 10.1007/BF00394867. [DOI] [PubMed] [Google Scholar]
- 9.Brown WH, Sharp LW. The closing response in Dionaea. Bot Gaz. 1910;49:290–302. [Google Scholar]
- 10.Ueda M, Nakamura Y. Metabolites involved in plant movement and ‘memory’: nyctinasty of legumes and trap movement in the Venus flytrap. Nat Prod Rep. 2006;23:548–557. doi: 10.1039/b515708k. [DOI] [PubMed] [Google Scholar]
- 11.Jaffe MJ. The role of ATP in mechanically stimulated rapid closure of the Venus's flytrap. Plant Physiol. 1973;51:17–18. doi: 10.1104/pp.51.1.17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Rea PA. The dynamics of H+ efflux from the trap lobes of Dionaea muscipula Ellis (Venus's flytrap) Plant Cell Environ. 1983;6:125–134. [Google Scholar]
- 13.Hodick D, Sievers A. On the mechanism of trap closure of Venus flytrap (Dionaea muscipula Ellis) Planta. 1989;179:32–42. doi: 10.1007/BF00395768. [DOI] [PubMed] [Google Scholar]
- 14.Forterre Y, Skotheim JM, Dumais J, Mahadevan L. How the Venus flytrap snaps. Nature. 2005;433:421–425. doi: 10.1038/nature03185. [DOI] [PubMed] [Google Scholar]
- 15.Bobji M. Springing the trap. J Biosci. 2005;30:143–146. doi: 10.1007/BF02703692. [DOI] [PubMed] [Google Scholar]
- 16.Volkov AG, Adesina T, Markin VS, Jovanov E. Kinetics and mechanism of Dionaea muscipula trap closing. Plant Physiol. 2008;146:694–702. doi: 10.1104/pp.107.108241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Fagerberg WR, Howe DG. A quantitative study of tissue dynamics in Venus's flytrap Dionaea muscipula (Droseraceae) II. Trap reopening. Am J Bot. 1996;83:836–842. [Google Scholar]
- 18.Lea HW. A muscle contracting substance from a plant's closing Fly-Trap. Planta. 1976;129:39–41. doi: 10.1007/BF00390911. [DOI] [PubMed] [Google Scholar]
- 19.Volkov AG, Adesina T, Jovanov E. Closing of Venus flytrap by electrical stimulation of motor cells. Plant Signal Behav. 2007;2:139–144. doi: 10.4161/psb.2.3.4217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ueda M, Nakamura Y, Okada M. Endogenous factors involved in the regulation of movement and “memory” in plants. Pure Appl Chem. 2007;79:519–527. [Google Scholar]
- 21.Beilby M, Coster H. The Action Potential in Chara corallina: Effect of Temperature. Aust J Plant Physiol. 1976;3:275–289. [Google Scholar]
- 22.Schaffner AR. Aquaporin function, structure and expression: are there more surprises to surface in water relations? Planta. 1998;204:131–139. doi: 10.1007/s004250050239. [DOI] [PubMed] [Google Scholar]
- 23.Franks PJ, Drake PL, Froend RH. Anisohydric but isohydrodynamic: seasonally constant plant water potential gradient explained by a stomatal control mechanism incorporating variable plant hydraulic conductance. Plant Cell Environ. 2007;30:19–30. doi: 10.1111/j.1365-3040.2006.01600.x. [DOI] [PubMed] [Google Scholar]
- 24.Angeli D, Ferrell JE, Sontag ED. Detection of multi-stability, bifurcations, and hysteresis in a large class of biological positive-feedback systems. Proc Natl Acad Sci USA. 2004;101:1822–1827. doi: 10.1073/pnas.0308265100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Fagerberg WR, Allain D. A quantitative study of tissue dynamics during closure in the traps of Venus's flytrap Dionaea muscipula Ellis. Am J Bot. 1991;78:647–657. [Google Scholar]
- 26.Van Volkenburgh E. Leaf expansion a an integrating plant behaviour. Plant Cell Environ. 2002;22:1462–1473. [Google Scholar]
- 27.Boyer JS. Water Transport. Annual Review of Plant Physiology. 1985;36:473–516. [Google Scholar]
- 28.Hodick D, Sievers A. The infulence of Ca2+ on the action potential in mesophyll cells of Dionaea muscipula Ellis. Protoplasma. 1986;133:83–84. [Google Scholar]
- 29.Molz FJ, Ferrier JM. Mathematical treatment of water movement in plant cells and tissue: a review. Plant Cell Environ. 1982;5:191–206. [Google Scholar]
- 30.Stuhlman O., Jr A Physical analysis of the opening and closing movements of the lobes of Venus' fly-trap. Bull Torrey Bot Club. 1948;75:22–44. [Google Scholar]
- 31.Markin VS, Volkov AG, Jovanov E. Active movements in plants: mechanism of fly catching by Venus flytrap. Plant Signal Behav. 2008;3:778–783. doi: 10.4161/psb.3.10.6041. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.