Rules extraction from neural networks applied to the prediction and recognition of prokaryotic promoters

Abstract

Promoters are DNA sequences located upstream of the gene region and play a central role in gene expression. Computational techniques show good accuracy in gene prediction but are less successful in predicting promoters, primarily because of the high number of false positives that reflect characteristics of the promoter sequences. Many machine learning methods have been used to address this issue. Neural Networks (NN) have been successfully used in this field because of their ability to recognize imprecise and incomplete patterns characteristic of promoter sequences. In this paper, NN was used to predict and recognize promoter sequences in two data sets: (i) one based on nucleotide sequence information and (ii) another based on stability sequence information. The accuracy was approximately 80% for simulation (i) and 68% for simulation (ii). In the rules extracted, biological consensus motifs were important parts of the NN learning process in both simulations.

Introduction

The determination of how and when genes are turned on and off is a challenge in the post-genomic era. Differences between two species are often more related to gene expression and regulation than to their structures (Howard and Benson, 2002). An adequate comprehension of the complex metabolic networks present in various organisms, including cellular differentiation and cellular responses to environmental change, can be facilitated by studying of promoter sequences, i.e., short sequences located before the transcription start site (TSS) of a gene (Jáuregui et al., 2003; Pandey and Krishnamachari, 2006).

Promoters act as gene expression regulators through their ability to interact with the enzyme RNA polymerase, thereby initiating transcription. The σ factor moiety of the RNA polymerase, of which there are several types, are involved in the recognition and primary interaction with the promoters. Various bacterial σ factors interact with different promoter sequences that are characterized by particular consensus motifs and properties. Most prokaryotic promoters have two consensus hexameric (six nucleotides) motifs: one centered at position −35 and another centered at position −10 relative to the TSS. For factor σ⁷⁰, the pattern sequences for these motifs are ‘TTGACA’ and TATAAT’ for positions −35 and −10, respectively, and are separated by ∼17 non-conserved nucleotides (Lewin, 2008).

As an analogy, the downstream sequences (genes) represent the “computer memory” while the upstream sequences (promoters) represent the “computer program” that acts on this memory. The study of promoters can provide new models for developing computer programs and for explaining how they operate (Howard and Benson, 2002). Despite the importance of promoters in gene expression, the shortness of their sequences, many of which are not highly conserved, makes them difficult to detect when compared to genes sequences. This characteristic limits the accuracy of in silico methods because many nucleotide alterations may not be significant in terms of promoter functionality (Howard and Benson, 2002; Burden et al., 2005; Kanhere and Bansal, 2005b).

There are many machine learning approaches for promoter recognition and prediction, including Hidden Markov Models – HMM (Pedersen et al., 1996), Support Vector Machines – SVM (Gordon et al., 2003) and Neural Networks – NN. The earliest NN used for promoter prediction had a simple architecture (Demeler and Zhou, 1991; O’Neill, 1991). In these papers, the prediction had good accuracy but the number of false positives was high. Mahadevan and Ghosh (1994) used two NN: one to predict motifs and another to recognize the complete sequence. The Neural Networks Promoter Prediction (NNPP) program was implemented by Oppon (2000) and improved by Burden et al. (2005), who included information about the distance between TSS and the first nucleotide translated, thereby decreasing the number of false positives.

Apart from consensus motifs, promoters have certain physical features, such as stability, curvature and bendability, that make them different from gene sequences, i.e., they are less stable, more curved and more bendable (Kanhere and Bansal, 2005a). The latter authors subsequently used promoter stability information to develop a procedure that recognizes promoters in whole sequences (Kanhere and Bansal, 2005b). However, despite the importance of these physical features, they have not been widely used in NN promoter prediction.

Neural networks are suitable for promoter prediction and recognition because of their ability to identify degenerated, imprecise and incomplete patterns present in these sequences. In addition, NNs perform well when processing large genome sequences (Kalate et al., 2003; Cotik et al., 2005). A further feature is that there is no need for prior knowledge when building a suitable model. An important procedure in NN methods is rule extraction from trained networks that can assist the user in identifying biological rules from the input data (Andrews et al., 1995). In this paper, we describe the use of a NN to predict and recognize prokaryotic promoters by comparing two data sets: (i) nucleotide sequence information and (ii) stability sequence information of E. coli promoters, regardless of the σ factor that recognizes the sequence.

Material and Methods

The promoter sequences used were obtained from the January 2006 version of the RegulonDB database (Gama-Castro et al., 2008). Nine hundred and forty promoters and 940 random sequences were used to train and test the NN. The promoters and sequences represented positive and negative examples, respectively. The random sequences were generated with a probability of 0.22 for guanine (G) or cytosine (C) nucleotides and 0.28 for adenine (A) or thymine (T) nucleotides, based on the distribution of these nucleotides in real promoter sequences (Kanhere and Bansal, 2005a). The examples were shuffled and allocated to one of ten files in order to generate the train and test set. Two simulations were done, one based on nucleotide sequences and the other on stability information. The procedures are described below.

Simulation based on nucleotide sequences

In the simulation using nucleotide sequences (referred to as the sequence-based simulation) the promoters and random sequences were initially aligned with the software ClustalW (Thompson et al., 1994) to accommodate the variable sequence length between the motifs. Without this initial alignment, the NN does not provide good accuracy. The alignment introduced gaps in the sequences, represented by a short line (-). The gaps were inserted where necessary (at the beginning, middle or end of a sequence) (Figure 1). The short line (-) was removed from the beginning and end of the sequence to avoid incorrect learning by the NN. Consequently, the resulting promoter sequences contained 72 nucleotides. After alignment, the nucleotides and gaps were encoded using a set of four binary digits as described by Demeler and Zhou (1991): A = 0100, T = 1000, C = 0001, G = 0010 and “-” = 0000.

Figure 1.

Examples of promoter sequences aligned by ClustalW software.

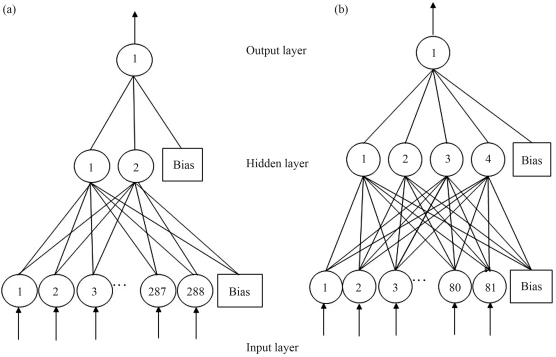
The architecture used to classify the sequences had 288 input neurons (72 bp x four digits for each nucleotide), two neurons in the hidden layer and one neuron in the output layer (Figure 2a). The presence of a large number of neurons in the hidden layer or in the output layer did not increase the accuracy of the procedure.

Figure 2.

(a) Architecture of the best NN used to classify promoter sequences in the sequence-based simulation. There were 288 neurons in the input layer, two neurons in the hidden layer and one neuron in the output layer. (b) Architecture of the best NN used to classify promoters in the stability-based simulation. There were 81 neurons in the input layer, four neurons in the hidden layer and one neuron in the output layer.

Simulation using promoter sequence stability

The stability of DNA molecules can be expressed in terms of their free energy (ΔG), which in turn depends on the mononucleotide and dinucleotide composition (SantaLucia and Hicks, 2004). The stability of a DNA duplex can be predicted from its sequence based on the contribution of each nearest-neighbor interaction (SantaLucia and Hicks, 2004; Kanhere and Bansal, 2005a). The contribution of each dinucleotide is described in SantaLucia and Hicks (2004).

To do the simulation using the free energy information, denoted as the stability-based simulation, ΔG was calculated using the following formula, described in SantaLucia and Hicks (2004)a and Kanhere and Bansal (2005a):

$$\Delta G^0\hspace{0.17em}=\hspace{0.17em}\Delta G_{\mathit{\text{ij}}}$$ (1)

where ΔG⁰_ij is the standard free energy change for dinucleotides of type ij. The original formula described in Kanhere and Bansal (2005a) was modified to adjust its adequacy to the goals of this paper. The best architecture obtained to classify the sequences had 81 neurons in the input layer, four hidden neurons and one output neuron (Figure 2b).

Training and analysis procedures

Both simulations were done in the R Environment (R Development Core Team, 2005). The algorithm back-propagation (BP) was chosen because it is the most popular algorithm for training feedfoward networks (Kalate et al., 2003). NNs based on the BP training algorithm have been successfully used for various applications in biology involving non-linear input-output modeling and classification (Mahadevan and Gosh, 1994; Kalate et al., 2003; Burden et al., 2005). The ten-fold cross-validation method was used to obtain statistically valid results. The k-fold cross-validation (k-FCV) technique consists in randomly sharing the examples’ archive in k equal portions. The train and validation were repeated k times, using k-1 archives to train and k^th archives for validation. In each interaction, the validation archive had a different k (Polate and Günes, 2007).

The accuracy (A), specificity (S) and sensitivity (SN) were calculated from the number of true positives (TP), true negatives (TN), false positives (FP) and false negatives (FN). The TP were promoter sequences classified as promoters, TN were random sequences recognized as non-promoters, FP were random sequences classified as promoters and FN, promoters classified as non-promoter sequences. The formulas used are given below:

$$A\hspace{0.17em}=\hspace{0.17em}\frac{\mathit{\text{TP}}\hspace{0.17em}+\hspace{0.17em}\mathit{\text{TN}}}{\mathit{\text{TN}}\hspace{0.17em}+\hspace{0.17em}\mathit{\text{TP}}\hspace{0.17em}+\hspace{0.17em}\mathit{\text{FN}}\hspace{0.17em}+\hspace{0.17em}\mathit{\text{FP}}}$$ (2)

$$S\hspace{0.17em}=\hspace{0.17em}\frac{\mathit{\text{TN}}}{\mathit{\text{TN}}\hspace{0.17em}+\hspace{0.17em}\mathit{\text{FP}}}$$ (3)

$$\mathit{\text{SN}}\hspace{0.17em}=\hspace{0.17em}\frac{\mathit{\text{TP}}}{\mathit{\text{TP}}\hspace{0.17em}+\hspace{0.17em}\mathit{\text{FN}}}$$ (4)

An input sequence was classified as a promoter if its output lay between 0.5 and 1.0. Otherwise, it was considered as a non-promoter (Kalate et al., 2003).

Rule extraction

Neural networks are applicable to many different problems, but the learning process is complex (Andrews et al., 1995). How a NN classifies a given sequence as promoter or non-promoter can be understood based on rule extraction. Here, we extracted rules using two approaches:

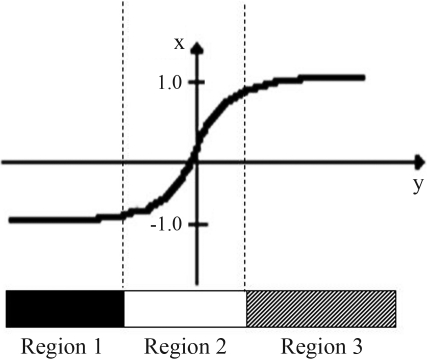
1. Rules based on hidden neurons: The sigmoid function was divided into three regions (Figure 3). For each input, the region of the sigmoid function corresponding to the best fit of the activation function of the hidden neurons was identified. The maximum number of combinations was 3ⁿ, where n is the number of neurons in the hidden layer. However, all of the possible combinations do not occur, and only the more frequent combinations were considered since they best represented the input data. The result of this approach was a rule prototype, which we defined as the input data set average. The rule can be written as a linear equation: “If x ≅ prototype then y = constant of a linear equation + (coefficients of the linear equation)”. Here, x is an input example, y corresponds to the NN output and the coefficients of the linear equation are the nucleotides of the sequence. This approach is referred to as FAGNIS, according to Cechin (1998). Rule extraction was done in the R Environment (R Developed Core Team, 2005).

2. Rules by a decision tree: These rules were obtained using the software Weka with the algorithm J-48 (Witten and Frank, 2005). The decision tree is an analytical tool to find rules and relations by subdividing information in the data analyzed. The tree consists of nodes that represent attributes and arches from the nodes that were assigned possible values for these attributes. The first node corresponds to the root from which the other nodes were derived. These derived nodes are referred to as leaf-nodes and represent the distinct classes of each training set. The possible ways of running the tree can be written in an if-then rule format.

Figure 3.

The three regions defined in the sigmoid function to analyze the input data and to extract rules from the trained NN.

Results and Discussion

Classification analysis

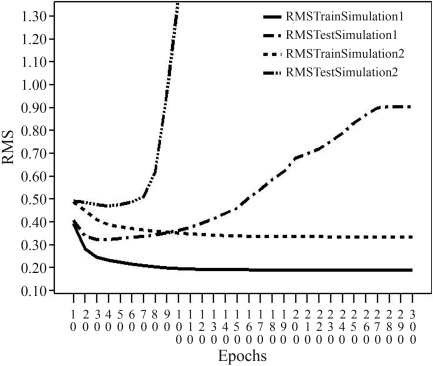
Analysis of the results initially involved a root mean square (RMS) evaluation. Figure 5 shows the RMS plot of the best NN architecture for both simulations. In the sequence-based simulation, the lowest RMS was achieved with 30 train epochs, i.e., this number of epochs yielded the best accuracy, which was 0.8 (80%) with a standard deviation of 0.04 (4%). For the stability-based simulation, the best NN yielded an RMS with 40 train epochs (Figure 3), an accuracy of 0.68 (68%) and a standard deviation of 0.023 (2.3%).

Figure 5.

Plot of the RMS for 300 train epochs. The RMS train showed a slow decrease in both simulations. In this test, the lowest RMS value was observed at epoch 30 in the sequence-based simulation and epoch 40 in the stability-based simulation.

The quality of the classification is shown by the confusion matrix for both simulations (Table 1). The specificity and sensitivity of the results for the sequence-based simulation was 0.9 (90%) and 0.65 (65%), respectively. For the stability-based simulation, the values for these two parameters were 0.7 (70%) and 0.67 (67%), respectively.

Table 1.

Confusion matrix for the NN architecture described in the text. The sequences were classified as promoters and non-promoter (random) sequences.

	Sequence-based simulation		Stability-based simulation
	Classified as promoter	Classified as non-promoter	Classified as promoter	Classified as non-promoter
Promoter	66	28	63	31
Non-promoter	9	85	28	66

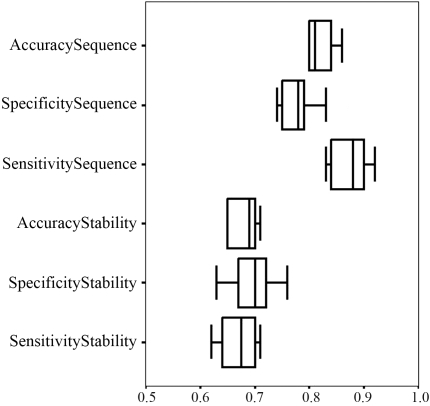
The box plot (Figure 4) shows the distribution of the values for accuracy, specificity and sensitivity in the tenfold cross-validation. The central line represents the median, the base of the rectangle is proportional to the number of cases, and the lower and upper boundaries of the box show the lower and upper quartiles, respectively. The length of the box therefore corresponds to the inter-quartile range, which is a convenient and popular measure of the spread. For both simulations, the small length of the boxes indicated low variation in accuracy and sensitivity; specificity showed the greatest variation.

Figure 4.

Box plot for accuracy, specificity and sensitivity in the ten-fold cross-validation for both simulations.

The classification results showed that the NN provided a good generalization for the input data in the sequence-based simulation. The NN classified random sequences more correctly than it did promoter sequences (Table 1). This fact probably reflected the incomplete conservation of the consensus hexameric sequence of the promoters and the presence of several consensus promoter sequences for each σ factor (Lewin, 2008). The NN was unable to learn a single pattern for the input data because of different motifs present in the σ factor family, e.g., the consensus sequences for σ24 are ‘CTAAA’ for the −35 region and ‘GCCGATAA’ for the −10 region. Consequently, the NN created a general classification rule based on similar features for all promoter sequences. For this reason, the sensitivity observed here was lower than that observed in other papers. This finding was reflected in the low number of epochs necessary for learning, an indication that the input data had noise typical of biological data (Losa et al., 1998). In contrast, the results from the stability-based simulation showed that the NN was unable to correctly classify the random sequences (Table 1). This finding can be explained by the lack of data synchronization since it was not possible to pre-align the sequences. Sequence alignment was not feasible because it was impossible to obtain stability values for the gaps inserted during alignment.

The results for the sequence-based simulation were very similar to those reported by others (Table 2). Burden et al. (2005) reported a specificity of 0.6 (60%) and sensitivity of 0.5 (50%) for their NN-based analysis. The usefulness of this tool (referred to as NNPP) was improved when the estimated probability that a given sequence was a true promoter was reduced by 60%. Gordon et al. (2003) developed an SVM-based approach using a sequence alignment kernel and reported an accuracy of 0.84 (84%), a specificity of 0.84 (84%) and a sensitivity of 0.82 (82%). Web tools such as BPROM claim an accuracy of 0.8 (80%). The papers or web tools described are only for σ⁷⁰ promoter sequences whereas our NN used all known promoter sequences. In addition, in most previous studies the number of sequences used was lower than that used here. The results of the stability-based simulation were poor, but this simulation can be useful for subsequent predictions and can expand the range of tools for promoter prediction.

Table 2.

Comparison of different methods used to calculate accuracy, specificity and sensitivity.

Procedure	Accuracy	Specificity	Sensitivity	Author
Sequence-based simulation	0.8	0.9	0.65	This paper
Stability-based simulation	0.68	0.7	0.67	This paper
Sequence alignment kernel	0.84	0.84	0.82	Gordon et al. (2003)
NNPP	N.I	0.6	0.5	Oppon (2000)
NNPP 2.2	0.49	N.I	N.I	Burden et. al (2005)

The numbers in bold indicate the highest scores for each parameter. N.I. = no information.

Rule extraction in the sequence-based simulation

In this simulation, five rules were extracted by the FAGNIS method. The decision tree was obtained by using the J-48 algorithm (Figure 7). To facilitate comprehension, only promoter rules will be discussed. The rules from FAGNIS yielded the promoter prototype shown in Figure 6 and identified the nucleotides that were most important in the learning process.

Figure 7.

Decision tree based on the J-48 algorithm. (a) Decision tree for the sequence-based simulation data. (b) Decision tree for the stability-based simulation data.

Figure 6.

Rule prototype for promoter sequence obtained from NN learning.

All of the nucleotides underlined in Figure 6 were the most important for the learning process. The nucleotides located in regions −35 and −10 (read left to right) are indicated in bold. The similarity of the nucleotides identified by the prototype with the consensus biological sequence was clear since most of the sequences belonging to the data set were recognized by σ⁷⁰. In addition to these consensus nucleotides, there are other nucleotides that are crucial for NN but they are not located in regions of known biological importance. The nucleotides in parentheses all have equal importance for NN. The pattern shown here was also observed with the decision tree discussed below.

The ten-fold-cross-validation method was used to obtain statistically valid results for the extraction rule based on the decision tree. The resulting tree had 31 nodes and 25 leaves (Figure 7a). The frequency of correctly classified sequences was 63% and the promoter precision was 68%. The trees showed nucleotide 25 (located in the −35 region) as the root. The presence of guanine at this position was sufficient to identify a given sequence as a non-promoter. The other nucleotides present in the rules were located in the −10 region that included nucleotides 46 to 54, approximately. Some of the rules identified by this approach included:

1. If Promoter then nucleotide_25 = A, nucleotide_45 = T and nucleotide_46 = A or G

2. If Promoter then nucleotide_25 = T and nucleotide_47 = A or T

3. If Promoter then nucleotide_25 = T and nucleotide_47 = C and nucleotide_50 = A or T

4. If Promoter then nucleotide_25 = C and nucleotide_45 = T

These rules shared many similarities with the prototype obtained with the trained NN. Clearly there is a strong relationship among the nucleotides located in the biological motifs. Despite the incomplete conservation of these motifs, they are still an important feature used by NN for learning. The rules generally agreed with current biological knowledge.

Rule extraction in stability-based simulations

For this simulation, rule extraction using FAGNIS generated seven rules, of which only one classified sequences as a non-promoter (rule 1). The prototypes of the rules are shown as plots for better comprehension (Figure 8). In four promoter prototypes (rules 4 to 7) there was a decrease in the ΔG values in the −10 region (located between nucleotides 45 and 52). These rules were valid for 135 promoter sequences, which were classified based on these rules. The two promoter prototypes that accounted for the majority of promoter sequences (total of 533) showed no evident decrease in this region. Four patterns of promoters were identified in the plots, in contrast to NN learning, and this explains the poor rate of correct sequence classification.

Figure 8.

Plot for the stability-based simulation data. This plot represents the rule prototype obtained with the FAGNIS method for rule extraction. Only rule 1 is for non-promoter sequences; the other rules are for prototype promoter sequences.

The rules obtained using the J-48 algorithm were extracted from the decision tree shown in Figure 7b. The ten-fold cross-validation method was also used. The resulting tree had 21 nodes and 11 leaves. The success rate for correctly classified sequences was 66.8% and the promoter precision was 68%. The rules that classified a sequence as a promoter are shown in Figure 7b. These rules showed that there was a relationship between the two consensus motifs of promoters. The root of the tree was nucleotide 49 (located in the −10 region), but there were other important nucleotides in the −10 and −35 regions. Some nucleotides (7, 13, 16, 17 and 32) occurred at positions with no known biological function. This analysis also revealed the stability low value of the nucleotides and the absence of guanine at position 49. This fact can explain the high ΔG value that this nucleotide has when it occurs as a neighbor of another nucleotide.

In conclusion, the usefulness of NN for promoter prediction and recognition was assessed using two data sets. The accuracy of the sequence-based simulation was 0.80 ± 0.04 while that of the stability-based simulation was 0.68 ± 0.02. These results were comparable to those reported in the literature. The rules extracted from NN learning can help to identify the most important nucleotide promoter patterns. The pattern obtained is representative of all sequences, despite the σ factor that recognizes each promoter. The data obtained by this approach can help in promoter prediction and increase our knowledge of the biological role of promoters. Generally, NN-based methods and machine learning techniques for promoter prediction rely on the stability of promoter sequences less frequently than on nucleotide sequence information. The confusion matrix showed that NN could differentiate promoters and random sequences based on nucleotide information, but this was not the case when stability information alone was used. The results of this study indicate that the use of nucleotide sequence and structural characteristics as input data may help to improve the prediction of bacterial promoters. This finding should provide a stimulus for developing more efficient algorithms for predicting such promoters.