Impact of myocyte strain on cardiac myofilament activation

Abstract

When cardiac myocytes are stretched by a longitudinal strain, they develop proportionally more active force at a given sub-maximal Ca²⁺ concentration than they did at the shorter length. This is known as length-dependent activation. It is one of the most important contributors to the Frank–Starling relationship, a critical part of normal cardiovascular function. Despite intense research efforts, the mechanistic basis of the Frank–Starling relationship remains unclear. Potential mechanisms involving myofibrillar lattice spacing, titin-based effects, and cooperative activation have all been proposed. This review summarizes some of these mechanisms and discusses two additional potential theories that reflect the effects of localized strains that occur within and between half-sarcomeres. The main conclusion is that the Frank–Starling relationship is probably the integrated result of many interacting molecular mechanisms. Multiscale computational modeling may therefore provide the best way of determining the key processes that underlie length-dependent activation and their relative strengths.

Introduction

This review article focuses on how myocyte strain (defined here, in the engineering sense, as the relative length of the cell) influences myofilament activation. The basic experimental finding is clear and universally agreed; cardiac myocytes develop more force if they are activated at a longer length. What is much less clear and indeed rather controversial is why this happens. Identifying the underlying principles is important because strain-dependent activation is probably the most important component of the Frank–Starling mechanism, and none of us would be alive for very long if it ceased to operate. In addition, if we could deduce how myocytes increase force development “naturally” in response to a length change, we might then be able to develop a treatment that stimulated the same pathway(s) “therapeutically.” This would provide a novel treatment for heart failure where muscle contraction seems to be depressed at all myocyte lengths.

Review of the Frank–Starling mechanism

As every undergraduate physiologist knows, the Frank–Starling mechanism is important because it ensures that the average amounts of blood pumped out of the left and right ventricles are equal. This ensures that blood does not have the opportunity to accumulate in either the systemic or pulmonary circulations and consequently (since total blood volume is essentially constant over the time-scale considered here) that neither side of the heart ever “runs dry.” Were a systematic imbalance to occur, the consequences would be catastrophic. If your left ventricle pumped 1 ml more than your right ventricle during each heartbeat, your pulmonary circulation (normally about 0.6 l) would be drained in less than 10 min. Failure would occur even sooner if you exercised and consequently increased your heart rate.

Clearly, because of their bias, a muscle physiologist might assume that equalizing the outputs of the left and right ventricles is too important to be left solely to the nervous and/or endocrine systems. However, evidence supporting this hypothesis did not start to accumulate until the nineteenth century [30], and it was not until 1895 that Otto Frank demonstrated that the basic mechanism existed in an isolated frog heart [12]. Frank showed that when he clamped the aorta leading from a frog heart (rendering all subsequent contractions isovolumic), the systolic pressure developed by the ventricle increased with the diastolic fluid volume. Two decades later, the more famous Ernest Starling, together with his collaborators, showed that when a canine heart–lung preparation was perfused with oxygenated blood, the stroke volume of the right ventricle increased as soon as the filling pressure in the right atrium was raised [46]. Left ventricular stroke volume increased thereafter as the blood flow through the lungs quickened and left atrial filling pressure started to increase. Since both Frank’s and Starling’s experiments were performed using isolated preparations, they demonstrated that the basic mechanism underlying length-dependent activation is intrinsic to the heart itself. Put simply, the ventricles pump more blood when they fill more during diastole, and they do this even when they are removed from the body.

If the total blood volume is assumed constant, this basic principle is sufficient to ensure that, on average, your ventricles pump equal amounts of blood. If, for some unspecified (and unimportant) reason, your left ventricle pumped more blood than your right, the “excess” blood would quickly work its way through the systemic circulation and arrive at the right atrium, at which point, cardiac output from the right ventricle would increase as a result of strain-dependent activation. Similarly, excess pumping from the right ventricle increases left ventricular output as soon as the blood passes through the pulmonary circulation. The two sides of the heart therefore act as demand pumps increasing their outputs as greater volumes of blood arrive at their inputs.

Toward the underlying mechanism

Although experiments performed with isolated hearts provide much of the information required for system-based analyses, they do not provide a great deal of information about the mechanisms underlying the Frank– Starling relationship. Consequently, beginning in the 1970s, many authors tried to investigate length-dependent activation in successively smaller preparations. These types of experiments were (and still are) demanding because of numerous technical difficulties including obtaining a stable preparation, preventing tissue hypoxia, and accounting for series compliance in the ends of the muscle. Eventually, however, length-dependent activation was demonstrated in papillary muscles [42], trabeculae [53], and ultimately in single cells [34]. This final step in particular was an important breakthrough because it demonstrated that the mechanism or mechanisms underlying length-dependent activation exist within each myocardial cell. The Frank–Starling mechanism is not therefore a “network effect” that is produced in each ventricle by interactions between the myocardial cells; it is an intrinsic property of the cells themselves.

Another important result that started to receive increasing attention in the 1970s was the finding that the force response of a myocardial cell to a sudden change in strain had two phases [42]. If the length of a rhythmically beating myocardial preparation was suddenly increased during the diastolic interval, the peak twitch force was increased during the next contraction producing an “immediate” strain-dependent effect. Force then continued to rise slowly, reaching a new plateau after a few minutes. Decreasing muscle strain by shortening the preparation also produced a two-phased response: a sudden drop in peak force that occurred contemporaneously with the shortening and a slower decline in force over the next few minutes. Again, since both of these effects were evident in small preparations, they seemed to reflect intracellular mechanisms rather than signals from extra-myocyte sources.

The next step in the discovery sequence was to perform experiments with chemically permeabilized samples. These experimental preparations are obtained by destroying the integrity of the cellular membranes by immersing the myocardial samples in a detergent such as triton. This is useful because the experimenter can then alter the ionic concentrations around the myofilaments at will by immersing the preparation in solutions with different compositions. It thus becomes possible to determine whether the strain dependence of contractile force reflects (1) strain-dependent changes in the activating Ca²⁺ signal, (2) strain-dependent changes in the response of the myofilaments to a fixed Ca²⁺ signal, or (3) some combination of the two preceding mechanisms.

The first experiments using chemically permeabilized myocardial preparations were performed by Fabiato and Fabiato [16]. They showed that when cardiac cells were immersed in solutions with a saturating Ca²⁺ concentration (and could thus be considered “maximally activated”), developed force increased with cell strain over a range of lengths comparable to that thought relevant for normal function. This implies that the contractile apparatus itself—the inter-digitating arrays of thick myosin and thin actin filaments—displays strain-dependent force-generating properties. One surprise, however, was that although force did decline when muscle length was reduced below optimal, the drop was not as great as that observed in living cardiac muscle. One interpretation of this result is that in living myocardium, muscle strain alters the relative activation level as well as the maximal force-generating capacity.

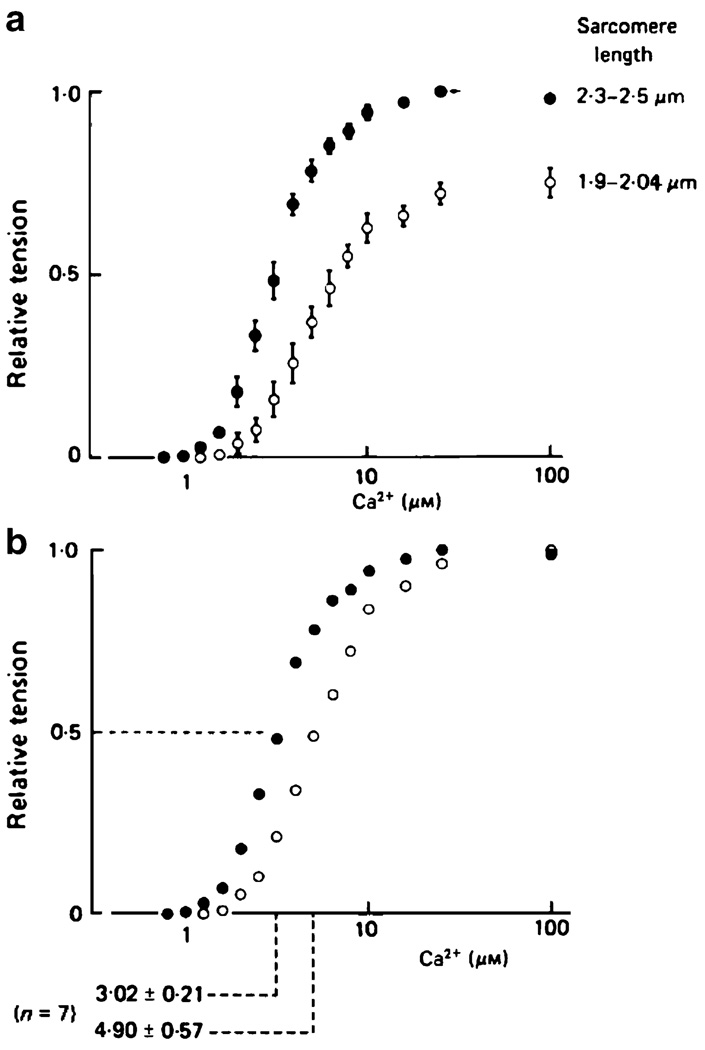
Another interesting result, summarized in Fig. 1, was obtained by Hibberd and Jewell using chemically permeabilized rat ventricular trabeculae [28]. They fitted their measurements of developed tension to a formula of the form

$$\text{Relative tension}=\frac{{[{\text{Ca}}^{2+}]}^n}{{[{\text{Ca}}^{2+}]}^n+{[{\text{Ca}}_{50}^{2+}]}^n}$$ (1)

and showed that Ca₅₀ ²⁺, the Ca²⁺ concentration required to produce half the maximal amount of force, was lower when the muscle was held at a longer length. It is now quite common in this research field to describe Ca²⁺ concentrations using pCa values where pCa = −log₁₀[Ca²⁺]. Hibberd and Jewell’s result therefore corresponds to an increased pCa₅₀ value, or a left-shift of the tension–pCa curve, with increasing sarcomere length.

Fig. 1.

Ca²⁺–force curves for chemically skinned rat ventricular muscle. Reproduced from Fig. 4, Hibberd and Jewell [28] with permission. The top panel shows pooled force data from seven preparations normalized to the maximal force generated by each muscle sample at the longer length. The bottom panel shows the same data normalized to the maximal force generated by the preparation at each length. The Ca²⁺ concentration required to produce half the maximal amount of force is lower at the longer sarcomere length

Hibberd and Jewell’s observation of length-dependent Ca²⁺ sensitivity has substantial physiological significance. Unlike skeletal muscle, where a saturating amount of Ca²⁺ is released from the sarcoplasmic reticulum during a contraction, cardiac muscle is never maximally activated in vivo. This means that the muscle operates on a fairly steep part of its tension–pCa curve. The increased strain imposed on cardiac cells when ventricular filling is enhanced therefore has the potential to increase developed force in two distinct ways. It can increase the number of cross-bridges that are able to participate in the contraction by optimizing filament overlap, and it can shift the system’s tension–pCa curve to the left, thus producing more force for a given Ca²⁺ signal. These effects seem to reinforce each other in living muscles and produce a very robust response, as is probably required for a mechanism as important as the Frank–Starling relationship.

Although chemically permeabilized muscle preparations have many advantages for this type of research work, they do also have some disadvantages. One of these is that they are not particularly stable. If a permeabilized ventricular preparation is held in maximally activating solution, for instance, contractile force starts to decline after a few tens of seconds. This makes it difficult to test whether the slow increase in force observed after a sudden length change results directly from altered behavior of the contractile apparatus or from alternative mechanisms.

The next breakthroughs therefore came again from experiments performed using “intact” (living) myocardial preparations. First, ter Keurs et al. [53] showed that electrically stimulated rat trabeculae exhibited length-dependent activation and suggested that “both calcium release from the sarcoplasmic reticulum and calcium binding by the myofilaments” contribute to the effect. Then Allen and Kurihara [1] used aequorin (a naturally occurring photoprotein that luminesces in the presence of Ca²⁺) to investigate whether the intracellular Ca²⁺ transient, the signal for activation, changed when a cell was suddenly strained. These experiments showed that the initial jump in developed force produced by a step increase in strain occurred without a change in the activating Ca²⁺ signal. However, the second slow phase of the force response was accompanied by a gradual increase in the peak Ca²⁺ signal.

The Frank–Starling relationship thus seems to have at least two cellular-level mechanisms. One is a change in the force developing characteristics of the myofilaments. The other involves changes to calcium handling mechanisms. The former effect seems to be much bigger than the latter and has become known as strain or length-dependent activation. It will be the focus of the remainder of this review. The latter mechanism is important and could arguably be simpler to target with pharmaceutical treatments, but will not be considered further in this work.

Current state of research in the field

Although it is now more than 100 years since Otto Frank’s pioneering work, the mechanistic basis of the Frank–Starling relationship is still unclear. Virtually everybody agrees that cardiac muscles develop more force when they are activated at longer lengths and that this is critically important for organ and thus whole-body function. It is also widely accepted that the Ca²⁺ sensitivity of cardiac muscle increases with muscle strain (that is, tension–pCa curves are left-shifted at long lengths). Beyond this point, however, things start to become quite controversial. For example, many active researchers think that the strain dependence of the Ca²⁺ sensitivity is related to some sort of cooperative mechanism (that is, changes in the local Ca²⁺ concentration produce a more than proportional change in active force) but even this is disputed by some (for example, [44]).

Work in the area has been dominated for the last few decades by reductionist approaches that seek to find the fundamental molecular mechanisms that underlie strain-dependent activation. This research has progressed to the extent that some scientists have started to focus on specific regions (and, in some cases, specific residues) of sarcomeric proteins. This is obviously very exciting, both for those interested in the basic mechanisms underlying strain-dependent activation and for those looking for “druggable” targets for heart failure therapies. It is pertinent to note, however, that different groups are currently focusing on different molecules. For example, the research team led by one of the editors of this journal issue, Dr. de Tombe, has published data [50] that “suggest that the presence of threonine at position 144 (in cardiac Troponin I) or 112 (in slow skeletal Troponin I) is both necessary and sufficient to impart length-dependent activation properties upon the cardiac sarcomere” [14]. In contrast, the other editor of this journal issue, Dr. Granzier, has recently published an article which supports the view that titin-based passive tension is important for strain-dependent calcium sensitivity [35].

If they took an extreme view, scientists favoring reductionist approaches might argue that the Frank–Starling mechanism could reflect either a specific interaction with troponin I, or a particular behavior of titin molecules, but not both. To this author, it seems more likely that molecular mechanisms are not a zero-sum game and that if one mechanism is important it does not necessarily mean that other mechanisms cannot be important too. My view is that many different molecular mechanisms probably have to work together inside the sarcomere to produce strain-dependent activation. The Frank–Starling relationship is compromised if any one of the underlying mechanisms fails, in the laboratory as the result of an experimental intervention, or in the clinic as a result of disease process. However, it is misleading to think that the Frank–Starling mechanism is due to any one of the parts in isolation. It is instead the end product of a complex system of interacting parts. Looked at in this way, strain-dependent activation emerges as a property of the contractile apparatus and is not the sole product of one of its isolated components.

What then are the main players that might contribute to strain-dependent activation? Research in recent years has focused on three general mechanisms: myofibrillar lattice spacing, titin-based effects, and cooperative activation. We will discuss each of these mechanisms briefly in the following paragraphs and then present two more potential contributors toward the end of the review.

Myofibrillar lattice spacing

Single cardiac cells behave as almost-constant volume systems [37]. This means very simply that if a cell is stretched longitudinally, it must become narrower. Since the myofibrils are comprised of a finite number of thick and thin filaments, the radial separation of these filaments must therefore diminish as the cell lengthens. It is widely recognized (for example, [20]) that this geometrical effect could underlie strain-dependent activation by increasing the local concentration of myosin heads near binding sites on the actin filaments. All other things being equal, the increased likelihood of S1 myosin heads being near binding sites would raise the probability of cross-bridges attaching to the thin filament and subsequently undergoing a force-generating power stroke. It is also possible that reducing the radial separation of the filaments increases the number of cross-bridges undergoing power-strokes by biasing the mean orientation of the S1 heads in such a way as to increase the rate constant for the force-generating transition.

One of the appealing features of this mechanism is that it is simple. At first thought, it seems almost inevitable that pushing myosin heads nearer the thin filaments will result in more force generation. Unfortunately, the experimental data to support this conjecture are much less clear. One of the first experiments to directly test the hypothesis was performed by McDonald and Moss [38]. These authors measured tension–pCa relationships using chemically permeabilized rat ventricular myocytes and then repeated the measurements when the preparations were immersed in solutions containing 2.5% dextran. Dextran is composed of many glucose molecules, and it is too large to diffuse between the myofilaments. It therefore exerts an osmotic stress on permeabilized muscle preparations and causes them to shrink. This is helpful because it allows the experimenter to reduce the radial separation of the actin and myosin filaments without having to change the preparation’s mean sarcomere length. McDonald and Moss observed that dextran reduced the pCa₅₀ value measured at short sarcomere lengths to a value close to that measured in cardiac cells without dextran at long sarcomere lengths. They therefore concluded that radial separation was a major component of length-dependent activation.

One of the potential weaknesses of the study was that the authors could not actually measure the radial spacing of the thick and thin filaments. Instead, McDonald and Moss monitored the experimental preparations with video microscopy and showed that dextran reduced their width at short sarcomere lengths close to that measured in the same preparations without dextran at long sarcomere lengths. While this is a practical solution to a difficult experimental problem, it is obviously possible (as McDonald and Moss noted) that dextran changes the cross-sectional profile of cardiac cells and/or their myofibrillar packing. This would mean that the preparation widths measured in these experiments did not provide an accurate indication of the radial separations of the thick and thin filaments.

Some years later, de Tombe and his colleagues performed more complex experiments which tried to overcome this potential issue [32]. They measured the average radial separation of the myofilaments by placing muscle preparations in an X-ray beam and recording the reflections. These experiments obviously have their own potential pitfalls [40], but the results did suggest that tension–pCa curves can be altered by cell strain without having to have an accompanying change in the radial separation of the myofilaments. Explaining these data is a formidable challenge for proponents of the myofibrillar lattice spacing hypothesis.

Titin-based effects

Titin is an extremely large protein (molecular weight >3 MDa) that forms single molecule filaments that run from near the M-line to the Z-line in each half-sarcomere. It is thought to be the main determinant of passive resting tension in cardiac sarcomeres under physiological conditions, and it has also been implicated as a key player in strain-dependent activation. Current thinking seems to suggest that it may influence activation in several different ways.

At long sarcomere lengths, the six titin molecules that surround each half-thick filament produce a radial as well as a longitudinal force vector. The radial component acts to pull the thick and thin filaments together and thus could contribute to length-dependent activation by keeping myosin heads close to binding sites on actin filaments. The evidence supporting this hypothesis came initially from experiments in which the Ca²⁺ sensitivity of force development was monitored while passive longitudinal tension (and thus presumably radial tension, which is harder to measure) was manipulated, either by treatment with trypsin [10, 22] or by changing the length of the preparation [11]. Recently new experimental data obtained with a genetic murine model have been published which supports these findings. The publication of Lee et al. [35] describes results obtained with cardiac myocytes in which the N2B region of titin has been genetically deleted. These myocytes have higher resting tensions (because the shorter titin molecules are more extended at a given sarcomere length) and importantly also exhibit greater strain-dependent activation.

While there are obvious similarities between the titin-based radial force mechanism described immediately above and the myofilament separation mechanism described in the previous section, titin also seems to have the potential to influence cross-bridge interactions in a more direct way. Some of the evidence for this comes from work by Muhle-Goll et al. [41]. These authors showed that the fn3 domains of titin, which are found exclusively in the A-band of the sarcomere, bind to the S1 heads of myosin. Muhle-Goll et al. also demonstrated that the addition of fn3 fragments of titin to the experimental solutions increased the force produced by chemically permeabilized murine myocytes. Intriguingly, the effect on force was greater at long sarcomere lengths than at short so that the muscle was relatively deactivated at short lengths and thus exhibited a striking strain-dependent sensitivity.

While the true mechanism underling strain-dependent sensitivity remains unclear, one could easily imagine that in the experiments of Muhle-Goll et al., the cells were strain sensitive because fn3–myosin interactions kept the S1 heads of myosin tethered close to the thick filament backbone. At long sarcomere lengths, the tethered heads could still interact with the thin filaments (because the myofilaments were packed closely together) but at short sarcomeres lengths the myofilaments were too widely separated for the tethered myosins to reach the nearest actin monomers. As an aside, it is interesting to speculate that other molecules which influence thick filament structure including, for example, myosin binding protein C [27] may be able to influence strain-dependent activation through similar mechanisms.

There are also intriguing data that suggest that the stiffness of titin filaments increases with the prevailing Ca²⁺ concentration (for example, [3, 33, 36]). In cardiac muscle, the effect seems to be isoform dependent [21] so whether or not this mechanism can underlie strain-dependent activation in all types of myocardium remains to be seen. It is also not yet clear that stiffening a structural element can, by itself, augment force production, but it is quite possible that Ca²⁺-dependent stiffening of titin molecules could produce a strain-dependent effect by altering the regulation of other processes.

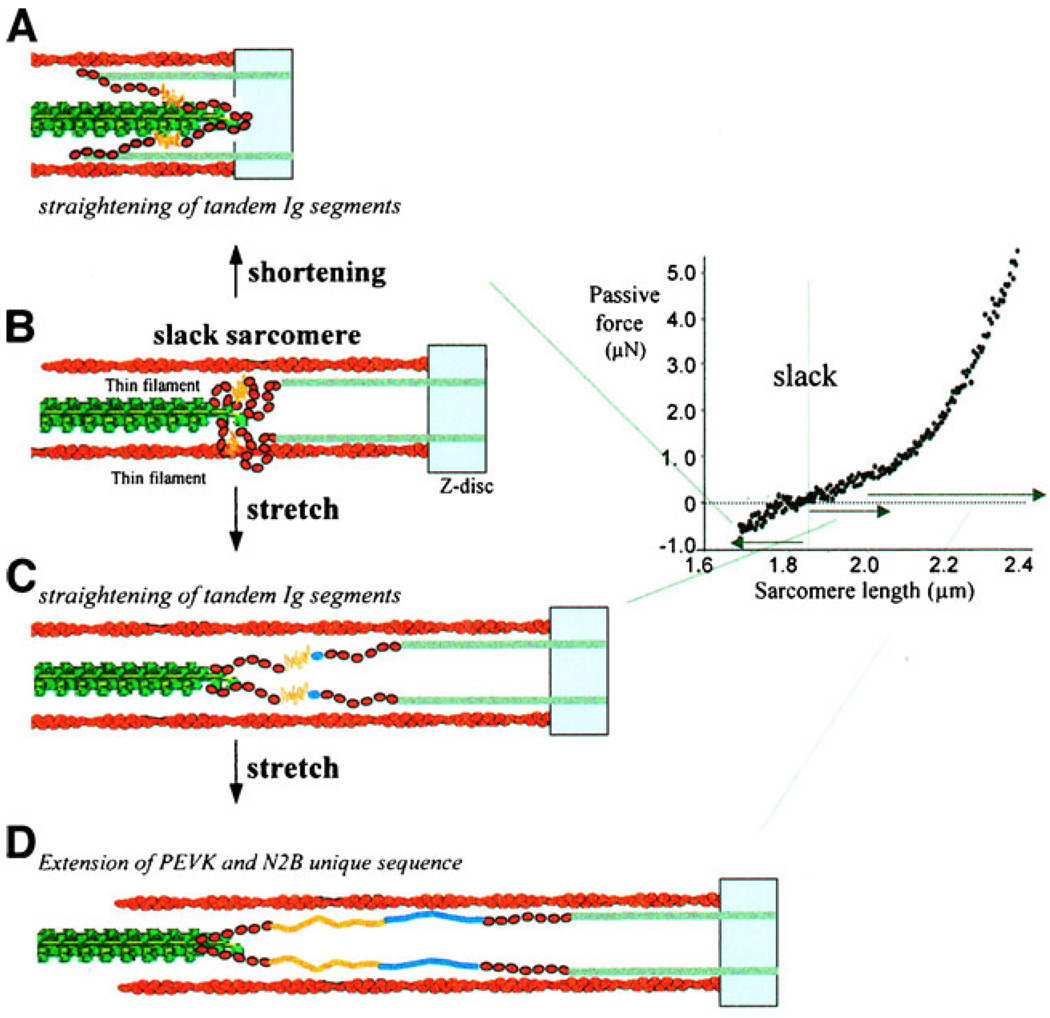
Finally, titin also seems to have the potential to influence the dynamics of cardiac muscle contraction. This aspect of titin’s properties is not readily apparent in measurements performed with isolated cells held at a fixed length, but it could be very important for the function of a beating heart [26]. The inferred behavior results from the fact that although titin molecules bind to the entire length of the thick filament they only bind to the ~100 nm of the thin filament that lies closest to the Z-line. If the half-sarcomere shortens below a length of ~0.9 µm, the unbound region of titin is therefore doubled backward as shown in Fig. 2. Titin molecules can therefore produce a restoring force that acts to lengthen the sarcomere if it shortens below a critical length [25].

Fig. 2.

Passive and restoring force generation by titin molecules. Reproduced with permission from Granzier and Labeit [24]. At short half-sarcomere lengths (a), part of the titin molecule is bent backward producing a recoil force that can help lengthen the half-sarcomere. As the half-sarcomeres length progressively (b, c, d) titin molecules are straightened and eventually stretched by progressive extension of the PEVK and N2B regions

In real hearts, this restoring force could increase ventricular filling and thus contribute to the Frank–Starling effect. Moreover, if the lengthening force caused cross-bridges to detach quickly near the end of a systolic contraction, it could quicken relaxation by destabilizing individual half-sarcomeres [52]. This type of mechanism would not change the biophysical properties of an isolated half-sarcomere, but it could influence the properties of the cells which groups of half-sarcomeres form. We will return to this concept later in the review.

Cooperative activation

When Hill curves Eq. 1 are fitted to experimental tension– pCa data, the Hill coefficient, n, is always greater than 1. Typically, values for cardiac muscle exceed 4 [23]. This implies that at low levels of force generation, small increases in the intracellular Ca²⁺ concentration produce more than proportional changes in active force. Cardiac muscle activation is therefore described as a “cooperative” process.

Since there is just one functional calcium binding site on cardiac troponin C, cooperative activation can only occur if there is at least one feedback process that causally links the probability of cross-bridges undergoing new force-generating power-strokes to the force exerted by cross-bridges that are already attached. The molecular mechanism(s) by which this occurs is/are currently unclear. It could be that force-generating heads recruit other heads to generate more force [4], but it is equally possible that the steepness of the tension–pCa curve reflects the suppression of new force-generating transitions at low overall activation levels [9]. Both types of process could also be “competing” simultaneously.

Many researchers in the field of cardiac muscle biophysics are currently trying to identify the key processes underlying cooperative activation and to determine their relative strengths. A consensus view has yet to emerge, but it is probably obvious to the reader that any mechanism which influences cooperativity could also control strain-dependent activation if its effectiveness varies as a function of sarcomere length. For example, image a situation in which (1) the binding of an S1 myosin head shifts the equilibrium position of the nearest tropomyosin molecule to expose a nearby binding site and (2) that this mechanism is less effective at the Z-disk end of the thin filaments where the tight binding of titin molecules stabilizes the position of the tropomyosin proteins. In this situation, at long sarcomere lengths, when the thick filaments do not overlap with the regions of the thin filaments that bind titin, bound cross-bridges will have the maximum opportunity to recruit other bound cross-bridges. However, at short sarcomere lengths, some myosin heads will bind to thin filaments at positions where they cannot move tropomyosin and thus will not be able to recruit other bridges. All other things being equal, this will result in a lower relative level of force generation at short sarcomere lengths for a given activating Ca²⁺ solution. In other words, the muscle will exhibit strain-dependent contractile activation.

The hypothetical mechanism described above was outlined in very general terms, but a variety of ongoing experiments are now providing information about the specific amino acids that might regulate cooperative mechanisms in real cardiac tissue. For example, as previously mentioned, Dr. de Tombe and his colleagues have shown that rat myocardium exhibits greater strain-dependent activation when there is a threonine residue at position 144 in cardiac troponin I than when a proline is present at the same position [50]. Exactly why this particular amino acid is so critical remains to be determined, but the result does suggest that the field might soon be able to test specific residue-level hypotheses.

In the simplest mathematical models of cooperative activation, the steepness of the tension–pCa curve (quantified by the Hill coefficient) is indicative of the strength of the interactions governing recruitment and/or suppression of new force-generating cross-bridges. If, for example, a single bound S1 head permits the recruitment of two additional myosin heads in the illustrative mechanism described above, the tension–pCa curve would be left-shifted and steeper than if it just recruited a single new attached head. There are, however, more complex mechanisms in which the pCa₅₀ value and the Hill coefficient can change independently of each other.

These more complex mechanisms are particularly relevant to strain-dependent activation because experimental results published by Dobesh et al. [15] suggest that the Hill coefficient does not change markedly with muscle length. This is an important result because in earlier experiments, Kentish et al. [31] had measured length-dependent activation in intact electrically simulated rat trabeculae and then repeated the measurements in the same preparations after they were chemically permeabilized. The results of these challenging experiments implied that the Hill coefficient increased with sarcomere length which raised the possibility that strain-dependent activation could result directly from a length-dependent change in the Hill coefficient. It now seems more likely that strain-dependent activation reflects a change in the Ca²⁺ concentration at which the cardiac muscle starts to activate rather than a change in the slope of the force–Ca²⁺ relationship.

Interesting new data about the molecular mechanisms underlying cooperative activation in cardiac muscle were published 2 years ago by Sun et al. [48]. These authors used polarized fluorescence to measure the orientation of probes attached to troponin C and tested whether the Hill coefficient describing the effects of Ca²⁺ on the probe movement was altered when myosin binding was inhibited by blebbistatin. The results showed that the Hill coefficient remained close to the control value of ~3 even though active force was largely eliminated by the myosin ATPase inhibitor. Sun et al. therefore concluded that the mechanism underlying cardiac cooperativity does not involve myosin binding and must therefore be intrinsic to the thin filaments.

The results of related experiments published in the last few months by Farman et al. [17] support the conclusion of Sun et al. Farman et al. demonstrated that blebbistatin did not alter the strain dependence of the tension–pCa relationship. If, as is commonly thought [2], blebbistatin really does inhibit force in cardiac muscle by preventing cross-bridge binding, this result seems to imply either that length-dependent activation is not a result of strain-sensitive cooperative activation or (as suggested by Sun et al.) that myosin binding is not a key player in cardiac cooperativity.

This view contrasts with the standard interpretation of experimental data collected by Fitzsimons and Moss [18]. These authors measured the tension–pCa curves of chemically permeabilized rat ventricular myocytes both in the absence and the presence of N-ethyl-maleimide-modified myosin S1 (NEM-S1). NEM-S1 molecules are myosin heads that are chemically modified so that they no longer hydrolyze ATP [49]. When they are added to the solution bathing a chemically permeabilized myocardial preparation, they diffuse into the myofilament lattice and bind tightly to the thin filaments in a rigor-like confirmation. If high concentrations of NEM-S1 are added, the chemically modified heads compete with the muscle’s own myosin heads for binding sites on actin, and active force falls. However, when added in low concentrations, the bound NEM-S1 molecules seem to recruit new cross-bridge attachments. The exact mechanism(s) by which this happens in a real muscle is/are not clear, but the treated preparations certainly generate more force at low Ca²⁺ concentrations than they do in the absence of NEM-S1. The net effects are that the measured tension–pCa curves are left-shifted and have a lower maximum slope.

Fitzsimons and Moss went on to show that NEM-S1 reduced the apparent effects of strain-dependent activation. Under control conditions (no NEM-S1), the mean pCa₅₀ value increased by ~0.10 when cell strain was raised by stretching the resting sarcomere length by ~0.3 µm. In the presence of NEM-S1, the corresponding shift in pCa₅₀ was just ~0.02. In other words, recruiting force-generating cross-bridges by a cooperative mechanism activated by NEM-S1 appeared to have almost the same effect on the pCa₅₀ value as increasing the longitudinal strain on the cell. Fitzsimons and Moss therefore concluded that strong-binding cross-bridges are the predominant mediators of strain-dependent activation.

This is clearly a controversial area. There are some published data that suggest that cooperative activation does not involve myosin binding and other data that suggest that it does. It is not yet obvious to this author how the different interpretations will be reconciled, but hopefully all of the data will be explained in the future with a single unifying mechanism. One potential idea, suggested by Rice et al. [43], is that cardiac muscles may regulate force by altering the proportion of thin filaments that are fully active as opposed to the proportion of active sites on each filament.

Alternative mechanisms

All of the mechanisms described to this point have been studied in great detail over the last few decades. Many different groups have performed clever, important work, and each mechanism seems to play at least some role in strain-dependent activation. In this section, we will discuss two other mechanisms that have received less attention to date but could potentially be as important. They are also particularly relevant to discuss in a journal issue that focuses on transduction of mechanical strain because they are based on the hypothesis that length-dependent activation results from localized forces that occur within and between half-sarcomeres.

Compliant realignment

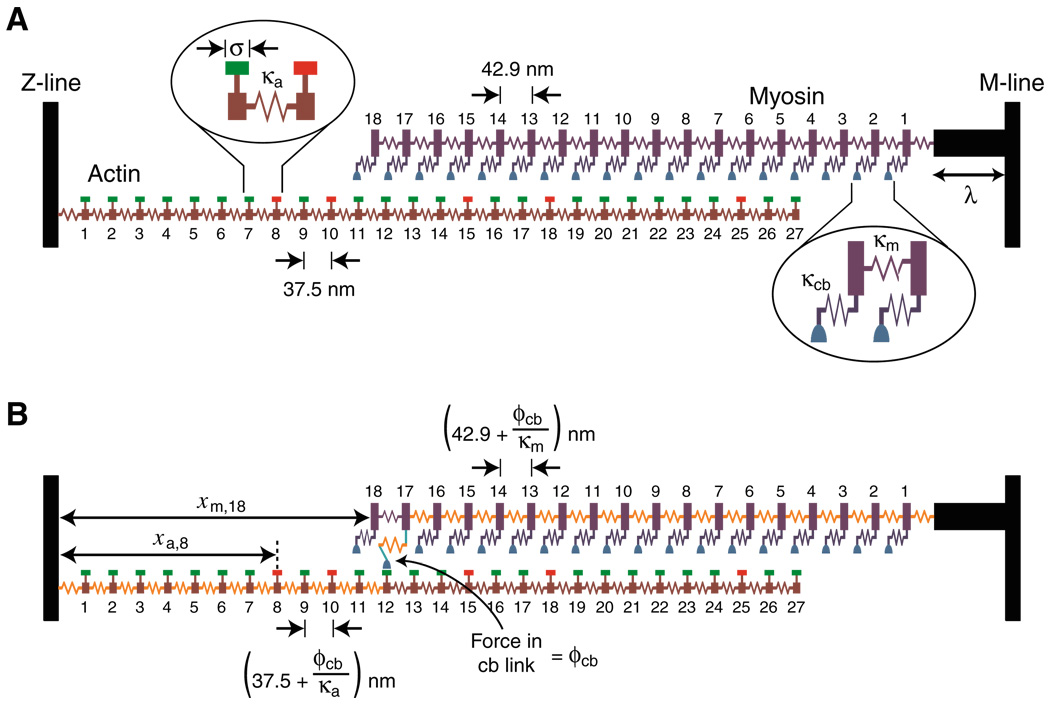
The term “compliant realignment” was introduced by Daniel et al. in a ground-breaking manuscript [13] which describes efforts to calculate the functional consequences of filament extensibility. Experiments performed by A.F. Huxley and his colleagues [19] had initially suggested that the thick and thin filaments were very stiff and therefore that the myosin heads acted as completely independent force generators. Later data, however [29, 54], showed that the filaments do in fact extend slightly when a muscle generates force. This was an important discovery because it implies that the relative position of myosin heads and binding sites can change when a single myosin head attaches. Thus, force development by one myosin molecule can potentially recruit additional myosin heads to the contraction in a cooperative process illustrated in Fig. 3.

Fig. 3.

Schematic diagram of a half-sarcomere composed of two filaments. Reproduced with permission from Campbell [5]. a The spacing of myosin heads along the thick filament is a non-integer multiple of the spacing of binding sites on the thin filament. There are therefore positions (e.g., myosin 10) where a myosin head is aligned close to a binding site on actin and places (e.g., myosin 14) where the myosin head may be positioned too far from a binding site to attach. b If the filaments extend slightly when a myosin head generates force, additional myosin heads may be pulled close enough to actin sites that they can interact with them

At this time, it is difficult to know whether or not compliant realignment plays an important role in length-dependent activation because the field does not have full quantitative information about the biophysical properties of the cardiac sarcomere. For example, X-ray data obtained with frog skeletal fibers suggest that the thick filaments extend by ~3 nm during an isometric contraction [29] (which corresponds to a filament stiffness of order 100 pN nm⁻¹), but similar experiments have yet to be performed with cardiac preparations. It is also unclear whether stiffness in any type of muscle preparation is uniform along the thick and thin filaments or whether it changes systematically along the filament length. This could obviously have a substantial impact on compliant realignment because different parts of the sarcomere might align in different ways. It is also possible that the passive force produced by titin molecules might be sufficient to strain the thick and thin filaments as the muscle lengthened and thus alter the realignment behavior. Such an effect could contribute to length-dependent activation in cardiac muscle even though it would be hard to measure in conventional experiments. Finally, the stiffness of the thick and thin filaments could be tuned [13, 51] to allow more cooperative recruitment of force-generating cross-bridges at high strains.

An alternative possibility is that strain-dependent changes in the geometry of the filament lattice influence the way that individual myosin heads generate force. Williams et al. [55] have advanced this area of research in the last few months by developing an efficient computational method to simulate the radial as well as the longitudinal forces generated by myosin heads. Their initial publication suggests that both the longitudinal forces generated by bound cross-bridges and the kinetics that govern their interactions with the thin filament, vary with lattice spacing. This suggests that the Frank–Starling mechanism could potentially reflect complex orientation-dependent properties of single actin–myosin links. The initial publication of Williams et al. does not describe calculations that test this hypothesis directly, but it is an exciting idea to investigate in future work. Certainly this new approach seems to have substantial potential.

Inter-sarcomere effects

The final potential explanation for strain-dependent activation discussed in this review does not attribute strain-dependent activation to the behavior of individual half-sarcomeres. Instead it reflects the functional consequences of linking half-sarcomeres together to form cell-sized preparations. When this is done, the half-sarcomeres can no longer operate independently of each other and instead interact to produce emergent mechanical properties that are not easily predicted from the theoretical behavior of a single half-sarcomere.

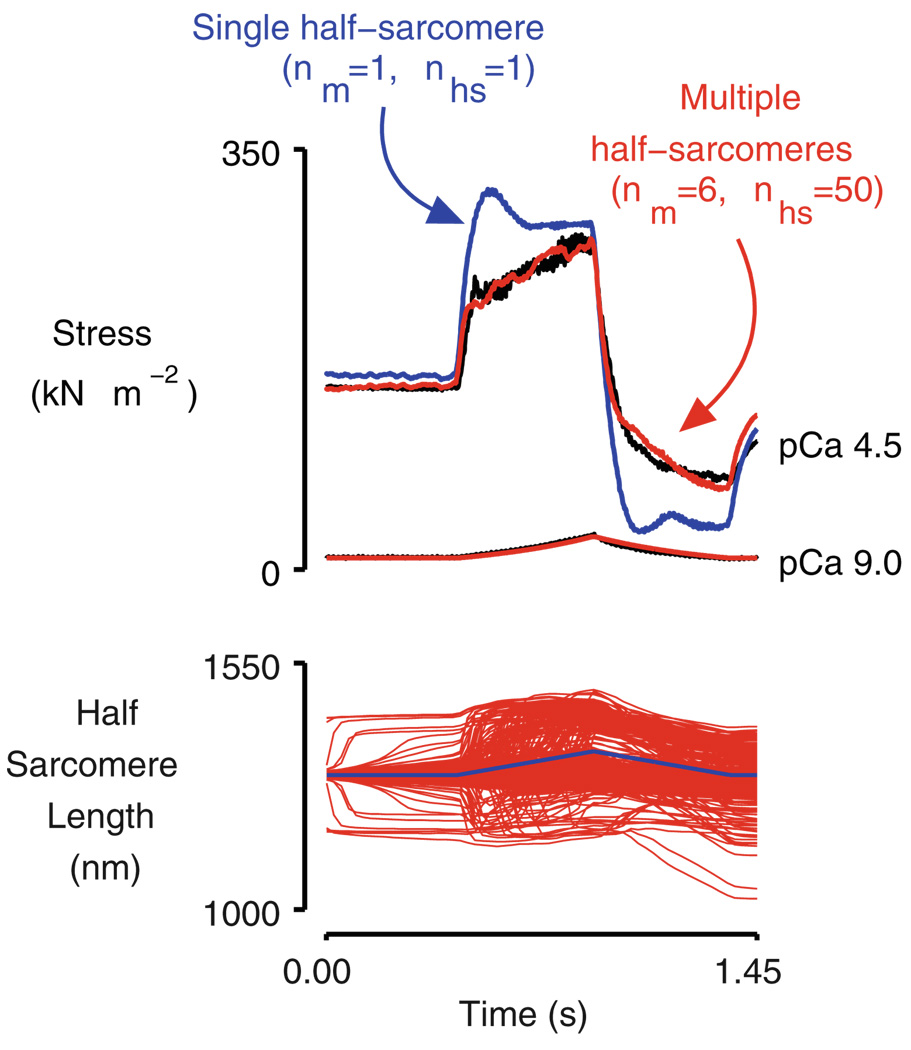
One of these emergent properties was discussed earlier in this review when it was mentioned that Telley et al. [52] showed that the force developed by an isolated myofibril drops very quickly during relaxation if one of the half-sarcomeres starts to lengthen. Another emergent property, this time calculated using computer simulations, is illustrated in Fig. 4. The red records in the top panel in this figure show the forces predicted by a computer model [6] composed of six myofibrils each of which contained 50 half-sarcomeres linked in series. The blue records show the forces predicted for a much simpler system, a single half-sarcomere, at the same two levels of activation. The plots show the behavior of the two systems—one with 300 half-sarcomeres, the other with just a single half-sarcomere—during a ramp stretch and subsequent release. At the high level of Ca²⁺ activation, both simulations show a marked short-range response [7], but force continues to rise thereafter for the large network (red trace) while it remains at a relatively stable plateau for the single half-sarcomere system (blue trace).

Fig. 4.

Simulated force and half-sarcomere length traces for single and multi-half-sarcomere frameworks. Reproduced with permission from Campbell [6]. Note that in the pCa 4.5 condition, force rises more quickly with muscle strain during the latter half of the stretch in the simulation of the multi-half-sarcomere system than it does for a single half-sarcomere. This is an emergent property of the contractile system. The black line is an experimental data record obtained using a chemically permeabilized rabbit psoas fiber [8]. n_m is the number of parallel myofibrils in the simulation. n_hs is the number of half-sarcomeres in series in each myofibril. The two simulations therefore correspond to networks of 1 half-sarcomere (n_m=1, n_hs=1, blue) and 300 half-sarcomeres (n_m=6, n_hs=50, red), respectively

This result is important because it shows that a system of half-sarcomeres can produce a force that increases with muscle strain much more quickly than would be predicted by looking at the properties of individual titin molecules and/or isolated actin–myosin links. Indeed, had the stretch been continued for a longer duration, force for the multiple half-sarcomere system would have continued to rise as long as the muscle continued to lengthen whereas the predicted force for the single half-sarcomere would have remained at an essentially constant plateau during the latter stages of the movement. This complex behavior results from the fact that in a multi-half-sarcomere system, the sum of the active and passive forces in each half-sarcomere has to balance along myofibrils. Slight variations in these forces (for example, due to different titin isoforms in different half-sarcomeres) thus produce mechanical effects that propagate along the myofibril and alter the force developed by the system. Stretching a cardiac muscle to different lengths would, at the very least, alter the passive mechanics of each half-sarcomere, which could in turn lead to different system-wide effects. The implication is that the Frank–Starling mechanism does not necessarily have to reflect the strain-dependent properties of individual half-sarcomeres but could instead be an emergent property of a network of connected half-sarcomeres that are subjected to transient internal strains.

The multi-half-sarcomere system displays the properties illustrated in Fig. 4 because in these simulations, each of the half-sarcomeres had a slightly different “strength.” This was implemented mathematically in this example by setting the number of myosin heads in each half-sarcomere to a slightly different number, but this was done primarily for computational convenience. How the half-sarcomeres differ does not make a material difference to the result. The key is that if the individual half-sarcomeres are not identical, the properties of the system that they form will be different from the properties of their “average member.” In the simulations described here, starting the stochastic calculations for each half-sarcomere with different random-number seeds is sufficient to produce emergent behavior. In real muscle, Brownian motion by itself could be enough to produce important system-wide effects. Random variation in the posttranslational status of sarcomeric proteins, local gradients in the intracellular Ca²⁺ concentration, ubiquitination of sarcomeric proteins, etc. could also influence the behavior. The bottom line is that if the half-sarcomeres that form a cell are not completely identical, the cell can be more than the sum of its parts.

Future directions

The Frank–Starling mechanism is critically important for cardiovascular function, and scientists have been trying to discover how strain-dependent activation, its most important component, works for many decades. Reductionist techniques have dominated the scientific chase, and many important advances have been made. For example, it now seems clear that filament spacing, cooperative activation, and titin-based mechanics are all at least somehow involved.

Saying much more than this is, however, problematic. It is difficult (the work of Dr. de Tombe and his colleagues with troponin I notwithstanding) to imagine that a single molecule or mechanism will ever be identified which is sufficient to explain the full range of cardiac muscle’s strain sensitivity. Instead, it seems more likely that strain-dependent myofilament activation is the product of a complex system of interacting molecular mechanisms. Disrupting any one of these mechanisms will impair strain dependency, but it is just as misleading to think of that mechanism as the source of the effect as it is to think of attributing muscle function to a single myosin head.

Where then will the next advance come from? The answer might be true multiscale computational modeling. Computers are now so fast and so cheap that it should soon be practical to simulate the dynamic mechanical properties of multiple spatially explicit half-sarcomeres. The basic techniques for modeling interactions between half-sarcomeres are well established [6, 39, 47], and several groups are working on models of the half-sarcomeres themselves [43, 45, 51, 55]. It should not be too hard to integrate these different scaled models into a single computational system. This could then be exhaustively probed to determine the relative strengths of the different mechanisms that potentially contribute to strain-dependent activation. For example, one could use the multi-scaled model to compute how changing the stiffness of titin filaments alters the strain dependence of activation in an otherwise unperturbed system.

The devil will undoubtedly be in the details but the future may be digital!