A cubic B-spline-based hybrid registration of lung CT images for a dynamic airway geometric model with large deformation

Abstract

The goal of this study is to develop a matching algorithm that can handle large geometric changes in x-ray computed tomography (CT)-derived lung geometry occurring during deep breath maneuvers. These geometric relationships are further utilized to build a dynamic lung airway model for computational fluid dynamics (CFD) studies of pulmonary air flow. The proposed algorithm is based on a cubic B-spline-based hybrid registration framework that incorporates anatomic landmark information with intensity patterns. A sequence of invertible B-splines is composed in a multiresolution framework to ensure local invertibility of the large deformation transformation and a physiologically meaningful similarity measure is adopted to compensate for changes in voxel intensity due to inflation. Registrations are performed using the proposed approach to match six pairs of 3D CT human lung datasets. Results show that the proposed approach has the ability to match the intensity pattern and the anatomical landmarks, and ensure local invertibility for large deformation transformations. Statistical results also show that the proposed hybrid approach yields significantly improved results as compared with approaches using either landmarks or intensity alone.

1. Introduction

Image registration is a process of determining an optimal spatial mapping that matches images collected at different times or using different imaging modalities. It has been extensively applied in various areas of medical image analysis (Crum et al 2004, Holden 2008). Of particular interest to this paper is the registration of computed tomography (CT)-derived three-dimensional (3D) lung volumes with applications to computational fluid dynamics (CFD) analysis of pulmonary gas flow in an attempt to extend from the rigid airway studies (Lin et al 2007, 2009, Choi et al 2009, 2010, Yin et al 2010, Lambert et al 2011) to breathing lungs with deforming airways and lung parenchyma. With pairs of images obtained at full inspiration and full or partial expiration or multiple images acquired at various time points during a breathing cycle, the registrations are performed to match those lung images to adjust the geometry of airway trees for changes in lung volumes.

Since lung motion varies from apex to base and ventral to dorsal, it is desirable to use non-rigid image registration to capture non-uniform expansion and contraction. There are two main approaches to implement non-rigid registration for lung CT images according to similarity measures: feature-based approaches and intensity-based approaches. The feature-based approach uses corresponding anatomical features, mostly landmarks or surfaces, to define the transformation from one lung dataset to the other (Fan et al 2001, Betke et al 2003, Coselmon et al 2004, Kaus et al 2007, Castillo et al 2009). In earlier landmark-based registration (LBR), several anatomical points, such as bifurcation points of airway and/or vascular trees, vertebra and so on, were manually selected by experts. Recent published work has shown the possibilities to generate large numbers of corresponding landmarks (more than 1000) from a pair of lung CT datasets with semi-automatic tools (Murphy et al 2008, Castillo et al 2009). Several LBR algorithms have been proposed based on thin-plate spline (TPS) (Rohr et al 2001, Johnson and Christensen 2002) or elastic-body spline (Davis et al 1997, Worz and Rohr 2008) or moving least squares (Castillo et al 2009). The use of B-spline was also proposed by Lee et al (1996) to compute a C² continuous and one-to-one mapping to warp two-dimensional (2D) points. Alternatively, intensity-based registration (IBR) matches the intensity patterns of the images by minimizing/maximizing a defined similarity measure. A representative though not exhaustive list of such studies can be found in Sundaram and Gee (2005), Guerrero et al (2006), Sarrut et al (2006), Schreibmann et al (2006), Christensen et al (2007), Staring et al (2007), Reinhardt et al (2008), Yin et al (2009b) and Ding et al (2010). Although both LBR and IBR have been applied in registering lung images, they each have limitations. IBR matches intensity patterns over the whole image but does not use anatomical knowledge. As a result, it may cause mismatch of important anatomical landmarks, such as airway bifurcations, when a registration falls into local minima. Conversely, LBR uses anatomical landmarks. Those landmarks, however, are usually sparsely distributed throughout the images leading to the mismatch of regions away from the landmarks. Thus, utilization of both anatomical landmark information and intensity patterns in image registration is desirable. In recent years, hybrid landmark- and intensity-based registration (LIBR) has been proposed to register lung images (Li et al 2003, 2008, Paquin et al 2007). In most of these LIBR methods, a TPS model, which minimizes the bending energy of a thin plate for a smooth transformation between designated landmarks is used to match landmarks. However, as pointed out by Holden (2008), the TPS transformation is a globally supported function so that it cannot accurately model localized deformation and it has high computational complexity when a large number of landmarks are used. More importantly, for large deformations a TPS model does not ensure local invertibility of the transformation, which is essential for biologically meaningful mapping and is especially important in our cases where the resulting deformation field is further used to deform the airway geometry for CFD simulation.

In this paper, cubic B-spline is adopted for both landmark- and intensity-based matching. Compared with other spline-based transformation models, such as TPS, B-spline is locally controlled, which makes it computationally efficient even when a large number of control nodes are used (Rueckert et al 1999, Kybic and Unser 2003, Tustison et al 2009). In addition, several algorithms have been proposed to ensure local invertibility of cubic B-spline by controlling the positivity of the Jacobian values (Choi and Lee 2000, Sdika 2008, Chun and Fessler 2009), among which Choi and Lee (2000) proposed an easy-to-implement sufficient injective condition for both 2D and 3D cases. According to their analysis, a transformation function is locally injective over the entire continuous domain if the displacement of each control node is bounded. Such small bound can also be extended to handle general cases based on the affine invariance property of B-spline (Choi and Lee 2000). In addition, a multilevel B-spline algorithm proposed in Lee et al (1996, 1997) is also helpful to capture the large deformation.

We propose a novel B-spline-based hybrid registration framework for lung CT datasets. A sequence of invertible B-splines is composed in a multiresolution framework to ensure local invertibility of the large deformation transformation. The resulting deformation is then applied to build a dynamic lung airway model. The proposed LIBR is first evaluated using 2D artificial binary images and then applied in matching inspiration/expiration 3D CT human lung dataset pairs. Each pair of lung datasets to be registered is acquired during breath-hold at approximately 90% vital capacity (near total lung capacity, TLC) and approximately 20% vital capacity (near functional respiratory capacity, FRC). The FRC and TLC image pairs show large lung volume changes, large tissue deformation, and large voxel intensity changes. Recently, we proposed an intensity-based mass-preserving registration method which uses the sum of squared local tissue volume difference (SSTVD) as the similarity measure to account for these differences between the images during registration (Yin et al 2009a, 2009b ). This intensity-based mass-preserving method has been shown to be effective at registering intra-subject datasets across large lung volume changes (Yin et al 2009b , Ding et al 2009). In this paper, we further incorporate the landmark information at bifurcations of airway and vascular trees to improve the registration accuracy, especially the alignment of the airway trees.

2. Methods

Given two N-dimensional (N-D) images F and R, referred to as the floating and reference images, the goal of the image registration is to determine a spatial mapping that matches one image to the other. Both images can be assumed as continuous functions f_F (x) and f_R(x) to determine intensity values at the position x (x ∈ ℝ^N).

2.1. Transformation model

Let Φ be an N-D uniform control grid with a grid spacing h (h ∈ ℝ^N). The displacement of the control node i is denoted by ϕ_i, where i ∈ I ⊂ ℤ^N and I is the set of all indexes of the control nodes on Φ. An ℝ^N → ℝ^N mapping T (x) can be defined in terms of displacements of control nodes as

$$T(\mathbf{x})=\mathbf{x}+\sum _{\mathbf{i}\in I_c\subset I}{\varphi }_{\mathbf{i}}\beta (\mathbf{x}/\mathbf{h}-\mathbf{i}),$$ (1)

where I_c is a set of control nodes which can influence the point x. $\beta (\mathbf{x})={\prod }_{k=1}^N\beta (x_k),$, with x = (x₁, … , x_N), is an N-D tensor product of basis functions of cubic B-spline. The basic algorithm described above may result in a non-invertible transformation, which causes folding of parts of the image upon nearby parts and further leads to failure of CFD simulation due to changes of topology. In order to ensure local invertibility of the large deformation, a sequence of B-splines with displacement constraints is composed in a multiresolution framework. For each B-spline level, an invertible transformation is obtained by bounding the displacement of control node by h/K, where K is a constant and it is approximately 2.046 392 675 for the 2D case and 2.479 472 335 for the 3D case (Choi and Lee 2000). The multilevel B-spline algorithm starts with the coarsest control grid. A smooth and invertible transformation can be obtained with the displacement constraints. This transformation has the ability to capture the global deformation. The local deformation is progressively handled by the subsequent transformations with finer control grids. The final transformation is defined as a composite operation of the sequence of transformations. Since the composite operation will not change the property of diffeomorphism, a final invertible transformation can be obtained by imposing the sufficient injective condition for each B-spline level. Namely, local invertibility for the large deformation is guaranteed by the combination of the displacement constraints and the multilevel B-spline technique.

2.2. Intensity-based registration with local invertibility

IBR matches intensity patterns by using mathematical or statistical criteria, also referred to as cost functions. The simplest cost function is the sum of squared intensity difference (SSD), which is defined as

$$E=\frac{1}{\mathrm{\Omega }}\sum _{\mathbf{x}\in \mathrm{\Omega }}{[f_F(T(\mathbf{x}))-f_R(\mathbf{x})]}^2,$$ (2)

The gradient of the cost function defined in (2) with respect to parameters of the transformation function is calculated by

$$\frac{\partial E}{\partial {\varphi }_{{\mathbf{i}}_m}}=\frac{1}{\mathrm{\Omega }}\sum _{\mathbf{x}\in \mathrm{\Omega }}\frac{\partial e}{\partial f_F}\frac{\partial f_F(\mathbf{z})}{\partial \mathbf{z}}{|}_{\mathbf{z}=T(\mathbf{x})}\frac{\partial T(\mathbf{x})}{\partial {\varphi }_{{\mathbf{i}}_m}},$$ (3)

where ϕ_im denotes the mth component of the displacement vector at the ith node. ∂e/∂f_F = 2[f_F (T (x)) − f_R(x)] and it reflects the current intensity errors between the corresponding points. The second term ∂f_F (z)/∂z is the intensity gradient of the floating image. The last term ∂T (x)/∂ϕ_im is the derivative of the transformation function with respect to its parameters.

The assumption of the SSD is that corresponding points in both images have the same intensity. This assumption is valid for matching the binary image while is not suitable for matching pulmonary CT images since the voxel intensity changes within lungs due to inflation. A similarity measure SSTVD was recently proposed as an extension of the SSD to account for such intensity changes (Yin et al 2009a, 2009b ). In this work, the SSD is used for matching 2D artificial binary images while the SSTVD is used for matching 3D pulmonary CT images.

The SSTVD minimizes the local tissue volume differences between matched regions. Its expression is given as

$$E=\frac{1}{\mathrm{\Omega }}=\sum _{\mathbf{x}\in \mathrm{\Omega }}{[V_F(T(\mathbf{x})){\stackrel{\sim }{f}}_F(T(\mathbf{x}))-V_R(\mathbf{x}){\stackrel{\sim }{f}}_R(\mathbf{x})]}^2,$$ (4)

where V_R and V_F are total volumes of corresponding regions in the reference and floating images, respectively, and V_F can be calculated from the Jacobian value J as V_F = JV_R. It should be noted that the Jacobian value must be positive here, which can be ensured for the invertible transformation. In addition, f̃ is the tissue fraction estimated from the Hounsfield unit (HU) by f̃ = [f (x) − HU_air]/[HU_tissue − HU_air], where HU_air and HU_tissue refer to the intensities of air and tissue, respectively (Hoffman 1985). Here, we assume that air is −1000 HU and tissue is 55 HU.

A limited-memory, quasi-Newton, bound constrained optimization method (L-BFGS-B) (Byrd et al 1995) is used as the optimization method to minimize the cost function. This optimization method has two main advantages. First, it is well suited for optimization with high dimensionality of parameter space. Second, it allows bound constraints on independent parameters, facilitating employment of displacement constraints for an invertible transformation.

2.3. Landmark-based registration with local invertibility

Let P = {p} and Q = {q} be a pair of corresponding N-D landmark sets from the reference and floating images, respectively. The goal of LBR is to find an ℝ^N → ℝ^N mapping to match the corresponding landmarks.

Given an initial configuration of the B-spline control grid ϕ⁰, the transformed point p′ of a landmark point p can be calculated from (1) as ${\mathbf{p}}^{\prime }=\mathbf{p}+{\sum }_{\mathbf{i}\in I_c}{\varphi }_{\mathbf{i}}^0{\beta }_{\mathbf{i}}$, where β_i = β(p/h − i). In order to move the point p to its corresponding point q, the displacements of control nodes must satisfy that q = p + Σ_i∈Ic ϕ_iβ_i. Thus, we can obtain

$$\mathrm{\Delta }\mathbf{q}=\mathbf{q}-{\mathbf{p}}^{\prime }=\sum _{\mathbf{i}\in I_c}\mathrm{\Delta }{\varphi }_{\mathbf{i}}{\beta }_{\mathbf{i}},$$ (5)

where $\mathrm{\Delta }{\varphi }_{\mathbf{i}}={\varphi }_{\mathbf{i}}-{\varphi }_{\mathbf{i}}^0$ and it is the desired deviation of displacement at the control node i. Among all possible solutions to (5), Lee et al (1996) chose the following one in the least-squared sense

$$\mathrm{\Delta }{\varphi }_{\mathbf{i}}=\frac{{\beta }_i\mathrm{\Delta }\mathbf{q}}{\sum _{\mathbf{i}\in I_c}{\beta }_{\mathbf{i}}^2}.$$ (6)

For this solution, the control nodes close to point p have larger deviations than others since β_i, which depends on the distance between the control node and p, decreases as the distance increases.

When multiple points in P are influenced by the same control node, the displacements of B-spline control nodes calculated for one point may mislead other points to other positions rather than the specified ones. Without loss of generality, we assume that P_s is a set of points in P which share a control node i. For each point in P_s, we can calculate Δϕ_i,s by (6). Since different points in P_s may result in different values of Δϕ_i,s, the final Δϕ_i can be chosen as a weighted average of all different Δϕ_i,s by minimizing Σ_s(β_i,sΔϕ_i − β_i,sΔϕ_i,s)², thus obtaining

$$\mathrm{\Delta }{\varphi }_{\mathbf{i}}=\frac{{\sum }_s{\beta }_{\mathbf{i},s}^2\mathrm{\Delta }{\varphi }_{\mathbf{i},s}}{{\sum }_s{\beta }_{\mathbf{i},s}^2},$$ (7)

where the point close to the control node have larger influence than others since β_i,s decreases as the distance increases. In addition, the displacement calculated by equation (7) must be truncated to satisfy the displacement constraints to ensure local invertibility.

The landmark-based matching technique proposed here has a low computational cost. Let m denote the number of landmark pairs to be matched and M is the number of B-spline levels. The time complexity is M * O(m), which is fast even when matching a large number of landmarks.

2.4. Landmark- and intensity-based registration with local invertibility

In this section, we combine both LBR and IBR algorithms described above as a LIBR algorithm. This LIBR algorithm is performed in a multiresolution framework, shown in figure 1. Both the image pyramid and the hierarchy transformation model consist of three different resolution levels. The whole registration is composed of six levels and starts with the coarsest scales of both images and control grid. The images and control grids are then alternatively refined until the finest versions. On each level, LBR is first performed. The resulting transformation is then used as the starting point to guide IBR in which the transformation is refined based on matching the intensity patterns of the images. The transformation obtained by IBR is then propagated to the next finer level and used as an initial transformation at that level. In order to ensure local invertibility, the displacement constraints are imposed during both LBR and IBR on each level. This is explicitly implemented by truncating the displacement of each control node during LBR while it is implicitly handled by the L-BFGS-B optimization method during IBR. The whole flow chart of the proposed LIBR method is given in figure 1.

Figure 1.

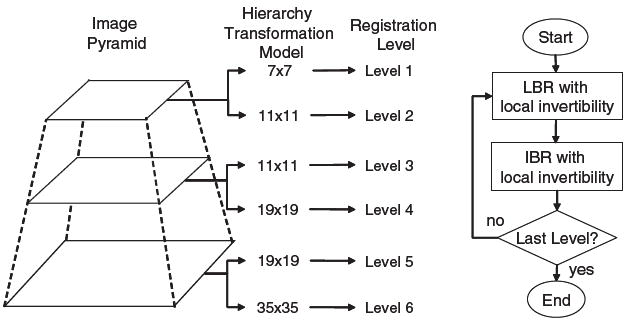
Sketch of the multiresolution framework and flow chart of the whole registration procedure for LIBR. The sketch of the framework is illustrated in 2D but the basic idea also works for 3D.

The current LIBR algorithm incorporates the landmark information with the image intensity patterns. The transformation produced by LBR is used to guide IBR, which helps the latter to avoid some local minima. This manner is similar to other commonly used hybrid registration approaches (Johnson and Christensen 2002, Li et al 2003, Rohr et al 2004, Paquin et al 2007, Li et al 2008). However, owing to the consistent deformation models, in the current LIBR algorithm the additional overhead for the transition from LBR to IBR is negligible and, more importantly, it is easy to ensure the local invertibility of the transformation.

2.5. Dynamic airway geometric model

Once the registration could match two volumetric datasets acquired at different lung volumes, registration-derived deformation field can then be used to deduce airway geometry at an arbitrary phase by using a suitable interpolation technique. Currently we assume that voxel trajectories are straight lines and the intermediate deformation field is defined as

$${\mathbf{u}}_s\left(\mathbf{x}\right)=s\left(t\right)\mathbf{u}\left(\mathbf{x}\right),$$ (8)

where u(x) is the registration-predicted displacement at the location x from the two CT images. s(t) is the displacement coefficient and is correlated with the actual respiratory trace (air flow) from the subject as monitored at the mouth.

3. Results

The performance of the proposed LIBR algorithm is first evaluated on 2D artificial binary images in section 3.1. The algorithm is then applied to match pairs of 3D CT lung datasets in section 3.2. The SSD is used for matching 2D artificial binary images with uniform intensity while the SSTVD is used for matching 3D lung CT datasets with variable intensity.

3.1. Experiments with 2D binary images

The performance of current algorithm is evaluated by two pairs of 2D binary images. The goal is to demonstrate that the proposed LIBR algorithm has the ability to recover the large deformations of the images. The results are compared with those obtained by LBR or IBR only, as shown in figures 2 and 3. In addition, TPS-LIBR, where TPS algorithm is used to match the landmarks instead of B-spline, is also performed for comparison. Each binary image has a size of 128 × 128 pixels and a spatial resolution of 1 × 1 mm. The pixel value is set to be 255 for the object and 0 for the background. In figures 2 and 3, column (a) shows the floating and reference images, where the landmarks are marked and labeled with the numbers showing the correspondence; columns (b)–(e) show the results obtained by LBR (b), IBR (c), LIBR (d) and TPS-LIBR (e), respectively. For each approach, the deformed image and the deformed grid are presented, where the deformed image is obtained by transforming the floating images from an Eulerian view while the deformed grid is obtained by deforming the regular grids from the reference image domain to the floating image domain from a Lagrangian view. The enlarged views of the deformed grids are also presented to show the details in regions where large deformations occur.

Figure 2.

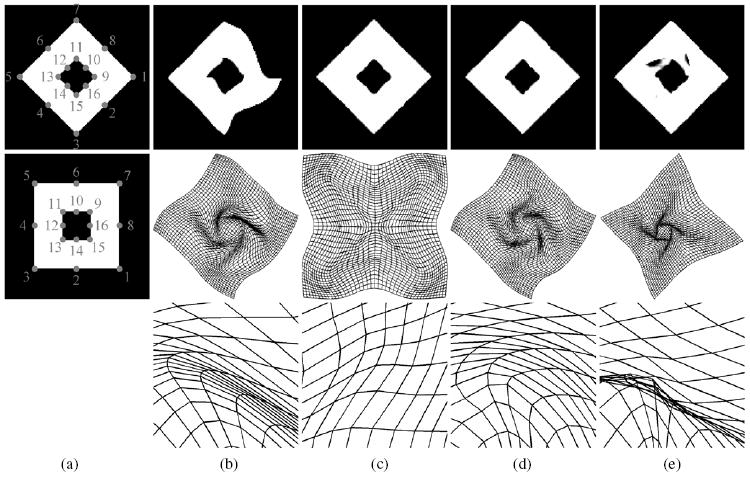
‘2D squares’ experiment. Column (a) shows the reference (top) and floating (middle) images, where the landmarks are marked and labeled with the numbers showing the correspondence; columns (b)–(e) show the results for registrations with LBR, IBR, LIBR and TPS-LIBR, respectively. The deformed image (top), the deformed grid (middle) as well as the enlarged view of the deformed grid (bottom) are presented for each approach.

Figure 3.

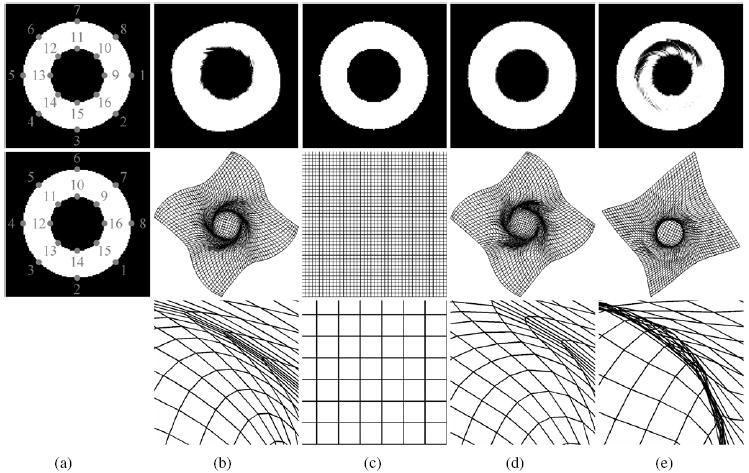
‘2D circles’ experiment. Column (a) shows the reference (top) and floating (middle) images, where the landmarks are marked and labeled with the numbers showing the correspondence; columns (b)–(e) show the results for registrations with LBR, IBR, LIBR and TPS-LIBR, respectively. The deformed image (top), the deformed grid (middle) as well as the enlarged view of the deformed grid (bottom) are presented for each approach.

In figures 2 and 3, the objects being mapped are two squares or circles with the same center point and a staggered pattern of landmarks. The outer square or circle rotates clockwise by 45° while the inner one rotates anticlockwise by 45°. In other words, the desirable transformation should be a non-rigid rotation. First of all, we see that no folding occurs in any deformed grids from (b)–(d), demonstrating that the transformations are invertible for all LBR, IBR and LIBR. By contrast, folding occurs in the TPS-LIBR deformed grid, as shown in (e). In addition, we can see that LIBR not only yields a good alignment over the whole image, but also avoids some local minima because of utilization of both the intensity and landmark information. IBR yields better alignment over the whole image than LBR while IBR fails to recover the non-rigid rotation.

The performance of the proposed LIBR algorithm is further quantified in table 1 by the landmark distance and metric value of SSD before and after registrations. The landmark distance is used to measure the agreement of the landmarks and the metric value of SSD is used as a measurement of agreement for intensity patterns.

Table 1.

2D binary image experiments. The landmark distance and metric value of SSD before and after registrations with four approaches: LBR, IBR, LIBR and TPS-LIBR. The minimum Jacobian value (J_min) and computational time for each approach are also listed.

	‘2D squares’				‘2D circles’
	SSD	Landmark distance (mm)	Jmin	Time (s)	SSD	Landmark distance (mm)	Jmin	Time (s)
Before Reg.	32.4	22.27 ± 12.66	–	–	0.0	27.58 ± 9.49	–	–
LBR	11.9	0.0 ± 0.0	0.19	0.04	9.5	0.0 ± 0.0	0.13	0.10
IBR	1.3	24.44 ± 13.03	0.44	0.56	0.0	27.58 ± 9.49	1	0.19
LIBR	1.4	0.74 ± 0.48	0.34	0.51	1.7	0.68 ± 0.44	0.19	0.71
TPS-LIBR	4.1	0.80 ± 0.40	−0.38	0.54	22.7	0.81 ± 0.36	0.51	0.84

In table 1, the initial landmark distance (before registration) is calculated between the corresponding landmarks in the floating and reference images while the landmark distance after registrations is calculated between the actual landmark positions in the floating images and the registration-predicted positions. The initial SSD (before registration) is calculated between the floating and reference images and the SSD after registration is calculated between the deformed and reference images. It is clear that LIBR yields low SSD values and small landmark mismatch errors compared with LBR and IBR. In addition, the minimum Jacobian values (J_min) are shown in table 1 and they are positive for LBR, IBR and LIBR. The minimum Jacobian is negative for TPS-LIBR, further demonstrating that folding of the deformation field exists.

The results above demonstrate that the current LIBR algorithm has the ability to match both the intensity patterns and the designated landmarks. It also has the ability to generate an invertible transformation to recover large deformation. In addition to good performance, the computational cost is low. The total computational time on a single 3 GHz processor is about 0.71 s, shown in table 1. The advantage of low computational cost becomes more obvious when a large number of landmarks are used. A test case was performed by using the ‘2D circles’ case while choosing 500 even-distributed landmarks on each circle (1000 landmarks in total). It takes 0.95 s for the current LIBR while 6.5 min for TPS-LIBR.

3.2. Experiments with 3D CT lung datasets

In this section, we apply the proposed LIBR method in matching pairs of 3D lung CT datasets. These datasets came from six normal human subjects (four males, two females; age: 22–39 years) examined under a protocol approved by the University of Iowa’s Institutional Review Board. For each subject, two volumetric scans were acquired with a Siemens Sensation 64 multi-detector row CT scanner (Forchheim, Germany) during breath-hold near FRC and TLC over the short periods of time in the same scanning session. The subject had no obvious movement during the scanning session and the scanner started at the same location along the z-axis of the subject. Each CT dataset contains 550–760 image sections with a section spacing from 0.5 to 0.7 mm and a reconstruction matrix of 512 × 512 pixels. In-plane pixel spatial resolution is approximately 0.6 × 0.6 mm². The total lung volume difference between the two volumetric scans ranges from 2.4 to 3.9 liters.

Bifurcations of major vascular and airway trees are selected as landmarks using a semi-automatic system (Murphy et al 2008). Each registration pair has 140–230 landmark pairs and approximately 20–40 are located in each lobe. In order to evaluate different approaches, we randomly chose half of the landmarks for matching and the rest for validation for each subject. Figure 4 shows an example of the landmark locations, where segmentations of lungs, vascular and airway trees are automatically obtained by using a segmentation software package PW2: VIDA Diagnostics (Coralville, IO, USA). It is noted that the beginning point of the trachea is used for both matching and validation. It is reasonable to assume that these beginning points at FRC and TLC have the correspondence in these cases since they are close to the vocal cord and the trachea is relatively rigid in that region.

Figure 4.

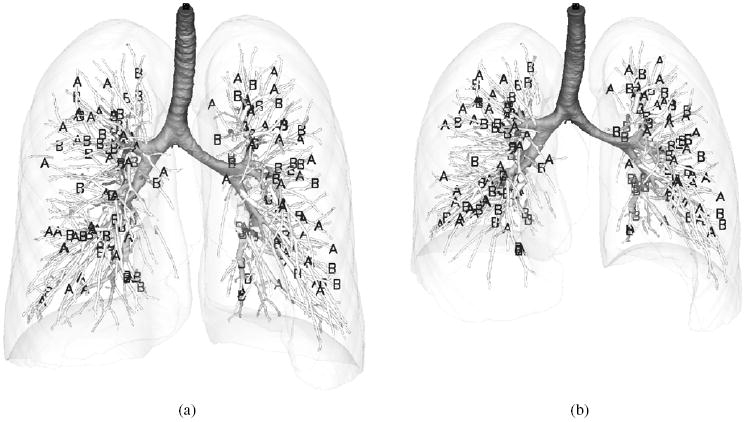
Illustration of landmark locations for (a) TLC and (b) FRC from one subject. The landmarks used for matching are marked by ‘A’ and the landmarks used for validation are marked by ‘B’. Surface rendering of airways, major vessels and lungs is shown for reference.

Table 2 shows the results for all six subjects. The metric values of SSTVD are calculated before and after registrations with LBR, IBR and LIBR. The distances of the validation landmarks and minimum Jacobian are also listed. It can be seen that LIBR yields the lowest metric values and also the smallest registration errors (landmark distance from validation landmark sets) since it combines both landmark and intensity information. A statistical analysis based on a linear mixed model that uses ‘method’ as the fixed effect and ‘subject’ as the random effect is further adopted to compare the average landmark errors among the three methods. The results show that LIBR yields a significant improvement against both LBR (with p-value < 0.001) and IBR (with p-value = 0.002). TPS-LIBR is also used for all six subjects but the registration fails for two subjects because negative Jacobian occurs after the landmark matching. If negative Jacobian occurs, the code has to be stopped. This is different from the 2D cases. In 2D, SSD is used and we can still run to get the final results even though negative Jacobian values appear after landmark matching. However, in 3D, if TPS landmark matching leads to negative Jacobian, the following intensity-based matching with SSTVD would be invalid. Statistical analysis is also performed to compare the average landmark errors by using TPS-LIBR and the proposed LIBR based on the other four subjects and the differences are not statistically significant (with p-value = 0.96). This shows that the proposed LIBR can produce accurate results as TPS-LIBR but ensure local invertibility for large deformation. In addition, the computational time is less than 10 min for LBR while is about 3–4 h for IBR, LIBR and TPS-LIBR. The most time-consuming part is to calculate the SSTVD and its derivatives with respect to the transformation parameters. We have also performed a simulated case with the CT lung dataset using a known deformation field. The experiments show that, given the same deformation field, different landmark sets would lead to invertible or non-invertible transformations for TPS-LIBR, depending on landmark locations. However, the proposed LIBR could ensure inevitability regardless the landmark sets. The details on the simulated case can be found in the appendix.

Table 2.

3D CT lung experiments. The landmark distance (LD)^a and metric value of SSTVD before and after registrations with four approaches: LBR, IBR, LIBR and TPS-LIBR. The minimum Jacobian value (J_min) for each approach is also listed.

	Subject 1			Subject 2			Subject 3
	SSTVD (mm3)	LD (mm)	Jmin	SSTVD (mm3)	LD (mm)	Jmin	SSTVD (mm3)	LD (mm)	Jmin
Before Reg.	0.104	26.03 ± 11.82	–	0.107	29.07 ± 14.77	–	0.0628	24.97 ± 13.56	–
LBR	0.0365	1.7 ± 1.36	0.37	0.0348	1.36 ± 1.07	0.27	0.0268	1.33 ± 1.05	0.40
IBR	0.0109	1.02 ± 1.08	0.24	0.0129	1.13 ± 0.96	0.23	0.008 28	0.88 ± 1.37	0.25
LIBR	0.0109	0.98 ± 1.01	0.23	0.0127	0.93 ± 0.69	0.23	0.008 20	0.71 ± 0.38	0.25
TPS-LIBR	0.0111	0.98 ± 0.81	0.22	0.0126	0.85 ± 0.66	0.19	0.008 26	0.72 ± 0.39	0.24
	Subject 4			Subject 5			Subject 6
	SSTVD (mm3)	LD (mm)	Jmin	SSTVD (mm3)	LD (mm)	Jmin	SSTVD (mm3)	LD (mm)	Jmin
Before Reg.	0.0748	25.13 ± 12.29	–	0.0861	29.15 ± 14.14	–	0.0921	29.73 ± 17.46	–
LBR	0.0291	1.56 ± 1.72	0.42	0.0310	1.93 ± 1.5	0.24	0.0339	2.12 ± 1.6	0.31
IBR	0.008 43	1.19 ± 2.21	0.25	0.009 74	1.45 ± 2.39	0.20	0.009 05	1.69 ± 2.94	0.17
LIBR	0.008 33	0.84 ± 0.63	0.26	0.009 76	1.12 ± 1.33	0.20	0.008 99	1.32 ± 1.45	0.18
TPS-LIBR	0.008 32	0.90 ± 0.87	0.23	–	–	–	–	–	–

^aDistances are calculated from landmark used for validation only.

Figure 5 shows the surface distance map of the registration-predicted FRC airway tree to the original FRC airway trees for LBR, IBR and LIBR. The registration-predicted FRC airway tree is obtained by applying the transformation to the airway surface mesh at TLC. By comparing these plots, LIBR yields the best matching result among all three approaches. LBR can match the airway tree at bifurcations but it yields a poor matching for the branches. IBR can match the branches well but it causes a shift at the beginning point of the trachea, which causes the trachea to erroneously shorten. The large distances in the distal ends of the airways do not represent mismatches but rather differences in the FRC versus TLC segmentations. At TLC the airways are detectible further out toward the peripheral lung.

Figure 5.

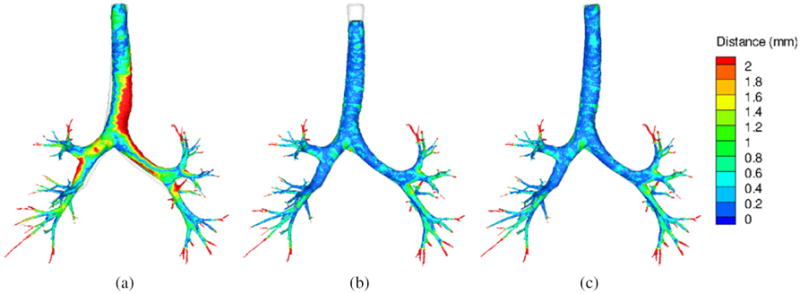
Surface distance map of the registration-predicted FRC airway tree to the original FRC airway trees for LBR (a), IBR (b) and LIBR (c). The original FRC airway trees are shown in white for reference.

The time-varying airway geometry could then be derived based on equation (8). Figure 6 demonstrates a dynamic airway geometrical model by using the LIBR method. The four panels shown in figure 6 correspond to four different time points in a breathing curve (t = 0, t = T/6, t = T/3 and t = T/2, with T as the period), where left and right panels correspond to the lower lung volume and higher lung volume, respectively.

Figure 6.

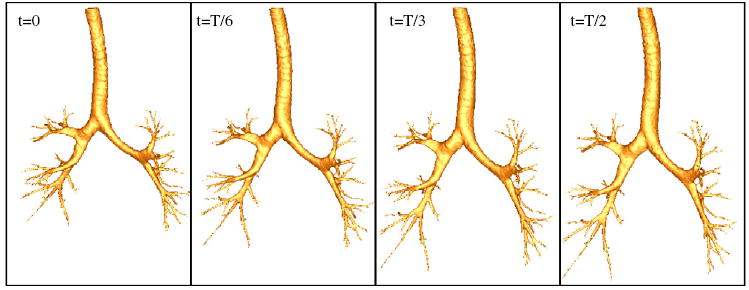
Airway geometries at four different time points from the dynamic airway geometrical model with the LIBR method. From left to right: t = 0; t = T/6; t = T/3 and t = T/2 (T is the period).

In addition, we have included supplementary downloadable material available at stacks.iop.org/PMB/56/203/mmedia that includes three multimedia AVI format animations showing the airway motion for LBR, IBR and LIBR. Note that IBR results in an obvious shift at the beginning of trachea. We recognize that non-straight-line displacement and the effect of hysteresis should not be neglected (Boldea et al 2008); however, these assumptions might be appropriate since a high-order parameterization cannot be fully utilized given only a pair of images. In this work, we aim to demonstrate the capability to develop a dynamic lung model based on image registration. This idea can be extended to account for non-straight-line displacement and hysteretic effects by using multiple lung volumes (or dynamic lung datasets) and the high-order trajectory modeling approach, such as in Castillo et al (2010).

4. Summary and conclusion

In this work, we propose a B-spline-based hybrid registration framework for pairs of lung CT datasets with large lung volume differences by incorporating anatomic landmark information and intensity patterns. We compose a sequence of invertible B-splines in a multiresolution framework to generate a locally invertible transformation and a physiologically meaningful similarity measure (SSTVD) to account for changes in voxel intensity between the TLC and FRC pairs. The registration-derived deformation field is then applied to deform the airway geometry for changes in lung volumes. The proposed LIBR algorithm is first evaluated by matching a pair of 2D binary images. The results show that LIBR has the ability to match the intensity patterns over the whole images and avoid mismatch of designated landmarks with an invertible transformation. We then apply LIBR to match six pairs of 3D CT human lung datasets. Statistical results show that LIBR yields the significantly improved results compared with LBR or IBR alone. LBR can match the airway tree at bifurcations but it yields a poor matching for the branches. By contrast, in spite of a good match in the branches, IBR yields a shift at the beginning point of the trachea, shortening erroneously the trachea. In addition, by using the registration-derived deformation field we demonstrate the ability to develop a dynamic airway model.

We seek to apply this approach to match multiple lung volumes acquired between TLC and FRC in the same scanning session or over short periods of time and adopt high-order interpolation to take into consideration to improve the current dynamic airway model for CFD simulation in future. Different from simulation with the fluid-structure interaction technique (Kumar et al 2009, Xia et al 2010, Tawhai and Lin 2010a, 2010b), the image-based CFD with moving airway geometries is only a one-way coupling analysis and, thus, requiring neither coupling with computational solid mechanics nor specifying tissue mechanical properties and tethering forces.

Appendix

A simulated experiment was performed using an actual chest CT dataset. The deformation field obtained from subject 6 was applied to the FRC image from subject 5 to obtain the artificial TLC image. 200 landmarks were randomly chosen inside lungs based on the given deformation field for matching. The registrations with both LIBR and TPS-LIBR were then performed to match the artificial TLC and the original FRC. To evaluate the quality of the registration, we measured the mean difference between the registration-derived deformation field T (x) and the ground truth T_g(x) by

$$\mathit{err}=\frac{1}{N}\sum _{\mathbf{x}\in \mathrm{\Omega }}\parallel T(\mathbf{x})-T_g(\mathbf{x}){\parallel }_2,$$ (A.1)

where N is the number of voxels inside lungs.

Several registration cases were performed using different landmark sets. It has been shown that different landmark sets would lead to invertible or non-invertible transformations for TPS-LIBR even though the deformation was the same one. However, the proposed LIBR could ensure inevitability regardless the landmark sets. In addition, the proposed LIBR could yield a better matching accuracy than the TPS-LIBR method with regard to the value of err. For a case with a landmark set leading to successful TPS-LIBR, the value of err is 0.77 mm for the current LIBR method and 1.03 mm for TPS-LIBR (the initial value of err is 35.23 mm).