High-Resolution Cardiac MRI Using Partially Separable Functions and Weighted Spatial Smoothness Regularization

Abstract

Imaging of cardiac morphology and functions in high spatiotemporal resolution using MRI is a challenging problem due to limited imaging speed and the inherent tradeoff between spatial resolution, temporal resolution, and signal-to-noise ratio (SNR). The partially separable function (PSF) model has been shown to achieve high spatiotemporal resolution but can lead to noisy reconstructions. This paper proposes a method to improve the SNR and reduce artifacts in PSF-based reconstructions through the use of anatomical constraints. These anatomical constraints are obtained from a high-SNR image of composite (k, t)-space data (summed along the time axis) and used to regularize the PSF reconstruction. The method has been evaluated on experimental data of rat hearts to achieve 390 µm in-plane resolution and 15 ms temporal resolution.

I. INTRODUCTION

Cardiac Magnetic Resonance (CMR) enables dynamic visualization of the beating heart and allows for the qualitative and quantitative analysis of cardiac anatomy, function, first pass myocardial perfusion, myocardial viability, ejection fraction, cardiac output, blood flow velocity, and various other diagnostic tests [1]. A major challenge of developing CMR imaging methods which produce accurate and reproducible representations of cardiac motion at high spatiotemporal resolution arises due to the limited imaging speed of MRI and its inherent tradeoffs between spatial resolution, temporal resolution, and signal-to-noise ratio (SNR). A large number of methods have been proposed to address this problem (see [2] and the references therein), including fast-scanning methods, parallel imaging methods, and model-based imaging methods. Model-based imaging methods have recently received significant attention because they are complementary to fast-scanning and parallel imaging methods. When used together, they can significantly accelerate MR acquisition. Some well-known model-based imaging methods are UNFOLD [3], PARADIGM [4], k-t BLAST [5], and k-t FOCUSS [6]. This paper is focused on improving the partially separable function (PSF) model-based imaging method [7].

The PSF method has been previously used to reconstruct “real-time” image sequences of beating rat hearts at high spatiotemporal resolution despite the significant challenges associated with the high heart rates (~300 bpm), respiratory motion (1 Hz), and high spatial resolution requirements (<500 µm) [8]. One practical problem with the PSF method is due to the ill-conditionedness of the underlying model fitting problem for highly sparse (k, t)-space data. This problem has been addressed using weighted spatial-spectral regularization [9] and spatial-spectral sparsity constraints [10], [11]. This paper describes a new method of data acquisition and image reconstruction involving the construction of a spatially-weighted smoothness constraint. The method has been evaluated on experimental data of rat hearts to achieve 390 µm in-plane resolution and 15 ms temporal resolution.

II. THEORY

With Fourier encoding, the measured data s(k, t) in a dynamic MR experiment is described by

$$s(\mathbf{k},t)={\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}}\rho (\mathbf{r},t)e^{-i2\pi \mathbf{k}·\mathbf{r}}d\mathbf{r},$$ (1)

where ρ(r, t) is the desired spatiotemporal image function [12]. The nature of MR data acquisition prevents dense sampling of (k, t)-space, leading to a direct tradeoff between the achievable spatial and temporal resolutions. The PSF model approach addresses this challenge by assuming partial separability of the spatial and temporal dimensions in the image function, thereby providing a new avenue for sparse sampling of (k, t)-space.

The Lth-order spatiotemporal PSF model [7] represents ρ(r, t) as

$$\rho (\mathbf{r},t)={\displaystyle \sum _{\ell =1}^L}{c}_{\ell }(\mathbf{r}){\phi }_{\ell }(t),$$ (2)

where φ_ℓ(t) and c_ℓ(r) are the ℓth temporal and spatial basis functions, respectively. There are various ways to collect sufficient data to determine {φ_ℓ(t)} and {c_ℓ(r)} while still satisfying MR data acquisition constraints. One basic strategy is to collect a set of “training” data with high temporal resolution (satisfying the Nyquist criterion) to determine {φ_ℓ(t)} and to collect regular imaging data with large k-space coverage (achieving high spatial resolution) to determine {c_ℓ(r)}. In this paper, we assume that such a data acquisition strategy is used, and thus that {φ_ℓ(t)} is known (or more precisely, pre-determined) [7]. Our goal is to determine {c_ℓ(r)} from the measured data, which is assumed to be highly sparse in (k, t)-space.

Let {s(k_m, t_n)} denote the measured data and be represented in vector form by d. Assuming the PSF model is correct, we have

$$\mathbf{d}=\mathbf{𝒰}\mathbf{ℱ}\mathbf{\Phi }\mathbf{c}+\mathit{\xi },$$ (3)

where c is the vector representation of {c_ℓ(r)}, Φ is a matrix constructed from {φ_ℓ(t)} that transforms c into ρ(r, t), ℱ is the Fourier operator which transforms ρ(r, t) into s(k, t), 𝒰 performs undersampling in (k, t)-space according to the data acquisition scheme, and ξ represents measurement noise.

In principle, c can be determined from (3) by solving a simple least-squares problem (assuming ξ is Gaussian noise). In practice, the undersampling operator 𝒰 often causes the forward matrix 𝒰ℱΦ to be ill-conditioned. The resulting noise amplification and potential for image artifacts make the direct least-square solution undesirable. We next discuss a regularization strategy to deal with this problem.

III. REGULARIZED RECONSTRUCTION

The proposed regularized solution of c is given by

$$\widehat{\mathbf{c}}=\underset{\mathbf{c}}{\text{arg min}}{\Vert \mathbf{𝒰}\mathbf{ℱ}\mathbf{\Phi }\mathbf{c}-\mathbf{d}\Vert }_2^2+\mathrm{\lambda }{\Vert \mathbf{\text{Bc}}\Vert }_2^2,$$ (4)

where the first term penalizes inconsistencies between the PSF model and the measured data, and the second term is a regularization penalty dependent on the regularization constant λ and the weighting matrix B. Equation (4) has a closed-form solution as

$$\widehat{\mathbf{c}}={({\mathbf{\Phi }}^H{\mathbf{ℱ}}^H{\mathbf{𝒰}}^H\mathbf{𝒰}\mathbf{ℱ}\mathbf{\Phi }+\lambda {\mathbf{B}}^H\mathbf{B})}^{-1}{\mathbf{\Phi }}^H{\mathbf{ℱ}}^H{\mathbf{𝒰}}^H\mathbf{d}.$$ (5)

Clearly both λ and B play a key role in selecting a stable PSF solution. The solution using B = I is referred to as the standard PSF solution in this paper. In the remainder of the paper, we will focus on defining B. We specifically propose formulating B to perform controlled smoothing of the image in order to recover SNR and penalize the formation of motion artifacts without blurring the edges of the object [13]. This controlled smoothing occurs according to a reference image, which we denote as ρ_ref (r).

Practically speaking, ρ_ref (r) is not always available in the form of a priori information. However, it is both simple and effective to generate ρ_ref (r) from a composite of the measured data {s(k_m, t_n)}. Ideally, ρ_ref (r) should be spatially unaliased and should exhibit high SNR. There are many methods for reconstructing such images from composite (k, t)-space data, even when the measured data violates the Nyquist condition [14]. In this paper, we reconstruct ρ_ref (r) from s̄(k_m), a weighted sum of {s(k_m, t_n)} over the time axis:

$$\overline{s}({\mathbf{k}}_m)=\frac{{\displaystyle {\sum }_n}s({\mathbf{k}}_m,t_n)}{{\displaystyle {\sum }_n}𝒰({\mathbf{k}}_m,t_n)},$$ (6)

where 𝒰 (k_m, t_n) is set to 1 for the (k, t)-space locations where s(k_m, t_n) is measured; otherwise, 𝒰 (k_m, t_n) takes the value of 0. The expression Σ_n 𝒰(k_m, t_n) gives the total number of samples which are collected at k_m, and (6) is therefore equivalent to averaging the measured data independently at each k_m. We obtain ρ_ref (r) from s̄(k_m) by Fourier reconstruction. This method for creating ρ_ref (r) requires that the measured k-space locations {k_m} collectively satisfy the spatial Nyquist condition. This condition is met by the imaging data in our acquisition scheme. It is useful to collect the imaging data so that the measurements at any given k_m are uniformly distributed over time; this helps prevent ρ_ref (r) from exhibiting certain motion artifacts.

We formulate B to penalize the weighted spatial smoothness of the PSF reconstruction, discouraging the formation of sharp image features in ρ(r, t) which are not represented in ρ_ref (r). This helps suppress both noise and motion artifacts in the reconstruction while protecting image edges from being smoothed. B operates on c in three steps. First, it applies {φ_ℓ(t)} to reconstruct ρ(r, t). Second, it convolves ρ(r, t) with multiple directional gradient kernels {g_n(r)} to localize image features and characterize the orientation of edges. Third, it multiplies the previous output by weighting functions {w_n(r)} that are generated from ρ_ref (r) as

$$w_n(\mathbf{r})=\text{min}(\frac{1}{g_n(\mathbf{r})⊛{\rho }_{\text{ref}}(\mathbf{r})},w_{\text{max}}),$$ (7)

where w_max is the maximum allowed penalty value [13]. The overall effect is that B penalizes the formation of image features in ρ(r, t) inversely proportional to their prominence in ρ_ref (r), excluding when w_n(r) = w_max. The use of w_max softens the penalties corresponding to very smooth areas of ρ_ref (r) and prevents these areas from overinfluencing the final solution. When (4) is viewed in a quasi-Bayesian context, the formulation of B to include weighting as defined in (7) may be interpreted as incorporating ρ_ref (r) into the model as a statistical prior [13]. For the purposes of this paper, we use two gradient kernels which compute vertical and horizontal finite differences.

B is specifically expressed as

$$\mathbf{B}=\left[\begin{array}{cccc}\hfill {\mathbf{W}}_1\hfill & \hfill \mathbf{0}\hfill & \hfill \dots \hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathbf{W}}_2\hfill & \hfill \dots \hfill & \hfill \mathbf{0}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \dots \hfill & \hfill {\mathbf{W}}_N\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\mathbf{G}}_1\hfill \\ \hfill {\mathbf{G}}_2\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathbf{G}}_N\hfill \end{array}\right]\mathbf{\Phi }$$ (8)

$$=\mathbf{\text{WG}}\mathbf{\Phi },$$ (9)

where Φ maps c to ρ(r, t), GΦc is equivalent to the convolution of ρ(r, t) with {g_n(r)}, W is a diagonal matrix which applies the weighting functions {w_n(r)}, and N is the number of directional gradients. When {φ_ℓ(t)} is orthonormal, we replace B with an alternative operator B_alt = WG that applies g_n(r) and w_n(r) directly to each c_ℓ(r) instead of to each timepoint of ρ(r, t). The operator B_alt preserves the property ${\Vert {\mathbf{B}}_{\text{alt}}\mathbf{c}\Vert }_2^2={\Vert \mathbf{\text{Bc}}\Vert }_2^2$ but is more computationally efficient than B by a factor of T/L, where T is the number of timepoints represented in {φ_ℓ(t)}.

For computational efficiency, we solve (5) using the conjugate gradient (CG) method [15]. The CG formulation of (5) is

$$({\mathbf{\Phi }}^H{\mathbf{ℱ}}^H{\mathbf{𝒰}}^H\mathbf{𝒰}\mathbf{ℱ}\mathbf{\Phi }+\lambda {\mathbf{B}}^H\mathbf{B})\mathbf{c}={\mathbf{\Phi }}^H{\mathbf{ℱ}}^H{\mathbf{𝒰}}^H\mathbf{d}.$$ (10)

For the purpose of comparing different regularization methods in this paper, we have selected all values of λ so the resulting solutions have a common data consistency error

$${\Vert \mathbf{𝒰}\mathbf{ℱ}\mathbf{\Phi }\widehat{\mathbf{c}}-\mathbf{d}\Vert }_2^2=\frac{2}{3}{\widehat{\sigma }}^2{N}_{\mathbf{𝒰}},$$ (11)

where σ̂² is the estimated noise variance of d and N_𝒰 is the number of (k, t)-space samples retained by 𝒰. The effect of (11) is closely related to Morozov’s discrepancy principle, and the resulting reconstructions have data discrepancies of the same order as noise with variance $\frac{2}{3}{\widehat{\sigma }}^2$.

IV. RESULTS

All experimental data in this paper were collected using a Bruker (Billerica, MA) Avance DRX 4.7 T, 40 cm equipped with a 12 cm, 40 G/cm shielded gradient set. A 5.5 cm custom built surface coil was used for the collections. A customized FLASH pulse sequence with a T_R of 7.5 ms and a T_E of 2.4 ms was used to acquire data at 102 × 128 resolution over a 4 cm × 5 cm Field of View (FOV) (an in-plane resolution of 390 µm) with a 1.5 mm slice thickness. Data were collected continuously with neither gating nor breath holding over 5 minutes, with interleaved acquisition of training and imaging data. All PSF reconstructions were performed at model order L = 16.

The animals used in the study were Dark-Agouti and Brown Norway rats as in [16]. All animals received humane care in compliance with the Guide for the Care and Use of Laboratory Animals, published by the National Institutes of Health, and the animal protocol was approved by the Carnegie Mellon University Institutional Animal Care and Use Committee.

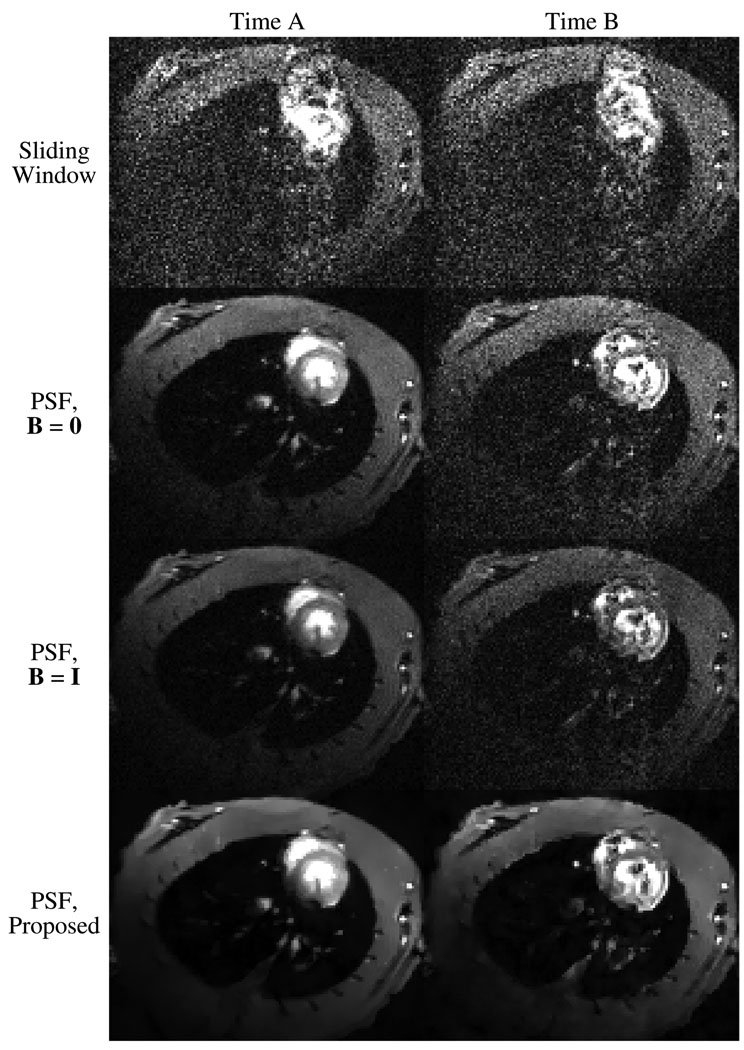
Fig. 1 shows results from multiple reconstruction methods applied to the same experimental data. The noise present in the PSF reconstructions varies with time; the two images displayed for each method represent the high and low extremes of this noise. The reconstruction methods shown are the sliding window reconstruction (direct Fourier reconstruction of the imaging data with zero-order temporal interpolation), the unregularized solution to the PSF model (B = 0), the standard PSF solution (B = I), and the proposed anatomically-constrained PSF solution. The proposed solution exhibits a significant reduction in noise and motion artifacts when compared to the other reconstruction methods. This improvement in image quality occurs without blurring edges or reducing temporal resolution.

Fig. 1.

Images corresponding to two timepoints from the sliding window reconstruction and from PSF reconstructions with different weighted regularization schemes. The bottom row shows images from the proposed anatomically-constrained regularization scheme.

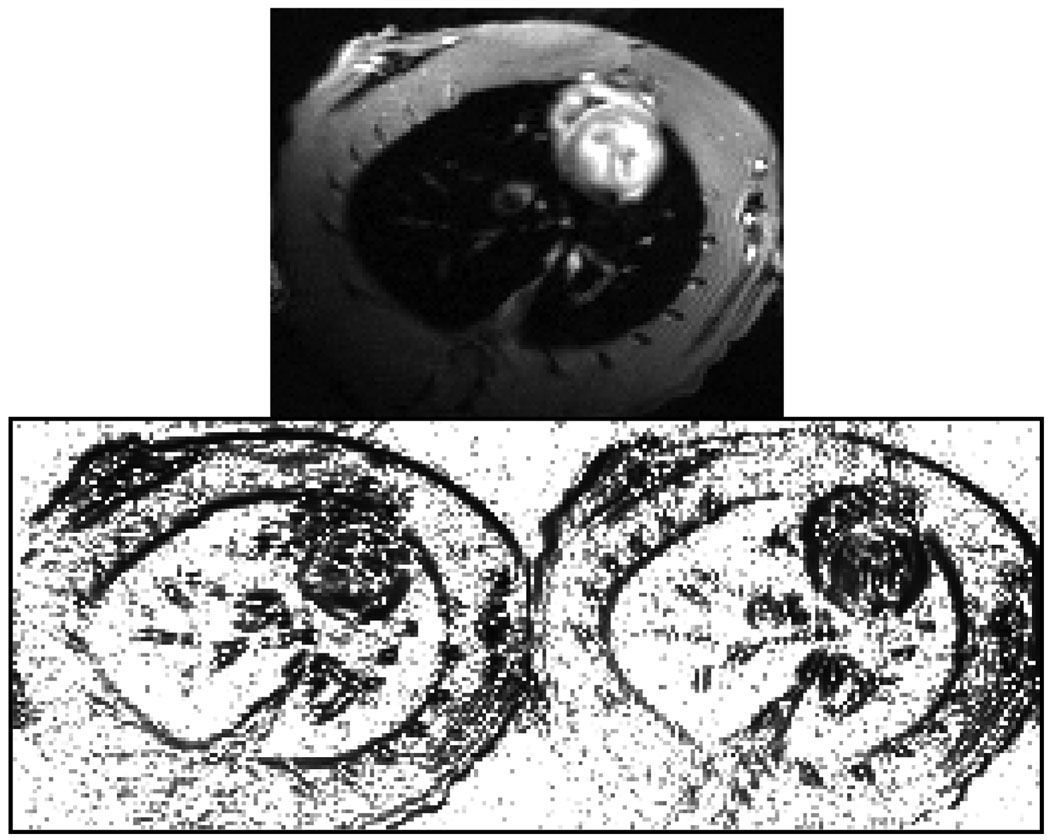
Fig. 2 shows the reference image ρ_ref (r) and penalty weightings {w_n(r)} used in the proposed reconstruction scheme.

Fig. 2.

The reference image ρ_ref (r) (top) and the resulting penalty weighting functions {w_n(r)} (bottom). Note that weighting is defined separately for the vertical (left) and horizontal (right) gradients.

V. DISCUSSION

The sliding window reconstructions shown in Fig. 1 represent Fourier reconstructions of the imaging data when no attempt is made to model the time-evolution of the object beyond nearest-neighbor interpolation. It should be noted that the interleaved acquisition of training and imaging data used in this experiment is not optimal for sliding window reconstruction: the sliding window reconstruction shown here has a temporal resolution of 1.53 s, whereas a non-interleaved acquisition of imaging data alone would yield a sliding window reconstruction with a temporal resolution of 765 ms. Nevertheless, neither temporal resolution is sufficient to resolve even respiratory motion in rats, let alone cardiac motion. The PSF reconstructions have a temporal resolution of 15 ms, with a spectral bandwidth of 33.3 Hz that covers six harmonics of cardiac motion. PSF theory does not exclude the use of parallel imaging or faster pulse sequences, so any performance gains from these techniques are equally applicable to both sliding window and PSF imaging [9].

The SNR improvement resulting from the proposed regularization method has farther-reaching implications than just those pertaining to image quality, as the PSF method features trade-offs between SNR and various other parameters such as experiment time and model order. The implications of the proposed method on experiment time will be examined here.

Although experiment times in PSF imaging are not as long as those required for gated imaging techniques, PSF experiment times are still generally longer than those required by other model-based imaging techniques, some of which require short experiment times within a single breath hold to function properly. Although the ability to reconstruct data over longer periods of time is one advantage of the PSF method, the sensitivity of SNR to experiment time is also a weakness. The SNR gained by the proposed regularization method can thus be interpreted as a time-saving technique when longer experiment times are inconvenient or impossible. Whereas the usual approach to improving the SNR of the unregularized or standard PSF solutions would be to acquire more data, the proposed regularization scheme has achieved this goal without resorting to an increase in experiment time.

It is possible that in some situations, such as when an object shifts in the scanner, a static reference image will be insufficient to reliably identify image features. In this case, it may be useful to define a time-variant reference image ρ_ref (r, t), perhaps generated from the measured data using a large temporal sliding window. The basic formulations of (7) and (9) will still apply, even for a dynamic reference image, although the computationally efficient operator B_alt will no longer be a valid alternative to B.

This work is complementary to other constrained PSF reconstruction techniques such as the weighted spatial-spectral regularization in [9] and spatial-spectral sparsity constraints in [10], [11]. In theory, the proposed penalty on the spatial smoothness should not conflict with such spatial-spectral penalties, and both can perhaps be used simultaneously. Weighted spatial smoothness regularization may also be useful in reconstructing radially-undersampled projection acquisitions or radial projection datasets which otherwise exhibit significant motion artifacts, assuming that an unaliased reference image is attainable. The control over edge orientation which results from using multiple spatial gradients seems particularly suited to the dampening of radial aliasing artifacts, which manifest as linear streaks in the image domain.

VI. CONCLUSION

An extension to PSF model-based dynamic imaging has been proposed and successfully used to perform real-time CMR imaging in breathing rats at 390 µm spatial resolution and 15 ms temporal resolution. Our results show that the quality of PSF image reconstruction regarding SNR and motion artifacts can be greatly improved by introducing a statistical prior to the model in the form of a spatially-weighted smoothness constraint. The proposed method would improve the practical utility of the PSF-based imaging method.