Mitochondrial membrane potential probes and the proton gradient: a practical usage guide

Abstract

Fluorescent probes for monitoring mitochondrial membrane potential are frequently used for assessing mitochondrial function, particularly in the context of cell fate determination in biological and biomedical research. However, valid interpretation of results obtained with such probes requires careful consideration of numerous controls, as well as possible effects of non-protonic charges on dye behavior. In this context, we provide an overview of some of the important technical considerations, controls, and parallel complementary assays that can be employed to help ensure appropriate interpretation of results, thus providing a practical usage guide for monitoring mitochondrial membrane potentials with cationic probes. In total, this review will help illustrate both the strengths and potential pitfalls of common mitochondrial membrane potential dyes, and highlight best-usage approaches for their efficacious application in life sciences research.

In recent years, fluorescent dyes for measuring the mitochondrial membrane potential (Δψ_m) have become commonly used tools for monitoring changes in this important physiologic mitochondrial parameter as it relates to cells’ capacity to generate ATP by oxidative phosphorylation. As such, the Δψ_m is a key indicator of cell health or injury. As a class, these dyes are typically lipophilic cationic compounds that equilibrate across membranes in a Nernstian fashion, thus accumulating into the mitochondrial membrane matrix space in inverse proportion to Δψ_m (1–4). A more negative (i.e., more polarized) Δψ_m will accumulate more dye, and vice versa. A handful of dyes can be used for this purpose, each with their own strengths and weaknesses (Table 1) (for review, see Reference 2). For best usage, all of these dyes require strict attention to technical details and controls to ensure appropriate interpretation of dye behavior as related to Δψ_m (2,5,6). Herein, we aim to complement other excellent, high-level reviews detailing theoretical and applied aspects of these dyes in life sciences research (e.g., References 1,2,3, and references therein) by offering a practical guide that lays out in one place—especially for laboratories using these tools for the first time—the range of controls and supporting experiments required to ensure meaningful interpretation of results obtained with these dyes.

Table 1.

Characteristics and typical usage paradigms for the most common probes of Δψ_m.

Probe	Spectra	Usage considerations
TMRM, TMRE: Best for slow resolving acute studies, or measuring pre-existing Δψm (nonquenching).		Lowest mitochondrial binding and ETC inhibition makes TMRM preferred for many studies (20). Used in non-quenching [~1–30 nM; use lowest possible concentration (6)] or quenching (>50–100 nM) modes; acute or chronic studies. Fast equilibration makes these less suited to some quenching studies than more slowly permeant Rhod123. If test treatment precedes dye loading, dye usually remains in bath for imaging in nonquenching mode; if test treatment succeeds dye loading, dye can remain in bath or not, in nonquenching or quenching modes.
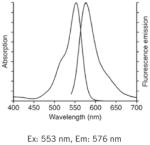
Rhod123: Best for fast resolving acute studies (quenching).		Often used in quenching mode (~1–10 μM), to monitor acute changes in Δψm after dye loading and washout. In this mode, due to dye aggregation and consequent quenching of fluorescence at higher dye concentrations, depolarization of Δψm causes unquenching and thus transiently increased fluorescence, and vice-versa. Slowly permeant means quenching/unquenching changes in Fwc are easier to spot. Slightly less ETC inhibition and mitochondria binding than TMRE, slightly more than TMRM (20).
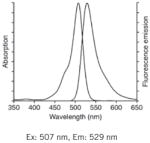
JC-1: Best for “Yes” or “No” discrimination of polarization state (e.g., apoptosis studies by flow cytometry or microscopy).		Monomer (m) and aggregate (a) forms allow dual-color, ratiometric assessment of Δψm, but also make JC-1 very sensitive to concentration to work correctly. JC-1 is usually loaded after experimental treatment, and then ideally will remain in bath during imaging, to prevent fluorescence changes from probe redistribution. Aggregate form reported sensitive to factors other than Δψm, such as S/V ratios, H2O2 (see text). If S/V ratios differ, slowly equilibrating aggregates could imply differences in Δψm where none exist. Likely requires load times longer than commonly reported.
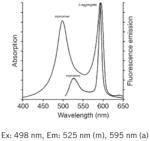
DiOC6(3): Best for flow cytometry.		Most widely employed as a measure of Δψm in flow cytometry studies. However, requires very low concentrations (<1 nM) to accurately monitor Δψm rather than Δψp, and to prevent respiration toxicity (6). See (56) for more detailed discussion regarding using this and other probes for assessing Δψm by flow cytometry.

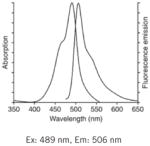
Notes: See Table 1 in Reference 2, upon which this table is loosely modeled, for additional complementary information on these probes. Fluorescence spectra are Molecular Probes technical data from www.invitrogen.com, copyright of Life Technologies Corporation, and used with permission.

Why is Δψ_m important?

As the energy power-plants of the cell, mitochondria generate ATP by utilizing the proton electrochemical gradient potential, or electrochemical proton motive force (Δp), generated by serial reduction of electrons through the respiratory electron transport chain (ETC). The reductive transfer of electrons through ETC protein complexes I–IV in the inner mitochondria membrane provides the energy to drive protons against their concentration gradient across the inner mitochondrial membrane (out of the mitochondrial cytoplasm). This results in a net accumulation of H⁺ outside the membrane, which then flows back into the mitochondria through the ATP-generating F₁/F₀ ATP-synthase (Complex V), thus producing ATP and completing the ETC. The total force driving protons into the mitochondria (i.e., Δp), is a combination of both the mitochondrial membrane potential (Δψ_m, a charge or electrical gradient) and the mitochondrial pH gradient (ΔpH_m, an H⁺ chemical or concentration gradient). Using a simplified Nernst factor for the second term, Δp can be represented at 37°C by the equation: Δp (mV) = Δψ_m − 60ΔpH_m (2,7,8). Using approximate physiological values of Δψ_m = 150 mV and ΔψpH_m = −0.5 units (mitochondrial matrix is alkaline), this equates to Δp = 150 – 60(−0.5) = 180 mV (mitochondrial matrix is negative) (2,7,9). Typical Δp values range 180–220 mV, with Δψ_m typically accounting for 150–180 mV of this value, and ΔpH_m of 0.5–1.0 units contributing the remaining 30–60 mV per the Nernst factor (2,7,10,11). This equation and the later case study (Box 2) also help illustrate an important distinction: the probes described herein are simply measuring the charge gradient Δψ_m across the inner mitochondrial membrane; they do not and cannot specifically measure the mitochondrial proton gradient, ΔpH_m. To assess this parameter, other tools are required (see Section 10, and the case study outlined in Box 2).

Box 2. Δψ_m is not ΔpH_m—mitochondrial membrane potential dyes and non-protonic charges (a cautionary case study).

Here we briefly highlight findings from our own laboratory, which demonstrate that under some conditions of intracellular stress, mitochondrial pH values are opposite what might be predicted by measuring Δψ_m alone. We found that in rodent cortical neurons, the neurotoxic HIV transactivator of transcription (Tat) gene product increased Δψ_m (5,45,50). This finding was surprising since, until more recently, hyperpolarization of Δψ_m in response to cellular insults had been infrequently reported (27,57–71) compared with many more reports of mitochondrial depolarization after cellular stressors. However, we validated this finding using both TMRE/TMRM and Rhod123 by nonquenching and quenching approaches (5,45,50), and ensured that our observations were not due to changes in mitochondrial morphology or mass (5), nor changes in Δψ_p (5). Moreover, both FCCP and oligomycin elicited the expected dye responses in all of our model systems (5,45,50).

At the same time, in these same cells under identical experimental conditions, mitochondrial pH was decreased (i.e., increased [H⁺]_mito) (45), as measured using a mitochondrially loaded pH-sensitive dye SNARF-1 (44). Control conditions again behaved as expected, with oligomycin increasing mitochondrial pH (less [H⁺]_mito), and FCCP decreasing mitochondrial pH (more [H⁺]_mito) (45). Such an increase in [H⁺]_mito (i.e., loss of the proton gradient) is commonly accompanied by decreased Δψ_m (depolarization), whereas our results suggested that Tat treated mitochondria had increased Δψ_m (more negative mitochondrial interior) despite increased [H⁺]_mito.

To explain this conundrum, using non–pH-sensitive mitochondria [YC3.1mito (72,73)]–or endoplasmic reticulum (D1ER; 51)– targeted ratiometric FRET constructs to monitor Ca²⁺_mito and Ca²⁺ _ER levels, we found that Tat induced Ca²⁺ release from both mitochondrial and ER stores (45,50). Only by preventing this Tat-induced dumping of Ca²⁺ _mito and Ca²⁺ _ER into the cytoplasm could we detect a mitochondrial depolarization that would be predicted on the basis of our observed increase in [H⁺]_mito alone (50). Our results strongly suggested that increased cytosolic [Ca²⁺], and not protonic charges, were responsible for Tat-induced hyperpolarization of Δψ_m.

These findings are important because they provide direct experimental evidence that Δψ_m does not always mirror changes in mitochondrial pH, thereby highlighting the fact that measuring Δψ_m solely with cationic dyes cannot be used to make direct inferences regarding ΔpH_m and respiratory status. For example, had we stopped after our initial findings that Tat increased Δψ_m, we might have erroneously concluded that Tat was increasing the proton gradient (thus increasing ATP generating capacity), whereas the opposite proved true—opposing scenarios with quite different energetic consequences.

Together, these factors help regulate mitochondrial control over energy metabolism, intracellular ion homeostasis, and cell death in eukaryotic cells. While Δp provides the bioenergetic driving force for and regulates ATP production, the Δψ_m component of Δp provides the charge gradient required for mitochondrial Ca²⁺ sequestration, and regulates reactive oxygen species (ROS) production, and thus is also a central regulator of cell health (2,12). During cellular stress, Δψ_m may in turn be altered by dysregulation of intracellular ionic charges [e.g., Ca²⁺ (2,7,12) or K⁺ (13)], consequently changing Δp and thus ATP production. When ionic fluxes surpass the ability of mitochondria to buffer these changes, ultimately Δp, Δψ_m, and/or ΔψpH_m may collapse, leading to a failure of ATP production and bioenergetic stress. Several extensive and excellent reviews explore these mitochondrial bioenergetics in more detail (7,14,15).

Dyes to measure Δψ_m

In this context, several fluorescent lipophilic cationic dyes [e.g., tetramethylrhodamine methyl (TMRM) and ethyl (TMRE) ester, Rhodamine 123 (Rhod123), DiOC₆(3) (3,3′-dihexyloxacarbocyanine iodide), and JC-1 (5,5′,6,6′-tetrachloro-1,1′,3,3′-tetraethylbenzimidazolylcarbocyanine iodide)] have become important tools for directly measuring the Δψ_m component of Δp. As positively charged molecules—and assuming that appropriate experimental controls and assay conditions are employed as discussed herein—these dyes will accumulate within mitochondria in inverse proportion to Δψ_m according to the Nernst equation. More polarized mitochondria (i.e., hyperpolarized, where the interior is more negative) will accumulate more cationic dye, and depolarized mitochondria (interior is less negative) accumulate less dye. Fluorescent dye accumulation in mitochondria is then optically detected by microscopy and CCD camera, confocal or multiphoton microscopy, flow cytometry, or fluorescent plate reader, thus allowing for at least qualitative or comparative assessments of Δψ_m among experimental conditions. (The choice of read-out mode is discussed in Section 2, and see Section 9 for discussion of how to use these probes yet more quantitatively). See Figure 1 for a demonstration of TMRE loaded into polarized mitochondria, whereas no detectable signal arises from mitochondria depolarized using p-trifluoromethoxy carbonyl cyanide phenyl hydrazone (FCCP).

Figure 1. TMRE loads specifically into polarized mitochondria.

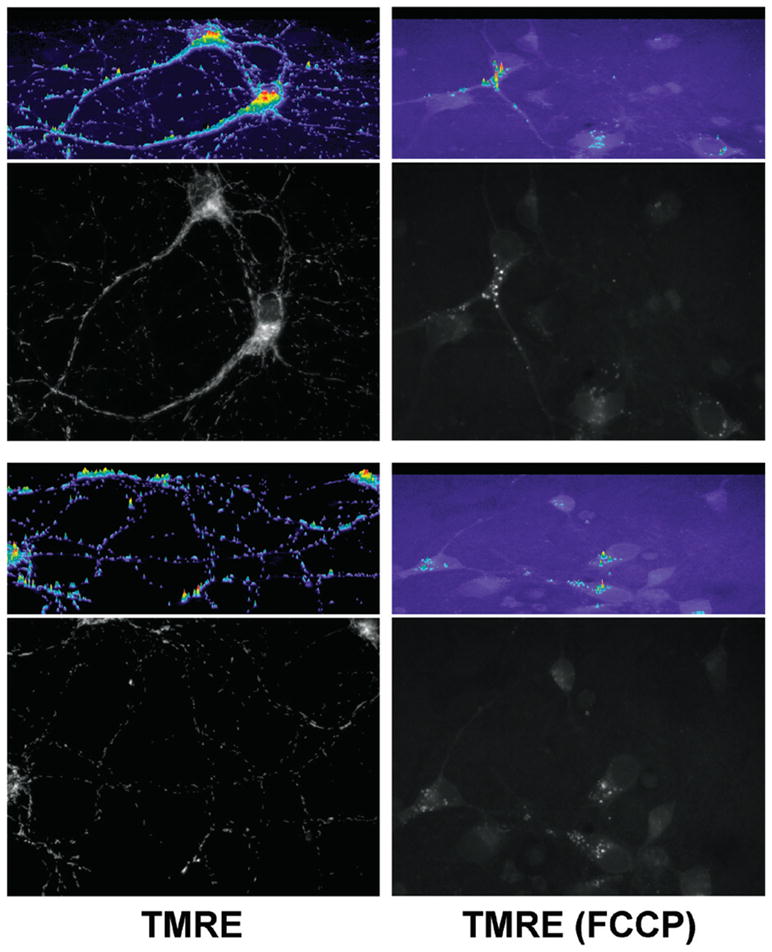
11–14-day-old primary mouse cortical neurons were loaded for 20 min at 37°C with 1 nM TMRE in Hanks Balanced Salt Solution (HBSS), either without (TMRE) or with [TMRE (FCCP)] 10 μM FCCP in the loading bath. After the 20-min loading, cells remained in the same loading bath, and images at 60× were taken for each condition (100-ms exposure times) using a Chroma HQ535/50x:Q565LP:HQ610/75m filter and dichroic set (Bellows Falls, VT, USA). Two images/condition are presented here. Images are the raw 12-bit grayscale images, converted to 8-bit grayscale for presentation using ImageJ. Immediately above each image, a relative intensity profile in color is presented for the whole image area (Metamorph). Note the specific mitochondrial TMRE loading—in neuronal soma and neurites but excluded from the nucleus as expected—that occurs only when mitochondria are polarized. Also note that contrary to conventional “cartoon” imagery of oval-shaped mitochondria, the elongated, fibrillar mitochondrial shape seen here is typical of many cell types (e.g., References 37 and 38). As demonstrated by the grayscale images and corresponding color intensity profiles, in the depolarized (FCCP) condition, mitochondrial TMRE labeling is completely absent reflecting a complete depolarization of Δψ_m, with only trivial signal arising from a small amount of cytoplasmic vesicular labeling that appears only in the FCCP condition. Note also the considerably higher background fluorescence in the FCCP condition, due to the TMRE remaining in the bath rather than being concentrated by mitochondria.

The comparative merits and pitfalls of each of these dyes and their suitability for differing experimental paradigms have been addressed by others (2–4,15–17), and thus we will first touch upon these areas briefly, in the context of experimental design. We will thereafter focus on practical experimental considerations, emphasizing controls and other complementary experiments that must be performed in parallel when measuring Δψ_m with these cationic dyes to ensure appropriate interpretation of results. We particularly emphasize techniques that can be applied by any laboratory, regardless of their level of experience with these probes. Box 1 summarizes some of these technical considerations and controls, which might be considered “best usage” practices for these probes for Δψ_m. We expand on each of these areas in more detail below.

Box 1. A practical guide to measuring Δψ_m with cationic probes.

• 1–3Determine the approach, then the best probe for the methods and experimental questions: acute or chronic studies, quenching or nonquenching mode, experimental treatments pre- or post-dye loading, whether or not dye is present in the bath for imaging, read-out method, etc.
• 4 Use pharmacologic controls such as FCCP/CCCP and oligomycin to confirm that directional changes in the dye signal are interpreted appropriately (19,45,50).
• 5 Use controls to ensure that changes in Δψ_p are not responsible for differences in mitochondrial dye loading in response to your treatment. For example, bis-(1,3-dibutylbarbituric acid) trimethine oxonol [DiBAC₄(3)] can be used as a relatively specific probe for changes in Δψ_p (5,30).
• 6Verify results for Δψ_m with a complementary dye and/or approach. For example, consider using one dye at low nonquenching concentrations, and another dye at high quenching concentrations to confirm treatment results (19,45,50). Quenching threshold will vary by experimental model and by fluorophore, but dye concentrations as low as <1–30 nM are frequently required to ensure no quenching (5,6,28).
• 7 In addition to measuring intensity levels, consider complementary numerical analyses of dye loading [e.g., coefficient of variance of F_wc pixel intensities (34)] to further verify interpretation of dye loading behavior.
• 8Use controls and observation to ensure that changes in dye signal are not due to changes in mitochondrial morphology, localization, or mass. Mitotracker dyes may be employed for this purpose, with the caveats that (i) mitochondrial loading of these dyes shows some sensitivity to Δψ_m, and (ii) these dyes also exhibit quenching behavior (35). See Reference 2 and references therein for additional considerations regarding Mitotracker probes. Alternatively, use mtGFP, mtDNA/nDNA, protein levels of ETC complexes, or citrate synthase assay; see Section 8.
• 9Use computer modeling and simulations to interpret dye behavior and kinetics, particularly as relates to changes in Δψ_m and Δψ_p. This approach can complement and/or substitute for some of the other controls listed here, and has been well detailed elsewhere (18,19,28,32).
• 10Use complementary methods to assess or model ΔpH_m, for comparison to Δψ_m changes as measured by mitochondrial dyes (e.g., References 42,43–45. Also see the case study in Box 2.
• 11As described herein and elsewhere, measure additional informative parameters related to mitochondrial function and metabolism [e.g., cellular ATP/ADP levels (5), ETC complex activities (45), NADH/NADPH (45,46), O₂ consumption/respiration (45,47,48), glycolysis (49), organellar calcium (45,50–54), and ROS (48,54,55)] to further substantiate or inform mitochondrial dye results.

Measuring Δψ_m with cationic probes: controls and practical applications

1. Planning the experiment

Foremost, it is important to outline the two general classes of experiments under which these dyes are typically used. In the first scenario (“Scenario 1”), the investigator wishes to determine how Δψ_m changes—usually in a population of cells—following chronic experimental treatment of the cells or tissues. Examples include analyzing the effects of chronic toxin exposure or knocked-in/knocked-out genes as they impact Δψ_m (on average) in the cell population under study. In the second scenario (“Scenario 2”), the investigator wishes to monitor real-time (i.e., rapid, short-term) changes in Δψ_m in response to acute application of an experimental treatment. Examples include investigations of the immediate localized effects of pharmacologic or toxic treatments on Δψ_m (as might be caused by rapid changes in respiratory capacity, Ca²⁺ dynamics, etc.), or investigations of acute real-time mitochondrial responses to secondary respiratory challenges following some other primary experimental treatment (e.g., gene knockout/knock-in). Although at first glance the second scenario may seem more technically daunting, in practice—because each sample/condition can serve as its own baseline or internal control prior to acute experimental treatment—it can often provide more readily interpretable results. On the other hand, not all experimental questions can be answered by Scenario 2, and in these situations Scenario 1 can provide meaningful results assuming rigorous attention is paid to the kinds of controls and technical details discussed herein. These considerations for both approaches are discussed in more detail.

2. Choosing a method and a dye to measure Δψ_m

The next considerations are (i) in which mode to use the dye, (ii) which dye to use, and (iii) what read-out method to use? As we discuss here, the best usage mode will be determined by the experimental requirements, which in turn will help determine the optimal dye for the studies, both of which in turn will help dictate the most suitable read-out for monitoring the fluorescent signal.

Typically, these dyes can be used in either quenching or nonquenching modes, as described in considerable detail elsewhere (2,15). Briefly, quenching mode utilizes higher dye concentrations (50–100 nM to several micromolar, determined empirically), such that dye accumulates within mitochondria in sufficient concentration to form aggregates, thus quenching some of the fluorescent emissions of the aggregated dye. Under these conditions, once dye is loaded into mitochondria, a subsequent mitochondrial depolarization will result in release of dye, thus unquenching the loaded probe, and (transiently) increasing fluorescent signal. Once all probe in the mitochondria is unquenched, fluorescent signal will decline as dye continues to leave the mitochondria and the cell under continued depolarization. Conversely, a subsequent mitochondrial hyperpolarization will result in more dye entering mitochondria, causing further quenching and thus a relative decrease in fluorescent signal. As such, and because quenching is a nonlinear event (15), quenching mode can only be appropriately used for monitoring the dynamic or acute effects of experimental treatments on Δψ_m after the dye has been loaded (i.e., Scenario 2 experiments). Furthermore, quenching mode is only appropriate for Scenario 2 studies when rapid and robust changes in Δψ_m occur during the imaging period (2,18,19). For following slower Δψ_m changes in real time (slower Scenario 2 experiments), or for determining differences in Δψ_m among two populations after an experimental treatment (Scenario 1), nonquenching mode (described in the next paragraph) should be used (2,18,19). See Figure 2 for a trace demonstrating both mitochondrial hyperpolarization (using oligomycin) and depolarization (using FCCP) in rat cortical neurons loaded with Rhod123 in quenching mode.

Figure 2. Rhod123 used in quenching mode.

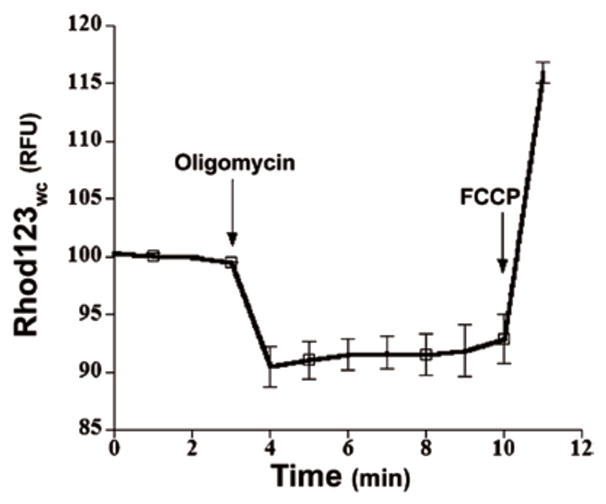
11–14-day-old primary rat cortical neurons were loaded for 30 min at 37°C with 10 μM Rhod123 in normal growth media as described (45). The Rhod123-containing loading medium was removed, and the cultures placed in CO2-insensitive, pH-stable Leibovitz’s L-15 medium (Invitrogen Life Technologies) and incubated at 37°C in room air for 15 min to allow for the Rhod123 fluorescent signal to reach steady state. Using a Chroma HQ560/55x:Q595LP:HQ645/75m filter and dichroic set, CCD images were captured 1/min for 5 min to establish a baseline. After 5 min, oligomycin or FCCP was added at the times indicated by the arrows, which respectively caused the characteristic quenching (hyperpolarization of Δψ_m) and unquenching (depolarization of Δψ_m) responses in F_wc as expected. Average traces of relative F_wc were taken from n = 4 neurons. This figure and legend is modified from Figure 1C in Reference 45, with permission.

In nonquenching mode, lower probe concentrations are used (0.5–30 nM, determined empirically) such that dye aggregation and quenching in the mitochondria does not occur. Therefore, depolarized (less negative) mitochondria will have lower cationic dye concentrations and lower fluorescence, and hyperpolarized (more negative) mitochondria will have higher dye concentrations and fluorescence. When using mitochondrial probes in nonquenching mode, acute experimental manipulations can be performed after probe loading (Scenario 2 experiments), or chronic treatments can be performed before dye loading to make a static comparison of pre-existing relative mitochondrial polarization between control and experimental treatments (i.e., Scenario 1 experiments). In summary, Scenario 2 (acute) experiments involve probe loading before the Δψ_m-affecting experimental treatments and can employ either quenching (if changes in Δψ_m are fast) or nonquenching modes (if changes in Δψ_m are slower), whereas Scenario 1 (chronic) experiments involve probe loading after Δψ_m-affecting experimental treatments and thereby should typically utilize probes in nonquenching modes (since quenching effects are nonlinear).

With the mode determined—quenching or nonquenching—the choice of probe then relates largely to their equilibration characteristics, which varies by probe and determines how each probe behaves in quenching or nonquenching modes. In addition to probe equilibration rates, which will be discussed in more detail below, each probe also has varying degrees of toxicity to mitochondria and cells, principally due to phototoxicity from singlet oxygen generation, and inhibition of the ETC. Each probe also varies in its degree of binding to mitochondria (i.e., non-Nernstian or non-ideal probe behavior), which will result in somewhat greater probe accumulation in mitochondria than would be predicted by the Nernst equation alone. For these reasons, it is always desirable to use the lowest possible probe concentration for any given experimental approach. Thus, as indicators of Δψ_m, each probe has relative strengths and weaknesses for different experimental paradigms. Table 1 briefly outlines fluorescent spectra, some key usage considerations, and potential pitfalls of each, and should be referred to in parallel with the further discussion of these issues (along with Box 1).

For example, TMRM inhibits the ETC less, and binds mitochondria less than either Rhod123 or TMRE (in that order), although in practice, at the nonquenching (0.5–30 nM) and lower quenching (>50 nM–1 μM) doses used experimentally, these factors will be negligible for all of these probes, with the possible exception of inhibition of the ETC by TMRE if used above 1 μM (which is not a typical usage paradigm for this probe) (20). For example, Figure 1 demonstrates that in the depolarized FCCP condition, 1 nM TMRE does not bind to mitochondria in any detectable amount; for these reasons, TMRE remains a common choice for nonquenching studies. Both TMRM and TMRE also equilibrate quickly, another factor making them well suited to nonquenching studies, but are somewhat more complicated to interpret in quenching studies (see below). Rhod123 has only slightly higher mitochondrial binding and ETC toxicity than TMRM, and is more slowly permeant, thus lessening the impact of plasma membrane potential (Δψ_p) changes on dye redistribution during short-term experimentation and making Rhod123 often the preferred choice for acute quenching studies to monitor rapid real-time changes in Δψ_m following acute cellular insults. DiOC₆(3) has been used most commonly for flow cytometry, but its higher toxicity toward mitochondrial respiration (see Reference 2, and references therein), and its ultra-low (<1 nM) concentrations required to accurately measure Δψ_m (6) somewhat limit the utility of this probe versus the others. All of the probes can be used for flow cytometry, typically in nonquenching mode.

In contrast to these monochromatic probes, the emission spectra of JC-1 shifts from green to red with increasing concentration (i.e., aggregation) in the mitochondria, thus allowing for a dual-color (green/red) and ratiometric semiquantitative assessment of mitochondrial polarization states. With regard to quenching versus nonquenching, this makes JC-1 something of a hybrid, because its usage relies on readings from both aggregated (red) and non-aggregated (green) probe forms, but in this case probe aggregation results in spectral shift rather than quenching. For some cell types and assay conditions, JC-1 has been reported to be a more reliable indicator of Δψ_m than other dyes described herein (21,22). On the other hand, while the monomeric (i.e., green-emitting) form of JC-1 appears to faithfully track Δψ_m under various experimental conditions, aggregate (i.e., red) JC-1 fluorescence may change independently of Δψ_m, for example with H₂O₂ treatment (23–25). Although pleasing to the eyes, this probe has several other traits and complexities that may render it less ideal for some applications. First, typical JC-1 usage as a ratiometric probe for Δψ_m relies on aggregation (threshold) effects, which may render it ill-suited to making reliable distinctions between subtle gradations in Δψ_m. It also means that in theory, and as shown in practice (22) and from our own unpublished data, getting the probe to properly work in this fashion is highly sensitive to probe loading concentrations and loading times. Complicating this matter further, JC-1 is very photosensitive (2) and its aggregates may not readily equilibrate with monomers. Moreover, all the mitochondrial probes are differentially permeant based on each probe’s distinct molecular structure, and JC-1 is slowly permeant. More specifically, while the monomer (green) form of JC-1 has been reported to equilibrate on a time scale similar to that of TMRM/TMRE (~ 15 min) (22), the aggregate (red) form of the dye—the formation of which is required in order to use JC-1 as a ratiometric probe for Δψ_m —takes ~90 min to reach equilibration in cardiomyocytes (22). Thus, since equilibration time is also closely linked to surface-to-volume (S/V) ratios, this means that in any cell populations where there may be significant heterogeneity in S/V ratios either across cells or within different subcellular regions (e.g., soma versus neurites in neurons), JC-1 may be particularly prone to indicating differences in Δψ_m when in fact they do not exist. Figure 3 illustrates neuronal staining with JC-1, and also highlights the fact that, depending on localized dye concentrations, either the monomer (green) or the aggregate (red) forms can be seen in polarized mitochondria, which could reflect real subregional differences in Δψ_m or it could simply reflect differential JC-1 equilibrium rates (and thus different aggregate formation rates) in subcellular regions with different S/V ratios. (See the Figure 3 legend for further description.) Thus results obtained with JC-1 must be evaluated with these issues in mind and interpreted with caution.

Figure 3. JC-1 in neuronal mitochondria.

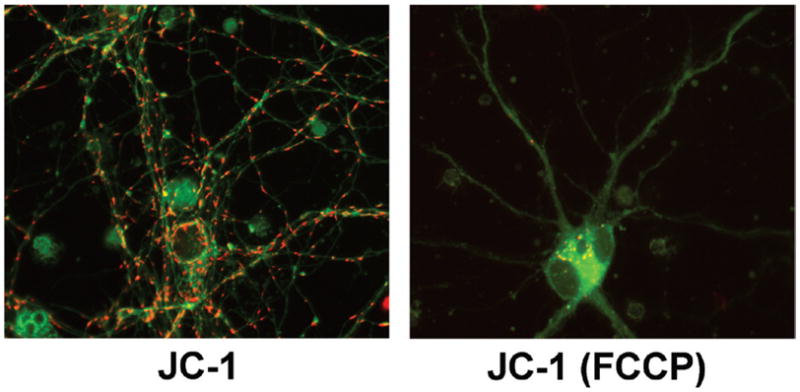
11–14-day-old primary mouse cortical neurons were loaded for 45 min at 37°C with 1 μg/mL (1.5 μM) JC-1 in Hanks Balanced Salt Solution (HBSS), either without (JC-1) or with [JC-1 (FCCP)] 10 μM FCCP in the loading bath. After the 45 min loading, cells remained in the same loading bath, and for each field sequential green (JC-1 monomers) and red (JC-1 aggregates) images at 60× were taken for each condition (100-ms exposure times) using HQ480/40x:Q505LP:HQ535/50m (green) and HQ560/55x:Q595LP:HQ645/75m (red) filters and dichroic sets; one green/red overlay image/condition is presented here. Images are the raw 12-bit images, converted to 8-bit for presentation using ImageJ. When combining green/red images, some adjustments to image stretch and tone were made to each green or red image, for overlay display contrast purposes only, to ensure that all red JC-1 aggregates in both conditions are visible. Note that even after 45 min loading at 1 μg/mL (1.5 μM) (Invitrogen product data sheet suggests 1 μg/mL for 30 min for neurons), in neuronal soma but not neurites, there appear to be concentrated JC-1 monomers (green) in polarized mitochondria (since completely depolarized mitochondria will not accumulate significant cationic JC-1. In the neuronal cell body at lower middle of the left-hand image, note the green fibrillar mitochondria labeling, similar in appearance to the TMRE staining in polarized mitochondria in Figure 1). While it is possible this reflects small “real” differences in Δψ_m between these cellular regions, it also possible that due to different S/V ratios in neurites versus soma and the slow permeance of JC-1, dye concentrations in soma mitochondria have not yet reached aggregation threshold (i.e., they have not yet become red), whereas aggregation threshold is reached sooner in neurites. This example highlights some of the complexities of using JC-1 that must be kept in mind. In the depolarized (FCCP) condition, specific mitochondrial JC-1 labeling appears nearly absent as reflected by a near complete loss of both mitochondrially concentrated monomers (green) and aggregates (red). The little bit of aggregate labeling that does exist in the FCCP condition may reflect a few remaining polarized mitochondria, or more likely, nonspecific vesicular labeling similar to that seen with FCCP+TMRE in Figure 1. Though not seen well here due to contrast adjustments, considerably higher background fluorescence again occurred in the FCCP condition, from JC-1 not concentrated by mitochondria.

For these reasons, and assuming adequate equilibration time is allowed, an investigator may find that JC-1 is best suited to more coarse “yes/no” assessments with the goal of determining whether mitochondria populations are either largely polarized or largely unpolarized (e.g., apoptosis-type studies), rather than discriminating finer gradations or differences in membrane potential across regions or populations, for which TMRM is likely better suited. On the other hand, as the extensive literature base indicates, JC-1 has been elegantly used in many studies—often chronic Scenario 1 type studies, but acute studies also (e.g., 26,27)—and thus in some cases can be a useful complement to the other probes discussed herein.

Another consideration for probe choice and read-out mode, which relates very closely to probe equilibration kinetics, is which fluorescence intensity will be monitored. Changes in dye distribution in response to changes in Δψ_m or Δψ_p will alter fluorescence signal in the mitochondria (F_m), in the cytoplasm (F_c), in both of these together (i.e., whole cell or cell soma fluorescence) (F_wc), and in the extracellular bath (F_ec). The direction and kinetics of dye response patterns will vary depending on exactly which of these F signals is being tracked, and on the equilibration rate and mode (quenching or nonquenching) of the dye in use. Dye behaviors in response to acute changes in Δψ_m have been expertly and thoroughly detailed elsewhere, and we refer the reader there for detailed discussion of these issues (2,19) (and see Section 7). Similar concepts will apply to determining how these regional intra/extracellular F intensities should vary in measurements of pre-existing Δψ_m among different populations (i.e., Scenario 1 studies), keeping in mind that in this situation one is only viewing a static snapshot of dye distribution, rather than tracking distribution changes.

As a somewhat coarse oversimplification of these issues for the sake of clarity to the first-time user, we might suggest the following:

1. For short time scale (minutes) studies to monitor rapid step changes in Δψ_m, using Rhod123 in quenching mode and monitoring F_wc is almost invariably a reliable choice. Rhod123’s slow equilibration may allow plasma membrane (PM) effects to be ignored over short time scales (2) and provides robust, relatively long-lasting whole-cell unquenching or quenching signals which are difficult to miss. In this paradigm, depolarization of Δψ_m leads to increased F_wc as Rhod123 unquenches from the mitochondria into the cytoplasm, whereas a hyperpolarization of Δψ_m leads to decreased F_wc as Rhod123 quenches from cytoplasm into the mitochondria. TMRE/TMRM can be used for these purposes as well, but these dyes’ shorter equilibration times means that PM effects must be accounted for, and make for much more transient unquenching (Δψ_m depolarization) or quenching (Δψ_m hyperpolarization) bursts in F_wc following step changes in Δψ_m, due to faster dye re-equilibration across the PM (compare Figure 2A and Figure 2B in Reference 19). This makes the initial change in F_wc easier to miss if capture frequency is not sufficient, and could lead to misinterpretation (i.e., opposite interpretation) of data. Another somewhat advanced distinction that Figure 2 in Reference 19 and Box 2 in Reference 2 nicely make clear is that in quenching mode, it is effectively the change in dye concentration in the cytoplasm/soma as dye is unquenched from or quenched into mitochondria that is responsible for the unquenching or quenching fluorescence burst—hence why F_wc and not F_m is monitored in this mode. This occurs because of the much greater S/V ratio of the mitochondrial inner membrane-matrix versus the PM-cytoplasm interface—i.e., dye leaves or enters mitochondria faster than dye leaves/enters the cell to compensate for this change in intracellular dye concentration—and is why the ΔF unquenching or quenching burst is easier to miss with faster equilibrating dyes like TMRM/TMRE versus slower equilibrating dyes like Rhod123.

2. For longer time scale (e.g., several tens of minutes to hours) but still ongoing real-time monitoring of Δψ_m, using the low-ETC inhibiting and low-binding TMRM in nonquenching mode (1–30 nM, best determined empirically) is often a good choice (28).

3. For measuring pre-existing Δψ_m across different chronically treated populations (Scenario 1 experiments), TMRM/TMRE in nonquenching mode will again usually provide good results. Again, TMRM is reported to exhibit somewhat less ETC inhibition and mitochondrial binding versus TMRE (20), but at low-nanomolar nonquenching concentrations, neither dye should have effects of concern in these areas.

In either of these latter nonquenching experimental paradigms (paradigm 2 or 3), the majority of TMRM/TMRE intracellular fluorescent signal will arise from polarized mitochondria, and therefore F_m can be monitored, which will correlate directly with changes in Δψ_m: depolarization of Δψ_m decreases F_m, and hyperpolarization of Δψ_m increases F_m. However, because in nonquenching mode the ratio of F_m/F_c is very high when mitochondria are polarized, if the read-out method lacks sufficient resolution to distinguish F_m from F_wc (e.g., flow cytometry or plate reader), then F_wc can serve as a satisfactory surrogate for F_m.

Finally, the mode and dye, and thus the signal that will be monitored (F_wc or F_m), will further help dictate the choice of read-out method. Certainly for quenching studies, or other studies requiring single-cell or single-mitochondria resolution, wide field fluorescence microscopy (WFM) (with CCD image capture) or confocal microscopy are reliable and proven choices. With either approach, light/laser intensities should be minimized as much as possible to prevent dye photobleaching and phototoxicity, and if at all possible, limited only to periods of actual image capture/image scanning. In addition, with either microscopy method, for acute studies the exposure (WFM) or scan (confocal) time for a single image must be fast enough to capture the kinetics of the dye response, and to minimize light exposure and prevent motion artifacts. Multiphoton microscopy is also being increasingly applied to studies with mitochondrial probes for Δψ_m, which will in theory not only allow real-time in vivo studies under some conditions (provided attention is given to all the considerations discussed herein, many of which are amplified in vivo), but should help reduce photobleaching and phototoxicity effects as well. Finally, read-out of F_wc by flow cytometry or fluorescent plate reader—while they lack the resolution of microscopy—may be effective choices for some population studies.

3. Other key dye loading, detection, and monitoring considerations

Regardless of experimental approach and dye method employed, correct interpretation of results requires a keen understanding of all the factors that can affect dye loading, distribution, and equilibrium. For chronic Scenario 1 experiments in particular, where each treatment group is not serving as its own internal baseline against which to measure fluctuations in dye fluorescence, this multitude of considerations in aggregate threatens to become all the more confounding, and thus (perhaps counterintuitively) obtaining reliable results in such chronic studies is sometimes more technically difficult than using the dyes in acute Scenario 2 studies.

For example, the concentration of dye loaded into mitochondria will be a function of, at minimum: bath dye concentration; Δψ_p; Δψ_m; mitochondrial size or mass (e.g., S/V ratios); and loading time (at least until equilibrium is reached). As detailed below, these variables must be controlled for in order to obtain interpretable results. For example, if the experimental treatment changes Δψ_p or mitochondrial mass, then the mitochondrial dye concentration—and thus F_m (and/or F_wc)—in experimental samples will differ from control independent of variations in Δψ_m. Despite these caveats, using low nonquenching dye concentrations and leaving the dye in the bath during image acquisition (i.e., no washout step; see next paragraph) should allow the investigator to make reproducible qualitative comparisons of post-treatment Δψ_m across different cell populations, assuming that total dye loading times and total light exposure times are precisely matched among the experimental conditions under comparison and that other factors discussed here are given due attention. In these kinds of Scenario 1 studies, leaving the dye in the bath helps avoid additional confounding experimental factors, such as if the experimental treatment were to affect the rate at which dye unbinds and/or repartitions across the mitochondrial and PM once dye is removed from the buffer—which in turn would change mitochondrial fluorescence independently of Δψ_m.

Another consideration is loading procedures. With perfectly free diffusion, the preferred approach would be to leave the dye in the perfusion bath during the course of the experiment so that the probe may equilibrate and re-equilibrate in Nernstian fashion with changes in Δψ_m. This approach, with dye continuously in the perfusion bath, has been frequently prescribed, tested, and applied in many published works. However, since all these dyes bind mitochondria to varying degrees, under many experimental paradigms a perfect Nernstian equilibrium may never be reached as dye remains in the perfusion buffer during the experiment. Despite this caveat, we have found that when TMRM or TMRE is loaded at sufficiently low concentrations (usually 1 nM) and left in the perfusion bath, the mitochondrial fluorescence intensity (F_m) will stop increasing after ~15–30 min (depending on sample conditions), meaning that an equilibrium—even if not a strictly Nernstian equilibrium due to some degree of unavoidable probe binding—has been reached. At this time, we find F_m will respond appropriately to known manipulations of Δψ_m.

On the other hand, under some experimental conditions the user may find that when probe remains in the perfusion bath, F_m may continue to increase with time, and never reach a stable equilibrium. There are several reasons this could occur. First, dye concentrations may be too high, and the user can determine whether the problem is corrected by lower dye loading concentrations. Second, the sample type may be such that unavoidable probe binding is very difficult to saturate, as might occur with very high cell densities, or tissue slices, for example. In this case, lower probe concentrations and/or lower cell densities can be explored. Other ways to remedy a continuously increasing F_m when probe remains in the perfusion bath include loading the mitochondrial dye for 15–30 min, followed by washout, then performing image acquisition with reduced concentrations or no dye in the perfusion buffer. (In some cases, by lowering fluorescence background, this approach may also improve signal-to-noise ratio.) Under these conditions, once bath dye concentrations are reduced or removed, mitochondria-loaded dye will repartition to equilibrium across both the mitochondrial and plasma membranes. Thus even if dye is completely removed from the perfusion buffer after dye loading, probe will still remain in the imaging bath buffer due to this re-equilibration. For these reasons, whenever the dye concentration in the imaging buffer is lower than the dye concentration in the loading buffer, it is imperative that the dye is allowed to fully re-equilibrate before imaging. This is particularly important for slow-equilibrating dyes such as JC-1. Despite the merit of this approach in some situations, at least for experiments in nonquenching mode, it may be preferable to maintain equivalent dye concentrations in loading and imaging buffers whenever possible to eliminate any possibility of misinterpreting Nernstian dye redistribution as an experimentally induced effect.

The converse situation may also exist whereby the mitochondrial dye loads slowly, and never appears to reach an equilibrium state. Often this may indicate efflux of the dye through rhodamine-sensitive multi-drug resistance transporters (MDR) (particularly in tumor cell lines) (6,29), which can be confirmed by blocking the MDR with verapamil or cyclosporin H.

Loading, equilibration, and binding considerations aside, there are other reasons that F_m may change independently of Δψ_m. Namely, these cationic probes also have varying degrees of phototoxicity, and others have shown that light exposure by itself can actually increase fluorescent TMRM signal, for reasons thought to be related to oxidant production (25). We have observed similar phenomena with TMRE under some experimental conditions (unpublished data). In other cases, significant and rapid photobleaching of these dyes may be observed with light exposure. In either case, minimizing total light exposure times is critical. For all these reasons, under Scenario 1 experiments, because experimental treatments are applied before probe loading, it is imperative that dye loading times and total duration of light exposure be precisely matched for any experimental conditions or individual fields under comparison. For example, following dye loading, the simple act of looking at fields of view under the microscope using mercury or xenon lamp illumination—unless total light exposure time and recovery time is identical for each condition (nearly impossible to achieve in practice)—will often impact the dye signal enough to render comparisons of F_m among the experimental conditions meaningless after such observation. Therefore for such Scenario 1 population studies, either fully automated microscopy (with automated field selection and image capture, such that specimens are only subject to low-intensity light during brief sub-second image exposures) or other read-out methods such as flow cytometry or a fluorescent plate reader may be most appropriate to minimize the confounds of light exposure on F_m.

With due attention to these kinds of details, verifiable and reproducible results can be obtained regardless of the approach chosen.

4. Use agents that affect Δψ_m to confirm directional dye behavior

Whatever method of dye usage one chooses for their experiments, it is critical to validate the approach in their experimental system using agents that affect Δψ_m to confirm that directional changes in mitochondrial fluorescence can be interpreted as predicted. For example, oligomycin (usually 2–5 μg/mL) will slightly hyperpolarize mitochondria by blocking proton re-entry via the ATP-synthase (7). Under nonquenching conditions, this will translate to a slight increase in F_m, and a slight (transient) decrease in F_wc under quenching conditions. It is important to note, however, that in unhealthy mitochondria with compromised energetics—for example, inhibited respiration and/or with proton leaks—the Δψ_m may be maintained by reversal of the ATP-synthase, in which case oligomycin treatment will cause increased interior [H⁺] and mitochondrial depolarization (7). Thus protonophores such as FCCP or carbonyl cyanide m-chloro phenyl hydrazone (CCCP) (usually ~0.25–5 μM), which depolarize mitochondria by increasing their permeability to protons, should be co-employed to further confirm dye behavior. In nonquenching mode, these compounds will decrease F_m. In quenching mode, FCCP/CCCP will transiently increase F_wc as quenched dye exits the mitochondria and becomes unquenched (thus brighter) in the cytoplasm, followed by a delayed decrease in F_wc as dye continues to exit mitochondria and cytoplasm and re-equilibrates across the PM with continued depolarization (see Box 2 in Reference 2). Following protonophore treatment, the duration of the transient increase in mitochondrial fluorescence caused by dye unquenching will differ with varying equilibration rates of each probe. These changes are well described in more detail elsewhere (2,7,19). The investigator should be aware of additional important considerations for FCCP/CCCP, namely that while lower concentrations (e.g., 250 nM) will specifically collapse Δψ_m, high concentrations (>2.5 μM) (likely to be variable with cell type) will also significantly diminish Δψ_p (18)—an important consideration if the investigator wishes to selectively collapse Δψ_m but not Δψ_p. Findings of another study suggested that in cerebellar granule neurons, FCCP may depolarize Δψ_p at least in part by glutamate release and NMDA receptor activation (28), perhaps either secondary to or downstream of its protonophoric or metabolic effects on Δψ_m. Addition of NMDA receptor antagonists/glutamate antagonists such as MK-801 may help determine if FCCP is acting in this fashion in a particular model system. These examples illustrate additional factors, likely to vary with cell type, that must be taken into account when interpreting effects of FCCP/CCCP on Δψ_m and Δψ_p.

5. Control or account for changes in Δψ_p

As discussed above, a cell’s Δψ_p will impact the amount of these cationic dyes entering the cytoplasmic space, thereby also affecting how much dye is available for mitochondrial uptake. Therefore, when using probes for Δψ_m, it is imperative to employ additional controls or modeling to ensure that altered Δψ_p is not responsible for any observed changes in F_m under the experimental conditions. Conversely, a change in Δψ_p that only occurs with experimental treatment could mask a legitimate (opposing) change in Δψ_m.

One approach is to use a complementary probe under parallel experimental conditions, such as bis-(1,3-dibutylbarbituric acid) trimethine oxonol [DiBAC₄(3)], a relatively specific probe for Δψ_p. An increase in the anionic DiBAC can be interpreted as a depolarization of Δψ_p, whereas decreased intracellular DiBAC fluorescence represents an increase in Δψ_p (5,30). In Scenario 1 experiments, this approach can be used to obtain a “static” snapshot of whether Δψ_p is also altered by experimental treatment, to help validate whether or not observed changes in F_m are due to altered Δψ_m alone, or to changes in Δψ_p (or both) (5).

Another clever approach is to obviate the dependence of F_m on Δψ_p by monitoring the ratio of fluorescence intensity between mitochondria-rich and mitochondria-poor regions of single cells (31); this method and the methods described herein may prove quite useful for many laboratories. However, it has been pointed out that this method requires nonquenching concentrations of probe (and thus may not be suitable for all experimental needs) and that estimating the rather small differences in fluorescence intensity between background and mitochondria-poor areas may introduce some measurement error (18).

Advanced methodologies have also been demonstrated for addressing relative contributions of Δψ_m and Δψ_p on F_m in real-time Scenario 2 type experiments, which include using computer modeling to simulate and isolate the effects of changes in Δψ_m and Δψ_p on F_m and F_c (19,32), parallel tracking of real-time changes in Δψ_p using DiBAC (28), and a method for simultaneous real-time tracking of both Δψ_m and Δψ_p using TMRM and a proprietary probe for monitoring Δψ_p (PMPI, Molecular Devices, Sunnyvale, CA) (18; also see Reference 33.)

These methods elegantly demonstrate, for example, that KCl or other cell-depolarizing treatments are indeed helpful for illustrating the impact of Δψ_p on mitochondrial dye equilibration behaviors in the context of real-time Scenario 2 type studies and simulation modeling (i.e., when the mitochondrial dyes are loaded before addition of KCl) (18,19,28,32). On the other hand, because regulation of Δψ_p and Δψ_m are intricately intertwined with intracellular ionic compositions and with each other—and because a depolarization of Δψ_p will severely limit the amount of dye available for mitochondrial uptake—investigators may find that for Scenario 1 studies (i.e., dye is loaded after experimental manipulation), loading the mitochondrial dye in the presence of KCl as a control for distinguishing the relative contributions of Δψ_p and Δψ_m to an experimentally observed F_m is of marginal diagnostic value. Rather, the other approaches described in this section should yield more useful information as to whether or not changes in Δψ_p are causing experimentally observed changes in F_m.

6. Verify results for Δψ_m with a complementary dye and/or approach

To support results obtained with a particular dye and methodological approach, it can be useful to further confirm the results with a complementary dye and/or approach. For example, one might examine chronic effects (e.g., 24-h time course) of an experimental treatment with TMRM used in nonquenching mode and loaded after experimental treatment (Scenario 1 studies), then support these results with acute treatments of the same agent after loading another probe (e.g., Rhod123) in quenching mode (Scenario 2 studies). Of course, acute versus chronic effects of any given agent on Δψ_m may differ. Therefore, one might instead employ two different dyes in quenching mode (e.g., TMRM and Rhod123) or in nonquenching mode (e.g., TMRM and JC-1) under otherwise identical experimental conditions. Given the complexities of using these dyes, this multimodal approach may better validate experimental findings than by using a single dye and methodology alone.

7. Utilize multiple approaches to quantifying fluorescent changes

Particularly if not employing software modeling of dye distribution behavior (see Section 5 above, and Section 9 below), investigators can consider using multiple analytical approaches to quantify changes in mitochondrial fluorescence under their experimental conditions. The most commonly employed approach is simply monitoring F_wc (in quenching mode) or F_m (in nonquenching mode) as described in Section 3 above. With changes in Δψ_m (or Δψ_p), changes in F_m will in turn be accompanied by opposing changes in F_c and F_ec fluorescence, as probe redistributes among mitochondrial, cytoplasmic, and extracellular compartments. However, F_c signal is small, especially at lower dye concentrations, and moreover, F_c changes that accompany F_m changes will be (often rapidly) transient as dye redistributes across the PM. Therefore, an approach that we have found useful is to instead monitor F_ec along with F_m (Figure 4). If F_m and F_ec are not mirroring each other in an opposing manner with oligomycin and FCCP treatment, for example, then the probes are not behaving in a fashion that will accurately predict Δψ_m and this methodological flaw must be identified and corrected before proceeding.

Figure 4. Acute tracking of nonquenching mitochondrial TMRE.

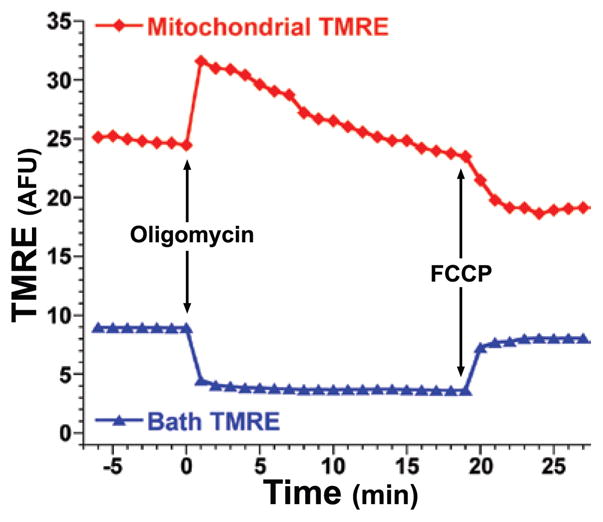
11–14-day-old primary mouse cortical neurons were loaded for >20 min at 37°C with 1 nM TMRE in HBSS. After the loading period, cells remained in the same loading bath, and using a Chroma HQ535/50x:Q565LP:HQ610/75m filter and dichroic set, CCD images were captured (1 image/min for 7 min) to establish a baseline; this was followed by direct addition of oligomycin (5 μg/mL) or FCCP (10 μM) at the times indicated by the arrows, which respectively caused the characteristic increase (hyperpolarization of Δψ_m) and decrease (depolarization of Δψ_m) of F_m as expected (red trace). These changes, as expected, were mirrored by an opposing decrease and increase in bath (background) TMRE signal (F_ec) (blue trace) as mitochondria absorbed or released TMRE in response to hyperpolarization and depolarization respectively. Monitoring F_m (or F_wc) and F_ec in parallel represents a simple and convenient approach to help verify expected redistribution behavior of these probes.

In addition, performing quantitative numerical analyses beyond measuring raw intensity changes in F_m can also further validate the interpretation of results. For example, examining the coefficient of variance of pixel intensities (CV = standard deviation/mean of F_wc pixel intensities)—a representation of the spatial heterogeneity of intracellular dye distribution between cytoplasmic and mitochondrial compartments—can further confirm results obtained from looking at F_m alone (34) and has the added benefit of helping to obviate any effects of a changing Δψ_p. By this method, depolarization of Δψ_m will lead to a more uniform intracellular distribution of probe as dye exits the mitochondrial pool, resulting in greater spatial homogeneity of the F_wc fluorescent signal, and thus a reduction in the variation of individual pixel values around the mean (i.e., a reduced CV). Hyperpolarization of Δψ_m will, in contrast, result in increased CV. While CV, like F_m, is still sensitive to changes in cell morphology or mitochondrial localization which must be accounted for (see Section 8), it nonetheless may provide a useful complementary analysis to confirm observed changes in F_m.

8. Control for changes in mitochondrial morphology, localization, or mass

Under some experimental conditions, it will be desirable to further ensure that any observed fluorescence changes correspond to changes in Δψ_m, rather than to changes in mitochondrial morphology, localization, or mass, changes in which can by themselves affect readings of F_m or F_wc. These controls are particularly important for nonquenching Scenario 1 type experiments in which dye fluorescence measurements are taken after experimental treatment using ensemble averaging (e.g., low-resolution analysis of dye fluorescence over whole cells) or over cell populations. Moreover, because of S/V ratios discussed in Section 2, more slowly permeant dyes like JC-1 used in a nonquenching experiment of this nature will still be more sensitive to the effects of changes in mitochondrial morphology or mass (i.e., volume). In fairness, even with best-practice efforts at some of these approaches below, we must note that quantifying mitochondrial morphology and/or mass can be a very difficult thing for any investigator do reliably, since (i) none of the assays themselves is without inherent sources of error, just as (ii) no one approach will be a perfect correlate for total mitochondrial mass/content under all conditions.

The first-line approach to control for these factors is to use qualitative (and if possible, quantitative, using image processing) visual assessment of whether changes in any of these parameters are occurring under the experimental conditions. Another complementary approach is to assess mitochondrial staining with Mitotracker (Molecular Probes, Invitrogen, Carlsbad, CA, USA) or other mitochondria binding fluorescent probes to determine whether these probes show intensity differences under experimental conditions identical to those used for monitoring Δψ_m. A key caveat to this approach is that many probes traditionally used in this fashion (e.g., Mitotracker probes or nonyl acridine orange) exhibit varying sensitivity to Δψ_m and/or inhibition of the ETC (35,36). Nonetheless, if used judiciously with these caveats and limitations in mind, mitochondria tracking probes of this nature may provide some relative impression of whether mitochondrial mass, morphology, or localization is changing under the experimental conditions and to determine if these factors may be contributing to changes in F_m or F_wc observed with TMRM, Rhod123, JC-1, or similar probes.

Another alternative to help control for mitochondrial localization and shape is the use of mitochondria-targeted fluorescent proteins [e.g., mtGFP (37,38)], which have been used for mitochondrial tracking and fusion/fission studies, among others (39,40). In many cases, these may prove more reliable than Mitotracker probes for assessing mitochondrial shape and localization, although mention of a few possible drawbacks and cautions is warranted. First, because these will require transfection or similar method to induce expression in cells, not all cells will be transfected, with transfection percentages depending on cell type. Second, because expression levels of the mitochondria-targeted fluorescent proteins will vary with many parameters besides mitochondrial mass and because their fluorescence intensity can also vary with many factors (e.g., with pH for some variants, see Section 10 and case study in Box 2), these tools are best used for assessment of mitochondrial localization and shape, rather than mass. Finally, if they are used simultaneously with any of the mitochondrial probes discussed herein, the investigator must be absolutely certain the two fluorophores can be spectrally separated with no cross-talk and that they do not interfere with the mitochondrial probe behavior, either of which will confound results.

Other means to assess relative mitochondrial mass under parallel experimental conditions include measuring the ratio of mitochondrial to nuclear DNA (mtDNA/nDNA), immunoblot analysis for key mitochondrial proteins (e.g., cytochrome c, Complex V), and/or analysis of mitochondrial protein content or weight following mitochondrial isolation procedures. Operating on a similar principle, one can also measure activity of the mitochondria-exclusive tricarboxylic acid (TCA) cycle enzyme citrate synthase (41), readily done with commercially available kits (Sigma Aldrich, St. Louis, MO, USA).

To further control for changes in mitochondrial localization that may affect quantification of mitochondrial dye signal when using ensemble-averaging approaches, F_m and F_ec under each experimental condition can be assessed and compared before and after addition of a protonophore (FCCP or CCCP). Analyzing the net change in F_m versus F_ec before and after complete mitochondrial depolarization can help to control for influences of mitochondrial mass or localization on F_m or F_wc when using ensemble averaging approaches. However, controls for Δψ_p must still be performed.

9. Use predictive computer simulations to interpret dye behavior and kinetics

Another approach to correctly interpreting F_m readings from cationic mitochondrial dyes involves using predictive computer simulations of dye behavior under various loading conditions (dye type, dye concentration, etc.) to aid or inform interpretation of single-cell fluorescence behavior during experimental treatments [e.g., under conditions of glutamate exposure and Ca²⁺ dysregulation in neurons (19,28)]. This modeling approach—which is particularly useful for dissecting changes in F_m that occur due directly to altered Δψ_m versus due to altered Δψ_p (see Section 5)—has been expertly validated and described elsewhere (see References 18, 19, 28, and 32, and references therein), and thus will not be described in detail here. While this approach can be technically and mathematically complex to implement, the recent addition of a freely available web-based service for TMRM trace analysis greatly enhances the availability and feasibility of this approach for biological researchers of all backgrounds (http://systemsbiology.rcsi.ie/tmrm/index.html) (32).

10. Employ complementary tools to assess the ΔpH_m component of Δp

With their utility as indicators of Δψ_m, coupled with the proton’s central role in mitochondrial bioenergetics, it is tempting to assume that distribution behavior of these mitochondrial dyes specifically reflects the H⁺ gradient between the mitochondrial exterior and interior (i.e., ΔpH_m, the pH component of Δp (recall from the Introduction that Δp = Δψ_m − 60ΔpH_m). In other words, one might be tempted to conclude that increased dye uptake (hyperpolarized mitochondria) also indicates decreased mitochondrial proton concentration ([H⁺]_mito), or that decreased mitochondrial dye uptake (depolarized mitochondria) reflects increased [H⁺]_mito. To do so would be to equate Δψ_m with ΔpH_m, when in fact these are each separate contributors to Δp (see the Introduction), or to assume that Δψ_m will always follow ΔpH_m. On the contrary, because Δψ_m ≠ ΔpH_m, and because changes in Δψ_m may often but do not necessarily follow changes in ΔpH_m, additional tools have been developed to assess the ΔpH_m component of Δp. For example, mitochondria-targeted pH sensitive fluorescent fusion reporter proteins whose fluorescence intensity varies with pH (42,43), or pH-sensitive probes like SNARF-1 targeted to mitochondria (44), can be used to directly assess mitochondrial pH. These tools can be used together with assessments of cytosolic pH using similar cytosol-targeted pH-sensitive fluorescent fusion reporter proteins (42) or the pH-sensitive fluorophore 2′-7′-bis(carboxyethyl)-5(6)-carboxyfluorescein acetoxymethyl ester (BCECF-AM) (43), to directly calculate ΔpH_m across the mitochondrial membrane. Precisely because cationic dyes for monitoring Δψ_m can only respond to charge gradients and not specifically to proton gradients, these additional tools are useful or even imperative (see case study in Box 2) complementary methods by which to assess both Δψ_m and ΔpH_m as independent and sometimes divergent components of Δp.

11. Measure additional parameters related to mitochondrial function and metabolism

Finally, to further substantiate interpretations of mitochondrial dye behavior, it is useful to measure additional parameters relevant to mitochondrial function, bioenergetics, metabolism, and/or respiration, to ensure that these additional observations are consistent with the predicted changes in Δψ_m. Complete details on all possible additional assays cannot be adequately covered here; however, some assays to consider, described elsewhere, include measuring: (i) cellular ATP/ADP levels (5), (ii) activities of the ETC complexes (45), (iii) NADH/NADPH levels (45,46), (iv) O₂ consumption/respiration (45,47,48), (v) glycolysis (49), (vi) organellar calcium (45,50–54), and/or (vii) reactive oxygen species (ROS) (48,54,55). Performing such additional assays of metabolic function along with measuring Δψ_m, together with the other approaches and controls discussed herein, will afford investigators the most comprehensive picture of how their experimental treatments affect cells’ bioenergetic status.