DESCRIBING DISABILITY THROUGH INDIVIDUAL-LEVEL MIXTURE MODELS FOR MULTIVARIATE BINARY DATA

Abstract

Data on functional disability are of widespread policy interest in the United States, especially with respect to planning for Medicare and Social Security for a growing population of elderly adults. We consider an extract of functional disability data from the National Long Term Care Survey (NLTCS) and attempt to develop disability profiles using variations of the Grade of Membership (GoM) model. We first describe GoM as an individual-level mixture model that allows individuals to have partial membership in several mixture components simultaneously. We then prove the equivalence between individual-level and population-level mixture models, and use this property to develop a Markov Chain Monte Carlo algorithm for Bayesian estimation of the model. We use our approach to analyze functional disability data from the NLTCS.

1. Introduction

1.1. Background

Data on functional disability are of widespread policy interest in the United States, especially with respect to planning Medicare and Social Security spending for a growing population of elderly adults. The concept of functional disability reflects difficulties in performing activities that are considered normal for everyday living. These activities are usually divided into two types, namely basic and instrumental activities of daily living (ADL and IADL). ADL and IADL outcomes are considered essential in health services research and form a cornerstone of geriatric medicine. In this article, we present a Bayesian analysis of functional disability among a sample of elderly individuals in the National Long Term Care Survey (NLTCS), using basic and extended Grade of Membership (GoM) models for multivariate binary response data.

The NLTCS began in 1982 and now extends over six waves through 2004, making it an important source of information on possible changes in disability over time among the elderly Americans. The NLTCS data on functional disability have been used to generate some major findings such as a persistent decline in chronic disability among the elderly Americans, e.g., see Manton and Gu [47] and Manton et al. [49, 53].

It is common practice to analyze functional disability data by using totals where individual scores are added together for all items or by subsets [47]. Statistically, adherence to the Rasch model [62] can provide researchers with a formal justification for reducing the multivariate data down to such total scores. It is often the case, however, that functional disability data have a high amount of heterogeneity that is not explainable by the Rasch model. It may be possible to circumvent this problem by reducing the set of functional disability items under consideration, as was illustrated, for example, in the gerontology literature by Spector and Fleishman [69]. This approach, however, obviously ignores potentially relevant information contained in the excluded items.

In this paper, we use individual-level mixtures to account for heterogeneity in functional disability data measured with a given battery of items without considering the issue of item reduction. We contrast the individual-level mixture assumption with population-level mixture models that assume individuals can be members of one and only one subpopulation, such as latent class models for discrete data [29, 40]. The central idea of all individual-level mixture models is to allow an individual’s membership to be a mixture with respect to population components [7, 60, 77]. A natural example of individual-level mixtures is genetic makeup of individuals who have various degrees of ancestry in several subpopulations of origin [60]. Such admixed individuals do not simply belong to one of the original subpopulations with some degree of uncertainty, but their genetic makeup is actually composed of genes that originated from different subpopulations. Specifically, we use the Grade of Membership (GoM) model introduced in 1978 by Woodbury et al. [77] and develop its extension to address the following questions: How many mixture categories are in the functional disability data under the assumption of mixed membership? What are characteristics of each mixture category? What is the population distribution of the individual membership scores?

We begin by introducing the NLTCS in Section 2. Next, we describe the GoM model and its relationship to latent class models via the fundamental representation theorem in Section 3. We use this result to develop a fully Bayesian approach in Section 4.1, and describe a variational approximation approach as an alternative estimation method in Section 4.2. Section 5 develops the extended mixture GoM model and corresponding estimation techniques. Section 6 considers the question of dimensionality selection in terms of the optimal number of mixture categories. Section 7 describes results from simulation studies. Finally, we present an individual-level mixture analysis of the NLTCS functional disability data and provide discussions in Sections 8 and 9.

2. National Long Term Care Survey functional disability data

The NLTCS aims to assess chronic disability in the U.S. Medicare-enrolled population age 65 or older (Corder and Manton [12]). The survey began in 1982 with a screening survey instrument that selected community-dwelling chronically disabled (based on basic and instrumental activities of daily living) persons for detailed in-home interviews. Once individuals screened-in, the NLTCS followed them longitudinally. The second wave of the survey was in 1984, and all subsequent waves occurred in five-year intervals with the most recent wave completed in 2004. The NLTCS replenishes its sample at each wave in order to reflect the current U.S. population 65 and older. While additional components have come and gone from post-1982 waves of the NLTCS, key disability questions have stayed the same. For more information on the NLTCS see [12, 52, 68].

We consider an extract from the NLTCS that contains data on 6 activities of daily living (ADL) and 10 instrumental activities of daily living (IADL) for community-dwelling elderly from 1982, 1984, 1989, and 1994 survey waves. These 16 binary functional disability measures are described in detail in Manton, et al. [46]. The 6 ADL items include basic activities of hygiene and personal care (eating, getting in/out of bed, getting around inside, dressing, bathing, and getting to the bathroom or using toilet). The 10 IADL items include basic activities necessary to reside in the community (doing heavy housework, doing light housework, doing laundry, cooking, grocery shopping, getting about outside, travelling, managing money, taking medicine, and telephoning). Positive responses are coded as 1=disabled, and negative as 0=healthy. In the NLTCS, positive ADL responses mean that during the past week the activity had not been, or was not expected to be, performed without the aid of another person or the use of equipment; positive IADL responses mean that a person usually could not, or was not going to be able to, perform the activity because of a disability of a health problem. For a more in-depth discussion, see Manton et al. [46], and Erosheva and White [22].

At each wave, the survey sample is representative of the 65 years and older U.S. population at that point in time. High follow-up rates and consistency in ADL and IADL questions over time makes the NLTCS a unique source of data for studying complex questions such as the dynamics of population changes in disability. For example, Manton and Gu [47] and Manton et al. [49, 53] used weighted total numbers of impaired ADL and IADL to show declines in disability, although they did not tackle the important question of “Why?” [13]. We believe that in order to move forward in our understanding of why disability is declining so rapidly and whether the decline can be expected to continue, an important first step is to describe heterogeneous multivariate disability manifestations.

Our ultimate goal is to develop a longitudinal version of the GoM model. Our analysis in this paper represents an attempt to learn disability mixture profiles that describe the underlying structure of functional disability in chronically disabled community-dwelling elderly U.S. population. We make three simplifying assumptions in this analysis. First, we assume that the nature of the mixture components stays the same over time. For a longitudinal version of the GoM model, keeping profiles the same over time and allowing the population distribution among the profiles to change would allow us to obtain an estimable model. For similar reasons, the assumption of time-invariant latent classes is common in latent class transition modeling (see [63], for example). In addition, our exploratory GoM analyses separately for each wave obtained profiles whose characteristics were fairly stable over time, thus confirming that the assumption of profile time-invariance is reasonable in our case. Second, we assume no inter-dependencies between longitudinal records on the same individuals. Violations of this assumption may reduce efficiency of our estimates but will not introduce bias. Third, we ignore the sample weights associated with differential probabilities of selection into the NLTCS. In fact, we have yet to understand how if at all we could incorporate the weights into the modeling process. We view these three assumptions necessary for this first step toward understanding changes in disability over time.

3. The grade of membership (GoM) model and its latent class representation

The GoM model originates in the context of medical applications: when a diagnosis is uncertain, partial membership reflects this uncertainty through allowing different disease symptoms correspond to different stages of the disease. GoM applications now cover a wide spectrum of studies, ranging from studying depression [14] and schizophrenia [50] to analyzing complex genotype-phenotype relations [48]; for a recent review, see Erosheva and Fienberg [20]. The model remains relatively unfamiliar to statistical audiences, however. Despite a multitude of published large-scale GoM applications, there are few statistical publications that explore basic GoM properties and provide simple examples that demonstrate model’s utility [18, 59, 76].

In particular, the relationship between individual-level and population-level mixture models does not appear to be clearly formulated in the literature. Singer [67] describes the GoM model as a new type of model that is not equivalent to usual mixture models. Likewise, when comparing the GoM and latent class models, in their 1994 book, Manton et al. [51] concluded: “latent class model is nested in the GoM model structure…”, but “…if we allow latent class model to have more classes, then it is potentially possible to “fit” the realized data set as well as with GoM” (p. 45). On the other hand, in his review of Manton et al., Haberman [32] suggested that the GoM model is a special case of latent class models. He pointed out that a set of constraints imposed upon a latent class model can specify a distribution of manifest variables that is identical to that specified by the GoM model.

In this section, we describe the GoM and latent class models and present the fundamental representation theorem of equivalence between individual-level and population-level mixture models [19].

GoM and latent class models

Let x = (x₁, x₂, …, x_J) be a vector of polytomous manifest variables, where x_j takes on values l_j ∈ L_j = {1, 2, …, L_j}, j = 1, 2, …, J, and L_j denotes the number of possible outcomes. Let $X={\prod }_{j=1}^J{L}_j$ be the set of all possible outcomes for vector x.

To define the GoM model, let K be the number of mixture components (extreme profiles), and let g = (g₁, g₂, …, g_K) be a latent partial membership vector of K nonnegative random variables that sum to 1. For discrete data, each extreme profile is characterized by a vector of conditional response probabilities, when a given kth component of the partial membership vector is 1 and the others are 0:

$$\begin{array}{ll}{\mathrm{\lambda }}_{kj{l}_j}=\mathrm{pr}\left(x_j=l_j\mid g_k=1\right),& k=1,2,\dots ,K,\\ & j=1,2,\dots ,J,\\ & l_j=1,2,\dots ,L_j.\end{array}$$ (1)

The set of conditional response probabilities must satisfy the following constraints:

$$\sum _{l_j\in L_j}{\mathrm{\lambda }}_{kj{l}_j}=1,k=1,2,\dots ,K;j=1,2,\dots ,J.$$

Given partial membership vector g ∈ [0, 1]^K, the conditional distribution of manifest variable x_j is given by a convex combination of the extreme profiles’ conditional response probabilities, i.e.,

$$\mathrm{pr}\left(x_j=l_j\mid g\right)=\sum _{k=1}^K{g}_k{\mathrm{\lambda }}_{kj{l}_j},j=1,2,\dots ,J,l_j=1,2,\dots ,L_j.$$ (2)

The local independence assumption states that manifest variables are conditionally independent, given latent variables. Under this assumption, the conditional probability of observing response pattern l is

$$f^{\mathit{GoM}}\left(l\mid g\right)=\mathrm{pr}\left(x=l\mid g\right)=\prod _{j=1}^J\mathrm{pr}\left(x_j=l_j\mid g\right)=\prod _{j=1}^J\left(\sum _{k=1}^K{g}_k{\mathrm{\lambda }}_{{\mathit{kjl}}_j}\right),l\in \chi .$$

The local independence assumption is common in latent structure models [40]; it says that latent variables fully account for associations among the observed responses.

Let us denote the distribution of g by D(g). Integrating out latent variable g, we obtain the marginal distribution for response pattern l in the form of an individual-level mixture

$$\begin{array}{ll}{f}^{\mathit{GoM}}\left(l\right)=\mathrm{Pr}\left(x=l\right)& =\mathit{\int }{f}^{\mathit{GoM}}\left(l\mid g\right)\mathit{dD}\left(g\right)\\ & =\mathit{\int }\prod _{j=1}^J\left(\sum _{k=1}^K{g}_k{\mathrm{\lambda }}_{{\mathit{kjl}}_j}\right)\mathit{dD}\left(g\right),l\in \chi .\end{array}$$ (3)

Using similar notation, we can derive the K-class population-level mixture (latent class) model as a special case of the K-profile GoM model by restricting components of the partial membership vector to only take values 0 and 1. Denote the restricted version of the membership vector by g* and its probability mass function by ${\mathrm{\pi }}_k=\mathrm{pr}\left(g_k^{\ast }=1\right)$. Assuming local independence, we see that the marginal distribution of the manifest variables under the latent class model simplifies to the K-component summation:

$$\begin{array}{ll}{f}^{\mathit{LCM}}\left(l\right)=\mathrm{pr}\left(x=l\right)& =\mathit{\int }{f}^{\mathit{LCM}}\left(l\mid g^{\ast }\right)\mathit{dD}\left(g^{\ast }\right)\\ & =\sum _{k=1}^K{\mathrm{\pi }}_k\prod _{j=1}^J{\mathrm{\lambda }}_{{\mathit{kjl}}_j},l\in \chi .\end{array}$$ (4)

The probability of observing response pattern l is the sum of the probabilities of observing l from each of the latent classes, weighted by their relative sizes, π_k. One can visualize the relationship between sets of individual-specific response probabilities under the GoM and latent class models with the same number of mixture categories using a geometric approach [18].

Fundamental representation theorem

Note that the GoM marginal or integrated likelihood in equation (3) does not simplify to a summation of K components. This is in contrast to the functional form of the likelihood for a population-level mixture of K latent classes. If we relax the requirement of equality of the number of latent classes and extreme profiles, however, following [32] we can construct a latent class model such that its marginal distribution of manifest variables is exactly the same as that under the GoM model.

Consider a vector of J polytomous latent variables z = (z₁, z₂, …, z_J), each taking on values from the set of integers {1, 2, …, K}. Vector z here is the latent classification variable. Denote by Z = {1, 2, …, K}^J the set of all possible vectors z. As before, $X={\prod }_{j=1}^J{L}_j$ is the set of all possible outcomes for vector x. Then X × Z is the index set for the cross-classification of the manifest variables x and latent classification variables z.

To obtain a latent class representation of the GoM model, we must find a way to interchange the summation and the product operator in equation (3). The following lemma provides algebra which allows us to do so.

Lemma 3.1

For any two positive integers J and K, and for any two sets of real numbers {a_k, k = 1, 2, …, K} and {b_kj, k = 1, 2, …, K, j = 1, 2, …, J},

$$\prod _{j=1}^J\sum _{k=1}^K{a}_k{b}_{\mathit{kj}}=\sum _{z\in Z}\prod _{j=1}^J{a}_{z_j}{b}_{z_{j}j},$$

where z = (z₁, z₂, …, z_J) is such that $z\in Z={\prod }_{j=1}^J\left\{1,2,\dots ,K\right\}$.

Define the distribution over latent classes z ∈ Z, conditional on the distribution of membership vector g ∈ [0, 1]^K:

$${\mathrm{\pi }}_z=E_D\left(\prod _{j=1}^J{g}_{z_j}\right).$$ (5)

If (g₁, g₂, …, g_K) has a joint distribution D(g) on [0, 1]^K, such that g₁ + g₂ + … + g_K = 1, then π_z is a probability measure on Z. From the functional form of π_z, it also follows that latent classification variables z₁, z₂, …, z_J are exchangeable.

To specify the conditional distribution of the manifest variables given the latent variables z, we need two additional assumptions. First, assume that x_j depends only on the jth component of the latent indicator variable z:

$$\mathrm{pr}\left(x_j=l_j\mid z\right)=\mathrm{pr}\left(x_j=l_j\mid z_1,z_2,\dots ,z_J\right)=\mathrm{pr}\left(x_j=l_j\mid z_j\right),$$ (6)

Where z_j ∈ {1, 2, …, K}, and l_j ∈ L_j} is the observed value of manifest variable x_j. In essence, equation (6) postulates that manifest variable x_j is directly influenced only by the jth component of the latent classification vector z. Second, assume that conditional response probabilities in equation (6) are given by

$$\begin{array}{ll}\mathrm{pr}\left(x_j=l_j\mid z_j\right)={\mathrm{\lambda }}_{z_{j}j{l}_j},& z_j=1,2,\dots ,K,\\ & j=1,2,\dots ,J,\\ & l_j=1,2,\dots ,L_{j,}\end{array}$$ (7)

where the set of λs is the same as the set of conditional response probabilities for the GoM model. These structural parameters must also satisfy the constraints:

$$\sum _{l_{j=1}}^{L_j}{\mathrm{\lambda }}_{z_j{\mathit{jl}}_j}=1,\mathrm{for}\mathrm{all}z\in Z,j\in \left\{1,2,\dots ,J\right\}.$$

Under the local independence assumption, we obtain the probability of observing response pattern l for the latent class model as

$$f^{\ast }\left(l\right)=\sum _{z\in Z}{\mathrm{\pi }}_z\left(\prod _{j=1}^J{\mathrm{\lambda }}_{z_j{\mathit{jl}}_j}\right),l\in \chi ,$$ (8)

where the probability of latent class z is the expected value of a J-fold product of the membership scores ${\mathrm{\pi }}_z=E_D\left({\prod }_{j=1}^J{g}_{z_j}\right)$. Thus, the probability of observing response pattern l in equation (8) is the sum of the conditional probabilities of observing l from each of the latent classes, weighted by the latent class probabilities.

Consider the marginal probability of an arbitrary response pattern l ∈ χ for the GoM model provided by equation (3). Applying lemma 3.1 with a_k = g_k, b_kj = λ_kjlj, and using properties of expectation, we obtain the marginal probability:

$$f^{\mathit{GoM}}\left(l\right)=\sum _{z\in Z}\left\{E_D\left(\prod _{j=1}^J{g}_{z_j}\right)\left(\prod _{j=1}^J{\mathrm{\lambda }}_{z_j{\mathit{jl}}_j}\right)\right\},$$

which is exactly the same as in equation (8). It follows that the GoM model is equivalent to a latent class model with a distribution on the latent classes given by a functional form of the distribution of membership scores. This equivalence statement can be generalized via the following fundamental representation theorem:

Theorem 3.2

Given J manifest variables, any individual-level mixture model with K components can be represented as a constrained population-level mixture model with K^J components.

The fundamental representation theorem applies to a wider class of mixed membership models introduced by Erosheva [16].

4. Estimation algorithms for the standard GoM model

4.1. Bayesian Estimation Algorithm

Data Augmentation

The fundamental representation theorem leads us naturally to a data augmentation approach in the spirit of those described by Tanner [74]. In this Section, we present the Bayesian estimation algorithm for the GoM model, described earlier in Erosheva [17].

Denote by x the set of observed responses x_ij for all subjects. Denote by λ the set of conditional response probabilities. For the functional disability data, λ_kj = pr(x_j = 1|gk = 1) is the probability of being disabled on activity j for a complete member of extreme profile k. For subject i, augment observed responses with realizations of the latent classification variables z_i = (z_i1, …, z_iJ). Denote by z the set of latent classifications z_ij on all items for all individuals. In the following, we use notation p(·) to refer to both probability density and probability mass functions.

We assume the distribution of membership scores is Dirichlet with parameters α. The joint probability model for the parameters and augmented data is

$$\begin{array}{ll}p\left(\mathrm{x},\mathrm{z},\mathrm{g},\mathrm{\lambda },\alpha \right)& =p\left(\mathrm{\lambda },\alpha \right)\cdot p\left(\mathrm{x},\mathrm{z},\mathrm{g}\mid \mathrm{\lambda },\alpha \right)\\ & =p\left(\mathrm{\lambda },\alpha \right)\prod _{i=1}^N\left[p\left(z_i\mid g_i\right)p\left(x_i\mid \mathrm{\lambda },z_i\right)\cdot D\left(g_i\mid \alpha \right)\right],\end{array}$$

where

$$\begin{array}{rl}p\left(z_i\mid g_i\right)=& \prod _{j=1}^J\prod _{k=1}^K{g}_{ik}^{z_{\mathit{ijk}}},\\ p\left(x_i\mid \mathrm{\lambda },z_i\right)=& \prod _{j=1}^J\prod _{k=1}^K{\left({\mathrm{\lambda }}_{\mathit{kj}}^{x_{\mathit{ij}}}{\left(1-{\mathrm{\lambda }}_{\mathit{kj}}\right)}^{1-x_{\mathit{ij}}}\right)}^{z_{\mathit{ijk}}},\\ \mathit{Dir}\left(g_i\mid \alpha \right)=& \frac{\mathrm{\Gamma }\left({\sum }_k{\alpha }_k\right)}{\mathrm{\Gamma }\left({\alpha }_1\right)\dots \mathrm{\Gamma }\left({\alpha }_K\right)}{g}_{i1}^{{\alpha }_1-1}\dots g_{\mathit{iK}}^{{\alpha }_K-1},\end{array}$$

and latent classification indicators z_ijk are such that z_ijk = 1, if z_ij = k, and z_ijk = 0 otherwise.

We assume the prior on extreme profile response probabilities λ is independent of the prior on the hyperparameters α. We further assume that the prior distribution of extreme profile response probabilities treats items and extreme profiles as independent. Thus

$$p\left(\mathrm{\lambda },\alpha \right)=p\left(\alpha \right)\prod _{k=1}^K\prod _{j=1}^{J}p\left({\mathrm{\lambda }}_{\mathit{kj}}\right).$$ (9)

We take p(λ_kj) to be Beta(η₁, η₂), and for simplicity in what follows we use η₁ = η₂ = 1.

If the hyperparameters α are known, it is possible to obtain complete conditional distributions and use standard software such as BUGS¹ to obtain a posterior distribution of the model parameters [16]. In reality, the hyperparameters are unlikely to be known and need to be estimated. Setting hyperparameters to some fixed values without prior knowledge may bias conclusions and affect model choice in individual-level mixture models (see the discussion in Airoldi et al. [1]).

If we assume that the Dirichlet parameter vector α is unknown, we obtain samples from its posterior distribution via a Metropolis-Hastings step within the Gibbs sampler. Consider a reparameterization of α = (α₁, …, α_K) with ${\alpha }_0={\sum }_{k=1}^K{\alpha }_k$ and $\xi =\left({\xi }_1,\dots ,{\xi }_K\right)$, where ${\xi }_k={\alpha }_k/{\alpha }_0$. Then components of vector ξ reflect proportions of the item responses that belong to each mixture category, and α₀ reflects the spread of the membership distribution. The closer α₀ is to zero, the more probability is concentrated near the mixture categories; similarly, the larger α₀ is, the more probability is concentrated near the population average membership score.

We assume that α₀ and ξ are independent since they govern two unrelated qualities of the distribution of the GoM scores. We also assume that the prior distribution on the GoM scores is independent of the prior distribution on the structural parameters. The joint distribution of the parameters and augmented data is

$$p\left(\mathrm{\lambda }\right)p\left({\alpha }_0\right)p\left(\xi \right)\left(\prod _{i=1}^{N}D(g_i\mid \alpha )\right)\prod _{i=1}^N\prod _{j=1}^J{\prod _{k=1}^K\left(g_{\mathit{ik}}{\mathrm{\lambda }}_{\mathit{kj}}^{x_{\mathit{ij}}}{(1-{\mathrm{\lambda }}_{\mathit{kj}})}^{1-x_{\mathit{ij}}}\right)}^{z_{\mathit{ijk}}}.$$ (10)

In the absence of a strong prior opinion about hyperparameters α₀ and ξ, we take the prior distribution p(ξ) to be uniform on the simplex and p(α₀) to be a proper diffuse gamma distribution.

Sampling from the posterior distribution

• Imputation step: We use a multinomial complete conditional distribution to obtain the (m + 1)st draw of latent class indicator variables z_ij for each i = 1, …, N, j = 1, …, J:

  $$z_{\mathit{ij}}^{\left(m+1\right)}~\mathit{Mult}\left(1,p_1,\dots ,p_K\right),p_k\propto g_{\mathit{ik}}{\mathrm{\lambda }}_{\mathit{kj}}^{x_{\mathit{ij}}}{\left(1-{\mathrm{\lambda }}_{\mathit{kj}}\right)}^{1-x_{\mathit{ij}}}$$ (11)

• Posterior step:

  • –
    Sampling λ. We use the complete conditional distribution to obtain the (m + 1)st draw of conditional response probabilities λ_kj, k = 1, …, K, j = 1, …, J:

    $${\mathrm{\lambda }}_{\mathit{kj}}^{\left(m+1\right)}~\mathit{Beta}\left(1+\sum _{i=1}^N{x}_{\mathit{ij}}{z}_{\mathit{ijk},}1+\sum _{i=1}^N(z_{\mathit{ijk}}-x_{\mathit{ij}}{z}_{\mathit{ijk}})\right)$$ (12)
  • –
    Sampling g. We use the complete conditional distribution to obtain the (m + 1)st draw of membership scores g_i, i = 1, …, N:

    $$g_i^{\left(m+1\right)}~D\left({\alpha }_1+\sum _{j=1}^J{z}_{\mathit{ij}1},\dots ,{\alpha }_K+\sum _{j=1}^J{z}_{\mathit{ijK}}\right).$$ (13)
  • –Sampling α₀ and ξ. Here we require Metropolis-Hastings steps.

Sampling α₀

Let the prior p(α₀) to be Gamma(τ, β) with shape parameter τ and inverse scale parameter β. The full conditional distribution for α₀, up to a constant of proportionality, is

$$p\left({\alpha }_0\mid \dots \right)\propto {\alpha }_0^{\tau -1}\exp \left[-\left(\beta -\sum _{k=1}^K{\xi }_k\sum _{i=1}^N\log g_{\mathit{ik}}\right){\alpha }_0\right]{\left[\frac{\mathrm{\Gamma }\left({\alpha }_0\right)}{\mathrm{\Gamma }\left({\xi }_1{\alpha }_0\right)\dots \mathrm{\Gamma }\left({\xi }_K{\alpha }_0\right)}\right]}^N,$$ (14)

Where … in $p\left({\alpha }_0\mid \dots \right)$ stands for all other variables.

In order to obtain the (m + 1)st draw of α₀ for the Metropolis-Hastings algorithm, we

1. draw a candidate point ${\alpha }_0^{\ast }$ from proposal distribution $p\left({\alpha }_0^{\ast }\mid {\alpha }_0^{\left(m\right)}\right)$;

2. calculate the proposal ratio

   $$r{\alpha }_0=\frac{p\left({\alpha }_0^{\ast }\mid \dots \right)p\left({\alpha }_0^{\left(m\right)}\mid {\alpha }_0^{\ast }\right)}{p\left({\alpha }_0^{\left(m\right)}\mid \dots \right)p\left({\alpha }_0^{\ast }\mid {\alpha }_0^{\left(m\right)}\right)};$$

3. assign ${\alpha }_0^{\left(m+1\right)}={\alpha }_0^{\ast }$ with probability $\mathit{min}\left\{1,r{\alpha }_0\right\}$ otherwise assign ${\alpha }_0^{\left(m+1\right)}={\alpha }_0^{\left(m\right)}$.

We take proposal distribution $p\left({\alpha }_0^{\ast }\mid {\alpha }_0^{\left(m\right)}\right)$ to be gamma with the expected value set at the value of the last draw, ${\alpha }_0^{\left(m\right)}$, and the shape parameter ω > 1. The inverse scale parameter for the proposal distribution is then $\omega /{\alpha }_0^{\left(m\right)}$, where ω plays the role of the tuning parameter for the Metropolis-Hastings step. The proposal ratio for the (m + 1)st draw of α₀ is the product of the likelihood component and the component that accounts for the asymmetric proposal distribution:

$$r{\alpha }_0=r_{{\alpha }_0}^L\cdot r_{{\alpha }_0}^A,$$

where

$$\begin{array}{rl}{r}_{{\alpha }_0}^L=& {\left(\frac{{\alpha }_0^{(\ast )}}{{\alpha }_0^{\left(m\right)}}\right)}^{\tau -1}\exp \left[-\left(\beta -\sum _{k=1}^K{\xi }_k\sum _{i=1}^N\log g_{\mathit{ik}}\right)({\alpha }_0^{\ast }-{\alpha }_0^{\left(m\right)})\right]\\ & \cdot {\left[\frac{\mathrm{\Gamma }({\alpha }_0^{\ast })\mathrm{\Gamma }({\xi }_1{\alpha }_0^{\left(m\right)})\dots \mathrm{\Gamma }({\xi }_K{\alpha }_0^{\left(m\right)})}{\mathrm{\Gamma }({\alpha }_0^{\left(m\right)})\mathrm{\Gamma }({\xi }_1{\alpha }_0^{\ast })\dots \mathrm{\Gamma }({\xi }_K{\alpha }_0^{\ast })}\right]}^N\\ r_{{\alpha }_0}^A=& {\left(\frac{{\alpha }_0^{\left(m\right)}}{{\alpha }_0^{\ast }}\right)}^{2\omega -1}\exp \left[-\omega ({\alpha }_0^{\left(m\right)}/{\alpha }_0^{\ast }-{\alpha }_0^{\ast }/{\alpha }_0^{\left(m\right)})\right].\end{array}$$

Sampling ξ

The full conditional distribution for ξ, up to a constant of proportionality, is:

$$p\left(\xi \mid \dots \right)\propto \exp \left[a_0\sum _{k=1}^K{\xi }_k\sum _{i=1}^N\log g_{\mathit{ik}}\right]{\left[\frac{\mathrm{\Gamma }\left({\alpha }_0\right)}{\mathrm{\Gamma }\left({\xi }_1{\alpha }_0\right)\dots \mathrm{\Gamma }\left({\xi }_K{\alpha }_0\right)}\right]}^N$$ (15)

where … in $p\left(\xi \mid \dots \right)$ stands for all other variables.

The Metropolis-Hastings sampling algorithm to obtain the (m+1)st draw of ξ has three steps:

1. draw a candidate point ξ* from the proposal distribution $p({\xi }^{\ast }\mid {\xi }^{\left(m\right)})$;

2. calculate the proposal ratio

   $$r_{\xi }=\frac{p({\xi }^{\ast }\mid \dots )p({\xi }^{\left(m\right)}\mid {\xi }^{\ast })}{p({\xi }^{\left(m\right)}\mid \dots )p({\xi }^{\ast }\mid {\xi }^{\left(m\right)})};$$

3. assign ξ^(m+1) = ξ* with probability min{1, r_ξ}, otherwise assign ξ^(m+1) = ξ^(m).

We chose the proposal distribution for ξ to be $\mathit{Dir}({\xi }^{\ast }\mid \eta K{\xi }_1^{\left(m\right)},\dots ,\eta K{\xi }_K^{\left(m\right)})$. The proposal distribution is centered at the previous draw and has reasonably small variance for each component, ${\xi }_k^{\left(m\right)}(1-{\xi }_k^{\left(m\right)})/(\eta K+1)$. The proposal ratio for ξ is

$$\begin{array}{ll}{r}_{\xi }=& \exp \left[{\alpha }_0\sum _{k=1}^K\sum _{i=1}^N\log g_{\mathit{ik}}({\xi }_k^{\ast }-{\xi }_k^{\left(m\right)})\right]{\left[\frac{\mathrm{\Gamma }({\xi }_1^{\left(m\right)}{\alpha }_0)\dots \mathrm{\Gamma }({\xi }_K^{\left(m\right)}{\alpha }_0)}{\mathrm{\Gamma }({\xi }_1^{\ast }{\alpha }_0)\dots \mathrm{\Gamma }({\xi }_K^{\ast }{\alpha }_0)}\right]}^N\\ & \cdot \frac{\mathrm{\Gamma }(\eta K{\xi }_1^{\left(m\right)})\dots \mathrm{\Gamma }(\eta K{\xi }_K^{\left(m\right)})}{\mathrm{\Gamma }(\eta K{\xi }_1^{\ast })\dots \mathrm{\Gamma }(\eta K{\xi }_K^{\ast })}\cdot \frac{{({\xi }_1^{\left(m\right)})}^{\xi \ast -1}\dots {({\xi }_K^{\left(m\right)})}^{\xi \ast -1}}{{({\xi }_1^{\ast })}^{\xi \left(m\right)-1}\dots {({\xi }_K^{\ast })}^{\xi \left(m\right)-1}},\end{array}$$

where η is a tuning parameter.

4.2. Variational approximation

For the GoM model, the integrated likelihood for an individual

$$p\left(x\mid \alpha ,\mathrm{\lambda }\right)=\mathit{\int }\prod _{j=1}^J\left(\sum _{k=1}^K{g}_k{\mathrm{\lambda }}_{\mathit{kj}}^{x_j}{(1-{\mathrm{\lambda }}_{\mathit{kj}})}^{1-x_j}\right)D_{\alpha }\left(dg\right),$$ (16)

does not have a closed form solution (the individual index i is omitted to simplify the notation). Variational approximation methods provide an alternative estimation approach by approximating a joint posterior distribution when the likelihood is intractable (see [37]). They assume the model parameters are unknown but fixed.

To compute the joint posterior distribution p(g, z∣x, α, λ) of the GoM scores g = (g₁, …, g_K) and the latent classifications variables z = (z₁, …, z_J), we consider N independent fully factorized joint distributions, one for each individual,

$$q\left(g,z\mid \mathrm{\gamma },\phi \right)=q\left(g\mid \mathrm{\gamma }\right)\prod _{j=1}^{J}q\left(z_j\mid {\phi }_j\right).$$

Here, (γ, ϕ) is a set of free variational parameters, where γ = (γ₁, …, γ_K) and ϕ is the matrix ϕ_jk, j = 1, …, J, k = 1, …, K. Assuming q (g∣γ) = Dir(g∣γ) and q(z_j ∣ ϕ_j) = M ult(1,ϕ_j1, …, ϕ_jK), we employ Jensen’s in-equality to approximate the log-likelihood by a lower bound which becomes a function of the variational parameters, (γ, ϕ).

We derive (pseudo) maximum likelihood estimates of the model parameters (α,λ) by using an approximate EM algorithm. In the E-step, we obtain values of variational parameters (γ,ϕ) that yield the tightest possible lower bound. In the M-step, we maximize the lower bound with respect to the parameters of the model, (α,λ).

Given the current estimates of the model parameters (α,λ), the E step consists of updates:

$${\phi }_{\mathit{jk}}\propto {\mathrm{\lambda }}_{\mathit{kj}}^{x_j}{(1-{\mathrm{\lambda }}_{\mathit{kj}})}^{1-x_j}\times \left(\mathrm{\Psi }({\mathrm{\gamma }}_k)-\mathrm{\Psi }(\sum _{k=1}^K{\mathrm{\gamma }}_k)\right),$$ (17)

$${\mathrm{\gamma }}_k={\alpha }_k+\sum _{j=1}^J{\phi }_{\mathit{jk}}.$$ (18)

Given the current values of the free parameters (γ,ϕ), we find (pseudo) MLE of λ in a closed form:

$${\mathrm{\lambda }}_{\mathit{kj}}\propto \sum _{i=1}^N{\phi }_{\mathit{ijk}}{x}_{\mathit{ij}},$$

where i is the individual index. Since no closed form solution is available for the pseudo MLE of α, we need to use an iterative method to maximize the lower bound with respect to α. The gradient and the Hessian for the Newton-Raphson algorithm are as follows:

$$\frac{\partial L}{\partial {\alpha }_k}=N\left(\mathrm{\Psi }(\sum _{k=1}^K{\alpha }_k)-\mathrm{\Psi }({\alpha }_k)\right)+\sum _{i=1}^N\left(\mathrm{\Psi }({\mathrm{\gamma }}_{\mathit{ik}})-\mathrm{\Psi }(\sum _{k=1}^K{\mathrm{\gamma }}_{\mathit{ik}})\right),$$ (19)

$$\frac{\partial L}{\partial {\alpha }_{k_1}{\alpha }_{k_2}}=N\left({\delta }_{k_1=k_2}\cdot {\mathrm{\Psi }}^{\prime }({\alpha }_{k_1})-{\mathrm{\Psi }}^{\prime }(\sum _{k_{2=1}}^K{\alpha }_{k_2})\right).$$ (20)

Computations for the variational approximation are simpler and less time-consuming than for MCMC, but the quality of approximation depends on a specific functional form of the likelihood.

5. Extended GoM mixture and its estimation

Although there is no time dimension in the basic GoM model, the latent class representation essentially describes individuals as stochastic “movers.” Here, individuals may move between extreme profiles when they respond to different items on the questionnaire. With this observation, it is natural to extend the GoM model to incorporate potential “stayers,” or those individuals that provide item responses in a deterministic fashion, analogous to longitudinal mover-stayer models [9]. In the extended GoM mixture model, one compartment represents “movers” determined by the GoM part and other compartments represent different kinds of “stayers” determined by specific extreme profiles or by particular cells in the contingency table. The extended GoM model can also be seen as a combination of latent class and GoM mixture modeling analogous to the extended finite mixture model by Muthen and Shedden [56].

For our analysis in this paper, we introduce one compartment of “stayers” for a specific cell in the table, and leave the question of choosing the number and nature of compartments open. Our choice of the “stayers” cell was motivated by two observations. First, in the functional disability data from the NLTCS, the cell that corresponds to the healthy people who report no disabilities is particularly difficult to fit with the standard GoM model. Thus, the excess of healthy people can be thought of as a set of outliers with respect to the standard GoM model. Second, it is known that elderly people move not only from being healthy to being disabled but also from being disabled to being healthy [27, 28, 44, 45]. Therefore, even though the NLTCS participants are initially screened for chronic disability, it is reasonable to assume the presence of healthy “stayers” in the data. Accordingly, we assume that some proportion of people has zero probability to report a functional activity problem at the time of the survey and that everyone else has nonzero chances to report a functional disability problem according to the basic GoM model. Our specific example of extended GoM mixture model can also be thought of as analogous to zero-inflated Poisson regression [39].

Parameter estimation for the compartmental GoM model would be identical to the estimation for the standard GoM model if we knew how many individuals are healthy “stayers”. Given that the number of healthy “stayers” is not observed, we need to modify parameter estimation taking into account a deterministic component.

More formally, we assume existence of: (1) a deterministic compartment of healthy individuals and (2) a stochastic GoM compartment. We denote by θ = (θ₁, θ₂) the respective weights such that θ₁ + θ₂ = 1. Assume individuals in the healthy compartment have no disabilities with probability 1. The distribution of responses for “movers” is given by the GoM model with parameters α, λ.

We further augment the data with compartmental indicators to derive the following modifications for the MCMC sampling algorithm. Let N be the total number of individuals in the sample and $n_2^{\left(m\right)}$ be the expected value of the all-zero cell count for the GoM compartment at the mth iteration. The expected value of the all-zero cell count from the healthy compartment, $n_1^{\left(m\right)}$, can be obtained by subtracting $n_2^{\left(m\right)}$ from the observed all-zero cell count. Denote the number of individuals with at least one positive and at least one zero response in their response pattern by n_mix. The total number of individuals from the GoM compartment at the mth iteration is then $n_2^{\left(m\right)}+n_{\mathrm{mix}}$. We let the prior distribution for compartmental weights θ to be uniform on the simplex, and update θ at the end of the posterior step with:

$${\theta }_1^{\left(m+1\right)}={\theta }_1^{\left(m\right)}+\frac{n_2^{\left(m\right)}-n_2^{\left(m+1\right)}}{N}$$ (21)

$${\theta }_2^{\left(m+1\right)}=\frac{n_2^{\left(m+1\right)}+n_{\mathrm{mix}}}{N}=1-{\theta }_1^{\left(m+1\right)}.$$ (22)

We can easily generalize the algorithm to more than two compartments.

6. Model selection: Choice of dimensionality

Choice of dimensionailty: Overview

Statistical model selection methods include the Pearson’s chi-square goodness of fit test [57], cross-validation techniques [33], penalized likelihood criteria such as the Akaike information criterion (AIC) [2], the Bayesian Information Criterion (BIC) [58, 66] and Bayes factors [38], reversible jump MCMC techniques [30], deviance information criteria (DIC) [72] and more recent simulation-based analogues to AIC and BIC, called Akaike Information Criterion Monte Carlo (AICM) and Bayesian Information Criterion Monte Carlo (BICM) [61], among others.

Some of these criteria, AIC and BIC in particular, have been criticized as being not applicable for assessing the number of mixture components due to violations of the regularity conditions [54]. However, in spite of this, researchers continue to apply both criteria and to study their performance in a mixture context. Findings in population-level mixture models suggest that AIC tends to overestimate the correct number of components [10], while BIC shows better results [41, 65].

Questions of dimensionality choice in mixed membership or individual-level mixture models have been approached by several authors [1, 8, 16, 31, 60]. With one recent exception [1], however, comparative performances of different selection criteria were not examined. Here, we provide an overview of several computationally feasible criteria and present results from a simulation study where we compare their performance in the context of the GoM model.

Model selection criteria: Overview

The Pearson chi-square test is one of the most common goodness-of-fit tests. It is not easily applicable to large sparse tables because of a large number of very small counts and, in the present context, because of the way in which the estimation is done, even if sparseness wasn’t a problem, it wouldn’t follow the usual chi-square distribution. We find it instructive, nonetheless, to examine deviations between expected and observed counts for cells with large observed values via the sum of squared Pearson residuals, c.f., [6]. We refer to this criteria as the truncated SSPR criterion or ${\chi }_{\mathit{tr}}^2$.

To calculate the truncated SSPR criterion, one needs to obtain expected values for selected response patterns r = (r₁, …, r_J), where r_j = 0 or 1. For example, using draws from the posterior distribution, ${\alpha }_k^{\left(s\right)}$ and ${\mathrm{\lambda }}_{\mathit{kj}}^{\left(s\right)}$, s = 1, … S, and a draw $g^{(s)}=\left(g_1^{\left(s\right)},\dots ,g_K^{\left(s\right)}\right)$ from Dir(α^(s)), the expected count for response pattern r can be computed as

$$\mathrm{Expected\; Count}=\left(\frac{1}{S}\sum _{s=1}^S\prod _{j=1}^J\left(\sum _{k=1}^K{g}_k^{\left(s\right)}{({\mathrm{\lambda }}_{\mathit{kj}}^{\left(s\right)})}^{r_j}{\left(1-{\mathrm{\lambda }}_{\mathit{kj}}^{\left(s\right)}\right)}^{1-r_j}\right)\right)\times N.$$

Note that label switching could present a problem for calculating posterior means and the model selection criteria based on them [73]

For the variational approximation, the expected count for response pattern r can be obtained as follows. Let α̂ and λ̂ be the pseudo MLE obtained via variational approximation and let g^(s), s = 1, …, S be draws from Dir(α̂), for some large S (for instance, S = 5000). Then, the expected count for response pattern r can be computed as above but with λ̂_kj in place of ${\mathrm{\lambda }}_{\mathit{kj}}^{\left(s\right)}$ and with $g_k^{\left(s\right)}$ computed using Dir(α̂).

A general formulation of the BIC is based on the log-likelihood l(x; θ) and a maximum likelihood estimate θ̂:

$$\mathit{BIC}=-2l\left(x;\widehat{\theta }\right)+p\log \left(N\right),$$

where p is the number of free parameters in the model and N is the number of data points. To obtain the BIC for the GoM model, we need to evaluate the integrated log-likelihood l(x; θ) at the maximum likelihood estimate of the parameter vector θ = (λ, α). Since the GoM integrated likelihood is intractable, we use variational methods described in Section 4.1 to obtain an approximation to the BIC:

$$\stackrel{\sim }{\mathit{BIC}}=-2\stackrel{\sim }{l}\left(x;\widehat{\lambda },\widehat{\alpha }\right)+p\log \left(N\right),$$

where λ̂ and α̂ are the (pseudo) maximum likelihood estimates obtained via variational approximation and $\stackrel{\sim }{l}\left(x;\widehat{\lambda },\widehat{\alpha }\right)$ is the lower bound on the log-likelihood. Models with larger values of $\stackrel{\sim }{\mathit{BIC}}$ are preferable.

Bayesian measures of model complexity and fit, namely DIC, AICM, and BICM, are analogous to AIC and BIC but are based solely on posterior simulation. While these criteria are attractive because of their computational simplicity for a given MCMC simulation, they may present other challenges such as choice of the parameters in focus [72].

A general formulation of DIC is based on the concepts of Bayesian deviance and the effective number of parameters. Bayesian deviance is defined as

$$D\left(\theta \right)=-2l\left(\theta \right)+2\log \left(h\left(x\right)\right),$$

where l(θ) = log p(x∣θ) and h(x) is function of the data only. Defining the effective number of parameters as

$$p_D=\overline{D\left(\theta \right)}-D\left(\overline{\theta }\right),$$

we compute DIC as follows

$$\mathit{DIC}=D\left(\overline{\theta }\right)+2_{\mathit{pD}}.$$

If we focus on GoM parameters θ = (g, λ), we can compute a version of DIC directly using S draws from the posterior distribution, $g_{\mathit{ik}}^{\left(s\right)}$ and ${\mathrm{\lambda }}_{\mathit{kj}}^{\left(s\right)}$, s = 1, …, S. The two pieces that we need to compute for DIC are:

$$D\left(\overline{g,}\overline{\mathrm{\lambda }}\right)=-2\sum _{i=1}^N\sum _{j=1}^J\log \left(\sum _{k=1}^K\overline{g_{\mathit{ik}}}{\overline{{\mathrm{\lambda }}_{\mathit{jk}}}}^{x_{\mathit{ij}}}{\left(1-\overline{{\mathrm{\lambda }}_{\mathit{kj}}}\right)}^{1-x_{\mathit{ij}}}\right)$$

Where $\overline{g_{\mathit{ik}}}=\frac{1}{S}{\sum }_{s=1}^S{g}_{\mathit{ik}}^{\left(s\right)},$ and $\overline{{\mathrm{\lambda }}_{\mathit{kj}}}=\frac{1}{S}{\sum }_{s=1}^S{\mathrm{\lambda }}_{\mathit{kj}}^{\left(s\right)}$, and,

$$\overline{D\left(g,\mathrm{\lambda }\right)=}-2\frac{1}{S}\sum _{s=1}^S\sum _{i=1}^N\sum _{j=1}^J\log \left(\sum _{k=1}^K{g}_{\mathit{ik}}^{\left(s\right)}{\left({\mathrm{\lambda }}^{\left(s\right)}\right)}_{\mathit{jk}}^{x_{\mathit{ij}}}{\left(1-{\mathrm{\lambda }}_{\mathit{kj}}^{\left(s\right)}\right)}^{1-x_{\mathit{ij}}}\right).$$

Models with smaller values of DIC are preferable.

AICM is a penalized version of the posterior mean of the log-likelihoods

$$\mathit{AICM}=2\left(\overline{l\left(\theta \right)}-s_{l\left(\theta \right)}^2\right),$$

that can be obtained using only the draws from the posterior simulation [61]. For the GoM model, the two pieces we need to compute are

$$\overline{l\left(\theta \right)}=\frac{1}{S}\sum _{s=1}^{S}l({\theta }^{\left(s\right)})\mathrm{and}{s}_l^2=\frac{1}{S}\sum _{s=1}^S{\left(l({\theta }^{\left(s\right)})-\overline{l\left(\theta \right)}\right)}^2,$$

where θ = (g, λ). Notice that l(θ) = −D(θ)/2.

7. Simulation Study

We conducted a simulation study to investigate performance of the MCMC and variational approximation methods with respect to parameter recovery and dimensionality selection. Here, we briefly report main findings from this study.

We selected data generating designs to reflect several important features of functional disability data. Most noticeably, contingency tables on disability data often have a large number of zero or very small observed cell counts and several very large cell counts. Large cell counts typically include the all-zero and the all-one response patterns.

We considered a 3- and a 7-profile data generation scenarios. In the first scenario, we generated 5, 000 individual responses on 16 binary items using the GoM model with K* = 3 extreme profiles. We choose the profiles to be considered as “healthy,” “disabled,” and “intermediate” by their conditional response probabilities. Respective proportions of the profiles were 0.7, 0.2 and 0.1, and the hyperparameter was set at α₀ = 0.25 to reflect the fact that individual responses to most items come from one extreme profile.

In the second scenario, we generated 5, 000 individual responses to 10 binary items using the GoM model with 7 extreme profiles. We chose conditional response probabilities for 4 profiles so that they could be considered as “very healthy,” “healthy,” “disabled,” and “very disabled.” The other 3 intermediate profiles did not follow the ordering. Profile proportions ranged from 0.05 for one of the intermediate profiles to 0.4 for the “healthy” profile, and the hyperparameter was set at α₀ = 0.2.

Under both scenarios, we carried out parameter estimation using the MCMC and variational approximation methods for the true values of K*. The variational methods consistently provided better estimation for the observed count at the all-zero pattern, however, the MCMC approach yielded an overall better fit for the second scenario with K* = 7. For K* = 3, conditional probabilities for the “healthy” and “disabled” profiles were recovered very well with both estimation methods. For the intermediate profile, the variational approximation consistently overestimated and the MCMC consistently underestimated the conditional response probabilities. Parameter recovery was noticeably better for K* = 3 than for K* = 7. This could indicate that the number of items and the sample size in the second scenario were too small to provide reliable distinction among different grades of membership, given the selected extreme profiles and hyperparameter values. Variational estimates of the profiles’ proportions were closer to the true values than corresponding MCMC estimates under both scenarios. In addition, the MCMC estimates of profile proportions had smaller range than the VA estimates.

For the MCMC method, given a sufficiently long run, the starting values of λ did not seem to influence the results, up to a relabelling of the extreme profiles. For smaller values of K, the posterior means obtained through MCMC simulations were very similar for all starting points considered. For this reason we did not use several starting points in higher dimensional cases that would have required substantial increases of computing time.

To investigate performance of different fit indices, we fitted the generated data sets using both the MCMC and variational methods separately for several values of K. For true K* = 3, models fitted with K = 2, 3, 4, 5 were considered; for true K* = 7, models fitted with K = 5, 7, 9 were considered. Table 1 summarizes results of six goodness-of-fit criteria, two of which rely on the variational approximation method while the rest rely on the full MCMC calculations. The values of ${\chi }_{\mathit{tr}}^2$ were calculated for response patterns with observed counts ≥ 30 in the first case and ≥ 40 in the second case.

Table 1.

Choices of optimal K according to different model selection criteria.

Criterion	Method	K* = 3	K* = 7
SSPR ${\chi }_{\mathit{tr}}^2$	VA	3	7
SSPR ${\chi }_{\mathit{tr}}^2$	MCMC	5	7
BIC	VA	2	7
DIC	MCMC	5	9
AICM	MCMC	3	7
BICM	MCMC	2	5

We see that ${\chi }_{\mathit{tr}}^2$ obtained with the variational method and AICM criteria perform well for both data generating scenarios, while BICM underestimates and DIC overestimates the true number of profiles in both cases. The variational approximation to BIC underestimates the model complexity for the 3-profile case while it points to the true optimal number of profiles in the 7-profile case.

8. Analysis of the NLTCS functional disability data

Data on 16 binary ADL and IADL items, pooled across four survey waves, 1982, 1984, 1989, and 1994, form a 2¹⁶ contingency table.² The total sample size is 21,574. Item marginal frequencies range from 0.1 for difficulty with eating to 0.7 for doing heavy housework. About 80% of cells in the contingency table have observed counts that are less than 5; 24 cells have observed counts greater than 100. These 24 most frequent response patterns account for 42% of the total observations (Table 2).

Table 2.

Expected cell counts for 24 most frequent response patterns under the basic GoM model with K profiles.

			Number of Latent Profiles K
n	Response Pattern	Observed	3	4	5	6	7	8	9	10	15
1	0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0	3853	2569	2055	2801	2889	3093	2941	3269	3016	3031
2	0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0	216	225	172	177	186	180	180	202	205	187
3	0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0	1107	1135	710	912	993	914	937	1010	944	940
4	0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0	188	116	76	113	200	199	181	190	198	201
5	0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0	122	64	88	58	199	90	89	116	127	127
6	0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0	351	344	245	250	274	274	259	331	303	357
7	0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0	206	20	23	116	86	80	137	116	111	149
8	0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0	303	200	126	324	255	236	213	273	264	325
9	0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 0	182	44	71	170	169	162	200	172	187	219
10	0 0 0 0 1 0 1 0 0 0 0 1 0 0 0 0	108	51	39	162	105	85	117	97	108	116
11	0 0 1 0 1 0 1 0 0 0 0 1 0 0 0 0	106	32	94	94	123	125	133	142	157	136
12	0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0	195	219	101	160	46	25	24	25	31	27
13	0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0	198	127	111	108	341	170	169	189	200	163
14	0 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0	196	41	172	90	104	224	214	174	187	160
15	0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0	123	96	86	132	131	120	109	95	108	110
16	0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0	176	136	162	97	67	167	149	152	167	157
17	0 0 1 0 0 0 1 0 0 0 1 1 1 0 0 0	120	144	104	41	57	47	96	75	72	80
18	0 0 0 0 1 0 1 0 0 0 1 1 1 0 0 0	101	127	90	54	41	68	72	70	74	124
19	0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0	102	44	38	22	18	18	85	103	85	61
20	1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 0	107	88	104	96	84	87	43	37	31	73
21	0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 0	104	269	239	202	52	50	50	63	53	66
22	1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0	164	214	246	272	274	276	224	166	143	115
23	0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1	153	291	261	266	250	230	235	189	167	137
24	1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1	660	233	270	362	419	418	582	612	474	423

From an interpretative standpoint, it is often desirable to have data that satisfy latent unidimensionality, as in the well-known Rasch model. We formally tested the hypothesis of latent unidimensionality, following the approach of Holland and Rosenbaum [36], using series of Mantel-Haenszel tests to detect negative conditional association among the 16 variables. We concluded that no monotone unidimensional latent structure model (e.g., one-factor or unidimensional logistic item response models) can provide an acceptable fit for the NLTCS data on 16 ADL/IADL items. Having rejected latent unidimensionality, our next step is to use the GoM analysis to determine characteristics and the number of disability profiles in the data.

The most apparent feature of the data is the very large observed count of “healthy” people. Almost 18% report no disabilities (Table 2), despite the fact that the majority of the NLTCS survey participants had been screened-in earlier as chronically disabled. A large fraction of “healthy” respondents includes disability recoveries as well as survey supplements of the healthy and oldest-old in the 1994 wave. Since most of the “healthy” individuals have been identified earlier as chronically disabled, it is important to incorporate these responses in our model. We use the compartmental GoM model to estimate weights of a deterministically healthy and a partially disabled components. In doing so, we allow the extended GoM model to fit the observed count for the all-zero pattern. In addition, we examine the impact of the introduction of the “healthy” compartment on parameter estimates and on model choice.

8.1. GoM analysis

MCMC sampling

We applied the fully Bayesian approach from Section 4 to estimate the posterior distribution of the GoM model parameters with the number of extreme profiles ranging from K = 3 to K = 15. Extreme profiles for K = 2 were identified as “healthy” and “disabled,” making the K = 2 GoM model to be a monotone unidimensional latent structure model. Having rejected latent unidimensionality earlier, we only considered results for K = 3 and beyond in the rest of our analysis.

We expected individual vectors of membership scores to be dominated by one component, hence we set the prior for α₀ to be Gamma(2, 10). We chose the prior for the relative proportions ξ to be uniform on the simplex and put uniform independent priors on the conditional response probabilities λ.

We fit the models sequentially in the order of K. For the GoM model with K extreme profiles, we set starting values for λ to the estimated conditional response probabilities from the latent class model with K classes. We took the posterior mean of α₀ from the GoM model with K – 1 extreme profiles to be the starting value for α₀ for the GoM model with K extreme profiles. We chose starting values for the hyperparameters ξ to be equal to the latent class weights estimated from the K class model.

For each value of K, we adjusted the tuning parameters ω (for α₀) and δ (for ξ) to reach a compromise between the acceptance rates of the Metropolis-Hastings steps and the amount of mixing. The acceptance rates for α₀ and ξ varied respectively from 11% and 28% in lower dimensions to 5% and 9% in higher dimensions. Since the acceptance rates were low, we introduced thinning parameter q and kept every qth draw and discarded the rest; q varied from 10 in lower dimensions to 140 in higher dimensions.

Choosing the length of a burn-in period did not appear to be a problem with our data. The chains generally did not experience long burn-in periods, except when starting values for the hyperparameters were very far from the posterior means. The burn-in period varied from 10,000 iterations in lower dimensions to 60,000 in higher dimensions.

For each parameter, we monitored univariate convergence via Geweke diagnostics, and Heidelberger and Welch stationarity and interval halfwidth tests, available from the CODA package [5]. In addition, we visually examined plots of successive iterations. To assess convergence of the multivariate posterior, we examined successive values of the log-likelihood with the same set of methods. The chains needed far fewer iterations to converge in posterior means than they needed to converge in distribution for all parameters and the log-likelihood.

We ran all chains long enough to reach acceptable convergence levels. We had to consider larger number of iterations for higher values of K to accommodate slow convergence of the hyperparameters due to slow mixing of the chains. The additional iterations needed to satisfy convergence criteria for hyperparameters (after the other parameters have reached convergence) had negligible effect on the posterior means of the conditional response probabilities.

Model selection

Table 2 provides 24 response patterns with observed cell counts ≥ 100 and corresponding expected counts obtained using draws from the posterior distribution for each K = 3, …, 9, 10, 15. We observe that the model with K = 9 replicated the marginal pattern abundance best. It is especially evident that models with K = 10 and K = 15 did not fit the three largest cell counts as well as the 9-profile model.

To select the number of profiles, we used all of the criteria that performed well in our simulation study described in Section 6 (the truncated SSPR criterion, the variational approximation to the BIC, and the AICM). We also calculated DIC for a further comparison, although it overestimated the correct number of profiles in the simulation study.

Table 3 gives values of the truncated SSPR criterion, ${\chi }_{\mathit{tr}}^2$, for three different levels of truncation, over cells with observed counts ≥ 100, 25, and 10. All three criteria indicate that K = 9 model has a better fit in an absolute sense, i.e., without correcting for differences in the degrees of freedom.

Table 3.

Sum of squared Pearson residuals for the basic GoM model with K profiles and different levels of truncation.

	Number of Latent Profiles K
Level	3	4	5	6	7	8	9	10	15
≥ 100	4889	5032	1840	2202	2458	1908	1582	1602	1604
≥ 25	14562	10458	6153	4337	3566	2194	1803	1997	1946
≥ 10	52288	20625	10839	7766	6251	4534	3931	4276	4258

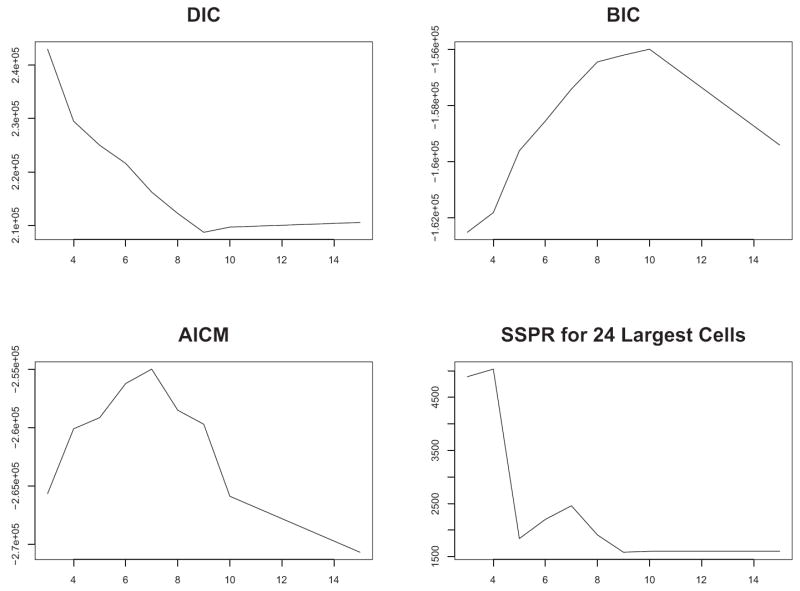
Figure 1 shows plots of the DIC, the BIC approximation, the AICM and the truncated SSPR criterion for the 100 level of truncation. All criteria agree that the optimal number of profiles is greater than 7. Recall that in the 7-profile simulation study the AICM, the BIC approximation and the truncated SSPR criterion all obtained the correct number of components. For the NLTCS data, these criteria point to 7, 10, and 9 profiles, respectively. Although the DIC overestimated the correct number of profiles in our simulation study, it indicates that 9 profiles is the optimal number for the NLTCS functional disability data. The value of K = 9 is in agreement with the results from truncated SSPR but is less than the optimal choice of K = 10 identified by BIC.

Fig 1.

Goodness-of-fit criteria for the basic GoM model.

We used the following steps to verify that no label switching had occurred in the MCMC chains. First, we postulated that label switching occasions should be visible as jumps in trace plots of the MCMC iterations when the extreme profiles are well separated in the multidimensional space. We found extreme profiles to be well separated in the multidimensional space for all K < 9. That is, there was at least one item for which posterior means were at least two standard deviations away from each other for each pair of the profiles (Table 4). We then visually monitored chains to identify jumps that could correspond to label permutations in the posterior distribution. We observed no jumps for models with K < 9 and concluded that no label switching occurred in those chains.

Table 4.

Posterior mean estimates for the basic GoM model with 9 profiles.

	Extreme Profile Number (k)
	1	2	3	4	5	6	7	8	9
λ̂k,1	0.001	0.035	0.002	0.005	0.239	0.002	0.738	0.001	0.002
λ̂k,2	0.001	0.071	0.003	0.269	0.891	0.437	0.967	0.001	0.001
λ̂k,3	0.001	0.285	0.001	0.706	0.994	0.875	0.976	0.001	0.004
λ̂k,4	0.009	0.158	0.029	0.076	0.674	0.080	0.970	0.004	0.013
λ̂k,5	0.070	0.550	0.171	0.453	0.974	0.627	0.998	0.039	0.266
λ̂k,6	0.011	0.114	0.026	0.208	0.774	0.317	0.894	0.005	0.026
λ̂k,7	0.008	0.985	0.973	0.607	0.999	0.948	0.999	0.007	0.761
λ̂k,8	<0.001	0.524	0.019	0.005	0.669	0.034	0.955	<0.001	0.011
λ̂k,9	0.001	0.909	0.093	0.034	0.864	0.412	0.997	0.001	0.208
λ̂k,10	0.001	0.822	0.014	0.001	0.694	0.067	0.998	0.001	0.055
λ̂k,11	0.002	0.977	0.080	0.077	0.920	0.856	0.995	0.002	0.752
λ̂k,12	0.042	0.692	0.146	0.933	0.950	0.998	0.936	0.076	0.448
λ̂k,13	0.037	0.836	0.109	0.219	0.838	0.847	0.894	0.037	0.849
λ̂k,14	0.012	0.626	0.013	0.002	0.230	0.144	0.908	0.007	0.282
λ̂k,15	0.022	0.489	0.055	0.029	0.345	0.068	0.909	0.010	0.127
λ̂k,16	0.024	0.386	0.021	0.007	0.061	0.027	0.768	0.017	0.099
ξ̂k	0.095	0.107	0.111	0.114	0.115	0.114	0.114	0.114	0.114
α̂0	0.095

ADL items: (1) eating, (2) getting in/out of bed, (3) getting around inside, (4) dressing (5) bathing, (6) using toilet. IADL items: (7) doing heavy housework, (8) doing light housework, (9) doing laundry, (10) cooking, (11) grocery shopping, (12) getting about outside, (13) traveling, (14) managing money, (15) taking medecine, (16) telephoning.

We weren’t able to carry out analogous assessments for the GoM models with K = 9 and higher since the profiles were no longer well separated (compare, for example, profiles k = 1 and 8 in Table 4). It is possible that label-switching did occur in those cases which would question validity of posterior mean estimates and the use of DIC and AICM. However, given that the approximate BIC, which is not impacted by label switching, indicated K* = 10, a choice of an optimal K around that value seems reasonable.

We examined the estimated profiles for K = 7 and K = 9 GoM models. Contrary to our expectations, we did not find the interpretation of the 7-profile model to be more appealing from a substantive point of view. Therefore, we report the estimated profiles for the 9-profile GoM model that is identified as the optimal by SSPR criteria. Table 4 provides posterior means and standard deviations for the conditional response probabilities, ${\mathrm{\lambda }}_{\mathit{kj}}=\mathrm{pr}\left(x_j=1\mid g_k=1\right)$; these are probabilities of being disabled on activity j for a complete member of extreme profile k. Estimation via variational methods yielded similar results in terms of profile interpretation, although variational estimates of conditional probabilities were generally closer to the boundaries of the parameter space.

Given that the fit of the all-zero pattern is still not very good for the 9-profile GoM model, we turn to the extended GoM mixture model, incorporating a “deterministically” healthy compartment.

8.2. The extended GoM mixture analysis

MCMC sampling

We carried out the extended GoM mixture analysis for K = 3, …, 9, 10, as described in Section 5. We chose initial values, ran MCMC samplers and determined convergence similarly as in Section 8.1. We set an initial value for the weight of the healthy compartment θ₁ to be a positive fraction that is less than the observed proportion of individuals with all-zero responses.

Model selection

Table 5 provides the expected and observed cell counts for the 23 most frequent response patterns; we excluded the all-zero pattern since the extended GoM mixture fits it precisely. It is difficult to choose among K = 7, 8 or 9 based on the expected counts in Table 5, but the model for K = 8 shows the best fit as indicated by the SSPR over the differing levels of truncation in Table 6.

Table 5.

Expected cell counts for 23 most frequent response patterns under extended GoM mixture model with K profiles and a healthy compartment.

			Number of Latent Profiles K
n	Response Pattern	Observed	3	4	5	6	7	8	9	10
2	0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0	216	77	133	139	151	136	152	201	148
3	0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0	1107	587	661	835	856	799	897	933	845
4	0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0	188	142	162	203	204	197	194	258	167
5	0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0	122	209	59	118	84	86	113	173	97
6	0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0	351	117	195	170	200	213	225	279	212
7	0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0	206	14	21	143	184	176	125	94	150
8	0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0	303	229	247	253	260	246	255	310	236
9	0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 0	182	56	63	213	230	192	195	156	197
10	0 0 0 0 1 0 1 0 0 0 0 1 0 0 0 0	108	75	73	122	122	114	98	113	87
11	0 0 1 0 1 0 1 0 0 0 0 1 0 0 0 0	106	56	76	119	120	106	158	125	102
12	0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0	195	38	26	38	29	26	36	33	31
13	0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0	198	287	139	222	183	183	177	244	148
14	0 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0	196	107	106	71	191	193	188	164	190
15	0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0	123	138	76	115	117	105	96	98	116
16	0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0	176	85	121	75	166	142	160	149	169
17	0 0 1 0 0 0 1 0 0 0 1 1 1 0 0 0	120	119	86	44	38	76	79	66	96
18	0 0 0 0 1 0 1 0 0 0 1 1 1 0 0 0	101	65	70	45	68	60	73	74	98
19	0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0	102	33	32	15	17	89	108	106	111
20	1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 0	107	74	99	64	99	41	40	39	40
21	0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 0	104	89	90	39	57	52	66	71	92
22	1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0	164	198	243	218	269	222	189	155	148
23	0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1	153	262	240	222	200	241	212	192	172
24	1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1	660	223	272	346	359	610	581	556	564

Table 6.

Sum of squared Pearson residuals for extended GoM mixture models with K profiles and a healthy compartment for different levels of truncation.

	Number of Latent Profiles K
Level	3	4	5	6	7	8	9	10
≥ 100	6169	4493	2541	2171	1666	1139	1265	1285
≥ 25	13611	8689	4605	4246	2582	1739	2211	2276
≥ 10	24638	14736	9120	6647	4678	3738	4028	4215

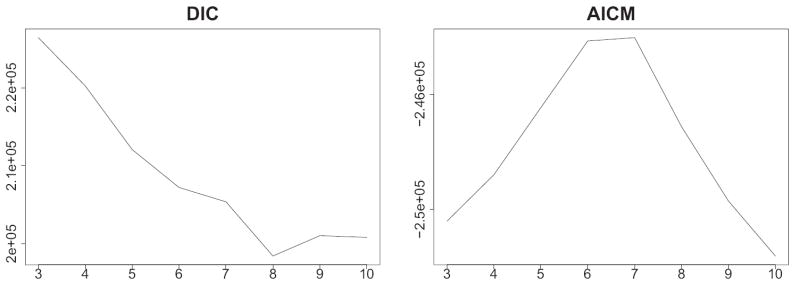
Analogously to the standard GoM model, we computed a version of AICM and a version of DIC obtained directly from the MCMC output. The AICM plot in Figure 2 picks K* = 7 profiles while the DIC plot in Figure 2 suggests the choice of K* = 8 profiles for the extended GoM mixture model, which is consistent with the SSPR selection. We therefore examine the 8-profile extended GoM mixture model.

Fig 2.

DIC (left) and AICM (right) for the GoM mixture model.

Table 7 provides the conditional response probabilities for the 8 profiles that we interpret in detail at the end of this section. Similarly to results from the standard GoM model with 9 profiles, estimated profile weights ${\widehat{\xi }}_k$, k = 1, …, K, are all close to 1/K. Estimated proportions of the healthy compartment for K = 3, …, 10, range from 14% to around 16% (Table 8). The estimated proportion of deterministically healthy individuals from the 8-profile GoM mixture model is θ̂₁ = 0.15 with the standard error of 0.006.

Table 7.

Posterior mean estimates for the extended GoM mixture model with 8 extreme profiles and a healthy compartment.

	Extreme Profile Number (k)
	1	2	3	4	5	6	7	8
λ̂k,1	0.004	0.243	0.002	0.008	0.002	0.740	0.034	0.002
λ̂k,2	0.005	0.900	0.448	0.288	0.003	0.970	0.079	0.001
λ̂k,3	0.003	0.996	0.889	0.742	0.001	0.978	0.296	0.005
λ̂k,4	0.025	0.685	0.083	0.081	0.029	0.972	0.158	0.013
λ̂k,5	0.196	0.978	0.634	0.445	0.165	0.998	0.554	0.263
λ̂k,6	0.039	0.783	0.327	0.212	0.024	0.897	0.116	0.024
λ̂k,7	0.101	0.999	0.946	0.604	0.938	0.999	0.982	0.772
λ̂k,8	0.001	0.686	0.032	0.005	0.017	0.956	0.525	0.013
λ̂k,9	0.002	0.873	0.412	0.036	0.088	0.998	0.908	0.221
λ̂k,10	0.002	0.705	0.065	0.001	0.014	0.998	0.820	0.057
λ̂k,11	0.038	0.923	0.858	0.081	0.067	0.995	0.975	0.769
λ̂k,12	0.234	0.949	0.998	0.916	0.146	0.934	0.697	0.444
λ̂k,13	0.180	0.838	0.853	0.212	0.095	0.892	0.833	0.834
λ̂k,14	0.046	0.222	0.141	0.002	0.010	0.909	0.619	0.278
λ̂k,15	0.057	0.343	0.066	0.029	0.053	0.909	0.484	0.122
λ̂k,16	0.066	0.054	0.025	0.005	0.020	0.768	0.379	0.092
ξ̂	0.104	0.120	0.126	0.129	0.130	0.130	0.130	0.130
α̂0	0.103
θ̂1	0.146

ADL items: (1) eating, (2) getting in/out of bed, (3) getting around inside, (4) dressing (5) bathing, (6) using toilet. IADL items: (7) doing heavy housework, (8) doing light housework, (9) doing laundry, (10) cooking, (11) grocery shopping, (12) getting about outside, (13) traveling, (14) managing money, (15) taking medecine, (16) telephoning.

Table 8.

Posterior mean estimates and standard deviations of the proportion in the healthy compartment for the extended GoM mixture model with K profiles.

K	3	4	5	6	7	8	9	10
θ1	0.162	0.159	0.152	0.148	0.152	0.146	0.141	0.154
SD(θ1)	0.0024	0.004	0.0045	0.0054	0.0047	0.0061	0.006	0.0045

Comparison of results for the basic and the extended GoM mixture models

The optimal dimensionality values identified by the SSPR, AICM, and DIC criteria for the extended GoM mixture model are one less than the corresponding optimal values for the basic GoM model. The presence of the deterministic healthy compartment therefore reduces the optimal number of profiles by one in the NLTCS disability data.

The preferred dimensionality choices are K* = 9 and K* = 8 for the basic GoM and extended GoM mixture models, respectively. Comparing DIC values for these models, we observe that the extended GoM mixture model provides an improved fit to the data. Comparing the estimated conditional response probabilities, we observe that all but two “healthy” profiles from the 9-profile basic GoM model match seven estimated profiles from the 8-profile GoM mixture model closely (see k = 6 in Table 7 and k = 7 in Table 4, for example). Moreover, the two “healthy” profiles from the 9-profile basic GoM model do not differ by much (see k = 1 and k = 8 in Table 4); in fact, taking standard errors into account, they are identical.¹ The unmatched profile from the 8-profile GoM mixture model (k = 1 in Table 7) is the new healthy profile.

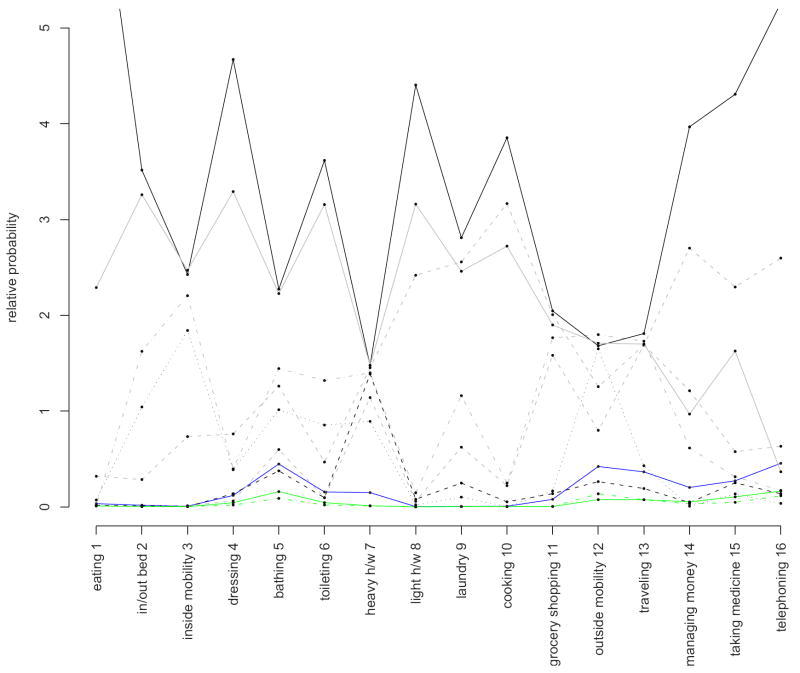
To aid interpretation, we compare the profiles’ estimated conditional response probabilities to the average probabilities for each functional disability item. We would like to see by how much the frequency of disability occurrence for each profile differs from the average frequency of occurrence of the same functional disability in the population as a whole. Relative frequencies for profile k, obtained as

$${\mathrm{\lambda }}_{\mathit{kj}}/{\mathrm{\lambda }}_{j,}j=1,\dots ,16,$$

where λ_j is the marginal probability for item j, indicate how frequently each disability is observed for a complete member of the extreme profile in relation to the population average (Table 9). For example, a complete member of extreme profile 6 is about seven times more likely to need help with eating than individuals in the NLTCS sample need on average (11%).

Table 9.

Functional disabilities average frequencies and relative frequencies by profile for the K = 8 GoM mixture model and for two healthy profiles from the basic K = 9 GoM model (green labels). Relative frequencies greater than 1 are in red.

Activities
profile 1	0.03	0.02	0.01	0.12	0.45	0.16	0.15	0.00	0.00	0.01	0.08	0.42	0.37	0.20	0.27	0.46
profile 2	2.29	3.26	2.47	3.29	2.23	3.16	1.48	3.16	2.46	2.72	1.90	1.71	1.70	0.70	1.63	0.37
profile 3	0.02	1.62	2.21	0.40	1.44	1.32	1.40	0.15	1.16	0.25	1.77	1.78	1.73	0.62	0.32	0.17
profile 4	0.07	1.04	1.84	0.39	1.02	0.85	0.89	0.02	0.10	0.00	0.17	1.65	0.43	0.01	0.14	0.04
profile 5	0.01	0.01	0.00	0.14	0.38	0.10	1.39	0.08	0.25	0.05	0.14	0.26	0.19	0.04	0.25	0.14
profile 6	6.98	3.52	2.43	4.67	2.27	3.62	1.48	4.41	2.81	3.85	2.05	1.68	1.81	3.97	4.31	5.26
profile 7	0.32	0.29	0.73	0.76	1.26	0.47	1.45	2.42	2.56	3.17	2.01	1.26	1.69	2.70	2.30	2.60
profile 8	0.02	0.00	0.01	0.06	0.60	0.10	1.14	0.06	0.62	0.22	1.58	0.80	1.69	1.21	0.58	0.63
profile 1*	0.01	0.00	0.00	0.04	0.16	0.04	0.01	0.00	0.00	0.00	0.00	0.08	0.07	0.05	0.1	0.16
profile 8*	0.01	0.00	0.00	0.02	0.09	0.02	0.01	0.00	0.00	0.00	0.00	0.14	0.07	0.03	0.05	0.12
average frequency	0.11	0.28	0.40	0.21	0.44	0.25	0.68	0.22	0.35	0.26	0.49	0.56	0.49	0.23	0.21	0.15

Table 9 shows values for relative probabilities greater than 1 in red ink. Among estimated extreme profiles in the 8-profile GoM mixture model, we find one healthy profile (k = 1) with all relative frequencies less than the corresponding population averages, while all other profiles have at least one activity with relative frequency greater than the population average. In addition, we find that each estimated profile in the 8-profile GoM mixture model has a unique set of functional disabilities with relative frequencies greater than the corresponding population averages (no two rows in the table have identical placements of values in red ink). We can say then that the estimated 8-profile GoM mixture solution defines a set of admissible profiles in the terminology of Berkman, Singer and Manton [4]. Moreover, taking into account standard errors of the estimates (not shown), we notice that all 8 disability profiles are now well separated.

Extreme profiles in black in Table 9 are the seven profiles from the 8-profile GoM mixture model that match corresponding profiles from the 9-profile basic GoM model closely. The two differing healthy profiles from the basic 9-profile GoM model are shown in green ink, and the new healthy profile from the GoM mixture model is in blue.

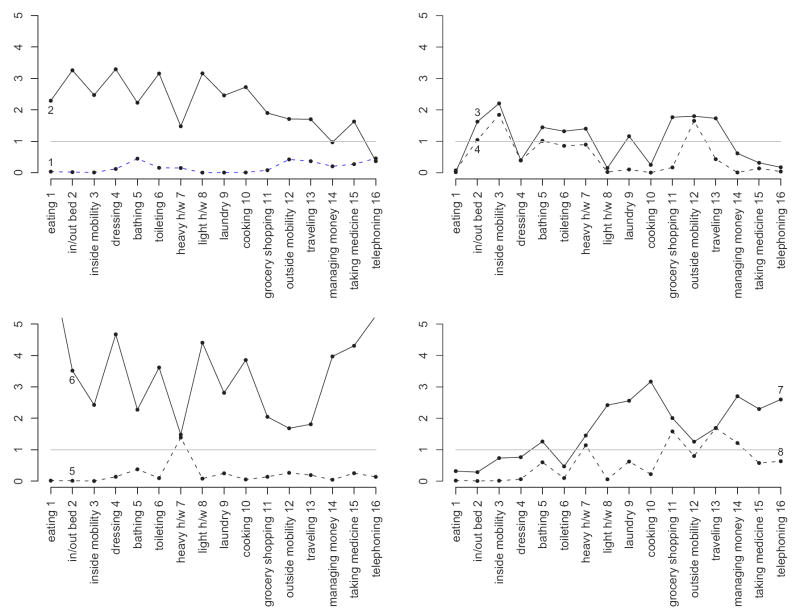
While Table 9 allows us to view all estimated profiles in relation to one other, it is not easy to trace each profile separately on this plot. Pairwise plots in Figure 3 allow us to view individual profiles in detail. Profile k = 2 exhibits relative conditional probabilities greater than 1 for all activities except managing money and telephoning. Relative probabilities for transferring in/out of bed, dressing, toileting and light housework for this profile are at least three times the corresponding averages in the population.

Fig 3.

Functional disabilities relative frequencies for extreme profile pairs for the K = 8 GoM mixture model. Horizontal lines indicate average frequencies in the sample.

Profiles k = 3 and k = 4 show patterns of frequencies that are somewhat similar to each other, indicating frequent difficulties with mobility activities, with profile 3 having noticeably higher frequencies on laundry, grocery shopping, and traveling.

Profile k = 6 is the profile of seriously disabled with most of the disability frequencies greater than 0.8 and greater than the corresponding average frequencies in the population. For a complete member of this profile, difficulties with each eating, dressing, light housework, managing money, taking medicine and telephoning occur at least four times more often than in the NLTCS sample on average. Profile k = 5 points to low probabilities for most ADL and IADL items but has a spike at the probability for doing heavy housework. An individual corresponding to this profile has difficulties with heavy housework one and a half times more often than the average chronically disabled person. This is a significant increase, given that the average frequency to experience difficulty with heavy housework is 0.68 in the NLTCS sample.

Profile k = 8 shows disability frequencies that are slightly higher than the average for heavy housework, grocery shopping, travelling, and managing money. Profile k = 7 exhibits high frequencies for all IADL items, especially for those with significant cognitive components such as cooking, managing money and telephoning.

Having the profile interpretations at hand, we recall that they represent extreme types of chronically disabled individuals aged 65 and over. Apart from an estimated 15% of healthy individuals who have no disabilities with probability one, each (partially disabled) person in the population can be described through a vector of membership scores for the eight estimated profiles. Since the hyperparameter estimate α̂₀ = 0.103 is small, the posterior distribution of grades of membership is bathtub-shaped which means that membership vectors are dominated by one component for a majority of individuals. Even though we focus on the population parameters in this paper, it is possible to use MCMC output to examine posterior distributions for each individual. One could also compute posterior estimates of various quantities of interest, such as the percentage of individuals in the sample that have membership vectors dominated by one profile (with g_k > 0.95, for example).

9. Discussion

Models that allow for specification of continuous latent constructs are increasingly popular among researchers in social, behavioral, and health sciences since many latent variables of interest can be thought of as having fine gradations. When substantive theory justifies distinct latent categories as well as continuous latent variables, approaches that describe heterogeneity of individuals with respect to those discrete categories often focus on class membership probabilities. To give a few examples, Foody et al. [24] emphasize the utility of posterior probabilities of class membership in the area of remote sensing; Muthen and Shedden [56] model the class membership probability as a function of covariates in a study of alcohol dependence; Roeder et al. [64] address a similar issue by modelling uncertainty in latent class assignments in a criminology case study. The GoM model also addresses the issue of uncertainty in class membership but by using a different approach that directly incorporates degrees of membership as model parameters.

Standard methods of estimating the GoM model described in Manton et al. [51] do not rely on the GoM representation as a discrete mixture model and have questionable properties [32] including instability of MLEs due to ridges in the likelihood function which are often present. The Bayesian GoM estimation algorithm developed originally in Erosheva [16, 17], on which the present paper is largely based, leans heavily on the structure provided by the latent class representation and has several advantages over likelihood-based estimation procedures for the GoM model. It is worth emphasizing one more time that the developed latent class representation of the GoM model places identical probability structure on observable variables and hence can not possibly be distinguished from the continuous mixture GoM model on the basis of data [19].

Understanding the latent class representation of the GoM model, and thus viewing it as a special instance of individual-level or mixed membership models, makes it easier to establish direct connections with models from other areas. For example, although a clustering model with admixture developed for genetic data by Pritchard et al. [60] and the standard GoM model appear to be quite different, they are both instances of the more general mixed-membership representation. The generalization is flexible enough to accommodate models for other data structures such as text documents [21].

Our goal for the NLTCS analysis in this paper was to explore the population characteristics of disability patterns as measured by the 16 ADL and IADL variables. Incorporation of covariates in the GoM modeling would be an obvious next step of great interest to social science researchers.

The preferred number of components identified by statistical criteria represents our best guess at the latent dimensionality in the NLTCS data under the GoM mixture model with a deterministically healthy compartment. Our choice of dimensionality is based on a number of assumptions, some of which may be worth exploring further. In particulary, the assumption of local independence for the full set of ADL and IADL variables may be questionable. One possible approach to relax this assumption suggested by a reviewer is to focus on fitting the GoM models separately for the set of ADL and for the set of IADL variables, producing two sets of correlated GoM scores. Such a split-GoM model may turn out to be more appealing to disability researchers and to produce gains in interpretability. We expect to consider this and other forms of model simplification as we work towards our ultimate goal of developing a longitudinal version of the GoM model.