Optimized molecular dynamics force fields applied to the helix-coil transition of polypeptides

Abstract

Obtaining the correct balance of secondary structure propensities is a central priority in protein force-field development. Given that current force fields differ significantly in their α-helical propensities, a correction to match experimental results would be highly desirable. We have determined simple backbone energy corrections for two force fields to reproduce the fraction of helix measured in short peptides at 300 K. As validation, we show that the optimized force fields produce results in excellent agreement with nuclear magnetic resonance experiments for folded proteins and short peptides not used in the optimization. However, despite the agreement at ambient conditions, the dependence of the helix content on temperature is too weak, a problem shared with other force fields. A fit of the Lifson-Roig helix-coil theory shows that both enthalpy and entropy of helix formation are too small. The helix extension parameter w agrees well with experiment, but its entropic and enthalpic components are both only about half the respective experimental estimates. Our structural and thermodynamic analyses point toward the physical origins of these shortcomings in current force fields, and suggest ways to address them in future force-field development.

Introduction

It is now more than 30 years since the development of the first molecular mechanics force fields^1,2 and the first molecular dynamics simulation of a protein.³ Simulations of biomolecules using classical energy functions have found widespread application, from protein structure determination and protein folding to studies of enzyme function and drug screening. While recent advances in computer power mean that sampling of the energy landscape is less of a limitation, the longer simulations now possible are making it increasingly evident that more accurate energy functions (force fields) will be important for reliable results.⁴ Force-field parameters are continually being improved, mainly by using a combination of ab initio quantum mechanical calculations augmented with empirical data from small molecules representing fragments of amino acids (for proteins).⁵ Recent developments in protein force fields have focused on improvements to the backbone potential based on comparisons with quantum calculations,^5–9 even leading to the implementation of new terms in the CHARMM energy function. ^5,8 The new force fields result in an improved treatment of folded proteins, giving better agreement with experimental data in solution (e.g., from nuclear magnetic resonance (NMR) measurements) and low root-mean-square deviations from the crystal structures (typically <1.5 Å for long MD trajectories) of small globular proteins. ^10,11

Although reproduction of native-state structure and dynamics of folded proteins is an important requirement for any force field, the properties of weakly structured peptides are a much more challenging target. With timescales of equilibration between different conformations being ≈ 0.1 − 1µs for helix formation or ≈ 1 − 10µs for β-hairpin formation,¹² obtaining equilibrium sampling from simulation is difficult. Furthermore, proper conformational sampling of peptides requires the correct statistical weights for different structures (as determined by the force field). This problem is exemplified by the need to balance α-helical, polyproline II (ppII), and β structure, posing a central issue in protein force-field development. Apart from direct relevance to so-called “natively unstructured” proteins, which have recently attracted a great deal of interest,¹³ the accurate balance of secondary structure in force fields is important because it is related to many other applications of biomolecular simulation, for example protein folding, aggregation, association and conformational change.

We recently compared an extensive set of experimental scalar couplings¹⁴ for Ala₅ with long equilibrium simulations of the peptide using 12 different force fields.¹⁵ This type of data is very useful because it reflects the backbone conformation of the peptide through its (ϕ, ψ) torsion angles, and can be simply calculated from the simulation trajectories via the Karplus equation.¹⁶ Since short peptides do not have a single dominant structure, such comparisons provide a sensitive test of the “intrinsic” secondary structure preferences of a given force field.¹⁷ We found that most of the force fields tested showed discrepancies with the experimental data, but that the more recent refinements were much closer to experiment than the older generation. However, even amongst these recent force fields, there were significant differences in secondary structure propensity.¹⁵ Similarly, simulations of loop closure dynamics in short peptides indicated markedly different structural propensities among the force fields used,¹⁸ as was also found in simulations of the helix-coil transition.¹⁹ All-atom folding simulations by other groups have also suggested that the secondary structure balance in current force fields may need adjustment.⁴

Although we had previously found that several force fields gave similar overall agreement with the experimental J-couplings,¹⁵ we focus here on Amber ff03ff03⁷ and Amber ff99SB.⁹ As shown below, their α-helical propensities are, respectively, too high and too low relative to experiment. We applied a perturbative energy correction (using torsional terms) to match experimental data for two peptides: (i) the scalar couplings for the short Ala₅ peptide used in our previous study^14,15 and (ii) helical populations determined from NMR chemical shift data for a longer helix-forming peptide, Ac-(AAQAA)₃-NH₂. The second data set was included because short peptides such as Ala₅ are too short to form a stable α helix:^14,15 mounting evidence for short Ala-based peptides indicates that they favor extended, ppII-like backbone conformations over the right-handed alpha-helical α_R region of the Ramachandran map;^14,20–24 however, longer Ala-based peptides do form α-helix.^25–27 To avoid detrimental effects from over-fitting the optimized force fields, we applied only the minimum correction to achieve an acceptable match to experiment. We show that the revised force fields match residual dipolar coupling (RDC) data for simulations of folded ubiquitin about as well as their parents or better, and are able to reproduce NMR scalar couplings for a longer 19-residue peptide with a significant helical population.¹⁴ However, the helix content in Ac-(AAQAA)₃-NH₂ depends more weakly on temperature in the simulations than in experiment, both for the parent and optimized force fields. Fits of the statistical mechanical Lifson-Roig (LR) model for helix formation to the simulation data suggest that the weak temperature dependence arises from the enthalpic and entropic contributions to helix formation both being too small. We discuss possible structural and energetic causes of this phenomenon in an effort to point the way for future force-field improvements.

Methods

Simulation Details

Simulations of Ala₅ were run using the simulation package Gromacs^28,29 using a protocol similar to that used in our previous work,¹⁵ and with the implementation of the Amber force fields by Sorin and Pande.³⁰ The peptide was unblocked and protonated at both N and C termini, corresponding to the experimental conditions of pH 2.¹⁴ Molecular dynamics simulations of each peptide in a 30 Å cubic simulation box of explicit TIP3P water³¹ were run at a constant temperature of 300 K and a constant pressure of 1 atm, with long range electrostatic terms evaluated using particle-mesh Ewald (PME) using a 1.0 Å grid spacing and a 9 Å cutoff for short-range interactions. For each force field, four runs of 50 ns each were initiated from different starting configurations. Further details of the simulation protocols are as published.¹⁵

Replica exchange molecular dynamics (REMD) simulations of the blocked peptide Ac-(AAQAA)₃-NH₂ were run using Gromacs^28,29 with 32 replicas spanning a temperature range of 278 K to 595 K. The peptide was solvated in a truncated octahedron simulation cell of 1022 TIP3P water molecules with an initial distance of 35 Å between the nearest faces of the cell. This cell was equilibrated for 200 ps at 300 K and a constant pressure of 1 atm. Subsequently, all REMD simulations were done at constant volume, with long range electrostatics calculated using PME with a 1.2 Å grid spacing and 9 Å cutoff. Dynamics was propagated with a Langevin integration algorithm using a friction of 1 ps⁻¹, and replica exchange attempts every 1 ps (every 500 steps with a time step of 2 fs). Typical acceptance probabilities for the replica exchange were in the range 0.1–0.5. All replica exchange runs used the same set of initial configurations, which were taken from the final configurations of a preliminary replica exchange simulation with ff99SB. The simulations were run for at least 30 ns per replica, of which the first 10 ns were discarded in the analysis (with an aggregate of ≈ 1 µs for each force field). To test for possible system size dependence, additional simulations of Ac-(AAQAA)₃-NH₂ in a 45 Å truncated octahedron box solvated by 2268 water molecules were run for 30 ns using a similar protocol, in this case with 32 replicas at 5 K intervals between 278 and 433 K.

Additional simulations were performed for the unblocked peptide HEWL19, derived from hen egg-white lysozyme with sequence KVFGRC(SMe)ELAAAMKRHGLDN. The structure and parameters for the S-methylated Cys 6 were adapted from those for methionine and are given in Supporting Information (SI) Figure 1 and Table 1 respectively. Both termini as well as all acidic side chains were protonated, corresponding to the experimental conditions of pH 2.¹⁴ The peptide was solvated in a truncated octahedron simulation cell with a 42 Å distance between nearest faces, and equilibrated at constant pressure for 200 ps at 300 K. Constant volume REMD was run with 32 replicas spanning the temperature range 278 K to 472 K, for 27 ns, of which the first 10 ns were discarded in the analysis. All other parameters were the same as for Ac-(AAQAA)₃-NH₂.

Native state simulations of ubiquitin were run starting from the crystal structure 1UBQ.³² The protein was solvated by 2586 explicit TIP3P water molecules in a cubic simulation box of 45 Å length with long range electrostatics calculated using PME with a 1.2 Å grid spacing and 9 Å cutoff. To neutralize the system charge, 7 sodium and 8 chloride ions were added. Dynamics was propagated for 30 ns at constant pressure (1 atm) and temperature (300 K) using a Nosé-Hoover thermostat³³ and Parrinello-Rahman barostat.³⁴

Definition of Helical States

We define helical structure in the spirit of the LR theory, that is to say, in terms of which regions of the Ramachandran map are occupied. We define two α-helical regions in the map:

• The α₊ region of the (ϕ, ψ) map is defined as¹⁵ ϕ ∈ [−160°,−20°] and ψ ∈ [−120°,50°]. This inclusive definition aims to capture all residues that are in the right-handed α_R free energy basin of the Ramachandran map, even if these are isolated and not part of a genuine helix (red squares in Figure 1), i.e., the α free energy minimum in the context of “random coil”.

• The α_h region of the (ϕ, ψ) map is defined more stringently as³⁵ ϕ ∈ [−100°, −30°] and ψ ∈ [−67°,−7°]. This definition is intended to capture the narrower (ϕ, ψ)-angle distribution of residues within actual α-helices (black squares in Figure 1; the insets show that this stringent definition covers the helical free energy minima for regions with defined secondary structure).

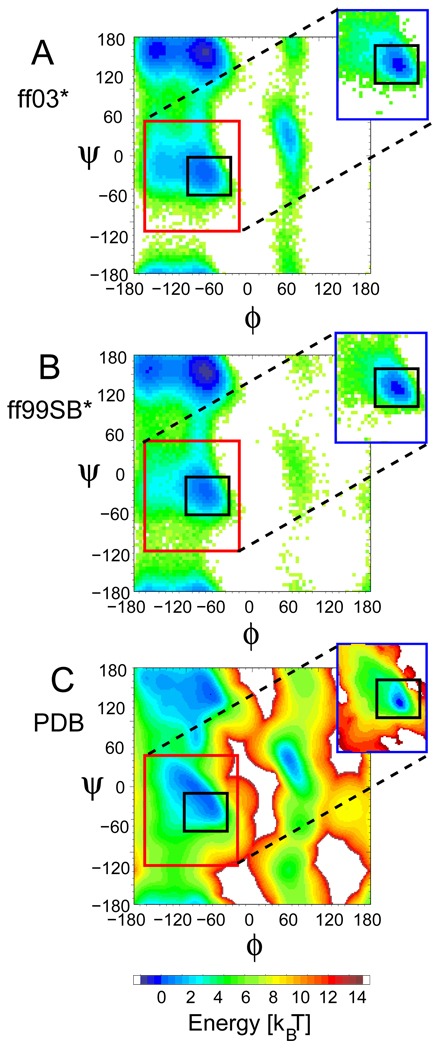
Figure 1.

Ramachandran potentials of mean force (PMFs), − log(P(ϕ, ψ)). To give an indication of the PMF in the absence of any helix formation, histograms of (ϕ, ψ) were constructed from the interior residues of Ala₅ (which forms almost no α-helix) in simulations using the modified force fields (A) ff99SB* and (B) ff03*, and (C) from a PDB database, excluding all residues in defined secondary structure.⁴⁸ The region defined as the α₊ basin¹⁵ is shown by a red box in each figure. A black box indicates the α_h region used in the definition of Of-helix.¹⁹ As an indication of the PMF within a helix, insets in (A) and (B) show the corresponding PMFs within an α-helix. This was calculated from simulations of the helix-forming peptide Ac-(AAQAA)₃-NH₂, by counting only segments of three or more consecutive residues whose (ϕ, ψ) angles are within the α basin. The inset in (C) shows the statistical potential derived by considering only residues in segments with secondary structure in the PDB database.⁴⁸

Residues which lie within the α_h region of the Ramachandran map are denoted as helical (h) for the purposes of LR analysis. All residues outside the α_h region are defined as “coil” (c). A helical segment is one which has at least three consecutive residues whose (ϕ, ψ) angles fall within the α_h boundaries (i.e., the smallest helix is … chhhc…); since the peptide Ac-(AAQAA)₃-NH₂ is blocked, all (ϕ, ψ) pairs are properly defined. The fraction of helix 〈h_i〉_sim for a given residue i in the simulation is calculated as the fraction of time spent by that residue within helical segments. Alternative definitions of helical structure are discussed in the SI text.

Calculation of Helix-Coil Parameters

We have analyzed the data using the LR model for the helix-coil transition. In this model, the statistical weight of a given conformation is the product of weights for individual residues. A residue in the coil conformation is assigned a relative weight 1, and a residue of type i in a helical conformation, but not within a helical segment, is assigned a weight v_i. Residues in helical segments receive a weight of w_i, except for the terminal residues in the segment which have weight v_i (since usually v ≪ w this creates a “nucleation penalty” for initial helix formation). The subscripts i indicate that, in some models, v and w depend on the residue types. The partition function of this model for a peptide with N amino acid residues can be written in a compact matrix form as:^36,37

$$Z=\left(001\right){\displaystyle \prod _{i=1}^N{\mathbf{M}}_i\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 1\hfill \\ \hfill 1\hfill \end{array}\right)}$$ (1)

in which the matrix M_i is defined as:

$${\mathbf{M}}_i=\left(\begin{array}{ccc}{w}_i\hfill & v_i\hfill & 0\hfill \\ 0\hfill & 0\hfill & 1\hfill \\ v_i\hfill & v_i\hfill & 1\hfill \end{array}\right)$$ (2)

The average “fraction of helix” for a given residue i is defined as the relative population of conformations where it has weight w_i, given by 〈h_i〉_LR = ∂ ln Z/∂ ln w_i. The average fraction of helix for the whole peptide, 〈f_h〉_LR, is the average over these for the non-terminal residues ${\langle f_h\rangle }_{\text{LR}}={(N-2)}^{-1}{\displaystyle {\sum }_{i=2}^{N-1}\langle h_i\rangle }$ (since terminal residues cannot have a w weight by definition). The average number of helical segments 〈n_s〉_LR is given by ${\langle n_s\rangle }_{LR}={\displaystyle {\sum }_{i=3}^N{\partial }^2\text{ln}Z/\partial \text{ln}{w}_{i-1}\partial \text{ln}{v}_i}$, in which ∂²lnZ/∂lnw_i−1∂lnv_i identifies the fraction of the ensemble in which residue i is at the C-terminal end of a helix.

We have fitted the simulation data to the model using a Bayesian formalism, where we estimate the probability of a set of chosen parameters, given the simulation data, via

$$p(\text{parameters}|\text{data})\propto p(\text{data}|\text{parameters})p(\text{parameters})$$ (3)

We use a uniform prior, p(parameters) = 1 with ln v and ln w as free parameters, and estimate the probability of the observed data arising from the LR model with a given set of parameters using the likelihood function:

$$L=p(\text{data}|\text{parameters})={\displaystyle \prod _{k=1}^{N_k}{\rho }_k={\displaystyle \prod _{k=1}^{N_k}\frac{1}{Z}{\displaystyle \prod _{i=1}^N{x}_{i,k}}}}$$ (4)

The N_k observations correspond to different conformations saved from the simulation, ρ_k is the equilibrium probability of observation k consistent with the LR partition function, and x_i,k is the weight of residue i in observation k (i.e., 1, w_i or v_i). The overall log-likelihood can then be written as

$$\text{ln}L={\displaystyle \sum _i{N}_{w,i}\text{ln}{w}_i+{\displaystyle \sum _i{N}_{v,i}\text{ln}{v}_i-N_k\text{ln}Z}}$$ (5)

where N_w,i (N_v,i) is the total number of times that residue i has weight w_i (v_i) in the N_k conformations. The model parameters, and their distributions, are inferred by running a Monte Carlo simulation in parameter space. Moves were made in ln w and ln v, with a move being always accepted if ln L increases, or accepted with probability L_trial/L if ln L decreases. The distribution of parameters is collected after an initial “equilibration” period.

Residual Dipolar Couplings

The RDC D_ab between nuclei a and b is calculated from the simulation structures as

$$D_{ab}=D_{ab}^{\text{max}}\langle \text{tr}\{\mathbf{A}{\mathbf{\Phi }}_{ab}\}\rangle =D_{ab}^{\text{max}}\langle {\widehat{\mathbf{r}}}_{ab}^T{\mathbf{A}\widehat{\mathbf{r}}}_{ab}\rangle$$ (6)

$${\mathrm{\Phi }}_{ab,\alpha \beta }={\widehat{r}}_{ab,\alpha }{\widehat{r}}_{ab,\beta },\alpha ,\beta \in \{x,y,z\}$$ (7)

where A is the alignment tensor describing the orientational distribution of the protein in a particular alignment medium,³⁸ and r̂_ab is a unit vector pointing from a to b, defined within an intramolecular coordinate frame. The constant $D_{ab}^{\text{max}}$ is related to the gyromagnetic ratios of the nuclei a and b and their distance r_ab via $D_{ab}^{\text{max}}=-{\mathrm{\mu }}_0\hslash {\mathrm{\gamma }}_a{\mathrm{\gamma }}_b/4{\mathrm{\pi }}^2{r}_{ab}^3$. Although in principle the bond length r_ab should be included in the ensemble average, all the RDCs were for backbone amide nitrogen and proton (NH) pairs, for which the bond lengths are constrained to the equilibrium values in the simulation. In practice r_ab was set to 1.04 Å,³⁹ although the actual value is irrelevant in this case as any change would be compensated by a scaling of the best-fit alignment tensor. Assuming that intramolecular motion is uncorrelated with the alignment tensor, Φ_ab can be replaced by an intramolecular ensemble average over the simulation, obtained after a least-squares alignment of the protein backbone to the crystal structure. The alignment tensor A for a particular alignment medium is determined by linear least-squares fitting of all the calculated dipolar couplings (eq 6) against the corresponding experimental couplings.⁴⁰ Agreement between experimental and simulation-derived dipolar couplings is quantified, for each alignment medium, in terms of $Q={\{{\displaystyle {\sum }_i{(D_{i,\text{sim}}-D_{i,\text{expt}})}^2}/D_{i,\text{expt}}^2\}}^{1/2}$, with Q_cum being the sum of Q over all alignment media.

Generalized Order Parameters

We compute Lipari-Szabo⁴¹ generalized order parameters $S_{ab}^2$ for backbone NH bonds. For nuclei a and b, $S_{ab}^2$ can be calculated from the simulation using the relation:⁴²

$$S_{ab}^2=\frac{3}{2}\text{tr}{\langle {\mathbf{\Phi }}_{ab}\rangle }^2-\frac{1}{2}{\left(\text{tr}\langle {\mathbf{\Phi }}_{ab}\rangle \right)}^2$$ (8)

where Φ_ab is defined in eq 7. This expression is valid provided that the simulation length (30 ns) is much longer than the correlation time for intramolecular fluctuations of the NH bond vector orientation;⁴² eq 8 will tend to underestimate the order parameters if intramolecular motions are present with time scales longer than the correlation time for molecular tumbling (≈ 2 ns).⁴³

Results

Peptide NMR Results for Original Force Fields

To measure the deviation between experimental data and observables calculated from simulation, we define a parameter χ² as the mean square deviation from experiment, normalized for the un-certainty.¹⁵ In the case of scalar couplings J, this gives:

$${\chi }^2=\frac{1}{N}{\displaystyle \sum _{i=1}^N\frac{{({\langle J_i\rangle }_{\text{sim}}-J_{i,\text{expt}})}^2}{{\sigma }_i^2}}$$ (9)

In this expression, 〈J_i〉_sim is the mean of coupling i, back-calculated from simulation, with J_i,_expt the corresponding experimental value. For the calculation of scalar couplings from simulation we use the “DFT2” set of Karplus equation parameters,¹⁵ based on the work of Case et al.⁴⁴ The uncertainties σ_i are assumed to be dominated by the uncertainty of the Karplus parameters.¹⁵ Using this metric, we found that, although many older force fields were in sharp disagreement with published J-couplings for Ala₅,¹⁴ a small group of recent force fields were in better accord with the experimental data¹⁵ (χ² ≤ 2.25). We note here that in our previous publication, the large disagreement reported for ff99SB was erroneous.⁴⁵ In fact, ff99SB is amongst the best performing force fields (χ² = 1.7). The scalar couplings for the two force fields are shown alongside the experimental data in Table 1. Thus, in terms of agreement with the scalar coupling data, ff03 and ff99SB are essentially indistinguishable, and the deviations from experiment are comparable to the experimental uncertainty. However the population in the α₊ basin in the Ramachandran map (defined as¹⁵ ϕ ∈ [−160, −20] and ψ ∈ [−120,50]) in ff03 is about double that in ff99SB (Table 1).

Table 1.

Structural characteristics of peptides used for parameter optimization. Populations of the α₊ β and ppII regions of the Ramachandran map¹⁵ averaged over all internal residues are listed (errors in parentheses), together with the fraction α-helix and the χ² with respect to the experimental data (scalar couplings J for Ala₅ and fraction helix per residue 〈h_i〉 for Ac-(AAQAA)₃-NH₂ (Figure 2). For ff99SB and ff99SB*, most of the unaccounted population in the Ramachandran map is located in the α_L region.

Peptide	Property	ff03	ff99SB	ff03*	ff99SB*
Ala5:
	%α+	29.3 (2.9)	15.7 (1.2)	16.4 (1.8)	22.5 (2.2)
	% β	28.5 (1.1)	37.8 (1.4)	32.5 (0.7)	34.5 (1.3)
	% ppII	41.5 (2.0)	42.3 (1.9)	50.5 (1.3)	39.8 (1.6)
	% α-helix	1.9 (0.9)	0.0 (0.2)	0.2 (0.2)	0.6 (0.3)
	χ2(J)	1.2	1.7	1.1	1.7
Ac-(AAQAA)3-NH2:
	%α+	93.9 (0.5)	26.9 (1.2)	45.9 (1.8)	48.5 (1.3)
	% β	2.7 (0.2)	32.4 (0.8)	26.4 (1.0)	22.7 (0.7)
	% ppII	3.3 (0.2)	31.8 (0.9)	27.1 (0.9)	21.8 (0.6)
	% α-helix	82.7 (0.7)	1.8 (0.3)	18.8 (2.1)	14.2 (2.1)
	X2(〈hi〉)	2600	570	1.9	3.7

Although isolated residues with α-helical (ϕ,ψ) angles occur in unblocked Ala₅, it forms only a very small amount of real α-helix (with at least three consecutive residues within the α-helical region of the Ramachandran map), as shown in Table 1. We have therefore augmented our training data set with ¹³C chemical shift data from the helix-coil transition in a longer helix-forming peptide. The fraction of helix in Ac-(AAQAA)₃-NH₂ has been estimated from a careful analysis of carbonyl chemical shifts,⁴⁶ as a function of temperature. This peptide is ideal for simulation, having a relatively high helix population for its size, and being uncharged. The absence of charged (e.g., lysine) residues may better reflect the intrinsic helix propensity of alanine.⁴⁷ We have carried out long replica exchange molecular dynamics simulations of this peptide in the two force fields and find dramatically different helical populations at ambient temperatures: with ff03, the peptide forms an α helix most of the time, whilst in ff99SB, the α-helical population is negligible. Figure 2 shows the fraction of helix in each force field obtained from the replica at 303 K. The correspondingly large χ² for deviations from the experimentally estimated fraction of helix at 303 K is also given in Table 1; in this case the errors σ_i are assumed to be dominated by the sampling error of the simulation. Clearly, ff03 and ff99SB have very different helical propensities and neither agrees particularly well with the experimental data for Ac-(AAQAA)₃-NH₂. Note that the exact definition of helix does not affect these conclusions (as is shown in SI Figures 2 and 3).

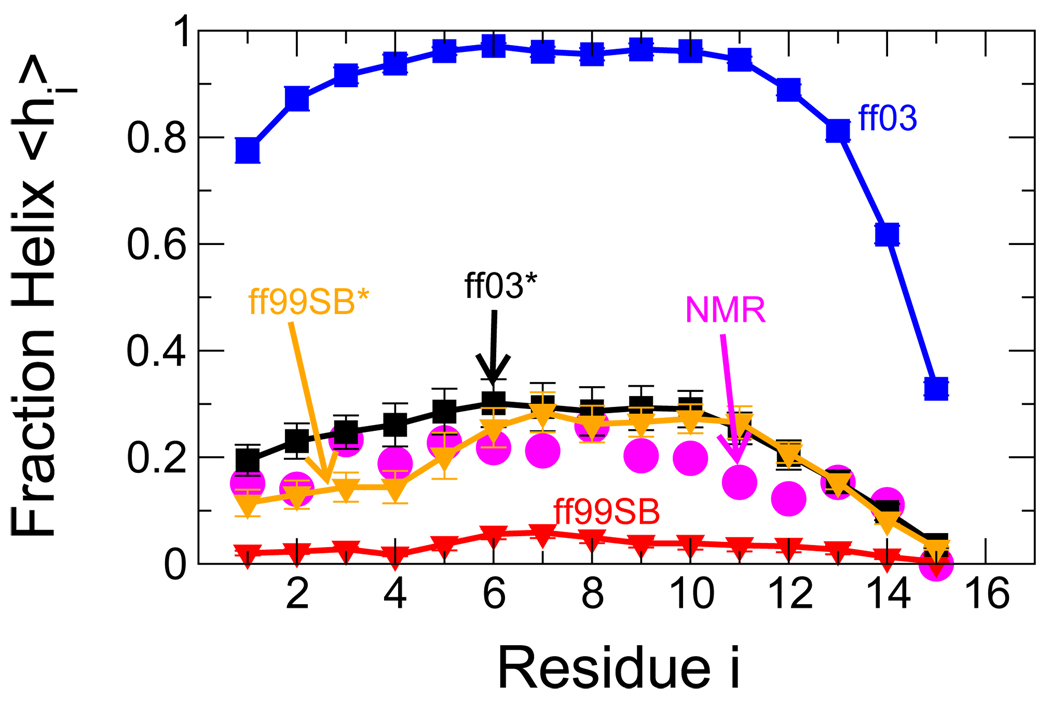
Figure 2.

Helix formation in the peptide Ac-(AAQAA)₃-NH₂. Fraction of helix 〈h_i〉 (see text) is given for each residue of Ac-(AAQAA)₃-NH₂ from NMR chemical shifts (magenta circles)⁴⁶ and from simulations at 303 K: ff03 (blue squares), ff99SB (red triangle down), ff03* (black squares), ff99SB* (orange triangle down). Where error bars are not visible, they are smaller than the symbol size.

Strategy for Correction of (ϕ, ψ) Surface

There are many terms in the force fields, most obviously charges, Lennard-Jones terms and torsion angles, which may influence their secondary structure preferences (i.e., for α, β or ppII structure) and there is surely much redundancy in methods for achieving a desired “correction”, given the number of available parameters. Following earlier efforts,^9,35 we focus on the ϕ, ψ torsional terms because these are most directly connected with the Ramachandran map. Moreover, ϕ, ψ, torsional modifications should not result in detrimental effects on the non-bonded (charge and Lennard-Jones) terms, which have been carefully parameterized for high quality condensed-phase simulations. Our choice can also be retrospectively justified by the small resulting corrections of around 0.5 k_BT (see below), indicating that the additional terms are merely fine tuning force fields which are already close to optimal.

To limit the number of free parameters and avoid over-fitting, we apply a simple cosine correc- tion term to ψ, since this torsion angle is the major determinant of helix propensity:

$$V_1(\psi ;k_{\psi },{\delta }_{\psi })=k_{\psi }[1+\text{cos}(\psi -{\delta }_{\psi })]$$ (10)

with parameters k_ψ and δ_ψ giving respectively the magnitude and phase offset of the correction. At first sight this correction does not fit within the “Amber philosophy” for torsional parameterization, which favors physically motivated torsion parameters (i.e., not allowing arbitrary phase offsets δ). However, since current Amber force fields include torsion parameters for both ψ (N-C_α-C-N) and ψ′(C_β-C_α-C-N), it is straightforward to map the correction terms with a phase offset δ to the existing terms with δ = 0 by recognizing that ψ′ ≈ ψ + 120°. For D-amino acids, the sign of the phase correction would be reversed.

We used two experimental data sets for parameter optimization. The first was a comprehensive set of scalar couplings for unblocked Ala₅, giving residue-specific information on (ϕ, ψ) torsion preferences.¹⁴ This is the minimal peptide which can form a single turn of α-helix, and so can be thought of as a model for helix nucleation. Although longer polyalanines were also studied by Graf et al.,¹⁴ like Ala₅, all formed very little helix (generally at least ten residues are required for significant α-helix population). As a model peptide which can form longer helices (a measure of helix extension), we chose the blocked 15-residue peptide Ac-(AAQAA)₃-NH₂. This peptide has a small but significant population of α-helix (≈ 20% at 300 K) and in addition (i) it is mostly alanine-based, like the peptides used in the scalar coupling study of Graf et al.,¹⁴ (ii) it is uncharged, and blocked at the termini, simplifying the system for simulation, and (iii) there is an extensive residue-resolved NMR study of helix formation as a function of temperature using chemical shifts.⁴⁶ Our approach was to find the minimal correction (eq 10) such that the force fields would reproduce both the scalar couplings for Ala₅ and the fraction of helix in Ac-(AAQAA)₃-NH₂ at 300 K.

A number of rounds of optimization were carried out to match the data for the longer peptide. In the first round a straightforward perturbation of the original force fields was used to estimate optimal correction parameters. Since simulations with these first round parameters revealed them to be an overcorrection, subsequent rounds kept δ_ψ fixed and used a simple binary search in order to pinpoint the optimal value of k_ψ. The final force-field parameters are given in Table 2. Plots of the final V(ψ) corrections are given in SI, Figure 4.

Table 2.

Optimized corrections to ff03 and ff99SB, yielding revised force fields ff03* and ff99SB*, respectively. The parameters refer to a cosine correction to ψ given by eq 10.

Parameter	ff03*	ff99SB*
kψ (kcal/mol)	0.3575	0.1788
δψ (degrees)	285.5	105.4

Below, we refer to the revised force fields as ff03* and ff99SB*.

Results with Optimized Force Fields

We first discuss the simulation results for Ala₅ with the modified force fields. The scalar coupling χ² values for both original and modified force fields are listed in Table 1 (a full list of the experimental and calculated couplings is available as SI Table 3). We find that the improvements in χ² with respect to the scalar couplings are very modest, indicating the parent force fields are already close to optimal, in terms of the Ala₅ data; the final parameters were therefore mainly determined by the data for the longer peptide. Note that early in the optimization process, we derived force fields with lower χ² for Ala₅. These force fields, however, formed only extended conformations with the longer peptide and were most likely overfitted. Despite the small change in χ², the populations of the various Ramachandran regions have shifted, with ff03* and ff99SB* having lower and higher populations in the helical region than their respective parents.

A much greater improvement was achieved with respect to the fraction of helix for the longer helix-forming peptide. This is demonstrated in Figure 2, where both revised force fields are much closer to the experimental estimate of fraction of helix than the parent force fields, at the temperature of interest (303 K). Both also correctly predict the trend toward lower helical propensity at the C-terminus. To further illustrate the difference between these force fields, snapshots of the structures obtained at this temperature are shown in Figure 3, selected at random from the trajectories. The almost complete helix in ff03 and lack of helix in ff99SB are evident from Figure 3 A and B, respectively; there is some evidence of β-turn formation in the latter. For both modified force fields, short helices are observed, with the structures being slightly more compact overall for ff99SB* than ff03*.

Figure 3.

Randomly selected conformations of Ac-(AAQAA)₃-NH₂ at 303 K in (A) ff03, (B) ff99SB, (C) ff03* and (D) ff99SB*.

To illustrate the effect of the modifications, we present in Figure 1 (A) and (B) the (ϕ, ψ) potential of mean force derived from the internal residues of Ala₅. Both modifications result in very similar final (ϕ, ψ) free energy surfaces (a comparison with the original force fields is given in SI Figure 5). These results can be compared with a statistical potential derived from observed (ϕ, ψ) frequencies in a library of coil residues drawn from the protein data bank (PDB).⁴⁸ For a fair comparison with the Ala5 peptide, which forms negligible α-helix (Table 1), in Figure 1 (C) we exclude all residues within secondary structure from this analysis. The positions and shapes of the minima derived from the simulations and the PDB are in good accord; note that the relative “free energies” of the major minima in the PDB reflect the biased frequency of different types of secondary structure in the PDB, and not the intrinsic structural preferences, and so would not be expected to agree with the simulation results. In SI Figure 6, we compare the potential energy surface of alanine dipeptide in the original modified force fields and from quantum mechanical (QM) calculations. ^5,8 The surfaces for the original and modified force fields compare equally well with the QM data.

Validation: NMR data for a Folded Protein

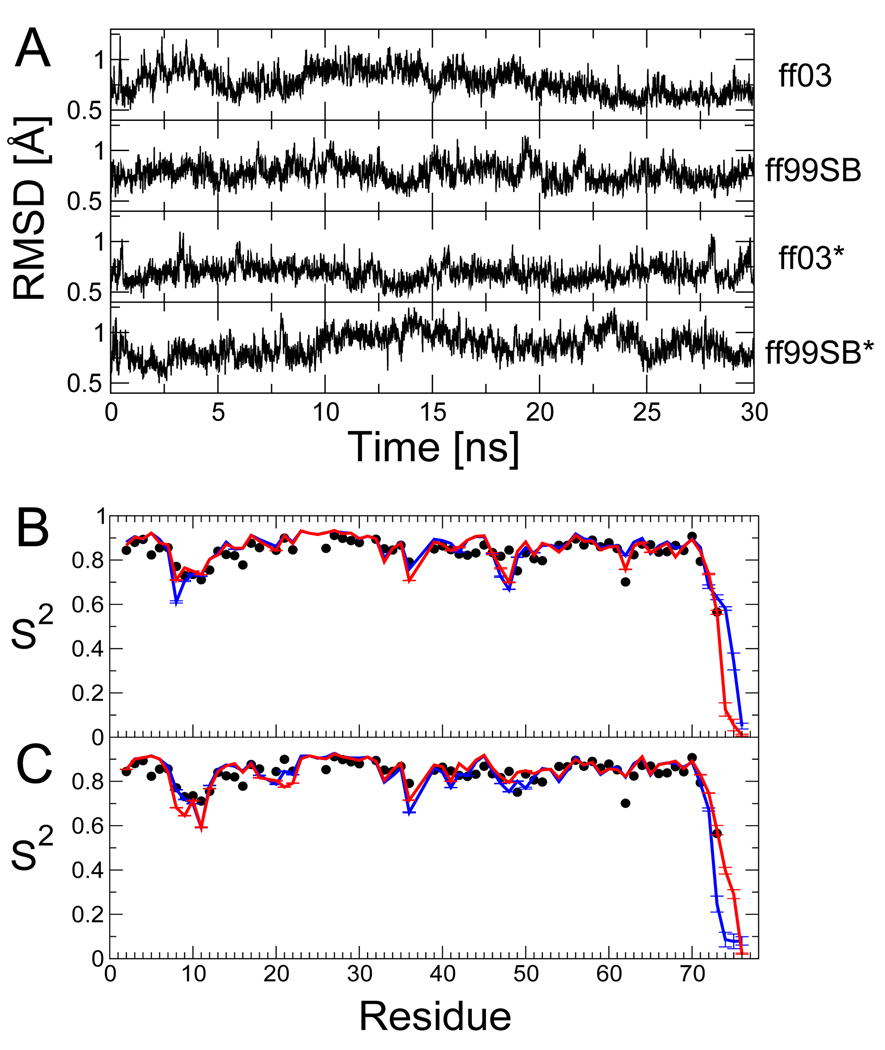
Although our primary aim is to obtain force fields that have properly balanced secondary structure preferences, with a view to simulations of non-native proteins, it is also important to obtain good results for folded proteins, where recent force fields have made large improvements. The relatively small shifts in the Ramachandran potentials of mean force suggest that our modifications should not have a large effect on native state simulations. To confirm this, we ran 30 ns simulations of folded ubiquitin, a protein for which a wealth of experimental NMR data is available in the literature. In Figure 4 A, we report the backbone root mean square deviation from the crystal structure for the various force fields. Note that this excludes the disordered C-terminal tail (residues 72–76). The performance of the modified force fields is comparable to that of the parent force fields, with deviations being less than 1 Å over most of the simulation. We have also calculated Lipari-Szabo generalized order parameters⁴¹ S² for NH bond vectors from the simulation. These parameters reflect the extent of orientational motion of the NH vector on a picosecond-to-nanosecond time scale. We find (Figure 4 B,C) that the order parameters determined from both the original and modified force fields are in excellent agreement with the experimental order parameters fitted to NMR relaxation data.⁴⁹

Figure 4.

Tests of refined force fields using 30 ns all-atom simulations of the native state of ubiquitin. Panels in (A) show the root-mean-square deviation of backbone heavy atoms (residues 1–71) from the crystal structure³² for each force-field (from top: ff03, ff99SB, ff03* and ff99SB*). Backbone generalized order parameters (S²) are shown in (B) for ff03 (blue) and ff03* (red) and (C) for ff99SB (blue) and ff99SB* (red); experimental order parameters from NMR relaxation measurements⁴⁹ are shown as black symbols.

Backbone RDCs are used for a second direct comparison of the simulation results with solution NMR experiments. The RDC data are a natural choice because they are exquisitely sensitive to small variations in geometry and a large set of dipolar couplings for ubiquitin in 10 different alignment media is available in the literature,⁵⁰ and has already been used to validate the ff99SB force field.⁵¹

We calculate the alignment tensor for each medium using only the ordered backbone residues, and assess the deviations from experiment by using the cumulative Q-factor, Q_cum, averaged over all alignment media. This procedure is the same as that used in earlier tests of ff99SB, in order to be comparable:⁵¹ we find a Q_cum of 2.38 for ff99SB, similar to the previous value of 2.22 obtained from longer simulations. The results for all force fields are summarized in Figure 4 (E). There is a substantial improvement in agreement with experiment for ff03* over ff03, while ff99SB* is comparable to ff99SB, within the uncertainty. Therefore, it appears that the new force fields are at least as good as the best current force fields at reproducing RDCs.

Validation: scalar couplings for HEWL19

As pointed out in the introduction, folded proteins represent rather a weak test of force-field secondary structure propensities, since the system explores only the narrow free energy basin around the folded structure. Ideally the force-field correction should be transferable to different peptides to predict helix content accurately for different sequences. In practice this will be limited by the accuracy of other factors that determine helix propensity, such as salt bridges. As a simple test we have run simulations of the 19-residue fragment HEWL19, consisting of residues 1–19 of hen egg-white lysozyme. This peptide has a naturally occurring trialanine sequence from residues 9–11, for which scalar couplings have been determined at 300 K.¹⁴ We ran replica exchange simulations of HEWL19 with both the original and modified force fields: the data are summarized in Table 4. We find that both the modified force fields show excellent agreement with the experimental data, with χ² close to 1. For the original force fields, ff03 shows a large discrepancy (χ² > 3), whilst χ² for ff99SB is only slightly larger than that for the modified force fields. However, both the population of the α region of the Ramachandran map, and the fraction of helix are much lower for ff99SB than for the modified force fields. The scalar coupling data for this peptide therefore appear to establish a strong upper bound for the amount of helix formed (as in ff03), but are less discriminating between force fields with a lower fraction of helix. For direct comparison, the scalar couplings for the central residue (Ala10) are also listed in Table 4, with the full data set available in SI Table 3.

Table 4.

Scalar couplings of the central residue (Ala 10) of HEWL19 for different force fields. The lower part of the table lists the Ramachandran populations and fraction helix averaged over the three consecutive Ala residues (errors in parentheses), and the χ² relative to the experimental J-couplings (complete data for Ala 9, 10, and 11 are given in SI Table 3).

	Expt.	σ	ff03	ff99SB	ff03*	ff99SB*
A10 1JNCα(ψ10)	10.58	0.59	10.04	10.84	10.51	10.27
A10 2JNCα(ψ9)	7.24	0.50	6.48	7.50	7.43	7.06
A10 3JHαC(ϕ10)	1.72	0.38	1.40	2.55	1.55	1.82
A10 3JHNC(ϕ10)	1.33	0.59	0.58	1.10	1.00	0.65
A10 3JHNCβ(ϕ10)	2.19	0.39	3.48	2.23	2.86	3.01
A10 3JHNHα(ϕ10)	5.10	0.91	5.72	7.08	5.95	6.46
A103JHNCα(ϕ10; ψ9)	0.46	0.10	0.24	0.52	0.46	0.39
% α+			91.6 (1.6)	34.9 (2.3)	60.6 (2.3)	69.4 (2.5)
% β			1.8 (0.7)	23.5 (1.3)	15.8 (1.7)	12.9 (1.3)
% ppII			6.3 (1.3)	27.9 (1.5)	22.6 (1.3)	15.2 (1.6)
% helix			78.6 (2.5)	4.5 (1.0)	35.1 (2.3)	30.9 (2.0)
χ2(J)			3.2	1.3	1.0	1.0

Temperature Dependence of Helical Content

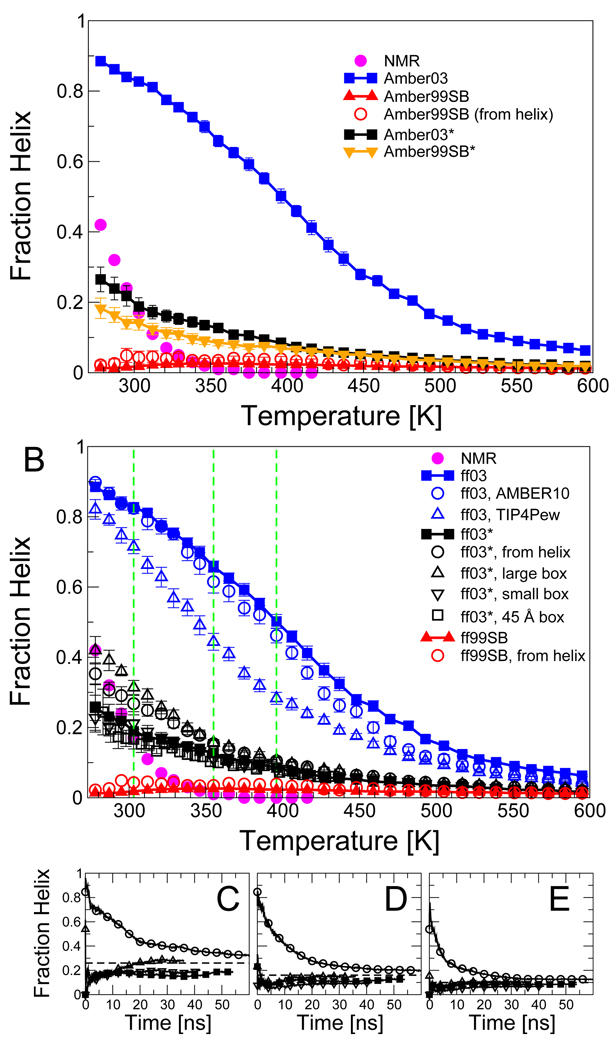
Since replica exchange sampling was used for the longer peptide, it is also possible to examine the temperature dependence of the helix content. Figure 5 (A) compares the overall fraction of helix of Ac-(AAQAA)₃-NH₂ determined from the various simulations to that estimated from NMR using chemical shifts.⁴⁶ Simulations with all force fields resulted in only a weak dependence of helical population on temperature, while the experiments suggest a much sharper transition, with all helix being lost above ≈ 350 K. A similar weak dependence of helical population on temperature was also observed in a recent simulation study by the Pande group, for their modified force field ff99ϕ.⁵² A number of simple explanations for the weak temperature dependence in simulations can be suggested: (i) lack of adequate statistical sampling in the simulations; (ii) effects of pressure (our replica exchange simulations are done at constant volume); (iii) poor temperature dependence in the water model; (iv) problems with simulation protocol; (v) imaging artifacts due to small simulation box; and (v) definition of “helix”. We address each possible cause here in turn:

Figure 5.

Temperature dependence of helix formation in Ac-(AAQAA)₃-NH₂. (A) Fraction helix as a function of temperature for ff03 (blue squares) ff99SB (red triangles), and the revised force fields ff03* and ff99SB*; experimental estimate from NMR chemical shifts given as magenta circles. (B) Effects of simulation parameters on results: ff03 (blue squares), ff03 run with Amber 10 instead of Gromacs 3.3.1 (blue circles), ff03 with TIP4P-Ew instead of TIP3P (blue triangles), ff03* (black filled squares), ff03* starting from helical conformations in all replicas (black open circles), ff03* with simulation cell with 6.1% larger volume (black triangle up), ff03* with simulation cell with 5.9 % smaller volume (black triangle down), ff03* with 45 Å simulation cell (black open squares), ff99SB (red triangle up), ff99SB from helix (red circles); experimental data as in (A). The convergence of the calculated helical fraction is shown by plotting a cumulative fraction helix against time for simulations with ff03* at temperatures of (C) 303 K, (D) 355 K and (E) 396 K. Symbols in (C)–(E) as in (B). Where error bars are not visible, they are smaller than the symbol size.

Statistical Sampling

Recent all-atom molecular dynamics simulations by Sorin and Pande have found that equilibration periods (without replica exchange) for the helix-coil transition may be as long as 30 ns,³⁰ and experimental relaxation times for helix formation are at least 100 ns.^53–56 We have addressed the question of statistical convergence for each of ff03* and ff99SB* by running simulations of Ac-(AAQAA)₃-NH₂ with all replicas starting (1) from random-coil initial conditions (the standard initial conditions, as used for all the other force fields), and (2) from a helical conformations. The average fraction of helix resulting from these two very different sets of initial conditions are similar (Figure 5 B), having clearly converged over time (Figure 5 C–E). We find a similarly slow rate of convergence to that seen in the earlier work.³⁰ Note also that the fraction of helix is only weakly dependent on temperature for both sets of initial conditions.

Effects of Pressure

Since constant pressure simulations in liquid water will be unstable at high temperatures, we have run the replica exchange simulations at constant volume. This was also justified from a study by Paschek et al. in which the results of two-dimensional volume-temperature replica exchange suggested a negligible effect of pressure on total fraction helix.⁵⁷ We have confirmed the absence of pressure/density effects on the helix-coil equilibrium by running replica exchange of Ac-(AAQAA)₃-NH₂ with the ff03* force field in a box with volume 5.9% smaller than the original, and one 6.1% larger. The results in both the larger and smaller box converge to the same values as those in the original box (Figure 5 D and C–E). A plot of the fraction helix as a function of density and temperature finds at most a weak density (or pressure) dependence, in agreement with the results of Paschek et al.⁵⁷ (SI Figure 7).

Water Model

TIP3P⁵⁸ is the water model with which the Amber force fields were intended to be used.^7,9,59,60 However, it is well known that this model does not reproduce well the temperature dependence of the properties of liquid water (e.g., density maximum). A more accurate recent model explicitly developed for use with Ewald-based electrostatics is TIP4P-Ew.⁶¹ Simulations of Ac-(AAQAA)₃-NH₂ with ff03 in TIP4P-Ew (Figure 5 B) indicate that this model clearly destabilizes helical structure; however it does not result in a sharper dependence of the helix-coil transition on temperature.

Force-Field Implementation and Simulation Protocol

We use Gromacs to run simulations with the Amber force fields. In addition to checking single-point energies with simple molecules in both simulation packages, we have also run replica exchange simulations of the same peptide Ac-(AAQAA)₃-NH₂ with ff03 in Amber with a set of simulation parameters as similar as possible to those used in Gromacs. The results (Figure 5 B) indicate that the results obtained using Amber and Gromacs are in good agreement.

Imaging Artifacts

When simulating unfolded polypeptides with periodic boundary conditions, some weak interactions between peptides in the primary image and its immediate neighbours are inevitable unless an impractically large simulation box is used. With the standard 35 Å box size used for most of our simulations, we find that the protein interacts with its image (minimum distance to nearest image less than 5 Å) in approximately 5 % of the configurations in the high temperature replicas where the peptide is most unfolded. To ensure that this artifact does not influence the temperature dependence of helix formation, we have run additional simulations of Ac-(AAQAA)₃-NH₂ with ff03* in a 45 Å truncated octahedron box. The results show (Figure 5 B) that imaging artifacts are negligible since an almost identical fraction helix is obtained with both 35 Å and 45 Å box sizes over the temperature range considered.

Definition of Helix

We have adopted a relatively conservative definition for the α_h region of (ϕ, ψ) space. We have also considered alternative definitions which define a larger region of the Ramachandran map as α_h, or which define helix using helical i, i + 4 hydrogen bonds. The more generous definitions do not alter the fraction helix much and result in a slightly weaker temperature dependence (see SI text and SI Figures 2 and 3). Therefore, the lack of temperature dependence is not a consequence of the specific helix definition employed.

We conclude from the above analyses that the weak temperature dependence of the helix-coil equilibrium in the simulations is not likely to be caused by the statistical sampling, pressure effects, the water model, possible problems with the simulation protocol, or the definition of “helix”. Instead, it points toward more fundamental issues with the force field. To provide a foundation for future improvements, we will in the following analyze the energetics of the helix-coil equilibrium by separating it into enthalpic and entropic contributions.

Thermodynamics of the Helix-Coil Transition

Lifson-Roig model for Helix-Coil Transition

We can gain some insight into thermodynamics of helix formation by considering a simple model for the helix-coil transition. We use the LR theory, which has been shown to be equivalent to the earlier Zimm-Bragg theory,⁶² at least for residues within α-helices.^36,37, Both theories are also closely related to the partition function used in the AGADIR algorithm for helix prediction.^63,64 The LR theory describes helix formation in terms of a nucleation parameter v and helix extension parameter w. Specifically, v is the statistical weight of a residue whose backbone (ϕ, ψ) torsion angles lie within the helical region, relative to the “coil”, or non-helical state: effectively, it is an equilibrium constant between these two states. Since v is a small number, the formation of helical structure is initially improbable. However, once sufficient helix has been formed, it can be stabilized by i, i + 4 hydrogen bonding (as well as other interactions). The parameter w represents the equilibrium constant for this favorable conversion of a coil residue to a helical residue at the end of a helix. Here we use common values of v and w for Ala and Gln. We also considered a separate treatment of Ala and Gln, as well as a variant of the LR theory that includes the possibility of helix-capping interactions,⁶⁵ which are known to be important^66–68 (SI text and SI Figures 8–10). These more complex models do describe the data slightly better, even after accounting for the additional parameters required, however, the results presented below do not depend strongly on the choice of model: for example, the fitted w and v when capping is included are almost identical to those when it is not (SI Figure 11). We therefore present here the simplest model.

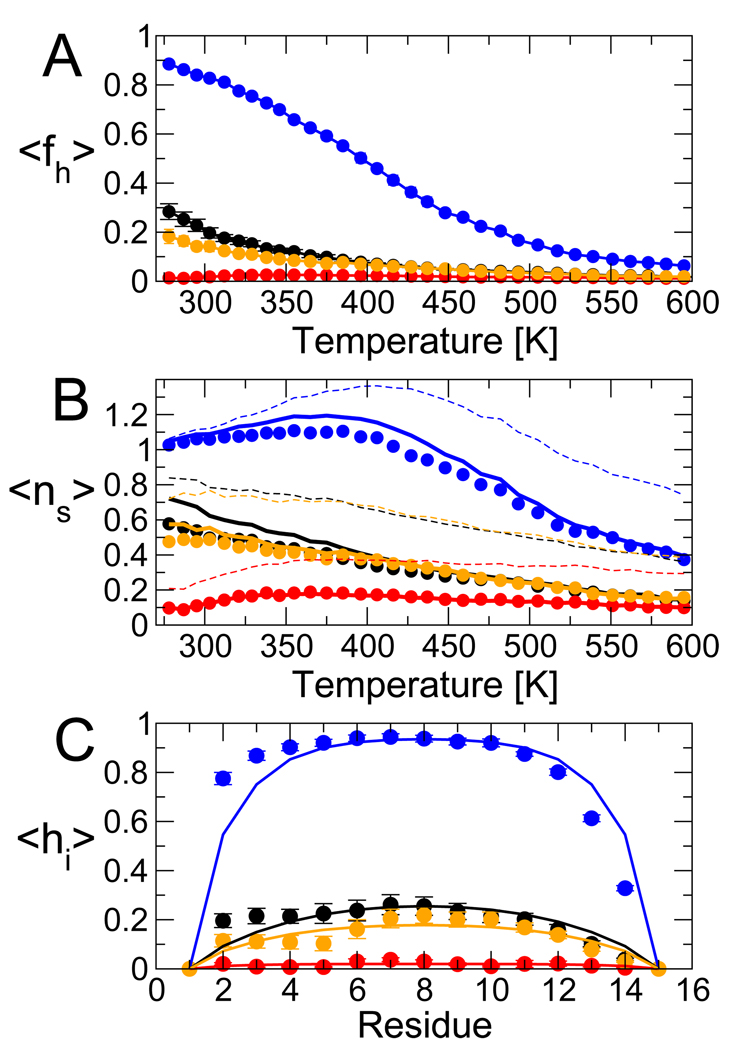
Using a Bayesian approach, we have determined the optimal LR parameters describing the helix formation with each force field and at each temperature. Even the simple form of the LR model used here provides a reasonable description of the simulation data, in the sense that it reproduces various characteristics of the distribution of helix within the peptide. Figure 6 (A) shows that the simplest LR model fits the total fraction of helix very well at all temperatures. There are small deviations between the number of helical segments predicted by the model, and the simulation data (Figure 6 (B)); these can be reduced by modeling Ala and Gln independently (SI text). The absence of capping interactions in the model results in a symmetric predicted distribution of helicity within the peptide (Figure 6 (C)): this misses the strong capping effect of the blocking acetyl group biasing helix formation toward the N-terminus. Inclusion of capping in the model reproduces this effect (SI text). We comment briefly on an expression commonly used to calculate the number of helical segments, ∂ lnZ/∂ lnv₁₂, where v₁₂ is the element in the first row and second column of the LR matrix M. This relation incorrectly counts …chhc … as a helix, and is a valid approximation only if v is very small. In general this expression will overestimate v (broken lines in Figure 6 (B)), hence helix-coil parameters (particularly v) obtained by fitting this expression to simulation data will tend to be underestimates.

Figure 6.

Quality of LR fit to simulations of Ac-(AAQAA)₃-NH₂. (A) The average fraction helix 〈f_h〉, with simulation data as symbols and model predictions as solid lines (blue: ff03, red: ff99SB, black: ff03*, orange: ff99SB*). (B) The average number of “helical segments”, 〈n_s〉, with simulation data as symbols and model predictions as solid lines; broken lines give the prediction using the approximate expression 〈n_s〉 ≈ Σ_i∂lnZ/∂lnv_12i. (C) Fraction of helix for each residue in the 303 K replica, symbols and lines as above.

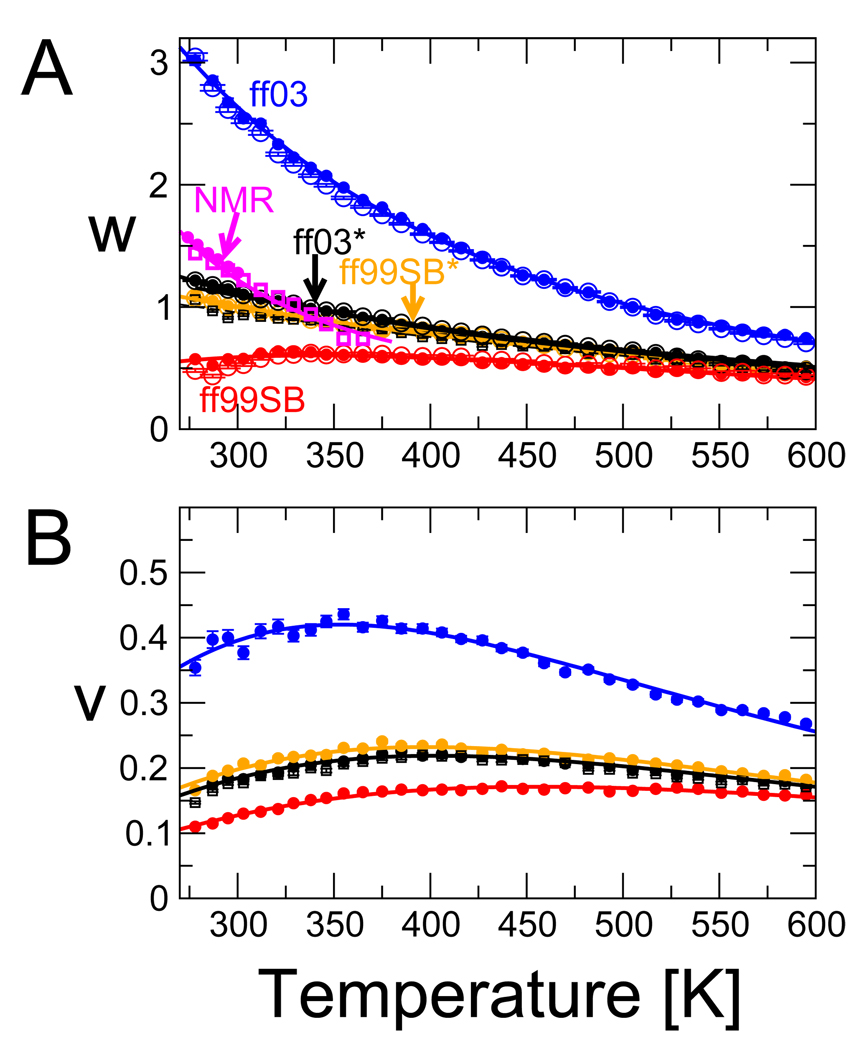
The fitted parameters w(T),v(T) are plotted as a function of temperature in Figure 7. Near 300 K, the fitted w, 1.10 and 1.00 for ff03* and ff99SB*, respectively, are somewhat too small relative to experimental estimates at this temperature (≈ 1.28⁶⁹); when w is independently fitted to Ala and Gln, the Ala results are closer to experiment (w ≈ 1.28 for ff03* from a fit using separate parameters for A and Q and helix capping; see SI text and SI Figure 11 A). The fitted v, 0.18 and 0.21 for ff03* and ff99SB* are too large with respect to the experimental estimates of 0.03–0.05;^65,69 a similar result was obtained from another simulation study.⁵² For reference the corresponding Zimm-Bragg parameters^36,37,62 σ = w/(1+v), s = v²/(1+v)⁴ are σ = 0.017, s = 0.93 for ff03* and σ = 0.020, s = 0.83 for ff99SB*. Thus, although the force fields match the overall fraction of helix in experiment, the higher nucleation parameters (v or σ) relative to experiment indicate that the helix formation in the simulations is less cooperative than inferred experimentally.

Figure 7.

Fitted LR parameters as a function of temperature. (A) The helix extension parameter w, with colors as in Figure 6. Solid circles are obtained from a free fit of w,v to simulations with each force field. Open circles are obtained by fitting only w, with v fixed to the average v obtained from the free fit, over the full temperature range. Data for the ten residue peptide Ac-(AAQAA)₂-NH₂ using ff03* is given by solid squares. NMR data are in magenta: solid circles, w from Rohl et al.;,⁶⁹ open squares, fit of w to the fraction helix in Ac-(AAQAA)₃-NH₂, assuming v = 0.04796. (B) The nucleation factor v, colors and symbols as in (A). Solid lines in (A) and (B) are the fit of a thermodynamic model with temperature-independent heat capacity (parameters in Table 5).

The LR extension parameter w closely mirrors the helical propensities of the different force fields, with ff03 and ff99SB having, respectively, the largest and smallest values, and ff03* and ff99SB* having similar w. Like the overall fraction of helix, w(T ) fitted to the simulation data exhibits a smaller temperature dependence than the experimental data. The temperature dependence of w is not suppressed by our assumption of a temperature-dependent v: w(T) is nearly unchanged in a fit with v fixed to its average over temperature in the free fit (open symbols in Figure 7 (A)).

When comparing parameters with experiment, it is important to note that the LR parameters v and w are not entirely independent in the fits. In the simulations, a LR model with the experimental v = 0.05 and a slightly increased w can fully account for the residue-specific fraction helix (SI Figure 12). However, the cooperativity of such a model is too high, as manifested in an average number of helical segments being about half of that seen in the simulations. In experiments probing the average fraction of helix,^70,71, such collective information is not available, and v is derived mostly from global fits to fraction-helix data for peptides of different length. In fitting the related Zimm-Bragg model to circular dichroism data from copolypeptides of alanine and ornithine or lysine, Yang et al.⁷² found that the nucleation parameter was very sensitive to the chosen dependence of circular dichroism (CD) signal on helix length, and could vary between σ = 0.004 (v ≈ 0.073) to σ = 0.02 (v ≈ 0.206) depending on this choice. A further nuance to the interpretation of experiments probing the helix- coil transition is the recent finding by Kennedy et al.²⁷ that the fitted w may depend on the length of the peptide (as we find when comparing the w for Ac-(AAQAA)₂-NH₂ and Ac-(AAQAA)₂-NH₃ - see Figure 7). These challenges together complicate the comparison of the LR parameters from theory and experiments.

Thermodynamic interpretation of Lifson-Roig parameters

We fit a thermodynamic model to the optimal LR parameters w(T) and v(T), including a temperature-independent heat capacity (Table 5). The fits are indicated by the solid lines in Figure 7. As expected, helix extension is favored by enthalpy ΔH (with the exception of ff99SB for which ΔH > 0) and opposed by entropy ΔS, with ff03* and ff99SB* having ΔH ≈ −0.5 kcal.mol⁻¹ and ΔS ≈ − 1.7 cal.mol⁻¹ .K⁻¹. The fitted heat capacity ΔC_V ≈ ΔC_p is negative (the opposite sign to that for protein folding), in qualitative agreement with a recent experimental estimate of −7.6 cal.mol⁻¹.K⁻¹.⁷³ We also fitted the experimental estimates by Rohl et al.⁶⁹ for w(T) (setting ΔC_p ≡ 0 because of the relatively small temperature range covered by this data). In this case, we obtain ΔH ≈ −1.3 kcal.mol⁻¹ and ΔS ≈ − 3.8 cal.mol⁻¹.K⁻¹. This value of ΔH is similar to estimates of between −0.9 and −1.3 kcal.mol⁻¹ from CD measurements at different temperatures⁷¹ and from calori-metric measurements.^73,74 Thus, although the free energy for helix extension, − k_BT ln w, is similar in simulation and experiment near 300 K, the enthalpic and entropic contributions are apparently about half the experimentally-derived estimates, resulting in an overall smaller temperature dependence.

Table 5.

Thermodynamic fits to the LR parameters w and v. Errors are given in parentheses and values with large uncertainties are indicated in italics. Note that since the Δ(PV) term is expected to be small,¹⁹ we assume ΔA ≈ ΔG, ΔU ≈ ΔH and ΔC_v ≈ ΔC_p; strictly speaking the simulation data are for the constant volume ensemble. Thus we fit k_BT ln w = ΔH_300K −TΔS_300K + ΔC_p[T − 300 K]−TΔC_p ln[T/300 K], with a similar relation for v.

Parameter: Force Field	ΔH300K kcal.mol−1		ΔS300K cal.mol−1.K−1		ΔCp cal.mol−1.K−1
w: ff03	−0.99	(0.02)	−1.37	(0.09)	−5.3	(0.4)
w: ff99SB	+0.23	(0.05)	−0.29	(0.17)	−5.7	(0.5)
w: ff03*	−0.61	(0.02)	−1.81	(0.06)	−3.6	(0.2)
w: ff99SB*	−0.47	(0.03)	−1.55	(0.09)	−3.3	(0.3)
w: Ref69	−1.28	(0.02)	−3.78	(0.05)
v: ff03	+0.44	(0.04)	−0.35	(0.12)	−8.3	(0.4)
v: ff99SB	+0.90	(0.04)	−1.08	(0.11)	−5.8	(0.3)
v: ff03*	+0.72	(0.03)	−0.94	(0.08)	−7.5	(0.2)
v: ff99SB*	+0.71	(0.04)	−0.86	(0.11)	−8.0	(0.3)
v: Ref69			−6.6

Since v is usually assumed temperature independent in experiment, we initially make this approximation for comparison. From our fitted v (for the optimized ff03* or ff99SB*) of 0.2, and the experimental estimate of 0.036,⁶⁹ we calculate ΔS to be −3.2 cal.mol⁻¹.K⁻¹ and −6.6 cal.mol⁻¹.K⁻¹, respectively: i.e., assuming there is no enthalphic contribution to v, the entropy loss on forming a helical h backbone conformation outside a helical segment in the simulation models is about half that in experiment. Fitting a more general thermodynamic model results in a significant gain in enthalpy on forming a helical conformation, ≈ 0.7 kcal.mol⁻¹ (details in Table 5). This result differs from the classical view of the helix-coil transition, in which the nucle-ation barrier (≈ v² in the LR model) is purely entropic in origin and v is consequently temperature independent. Interestingly, the enthalpic contribution to v is increased by 0.28 kcal.mol⁻¹ by the correction to ff03, and decreased by 0.19 kcal.mol⁻¹ by the correction to ff99SB, similar to the magnitudes of the ψ corrections (Table 2). This suggests that the main difference between the nucleation parameters v of the parent and optimized force fields comes from the enthalpic contributions of the torsional correction, with the entropic contribution relatively unaffected.

The thermodynamic fits of the helix-coil parameters indicate that while the torsional correction to ψ can approximately reproduce free energies at a given temperature, the enthalpic and entropic contributions to the helix-coil equilibrium are too small, each about half the experimental estimate. This error is reflected in part in the Ramachandran maps. As a rough measure of the conformational entropy lost upon helix formation we have calculated a Shannon entropy over the α₊ region of the maps as $-k_B{\int }_{-160}^{-20}d\varphi {\int }_{-120}^{50}d\psi p(\varphi ,\psi )\text{ln}p(\varphi ,\psi )$ where p(ϕ, ψ) is the distribution of backbone dihedral angles normalized over the region of integration (i.e., the red squares in Figure 1). Specifically, we calculate the difference in this “entropy” for residues in helical states with and without helical hydrogen bonds. For the PDB,⁴⁸ ff03* and ff99SB*, these differences are −3.4, −1.8 and −1.4 cal.mol⁻¹.K⁻¹, respectively. By this entropy measure, residues within helices are more structured in the PDB, relative to coil residues in the helical basin, than in the force fields. This structuring is evident in the insets of Figure 1, which show the α₊ region for residues within helices: the potential well for residues with helical hydrogen bonds is much narrower in the PDB than in the force fields. A comparable measure of entropy loss upon hydrogen bonding can be obtained by taking the difference between the entropy associated with the LR parameters w (which includes both a c to h conformational change and hydrogen bond formation) and v. This results in a loss of entropy of approximately 3 cal.mol⁻¹.K⁻¹ in experiment, versus only about 0.8–1.0 cal.mol⁻¹.K⁻¹ for the modified force fields, in qualitative agreement with the Shannon entropy estimates.

Discussion

Our work builds on many years of AMBER force field improvements, many using similar correction terms (consequently, it is important to specify exactly which one is being used). For example, the original AMBER force field intended for condensed phase simulation, ff94,⁵⁹ had a known propensity for strongly overstabilizing helical structure, prompting two corrective modifications: (i) the ff96 release which changed only the ϕ and ψ torsion parameters,⁷⁵ but proved to overstabi-lize extended structure; (ii) the ff94GS variant of García and Sanbonmatsu in which both the ϕ and ψ torsion parameters were set to zero.³⁵ Although ff94GS achieves a better balance, it still retains too much helical structure as assessed by comparison with NMR scalar coupling data.¹⁵

The more recent ff99 parameters, also based on ff94, included extensive changes to the torsional potentials.⁶⁰ While reasonably balanced between α and extended structure, this force field was found to have a large barrier to rotation in ϕ. To address this, Sorin and Pande replaced the ϕ torsional potential of ff99 with that of ff94 to create ff99ϕ³⁰. In a more extensive optimization, Simmerling and co-workers used quantum chemical calculations on longer alanine peptides in order to optimize both the ϕ and ψ torsions;⁹ the resulting ff99SB potential gave improved agreement with NMR data for proteins.^9,51 The most recent release of the AMBER all-atom force field, ff03, is a major departure from ff94 in that both the charges and torsional potentials have been refitted to high level quantum calculations. In particular, a new approach was applied to deriving the charges in order to make them more compatible with condensed phase simulation.⁷ Our recent comparison with NMR scalar coupling data for (Ala)₅ showed that both ff99SB and ff03 were amongst the force fields showing the best agreement with experimental data.¹⁵

By modifying the backbone dihedral potentials of ff03 and ff99SB to match experimental data related to the helix-coil transition, we have obtained force fields that produce the proper balance between average helix and coil populations at ambient conditions. This balance is essential for simulations of unfolded or disordered peptides and protein loops. The transferability of the optimized force fields was demonstrated by reproducing experimental NMR data for peptides not used in parameterization, as well as excellent structural results for a folded protein. However, despite these overall improvements the resulting force fields still exhibit a number of deficiencies that become apparent upon examination of the LR parameters v and w, and their temperature dependence. We find that the force fields underestimate w and overestimate v compared with experiment. As a consequence, the helix-coil transition is less cooperative in the simulations than in experiment. On this basis, we expect that long helices will be more fragmented in the simulations than in experiment, despite the match in average helicity for short helices.

The explanation for the discrepancies between the v,w for experiment and simulation lies in the entropy loss upon helix formation and the compensating enthalpy gain both being too small in magnitude. This thermodynamic analysis of the improved force fields points the way toward further important corrections. The small change in entropy relative to experiment could be explained by a lack of orientational specificity in hydrogen bonding in the force field. For example, it has been shown that although the orientational distribution of side-chain hydrogen bonds in the PDB matches quantum mechanical calculations, the orientational dependence shown by current force fields is too small.⁷⁶ This is particularly true of the geometry with respect to the hydrogen-bond acceptor, where there is a slight preference for hydrogen bonding in the direction of the “lone pairs”. This preference is also evident in the distribution of hydrogen bonds in small molecule crystal structures;⁷⁷ inclusion of orientation-dependent hydrogen bonding potentials has produced improvements in NMR structure calculations⁷⁸ and the prediction and design of protein-protein complexes.⁷⁹ The additional geometric requirements for hydrogen bonding would be expected to increase the entropic component of w: our analysis of the Shannon entropy in Ramachandran maps is consistent with a larger loss of entropy upon hydrogen-bond formation in the PDB, relative to the simulation. This effect might be addressed in force fields either by the inclusion of a geometrically specific hydrogen-bond energy term⁸⁰ or the introduction of “off-center” charges in addition to the current “atom-centered” charges.^81,82

A second major effect is the neglect of electronic polarization (or induction) effects in current force fields.⁸² A recent density functional theory study has suggested, for example, that as much as half of the hydrogen-bonding energy in a helix may arise from electron density re-distribution on helix formation.⁸³ Other studies of hydrogen-bonded chains of formamide molecules⁸⁴ and in long helices⁸⁵ have led to similar conclusions. An experimental finding that the LR w may depend on helix length is consistent with this cooperativity.²⁷ The increase in enthalpy associated with this effect approximately matches the discrepancy between the enthalpy for the formation of hydrogen bonds in the non-polarizable force fields used here, and the experimental values.

Improved future force fields should, at the minimum, account for the two effects of hydrogen bond geometry and polarization, which appear to account for the observed differences between the simulated and measured thermodynamics of the helix-coil transition. Improvements could be achieved by using multi-center atom charges (or directional potentials) and by adding polarizability,⁸⁶ at least for the groups involved in backbone hydrogen bonds. When making alterations to the protein hydrogen bonding potential, it will also be necessary to consider the balance of interec-tions with the water model which may be altered by such changes. To be consistent, it may also be necessary to introduce similar terms for protein-water and water-water interactions.

We stress that, desp still be adequate for reproducing equilibrium properties of both unfolded and folded peptides and proteins near 300 K. The fact that the corrections necessary are around 0.5 k_BT per residue shows that the parent force fields ff03 and ff99SB are already of high quality; the modifications are simply a “fine tuning” step. Nonetheless, when summed over all the residues, we find that the correction terms have a substantial effect on the conformational distribution. We would therefore recommend using the modified force fields ff03* and ff99SB* for simulations of weakly structured or unfolded peptides and proteins; we note that initial tests suggest that the refined force fields give an improved description of β-hairpin forming peptides. Future development of more sophisticated force fields will be greatly facilitated by experimental data for weakly structured peptides that can be readily calculated from simulation (e.g., NMR scalar couplings, NOE’s), particularly if this is determined at different temperatures.

Table 3.

NMR RDCs for ubiquitin. The agreement between RDCs from 30 ns simulations with each force field, and experimental NMR data recorded in 10 different alignment media⁵⁰ is assessed by the cumulative Q-factor, Q_cum⁵¹

Force Field	Qcum	uncertainty
ff03	2.80	0.10
ff99SB	2.30	0.05
ff03*	2.58	0.05
ff99SB*	2.49	0.09
X-ray structure	2.45