Data interpretation: using probability

Experimental data are analysed statistically to allow us to draw conclusions from a limited set of measurements. The hard fact is that we can never be certain that measurements from a sample will exactly reflect the properties of the entire group of possible candidates available to be studied (although using a sample is often the only practical thing to do). It's possible that some scientists are not even clear that the word ‘sample’ has a special meaning in statistics, or understand the importance of taking an unbiased sample. Some may consider a ‘sample’ to be something like the first ten leeches that come out of a jar! If we have taken care to obtain a truly random or a representative sample from a large number of possible individuals, we can use this unbiased sample to judge the possibility that our observations support a particular hypothesis. Statistical analysis allows the strength of this possibility to be estimated. Since it's not completely certain, the converse of this likelihood shows the uncertainty that remains. Scientists are better at dealing with ‘uncertainty’ than the popular press, but many are still swayed by ‘magical’ cut-off values for P values, such as 0.05, below which hypotheses are considered (supposedly) proven, forgetting that probability is measured on a continuum and is not dichotomous. Words can betray, and often cannot provide sufficient nuances to describe effects which can be indistinct or fuzzy (Pocock & Ware, 2009). Indeed, many of the words we use such as significance, likelihood and probability, and conclusions such as ‘no effect’, should be used guardedly to avoid mistakes. There are also differences of opinion between statisticians: some statisticians are more theoretical and others more pragmatic. Some of the different approaches used for statistical inference are hard for the novice to grasp. Although a full mathematical understanding is not necessary for most researchers, it is vital to have sufficient understanding of the basic principles behind the statistical approaches adopted. This avoids merely treating statistical tests as if they were a fire appliance, to pick up when smoking data need to be dealt with, and vaguely hoping you have got the correct type. Better to know how the data should be properly analysed (as it is to know which extinguisher works best). The wrong statistical approach could be like using water on an electrical fire!

Ideally, the appropriate method of analysis should be anticipated, because it should have been considered when the study was set up. A properly designed study that aims to answer specific questions will have defined outcomes of interest at the outset, before data collection has started. These questions are then recast as hypotheses that need to be tested. We use the collected measurements on an appropriate outcome to test how probable these observations would have been if a particular hypothesis of interest is correct. Assuming that the reader followed our previous instructions to properly display the data obtained (Drummond & Vowler, 2011) we hope that a review of these data displays will confirm the planned analysis that is to be used, or suggest alternatives.

As an example, and with no apology for a basic approach, we shall explain the principles of statistical inference in a simple example involving probability, the bedrock of statistical analysis. We hope that the example will be sufficiently concrete to allow insight into some of the concepts, such as significance, effect size, and power. More specific and practical aspects will be addressed later in the series.

Key points

• Ensure that a sample is random

• Use observations of a sample to judge the features of the population

• Plan the study: this includes the appropriate analysis

• Establish a hypothesis: usually that there is no difference

• Estimate the probability that the observed data could have occurred by chance

• Consider the probabilities of more extreme data as well

• If you find ‘no difference’ this is no DETECTABLE difference

• Absence of evidence is NOT evidence of absence

Suppose we set up a very simple experiment to find out if a flu virus is more lethal in one strain of cell than another. We have 20 A cells and 20 B cells to study. We assume that the cells chosen are representative of A and B cells in general. We infect these 40 cells with the virus. We find that 8 cells out of 40 die (Fig. 1). We start the analysis with a hypothesis: that the probability of death after infection is equal for each strain. The hypothesis is of independence (i.e. no association) between death and strain. It also corresponds to the null hypothesis that there is no difference in the capacity of the virus to kill A and B cells. This hypothesis lets us calculate the probability of observing a number of potential results from our study and also predict what would be found if the virus were equally lethal in A cells and B cells. For instance, given that there are a total of 8 deaths, we could predict, under this null hypothesis, that the likely splits of these 8 deaths could be 4 dead A cells and 4 dead B cells, or maybe even 5 and 3. However, we discover that 6 of the dead cells are strain B. Is this finding evidence that the mortality rates are different? Are A cells more resistant? Or is this just chance at work?

Figure 1. A hypothetical experiment, exposing two strains of cells (n = 20 of each strain) to viral infection and assessing cell death and survival.

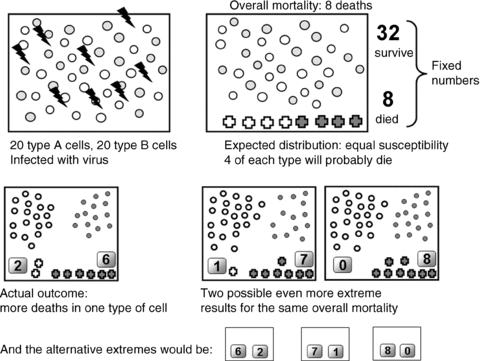
The hypothesis of equal deaths is suggested in the upper right panel. Below, we illustrate the actual result and two possibilities that are less likely than the observed result, if there were in fact no difference in death rates between the groups.

If we wished to observe how chance works we could toss a fair coin eight times to predict the strain of the dead cells (heads, it's an A; tails it's a B). We would find that eight throws could unsurprisingly yield six heads and two tails: so maybe the way things have happened is not that unlikely. But, if we tossed the coin 80 times, then we would be less likely to get 60 heads and 20 tails: we would expect the number of times the coin came up heads or tails would be nearly the same. If the coin is a fair one, P for heads is about 0.5. A coin was in fact tossed 24,000 times by Karl Pearson and there were 12,012 heads, so that experiment gave an estimate close to the theoretical value. (Indeed it would be improbable that the number would be exactly 12,000!) So, one way to answer our question ‘Have six dead B cells and only two dead A cells occurred just as a matter of chance?’ would be to carry out a bigger experiment. With more cells in the experiment, and more dead cells, we could be more certain that a difference of this degree in death rates was evidence against the hypothesis of independence, rather than just a chance event. However, we only had a small plate of expensive cells, and the experiment is over. Can we use statistical inference to predict the probability of our result, or something more extreme, under the assumption of independence? If this probability is small, the evidence would lean towards the cells having different susceptibilities.

In this study, we observed eight deaths. Working with the hypothesis that the probability of death was the same for each cell type, we would expect that the distribution of deaths between the groups would be similar. However, given this total of eight deaths, there is a range of possible results. These range from the possibility that all the deaths occurred in one type, through to all the deaths being in the other type. Neither of these extremes is consistent with our hypothesis that the cells are equally susceptible (Fig. 1). That is, if the actual probability of death was the same for each cell type, it would be improbable (in the sense of odd, strange, unlikely) that we would find the extreme circumstances where all the deaths were in one type of cell, either A cells or B cells.

This is a simple version of Fisher's exact test (Fig. 2). There is a formula that allows us to calculate the probability of each distribution of deaths, given a total of eight deaths over both cell types, using the notation shown in the figure.

Figure 2.

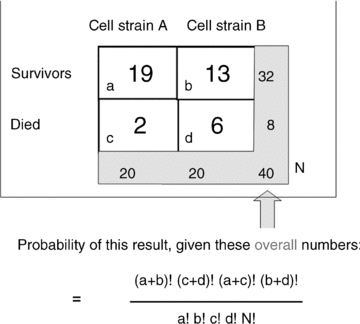
Basis of Fisher's exact test

This formula calculates the probability of this specific configuration occurring, in relation to the assumption that deaths are equally distributed, and is based on the theory of permutations. In a permutation, as each circumstance is set, the remaining possible options are reduced. In the formula, the reducing options are indicated in the factorial values: a! is a factorial (e.g. 4! is 4 × 3 × 2 × 1, which gives a value of 24, and 0! is defined to be 1). For the values shown here (Fig. 2), and if the mortality rate were the same for each type of cell, the probability of this specific configuration is 0.0202. Since all the probabilities added together has to be 1, the other possible configurations apart from the one we've observed will have a total probability of (1 − 0.0202). Out of these remaining alternative configurations, probability 0.9798, there can be other more extreme and unlikely configurations, For example there could be no deaths of A cells, and eight deaths of B cells. This distribution would be quite unlikely if the actual probability of being killed by the flu virus were the same for both cell types.

Using the formula we calculate the probability of this configuration (no A deaths and eight B deaths) to be 0.0016. We can add another unlikely distribution: the possibility of counts of one A death and seven B deaths. These two possibilities, together with the observed result of two and six, give a total probability of 0.1176 that these three extreme configurations would occur, if it were true that the actual probability of cell death was equal in the two cell types. What we have done is compute the probabilities that the observation we made, and some even more extreme observations, could have occurred, if the mortality rate were the same for each type of cell. Given the original hypothesis, of no difference in the probability of being killed by the flu virus, are there other possible extreme or strange distributions to consider? Yes, we should also consider unlikely values at the other end of the scale: the unlikely distributions of six A deaths and two B deaths, seven A deaths and one B, and finally eight As and no Bs. By considering all unlikely values (given the hypothesized equal probability) we are carrying out a ‘two-tailed’ test. Thus the total possibility of all the results that are either similar to, or more extreme than, the one we have observed now becomes 0.2351. Put as a chance, this is about 1 out of 4. This suggests that the probability of our findings is substantial: a 24% chance that what we've found could have occurred as a random event, even if there were really no difference between the cells’ likelihood to be killed. We would be foolish to discount the possibility that there is a difference, but our observed events could be the workings of chance. What we must NOT say is ‘these cells have the same susceptibility to the virus’ because the analysis we have done has merely made us accept that there is not a detectable difference. This is not the same as ‘there is no difference’. To conclude ‘this shows that there is no difference’ here is to make perhaps one of the commonest errors in biology. A useful summary phrase is ‘absence of evidence is NOT evidence of absence’ (Altman & Bland, 1995).

Is it a bad idea to accept the hypothesis, and conclude that there is no difference in probability of death after infection? In this case, perhaps yes. We could be missing an important effect. One type of cell appears (on the basis of these limited numbers) to be three times less likely to die when exposed to the virus. That could be an important difference. Here – as very often is the case – we should say ‘at present, there could be an effect; the probability that there is no difference is not very small’. If we could afford it, we should conduct another, larger, experiment to be clearer about what we have found. If we used double the numbers, and got the exact same pattern of results (although because of random variation, this is highly unlikely), the null hypothesis could possibly be rejected. When the total number is 80 and the cell death frequencies are 4 and 12, the possibility that this or a more extreme result could occur would only be likely 4.8% of the time, if the null hypothesis were correct. In most people's judgement, that approaches a sufficiently small possibility to accept that the null hypothesis could be rejected. However, even here the judgement should be balanced: other factors are relevant in judging these probabilities. If a big investment in equipment to manufacture antiviral therapy depended on the result, responsible financiers might want to be more than 95% certain that a big investment was worth it.

The important concepts of power, effect size, and scientific relevance will receive further attention, in more detail, in a subsequent article.