The effect of solvation on vertical ionization energy of thymine: from microhydration to bulk

Abstract

The effect of hydration on the vertical ionization energy (VIE) of thymine was characterized using equation-of-motion ionization potential coupled-cluster (EOM-IP-CCSD) and effective fragment potential (EFP) methods. We considered several microsolvated clusters as well as thymine solvated in bulk water. The VIE in bulk water was computed by averaging over solvent-solute configurations obtained from equilibrium MD trajectories at 300 K. The effect of microsolvation was analyzed and contrasted against the combined effect of the first solvation shell in bulk water. Microsolvation reduces the ionization energy (IE) by about 0.1 eV per water molecule while the first solvation shell increases the IE by 0.1 eV. The subsequent solvation lowers the IE, and the bulk value of the solvent-induced shift of thymine’s VIE is approximately −0.9 eV. The combined effect of the first solvation shell was explained in terms of specific solute-solvent interactions, which were investigated using model geometries. The convergence of IE to the bulk value requires the hydration sphere of approximately 13.5 Å radius. The performance of the EOM-IP-CCSD/EFP scheme was benchmarked against full EOM-IP-CCSD using microhydrated structures. The errors were found to be less than 0.01–0.02 eV. The relative importance of the polarization and higher multipole moments in EFP model was also investigated.

1 Introduction

Ionization of nucleic acid bases (NABs) is relevant to radiation and photoinduced damage of DNA.^1–7 In realistic environments, several types of interactions affect ionization energies (IEs) of the nucleic acid bases, quantities that govern charge migration, radiationless relaxation, proton transfer and other photoinduced chemical changes and, therefore, ultimately control the redox properties and photostability of DNA. These include h-bonding interactions between the Watson-Crick pairs, π-stacking interactions between neighboring bases, interactions with sugar-phosphate backbone, counterions, and, of course, omnipresent biological solvent — water.

Numerous gas-phase studies have characterized some of the above factors using model systems.^{8, 9} For example, recent studies of NABs,^{10, 11} their dimers^11–15 and microhydrated NABs^{16, 17} illuminated the effects on different noncovalent interactions on IEs and hole delocalization patterns in ionized species. It was found that both π-stacking and h-bonding can reduce IEs by 0.4–1.0 eV via two distinctly different mechanisms.^{11, 14} In π-stacked isomers, the IE reduction is due to the hole delocalization over the extended π-systems. In h-bonded species, large IE reduction is achieved via electrostatic stabilization of the localized hole by its interactions with the dipole moment of the favorably oriented “neutral” moiety.^{11, 14} Similar mechanism is at play in microhydrated species.¹⁶

Microsolvation has been found to decrease the IEs of nucleobases by about 0.1 eV per water molecule,^{17, 18} however, these findings cannot be extrapolated to bulk because, in addition to specific solvent-solute interactions, there are long-range contributions due to electrostatic screening and solvent polarization.^{19, 20}

Solvent effects are expected to lower IEs of nucleobases and stabilize charged phosphate groups (thus increasing their detachment energies) reducing the gap between nucleobases and phosphate IEs suggesting that nucleotide ionization becomes more favorable in water.¹⁹ Ab initio calculations of isolated thymidine using CASPT2 have suggested that the preferred oxidation site in the nucleotide corresponds to the π orbital of the thymine base.²¹ This conclusion has been reassured by recent experimental study by Bradforth and coworkers²² who concluded that NABs are indeed preferred sites for ionization in DNA based on photoelectron measurements of vertical IEs of the pyrimidine nucleosides and DNA in aqueous microjets. This study reported that vertical ionization energy (VIE) of deoxythymidine in water is around 8.3 eV (i.e., red shifted by 0.7–0.9 eV relative to gas phase). Based on DFT and continuum solvent model calculations, the authors concluded that the ionization occurs predominantly from the NAB and not the sugar or phosphate moiety.²²

Due to inherent complexity of the problem causing experimental and computational challenges, there are still open questions regarding the effect of bulk solvation on IEs of the building blocks of DNA. For example, there are still no experimental measurements of VIEs of solvated nucleobases. Most of the computational studies focused on either model microhydrated systems^16,23–25 or employed implicit solvent models^{21,22,26–28} such as polarized continuum model (PCM) lacking the ability to describe specific solvent-solute interactions (e.g., h-bonding). Most of the PCM calculations focused on the adiabatic IEs, although the so-called non-equilibrium PCM has been used to calculate VIEs.²² A recent study²⁹ by Cauët et al have attempted to bridge this gap by modeling the effect of solvent and backbone environment on the lowest VIE of DNA bases by using a quantum mechanics/molecule mechanics (QM/MM) approach that includes explicit solvent-solute interactions (albeit empirically described). They have reported²⁹ unphysically large blue shifts (3.2–3.3 eV) due to the environment, in disagreement with the experiment.^22,30

This work presents calculation of the VIE of thymine in bulk water using explicit first-principle treatment of the solvent and high-level ab initio description of the solute. We employ a hybrid quantum mechanics/effective fragment potential (QM/EFP) approach, which is similar to QM/MM but does not rely on empirical force fields. The ab initio or QM part consists of the thymine molecule described by equation-of-motion ionization potential coupled-cluster with single and double substitutions (EOM-IP-CCSD).^31–36 The water-thymine interactions are described by effective fragment potential (EFP) which includes Coulomb interactions with multipoles as high as octopoles as well as self-consistently calculated polarization.^37–40

We benchmarked the performance of the EOM-IP-CCSD/EFP scheme against full EOM-IP-CCSD using microhydrated structures. The errors were found to be less than 0.01–0.02 eV. We also investigated the relative importance of the polarization and higher multipole moments in EFP model and found that multipoles up to quadrupoles and polarization effects are very important for capturing solvent-induced shifts in IEs.

We found that bulk solvation results in a red shift of thymine’s VIE of about 0.9 eV, in agreement with the findings of Bradforth and coworkers.²² Our calculations revealed the importance of both specific solvent-solute interactions and long-range solvent polarization. We demonstrate that the overall solvent shift is a result of several opposing effects. While microsolvation reduces the IE by about 0.1 eV per water molecule, the combined effect of the first solvation shell is the IE increase by 0.1 eV. The subsequent solvation shells lower the IE slowly approaching the bulk value. Thus, neither implicit solvent models nor QM/MM with non-polarizable force fields capture the correct physical picture of solvation.

The structure of the paper is as follows. Sections 2 and 3 describe the methodology employed and computational details. Section 4 presents our results and discussion including the benchmark results for microsolvated systems (Sec. 4.1), calculations on model systems quantifying the effects of individual hydrogen-bonds (Sec. 4.2) and bulk hydration (Sec. 4.3).

2 Methodology

EFP coupled with EOM-IP-CCSD allows reliable calculation of solvated ionized species. EOM-IP-CCSD^31–36 is a method of choice for ionized systems as it is free from spin-contamination, artificial symmetry breaking and self-interaction errors that plague many other electronic structure methods. EOM-IP-CCSD has been successfully applied to study a variety of ionized species.^{11–15,35,41–44} EOM-IP-CCSD describes problematic target open-shell wave functions by Koopmans-like operators acting on well-behaved closed-shell reference states.^31–36 EOM-IP-CCSD simultaneously includes dynamical and non-dynamical correlation, describes multiple electronic states in one calculation, and treats the states with different number of electrons on the same footing.

Unfortunately, the computational cost of EOM-IP-CCSD calculations increases as N⁶ with the system size, which makes the calculations of bulk solvation prohibitively expensive. Thus, an approximate description of the environment is necessary. This can be achieved by the EFP approach^37–40 which is similar to a popular QM/MM scheme but does not involve any empirical parameters. EFP is an explicit (or discrete) solvent model that includes the effect of Coulomb (multipoles up to octopoles obtained by Stones distributed multipole analysis^45,46) and polarization interactions (see Ref. 40 for details on the EFP implementation employed in this study).

The effect of the environment (water) on the QM subsystem (thymine) is included via a perturbative technique (electronic embedding) in which the perturbed Hamiltonian of the QM system is:

$$\widehat{H}={\widehat{H}}_0+\widehat{V},$$ (1)

and the perturbation V̂ is given by:

$$\widehat{V}={\displaystyle \sum _{p,q}{\displaystyle \sum _A({\displaystyle \sum _{k\in A}{d}_{pq}\langle p|V_k|q\rangle +{\displaystyle \sum _{I\in A}\langle p|\frac{Z_I}{R}|q\rangle ),}}}}$$ (2)

where p,q are the atomic orbitals in the ab initio region, A is an effective fragment, k denotes the multipole or polarization points depending on V_k, and I denotes nuclei in the fragment.

The induced dipoles of the effective fragments are iterated until self-consistency with each other and with the electronic wave function. Dispersion and exchange-repulsion interactions between the ab initio region and the effective fragments are treated similarly to the fragment-fragment interactions, i.e., as additive corrections to the total energy. Thus, the total ground-state (or, more precisely, reference-state) energy of the QM/EFP system is:

$$E_{\text{gr}}^{\text{QM}/\text{EFP}}=\langle {\mathrm{\Phi }}_{\text{gr}}|{\widehat{H}}_0+{\widehat{H}}^{\text{Coul}}+{\widehat{H}}_{\text{gr}}^{\text{pol}}|{\mathrm{\Phi }}_{\text{gr}}\rangle +E_{\text{Coul}}+E_{\text{pol},\text{gr}}+E_{\text{disp}}+E_{\text{exrep}}$$ (3)

where Φ_gr is the reference-state wave function, Ĥ^Coul and ${\widehat{H}}_{\text{gr}}^{\text{pol}}$ are Coulomb and polarization EFP contributions to the Hamiltonian (subscript “gr” means that the induced dipoles corresponding to the electronic density of the reference state, which is often referred to as “ground state”, are used). E_Coul is the electrostatic EFP-EFP energy; E_exrep and E_disp include the exchange-repulsion and dispersion energies of both the EFP-EFP and the ab initio-EFP regions. E_pol,gr is the self-consistent ground-state polarization energy of the QM/EFP system given by the following expression:

$$E_{\text{pol},\text{gr}}=-\frac{1}{2}{\displaystyle \sum _k{\displaystyle \sum _a^{x,y,z}{\mu }_a^k(F_a^{\text{mult},k}}}+F_a^{\text{nuc},k})+\frac{1}{2}{\displaystyle \sum _k{\displaystyle \sum _a^{x,y,z}{\tilde{\mu }}_a^k{F}_a^{\text{ai},k},}}$$ (4)

where F^mult and F^nuc are the fields due to the static fragment multipoles and the nuclei of the quantum region; F^ai is the field due to the electronic density of the reference (Hartree-Fock, HF) state. μ^k and μ̃^k are the induced dipole and the conjugated induced dipole at the distributed polarizability point k. Note that the polarization contributions appear both in the quantum Hamiltonian through Ĥ^pol:

$${\widehat{H}}^{\text{pol}}=-\frac{1}{2}{\displaystyle \sum _k{\displaystyle \sum _a^{x,y,z}\frac{({\mu }_a^k+{\tilde{\mu }}_a^k)a}{R^3}}},$$ (5)

and in the EFP energy as E_pol,gr.

The derivation and the programmable expressions of all EFP terms were discussed in the previous EFP papers.^38,47–50 The details of the implementation used in this study can be found in Ref. 40.

In the EOM-IP-CCSD/EFP calculations, the reference-state CCSD equations for the cluster amplitudes T are solved with the HF Hamiltonian modified by the electrostatic and polarization contributions due to the effective fragments, Eq. (1). The induced dipoles of the fragments are frozen in the coupled-cluster calculation. Such treatment, in which the dipoles are not reoptimized for the coupled-cluster wave function, is justified when the HF density provides a good zero-order approximation to the electron density of the coupled-cluster wave function and, consequently, the electric fields due to these densities are similar. For the systems considered in this work, the errors due to the neglect of the electron correlation contribution to the EF polarization were estimated to be less than 0.001 eV.

In EOM-CCSD, the target states energies, E_k, are found by diagonalizing the similarity-transformed Hamiltonian H̄ ≡ e^−T H e^T:

$$\overline{H}{R}_k=E_k{R}_k,$$ (6)

where R_k is the excitation operator (with respect to the reference state Φ₀) describing k-th target state In EOM-IP, the reference and target states have different number of electrons and the operator R is of a Koopmans-like type.

The transformed Hamiltonian H̄ includes Coulomb and polarization contributions from the EFP part. As H̄ is diagonalized (using Davidson iterative procedure) in an EOM calculation, the induced dipoles of the effective fragments are frozen at their reference-state values, i.e., the EOM equations are solved in a constant EFP field. To account for solvent response to electron rearrangement in the EOM target states (i.e., due to excitation or ionization), a perturbative non-iterative correction is computed for each EOM root as follows. The one-electron density of each target EOM state (excited or ionized) is calculated and used to re-polarize the environment, i.e., to recalculate the induced dipoles of the EFP part in the field of this EOM state. These dipoles are used to compute the polarization energy corresponding to this state.

Following Ref. 39, the total energy of the ionized state with the inclusion of the per - turbative response of the EFP polarization is:

$$E_{\text{IP}}^{\text{QM}/\text{EFP}}=E_{\text{IP}}+\mathrm{\Delta }{E}_{\text{pol}},$$ (7)

where E_IP is the energy found from Eq. (6) and ΔE_pol has the following form:

$$\mathrm{\Delta }{E}_{\text{pol}}=\frac{1}{2}{\displaystyle \sum _k{\displaystyle \sum _a^{x,y,z}[-({\mu }_{\text{ex},a}^k-{\mu }_{\text{gr},a}^k)(F_a^{\text{mult},k}+F_a^{\text{nuc},k})}}+({\tilde{\mu }}_{\text{ex},a}^k{F}_{\text{ex},a}^{\text{ai},k}-{\tilde{\mu }}_{\text{gr},a}^k{F}_{\text{gr},a}^{\text{ai},k})-({\mu }_{\text{ex},a}^k-{\mu }_{\text{gr},a}^k+{\tilde{\mu }}_{\text{ex},a}^k-{\tilde{\mu }}_{\text{gr},a}^k)F_{\text{ex},a}^{\text{ai},k}],$$ (8)

where $F_{\text{gr}}^{\text{ai}}$ and $F_{\text{ex}}^{\text{ai}}$ are the fields due to the reference (HF) state and the excited-state electronic densities, respectively. ${\mu }_{\text{gr}}^k$ and ${\tilde{\mu }}_{\text{gr}}^k$ are the induced dipole and conjugated induced dipole at the distributed polarizability point k consistent with the reference-state density, whereas ${\mu }_{\text{ex}}^k$ and ${\tilde{\mu }}_{\text{ex}}^k$ are the induced dipoles corresponding to the excited state density

The first two terms in Eq. (8) describe the difference of the polarization energy of the QM/EFP system in the ionized and ground electronic states; the last term is the leading correction to the interaction of the ground-state-optimized induced dipoles with the wave function of the excited state.

As discussed in detail in Ref. 39, the EOM states have both direct and indirect polarization contributions. The indirect term comes from the orbital relaxation of the solute in the field due to induced dipoles of the solvent. The direct term given by Eq. (8) is the response of the polarizable environment to the change in solute’s electronic density upon excitation. Unlike EOM-CCSD/EFP for the excitation energies, the direct polarization contribution in EOM-IP-CCSD/EFP can be very large (up to 0.7 eV for the systems considered in this study) since the electronic densities of the neutral and the ionized species are very different.

An important advantage of the perturbative EOM/EFP scheme described above is that it does not compromise multi-state nature of EOM and that the electronic wave functions of the target states remain (bi-)orthogonal to each other since they are obtained with the same (reference-state) field of the polarizable environment. This would not be the case if polarization of the environment were treated fully self-consistently with the density of each electronic state.⁵¹

3 Computational details

The equilibrium geometries of microhydrated thymine clusters optimized by RI-MP2/cc-pVTZ are from Ref. 16 (the structures are also given in supplementary materials). These structures were used in the EOM-IP-CCSD calculations with the cc-pVTZ and 6–31+G(d) basis sets. The RI approximation was used in the former calculations.

In the QM/EFP calculations, the QM region consisted of the thymine molecule and was described by EOM-IP-CCSD/6–31+G(d). The water molecules were treated as effective fragments.

The EOM-IP-CCSD/EFP calculations were carried out using Q-Chem.⁵² The EF potentials of water are from the Q-Chem fragment library.⁴⁰ These potentials were computed by using GAMESS⁵³ following the protocol⁵⁴ described in Ref. 40.

In the model systems, the structure of the thymine molecule was frozen at its equilibrium geometry (optimized by RI-MP2/cc-pVTZ) and the water molecule geometries are taken from the Q-Chem fragment library.

The equilibrium snapshots for thymine in bulk water were generated using molecular dynamics (MD) simulations carried out as follows. The AMBER-parm99SB/TIP3P^55–57 solute-solvent model was employed for the classical MD simulation of thymine and 1544 water molecules. For parm99SB, Restrained Electrostatic Potential fit (RESP) charges were calculated using the antechamber suite of AMBER9 package⁵⁸ following a geometry optimization at the B3LYP/cc-pVTZ level. Periodic boundary conditions were applied treating long range electrostatic interactions with the particle-mesh Ewald technique.⁵⁹ Prior to running production step, water box was allowed to relax. At this stage, position restraints were applied on all atoms of thymine. The following relaxation of the entire system was performed at constant volume periodic conditions. Slow heating of the system up to 300 K was performed during the next 20 ps. Constant temperature (300 K) and constant pressure (1 atm) periodic boundaries were turned on during the production run only. After discarding the first 20 ps of production, the snapshots were taken every 500 fs on a trajectory of 10 ns. Langevin temperature control and the barostat were used whenever it was required for maintaining constant temperature and pressure, respectively. The SHAKE constraints⁶⁰ on hydrogen atoms and 2 fs time step were used during equilibration and production runs. Detailed discussion of this simulation is presented elsewhere.⁶¹

The geometry of the thymine moiety in the MD snapshots is slightly different from the optimized gas-phase structure however, the effect on VIE is small, e.g., the average VIE of thymine at the geometries from the MD snapshots (averaged over 20 snapshots) is 8.91 eV versus 8.97 eV of the gas-phase structure [EOM-IP-CCSD/6–31+G(d)]. Thus, the effect of structural fluctuations of thymine’s about −0.06 eV.

The IEs were calculated using EOM-IP-CCSD/6–31+G(d)/EFP with the EFP parameters described above.⁶²

4 Results and Discussions

4.1 Benchmark calculations of thymine microhydrates

Table 1 compares the values of the lowest VIE of microsolvated thymine computed by EOM-IP-CCSD/EFP and full EOM-IP-CCSD in the 6–31+G(d) basis set. The errors in IEs due to EFP approximation are less than 0.02 eV. Moreover, the correct ordering of the IEs in the different structures is preserved in the EFP calculations. Another important point is that the errors in EOM-IP-CCSD/EFP VIEs remain almost constant when going from one to two water molecules.

Table 1.

VIEs (eV) of microsolvated thymine computed using the EOM-IP-CCSD/EFP, EOM-IP-CCSD/TIP3P and full EOM-IP-CCSD with the 6–31+G(d) basis set.

System	Full IP-CCSD	IP-CCSD/EFP	ΔIE (EFP)	IP-CCSD/TIP3P	ΔIE (TIP3P)
T(H2O) (T1)	8.84	8.85	0.01	8.99	0.15
T(H2O) (T2)	8.88	8.90	0.02	8.89	0.01
T(H2O) (T3)	8.91	8.91	0.00	8.91	0.00
T(H2O)2 (T11)	8.72	8.72	0.00	8.84	0.12

Table 2 demonstrates that the effect of the basis set on the solvent-induced shift in VIE (ΔVIE) is negligible. However, the effect of the basis set on the absolute values of VIEs is considerable, i.e., the difference between the cc-pVTZ and 6–31+G(d) values is about 0.17 eV. Thus, VIE of thymine in water can be reliably computed by combining solvent shifts (ΔVIE) calculated with a smaller basis set and the VIE value of a bare thymine computed with a larger basis set. Using a smaller basis set in solvent-shift calculations allows us to perform extensive sampling over solvent configurations which is important for converged results.

Table 2.

The effect of the basis set on VIE (eV) of microsolvated thymine calculated using full EOM-IP-CCSD. VIE and ΔVIE refer to the vertical ionization energy and change in vertical ionization energy due to solvation. EOM-IP-CCSD calculations are done using the cc-pVTZ and 6–31+G(d) basis sets.

System	VIE	ΔVIE	VIE	ΔVIE
	(CCSD/cc-pVTZ)	(CCSD/cc-pVTZ)	(CCSD/6–31+G(d))	(CCSD/6–31+G(d))
Thymine	9.14	n.a.	8.97	n.a.
T(H2O) (T1)	9.01	−0.13	8.84	−0.13
T(H2O) (T2)	9.05	−0.09	8.88	−0.09
T(H2O) (T3)	9.08	−0.06	8.91	−0.06
T(H2O)2 (T11)	8.89	−0.25	8.72	−0.25

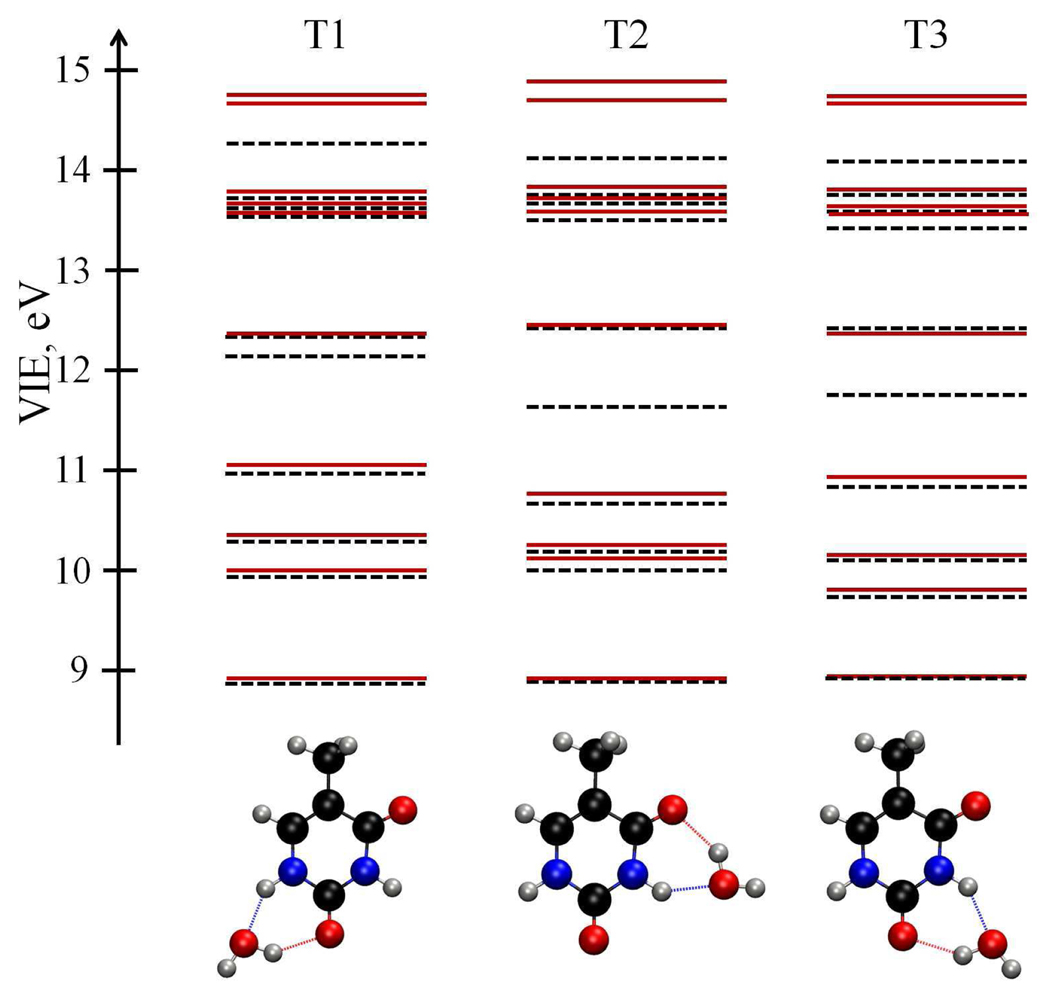
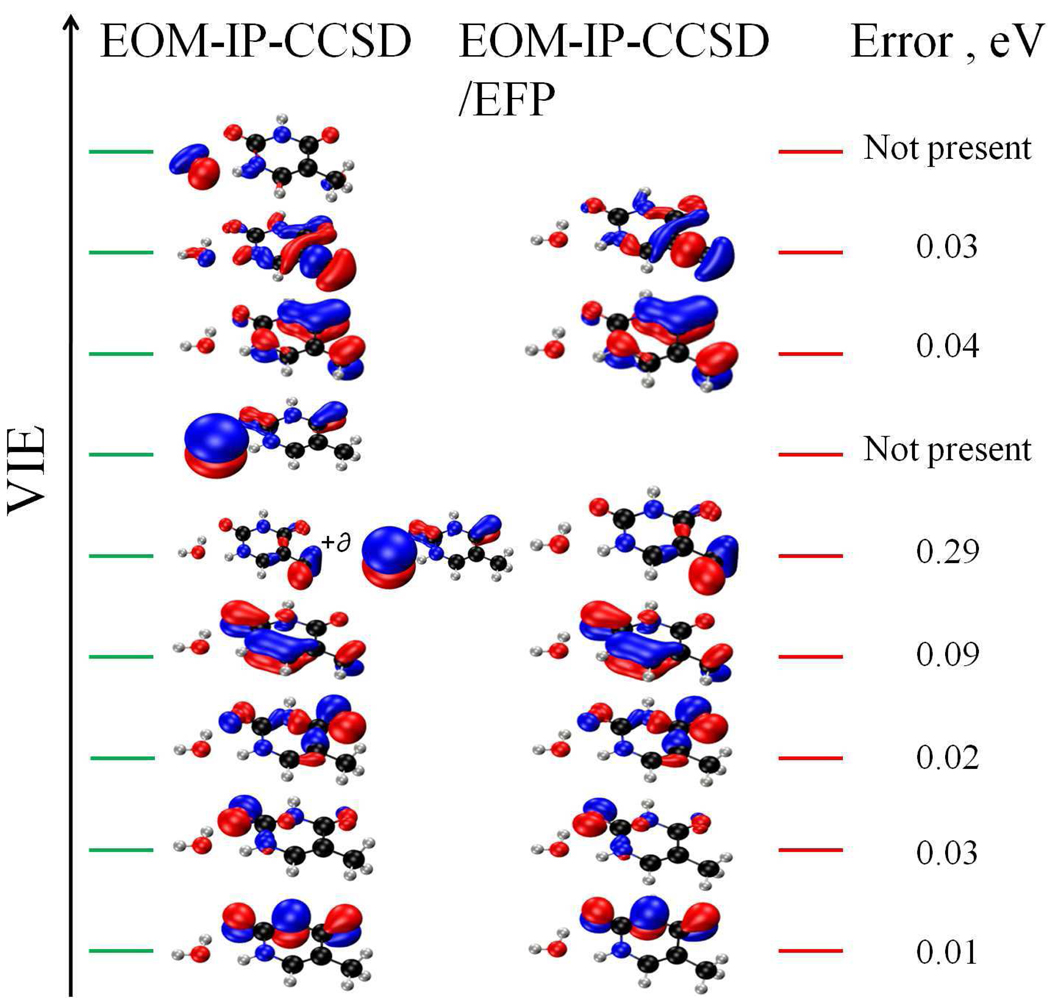
Figure 1 shows the results for higher VIEs. The EOM-IP-CCSD and EOM-IP-CCSD/EFP values agree well below 11.5 eV. The errors increase above 11.5 eV, as we approach the lowest VIE of water (≈ 11–13 eV^{44, 63,64}). As expected, the largest errors are observed for the states that have a significant electron density on the water molecule (see Figure 2). The state corresponding to removing the electron from the water moiety is simply missing in EOM-IP-CCSD/EFP. When the electron hole is delocalized over thymine and water, our separation of the system into the QM and EFP region becomes qualitatively incorrect — the QM/EFP approximation is valid as long as the orbitals (perturbed by the solvent) are localized on thymine. Fortunately, the gap between the IEs of the solute and the solvent provide a guideline for choosing QM/EFP (or QM/MM) separation — the ionized states are localized on the solute as long as they are considerably below the lowest IE of the solvent.⁶⁵

Figure 1.

Higher VIEs (eV) of T(H₂O) calculated using the EOM-IP-CCSD (black dashed lines) and EOM-IP-CCSD/EFP (red lines) methods with the 6–31+G(d) basis set.

Figure 2.

The MOs representing the ionized states of the T1 monohydrate computed by EOM-IP-CCSD and EOM-IP-CCSD/EFP. The errors in IEs due to the EFP approximation are also shown.

4.2 Solvent shifts due to specific integrations

To understand the effect of individual hydrogen bonds at the different sites of thymine as well as the length over which the hydrogen-bond network affects VIE, we considered several model structures with water molecules placed at different parts of the thymine molecule. Note that these structures do not represent equilibrium geometries of microhy-drates (shown in Fig. 1).

4.2.1 The effect of a single hydrogen bond

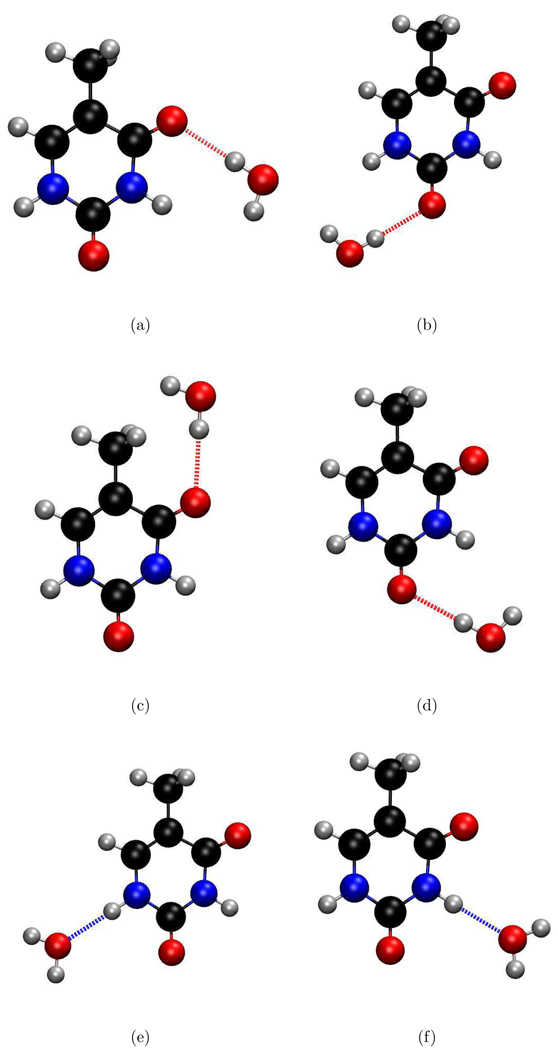
In water-thymine hydrogen-bonding, the water molecules can act as donors or as acceptors. Figure 3 shows the positions of the water molecules with respect to thymine in the model structures constructed to probe the effect of different types of h-bonds on IE. When the water molecule is h-bonded to the NH groups of thymine, it acts as the electron donor and, therefore, reduces the VIE. Likewise, water that is hydrogen-bonded to the carbonyl groups acts as the electron acceptor, thereby increasing the VIE.

Figure 3.

Model structures of thymine with one h-bonded water. Subfigures a,b,c,d refer to the structures with thymine and one water h-bonded to the CO group, whereas e and f refer to the structures with water h-bonded to the NH group.

Table 3 shows the VIE shifts due to water molecules forming h-bonds with the CO and NH groups of thymine. We observe that a single water molecule h-bonded to a carbonyl group increases the VIE by ≈ 0.29 eV while a molecule h-bonded to an NH group reduces the VIE by ≈ 0.34 eV. The magnitude of these opposing effects due to the different types of h-bonds provides a rationale for the observed VIE changes due to microhydration by a single water molecule. In the lowest-energy monohydrates (e.g., T1 structure shown in Figure 1), water is h-bonded to both the CO and the NH group, which yields the red shift of about 0.1 eV. Other microhydrates exhibit similar trend — about 0.1 eV reduction in VIE per water molecule.^16–18

Table 3.

The effect of specific h-bonds on ΔVIE (eV) of thymine using model geometries shown in Figure 3. The errors due to EFP treatment of water are also shown. The CO columns refer to structures a,b,c and d, whereas the NH columns refer to structures e and f.

ΔVIE	CO				NH
Method	a	b	C	d	E	f
Full IP-CCSD	+0.27	+0.30	+0.31	+0.28	−0.39	−0.29
IP-CCSD/EFP	+0.27	+0.30	+0.33	+0.28	−0.40	−0.30
Error	+0.00	+0.00	+0.02	+0.00	−0.01	−0.01

The comparison between the VIEs calculated using EOM-IP-CCSD and EOM-IP-CCSD/EFP (see Table 3) further reinforces the excellent performance of the EFP treatment of water.

In sum, owing to their different nature, the h-bonds to CO and NH groups have opposing effects on VIEs. When water is bound to CO acting as electron acceptor, the VIE increases, whereas electron-donating water bound to NH leads to the IE decrease. These effects of solvent-solute specific interactions cannot be described by continuum solvent models.

4.2.2 The length scale of water-thymine interactions

The h-bond network acts as a conduit for the electrostatic interactions, thereby increasing or decreasing electron density on thymine and, consequently, affecting its IE. To understand the VIE of thymine in bulk water and to obtain a converged result, we need to determine the length scale over which water molecules can affect the VIE of thymine.

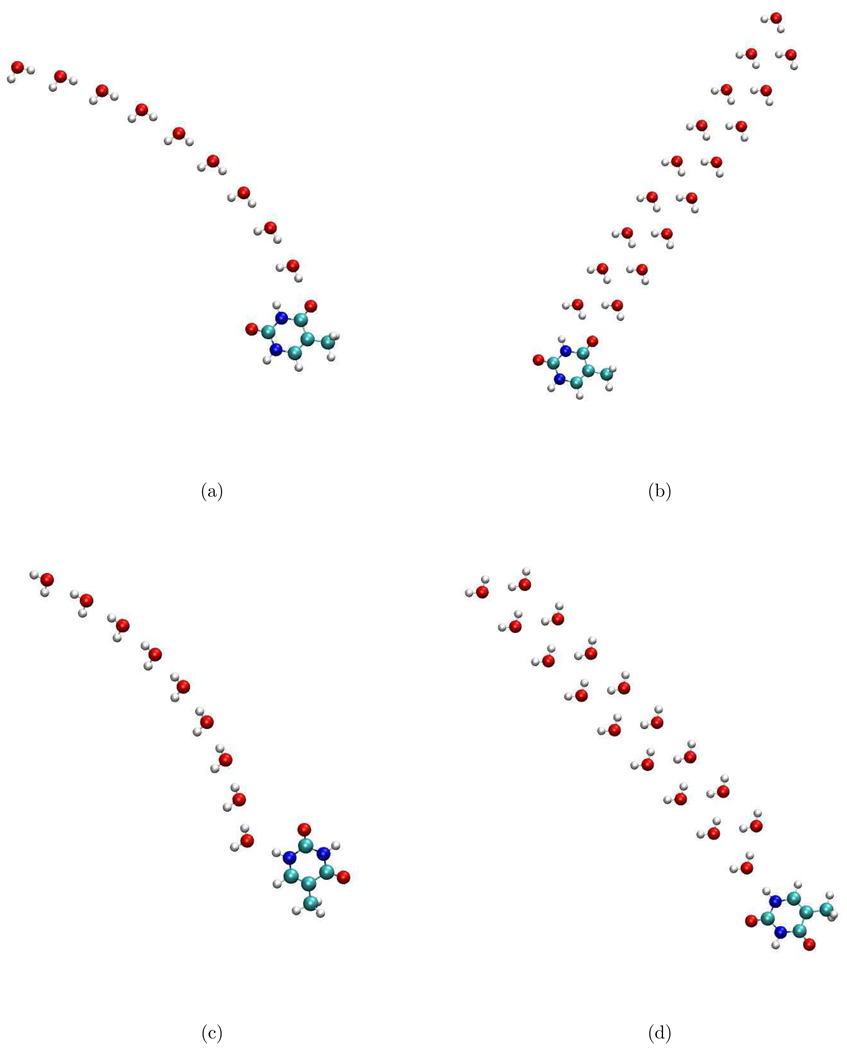
In liquid water, there are instantaneous h-bonds acting as electron density donors or acceptors. These competing effects cancel out quite efficiently obscuring the real length scale of water-thymine interactions. Therefore, to determine the maximum distance over which water can affect thymine’s IE, we considered artificial chains of water molecules enhancing the electron donation/accepting effects. Four such model structures are shown in Figure 4. Model systems a and b are constructed by adding water molecules to the structure with water forming a single h-bond with the CO group. The subsequent waters are h-bonded to the O atom of the preceding water molecule (i.e., acting as h-donors). Model systems c and d are constructed by adding hydrogen-accepting water molecules to the structure with water forming a single h-bond with the NH group.

Figure 4.

Different model structures used to study the length scale of water-thymine interactions.

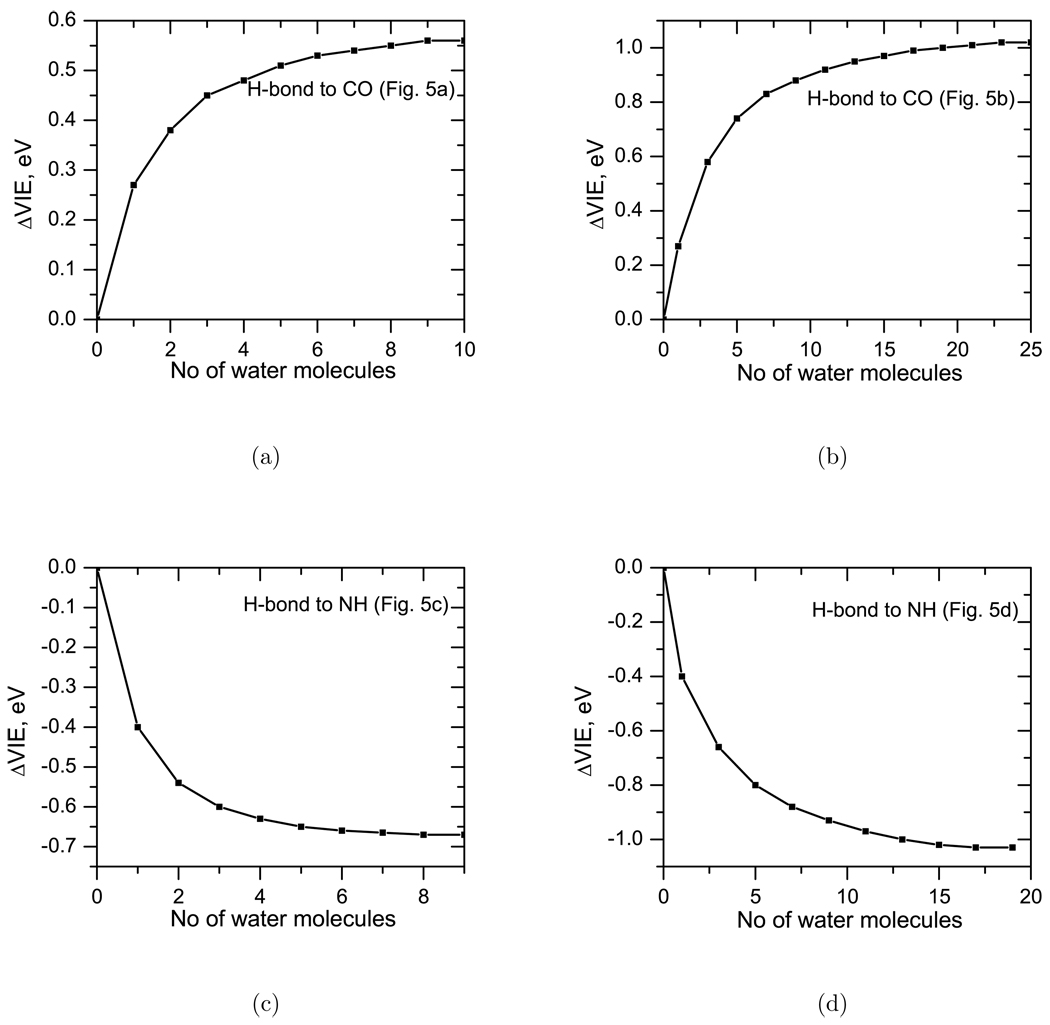
Fig. 5 shows the convergence of VIE with respect to the number of water molecules in these structures. As one can see, the apparent length scale of the interactions is different in these structures. Structure b exhibits the slowest convergence. In general, the structures that have water molecule h-bonded to the NH group of thymine have shorter range of interaction than those in which water is h-bonded to the CO group. Figure 5 shows that the VIEs are affected by up to 9^th and 20^th water molecules in the case of water molecules h-bonded to the NH group, to be compared to 10^th and 25^th water molecules h-bonded to the CO group.

Figure 5.

The shift in VIE (ΔVIE, eV) as a function of number of water molecules in the model structures shown in Figure 4.

These results show that water molecules that are as far as 30 Å away from thymine can affect its VIEs. However, in a disordered system like liquid water, numerous instantaneous opposing interactions cancel out resulting in a reduced apparent interaction length.

4.3 VIE of thymine in bulk water

4.3.1 Convergence to the bulk limit with respect to the system size

The convergence of IEs (or detachment energies, DEs) with respect to the model system size has been shown to be quite slow. For example, the computed DE of iodide increases by about 2 eV when the first solvation shell of iodide (consisting of six water molecules) is encapsulated in a cluster of additional 858 waters.⁶⁶ Even slower convergence of VDE with respect to the model system size was reported in Ref. 29 in which the convergence of VDE of aqueous chloride required using the box size of 30 Å including approximately 1,000 water molecules.

To estimate the minimum box size needed for converged VIE of solvated thymine we computed the VIEs averaged over multiple solvent configurations obtained from MD snapshots including different number of solvation shells.

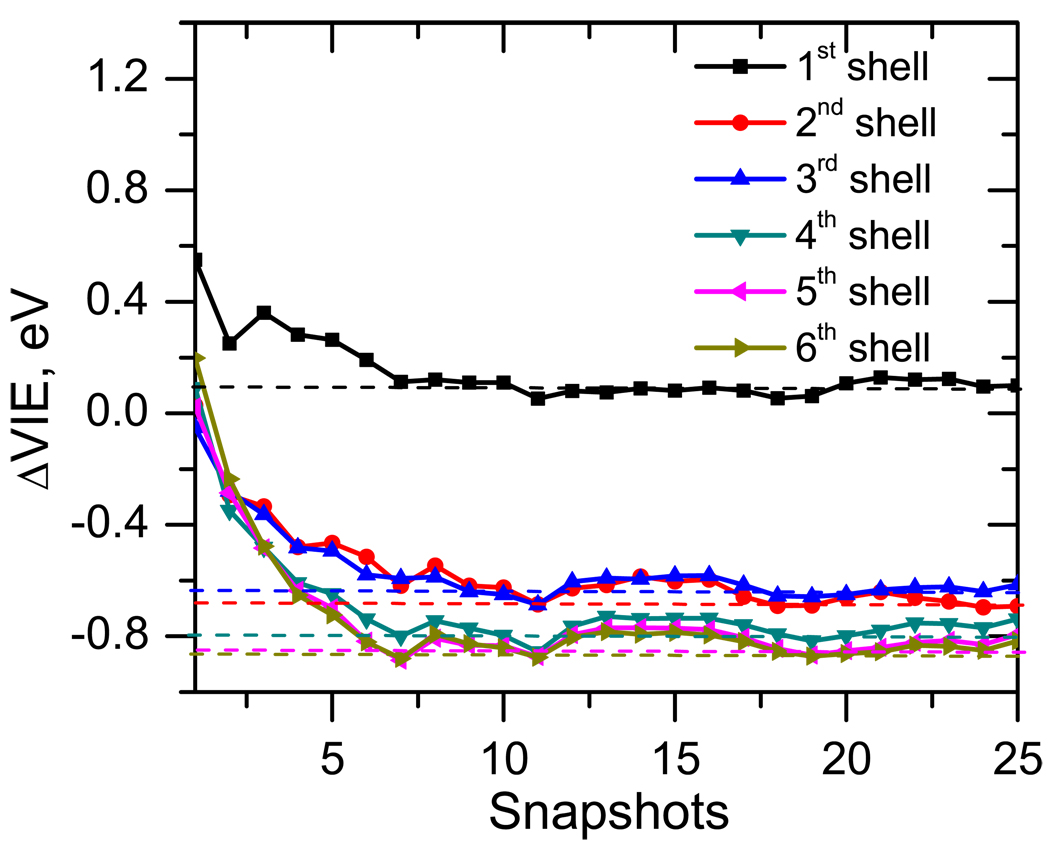
We define solvation shells as follows. The first shell was defined to include water molecules whose H atoms are within of 2.7 Å from the O atoms of thymine and those with O atoms that are within 2.7 Å of the H atoms of thymine. Distance of 2.7 Å was chosen as the cut-off radius based on the position of the first minima in the radial distribution function between NH–O and CO–H. The position of the first minima are at 2.45 Å, 2.65 Å, 2.6 Å and 2.5 Å, respectively (as shown in the supplementary materials). Thus, the first shell was designed to include all water molecules that have a direct h-bond to thymine. The n^th shells are designed to include water molecules with the center of mass within n × 2.7 Å from thymine. With these definitions, the first six hydration shells contain approximately 10, 50, 150, 300, 500, and 800 water molecules.

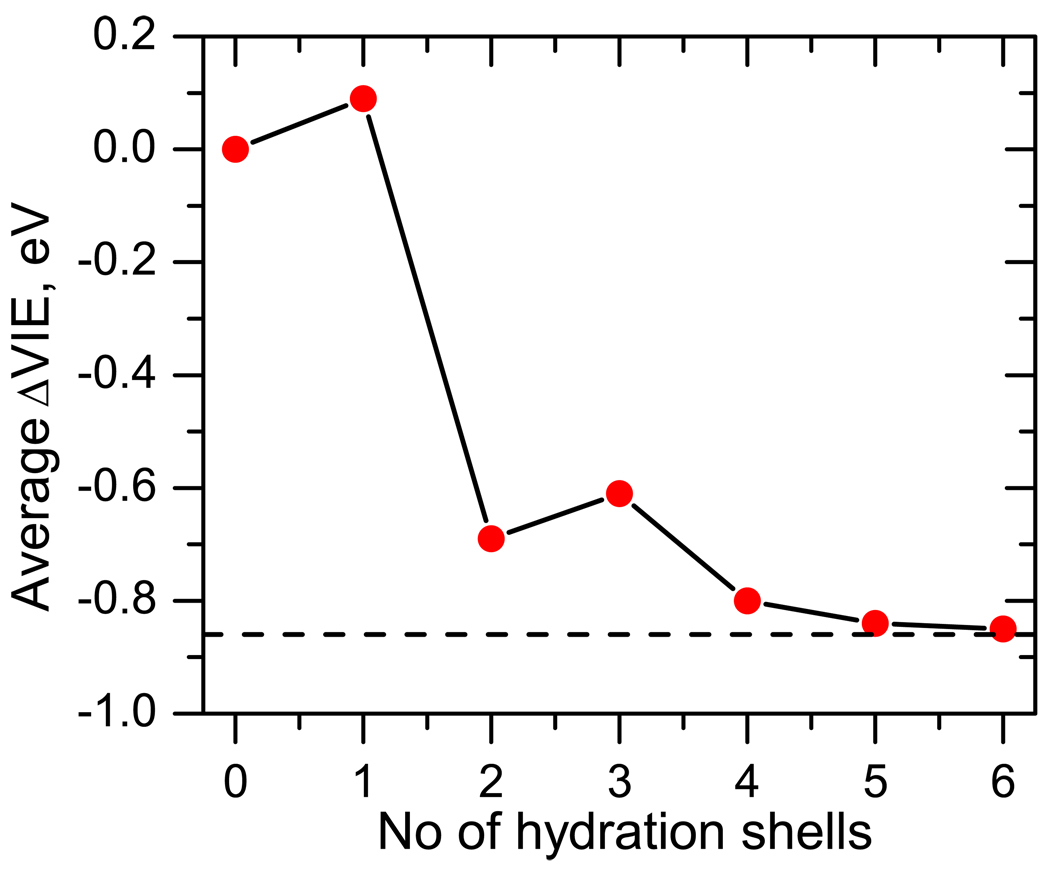
Using this criterion and averaging the IEs over 25 MD snapshots, Figure 6 shows that the IE converges to the bulk value within the fifth shell. Thus, a simulation box of at least 30 Å (2.7 × 5 = 13.5 Å radius around thymine) is required for the converged result. Such sphere contains about 500 molecules. This cut-off radius is very similar to the one observed in Ref. 29, contrary to our expectation that the IEs of the neutral species may be less sensitive to the solvent than DEs of the anions, which exhibit much stronger solvent-induced shifts (several eV are common). Interestingly, the convergence is not monotonous — the first shell increases the IE, whereas the bulk value is lower than the gas-phase IE. The increase of the IE due to the interactions with the first shell is somewhat surprising, in view of the results for microhydrated species in which the IEs were shown to decrease with each water molecule. This finding is explained below.

Figure 6.

Average shift of VIE (ΔVIE, eV) of thymine solvated in n shells of water molecules. The VIE converges around fifth solvation shell.

4.3.2 The effect of the first hydration shell on the VIE of thymine

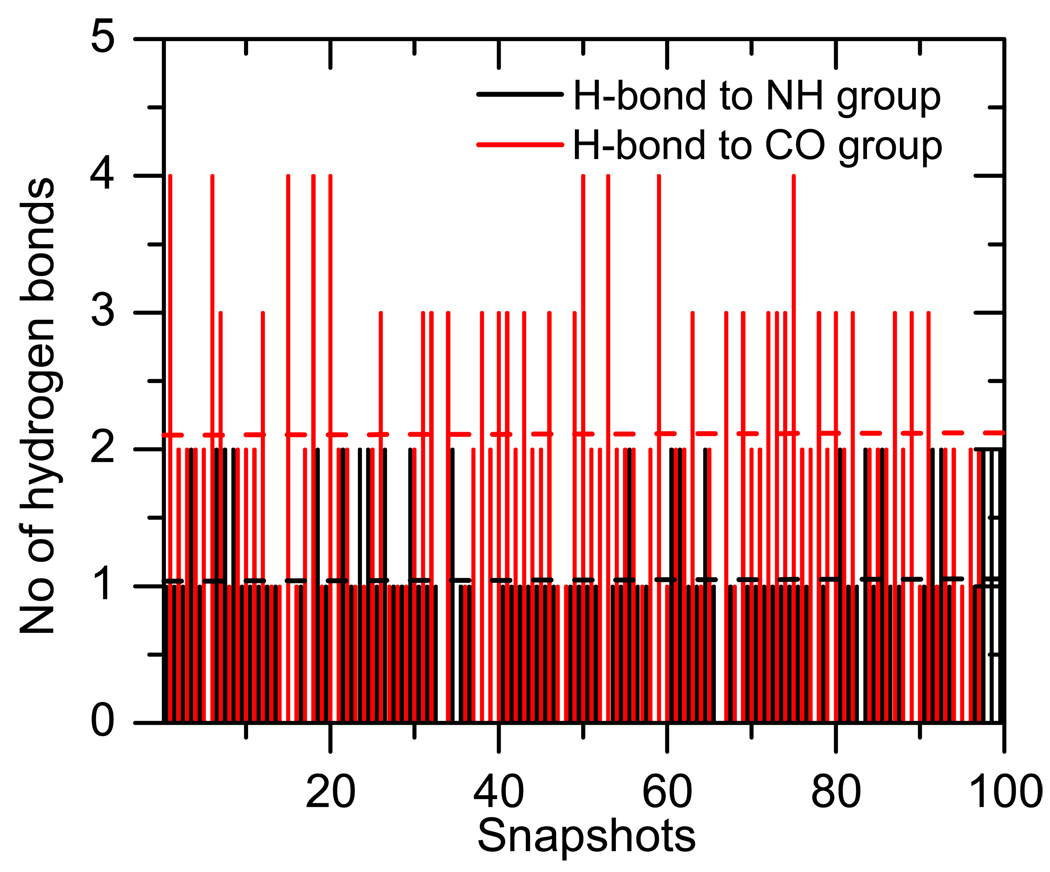
Figure 7 shows the VIE shift due to the first solvation shell. The average ΔVIE is about +0.09 eV relative to the gas-phase value. Taking into account small red shift (− 0.06 eV) due to structural fluctuations of thymine, the solvent-induced shift is 0.15 eV. The increase in VIE can be rationalized by analyzing the instantaneous configurations of waters around thymine in the MD snapshots used for averaging. Figure 8 presents the analysis of instantaneous h-bonds formed at each snapshot. On average, there are 2.1 h-bonds with the CO group and 1.02 h-bonds with the NH moiety of thymine. The average increase in IE due to h-bond to CO (+0.29 eV) is smaller than the decrease in IE due to hydrogen-bond to NH (−0.34 eV), however, since there are more h-bonds to CO than to NH, we observe a net increase in VIE relative to the gas phase value. A simple estimate of the shift based on the average number of different h-bonds and assuming that the effects are additive is +0.2 eV, which is remarkably close to the observed value of +0.1 eV.

Figure 7.

ΔVIE (eV) of thymine due to the first solvation shell. The averaging was performed over the configurations from the MD snapshots until convergence [i.e., when the change in the cumulative average VIE becomes less than 0.05 eV], which required 25 snapshots.

Figure 8.

Number of hydrogen-bonds with the carbonyl and amine groups of thymine from MD snapshots.

To summarize, the first hydration shell increases the VIE, in stark contrast to the observed VIE decrease in microhydrated clusters (Sec. 4.1). This is because in the microhydrates, the water molecules form the maximum number of the strongest h-bonds with thymine in order to form the most stable structure. Typically, such structures are not representative of the true distribution of water molecules around the base, as in bulk water the interaction with other water molecules influences the positions of the water molecules in the first hydration shell. Moreover, the real structure of the first hydration shell at room temperature possesses not static (0 K global minima) but a statistic character. We observe that average coordination number for CO is larger than for NH (2.1 vs. 0.9).⁶¹ Consequently, statistically there are more h-bonds with CO than with the NH group, which leads to the increase in VIE.

4.3.3 The effect of the outer hydration shells (2–6) on VIE

The effect of the subsequent water shells is shown as a function of number of configurations in Figure 9. The cumulative averages of ΔVIE were computed. We notice that after the first hydration shell, all the subsequent shells lower the VIE. Although the convergence is achieved only around fourth or fifth shell, the effect of outer shells is relatively small compared to the first two shells and the VIE computed with the first and second shells is quite close to the bulk value.

Figure 9.

Average shift in VIE (eV) of thymine computed using an increasing number of solvation shells. An increase in VIE due to the first shell of water is reversed when the outer shells are included.

The effect of the subsequent shells on VIE is more difficult to rationalize within a simple statistical picture, as was done for the first shell above, because the h-bond statistics becomes increasingly complicated. Electrostatic interactions, which provide leading contribution to the long range water-solute interactions, are responsible for the observed VIE change due to third-sixth shells.

4.3.4 VIE of thymine in bulk solution

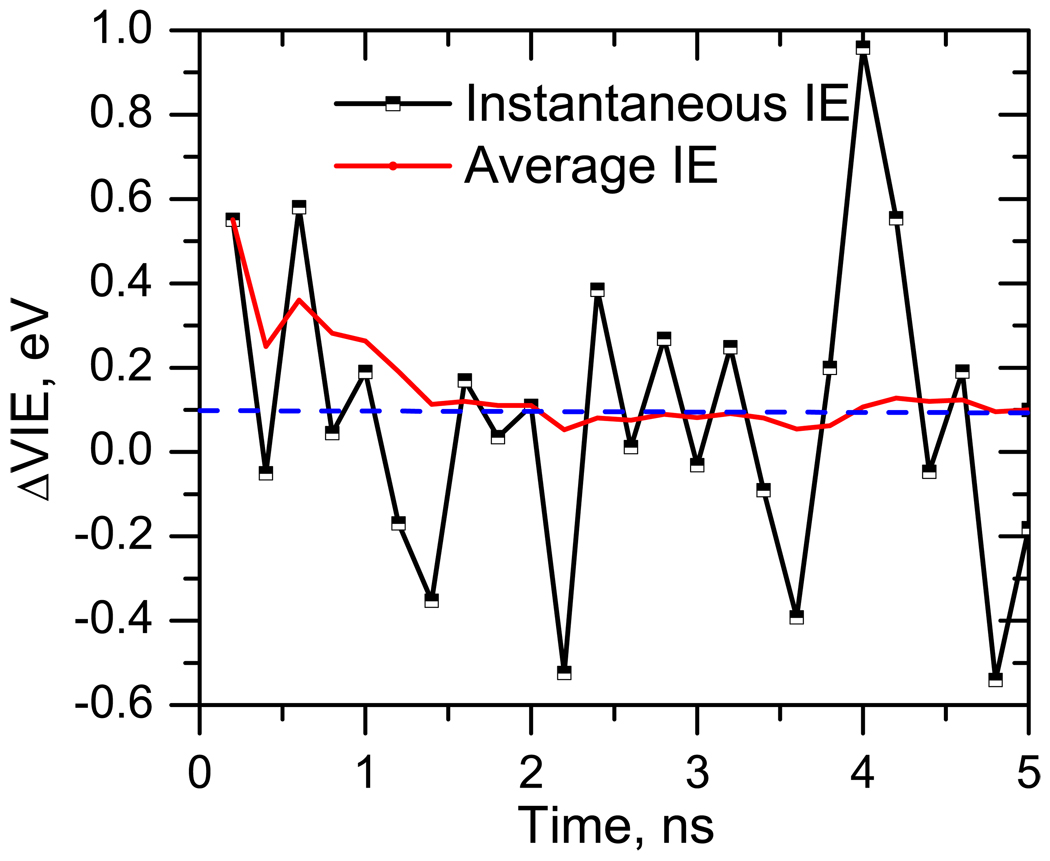
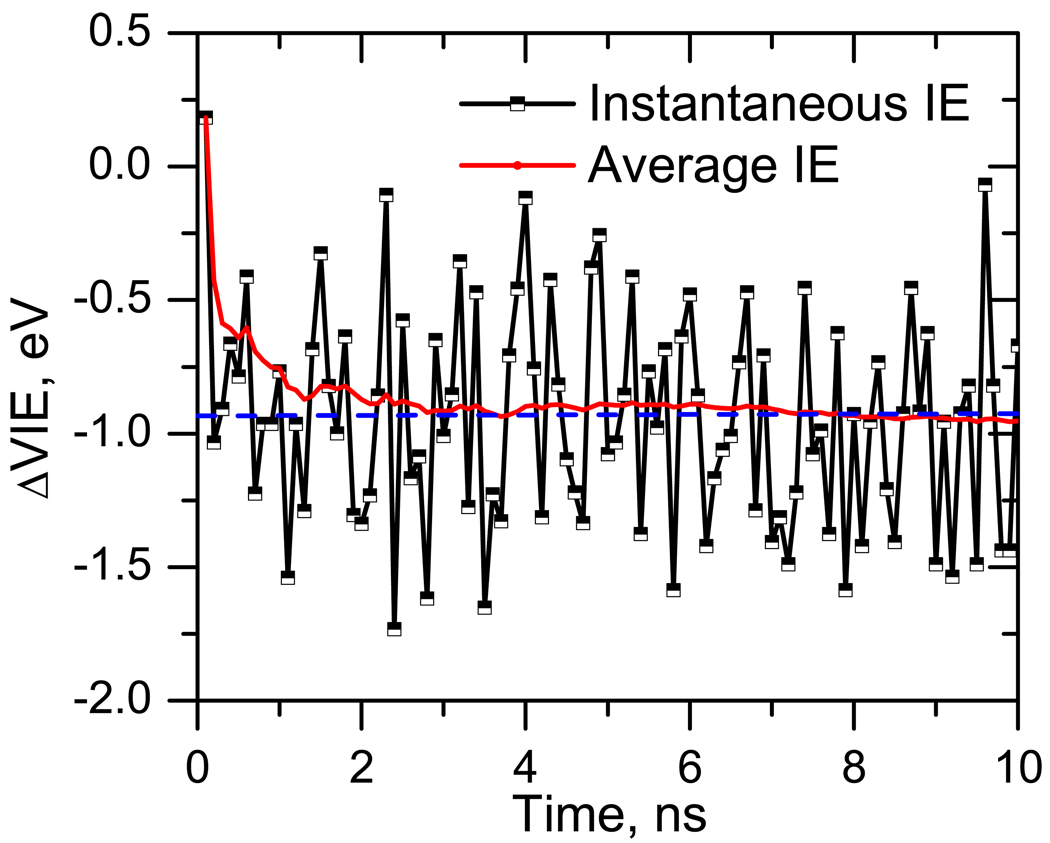
The bulk VIE was calculated by averaging instantaneous VIEs over 100 configurations obtained from 10 ns trajectory at 300 K. All water molecules (≈ 1500) present in the simulation box (36 Å) are included in the EOM-IP-CCSD/EFP calculations.

Figure 10 shows ΔVIEs computed using 100 configurations from the MD snapshots. The average ΔVIE converges around 25–50 configurations. Thus, 100 configurations provide sufficient sampling. The converged solvent-induced VIE shift is −0.9 eV.

Figure 10.

ΔVIE (eV) of thymine in bulk (1500 water molecules in a 36 Å box with one thymine molecule).

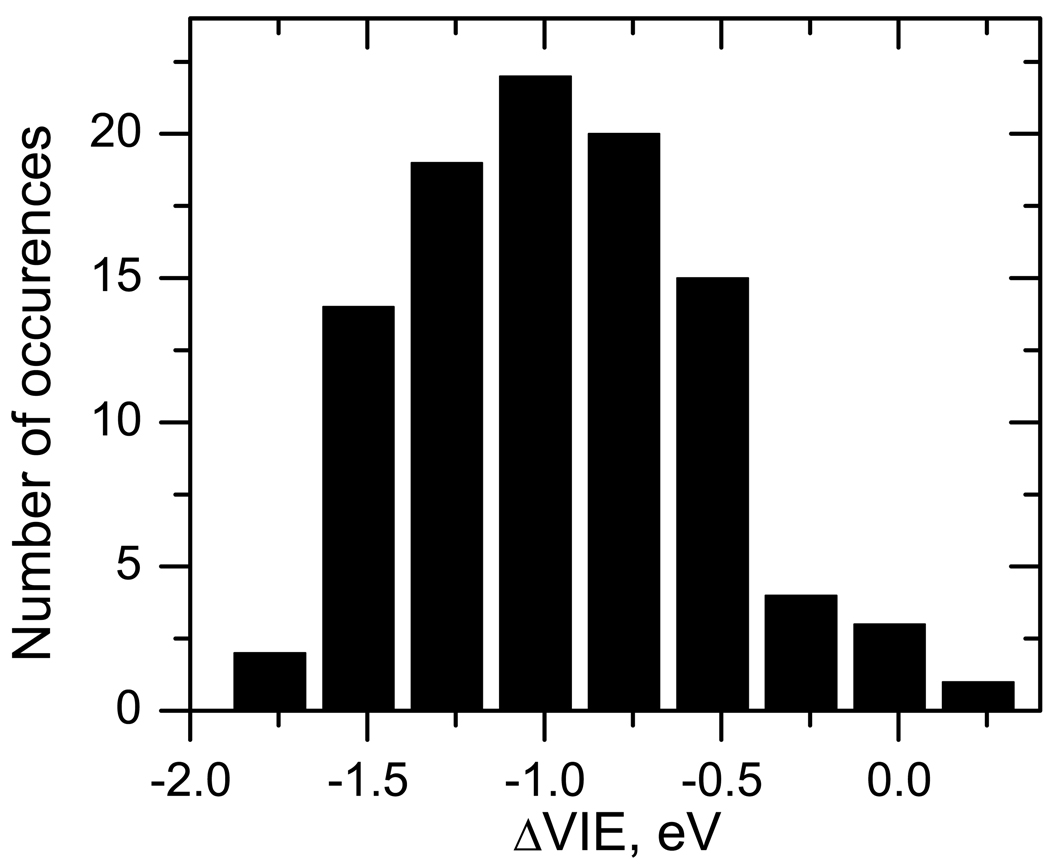
Using QM/MM, Cauët et al²⁹ reported that the combined effect of the environment (water and DNA backbone) on nucleobases leads to the VIE increase of about 3.4 eV. We observe an opposite effect due to solvation, possibly because we are considering only water environment. However, differences in methodology can contribute as well. Using the EOM-IP-CCSD/EFP/6–31+G(d) solvent shifts (ΔVIE) and the gas-phase VIE from the EOM-IP-CCSD/cc-pVTZ calculation, we obtain the VIE of bulk solvated thymine at ≈8.3 eV (9.2 eV −0.9 eV). This is in excellent agreement with the experimentally observed VIE of nucleotides (8.3 eV).²² Figure 11 shows the distribution of the instantaneous ΔVIE of thymine at solvent configurations sampled in liquid water. The shifts are distributed from −1.75 to +0.25 eV. The most probable ΔVIE is −1.0 eV, which corresponds to the peak maximum in the photoelectron spectra of the first band. The lowest observed VIE corresponding to the onset of the first peak is ≈7.45 eV (9.2 eV − 1.75 eV).

Figure 11.

Distribution of instantaneous solvent-induced shift (ΔVIE, eV) in bulk water.

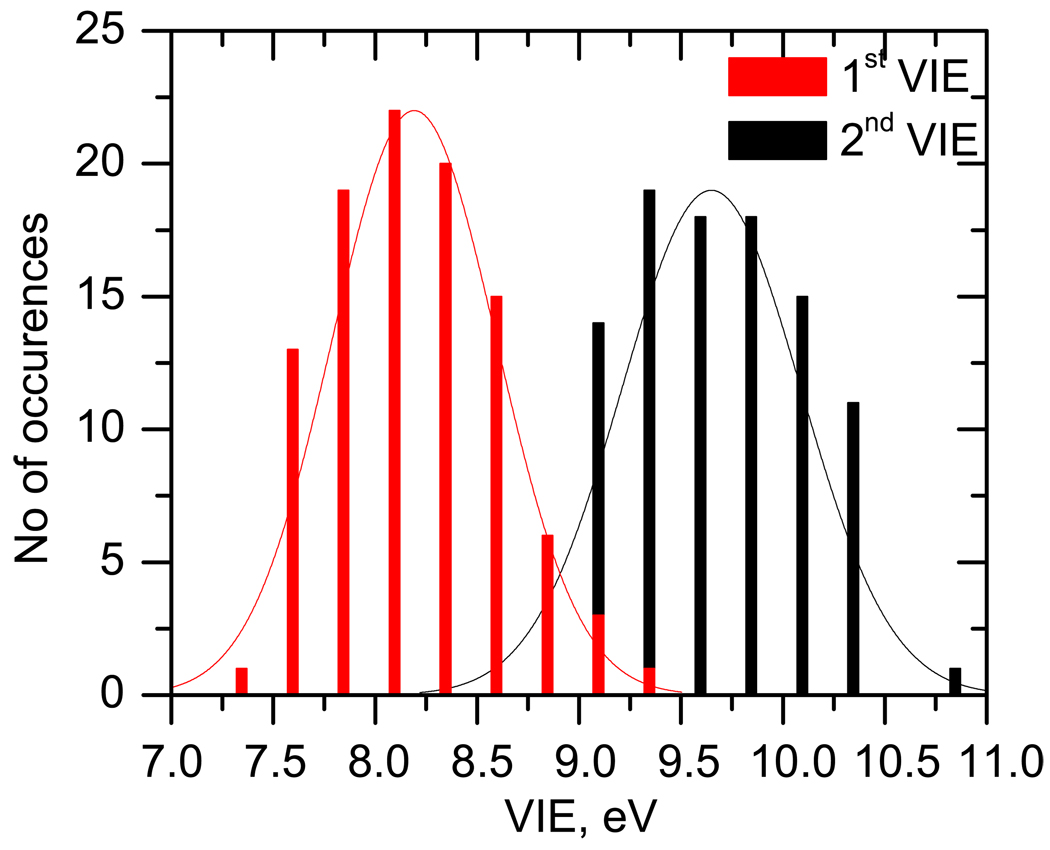
Figure 12 shows the distributions of the instantaneous 1st and 2nd VIEs of thymine in bulk water. We notice that there is some overlap between the two peaks (around 8.5 eV to 9.4 eV). The most probable VIEs corresponding to the first and second band maxima are 8.3 eV and 9.5 eV, respectively. The widths of the peaks due to solvation (full width at half maxima) are ≈ 0.75 eV and 1.0 eV respectively which is in excellent agreement with the experimental spectra.²²

Figure 12.

Simulated peak shapes corresponding to the 1st and 2nd lowest ionized states of thymine in bulk water. Red denotes the distribution of the 1st and black – of the 2nd VIE, respectively.

4.4 The effect of various EFP components on the VIE of thymine

The change in VIEs of the thymine molecule due to water can be analyzed in terms of different components of the EFP potential, i.e., Coulomb (charge, dipole, quadrupole and octopole) and polarization energies. Such analysis is important for understanding the nature of water-thymine interactions. It is also of methodological significance as it may guide the development of new empirical water models and force fields.

The polarization component accounts for 23% of the fragment interaction energies owing to expected strong polarizability of extensive h-bonded systems. This is because polar molecules such as water and thymine which can strongly perturb each others wave functions and their interactions will result in significant charge redistribution. For example, our calculations show that the average dipole moment of thymine in water is 6.5 Debye, to be compared against the respective gas-phase value of 4.1 Debye. Likewise, the dipole moment of water in bulk water increases up to 2.9 Debye (the gas-phase value is 1.85 Debye).⁶⁷ Our calculations also show that the dipole moment of water increases significantly even in microhydrates, e.g., the values for thymine+1H₂O structures are 2.25, 2.45 and 2.35 Debye (in T1, T2 and T3), and in the dihydrate, the water dipole moment is 2.65 Debye. These changes in dipole moment quantify how strongly thymine polarizes the solvating waters.

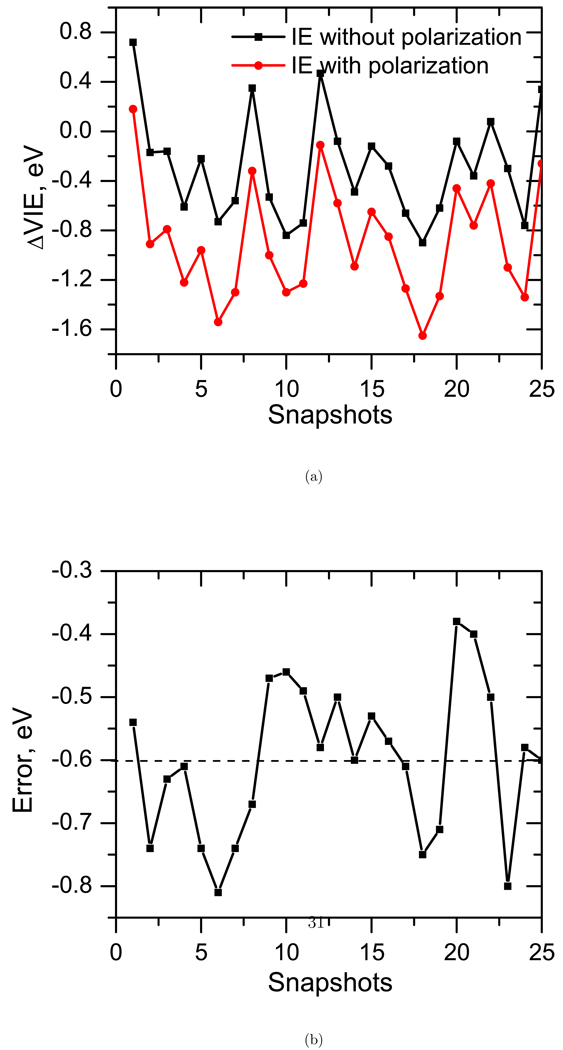
Figure 13 shows the effect of polarization on the VIEs and the error due to the neglect of polarization. We observe errors as high as −0.8 eV (average error is ≈ −0.6 eV). Thus, polarization is crucial for accurate calculations of VIEs in water.

Figure 13.

The effect of polarization on the VIE of thymine in water.

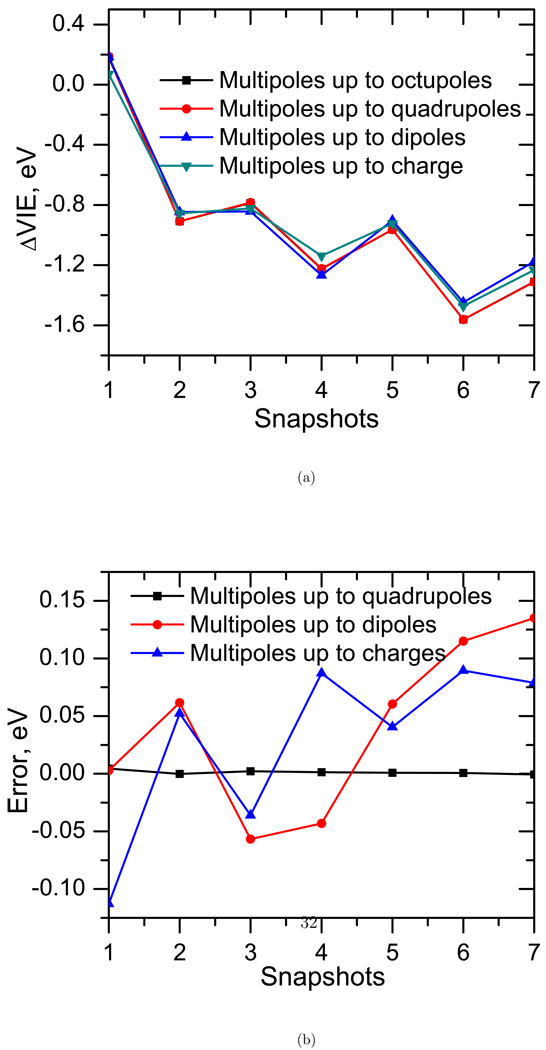
The dipole, quadrupole and octopole components account for 9%, 12% and −0.2%, respectively, of the fragment interaction energies. The errors in the VIEs (see Figure 14) show similar trends due to the neglect of the dipole, quadrupole and octopole moments, respectively. Thus, in this system, multipoles up to quadrupoles are of considerable importance. The effect of octopoles is small. Note that the multipoles used to carry out these benchmark calculations were not re-computed assuming the new truncation of multipoles (i.e., the multipoles are kept constant once calculated using up to octopole expansion).

Figure 14.

The effect of higher multipole moments on the VIE of thymine in water.

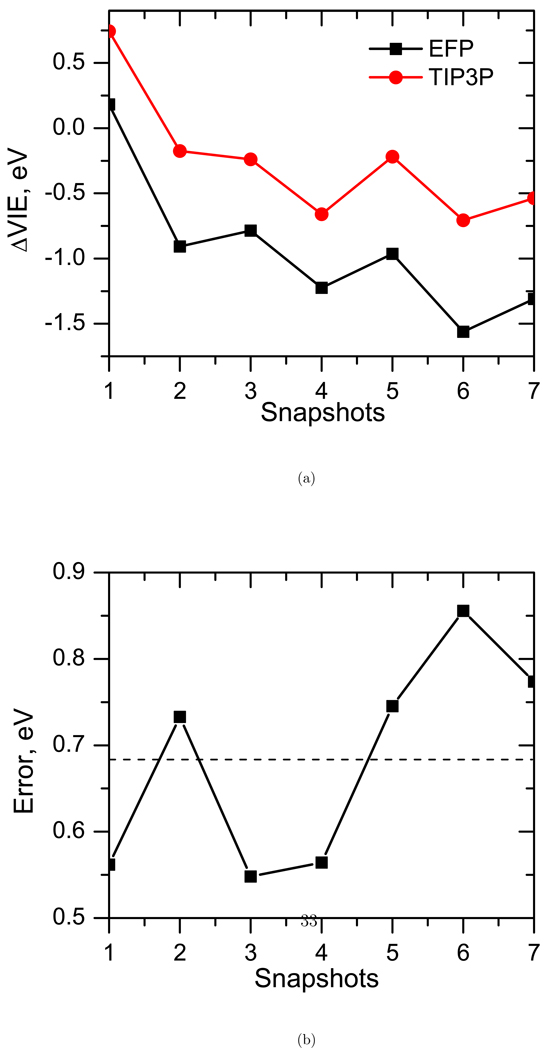
Finally, for the benchmark purposes, we also employed the TIP3P point charges in calculations of VIEs of solvated and microsolvated thymine. Figure 15 shows the ΔVIE due to solvation in TIP3P water compared to the EFP waters and the differences between the respective VIEs. The average error (of the TIP3P VIE relative to EFP) is around 0.68 eV. About 80% of it is due to the neglect of polarization, and the remaining 20% is due to the neglect of higher multipole moments. Table 1 shows the VIEs of microsolvated water calculated with the TIP3P point charges. We notice that the errors can be as high as 0.15 eV in the case of the T1 structure.

Figure 15.

Comparison of VIEs (eV) calculated using EFP (up to octopoles) and TIP3P.

To summarize, we conclude that point charges alone provide a poor description of the water molecules around thymine and higher multipole moments up to quadrupoles and polarization are necessary in order to accurately describe the VIEs.

5 Conclusion

We investigated the effect of microsolvation and bulk water on the lowest VIE of thymine using the EOM-IP-CCSD/EFP method. We benchmarked EOM-IP-CCSD/EFP against full EOM-IP-CCSD for small systems [T(H₂O)_n, n = 1,2]. EOM-IP-CCSD/EFP values agree well with the full EOM-IP-CCSD calculations for VIEs below the lowest VIE of the solvent molecules (11–13 eV for various water clusters^{42–44,63,64}). For the lowest ionized states, the errors are below 0.02 eV. Using TIP3P point charges yields much larger errors even for small systems (about 0.15 eV for monohydrates), which increase with the system size approaching 0.7 eV for bulk water.

Calculations on the model systems demonstrated that the effect of water molecules on VIE depends on whether they form donor or acceptor h-bonds. Thus, a discrete QM/MM method is mandatory for a qualitatively correct description of such systems. The range of solvent-solute interactions and the effect of the various hydration shells also exhibits a delicate interplay of the specific h-bonds and long-range electrostatic/polarization effects. Our results allow us to estimate the smallest system required to understand the bulk effect of the water. We observed the convergence of VIE to the bulk value with respect to the system size by increasing the number of water molecules around thymine. Our data suggest that minimum 4–5 of water shells are needed, which corresponds to the approximately 30 Å simulation box.

We determined that the average value of VIE of thymine in bulk water is reduced by 0.9 eV. Thus, the predicted peak maximum of the lowest ionization band is 8.24 eV. Due to the solvent-induced broadening, the threshold value of the VIE is 7.39 eV. The computed second band maximum is at 9.4 eV. These values are in excellent agreement with the experimental VIE measurements by Bradforth and coworkers²² supporting their conclusion that the phosphate moiety has little effect on the ionized states of nucleobases, possibly due to the screening effects. However, accurate calculations of solvated nucleotides (i.e., using EOM-IP-CCSD/EFP) are required to investigate this phenomenon.

A complete picture of the ionization process requires calculations of adiabatic IEs that involve solvation energy of the electron and re-organization energy of the solvent around the base. Furthermore, other bases should also be investigated, and the effect of the DNA backbone, inter-base interactions, and counterions should be included. This is a subject of a future work.

Table 4.

Average shift and standard deviation of thymine’s VIE (eV) computed using increasin number of solvation shells.

No of solvation shells	ΔVIE	Std. deviation
1	+0.09	0.35
2	−0.69	0.46
3	−0.61	0.37
4	−0.80	0.45
5	−0.84	0.45
6	−0.85	0.44