Application of spectral derivative data in visible and near-infrared spectroscopy

Abstract

The use of the spectral derivative method in visible and near-infrared optical spectroscopy is presented, whereby instead of using discrete measurements around several wavelengths, the difference between nearest neighbouring spectral measurements is utilized. The proposed technique is shown to be insensitive to the unknown tissue and fibre contact coupling coefficients providing substantially increased accuracy as compared to more conventional techniques. The self-calibrating nature of the spectral derivative techniques increases its robustness for both clinical and industrial applications, as is demonstrated based on simulated results as well as experimental data.

1. Introduction

The use of near-infrared (NIR) spectroscopy in functional imaging of soft tissue relies on the low absorption of tissue in the wavelength range of 650–900 nm, and is a widely used method for the measurement of tissue function and scattering properties (Bank et al 1998, Breit et al 1997, Chance 2001, Colier et al 2001, Delpy and Cope 1997, Gopinath et al 1995, Mancini et al 1994, Matcher and Cooper 1994, Tromberg et al 2000, Leung et al 2009, Smith and Elwell 2009). The advantages of NIR spectroscopy include the fact that light–matter interactions in this spectral range are non-ionizing and that data acquisition can be performed on time scales compatible with several industry applications such as pharmaceutical powder (Torrance et al 2004) and polymer analysis (Lachenal 1998). Typically measurements of NIR light epi-illumination and/or trans-illumination at two or more wavelengths are used to determine the spectral absorption and scattering properties of tissue. Spectroscopy technique to date has been used for the study of brain function (Smith and Elwell 2009), breast cancer detection and characterization (Shah et al 2001). Several other studies have combined the use of multiple source and measurement NIR spectroscopy to topographically image brain activation studies (Fantini et al 1999, Taga et al 2003).

Due to recent instrumentation advancements, many current spectroscopy systems are capable of measuring the complete spectrum of reflected and/or transmitted NIR signals following white light excitation with high bandwidth, therefore allowing the acquisition of a comprehensive spectral dataset for the determination of tissue function and structure. In several types of biological tissues the main chromophores contributing to absorption in the NIR are oxyhaemoglobin and deoxyhaemoglobin as well as, to a lesser extent, water. Moreover the intrinsic scattering properties of tissue have been shown to be closely related with bulk tissue scatter size and density (Wang et al 2006). Additionally, through the use of novel spectral imaging techniques, it has been shown that by the direct incorporation of all spectral measurements simultaneously, it is possible to estimate tissue chromophore and scattering properties with improved quantitative and qualitative accuracy (Corlu et al 2005, Eames et al 2008, Srinivasan et al 2005a).

Most spectroscopic measurements rely on pre-measurement calibration routines that are needed to determine source strength and spectral characteristics as well as camera efficiency and in the case of most systems, the calibration due to the optical fibre assembly and tissue contact. However, it is well accepted that fibre and tissue contact varies from case to case and it may not be possible to allow for complete calibration to allow accurate spectral measurement and quantification. These parameters have a parasitic effect for online application resulting in frequent and often difficult model maintenance (re-calibration). Recently, a novel NIR image reconstruction algorithm was developed that aims to recover these fibre/tissue contact coefficients by their direct corporation within the imaging algorithms (Boas et al 2001). However, application of this technique may not be suitable in NIR spectroscopy since the addition of these unknowns can overwhelm the number of parameters recovered.

The use of second differential NIR spectroscopy of water to determine the mean optical path length of the neonatal brain has been previously demonstrated to monitor the absolute cerebral concentration of deoxyhaemoglobin (Cooper et al 1996). Second-derivative preprocessing of data has also been utilized to remove spectral baselines and dc offsets (Arakaki and Burns 1992). Second derivative analysis of visible data (500–650 nm) has been shown to accentuate the differences between myoglobin and haemoglobin spectra and to remove baseline offsets between spectra, and decrease the effect of scattering on the spectra (Arakaki et al 2007). However, in the presence of noise in data, the use of second derivative multi-spectral data can lead to over amplification of noise in the absolute evaluation of tissue function and physiology.

In a previous small animal NIR tomography study, the use of spectral derivative data has been introduced (Xu et al 2005). It was demonstrated that instead of using NIR measurements at each wavelength, when the difference between each neighbouring wavelength is instead utilized, the resulting reconstructed images were insensitive to source and detector coupling and location. In this presented study, the theory and concept of spectral derivative method, as applicable to NIR spectroscopy, is introduced. The underlying theory as to the self-calibrating nature of this technique is presented, together with the algorithm adapted for bulk parameter recovery. Detailed simulated studies are presented whereby the effect of noise on the data is illustrated, together with preliminary experimental data demonstrating the effectiveness of the proposed method.

2. Methods and results

2.1. Semi-infinite frequency domain analytical model

Consider a semi-infinite diffusive medium where scattering dominates over absorption with a physical boundary at z = 0 associated with a finite index of refraction mismatch. For the zero boundary condition, if the real source is at position r_s = (x_s, y_s, z_s), the image source will be at a position r_s′ = (x_s′, y_s′, −z_s′). The excitation diffuse photon density wave is then given by (Li et al 1996)

$$\mathrm{\Phi }(r^{\prime },r_s)=\frac{v{M}_0}{D}\left[\frac{exp(\text{i}k\left|r^{\prime }-r_s\right|)}{4\pi \left|r^{\prime }-r_s\right|}-\frac{exp(\text{i}k\left|r^{\prime }-r_{s^{\prime }}\right|)}{4\pi \left|r^{\prime }-r_{s^{\prime }}\right|}\right],$$ (1)

where Φ(r′, r_s) is the fluence (J cm⁻²) at location r′ due to a source at r_s, v is the speed of light in the medium, $D=v/3{\mu }_s^{\prime }$, ${\mu }_s^{\prime }$ is the reduced scatter, k² = (−vμ_a + iω)/D, μ_a is the absorption coefficient, ω is the modulation frequency (ω = 2π f), and M₀ is the source dc intensity. In order to allow for a diffuse source to be modelled accurately, the location of the real source is modified so that it lies at one reduced scattering distance inside the z = 0 boundary, i.e. at $z_s=1/{\mu }_s^{\prime }$. Additionally, to allow for more accurate incorporation of the boundary condition, the zero-boundary condition is modified to the extrapolated boundary condition, so that the fluence vanishes on an extrapolated outer boundary (Haskell et al 1994). Therefore instead of having a physical boundary at z = 0, an extrapolated boundary condition is imposed at z_e = 2AD where A is the boundary coefficient calculated using Fresnel's law (Schweiger et al 1995). This would lead to a new image source r_s′ at a position placed at $z_s=2z_e+1/{\mu }_s^{\prime }$. Although the frequency domain expression is defined in equation (1), the remainder of the presented work will concentrate on continuous wave measurements for simplicity (intensity only); however, all the presented work is valid for complex measurements.

2.2. Effect of unknown source and detector coupling coefficients

2.2.1. Spectral reflectance data analysis

Consider a set of reflectance spectroscopic point measurements (Y_i,j, for i = 1, …, n, where n is the total number of detectors, and j = 1, …, L, where L is the total number of wavelengths) due to a point source (S) as shown in figure 1. The optical parameters within the volume of interest are given by absorption (μ_a) and reduced scattering coefficients $({\mu }_s^{\prime })$, where ${\mu }_s^{\prime }=(1-g){\mu }_s$ where μ_s is the scattering coefficient and g is the anisotropic factor. The tissue optical properties (absorption and reduced scatter) are a function of the wavelength of the applied source (λ), whose attenuation response depends on the concentration of each chromophore as well as on the scattering properties, as shown in figure 2 (Prahl 2009). Assuming the main absorbers to be oxyhaemoglobin (HbO), deoxyhaemoglobin (Hb) and water, Beer's law can be used to compute overall tissue absorption with reasonable accuracy:

Figure 1.

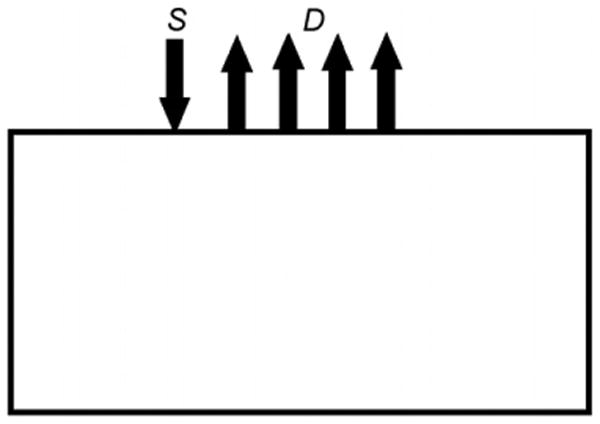
Schematic of the reflectance spectroscopic measurements, where S denotes the source (placed at one scattering distance beneath the boundary) and D denotes the location of the measurements at 50–100 mm away from the source with a 10 mm spacing.

Figure 2.

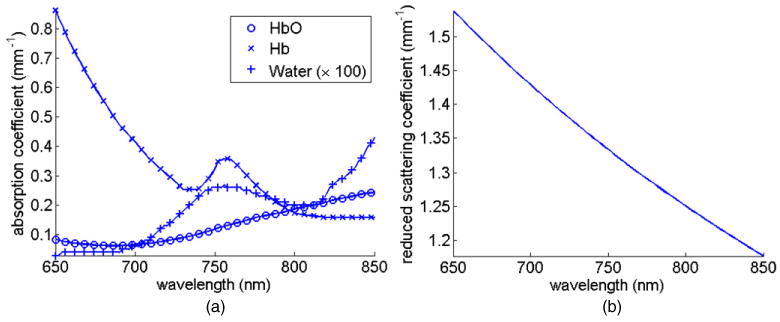
The spectral response of tissue: (a) absorption due to oxyhaemoglobin (HbO), deoxyhaemoglobin (Hb) and water, and (b) reduced scatter based on Mie theory.

$${\mu }_a(\mathrm{\lambda })=\sum _{k=1}^3{\mathit{\varepsilon }}_k(\mathrm{\lambda })c_k,$$ (2)

where ε_k and c_k are the molar absorption spectra and the concentration of the kth chromophore, respectively. The reduced scattering coefficient can be approximated using Mie theory (Mourant et al 1997):

$${\mu }_s^{\text{'}}=a{\mathrm{\lambda }}^{-b},$$ (3)

where a is assumed to be the scattering amplitude and b the scattering power. The coefficient ${\mu }_s^{\prime }$ has units of inverse millimetres, and b is dimensionless so that scatter amplitude has units given by 10^−3b(mm)^b−1 and the wavelength is in micrometre (Srinivasan et al 2005b). Strictly speaking Mie theory is valid when interactions between scatter sites and photons can be considered to be elastic and when the scatter sites are spherical and independent scatter events are considered (Mourant et al 1998, Wang et al 2006). The reflectance measurements at each detector location Y_i,j is then given by a light propagation model:

$$Y_{i,j}=F(c_k,a,b,{\mathrm{\lambda }}_j,r_i),$$ (4)

where r_i is the Euclidian distance of each detector from the source S. The model F used in this work is the semi-infinite analytical expression in equation (1), whereby for each wavelength λ the absorption and scattering coefficients are calculated using equations (2) and (3). The reflectance measurement Y_i,j at each detector location and for each wavelength is proportional to the source power and other coupling factors to the medium, which are absorbed into a multiplicative calibration factor N_S. Similarly a calibration constant N_D applies for the detector gain factors, the coupling coefficients from the medium and the varying filter attenuation factors across the multi-spectral detection domain. Therefore, the detector measurement at each point becomes

$$Y_{i,j}=N_S{N}_{D}F(c,a,b,{\mathrm{\lambda }}_j,r_i).$$ (5)

Typically the source power and coupling coefficient N_S are constant for all detectors (but may also vary spectrally for the un-calibrated system), whereas the detector gain and coupling coefficient N_D can vary by substantial amounts depending on the individual detector contact with the medium as well as the detection optics setup (Boas et al 2001). In an experimental setup, although N_S can be calculated to some accuracy and the data calibrated, these coefficients depend on each volume of interest and can vary substantially from case to case, as well as the intensity of the source may have a spectral dependence.

Consider a case whereby measurements are taken from an experimental setup as depicted in figure 1. Reflectance boundary data Y_i,j (intensity only at 100 MHz) have been calculated for the wavelength range of 650–850 nm using the semi-infinite model based on equation (1) with typical chromophore concentrations of soft tissue consisting of HbO = 0.01 mM, Hb = 0.01 mM, water = 75%, a = 0.87 and b = 1. A source is placed one scattering distance underneath the tissue surface, and detector measurements (henceforth referred to as ‘noise-free’ data) have been calculated at six distances from 50 to 100 mm away from the source. For the ‘noise-added’ data, a linear spectral dependence of the N_S coefficients (90% – 75%, from 650 nm to 850 nm) is assumed with the detector coupling coefficients N_D taking values of 80%, 60%, 90%, 40%, 85% and 91% for detection points placed at 50, 60, 70, 80, 90 and 100 mm, respectively. These simulated noise conditions are under the assumptions that for each specific wavelength, the source strength can vary by an unknown amount (but constant for each source) and for each detector, due to the detector coupling coefficient, the measured intensity can also vary by an unknown amount (but constant for each detector).

Figure 3(a) shows the log intensity plot from both the noise-free and noise-added data for a single detector point at 70 mm away from the source. The large variation seen between the data represents the often unknown N_S coefficient as well as N_D. Nonetheless, it is often well accepted that in order to account for such variation in N_S it is either possible to calibrate the data for the unknown source strength using well-defined phantom experiments, or more commonly in spectroscopic experiments to normalize each data point with respect to measurements at a given detector. In this latter approach, figure 3(b) shows the same data as in figure 3(a) but normalized with respect to detector measurements at 50 mm away from the source. As evident, although such normalization could eliminate the effect of the unknown source strength, it does not however eliminate the effect of the unknown detector coupling coefficients N_D because the two measurements used when ratioing are acquired at different tissue locations. The calculated error between the noise-free and noise-added data can be shown to equal the ratio of the modelled N_D value at detectors 1 and 3, i.e. 12.5%.

Figure 3.

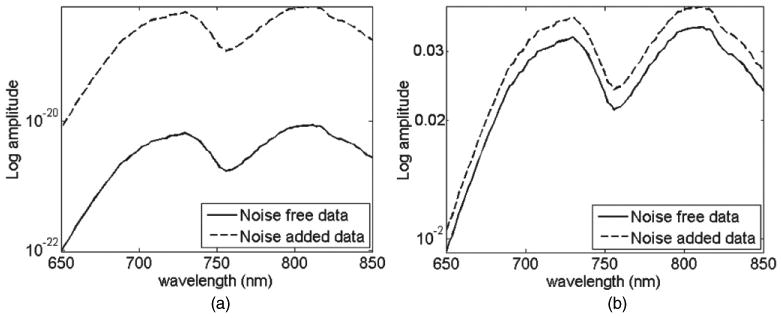
Effect of the unknown source power and coupling coefficient (N_s) on the detector placed 70 mm away from the source: (a) raw un-normalized data and (b) normalized data with respect to the detector at 50 mm away from the source.

Figure 4(a) shows the log intensity plot from both the noise-free and noise-added data for all detectors at a single wavelength of 780 nm. The large variation between the two datasets represents the unknown detector coupling coefficients N_D. As in the previous case, it is possible to normalize the data with respect to measurements at a given detector. In this latter approach, figure 4(b) shows the same data as in figure 4(a) but normalized with respect to detector measurements at 50 mm away from the source. As evident, although such normalization could eliminate the effect of the unknown source strength and N_D at the detector placed at 50 mm, it does not however eliminate the effect of the unknown detector coupling coefficients for all other detectors. It is worth noting that although the mismatched seen appears minimal, the calculated error, figure 4(c), corresponds to the ratio of the unknown N_D factors equalling an error of up to more than 40%.

Figure 4.

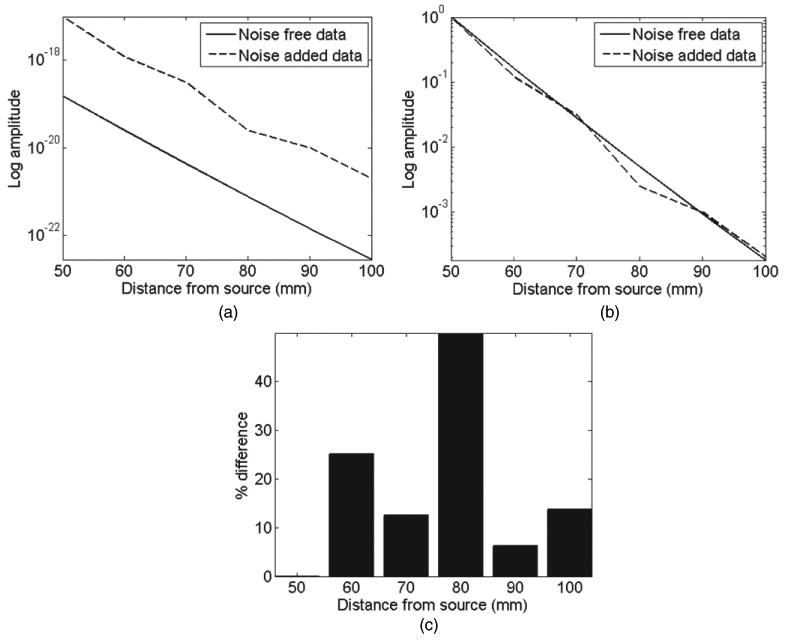
Effect of detector gain factors and coupling coefficients (N_D) at 780 nm: (a) raw un-normalized data and (b) normalized data with respect to the first detector point at 50 mm. (c) Percentage error between normalized noise-free and noise-added data.

2.2.2. Spectral derivative reflectance data analysis

Assuming that the source and detector coupling coefficients have a small spectral dependence, that is N_Sj ∼ = N_Sj+1 and N_Dj ∼ = N_Dj+1, the spectral derivative method can be utilized to account for these unknown coefficients. Equation (5) can be modified such that

$$\frac{Y_{i,j+1}}{Y_{i,j}}=\frac{N_{Sj+1}{N}_{Dj+1}F(c,a,b,{\mathrm{\lambda }}_{j+1},r_i)}{N_{Sj}{N}_{Dj}F(c,a,b,{\mathrm{\lambda }}_j,r_i)}=\frac{F(c,a,b,{\mathrm{\lambda }}_{j+1},r_i)}{F(c,a,b,{\mathrm{\lambda }}_j,r_i)}.$$ (6)

As evident by equation (6), assuming that the coupling coefficients between neighbouring wavelengths are equal, by taking the ratio of each dataset for each detector with respect to its nearest wavelength, it is possible to eliminate the effect of these errors.

Using the same data as in the previous case, figure 5 shows the spectral derivative data (normalized log intensity plot of each wavelength with respect to its next highest wavelength with 2 nm separation) from both the noise-free and noise-added data for a single detector point at 50 and 70 mm away from the source. As shown, despite a non-constant source coupling coefficient, N_Sj, the spectral derivative calculations as derived in equation (6) allow self-calibration of data with respect to both the unknown coupling coefficients. Therefore the use of spectral derivative data should in principle provide a much more accurate information regarding the spectrally dependent optical parameters. The percentage error for the spectral derivative data between the noise-free and noise-added dataset is shown in figure 5(c). It is seen that the maximum error seen is less than 0.2%, which is equal to the linear spectral error variation of N_S.

Figure 5.

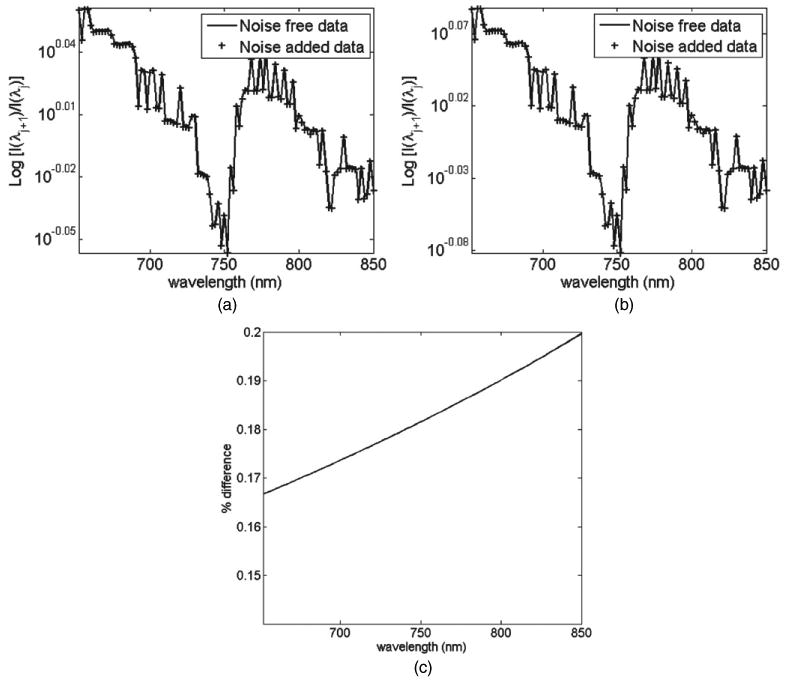
Spectral derivative data for both noise-free and noise-added measurements at (a) 50 mm, and (b) 70 mm distance detectors. (c) Percentage error between normalized noise-free and noise-added data for all detectors.

2.3. Errors due to different models of light propagation

Many models and methods exist for the calculation of boundary data based on some input such as geometry, optical properties and source/detector separation (Arridge 1999, Dehghani et al 2009). Numerical models provide flexibilities in the number of degrees of freedom and they are computationally complex, whereas analytical models, although limited to simple homogeneous cases, are computationally fast and efficient. Assuming that the true spectroscopic data from a domain is given by equation (1), it is possible to express any error due to the model used as α, such that

$$Y_{i,j}={\alpha }_{i,j}F(c,a,b,{\mathrm{\lambda }}_j,r_i),$$ (7)

where α_i,j is the model error coefficient which can be detector dependent and a spectrally varying function. As in the previous example, if we assume that α_i,j+1 ∼ = α_i,j, then using the spectrally derived data, equation (5), it can be shown that the effect of such a scaling factor can be ignored.

As an example, consider the same analytical data used in the previous section. Using the same optical parameters and source/detector geometry, equivalent spectral data were calculated using a 2D and 3D finite element model (FEM) package, NIRFAST (Dehghani et al 2008). A 2D model is used to assess the accuracy of such an approach, since the numerical solutions of 2D models although not as accurate, are much faster than those of 3D. For the 2D model, figure 6, the domain consisted of a slab of length 200 mm and a thickness of 100 mm, with the source placed at one scattering distance on the top face at 50 mm from the left boundary. The 2D FEM mesh consisted of 80 601 nodes corresponding to 160 000 linear triangular elements. For the 3D FEM mesh, figure 7, the domain consisted of a slab with a length (x-axis) of 140 mm, width (y-axis) of 100 mm and depth (z-axis) of 50 mm. The source was placed at one scattering distance on the top face at 20 mm from the left boundary. The 3D FEM mesh consisted of 49 098 nodes corresponding to 263 562 linear tetrahedral elements.

Figure 6.

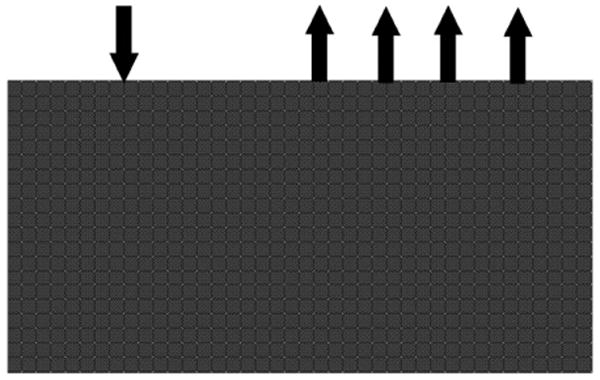
2D FEM mesh used. The arrows indicate the location of the source and detectors.

Figure 7.

3D FEM mesh used with the (a) x−z plane and (b) x−y plane. Note high density mesh resolution in the source/detector locations.

For both the 2D and 3D FEMs, as in the analytical case, detector measurements have been calculated at a 50–100 mm distance away from the source on the same boundary. Figure 8(a) shows the log intensity plot from all the three models for a single detector point at 70 mm away from the source. The large variation seen between the data represents the large mismatch seen between the three models. Figure 8(b) shows the same data in figure 8(a) but normalized with respect to detector measurements at 50 mm away from the source. As evident, although such normalization could eliminate the effect of the unknown model mismatch, it does not however eliminate the effect entirely. The calculated errors between the analytical models and the FEMs are shown in figure 8(c). As seen, the largest error is found with the 2D model at about 18%, whereas the 3D model has errors less than 9%.

Figure 8.

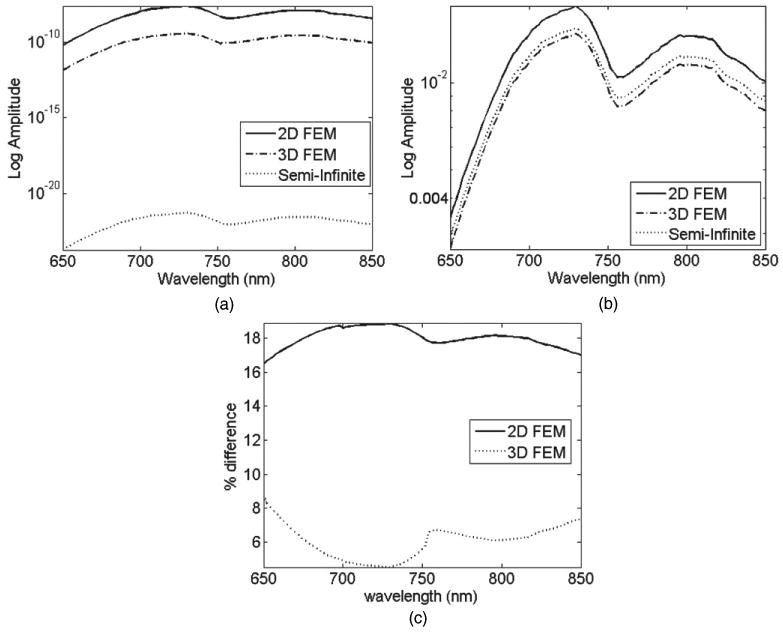
Calculated data using three models for the detector placed 70 mm away from the source: (a) raw un-normalized data and (b) normalized data with respect to the detector at 50 mm away from the source. (c) Percentage error between the FEM and the analytical model.

Figure 9(a) shows the log intensity plot from all models at a single wavelength of 780 nm. Figure 9(b) shows the same data as in figure 9(a) but normalized with respect to detector measurements at 50 mm away from the source, and figure 9(c) shows the calculated error between these data. Large errors can be seen between the FEMs and the analytical models ranging up to 35% with the best results from the 3D model.

Figure 9.

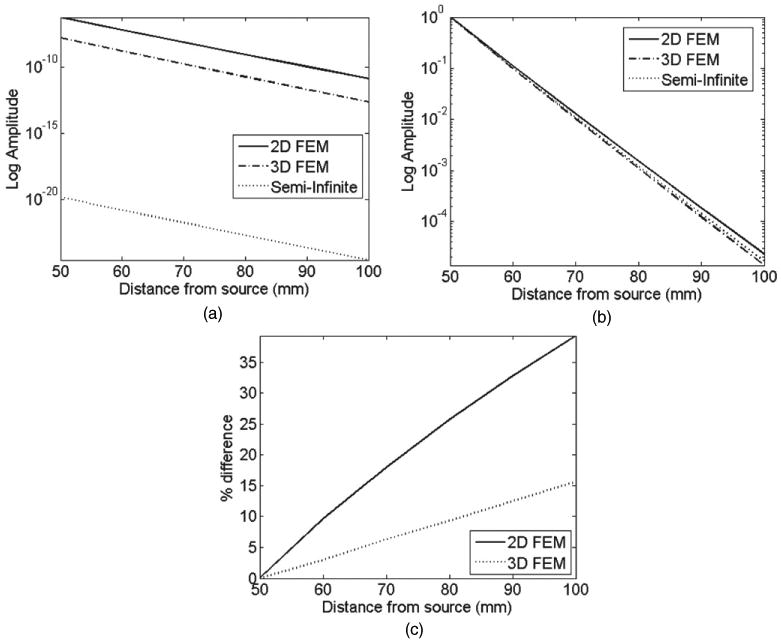
Calculated data using three models for all detectors at 780 nm: (a) raw un-normalized data and (b) normalized data with respect to the first detector point at 50 mm. (c) Percentage error between FEM and analytical models.

Figure 10 shows the spectral derivative data from all models for single detector points at 50 and 70 mm away from the source. As shown, despite the use of three inherently different models, the spectral derivative calculations allow self-calibration of data with respect to both the unknown coupling coefficients and model mismatch parameter. The percentage error for the derivative spectral data between FEMs and analytical models is shown in figure 10(c). It is seen that the maximum error seen for the 3D model is less than 0.3% and less than 0.85% for the 2D model, which is much smaller than those shown in figures 8(c) and 9(c). Therefore the use of spectral derivative data should in principle provide a much more accurate information regarding the spectrally dependent optical parameters.

Figure 10.

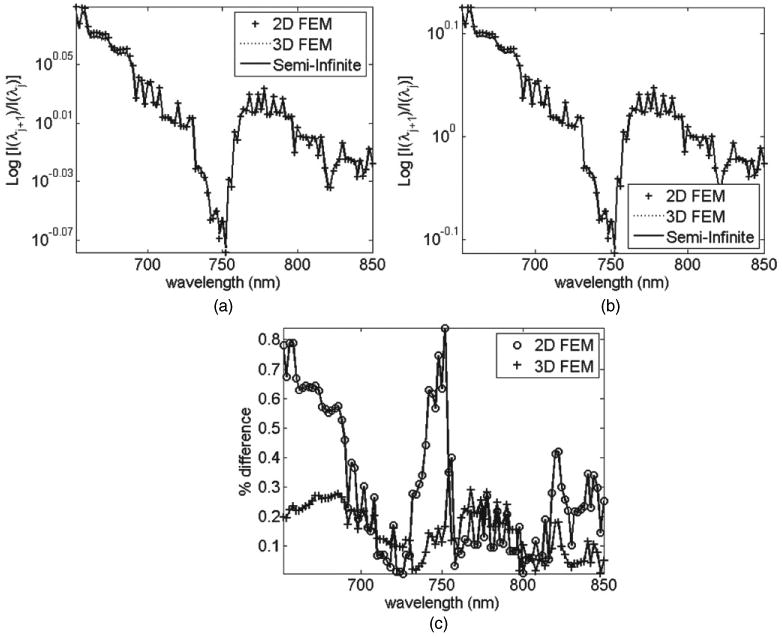
Spectral derivative data for all light transport models at (a) 50 mm and (b) 70 mm distance detectors. (c) Percentage error of derivative data between FEM and analytical models.

2.4. Inverse model

2.4.1. The spectral case

The goal of the inverse problem is the recovery of optical parameters within the imaging domain based on the measurements of light fluence at the tissue surface. This is accomplished based on a least-squares error optimization method allowing the formation of images in terms of the chromophore concentrations and the scattering parameters. This is done by assuming that light transport can be modelled as a diffusive process and that physical quantities of interest can be expressed in terms of physiologically relevant parameters through equations (2) and (3). The inverse solution is achieved by minimizing the two-norm difference between measured fluence at all wavelengths, Φ^o, and the calculated spectral data Φ^c from a given model:

$$\mathrm{\Psi }={\Vert {\mathrm{\Phi }}^c(x)-{\mathrm{\Phi }}^o\Vert }_2^2.$$ (8)

The fluence fields are n×L elements vectors, i.e. one element for each source-detector pair and wavelength values. The vector x = [c_k a b] parametrizes all the unknown in problem, namely the chromophore concentrations and the scattering parameter at each node in the FEM mesh. The iterative update formula for the least-squares method can be derived and found to be (Dehghani et al 2008, Srinivasan et al 2005b)

$$\mathrm{\Delta }x={(J^{T}J+\rho I)}^{-1}{J}^T\mathrm{\Delta }{\mathrm{\Phi }}^{c-o},$$ (9)

where typically ΔΦ^c−o = ln(Φ^c) − ln(Φ^o) = ln(Φ^c/Φ^o), ρ is the regularization parameter and J is the Jacobian matrix comprising the sensitivity (i.e. the rate of change of natural log of fluence with respect to a small change in x, δlnΦ/δx) for each unknown parameter:

$$J=\left[J_a{J}_b{J}_{c_1}{J}_{c_2}{J}_{c_2}\right]=\left[\begin{array}{ccccc}{J}_{a,{\mathrm{\lambda }}_1}& J_{b,{\mathrm{\lambda }}_1}& J_{c_1,{\mathrm{\lambda }}_1}& J_{c_2,{\mathrm{\lambda }}_1}& J_{c_3,{\mathrm{\lambda }}_1}\\ J_{a,{\mathrm{\lambda }}_2}& J_{b,{\mathrm{\lambda }}_2}& J_{c_1,{\mathrm{\lambda }}_2}& J_{c_2,{\mathrm{\lambda }}_2}& J_{c_3,{\mathrm{\lambda }}_2}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ J_{a,{\mathrm{\lambda }}_j}& J_{b,{\mathrm{\lambda }}_j}& J_{c_1,{\mathrm{\lambda }}_j}& J_{c_2,{\mathrm{\lambda }}_j}& J_{c_3,{\mathrm{\lambda }}_j}\end{array}\right].$$ (10)

2.4.2. The spectral derivative case

In the spectral derivative approach, the objective function is modified from equation (8) to

$${\mathrm{\Psi }}_2={\Vert \mathrm{\Delta }{{\mathrm{\Phi }}^{\prime }}^{c-o}\Vert }_2^2={\Vert \left\{\begin{array}{c}{\mathrm{\Phi }}_{{\mathrm{\lambda }}_1}^c(x)-{\mathrm{\Phi }}_{{\mathrm{\lambda }}_2}^c(x)\\ {\mathrm{\Phi }}_{{\mathrm{\lambda }}_2}^c(x)-{\mathrm{\Phi }}_{{\mathrm{\lambda }}_3}^c(x)\\ ⋮\\ {\mathrm{\Phi }}_{{\mathrm{\lambda }}_{j-1}}^c(x)-{\mathrm{\Phi }}_{{\mathrm{\lambda }}_j}^c(x)\end{array}\right\}-\left\{\begin{array}{c}{\mathrm{\Phi }}_{{\mathrm{\lambda }}_1}^o-{\mathrm{\Phi }}_{{\mathrm{\lambda }}_2}^o\\ {\mathrm{\Phi }}_{{\mathrm{\lambda }}_2}^o-{\mathrm{\Phi }}_{{\mathrm{\lambda }}_3}^o\\ ⋮\\ {\mathrm{\Phi }}_{{\mathrm{\lambda }}_{j-1}}^o-{\mathrm{\Phi }}_{{\mathrm{\lambda }}_j}^o\end{array}\right\}\Vert }_2^2.$$ (11)

Here ΔΦ′^c−o denotes the finite difference operator. Equation (9) can then be modified to

$$\mathrm{\Delta }x={({\stackrel{\sim }{J}}^T\stackrel{\sim }{J}+\rho I)}^{-1}{\stackrel{\sim }{J}}^T\mathrm{\Delta }{{\mathrm{\Phi }}^{\prime }}^{c-o},$$ (12)

where

$$\stackrel{\sim }{J}=[{\stackrel{\sim }{J}}_a{\stackrel{\sim }{J}}_b{\stackrel{\sim }{J}}_{c_1}{\stackrel{\sim }{J}}_{c_2}{\stackrel{\sim }{J}}_{c_2}]=\left[\begin{array}{ccccc}{J}_{a,{\mathrm{\lambda }}_1}-J_{a,{\mathrm{\lambda }}_2}& J_{b,{\mathrm{\lambda }}_1}-J_{b,{\mathrm{\lambda }}_2}& J_{c_1,{\mathrm{\lambda }}_1}-J_{c_1,{\mathrm{\lambda }}_2}& J_{c_2,{\mathrm{\lambda }}_1}-J_{c_2,{\mathrm{\lambda }}_2}& J_{c_3,{\mathrm{\lambda }}_1}-J_{c_3,{\mathrm{\lambda }}_2}\\ J_{a,{\mathrm{\lambda }}_2}-J_{a,{\mathrm{\lambda }}_3}& J_{b,{\mathrm{\lambda }}_2}-J_{b,{\mathrm{\lambda }}_3}& J_{c_1,{\mathrm{\lambda }}_2}-J_{c_1,{\mathrm{\lambda }}_3}& J_{c_2,{\mathrm{\lambda }}_2}-J_{c_2,{\mathrm{\lambda }}_3}& J_{c_3,{\mathrm{\lambda }}_2}-J_{c_3,{\mathrm{\lambda }}_3}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ J_{a,{\mathrm{\lambda }}_{j-1}}-J_{a,{\mathrm{\lambda }}_j}& J_{b,{\mathrm{\lambda }}_{j-1}}-J_{b,{\mathrm{\lambda }}_j}& J_{c_1,{\mathrm{\lambda }}_{j-1}}-J_{c_1,{\mathrm{\lambda }}_j}& J_{c_2,{\mathrm{\lambda }}_{j-1}}-J_{c_2,{\mathrm{\lambda }}_j}& J_{c_3,{\mathrm{\lambda }}_{j-1}}-J_{c_3,{\mathrm{\lambda }}_j}\end{array}\right]$$ (13)

and

$$\mathrm{\Delta }{{\mathrm{\Phi }}^{\prime }}^{c-o}=ln\left(\frac{{\mathrm{\Phi }}_{j-1}^c}{{\mathrm{\Phi }}_{j-1}^o}\right)-ln\left(\frac{{\mathrm{\Phi }}_j^c}{{\mathrm{\Phi }}_j^o}\right)=ln\left(\frac{{\mathrm{\Phi }}_{j-1}^c\times {\mathrm{\Phi }}_j^o}{{\mathrm{\Phi }}_{j-1}^o\times {\mathrm{\Phi }}_j^c}\right).$$ (14)

2.4.3. Simulated data

To demonstrate the flexibility of the proposed method, an approach based on experimental design is used (Cela et al 2009) which has shown to be a robust and accurate method to decrease the total number of experiments or simulations in order to calculate complete system responses for a large number of case scenarios (Nguyen et al 2008). In order to analyse the behaviour of the spectral derivative approach, several simulations were run according to changes in HbO, Hb water, scattering amplitude (a) and scattering power (b) with the level of factors defined according to a central composite design. Five levels of variation were defined for each factor according to the central composite design, consisting of one central point, two axial points and two factorial points and the levels were calculated in order to take into account the curvature of the surface response. A set of data are therefore composed of 52 experiments (run of simulation) for each approach and each type of added noise with the maximum variations of chromophore concentrations and scattering parameters (as expected for soft tissue) given as HbO = 0.01–0.05 mM, Hb = 0.01–0.05 mM, water = 30–90%, a = 0.2–1.2 and b = 0.5–1.5.

Reflectance spectral measurements from 650 to 850 nm (2 nm separation) were simulated using the model in equation (1) for a set of detectors ranging from 5 to 50 mm with 5 mm spacing (see figure 1). The simulated data were then corrupted using three types of noise: (a) 1% randomly distributed Gaussian noise, (b) 1% randomly distributed Gaussian noise plus random (ranging from 0 to 100%) detector coupling coefficient (N_D), and (c) 1% randomly distributed Gaussian noise plus random detector coupling coefficient (N_D) plus the linear varying N_S coefficient (80% – 75%, from 650 nm to 850 nm). These noise-added datasets were then used together with equations (9) and (12) to reconstruct the chromophore and scattering parameters using the spectral and spectral-derivative techniques, respectively. For the inverse model, the regularization parameter ρ was set to 1% of the maximum of the diagonal of the matrix J^TJ (or J̃^T J̃) with a total of 50 iterations. The Jacobians were calculated using the perturbation method (Arridge 1999) using equation (1) and the initial guess for all reconstructions was set as HbO = 0.03 mM, Hb = 0.03 mM, water = 50%, a = 1.0 and b = 1.0.

For each reconstructed model, the maximum and average relative error between each of the expected and reconstructed parameter is shown in table 1. For case (a), the spectral method provides the smallest relative error as expected, since the only noise present in the data is 1% random noise. Using the spectral derivative method, the results from case (a) and case (b) are identical, demonstrating that the noise due to the detector coupling coefficient is effectively cancelled, since spectral derivative data are used. However, the addition of this detector coupling coefficient demonstrated a large effect when conventional spectral method is utilized, leading to errors well over 1000% for the recovery of scattering amplitude. The results from case (c) show that the spectral method has produced unreliable results, whereas the spectral derivative method is still accurate within 27% in the worst scenario case, but greatly improved as compared to the spectral method. This is not surprising as the effect of the source coupling coefficient is not entirely cancelled using the spectral derivative method.

Table 1.

The maximum and average (in parentheses) relative percentage error between the expected and reconstructed parameter from noise-added simulated data. For each case ((a)–(c)) different types of noise are added as described in section 2.4.3.

	HbO	Hb	Water	a	b
Spectral derivative: case (a)	9.2 (2.4)	9.3 (2.4)	9.3 (3.2)	10.7 (2.8)	2.3 (0.8)
Spectral derivative: case (b)	9.2 (2.4)	9.3 (2.4)	9.3 (3.2)	10.7 (2.8)	2.3 (0.8)
Spectral derivative: case (c)	27.1 (15.8)	24.5 (13.4)	25.9 (13.4)	20.1 (11.4)	5.2 (2.8)
Spectral: case (a)	0.2 (0.06)	0.1 (0.04)	0.9 (0.1)	0.2 (0.05)	0.6 (0.1)
Spectral: case (b)	250 (86)	279 (78)	602 (98)	1456 (359)	146 (45)
Spectral: case (c)	1334 (121)	338 (84)	831 (111)	259 280 (5445)	874 (67)

2.4.4. Experimental data

A set of reflectance spectral measurements from 650 to 850 nm (2 nm separation) were acquired on the forearm of three human subjects, using the SAM-Spec® system from Indatech. The measuring head is composed of a probe consisting of one irradiating fibre bundle (2.5 mm diameter consisting of 55 fibres of 250 μm diameter) and three measurement fibres (600 μm) which are fixed at pre-fabricated locations of 1.48, 2.78 and 3.89 mm away from the source. The irradiation bundle was connected to a halogen light source (Leica CLS 150 XD). The spectral data at all detectors were measured using a Vis–NIR spectrometer (Zeiss, Vis–NIR enhanced, spectral range of 330–1100 nm). For each subject, three sets of spectral data were recorded at resting state, and were used together with the spectral derivative technique outlined above (equation (12)) and the semi-infinite model (equation (1)) to calculate the bulk properties of total tissue haemoglobin (HbT), oxygen saturation (StO), water, scattering amplitude and scattering power. An example for the experimental spectral derivative data for a single subject, together with the fitted modelled data is shown in figure 11(a). The calculated average of each parameter, for each subject is shown in figure 11(b) together with the published bulk value of adipose tissue (Alexandrakis et al 2005). It is seen that although the results from all subject show similar trends, the largest discrepancies are found between the values for water content (expected 50%, average for all subjects of 17%) and scatter power (expected 5.3, average for all subjects of 25.5). There is a good agreement between the calculated oxygen saturation (expected 70%, average for all subjects of 66.6%) as well as scatter amplitude (expected 38 mm⁻¹, average for all subjects of 28.9 mm⁻¹); note that the calculated values for scatter amplitude have been modified accordingly to have units of mm⁻¹, as reported by others (Alexandrakis et al 2005). The same data were also used together with conventional spectral technique (equation (9)), and the reconstructed values did not converge to a stable solution.

Figure 11.

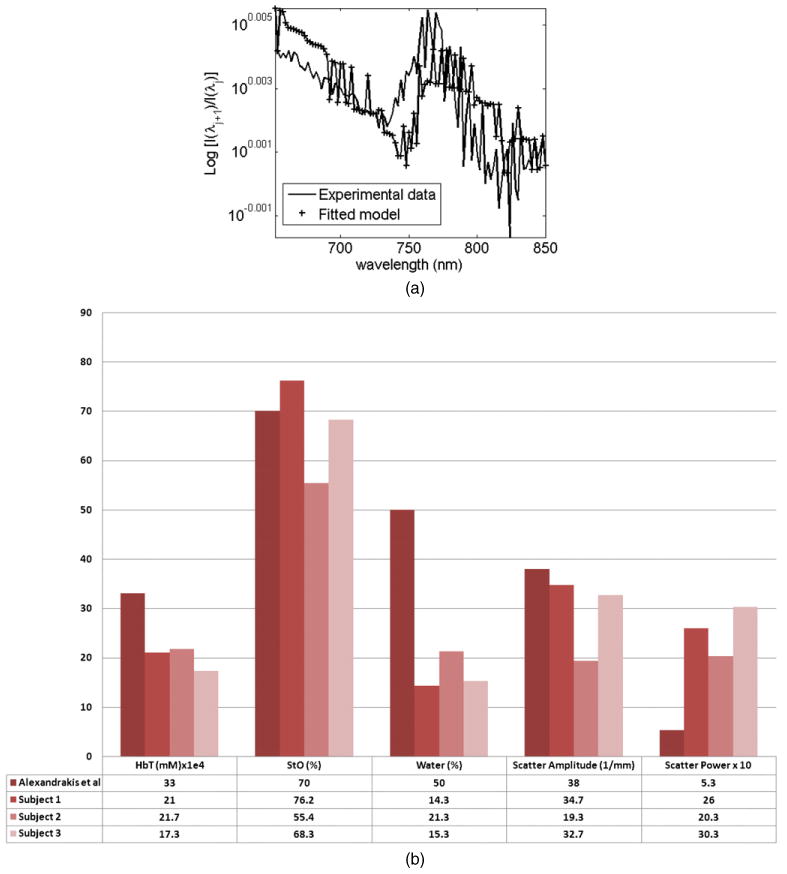
(a) Plot of the spectral derivative of experimental data and fitted model for a single detector at 2.78 mm from the source, (b) the average bulk properties of the forearm calculated using the spectral derivative method, together with the published values of bulk adipose tissue (Alexandrakis et al 2005).

3. Discussions

Using an analytical semi-infinite model, spectral NIR data have been presented whereby the effect of the unknown source and detector coupling coefficient is shown. As expected, figure 3(a) shows that spectral measurements in the presence of unknown source coupling coefficients can add an undesirable offset to the measurements. Although it is often common to normalize the measured data with respect to a given detector point, evidence is also provided through figure 3(b) that this does not completely eliminate the effect of the unknown source coupling coefficient which can therefore lead to incorrect quantification of physiologically relevant tissue parameters. The effect of the unknown detector coupling coefficient is also investigated. With figure 4 as supporting evidence, it is demonstrated that although normalizing the data with respect to a given measurement point can reduce the magnitude of this type of noise, it does lead to an error in measurement which is a function of this unknown detector coupling coefficient. It has been previously demonstrated that these unknown source and detector coupling coefficients can be incorporated as part of the inverse problem (Boas et al 2001), but in the case of spectroscopic bulk imaging as presented here, whereby the number of these optode coupling coefficients can equal the number of the unknown parameters, such methods are less than desirable.

The concept of spectral derivative data has been presented. It is shown that assuming the unknown optode coupling coefficients to be equal between nearest wavelengths, their effects can essentially be cancelled (equation (6)), figure 5. This is of profound importance, since instead of using raw spectral data to obtain information regarding tissue properties, it is possible to normalize each dataset for the same purpose, which inherently incorporates a self-calibrating mechanism. It is shown that using these schemes, the maximum error between noise-added and noise-free data is less than 0.2%, figure 5(c), as compared to over 40% using conventional spectral analysis, figure 4(c).

The presented concept of the self-calibrating nature of spectral derivative data is further extended to the analysis of spectral data from three different models. It is shown that for a given geometry and set of optical parameters, if data is calculated using (a) semi-infinite analytical model, (b) 2D and (c) 3D FEMs, the raw spectral data can present large discrepancies when compared, figure 8. The mismatch between 2D and analytical model is shown to be as great as 18%, whereas 3D model shows a better match, due to its more accurate representation of a semi-infinite medium. It is also shown that although it is possible to minimize this model-mismatch through the use of data normalization with respect to a given wavelength, the mismatch errors between 2D and analytical model can be as great as 35%, figure 9(c), which would lead to errors in calculated parameter values. The data from these three models were further analysed using the spectral derivative data. It is shown through the analytical expression (equation (7)) that assuming the model mismatch between each nearest wavelength to be equivalent, the effect of this parameter can theoretically be eliminated using the spectral derivative algorithm. This is demonstrated, using modelled data, figure 10, showing that the mismatch error in spectral derivative data between the FEM models and the analytical models is less than 1% for 2D and less than 0.4% for 3D models. This presents a dramatic improvement as compared to raw and otherwise un-normalized data. This concept is important, as it would suggest that this self-calibrating nature of spectral derivative data can be used for problems which can be considered geometry and optical parameter independent.

The concept of spectral derivative data has been further expanded within the inverse problem for spectroscopic bulk imaging of tissue. It has been shown that the use of spectral derivative data can lead to direct reconstruction of chromophore and scattering properties, in the same manner as conventional spectral method. The only difference between these two methods is that instead of using a sensitivity matrix that relates the change of each optical property with respect to measurement at each wavelength, the problem is now concerned with the spectral change of these sensitivities between nearest wavelengths. To validate these, a set of simulated data for a range of chromophore and scattering parameters were calculated and then corrupted using random noise, as well as source and detector (optode) coupling coefficients. These noise-added data were then used together with both conventional spectral as well as spectral derivative inverse algorithms to calculate the unknown optical parameters. It is shown that using spectral derivative method outperforms the conventional spectral method in all cases except the case where the only noise present is the random noise of 1%, table 1. This is as expected, as the effect of random noise will be amplified using the spectral derivative method, since it is not reasonable to assume that such noise would be equivalent at each wavelength. Furthermore, it is shown that the spectral derivative method provides the same calculated parameters with or without detector coupling coefficient noise, demonstrating that the expression of equation (6) is valid whereby this unknown coefficient is effectively eliminated. The results from the conventional spectral method in the presence of optode coupling coefficient have performed poorly, in some cases leading to negative and unrealistic results. These findings again highlight the unique property of the spectral derivative method of being self-calibrating which provides a mechanism to improve quantitative accuracy of the calculated parameters without the need for complex and time consuming data calibration. There clearly is a trade-off between the spectral and spectral derivative method in the presence of noise, whereby in the absence of coupling coefficients, the conventional spectral method performs better. However, given that most experimental measurements will contain some form of unknown model or fibre coupling coefficient noise, it is expected that the proposed spectral derivative method will always provide more quantitative accuracy.

Finally, a set of spectral reflectance measurements were made on the forearm of three subjects. Each dataset was used, together with the spectral derivative algorithm to reconstruct values for bulk properties of total tissue haemoglobin (HbT), oxygen saturation (StO), water, scattering amplitude and scattering power. For comparison, these reconstructed values are plotted in figure 11(b), together with published values for adipose tissue. It is evident that the reconstructed parameters for all three subjects show a similar trend, with good quantitative accuracy in terms of the calculated StO value and scatter amplitude. However, there is some disagreement between calculated and published values for water content as well as scatter power. There could be several explanations for these discrepancies. It has been previously shown that there may exist a set of unique wavelengths that would provide a much better quantitative accuracy when using spectral data for the inverse problem (Eames et al 2008). Furthermore, the spectral derivative method used here was based upon a wavelength separation of 2 nm, which could in principle be reduced, depending on spectrometer accuracy and can be further investigated using simulated models. It has been shown that the use of spectral derivative data can reduce the errors due to different modelling approaches (2D versus 3D versus analytical). Nonetheless, since an analytical model was used for the calculation of these parameters, quantitative accuracy may be improved by the use of more appropriate realistic 3D layered higher ordered models. Additionally, the probe available for measurements consisted of detectors which are near the source (i.e. not far enough to allow a diffuse propagation of NIR light through tissue). It may be argued that the model used based on the diffusion approximation is not certainly valid, particularly in the conventional spectral method used. However, the use of the proposed spectral derivative method, as demonstrated earlier, could provide some accuracy in model-mismatched errors. Also it is unclear whether the comparison of these calculated values with adipose tissue is most appropriate, since the forearm is a multi-layered medium consisting of haemoglobin, fat and muscle tissue. Nonetheless, it is shown that the calculated values for all datasets for all subjects are repeatable and provide realistic measurements without the need of complex and often unreliable data calibration. Although not shown, the values calculated using the conventional spectral technique did not provide consistent or realistic values and were therefore deemed unreliable.

4. Conclusions

The concept of spectral derivative data in optical spectroscopy is introduced, demonstrating that by the use of this technique, the effect of unknown fibre coupling with tissue can be effectively eliminated by the assumption that these coefficients have a similar value when compared with neighbouring wavelengths. Using theoretical models based on the analytical solutions for semi-infinite diffusive medium, the effect of these coupling coefficients is demonstrated, showing that simple data normalization based on a given measurement (spatial or spectral) is not adequate and will lead to inaccuracies which are magnified when propagated into the inverse problem solutions. It is also demonstrated that the use of the spectral derivative method can dramatically reduce any error due to light transport model mismatch. This has been demonstrated by comparing 2D and 3D FEM simulations with the analytical solutions. The errors in spectral derivative data were reduced to less than 1% independent of which the modelling method was used.

The concept of the inverse model to calculate bulk tissue properties from hyper-spectral data has been presented. It is shown using the spectral derivative method that it is possible to calculate directly the chromophore and scattering coefficients of tissue without the need of complex, and often unreliable, data calibration routines. This has been further demonstrated using a simulated study, showing that the spectral derivative method can produce consistently the reliability of the results, regardless of noise (both stochastic and fibre related) within the data. In comparison, it is shown that using conventional spectral techniques, although the presence of small random noise in data is of little detriment, the effect of the unknown fibre coupling coefficient produced inaccurate results preventing the use of such techniques as diagnostic tools when calibration is not done correctly.

Finally, the spectral derivative technique has been used together with measurements from the human forearm. It is shown that although there is some inconsistency between the expected and calculated values of bulk tissue, the reconstructed parameters are realistic and consistent within the given setting. The work presented here, although confined to reflectance measurements in the NIR range, is fully transferable to other wavelengths as well as tomographic imaging measurements. Further work is planned to investigate the effect of the wavelength resolution, number of measurements and wavelength selection to improve the accuracy of the proposed method further.