Abstract
During adaptation, motor commands tend to repeat as performance plateaus. It has been hypothesized that this repetition produces plasticity in the motor cortex (M1). Here, we considered a force field reaching paradigm, varied the perturbation schedule to potentially alter the amount of repetition, and quantified the interaction between disruption of M1 using transcranial magnetic stimulation (TMS) and the schedule of perturbations. In the abrupt condition (introduction of the perturbation on a single trial followed by constant perturbation), motor output adapted rapidly and was then followed by significant repetition as performance plateaued. TMS of M1 had no effect on the rapid adaptation phase but reduced adaptation at the plateau. In the intermediate condition (introduction of the perturbation over 45 trials), disruption of M1 had no effect on the phase in which motor output changed but again impaired adaptation when performance had plateaued. Finally, when the perturbation was imposed gradually (over 240 trials), the motor commands continuously changed during adaptation and never repeated, and disruption of M1 had no effect on performance. Therefore, TMS of M1 appeared to reduce adaptation of motor commands during a specific phase of learning: when motor commands tended to repeat.
Keywords: force-field adaptation, motor control, primary motor cortex, repetition-dependent plasticity, transcranial magnetic stimulation
Introduction
Studies of motor adaptation rely on scenarios in which an externally imposed perturbation disturbs a movement, resulting in performance errors, that is, a difference between the expected and observed sensory consequences of motor commands. In reach adaptation (Donchin et al. 2003) and saccade adaptation paradigms (Ethier et al. 2008; Srimal et al. 2008), an error in a given trial induces changes in the motor output of the subsequent trial, suggesting that the brain learns from prediction errors. The neural basis of this error-dependent adaptation includes the cerebellum, as studies on reaching (Smith and Shadmehr 2005; Tseng et al. 2007; Criscimagna-Hemminger et al. 2010) and saccade paradigms (Barash et al. 1999; Xu-Wilson et al. 2009) have found that damage to the cerebellum produces profound deficits in adaptation. In a recent experiment, however, cerebellar patients demonstrated improved adaptation when the perturbation was gradually introduced over hundreds of trials as compared with when the full perturbation was abruptly introduced on the first trial (Criscimagna-Hemminger et al. 2010). Is the neural basis of adapting to a gradual perturbation distinct from an abrupt perturbation?
Psychophysical evidence suggests that gradual and abrupt introduction of perturbations produce motor memories with distinct properties. For example, in force-field adaptation tasks, gradual introduction of a perturbation leads to better retention (Kagerer et al. 1997; Michel et al. 2007; Huang and Shadmehr 2009) and a distinct pattern of generalization (Malfait and Ostry 2004; Michel et al. 2007; Kluzik et al. 2008). Similarly, adapting to a gradually increasing visuomotor rotation causes subjects to rely more on sensory feedback during the reach and reduce their reaction time (Saijo and Gomi 2010). The altered patterns of generalization and response to sensory feedback suggest that the neural basis of adapting to statistics of error in the gradual versus abrupt perturbations may be distinct.
Neurophysiological studies have highlighted changes in the primary motor cortex (M1) during learning of force field or visuomotor rotation (Gandolfo et al. 2000; Li et al. 2001; Paz et al. 2003; Paz and Vaadia 2004; Arce et al. 2010). Some of these studies (Paz et al. 2003; Paz and Vaadia 2004) have found that changes in M1 occur not during the early stage of adaptation when errors are large, but during a later stage when performance errors are small. Here, we controlled the schedule of the perturbation and attempted to assay the role of the human M1 during adaptation. To this end, we used a single-pulse transcranial magnetic stimulation (TMS) procedure to disrupt the function of M1 during reach adaptation (Hadipour-Niktarash et al. 2007). This disruption produced adaptation deficits that were specific to the schedule of perturbations. Our result suggests that the repetition of the motor commands plays a significant role in how much M1 contributes to changes in motor output during adaptation.
Methods
Sixty-six right-handed volunteers with no known neurological disorders participated in this study. All participants were naive to the purpose of the experiment. All procedures were approved by the Institutional Review Board of the Johns Hopkins School of Medicine, and all participants signed a consent form.
Behavioral Training
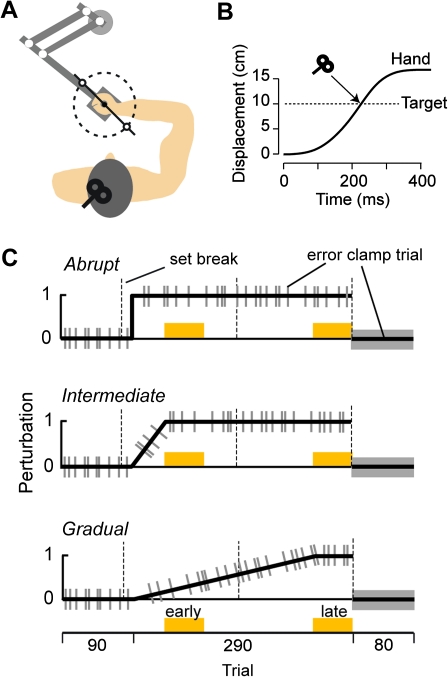
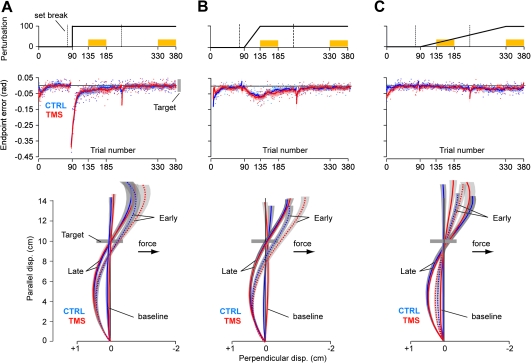
The experiment is illustrated in Figure 1A. Subjects performed a “shooting task” while holding the handle of a robotic manipulandum (Huang and Shadmehr 2009). Their hand was covered by a horizontal screen upon which a small white cursor (5 × 5 mm) representing hand position was displayed at all times. A target (5 × 5 mm) was positioned at 10 cm from the center of the screen at either 121.5° or 301.5° in a pseudorandom sequence. The volunteers were instructed to “shoot” through the target, beyond which the robot produced a dampening field (as if punching a pillow). As the cursor crossed an imaginary 10-cm radius circle centered at the start position of the movement, a yellow dot appeared at the crossing point to emphasize the endpoint error. Once they had “punched the pillow,” the subjects brought their hand back to the target, and then, the robot brought the hand back to the center. Subjects were rewarded with a target explosion. In order to receive this reward, the cursor had to cross the target area in less than 230 ms after movement start. If the movement duration was longer than 230 ms, a blue dot appeared to indicate a slow movement. Because the subjects were instructed to strike quickly through the target, peak velocity was usually achieved near the crossing point (Fig. 1B). During the experiment, subjects received 3 set breaks (about 1 min in duration), as noted by the dashed lines in Figure 1C. Hand position, hand velocity, and force at the handle were recorded at 100 Hz.
Figure 1.
(A) Experimental setup. Subjects were seated in front of a robotic arm and were asked to hold the handle and shoot through a 10 cm distant target. The two targets that we used are plotted here. (B) TMS was delivered when the hand crossed the target during the force-field trials. (C) Subjects participated in one of the three experiments: abrupt, intermediate, or gradual. In the first 90 trials, the robot did not produce any forces. In the subsequent 290 trials, a curl force field was introduced, perturbing the hand perpendicular to its direction of motion. It was introduced either over 1 trial (abrupt condition), over 45 trials (intermediate condition), or over 240 trials (gradual condition). The gray bars represent error-clamp trials (see Methods).
To control for repetition-dependent and error-dependent signals that might contribute to learning (see definitions and simulations results below), we considered 3 protocols: abrupt, intermediate, and gradual (Fig. 1C). The first 90 trials of all 3 protocols were in a null field. Following these null field trials, the subjects experienced a force field. The perturbation in field trials was a velocity-dependent curl field in which the robot pushed the hand perpendicular to the direction of motion. In the “abrupt condition,” subjects experienced 290 field trials in which the force exerted by the robot was introduced at the maximum magnitude [0 -13; 13 0] N·s/m on the first field trial. We recruited a control group of subjects who experienced the abrupt condition without TMS (CTRLABR, n = 9) and a group of subjects who received a single TMS pulse over the primary motor cortex at the end of each of the 290 trials (TMSABR, n = 9). Further information about the TMS condition is provided below. In the “intermediate condition,” the field strength was ramped up linearly over 45 trials. In this condition, n = 10 subjects participated in the control group (CTRLINT), and n = 11 subjects participated in the TMS group (TMSINT). In the “gradual condition,” the field strength was ramped up linearly over 240 trials. In this condition, n = 9 subjects participated in the control group (CTRLGRA), and n = 9 subjects participated in the TMS group (TMSGRA). In all conditions, error-clamp trials were randomly interspersed with a one-fifth probability. In error-clamp trials, hand motion was constrained to a straight line to the target by a stiff virtual wall (spring coefficient: 2500 N·m and damping coefficient: 25 N·s/m). The error-clamp trials allowed us to measure the forces that the subjects predicted on that trial while minimizing performance errors. The 290 field trials were followed by a block of 80 error-clamp trials.
To assess the specificity of our TMS results to the motor cortex, we recruited an additional group (n = 9) that trained in the abrupt condition but received a TMS pulse over the occipital cortex.
TMS Protocol
To stimulate the motor cortex, TMS was applied over the biceps and deltoid representations of the left primary motor cortex at 120% of the resting motor threshold (Desmurget et al. 1999; Della-Maggiore et al. 2004; Cothros et al. 2006; Hadipour-Niktarash et al. 2007; Brown et al. 2009). The coil was placed tangential to the scalp with the handle pointed backwards at a 45° with respect to the anterior–posterior axis. In order to stimulate the occipital cortex, TMS was applied on the inion–nasion line, above the inion, with the handle pointing upward. The resting motor threshold was defined as the minimum stimulator intensity that produced a 50 μV motor–evoked potential in the right first dorsal interosseous muscle in 5 of 10 stimulations. During reach adaptation, the pulse was delivered when the hand crossed an imaginary 10 cm radius circle centered at the start position of the movement (Fig. 1B). Because the TMS pulse arrived after completion of the trial, it did not alter the movement. However, earlier work had demonstrated that the temporal proximity of the TMS pulse and trial completion are critical to disruption of learning in the motor cortex (Hadipour-Niktarash et al. 2007). We did not deliver the pulse at the start or during the movement, leaving movement execution unimpaired.
Data Analysis
Endpoint error was defined as the angle between a straight line to the target and endpoint position. Perpendicular velocity at the end of the movement was assessed at 90% of movement duration. We excluded trials that completed in more than 300 ms or had endpoint error of more than 30° (less than 5% of all movements). For each error-clamp trial, the ideal force was computed as the field magnitude times the hand velocity. The baseline force trajectory that subjects produced during null trials was subtracted from the force they produced during adaptation trials. For some analyses of field trials, movement trajectories were divided into an early and a late phase at the halfway point to the target. In error-clamp trials, the dependent measure was the maximum force exerted by the subjects against the channel walls. For some analyses of error-clamp trials, the force profile for each trial was normalized in time (0% is the movement onset and 100% is the movement offset) and then resampled in 5% time intervals. The intermediate data points were computed from a spline curve fitted on the raw data points (spline function in Matlab; Mathworks Inc.).
The post-adaptation retention period was composed entirely of a sequence of error-clamp trials. We examined the rate of decay of the force output during the error-clamp trials of the test period. This rate was estimated by fitting a single exponential of the form to the data set for each subject. In this equation, is the peak force on trial n. This continuous domain equation can be well approximated in the discrete domain: and in which (1−b) is an estimate of sensitivity of the memory to trial. Therefore, b is fraction of the force that is lost from one trial to the next. To assess between-group differences in rate of decay, we ran a bootstrap analysis on the parameter b with 10 000 resamplings (bootstrap function in Matlab). The same technique was used to assess the rate of learning during the first 25 trials in the abrupt condition. To do so, we approximated the exponential learning function with the following discrete function . To estimate the running standard deviation of the force output, we smoothed the maximum force data from our subjects using a running average of 10 trials and then found the running standard deviation with a window of 7 trials. The normalized running standard deviation was obtained by dividing the running standard deviation by the running average.
In some instances, we used an analysis of covariance (ANCOVA) in order to test for the possible influence of covariate measure on the results of an analysis of variance (ANOVA). Before performing this analysis, we first performed a homogeneity-of-slope test that confirmed the significant relationship between the covariate and the dependent measure and the necessary hypothesis that this relationship was similar for the different groups. Statistical analyses were implemented in Statistica (Statsoft).
Results
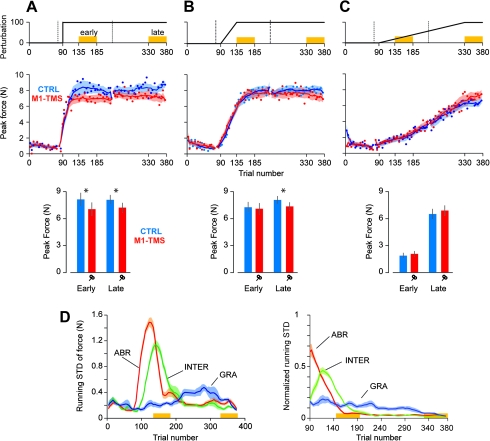
We asked whether disruption of M1 produced impairments in performance during adaptation and whether this impairment was dependent on the schedule of the perturbations. Our primary measure of performance was the force that subjects produced in error-clamp trials (Fig. 2).
Figure 2.
Force output in the abrupt, intermediate, and gradual protocols. (A) Performance of the abrupt group. Top row: perturbation schedule. Middle row: peak force in error-clamp trials over the course of the training. The solid curves represent the running average over a window of 10 trials, which are interrupted during set breaks. Error bars are standard error of the mean. Bottom row: output of the ANCOVA on peak force in error-clamp trials during the early and late periods of training (factor: group and covariate: peak velocity). Error bars are CI. (B) Performance of the intermediate group. (C) Performance of the gradual group. (D) Running standard deviation of the peak force for the control groups (blue curves of middle row) is presented on the left panel. In the normalized version of this plot (right panel), the standard deviation of the force is divided by its magnitude.
In the abrupt condition, M1-TMS produced an impairment in force output in the trials following the introduction of the perturbation (Fig. 2A), and this impairment was sustained for the entire course of the experiment. To quantify this pattern, we considered the peak force exerted in the error-clamp trials during the early phase of adaptation (trials 136–185) and the late phase of adaptation (trials 331–380). We performed an ANOVA with period (early and late) as a within-subject factor and group (CTRLABR and TMSABR) as a between-subject factor. We found a main effect of group, F1,16 = 15.1, P = 0.001, but no effect of period, F1,16 = 0.03, P > 0.80, or interaction, F1,16 = 0.17, P > 0.60. To ask whether the differences in force were due to differences in individual movement speeds, we performed an ANCOVA analysis in which the peak force was the dependent measure, group was the between-subject factor, and peak velocity was the covariate. We found that group differences in peak force were maintained (early: F1,15 = 4.54, P = 0.049 and late: F1,15 = 5.76, p = 0.03).
In the intermediate condition, as the perturbation was ramped up (trials 90–135), the forces that subjects produced increased rapidly. During this transient period of adaptation, we observed no reliable effect of TMS. However, by the end of the training period, the CTRLINT subjects were producing significantly more force than the TMSINT subjects (Fig. 2B): There was an interaction between group and period, F1,19 = 4.95, P = 0.038, and a significant difference between the force in the 2 groups (t19 = 2.12, P = 0.047). Importantly, from the early to the late adaptation period, the CTRLINT group showed a 15% increase in peak force (t10 = 3.9, P = 0.003), whereas during the same period, TMSINT group showed no significant changes (2% increase, t9 = 0.39, P > 0.40). This group difference in peak forces during the late period was maintained when we considered the individual differences in movement speeds: ANCOVA main effect of group, F1,18 = 5.58, P = 0.03.
In contrast to the abrupt and intermediate conditions, in the gradual condition, we observed no reliable differences between groups throughout the experiment: main effect of group, F1,16 = 3.53, P = 0.08; of period, F1,16 = 366, P < 0.001; and interaction, F1,16 = 1.29, P = 0.27. The small trend toward a higher force by the end of training for the TMSGRA group disappeared when we took into account differences in individual movement speeds: ANCOVA, effect of group, F1,15 = 0.95, P = 0.35.
In summary, we found that force adaptation in response to an abruptly imposed perturbation was impaired when M1 was stimulated, and this impairment was present in both the early and the late periods of training. When the perturbation was imposed less abruptly (intermediate condition), disruption of M1 impaired the adaptation only in the late period of training. When the perturbation was imposed gradually, disruption of M1 had no effect on adaptation.
Repetition-Dependent Learning and the Motor Cortex
Why should the disruption of M1 affect performance in the abrupt (early and late) and intermediate (late) conditions but not the gradual condition? An important clue is previous research regarding disruption of M1 in tasks that do not involve adaptation. For example, when people move their thumb repeatedly in a given direction, stimulation of M1 is more likely to reproduce the practiced movement than other movements (Classen et al. 1998). Therefore, a brief period of repetition alters the response of M1 to a given external input (Liepert et al. 1998), implying that even short-term repetition of a movement enhances representation of that particular movement in the motor cortex. This enhancement of representation is termed use-dependent plasticity and appears to rely on synaptic alterations within M1 (Butefisch et al. 2000, 2004; Galea and Celnik 2009). Interestingly, 2 recent experiments (Huang et al. 2009; Diedrichsen et al. 2010) demonstrated that during reach adaptation, a component of the change in the motor output was driven by the act of repetition, while another component was driven by sensory prediction errors. For example, Diedrichsen et al. (2010) suggested that learning in even short-term adaptation experiments depends on at least 2 signals: prediction errors and repetition. Here, we wondered whether the results that we had observed in disrupting M1 were consistent with an effect that was due to disruption of learning from repetition.
Our intuition was that in the abrupt condition and late in the intermediate condition, the subjects were likely to repeat their motor commands (after an initial transient in force output). In the gradual condition, the subjects needed to continuously update their force output in order to maintain performance. Therefore, a proxy for the degree of repetition in the motor commands is the inverse of the variability of the motor commands across the trials. That is, the smaller the trial-to-trial change in motor commands (as measured by force during error-clamp trials), the greater the repetition. To estimate the degree to which the forces repeated in various conditions, we computed the running standard deviation of the forces in each control subject in error-clamp trials and then normalized this STD with respect to the mean force output (Fig. 2D). We found that in the abrupt and intermediate conditions, after an initial transient, the between-trial force variability became low, whereas in the gradual condition, this variability stayed high as the perturbation continued to change. Therefore, the impairment that M1-TMS caused was greatest in the condition for which repetition of motor commands was greatest and between-trial variability of force output was low (abrupt condition), less in the condition for which repetition was smaller (intermediate condition), and none in the condition for which repetition was smallest and between-trial variability was high (gradual condition).
The absence of TMS effect during the sharp rise in force output (Fig. 2A; first 25 trials in the abrupt condition) suggests that TMS did not disrupt an error-based learning process. This observation is reinforced by the use of a bootstrap analysis to quantify any difference in the initial rate of learning. To do so, an exponential function was fit to the force measured during error-clamp trials (see Methods). This analysis did not reveal any differences in the rate of learning (d) between the 2 groups (CTRLABR: 0.26 ± 0.11 and TMSABR: 0.2 ± 0.05, mean ± confidence interval [CI], t-test, P = 0.33).
Regional Specificity of the Effect of TMS
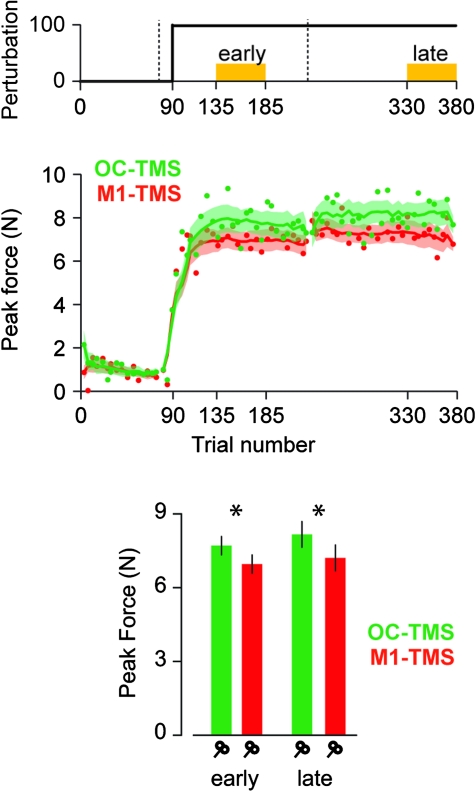
The strongest effect of TMS was in the abrupt condition. In order to control for regional specificity of TMS, we enrolled an additional group of subjects in the abrupt condition and applied the stimulation over the occipital cortex (OC-TMS). We found that the force output in the M1-TMS group was impaired compared with the OC-TMS group, and this impairment was present both in the early and in the late adaptation periods (Fig. 3). An ANOVA revealed a significant main effect of group (F1,16 = 6.69, P = 0.02) but no significant effects of period (F1,16 = 2.22, P = 0.15) or interaction (F1,16 = 0.39, P = 0.54). This difference among the OC-TMS and M1-TMS groups was maintained when we controlled for differences in movement speed (ANCOVA early: F1,15 = 9.18, P = 0.008 and late: F1,15 = 7.5, P = 0.015). Furthermore, we found no significant differences in force patterns between the OC-TMS group and the control group: ANOVA: F1,16 = 0.31, P = 0.59; ANCOVA early: F1,15 = 0.47306, P = 0.5; and late: F1,15 = 0.4, P = 0.54.
Figure 3.
Site specificity of the TMS effect. TMS impaired peak force when it was delivered over the primary motor cortex (red curve, same as Figure 2A) but not when delivered over the occipital cortex (green curve). Figure structure is similar to Figure 2.
TMS During Adaptation Did Not Affect the Rate of Decay after Adaptation
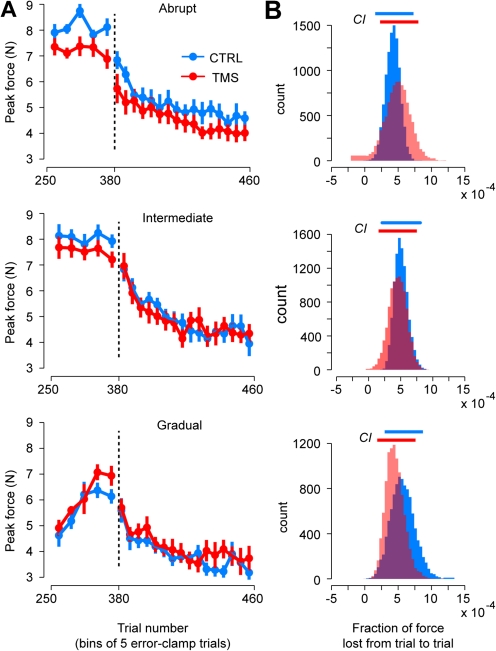
The adaptation blocks were followed by 80 error-clamp trials in which we assayed the rate of decay of the motor output (Fig. 4A). TMS was discontinued at this stage of the experiment. To compare the rate of decay between groups, single exponentials of the form were fit to the trial-to-trial force data of each group, and a bootstrap analysis was used to estimate mean and CI of the decay parameter b (Fig. 4B). We found that TMS during adaptation had no reliable influence on the rate of decay of motor output after adaptation (t-tests of the mean rate of decay, P > 0.5 for all conditions).
Figure 4.
Force output during the end of training period and throughout the posttraining period. (A) Peak force over the course of last 25 error-clamp trials during the training period and the 80 ensuing ones. Trial bins consisted of 5 trials each. Error bars are standard error of the mean. (B) Bootstrap estimate population of the decay parameter b(10 000 resamplings). Top horizontal bars represent CI. Top row: abrupt condition, middle row: intermediate condition, and bottom row: gradual condition.
Effect of TMS on Reach Trajectories and Feedback Control
Our results that disruption of M1 impaired performance in the abrupt and intermediate conditions are surprising because a number of previous TMS studies have found that disruption of M1 did not affect learning (Richardson et al. 2006; Hadipour-Niktarash et al. 2007). Previous work relied on measures that quantified reach trajectories, whereas here, we relied on forces that were produced in channel trials. Is there a fundamental difference between these 2 measures of performance? Endpoint errors and reach trajectories are plotted in Figure 5. We found that while M1-TMS affected the forces that subjects produced in error-clamp trials (Fig. 2), it had no reliable effect on endpoint errors in field trials (Fig. 5). For example, in the abrupt condition (Fig. 5A), an ANOVA with period (early and late) as a within-subject factor and group (CTRLABR and TMSABR) as a between-subject factor revealed that the error patterns were comparable in the 2 groups: main effect of period, F1,16 = 51.63, P < 0.001; main effect of group, F1,16 = 0.018, P > 0.40; and interaction, F1,16 = 0.73, P = 0.4. In the intermediate condition (Fig. 5B), the error patterns were also comparable in the 2 groups: main effect of period, F1,19 = 77.7, P < 0.001; main effect of group, F1,19 = 2.26, P = 0.15; and group by period interaction, F1,19 = 1.4, P = 0.25. Finally, in the gradual condition (Fig. 5C), the error patterns were also comparable in the 2 groups: main effect of group, F1,16 = 0.16, P > 0.40, and interaction, F1,16 = 0.31, P > 0.4. Thus, TMS did not produce an impairment of performance in terms of endpoint errors.
Figure 5.
Kinematics of the reach in the abrupt, intermediate, and gradual protocols. (A) Performance of the abrupt group. Top row: perturbation schedule. Middle row: endpoint error over the course of the training. The solid curves represent the running average over a window of 14 trials, which are interrupted during set breaks. Error bars are standard error of the mean (SEM). Bottom row: average trajectory profiles during baseline (trials 41–90), early (trials 136–185), and late periods (trials 331–380). Trials were rotated such that the target is represented 10 cm away in the North direction. Areas around the curves represent SEM. (B) Kinematics of the intermediate group. (C) Kinematics of the gradual group.
The best policy (in terms of minimum effort, where effort is defined as the sum of squared forces) that can bring the hand to the target in a curl field is to overcompensate early in the movement when the field is weak and then allow the robot to bring the hand back to the target (Izawa et al. 2008). All groups produced reach trajectories that exhibited overcompensation, as shown by the hand paths in the lower part of Figure 5, and this overcompensation increased over the course of trials (from early to late). Thus, if we view the overcompensation as the result of an optimization process, TMS of the motor cortex did not appear to affect the ability of the subjects to find the trajectory of minimum effort to the target.
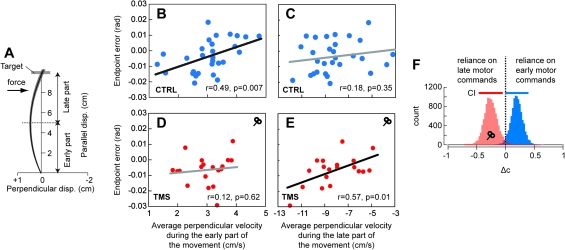
How could TMS affect force production during error-clamp trials but not influence the endpoint errors during field trials? We closely analyzed the reach trajectories of each subject and looked for clues that might help answer this question. Our first clue was that during the late phase of adaptation in the control subjects, an individual’s motor output in error-clamp-trials was a predictor of their endpoint kinematics in free reaching but not for the TMS subjects. For example, in the control groups (CTRLABR, OC-TMSABR, and CTRLINT), the force recorded in error-clamp trials at midway into the movement was a predictor of perpendicular velocity at the end of free reaching (r = 0.41, P = 0.026). In contrast, this correlation did not exist in the TMS groups (TMSABR and TMSINT, r = 0.09, P> 0.70). Furthermore, in the control groups, the early motor commands in free reaching (average perpendicular velocity in the first half of the movement, see Fig. 6A) were predictors of endpoint errors of the same movements (Fig. 6B, r = 0.49, P = 0.007) but not in the TMS groups (Fig. 6D, r = 0.12, P = 0.62). (A positive perpendicular velocity early into the movement implies an overcompensation. Therefore, Figure 6B suggests that in the control group, the greater this early overcompensation, the greater the likelihood that the endpoint error would be positive [the hand would pass to the right of the target.]) That is, motor commands that control subjects produced to start their movements were generally good predictors of their endpoint kinematics. In the TMS groups, however, these early motor commands were poor predictors of endpoint kinematics.
Figure 6.
Effect of TMS on early and late components of movement trajectories. (A) Schematic representation of how the trajectories were spatially divided into 2 phases (early phase: parallel position <5 cm and late phase: parallel position >5 cm). (B), (C), (D), and (E): intersubject relationship between the average perpendicular velocity and endpoint error for the CTRL and TMS groups (B and C and D and E, respectively) during the late training period. The average perpendicular velocity was computed either during the early (B and D) or late (C and E) phase of the movements. (E) Bootstrap estimate population of the Δc parameter (10 000 resamplings). This parameter represents the difference between the standardized coefficients of the multiple regression. In this regression, endpoint error is the dependent measure, and average perpendicular velocities of the early and late phases of the movement are the 2 factors. For this analysis, CTRL (CTRLINT, CTRLABR, and TMSOC) and TMS (TMSINT and TMSABR) groups across the intermediate and abrupt conditions were collapsed together.
Our second clue was that in the TMS groups, endpoint kinematics were more closely related to motor commands that arrived late in the movement, but not for the control groups. For example, for the second half of the movement, the average perpendicular velocity was a predictor of endpoint error for the TMS groups (Fig. 6E, r = 0.57, P = 0.01) but not for the control groups (Fig. 6C, r = 0.18, P = 0.35). To explore this idea further, we fit a multiple regression model to predict endpoint error from the measures of perpendicular velocity in the early and late phases of free reaching movements (). The multiple regression analysis provided good fits of the data (r2 = 0.7 for the control groups and r2 = 0.85 for the TMS groups). However, the weight of the independent factors differed between the control and TMS groups (given here with standardized coefficient):
For all groups, the independent factors were always significant (P < 0.0002). Standard error of the standardized regression coefficients was 0.142 and 0.136 for the control and TMS groups, respectively. The results of this analysis suggested that whereas in the control group, the early motor commands were a better predictor of endpoint errors, in the TMS group, the late motor commands were a better predictor. To test the statistical strength of this result, we performed a bootstrap analysis by computing the difference in weight between the different components: . A positive Δc suggests that the endpoint error was more strongly dependent on the early motor commands, whereas a negative Δc suggests a stronger dependence on the late motor commands. We found that Δc estimates were significantly different across populations (Fig. 6F), as the 95% CIs did not overlap (t-test, P = 0.001). The mean estimate of Δc was positive for the control population but negative for the TMS population.
In summary, the results of our analysis suggest that during free reaching, the endpoint errors were indistinguishable between the TMS and control groups. However, the motor commands that the control groups produced in error-clamp trials were a better predictor of their performance in free reaches than for the TMS groups. This suggests that the TMS groups relied more on the late phase of the movement (i.e., relying on sensory feedback to correct the movement), whereas the control groups relied more on the early phase (i.e., relying on prediction).
Discussion
We considered 3 ways of introducing a perturbation: suddenly on a single trial (abrupt condition), over 45 trials (intermediate condition), and over 240 trials (gradual condition). We found that despite disruption of M1 using TMS, in response to the abrupt perturbation, the motor output (force in error-clamp trials) adapted quickly. However, within 50 trials after the onset of the abrupt perturbation, the motor output of the control group reached a higher level of adaptation than the TMS group. This impairment persisted for an additional 200 trials during which the perturbation was held constant. That is, in the abrupt condition, TMS over M1 impaired both the early and the late stages of adaptation. In contrast, in the intermediate condition, disruption of M1 only impaired the late training period. When the perturbation was imposed gradually, disruption of M1 had no effect on adaptation. Therefore, we found that disruption of M1 produced the strongest effects on adaptation in the abrupt condition, less in the intermediate condition, and none in the gradual condition.
One way to interpret our results is in the framework of a 2 rate error-dependent learning process: a fast process that adapts strongly to error but has poor retention and a slow process that adapts weakly to error but has strong retention (Smith et al. 2006). Thus, the contribution of the slow process is most significant when errors are small. In the abrupt and intermediate conditions, our results show an impairment when errors are small, consistent with a mechanism that disrupted the slow process but spared the fast process. However, this framework would also predict impairment in the gradual condition where errors are small throughout learning. The fact that disruption of M1 left no measurable impairment in the gradual condition appears inconsistent with the hypothesis that the slow process, at least as defined as an error-dependent learning process, was affected.
Another way to consider our results is in a framework in which learning depends on separate processes that rely on prediction error and repetition. For example, in a recent experiment, Diedrichsen et al. (2010) demonstrated that the history of the motor commands experienced during training produced a memory that acted in parallel with a memory that depended on the errors present during that training. They suggested that whereas the fast adaptive process learned from prediction errors, the slow process did not depend on error but on the history of the motor commands. A hypothesis that emerges from these studies is that in a typical adaptation task in which training allows performance errors to become small, motor commands tend to change little from trial to trial, enhancing the possibility of reinforcement through repetition. Our proxy for repetition of the motor commands was the trial-to-trial variance of the force that subjects produced in error-clamp trials. Using this measure, we found that in the abrupt condition, there was a long period in which control subjects tended to repeat their motor commands, resulting in a decreased variability in force output (Fig. 2D). This period was shorter in the intermediate condition and shortest in the gradual condition. If learning from repetition can be assayed through a measure of trial-to-trial force variance, then the greatest opportunity for repetition-dependent plasticity likely occurred in the abrupt condition and smallest opportunity occurred in the gradual condition. While trial-to-trial force variance is one plausible proxy of the signal required for repetition-dependent learning, the variability in the magnitude of the perturbation may instead be the signal driving learning. Future studies are required to assay the effect of performance variability on the repetition-dependent learning mechanism.
The role of M1 in repetition-dependent plasticity has been highlighted in other experiments in which a movement or sequence of movements is repeated without an explicit performance error. In these experiment, the act of repetition induces both improvements in performance and parallel changes in the motor cortex (Karni et al. 1995; Classen et al. 1998; Matsuzaka et al. 2007). For example, the act of repeating a thumb flexion produces a greater likelihood of generating that thumb flexion in response to a TMS pulse to M1. This cortical plasticity appears to occur despite the absence of performance errors. If we view repetition as a signal that drives plasticity in the motor cortex, then we might expect that disruption of the motor cortex should have little or no effect on performance when learning is driven by errors and motor commands are changing rapidly, but impair performance when repetition is driving plasticity. Although our study was not designed to dissociate learning from error versus learning from repetition, our data are consistent with a role for M1 in repetition-dependent, but not error-based learning: 1) When errors were large, forces produced by the subjects adapted rapidly, and we saw no effects of M1 TMS on adaptation. 2) When errors were small, in some conditions (abrupt and intermediate), there was impairment due to TMS of M1, but in another condition (gradual), there was no impairment. One difference between the conditions was the degree of repetition in the motor commands. TMS of M1 produced adaptation impairments when both the errors were small, and there was a greater number of trials in which the motor commands showed a small variance.
There is now substantial data regarding the mechanisms that support repetition-dependent learning in the motor cortex. Repetition of a movement during a single session of training (particularly when this repetition is reinforced with reward) strengthens horizontal excitatory connections (Rioult-Pedotti et al. 1998), weakens inhibitory connections (Floyer-Lea et al. 2006), and induces formation of postsynaptic dendritic spines (Xu et al. 2009; Yang et al. 2009). All 3 of these processes combine to produce neural plasticity. It is possible that a low-variance training schedule (resulting in high repetition) enhances this plasticity, whereas a high-variance training schedule reduces this plasticity. These effects are likely to underlie the observation that response of the human M1 to cortical or peripheral stimulation undergoes rapid changes after a few minutes of movement repetition (Rosenkranz et al. 2007). Furthermore, drugs that enhance γ-aminobutyric acid (GABA) or block N-methyl-D-aspartic acid transmission and uptake tend to inhibit formation of cortical long-term potentiation (Hess and Donoghue 1994), resulting in reduced repetition-dependent plasticity in the motor cortex (Butefisch et al. 2000). The same drugs impair learning of reaching movements in response to an abrupt perturbation (Donchin et al. 2002).
Neurophysiological results from adaptive control of reaching have demonstrated that as monkeys learn to compensate for a perturbation, the motor output undergoes rapid adaptation, but this rapid adaptation is not reflected in corresponding changes in the discharge of M1 cells before onset of the movement (Paz et al. 2003). Instead, robust changes in M1 delay-period activity appear later in training when there has been a period of repetition in the motor commands (Paz et al. 2003, 2005). Based on this result, one would expect that disruption of M1 should affect adaptation, particularly late in the learning period. However, while stimulation of the posterior parietal cortex 40 ms after movement onset during reaching and pointing has been shown to disrupt online correction mechanisms (Desmurget et al. 1999) and induce changes in movement kinematics during the late part of the training period (Della-Maggiore et al. 2004), a number of previous TMS studies have found that disruption of M1 has no effect on performance during training (Richardson et al. 2006; Hadipour-Niktarash et al. 2007). Our results here provide a potential explanation for this apparent contradiction of the role of M1: Previous works have assayed performance via kinematic measures of reaching. Using these measures, we also found no effect of TMS. However, when we assayed performance via forces that subjects produced in error-clamp trials, the effect of TMS was evident. Why was there a difference in the patterns of force produced in error-clamp trials but not movement kinematics in free trials?
One possibility is that the force in error-clamp trials measures a feed-forward predictive component of the movement. In contrast, both feedback and feed-forward processes may affect motor output in the free reaching movements. In the control subjects, forces in error-clamp trials were good predictors of endpoint errors in free reaching but not in the TMS subjects. In the control subjects, motor commands early in free reaching were also good predictors of endpoint errors but again not in the TMS subjects. However, in the TMS subjects, motor commands late in the free reaches were good predictors of endpoint errors but not in the control subjects. Based on this double dissociation, we speculate that in the TMS subjects, kinematic performance appeared unaffected not because the motor commands that initiated their movement were comparable with the control subjects but because there was compensation via some form of internal or sensory feedback. This view is consistent with the observation that there is decreased M1 activity during arm movements that require higher reliance on feedback (Seidler et al. 2004).
Does discharge of cells in M1 reflect contributions of both error- and repetition-dependent signals? Green et al. (2007) found that during curl field adaptation, discharge of caudal M1 cells during reaching encoded the ongoing error at roughly 100 ms latency. When perturbations were random, the latency remained constant. As perturbations repeated, the latency declined, suggesting a transition from an error-dependent feedback response to a predictive feed-forward response. It seems reasonable that at least part of this predictive response is conveyed via the cerebellum to the motor cortex. That is, the cerebellar input corrects the M1 response. However, as the movement is repeated, M1 cells may undergo plasticity so that they produce the feed-forward response not through internal feedback from the cerebellum (Tseng et al. 2007), but in their response to inputs from premotor or parietal areas. Based on this conjecture, one would predict that disruption of synaptic plasticity in M1 should not alter the rapid phase of reach adaptation, but impair the later component in which motor commands repeat.
Motor learning is a complex process supported by multiple brain structures (Shadmehr and Krakauer 2008). Error-dependent and repetition-dependent signals appear to be some of the driving forces in motor learning (Huang et al. 2009) with potentially distinct timescales (Diedrichsen et al. 2010). Studies from our laboratory have shown that cerebellar patients are impaired when adapting to an abrupt perturbation (Smith and Shadmehr 2005) but show much less impairment when adapting to a gradual perturbation (Criscimagna-Hemminger et al. 2010). Our finding was reminiscent of a study in knockout mice that were unable to maintain long-term depression (LTD) over time (Boyden et al. 2006). In those animals, skill was maintained when acquired through small errors but not through large errors. The interaction between the disruption of LTD maintenance in the cerebellum and the size of the errors suggests that the gradual and abrupt conditions might involve very different mechanisms at the level of the cerebellum. In the present study, we also found an interaction between the perturbation scheduled and the role of the motor cortex in motor learning. Disruption of M1 caused the greatest impairment in the abrupt protocol and no effect in the gradual protocol, hence pointing to a repetition-dependent process. However, the time course of the impairment was very different. Error-based learning was impaired in cerebellar patients (Criscimagna-Hemminger et al. 2010) as evidenced from their impairment during the very first trials of the learning period. In contrast, TMS over M1 only disrupted the late part of the learning. In light of our current results that TMS of M1 has little or no effects in the gradual condition, we speculate that the learning that we observed in the cerebellar patients was not due to repetition and the involvement of M1 but possibly due to spared learning in the deep cerebellar nuclei or elsewhere. Future studies are required in order to investigate how cerebellar degeneration patients are able to learn in the gradual condition.
Funding
National Institutes of Health (NIH, NS37422); Belgian American Educational Foundation, internal research grant (Fonds Spéciaux de Recherche) of the Université catholique de Louvain (Belgium), Fondation pour la Vocation (Belgium) to J.J.O.d.X.; predoctoral fellowship from the NIH (NS062647 to S.E.C.-H.).
Acknowledgments
Conflict of Interest: None declared.
References
- Arce F, Novick I, Mandelblat-Cerf Y, Israel Z, Ghez C, Vaadia E. Combined adaptiveness of specific motor cortical ensembles underlies learning. J Neurosci. 2010;30:5415–5425. doi: 10.1523/JNEUROSCI.0076-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barash S, Melikyan A, Sivakov A, Zhang M, Glickstein M, Thier P. Saccadic dysmetria and adaptation after lesions of the cerebellar cortex. J Neurosci. 1999;19:10931–10939. doi: 10.1523/JNEUROSCI.19-24-10931.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyden E, Katoh A, Pyle J, Chatila T, Tsien R, Raymond J. Selective engagement of plasticity mechanisms for motor memory storage. Neuron. 2006;51:823–834. doi: 10.1016/j.neuron.2006.08.026. [DOI] [PubMed] [Google Scholar]
- Brown L, Wilson E, Gribble P. Repetitive transcranial magnetic stimulation to the primary motor cortex interferes with motor learning by observing. J Cogn Neurosci. 2009;21:1013–1022. doi: 10.1162/jocn.2009.21079. [DOI] [PubMed] [Google Scholar]
- Butefisch CM, Davis BC, Wise SP, Sawaki L, Kopylev L, Classen J, Cohen LG. Mechanisms of use-dependent plasticity in the human motor cortex. Proc Natl Acad Sci U S A. 2000;97:3661–3665. doi: 10.1073/pnas.050350297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butefisch CM, Khurana V, Kopylev L, Cohen LG. Enhancing encoding of a motor memory in the primary motor cortex by cortical stimulation. J Neurophysiol. 2004;91:2110–2116. doi: 10.1152/jn.01038.2003. [DOI] [PubMed] [Google Scholar]
- Classen J, Liepert J, Wise S, Hallett M, Cohen L. Rapid plasticity of human cortical movement representation induced by practice. J Neurophysiol. 1998;79:1117–1123. doi: 10.1152/jn.1998.79.2.1117. [DOI] [PubMed] [Google Scholar]
- Cothros N, Köhler S, Dickie E, Mirsattari S, Gribble P. Proactive interference as a result of persisting neural representations of previously learned motor skills in primary motor cortex. J Cogn Neurosci. 2006;18:2167–2176. doi: 10.1162/jocn.2006.18.12.2167. [DOI] [PubMed] [Google Scholar]
- Criscimagna-Hemminger S, Bastian A, Shadmehr R. Size of error affects cerebellar contributions to motor learning. J Neurophysiol. 2010;103:2275–2284. doi: 10.1152/jn.00822.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Della-Maggiore V, Malfait N, Ostry DJ, Paus T. Stimulation of the posterior parietal cortex interferes with arm trajectory adjustments during the learning of new dynamics. J Neurosci. 2004;24:9971–9976. doi: 10.1523/JNEUROSCI.2833-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desmurget M, Epstein C, Turner R, Prablanc C, Alexander G, Grafton S. Role of the posterior parietal cortex in updating reaching movements to a visual target. Nat Neurosci. 1999;2:563–567. doi: 10.1038/9219. [DOI] [PubMed] [Google Scholar]
- Diedrichsen J, White O, Newman D, Lally N. Use-dependent and error-based learning of motor behaviors. J Neurosci. 2010;30:5159–5166. doi: 10.1523/JNEUROSCI.5406-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donchin O, Francis J, Shadmehr R. Quantifying generalization from trial-by-trial behavior of adaptive systems that learn with basis functions: theory and experiments in human motor control. J Neurosci. 2003;23:9032–9045. doi: 10.1523/JNEUROSCI.23-27-09032.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donchin O, Sawaki L, Madupu G, Cohen LG, Shadmehr R. Mechanisms influencing acquisition and recall of motor memories. J Neurophysiol. 2002;88:2114–2123. doi: 10.1152/jn.2002.88.4.2114. [DOI] [PubMed] [Google Scholar]
- Ethier V, Zee D, Shadmehr R. Spontaneous recovery of motor memory during saccade adaptation. J Neurophysiol. 2008;99:2577–2583. doi: 10.1152/jn.00015.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Floyer-Lea A, Wylezinska M, Kincses T, Matthews P. Rapid modulation of GABA concentration in human sensorimotor cortex during motor learning. J Neurophysiol. 2006;95:1639–1644. doi: 10.1152/jn.00346.2005. [DOI] [PubMed] [Google Scholar]
- Galea J, Celnik P. Brain polarization enhances the formation and retention of motor memories. J Neurophysiol. 2009;102:294–301. doi: 10.1152/jn.00184.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gandolfo F, Li C, Benda B, Schioppa C, Bizzi E. Cortical correlates of learning in monkeys adapting to a new dynamical environment. Proc Natl Acad Sci U S A. 2000;97:2259–2263. doi: 10.1073/pnas.040567097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green AM, Shadmehr R, Kalaska JF. Program no. 413.4. 2007 Neuroscience Meeting Planner. San Diego (CA): Society for Neuroscience; 2007. Motor cortex: converting errors into predictions. online. [Google Scholar]
- Hadipour-Niktarash A, Lee C, Desmond J, Shadmehr R. Impairment of retention but not acquisition of a visuomotor skill through time-dependent disruption of primary motor cortex. J Neurosci. 2007;27:13413–13419. doi: 10.1523/JNEUROSCI.2570-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hess G, Donoghue J. Long-term potentiation of horizontal connections provides a mechanism to reorganize cortical motor maps. J Neurophysiol. 1994;71:2543–2547. doi: 10.1152/jn.1994.71.6.2543. [DOI] [PubMed] [Google Scholar]
- Huang V, Shadmehr R. Persistence of motor memories reflects statistics of the learning event. J Neurophysiol. 2009;102:931–940. doi: 10.1152/jn.00237.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang VS, Mazzoni P, Krakauer JW. Program no. 369.13. 2009 Neuroscience Meeting Planner. Chicago (IL): Society for Neuroscience; 2009. Learning of a visuomotor rotation through a combination of use-dependent shaping and error-based adaptation. online. [Google Scholar]
- Izawa J, Rane T, Donchin O, Shadmehr R. Motor adaptation as a process of reoptimization. J Neurosci. 2008;28:2883–2891. doi: 10.1523/JNEUROSCI.5359-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kagerer FA, Contreras-Vidal JL, Stelmach GE. Adaptation to gradual as compared with sudden visuo-motor distortions. Exp Brain Res. 1997;115:557–561. doi: 10.1007/pl00005727. [DOI] [PubMed] [Google Scholar]
- Karni A, Meyer G, Jezzard P, Adams M, Turner R, Ungerleider L. Functional MRI evidence for adult motor cortex plasticity during motor skill learning. Nature. 1995;377:155–158. doi: 10.1038/377155a0. [DOI] [PubMed] [Google Scholar]
- Kluzik J, Diedrichsen J, Shadmehr R, Bastian A. Reach adaptation: what determines whether we learn an internal model of the tool or adapt the model of our arm? J Neurophysiol. 2008;100:1455–1464. doi: 10.1152/jn.90334.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li C, Padoa-Schioppa C, Bizzi E. Neuronal correlates of motor performance and motor learning in the primary motor cortex of monkeys adapting to an external force field. Neuron. 2001;30:593–607. doi: 10.1016/s0896-6273(01)00301-4. [DOI] [PubMed] [Google Scholar]
- Liepert J, Classen J, Cohen L, Hallett M. Task-dependent changes of intracortical inhibition. Exp Brain Res. 1998;118:421–426. doi: 10.1007/s002210050296. [DOI] [PubMed] [Google Scholar]
- Malfait N, Ostry D. Is interlimb transfer of force-field adaptation a cognitive response to the sudden introduction of load? J Neurosci. 2004;24:8084–8089. doi: 10.1523/JNEUROSCI.1742-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsuzaka Y, Picard N, Strick P. Skill representation in the primary motor cortex after long-term practice. J Neurophysiol. 2007;97:1819–1832. doi: 10.1152/jn.00784.2006. [DOI] [PubMed] [Google Scholar]
- Michel C, Pisella L, Prablanc C, Rode G, Rossetti Y. Enhancing visuomotor adaptation by reducing error signals: single-step (aware) versus multiple-step (unaware) exposure to wedge prisms. J Cogn Neurosci. 2007;19:341–350. doi: 10.1162/jocn.2007.19.2.341. [DOI] [PubMed] [Google Scholar]
- Paz R, Boraud T, Natan C, Bergman H, Vaadia E. Preparatory activity in motor cortex reflects learning of local visuomotor skills. Nat Neurosci. 2003;6:882–890. doi: 10.1038/nn1097. [DOI] [PubMed] [Google Scholar]
- Paz R, Natan C, Boraud T, Bergman H, Vaadia E. Emerging patterns of neuronal responses in supplementary and primary motor areas during sensorimotor adaptation. J Neurosci. 2005;25:10941–10951. doi: 10.1523/JNEUROSCI.0164-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paz R, Vaadia E. Specificity of sensorimotor learning and the neural code: neuronal representations in the primary motor cortex. J Physiol Paris. 2004;98:331–348. doi: 10.1016/j.jphysparis.2005.09.005. [DOI] [PubMed] [Google Scholar]
- Richardson AG, Overduin SA, Valero-Cabre A, Padoa-Schioppa C, Pascual-Leone A, Bizzi E, Press DZ. Disruption of primary motor cortex before learning impairs memory of movement dynamics. J Neurosci. 2006;26:12466–12470. doi: 10.1523/JNEUROSCI.1139-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rioult-Pedotti M, Friedman D, Hess G, Donoghue J. Strengthening of horizontal cortical connections following skill learning. Nat Neurosci. 1998;1:230–234. doi: 10.1038/678. [DOI] [PubMed] [Google Scholar]
- Rosenkranz K, Kacar A, Rothwell J. Differential modulation of motor cortical plasticity and excitability in early and late phases of human motor learning. J Neurosci. 2007;27:12058–12066. doi: 10.1523/JNEUROSCI.2663-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saijo N, Gomi H. Multiple motor learning strategies in visuomotor rotation. PLoS One. 2010;5:e9399. doi: 10.1371/journal.pone.0009399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seidler R, Noll D, Thiers G. Feedforward and feedback processes in motor control. Neuroimage. 2004;22:1775–1783. doi: 10.1016/j.neuroimage.2004.05.003. [DOI] [PubMed] [Google Scholar]
- Shadmehr R, Krakauer J. A computational neuroanatomy for motor control. Exp Brain Res. 2008;185:359–381. doi: 10.1007/s00221-008-1280-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith MA, Ghazizadeh A, Shadmehr R. Interacting adaptive processes with different timescales underlie short-term motor learning. PLoS Biol. 2006;4:e179. doi: 10.1371/journal.pbio.0040179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith MA, Shadmehr R. Intact ability to learn internal models of arm dynamics in Huntington's disease but not cerebellar degeneration. J Neurophysiol. 2005;93:2809–2821. doi: 10.1152/jn.00943.2004. [DOI] [PubMed] [Google Scholar]
- Srimal R, Diedrichsen J, Ryklin E, Curtis C. Obligatory adaptation of saccade gains. J Neurophysiol. 2008;99:1554–1558. doi: 10.1152/jn.01024.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tseng Y, Diedrichsen J, Krakauer J, Shadmehr R, Bastian A. Sensory prediction errors drive cerebellum-dependent adaptation of reaching. J Neurophysiol. 2007;98:54–62. doi: 10.1152/jn.00266.2007. [DOI] [PubMed] [Google Scholar]
- Xu T, Yu X, Perlik A, Tobin W, Zweig J, Tennant K, Jones T, Zuo Y. Rapid formation and selective stabilization of synapses for enduring motor memories. Nature. 2009;462:915–919. doi: 10.1038/nature08389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu-Wilson M, Chen-Harris H, Zee D, Shadmehr R. Cerebellar contributions to adaptive control of saccades in humans. J Neurosci. 2009;29:12930–12939. doi: 10.1523/JNEUROSCI.3115-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang G, Pan F, Gan W. Stably maintained dendritic spines are associated with lifelong memories. Nature. 2009;462:920–924. doi: 10.1038/nature08577. [DOI] [PMC free article] [PubMed] [Google Scholar]