Noninvasive Methods for Determining Pulmonary Vascular Function in Children with Pulmonary Arterial Hypertension: Application of a Mechanical Oscillator Model

Abstract

Objective

Noninvasive diagnostics for pulmonary arterial hypertension (PAH) have traditionally sought to predict main pulmonary artery pressure from qualitative or direct quantitative measures of the flow velocity pattern obtained from spectral Doppler ultrasound examination of the main pulmonary artery. A more detailed quantification of flow velocity patterns in the systemic circuit has been obtained by parameterizing the flow trace with a simple dynamic system model. Here, we investigate such a model’s utility as a noninvasive predictor of total right heart afterload and right heart function.

Design

Flow velocity and pressure was measured within the main pulmonary artery during right heart catheterization of patients with normal hemodynamics (19 subjects, 20 conditions) and those with PAH undergoing reactivity evaluation (34 patients, 69 conditions). Our model parameters were obtained by least-squares fitting the model velocity to the measured flow velocity.

Results

Five parameter means displayed significant (P < .05) differences between normotensive and hypertensive groups. The model stiffness parameter correlated to actual pulmonary vascular resistance (r = 0.4924), pulmonary vascular stiffness (r = 0.6811), pulmonary flow (r = 0.6963), and stroke work (r = 0.7017), while the model initial displacement parameter had good correlation to stiffness (r = 0.6943) and flow (r = 0.6958).

Conclusions

As predictors of total right heart afterload (resistance and stiffness) and right ventricle work, the model parameters of stiffness and initial displacement offer more comprehensive measures of the disease state than previous noninvasive methods and may be useful in routine diagnostic monitoring of patients with PAH.

Introduction

Evaluation of pulmonary arterial hypertension (PAH) requires the invasive measurement of cardiac output, mean pulmonary artery pressure (MPAP), and pulmonary capillary wedge pressure. The baseline values and reactivity of these measurements to clinical challenges provide the primary diagnostic for this disease: pulmonary vascular resistance (PVR), which is the ratio of the pressure drop across the vasculature to the cardiac output.

A reliable noninvasive predictor of PAH status would be invaluable to its diagnosis and treatment. Many existing noninvasive diagnostics for the disease rely on echocardiography (ultrasound Doppler)¹ to quantify the velocity in the main and first branch pulmonary arteries, and to estimate pressure. One approach has found that the pulmonary flow acceleration time (AcT), i.e., the time shown in the Doppler trace from the onset of flow to the maximum flow, is significantly smaller in hypertensive patients, and that this time and its ratio to the right ventricle ejection time (RVET) strongly correlate with MPAP.^2–7 Another utilizes a simplified form of the Bernoulli equation to estimate right ventricular systolic pressure in thepresence of a tricuspid regurgitant (TR) jet.^8–10 Implementing these methods clinically can present difficulties that have precluded their use in all patients as routine diagnostics for this disease.^10–14

A more mechanistic approach for noninvasive characterization of heart and/or vascular status relies on fitting ultrasound Doppler velocity profile data to the motion predicted by a simple single-degree-of-freedom mass-spring-damper oscillator model, also known as the damped, free classical mechanical oscillator (CMO), seen in Figure 1A. This entails finding model parameters that generate the best match between model response and experimental data. In one common method,^15–17 the systemic A- and E-waves, which characterize mitral flow, were fitted to the predicted motion of the CMO model. The model was assumed to approximately represent the ventricular wall motion and contained lumped elements of inertance, resistance, and compliance. Such a model has also been applied to the systemic circulation to quantify diastolic function,¹⁸ differentiate hypertensive and normotensive status,¹⁹ and examine diabetes and heart failure;^20,21 additional applications may be found in the literature.

Figure 1.

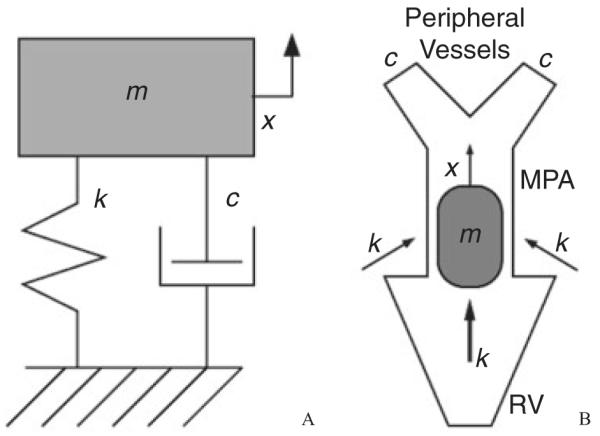
(A) Classical mechanical oscillator with components of mass (m), stiffness (k), and damping (c). The mass displaces only along the x-axis. (B) For our model, we postulate correspondence between the mass component and the fluid bolus traveling through the main pulmonary artery (MPA), between the spring (stiffness) and the driving force provided by the right ventricle (and the proximal arteries after systole), between the damper and the fluid viscous drag in the peripheral vessels, and between the displacement (x) and the flow through the MPA. RV, right ventricle.

In the present study we investigate the CMO model’s utility as a noninvasive diagnostic for pediatric PAH by fitting its motion to the blood velocity time-history obtained at the centerline of the main pulmonary artery (MPA). We hypothesize that the resulting model parameters may be used to quantify overall right heart afterload. Recently we have developed an invasive measure of total afterload;^22,23 this work could eventually enable the measurement to become part of an initial noninvasive assessment of the disease. Total afterload better characterizes the dynamic behavior of the pulmonary vasculature compared with invasively obtained PVR or pressure because it additionally quantifies pulmonary vascular stiffness (PVS). Inclusion of stiffness in diagnosis should provide a more comprehensive description of the disease state, and has already been shown to better predict pulmonary hypertension mortality in adults²⁴ and PAH heart outcomes in children.²³ The goals of this study were to: (1) calculate CMO parameters from echo data obtained from a large pediatric population (53 patients, 89 reactivity conditions) of both normotensive and hypertensive individuals; (2) determine which parameters produce significant differences between the parameter sets of normal and hypertensive populations; and (3) investigate correlations between the parameters and invasively obtained hemodynamic measurements.

Methods

Clinical Study

Patient Selection

After institutional review board approval and informed consent and assent had been obtained, spectral Doppler ultrasound data were obtained during cardiac catheterization for routine evaluation and treatment at the Children’s Hospital in Denver, CO, USA. The patient population was divided into two groups. Group 1 studies were conducted after intervention to correct congenital heart defects (12 patent ductus arteriosus, 7 atrial septal defect), had normal MPAPs, and were considered the control (19 patients, 20 reactivity conditions; median age = 2 years, range 0.33–16 years, 12 females). The remainder of patients were placed in group 2 (34 patients, 69 reactivity conditions; median age = 3.5 years, range 0.25–17 years, 13 females) and suffered from pulmonary hypertension; most underwent tests for PV reactivity with the administration of oxygen, nitric oxide, or other therapeutic agents (epoprostenol, diltiazem, sidenafil, iloprost). A summary of patient characteristics is in Table 1.

Table 1.

Baseline Patient Characteristics (Mean ± Standard Deviation) at Control (Group 1) and with PAH (Group 2)

	Control (Group 1)	PAH (Group 2)	P
Demographics
N	19.00	34.00	na
Age (months)	52 ± 61	69 ± 65	.3636
BSA (m2)	0.74 ± 0.48	0.74 ± 0.41	.9733
Female/Male	12/7	13/21	.0842
Heart rate	111 ± 25.3	105 ± 27.0	.4172
Hemodynamics
Mean pulmonary artery pressure (mm Hg)	20.1 ± 8.1	40.5 ± 18.9	<.0001
Cardiac index (L/min/m2)	7.8 ± 4.5	5.1 ± 2.9	.0296
Stroke volume (mL)	54.9 ± 51.6	37.4 ± 28.2	.1836
Pulse pressure (mm Hg)	18.5 ± 4.3	34.8 ± 5.9	<.0001
Pulmonary artery resistance (mm Hg min/L)	3.5 ± 2.5	11.7 ± 12.2	.0004
Pulmonary artery stiffness (PP/SV) (mm Hg/cc)	0.56 ± 0.37	1.65 ± 1.86	.0021
Stroke work (SV*MPAP) (mm Hg*cc)	1000 ± 770	1620 ± 1650	.0687
Stroke power (CO*MPAP) (mm Hg L/min)	103 ± 69.5	157 ± 154	.0855
Acceleration time/right ventricle ejection time	0.659 ± 0.058	0.616 ± 0.082	.0121

PAH, pulmonary arterial hypertension; BSA, body surface area; MPAP, mean pulmonary artery pressure; PP, pulse pressure; SV, stroke volume; CO, cardiac output. Significant p-values are shown in bold.

Clinical Data Acquisition

Pulse wave Doppler velocity measurements were taken with a commercial ultrasound scanner (Vivid 5, GE Medical Systems Inc., Waukesha, WI) from a parasternal short axis view within the midpoint of the MPA. Two-dimensional echo and color Doppler was used to align the ultrasound beamline parallel to the main flow direction. We estimate minimal errors due to ultrasound beam angulation (<5°). Pressure measurements were made with standard fluid-filled catheters (Transpac IV, Abbott Laboratories, Abbott Park, Illinois), also within the MPA. Cardiac output was measured by Fick’s method with measured oxygen consumption in cases where intracardiac shunts were in place and by thermodilution otherwise. Ultrasound and catheter measurements were made simultaneously for approximately 16 seconds in each patient; this typically encompassed 20 cardiac cycles.

Data Analysis

Automated MPA Velocity Acquisition

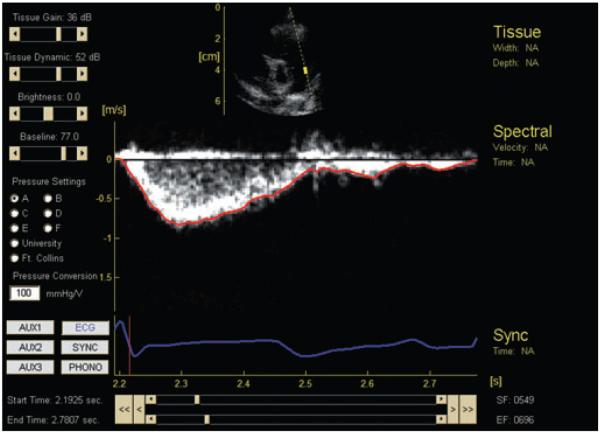
Offline, MPA midline velocity time-histories were obtained semiautomatically from the digitally recorded PW Doppler images. Figure 2 shows the complete interface (based on EchoMAT v2.1, GE Medical Systems Inc, Waukesha, Wis) used to conduct the analysis; below the PW Doppler data and overlaying computed velocity trace (red) is an ECG trace (blue) used to separate cardiac cycles. Only the red trace (i.e., Doppler velocity in the MPA) is used in the modeling procedure. The method is referred to as “semiautomatic” in that user input was occasionally needed to remove velocity spikes from the trace due to noise and/or valve clicks. As implemented, the method requires less than 5 seconds to obtain a velocity trace for 16 seconds of spectral data. After the trace was obtained, the user manually established individual systolic time intervals and forced the start and end velocities of these intervals to zero. This created short starting and ending portions of the velocity trace that deviated from the spectral image, but typically the velocity in these areas was already at a level equal to or below the level of noise in the image. More details of the velocity trace acquisition may be found in the Appendix.

Figure 2.

Graphical user interface for semiautomatic impedance computation. At center transient PW Doppler data with an overlain computed velocity trace (red); at center bottom, the corresponding ECG signal (blue).

Systolic Flow Model

The velocity data acquired from each systolic time interval was fitted to the CMO model (Figure 1A). It consists of a body of mass m affixed to a rigid wall via a spring with stiffness k and a viscous dashpot with damping factor c. To account for the initial system energy—i.e., the energy provided to the blood by the right heart—the model is assumed to begin with the body displaced a distance x₀ from its rest position, so that the spring initially has preload. Our expected correspondence between model parameters and the pulmonary vasculature is shown in Figure 1B. At the beginning of systole, the mass is released from its stretched position and the spring acts to move it; in this way, the spring models the driving pressure or force that acts on the bolus of blood moved during systole, represented by the mass itself. The model’s damping c should be proportional to the peripheral resistance, i.e., the viscous retarding force present in the smaller peripheral arteries. Finally, because the mass moves through the distance x₀ after being released, we consider x₀ to be representative of a flow distance or flow quantity per cardiac cycle.

Values for three of the four model parameters (k, c, x₀) are obtained from the fitting process, while the body mass m may be set to one without loss of generality. For the solutions obtained, increasing c generally yields velocity traces of shorter cycle duration and increased peak velocity; increasing k generally yields increased cycle duration and reduced peak velocity; and increasing x₀ yields increased peak velocity at constant cycle duration. Additional parameters corresponding to equation constants or meaningful system properties (such as kinetic or potential energy) were also computed postfit for comparison with hemodynamic data; these are described more fully in the Appendix, along with mathematical details of the model and the fitting procedure.

Statistical Analysis

Statistical analysis was performed with the S-Plus package (Insightful, Seattle, Wash) on groups corresponding to normotensive (control) and hypertensive patient status in addition to the pooled data set. The distributions of both the grouped and pooled data set were first tested for skewness to determine the appropriateness of applying a normalizing parameter (body surface area), a normalizing transform (in this case, the natural logarithm), or both. For each variable in the grouped data, an F-test was first performed to determine if the group variances were equal; then the appropriate (equal or unequal variance) t-test was performed to determine if the group means were equal. Univariate regressions were performed to determine if the CMO model parameters were significant predictors of the hemodynamic variables. Coefficients of determination for the regressions are calculated according to standard procedure (see, e.g., Johnson and Wichern²⁵). Throughout our results, significance is set at 95%, P values refer to the two-tailed value, and data are reported as mean ± standard deviation.

Reproducibility was assessed through the calculation of intraobserver and interobserver variability. Fitting was performed by two experienced modelers (KSH and JKG) on separate days. Variability was computed for each fitted parameter as the difference between observations divided by the mean of the observations.

Results

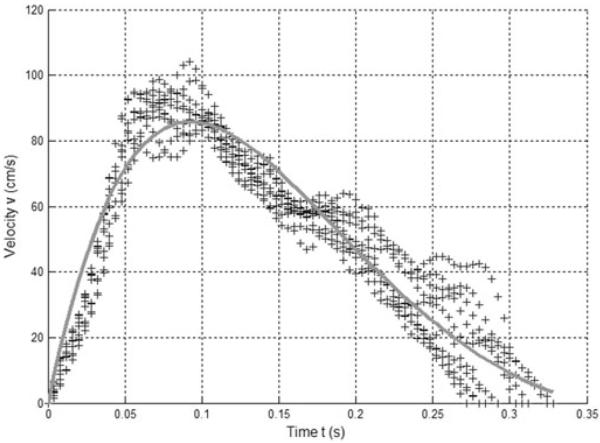
Data points (represented as “+” symbols) from 10 representative velocity envelopes from a single patient condition are shown in Figure 3, along with the average parameter data from multiple optimized CMO fit traces (shown as a solid line). This example has 75.6 ± 4.9 experimental points per cycle; the 250 Hz sample rate gives a total systolic time of 301.6 ± 19.6 milliseconds. Over all the data, the systolic traces were represented by 78.0 ± 15.9 data points.

Figure 3.

Multiple sets of experimental data (+) and average classical mechanical oscillator model fit obtained from multiple optimizations (line).

Patients in the control group have normal pulmonary pressures (MPAP = 20.1 ± 8.1 mm Hg), whereas patients in the hypertensive group show PAH (MPAP = 40.5 ± 18.9 mm Hg, baseline condition). The mean cardiac index of the control group is higher, at 7.8 ± 4.5 L/min/m²), compared with 5.1 ± 2.9 L/min/m²) for the hypertensive group. Both pressure and flow differences were significant (P < .0001 and P = .0296, respectively). The mean heart rates, age, and body surface area (BSA) for the two groups are similar (P = n.s.). Patient characteristics and significance levels, calculated at the patient level (n = 53), appear in Table 1.

Table 2 provides t-test results for the 10 CMO parameters in normal form; also shown are two parameters significant only in logarithmic form. The parameter means of x₀, kx₀, and kx₀² all increase significantly in control subjects. The initial displacement x₀ is significant in both standard (listed) and log-transformed forms. Differences in the means of kx₀, an acceleration constant, and kx₀², characterizing the initial system energy, were most significant when they were indexed and log-transformed (P = .0003 and P = .0001, respectively); however, significance is <.02 for all four forms of the variables. Additionally, differences in means of the damping c and the velocity constant V₀ are nearly significant in normal form, and gain significance in log-transformed form.

Table 2.

Grouped Parameters Derived from CMO Model (Mean ± Standard Deviation) at Control (Group 1) and with PAH (Group 2).

	Control (Group 1)	PAH (Group 2)	P
Direct
k (g/s2)	137.9 ± 64.1	121.3 ± 62.3	.3013
c (g/s)	10.14 ± 4.42	8.13 ± 6.61	.1203
x0 (cm)	−15.77 ± 4.67	−12.34 ± 4.92	.0068
X0 (cm)	−8.38 ± 5.02	−8.89 ± 14.40	.8044
V0 (cm/s)	−103.5 ± 38.1	−87.0 ± 73.2	.1839
A0(cm/s2)	−1140 ± 720	−1070 ± 1780	.7996
kx0 (dyne)	−2150 ± 1150	−1400 ± 730	.0107
kx02 (dyne · cm)	36.8e3 ± 28.8e3	19.5e3 ± 17.2e3	.0174
V02 (cm2/s2)	12.1e3 ± 9.5e3	12.8e3 ± 28.5e3	.8535
tc (s)	0.309 ± 0.062	0.316 ± 0.062	.6664
Log-transformed
ln(c) [ln(g/s)]	2.10 ± 0.91	1.07 ± 3.38	.0257
ln(V0) [ln(cm/s)]	4.57 ± 0.37	4.27 ± 0.60	.0151

Direct entries come directly from the model; indexed entries have been scaled by body surface area and log-transformed entries are the natural log of direct values. Significant p-values are shown in bold. CMO, classical mechanical oscillator; PAH, pulmonary arterial hypertension.

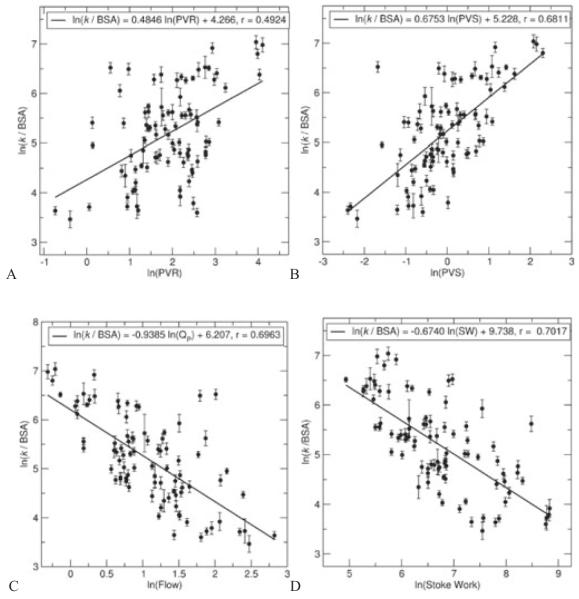
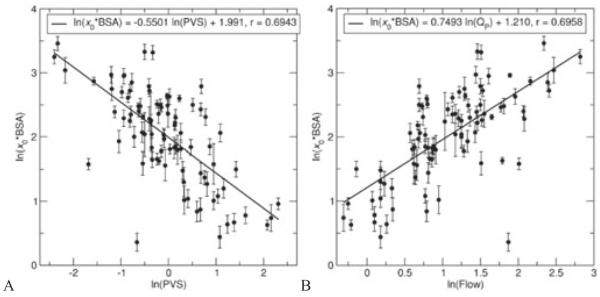
It was found that the three primary model variables (k, c, x₀) displayed high skewness (>0.5 in absolute value); thus, the variables were log-transformed prior to attempting correlations, which reduced skewness in all cases. Shown in Figure 4 are noteworthy univariate correlations found between the hemodynamically measured variables and the stiffness parameter k. In the entire cohort, ln(k/BSA) was positively correlated with PVR (Figure 4A; ln(k/BSA) = 0.4846 · ln(PVR) + 4.266, r = 0.4924), PVS (Figure 4B; ln(k/BSA) = 0.6753 · ln(PVS) + 5.228, r = 0.6811), flow (Figure 4C; ln(k/BSA) = −0.9385 · ln(Q_p) + 6.207, r = 0.6963), and stroke work (Figure 4D; ln(k/BSA) = −0.6740 · ln(SW) + 9.738, r = 0.7017). Figure 5 shows notable univariate correlations for the log-transformed indexed form of x₀, which was positively correlated with PVS (Figure 5A; ln(x₀ · BSA) = −0.5501 · ln(PVS) + 1.991, r = 0.6943) and with flow (Figure 5B; ln(x₀ · BSA) = 0.7493 · ln(Q_p) + 1.210, r = 0.6958). We note that P < .0001 for all these correlations.

Figure 4.

Univariate correlations between normalized classical mechanical oscillator model stiffness (k/BSA) and hemodynamically measured variables (A, B, pulmonary vascular resistance and stiffness—PVR and PVS, respectively; C, pulmonary flow—Q_p; D, stroke work—SW).

Figure 5.

Univariate correlations between normalized classical mechanical oscillator model initial displacement (x₀ · BSA) and hemodynamically measured variables (A, pulmonary vascular stiffness—PVS; B, pulmonary flow—Q_p). BSA, body surface area.

For the correlation involving PVR, we find that k/BSA predicts a PVR of >3 m³ mm Hg/(L/min) with 68.2% sensitivity and 50% specificity. Although PVS is not a routine clinical diagnostic, it was significantly different between the two populations; here we examine its potential use as such, and choose the value 1.11 mm Hg/m³ (the mean of all baseline clinical values) as a differentiator between a “compliant”/healthy state and a “stiff”/PAH state. For the two correlations involving PVS, we find that k/BSA predicts PVS >1.11 mm Hg/m³ with 72.2% sensitivity and 62.9% specificity, while x₀ · BSA predicts with 66.7% sensitivity and 77.1% specificity.

Interobserver variability was found to be 3.3%, 7.6%, and 2.9% for k, c, and x₀, respectively, while intraobserver variability for the same parameters was found to be 3.4%, 24.7%, and 7.1%, respectively.

Discussion

At present, use of invasively obtained hemodynamic variables is standard in the evaluation of PAH. Previous attempts to noninvasively diagnose this disease have relied on direct measurements of Doppler ultrasound velocity waveforms^2–7 or on the existence of valve incompetence^8–10 to predict MPAP. The CMO model parameters presented herein more completely quantify the shape of the velocity waveform in the MPA than previous studies of the pulmonary vasculature and, to the best of our knowledge, have never been applied as a noninvasive diagnostic of PAH. This study, which uses only simple groupings of the patient data, is a pilot investigation into the model’s utility.

As the survival rate of childhood PAH increases, so too does the need for routine noninvasive non-ionizing image-based diagnostics. This work complements previous studies by our team^26,27 in providing such ultrasound-based diagnostics for PAH. While these previous studies examined specific predictors of PVR and local vascular stiffness, here our preliminary results found more generally that the CMO model parameter k holds promise as a predictor of overall right heart function (stroke work and pulmonary flow) and global right heart afterload (PVR and PVS), and the parameter x₀ may be useful as an additional predictor of flow and PVS; we propose further investigation of these parameters as useful new noninvasive diagnostic measures. Should such additional work demonstrate their utility, we believe these CMO parameters will first and foremost belong as part of an initial noninvasive assessment of a PAH patient, either alone or in concert with our other ultrasound-based diagnostics. In this capacity, they could provide more quantitative measures to this traditionally more qualitative assessment.

Vascular stiffness has been found recently as an important additional predictor of morbidity and mortality²⁴ and outcomes²³ for PAH, the prevailing hypothesis being that vascular remodeling yields permanent stiffening of the pulmonary tree, which leads to increases in RV afterload; proximal arterial stiffness has also been shown to affect wall shear in recent computational studies.²⁸ Changes in wall shear may also affect a reduction in vasodilator release.^29–32 Of significance is the method’s relative strength in prediction of PVS; additionally, its capability to predict global PVS complements our noninvasive measure of local, proximal compliance,²⁶ and is superior in the absence of a TR jet. Because the set includes significant predictors of both PVR and PVS, it could potentially provide a better noninvasive diagnostic for disease outcomes than previous studies in this area. Thus, further work holds promise to establish the diagnostic as a good predictor of total afterload, and subsequently, of outcomes.

This diagnostic causes minimal discomfort to the patient, may be performed routinely, and with ongoing reductions in ultrasound equipment size, may eventually become a “routine bedside” evaluation. The model’s use of Spectral data from the MPA should ease possible implementation in the clinical environment, since no unusual or non-routine imaging views are required. While this method is currently only performed as a postprocessing step, generation of the model parameters is not computationally intensive and could be readily implemented as an automatic calculation on commercial ultrasound equipment.

We hypothesized that significant differences could be found between the CMO parameters representing control and hypertensive velocity waveforms. Prior to any discussion of model parameters, we note that the two groups display significant differences in their hemodynamic variable means for MPAP, PVR, PVS, and AcT/RVET, as expected from previous studies of PAH.^1,22,23 Significant differences also exist in the group means of five of the 10 model variables examined. The first three means of interest, x₀, V₀, and kx₀, all show significant increases in absolute value in the control group, and are suggestive of an overall increase in flow, velocity, and acceleration in the MPA. Analogous increases are present in hemodynamically measured quantities of cardiac index and the mean peak velocity (control, 117.0 ± 43.25 cm/s; hypertensive, 89.12 ± 23.58 cm/s: P = .0114). The model damping c is larger for the control group, contrary to our expectation that this parameter is comparable to flow losses in the pulmonary circuit. Clearly, such flow losses—i.e., overall pressure drops due to resistance—are larger in patients with greater PVR (i.e., that are hypertensive); thus, the connection between the model damping parameter, c, and viscous loss through downstream arteries is not appropriate. The remaining significant parameter, kx₀², which quantifies initial system energy, increases in the control group. This suggests that the normotensive flow waveforms display more flow energy, despite the smaller mean right heart power output seen from hemodynamic quantities in this group, and points towards substantially smaller flow losses in the pulmonary circuit of such individuals. With additional clinical study and confirmation, these five measures together might be useful as initial determinants of a patient’s hemodynamic state, and, with commercial implementation of the method, could be obtained regularly in order to track hemodynamic status on a day-to-day basis. Also possible is more sensitive estimation of hemodynamic data through the use of all these significant parameters in multivariate prediction; development of such capability is ongoing.

We note that there are small but significant decreases of the hypertensive group’s AcT/RVET in both the experimental data (control, 0.659 ± 0.058; hypertensive 0.616 ± 0.082: P = .0121) and the model data (control, 0.623 ± 0.048; hypertensive, 0.587 ± 0.073: P = .0129). Such decreases are not as large as previously reported.^2–7 However, our groups display significant differences in flow, and nearly significant differences in peak velocity, which are features noted as being not significantly different in some previous studies (flow;^4,6 velocity,³). These previous studies also only included hemodynamics measured under room conditions, whereas 44% of our hypertensive patients had measurements obtained only under reactivity conditions (i.e., under hypoxia, or after delivery of NO or other therapeutic agents).

There are several limitations to this study that should be recognized. First, we acknowledge that this is a pilot study, and as such, further work is needed to determine if these measures are useful for clinical decision making. Additional patient numbers and statistical work are needed to clarify the relationships shown here, to further investigate the use of the parameter set as multivariate predictors of PAH status, and to produce robust prediction equations suitable for use as clinical diagnostics. Such multivariate analysis will also attempt to improve the model’s sensitivity and specificity in prediction of PVR and PVS. Further, we note that the CMO model represents a simple, single frequency system, whereas the flow through the MPA is coupled to the right heart and distal pulmonary vasculature, which is a complex assembly capable of multi-frequency response. Thus, meaningful physics-based connections between the CMO model parameters and physiologically measured responses are tentative; however, further effort should be made to better understand the predictive relationships between model parameters and hemodynamic variables.

We conclude that the CMO model parameters provide noninvasive prediction of total right heart afterload (PVR and PVS), stroke work, and flow. These predictors and the existence of significant differences between control and hypertensive waveform parameters support the potential future use of the model as a noninvasive diagnostic of PAH.

Appendix

Automated MPA Velocity Acquisition

The velocity acquisition process used a pixel-decimation method in which any image pixel having an intensity value below a specified threshold level was eliminated; this process essentially removes noise from the image. The centerline velocity was then found from the decimated image as the envelope value (i.e., the maximum nondecimated velocity) in each image time-slice. The velocities were found starting from the beginning of the spectral data set, which allowed each value after the first to be checked against the previous velocity to prevent nonphysical accelerations from appearing in the final trace; if the velocity change between two times exceeded a preset limit (taken here as 30 m/s²), it was rejected and a new final nonzero value was found. The raw trace was then smoothed by re-approximating it with a cubic smoothing spline³³ and was presented to the user; this final trace is shown in red, along with the gamma-corrected, decimated image, in the center of Figure 2.

Systolic Flow Model

The motion of the flow velocity in the MPA is represented herein by the CMO model (Figure 1), which is described by the equation

$$m\ddot{x}\left(t\right)+c\stackrel{.}{x}\left(t\right)+kx\left(t\right)=0,$$ (1)

in which x(t) is the mass displacement, an overdot indicates a time derivative, and m, c, and k are the system mass, damping, and stiffness parameters. Without loss of generality we may set m = 1 g, leaving the equation with two floating parameters which are specified on a per-mass basis. With real initial conditions x(t₀) = x₀ and $\stackrel{.}{x}\left(t_0\right)=0$, the general solution (displacement) is then given by the real part of

$$\begin{array}{cc}\hfill x\left(t\right)=& {\mathrm{e}}^{-ct∕2}{x}_0[\mathrm{Cosh}(½\sqrt{{\mathrm{c}}^2-4kt})+\phantom{]}\hfill \\ \hfill & \phantom{[}\frac{c\mathrm{Sinh}(½\sqrt{{\mathrm{c}}^2-4kt})}{\sqrt{{\mathrm{c}}^2-4kt}}].\hfill \end{array}$$ (2)

This is then differentiated in time to obtain velocity and acceleration:

$$\stackrel{.}{x}\left(t\right)=-\frac{2k{x}_0{\mathrm{e}}^{-ct∕2}\mathrm{Sinh}(½\sqrt{{\mathrm{c}}^2-4kt})}{\sqrt{{\mathrm{c}}^2-4kt}},$$ (3)

$$\begin{array}{cc}\hfill \ddot{x}\left(t\right)=& {\mathrm{e}}^{-ct∕2}k{x}_0[\mathrm{Cosh}(½\sqrt{{\mathrm{c}}^2-4kt})+\phantom{]}\hfill \\ \hfill & \phantom{[}\frac{c\mathrm{Sinh}(½\sqrt{{\mathrm{c}}^2-4kt})}{\sqrt{{\mathrm{c}}^2-4kt}}].\hfill \end{array}$$ (4)

We note that only the real parts of (3) and (4) are of interest to our procedure. Equation (3) is actually used in fitting, while the other two equations yield potentially useful parameter combinations, as noted below.

For each systolic time interval (of the typically 20+ available in each echo data set), a nonlinear least-squares (NLS) fitting procedure^34,35 as implemented in MATLAB (The Mathworks, Natick, MA) was used to find the values for k, c, and x₀ that optimized the correspondence between the velocity expression (3) and the clinical velocity data. An analytic Jacobian (i.e., [$\partial \stackrel{.}{x}∕\partial k$, $\partial \stackrel{.}{x}∕\partial c$, $\partial \stackrel{.}{x}∕\partial x_0$]) was used in the method to aid fit convergence. We note that (2)–(4) do not presume the exact nature of the solution; whether the system was underdamped or overdamped was determined only through the fitting procedure. Parameters representing an under-damped solution were provided to the NLS algorithm as an initial guess; notably, large variations to this guess examined in 10 cases—including providing values of c that would yield an over-damped solution—produced insignificant changes to the final parameter values. Means and standard deviations of the fit results (i.e., k, c, and x₀) were obtained for each patient after all the cycles were analyzed, allowing for the calculation of uncertainties due to cycle-to-cycle variability, and a plot of the mean data against all cycle data was provided to the user as a visual check of the fit.

Ten parameters in total were extracted from the CMO model for comparison with hemodynamically measured data. These parameters were, in addition to the three fitted parameters k, c, and x₀: the second displacement constant $X_0=x_{0}c∕\sqrt{{\mathrm{c}}^2-4kt}$; the velocity constant $V_0=2k{x}_0∕\sqrt{{\mathrm{c}}^2-4kt}$; the two acceleration constants kx₀ and A₀ = cV₀/2; kx₀², a measure of the system potential energy; the squared velocity constant V₀², a measure of the system kinetic energy; and the duration of systole, t_s, which is essentially RVET. Because both the hemodynamic variables and the model parameter sets had skewed probability distributions, both log-transformed and indexed (i.e., multiplied or divided by BSA) forms of both the hemodynamically measured data and the CMO model parameters were also examined for possible correlation.

Analysis Implementation

As previously noted, the method is implemented in MATLAB and thus cannot yet be performed directly in the clinical workflow. The offline analysis is graphical user interface based and requires only basic computer skills, a business-class personal computer, and a license for MATLAB ($800 commercial). The software can currently read and process data formats native to either the CFM800/System 5/Vivid 5 (EchoPAC format, GE Medical Systems Inc, Waukesha, WI) or Vivid 7 (Revision BT08, HDF output from Raw-DICOM, GE Medical Systems Inc.) series ultrasound machines; other formats are in development.