Number-Knower Levels in Young Children: Insights from Bayesian Modeling

Abstract

Lee and Sarnecka (2010) developed a Bayesian model of young children’s behavior on the Give-N test of number knowledge. This paper presents two new extensions of the model, and applies the model to new data. In the first extension, the model is used to evaluate competing theories about the conceptual knowledge underlying children’s behavior. One, the knower-levels theory, is basically a “stage” theory involving real conceptual change. The other, the approximate-meanings theory, assumes that the child’s conceptual knowledge is relatively constant, although performance improves over time. In the second extension, the model is used to ask whether the same latent psychological variable (a child’s number-knower-level) can simultaneously account for behavior on two tasks (the Give-N task and the Fast-Cards task) with different performance demands. Together, these two demonstrations show the potential of the Bayesian modeling approach to improve our understanding of the development of human cognition.

Introduction

Young children’s number knowledge is a classic domain of research in cognitive development. On the one hand, evolution has given humans (like other animals) the ability to represent implicitly small, exact set sizes (up to about 4), and to represent explicitly larger, approximate cardinalities (e.g., approximately 50 vs approximately 100; see Feigenson, Dehaene & Spelke, 2004 for review). On the other hand, many types of numbers (e.g., negative integers; pi and other irrationals; etc.) are better understood as cultural products (Piaget, 1952). This combination of innate or early-developing, preverbal knowledge with painstakingly-acquired, verbalized knowledge makes the case of number a perennially interesting one for cognitive development. The present work uses examples from the domain of number to show how Bayesian models can be useful for studying cognitive development.

The first goal of the paper is to show how a model can be used to decide between competing theories of young children’s number knowledge. In our example, one theory, the knower-levels theory, describes development as stage-like, involving qualitative discontinuities in knowledge development. The other theory, the approximate-meanings theory, describes development as essentially continuous, with improvements in children’s performance, but no real qualitative changes in their underlying knowledge state. Our version of number knower-levels theory will make three claims. The first is that children learn the exact, cardinal meanings of the number words ‘one,’ ‘two,’ ‘three’ and ‘four,’ one at a time, and in order. The second claim is that children figure out the meanings of all higher number words at once when they learn the cardinality principle (Gelman & Gallistel, 1978), which connects cardinal numerosity to counting; (e.g., Carey, 2009; Le Corre, Van de Walle, Brannon, & Carey, 2006; Sarnecka & Carey, 2008; Wynn, 1992). The third claim is that, before learning the cardinality principle, children do not know the meanings (even approximately) of any higher number words.

Our version of approximate-meanings theory will make the claim that by the time children have learned the number words of their language (i.e., have learned to recite the conventional number-word list up to ten), they already know the approximate cardinal value of each number word, although their ability to demonstrate that knowledge may be very poor (especially for the higher numbers).

Note that we have chosen relatively simple versions of each theory as examples. More nuanced and complicated theories could be tested by this same method. For present purposes, it is not the exact details of particular theories that matter, but the demonstration of how a Bayesian graphical model can be used to decide among them.

The second goal of the paper is to show how a model can be used to ask whether the same latent psychological variable can simultaneously account for behavior on two different tasks. In our example, the psychological variable is a child’s number-knower level. One task is Give-N (Wynn, 1992), where children are told a number word and must generate a set. The other task is Fast-Cards (Le Corre & Carey, 2007), where children are shown a set and must generate a number word. We show how a formal model can be used to identify regularities in children’s behavior (potential indicators of the same underlying knowledge) across the two different tasks.

We first presented a version of this model in a recent paper (Lee & Sarnecka, 2010). In that paper, we considered a dataset that contained only Give-N behavior. In this paper, we apply the same model to new Give-N data. We then extend the modeling approach in two fundamental ways, to address our two research goals. First, we embed an approximate-meanings theory within the same modeling framework, to show how the theories can be compared using Bayesian methods. Second, we extend the model to apply to both Give-N and Fast-Cards data simultaneously, to show how multiple tasks dependent on the same latent knowledge can be modeled using Bayesian methods.

Data

Participants

Participants included 56 children (26 girls; 30 boys), ages 2 years, 3 months to 5 years, 3 months (mean age 3;9). All children were monolingual and native speakers of English, as determined by parental report. Children were recruited from private child-care centers in Irvine, California. Families received a prize (e.g., a small stuffed animal or rubber duck) when they signed up to participate in the study; no prizes were given at the time of testing. No questions were asked about socio-economic status, race, or ethnicity, but participants were presumably representative of the middle-to-upper income, predominantly white and Asian community from which they were recruited.

Procedure

Children were given three tasks (Intransitive counting, Give-N and Fast-Cards) as part of a larger study. Intransitive counting was always given first; Give-N and Fast-Cards were presented in counterbalanced order afterward.

Intransitive counting task

The purpose of this task was to assess the child’s knowledge of the conventional English number-word sequence up to ten. The experimenter prompted the child to count by saying, “Let’s count. Can you count to ten?” If a child hesitated, the experimenter said, “Let’s count together” and counted to ten slowly, encouraging the child to join in. Afterward, the experimenter said “Great. Now you,” prompting the child to count alone. If a child stopped counting before ten (e.g., at five), the experimenter repeated the last three numbers with an encouraging tone of voice (e.g., “three, four, five, …?”) or asked, “What comes after five?” If a child got to ten but skipped one or more numbers along the way, the experimenter did not provide correction, but encouraged the child to count again (e.g., “OK! Do you want to count again?”), up to a total of three attempts.

Give-N task

This task asked children to generate sets of a given number. Materials included a stuffed animal, a plastic plate (approximately 11cm in diameter), and three sets of 15 plastic counters each (fish, dinosaurs and oranges, each approximately 2–3 cm in diameter). Items in each set were homogenous. The experimenter began the task by saying, “The way we play this game is, I will tell you what to put on the plate, and you put it there and sli-i-i-de it over to Pig, like this (demonstrating). OK, can you give one fish to Pig?”

After the child slid the plate toward the stuffed animal, the experimenter asked one or more follow-up questions. On low-number trials (those asking for one, two, three or four items), there was only one follow-up question, repeating the original number word (e.g., “Is that one?”) If the child said “yes,” then the experimenter said, “Thank you!” and placed the item(s) back in the bowl. If the child said “no,” then the experimenter restated the original request, starting the trial over.

On high-number trials (those asking for five, eight or ten items), the follow-up questions encouraged the child to count. (For children who had spontaneously counted out the items already, the follow-up was the same as on low-number trials.) For children who had not counted the items, the first follow-up question was the same (e.g., “Is that five?”). If the child said “yes,” the experimenter said, “Can you count and make sure it’s five?” If the child counted and ended with a number other than five, the experimenter said “Can you fix it so it’s five?” If the child answered no” to the original follow-up question, the experimenter said “Can you count and fix it so it’s five?” The child’s final response (after counting and fixing) was the response used for the analysis.

Each child was given 21 trials: three trials each of the numbers 1, 2, 3, 4, 5, 8 and 10. Trials were presented in blocks of seven (one trial of each number). For each block, a new set of items was used. Order of trials was randomized within each block.

Fast-Cards task

This task (adapted from Le Corre & Carey, 2007) asked children to estimate the numerosities of briefly presented sets. Materials included 21 laminated cards with pictures of small plastic counters (ducks, fire trucks and bananas, each approx 2–3 cm in diameter). Items in each set were homogenous. The experimenter began the task with a warm-up trial. The experimenter showed the child a picture of just one item and said, “What’s on this card?” The child usually answered with a noun (e.g., “a pig”). The experimenter said “That’s right, it is a pig! But in this game, we use our number words, so you say, ONE’. (Here the child would usually say, “one.”) Then the experimenter said “Good job! OK, what do you think you say for this card?” and began the test trials.

If a child did not give a number-word response, the experimenter prompted with one of the following questions: “Can you think of a number word for this picture?” “How about a number?” “What number do you think goes with this picture?” After one such prompt, the child’s response was recorded and the experimenter moved on to the next trial. The phrase “how many” was avoided, because previous research has shown that it prompts children to count (Sarnecka & Carey, 2008). When children did start to count the items, the experimenter lowered the card and said, “This isn’t a counting game. You can just guess a number.”

Each child was given 21 trials: three trials each with pictures of 1, 2, 3, 4, 5, 8 and 10 items. Trials were presented in blocks of seven (one trial of each set size). For each block, a new set of cards was used. Order of trials was randomized within each block.

A Model of Behavior on Number Tasks

Lee and Sarnecka (2010) developed a model of behavior on the Give-N task, formalizing the number-knower-levels theory. The model is inherently Bayesian, based on the premise that children use task instructions to update a prior belief about appropriate behavior into a posterior belief.

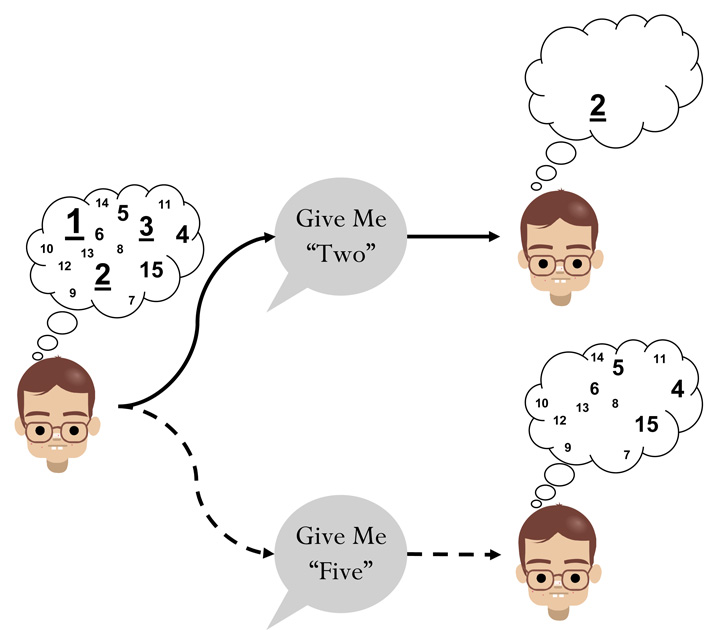
A schematic account of the Lee and Sarnecka (2010) model is presented in Figure 1. The child on the left is shown in a prior belief state, for a Give-N task with 15 toys. As their thought bubble shows, the child permits the belief that any number of toys between 1 and 15 might be appropriate behavior. But, the child is pre-disposed to give some set sizes rather than others, purely because of the nature of the task. These pre-dispositions are represented by the size of the numerals.

Figure 1.

Intuitive operation of model, showing a child who is a 3-knower responding to instructions to ‘give “two”’ and to ‘give “five”’.

This pre-disposition takes the form of a base-rate, which specifies how likely each response would be in the absence of any instructions at all. In Figure 1, the child is a priori more likely to construct small sets (e.g., 1, 2, 3 or 4 items) or to give all 15 objects, than to construct larger sets that stop short of the whole (e.g., 7–14 items).

Figure 1 shows how two different instructions—‘give me “two”’ and ‘give me “five”’—lead the base-rate to be updated, based on knower-level theory. To make this demonstration concrete, we assume the child is a 3-knower (i.e., the child knows the exact, cardinal meanings only of the underlined numbers). For the ‘give me “two”’ instruction, updating simply corresponds to making 2 the most likely response, since it is known.

For the “give me ‘five’” instruction, the updating is more subtle, and involves two parts. First, those numbers that are known, and are not the target number, become very unlikely responses. This is why the numbers 1, 2 and 3 do not appear in the lower-right thought bubble—the likelihood of the child giving any of those responses is negligibly small. Secondly, the remaining numbers keep the same relative likelihood (e.g., 5 is still a more likely response than 12, and less likely than 15) but they all have a greater absolute likelihood, because the total probability still adds up to one. Acting on this posterior belief, the child at the bottom right of Figure 1 is most likely to give 4, 5, or 15 toys.

In general, the model works by making relatively more likely a target number that is known, relatively less likely a number that is known but is not the target number, and leaving relatively equally likely a number that is not known. In this way, the task base-rate, the knower-level of the child, and the instructions giving the target number all interact to produce a belief that is the basis for behavior.

Formal Implementation of Model

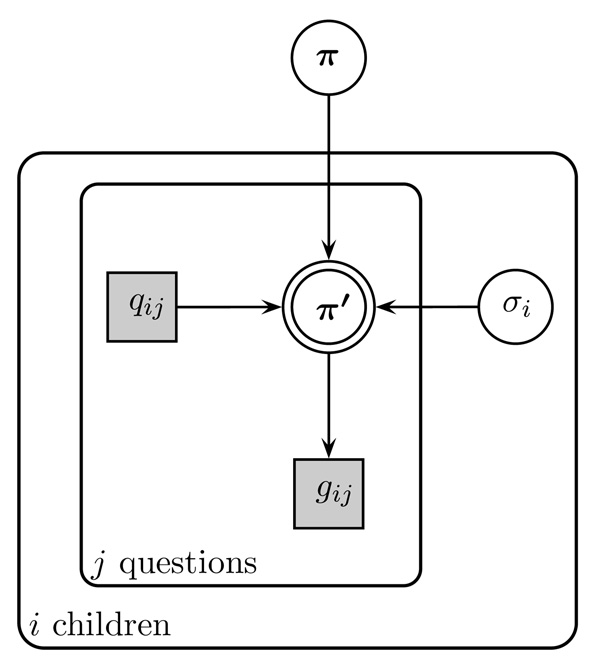
Lee and Sarnecka (2010) implemented their model using the formalism provided by graphical models. This is a standard approach in machine learning and statistics for specifying probabilistic generative models (e.g., Jordan, 2004; Koller, Friedman, Getoor, & Taskar, 2007), and is becoming increasingly popular in the cognitive sciences (e.g., Griffiths, Kemp, & Tenenbaum, 2008; Lee, 2008; Shiffrin, Lee, Kim, & Wagenmakers, 2008). The basic idea is that unobserved variables (i.e., model parameters) and observed variables (i.e., data) are represented by nodes in a graph, their dependencies are indicated by the graph structure, and encompassing plates are used to indicate replications.

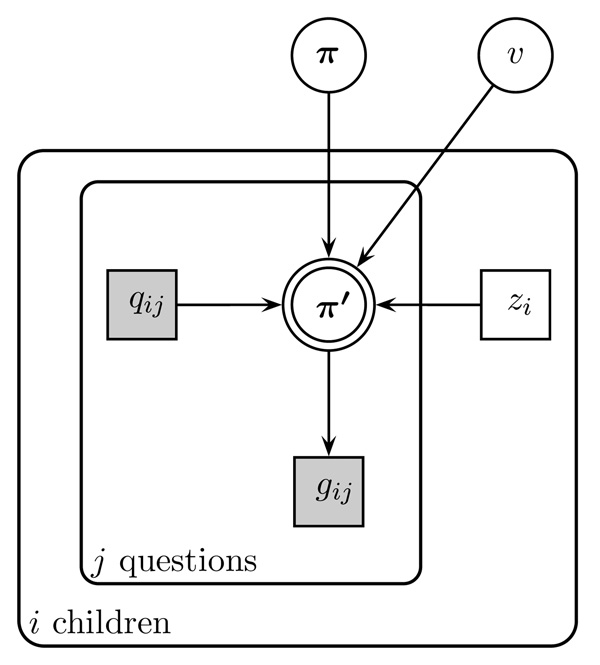
Figure 2 shows the graphical model for the Bayesian account of knower-level behavior on the Give-N task. The observed data are the question q_ij, which corresponds to the number of toys the ith child is instructed to give on their jth question, and the answer g_ij, which corresponds to how many toys they actually gave.

Figure 2.

Graphical model for a knower-level account of task behavior.

The base-rate is represented by the vector π, with the element π_k giving the initial probability of giving k toys. The evidence value υ is a model parameter, controlling how much more or less likely behaviors become, when the instructions provide evidence for or against them. The discrete state parameter z_i gives the knower-level of the ith child, ranging from pre-number (PN)-knower level, where the child does not yet know the exact meanings of any number words, to the 1-knower level (where the child knows the meaning only of “one”), and so on up to the cardinal-principle (CP)-knower level. All of these parameters are unknown, and must be inferred from data.

The base-rate, evidence and knower-level parameters interact with the task instruction to generate the updated belief represented by π′ with ${\pi }_{ijk}^{\prime }$ giving the probability the ith child will give k toys in response to a question about number j. Following the logic of the model intuitively outlined above, and described in more detail by Lee and Sarnecka (2010), this updating is given by

$${\pi }_{ijk}^{\prime }\propto \{\begin{array}{ll}{\pi }_{ijk}\hfill & \text{if}k>z_i\hfill \\ \upsilon \times {\pi }_{ijk}\hfill & \text{if}k\le z_i\text{and}k=q_{ij}\hfill \\ \frac{1}{\upsilon }\times {\pi }_{ijk}\hfill & \text{if}k\le z_i\text{and}k\ne q_{ij}.\hfill \end{array}$$ (1)

The observed behavior is simply sampled from the updated probabilities, so that g_ij ~ Discrete (π′).

The three parts of this updating rule correspond to the three cases described intuitively earlier. The first case applies to numbers that are greater than the child’s knower-level, and so the base-rate for giving that number guides their behavior. The second case applies when the number is known, and is being asked for, so its likelihood of being given is increased by a factor of υ. The third case applies when the number is known, but it not being asked for, so its likelihood is decreased by a factor of υ.

Our modeling approach uses Bayesian inference in two separate ways, both as a model of a child’s inference about how many toys to give, and as a method for us as scientists making inferences about what a child knows based on their behavior (see Kruschke, 2010; Lee, 2010; Lee & Sarnecka, 2010, for detailed discussion). Because of the second, methodological, use of Bayesian principles, we need to place priors on the unobserved parameters. These are given by the relatively non-informative choices π ~ Dirichlet (1,…, 1), υ ~ Uniform (1,1000), and z_i ~ Discrete $(\frac{1}{6},\dots ,\frac{1}{6})$.

Basic Results

Intransitive counting task

All the children except one produced the number-word sequence correctly up to 10. The exception was a boy (age 3 years, 6 months) who produced the sequence only up to 7. We chose to include this child’s data in the analysis after determining that excluding them did not change the results in any noticeable way.

Give-N task

For comparison with previous studies and with the model’s sorting below, we first present the breakdown of children into knower-levels by the standard heuristic method. In this method, a child is counted as ‘knowing’ a number N, if that child successfully generated sets of N for at least two of the three trials asking for that number, and did not generate a set of N more than once during the 18 trials asking for other number words. For this set of Give-N data, that sorting produced 4 pre-number-knowers; 7 one-knowers; 10 two-knowers; 6 three-knowers; 8 four-knowers; and 21 CP-knowers. This distribution is similar to those in previously reported sets of Give-N data from children of comparable age and SES background (e.g., Le Corre & Carey, 2007; Lee & Sarnecka, 2010; Sarnecka & Carey, 2008; Sarnecka & Lee, 2009).

Fast-Cards task

Using sorting criteria analogous to those in the Give-N sorting above, children were counted as ‘knowing’ a number N if they successfully said N on at least two of the three trials presenting pictures of N objects; and did not say N on more than one of the eighteen other trials. This sorting produced the following distribution: 4 pre-number-knowers; 7 one-knowers; 21 two-knowers; 15 three-knowers; and 9 four-knowers/CP-knowers. (The difference between four-knowers and CP-knowers cannot be reliably detected by the Fast Cards task, as the difference depends on counting.)

Modeling Results

In this section we apply the model to the current Give-N data. We do not work through all of the analyses in the same detail as Lee and Sarnecka (2010). Instead, we focus on the key results that show how modeling the new data confirms the earlier findings. In particular, we focus on the ability of the model to provide a good descriptive fit to the observed task behavior of the children, and to infer meaningful and useful characterizations of the processes generating this behavior.

The posterior distributions for the latent knower-level states z_i classified the 56 children into 3 PN-knowers, 7 1-knowers, 10 2-knowers, 6 3-knowers, 10 4-knowers and 20 CP-knowers. The standard Cohen’s kappa measure of agreement (Cohen, 1960) was 0.63, indicating what is usually considered “substantial agreement” between the heuristic and model-based classifications of children into knower-levels, although clearly they are not identical assessments.

Consistent with the detailed analysis presented by Lee and Sarnecka (2010), the posterior distributions were highly peaked, often giving almost all their mass to a single knower-level. For those cases with uncertainty, it is always with respect to neighboring knower-levels, even though no such constraint is built into the model. As Lee and Sarnecka argued, both of these properties are consistent with latent knower-levels being meaningful psychological characterization of the individual differences between children. The mean posterior for the evidence parameter υ was about 23 (i.e., when a 3-knower is asked to give 2, that response becomes about 23 times more likely than it was in the prior distribution, whereas all other responses become about 23 times less likely.). This is comparable with the value of 29 found by Lee and Sarnecka for the earlier dataset.

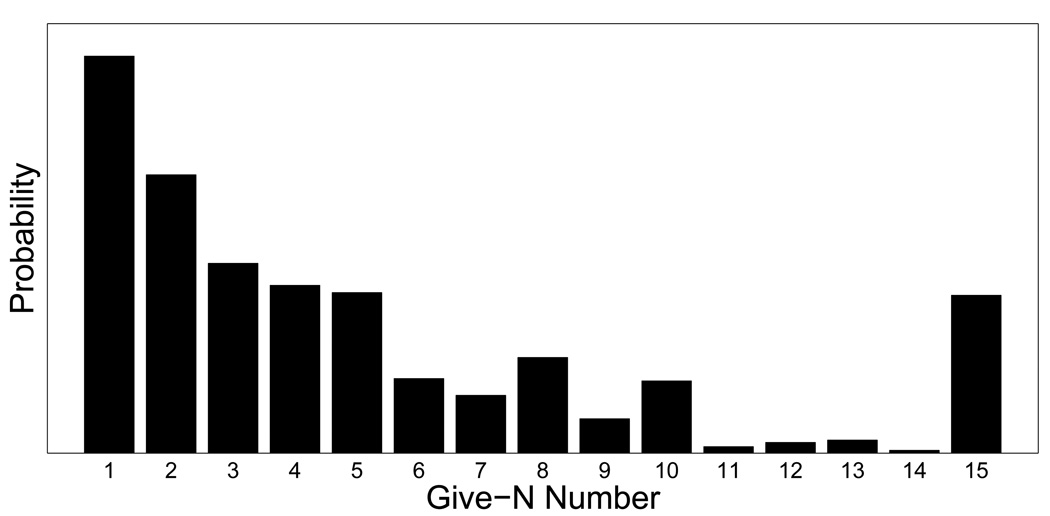
Figure 3 shows the base-rate that is inferred from the current data, and highlights a key contribution of the model. As with the data considered by Lee and Sarnecka (2010), the base-rate assigns high probabilities to small numbers, consistent with the child giving one to four toys. High probability is also assigned to 15, consistent with the child’s giving the entire set. In the context of the Give-N task, this base rate makes strong intuitive sense. The fact that the model infers this base rate from the data shows that the model is useful in quantifying an aspect of children’s behavior (i.e., their pattern of ‘chance’ responding) that had never been specified before.

Figure 3.

Inferred base-rates for the Give-N task.

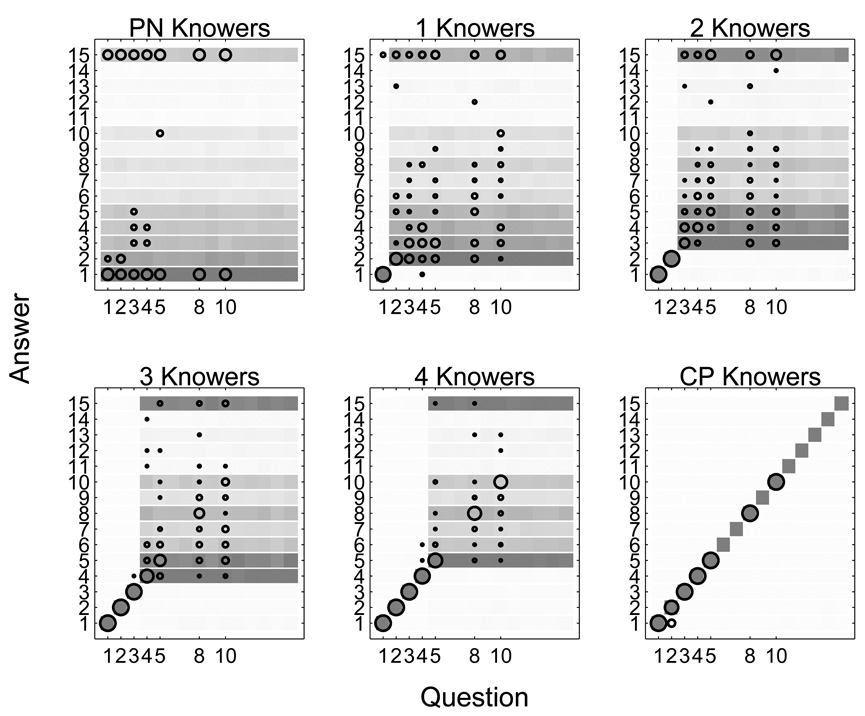
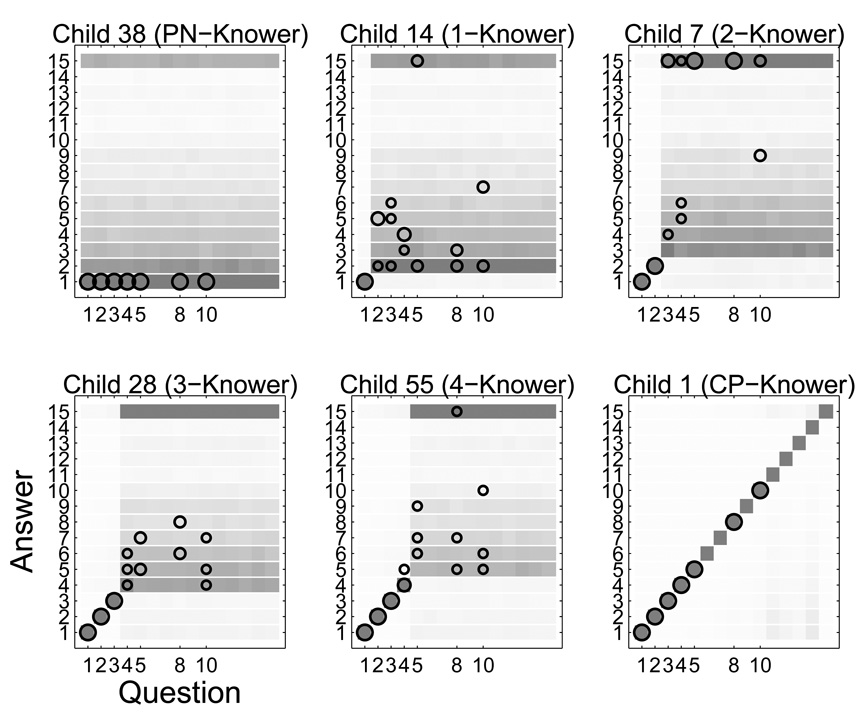
Figure 4 shows the fit between the model and data, examining how well the interaction of the inferred base-rate, evidence value, and knower levels can account for trial-by-trial task behavior. Each panel corresponds to a knower-level stage, with the x-axis listing the number of toys asked for, and the y-axis listing the number given. The darkness of the shading in each cell thus represents the posterior predicted probability the model gives to each combination of question and answer. Overlayed in each panel by circular markers are the observed data, for just those children inferred to belong to the appropriate knower-level. The area of each circle represents the number of times each question and answer pair was observed for children at that knower-level.

Figure 4.

Posterior predictive fit of the knower-level model to task behavior for all children.

The model predictions fit the data very well, as Figure 4 shows. The distinctive pattern of near-perfect behavior up to a child’s knower-level, but completely different behavior beyond their knower-level, is evident in both observed and model behavior. An especially important feature of the fit is the way the base-rate accounts for the task-specific nature of the non-accurate behavior. It is clear in Figure 4 that this behavior is consistent with a base-rate—giving emphasis to small numbers immediately above the knower-level, and to 15—as formalized by the updating process within the model. In this way, the model explains task behavior in terms of an interaction between the child’s conceptual knowledge of numbers, and superficial aspects of the task.

Using the Model to Compare Alternative Theories

The model developed by Lee and Sarnecka (2010) accounts for several Give-N data sets well, and provides the ability to measure interpretable aspects of the behavioral process. It does this assuming a discontinuous (stage-like) developmental trajectory. That is, it assumes that children learn exact meanings for the first 3–4 number words one at a time and in order, and that during this time they do not have even approximate cardinal meanings for the higher number words in their counting list.¹ A natural question is how alternative accounts of number-concept development fare within the same framework for modeling task behavior. One obvious alternative is to assume that children know the meanings of all the number words in their counting list (at least approximately), and that the answers given are noisy estimates of the numbers asked for. Under this theory, there are no such things as number-knower-levels. Some children merely estimate more accurately than others. This theory also explains why children would get all trials correct up to a given number, and few or none correct above that number—it’s simply because small set sizes are easier to estimate than large ones. Finally, the theory explains why children’s performance would improve over time: As children get older, their estimation ability improves, and the numbers they can reliably estimate get larger.

Figure 5 shows a modified graphical model that introduces an approximate-meanings assumption into the basic Bayesian task model. As before, a base-rate π is updated to π′ based on the question, and on a parameter controlling each child’s number representation. In this case, the parameter is σ_i, corresponding to the coefficient of variation for the ith child from approximate-meanings theory. The updating is now given by

$${\pi }_{ijk}^{\prime }\propto {\pi }_{ijk}\times \frac{1}{\sqrt{2\pi {\sigma }_i^2}}\text{exp}\left(-\frac{1}{2{\sigma }_i^2}{(q_{ij}-k)}^2\right),$$ (2)

but the remainder of the model is formally identical to the knower-level version.

Figure 5.

Graphical model for an approximate-meanings account of task behavior.

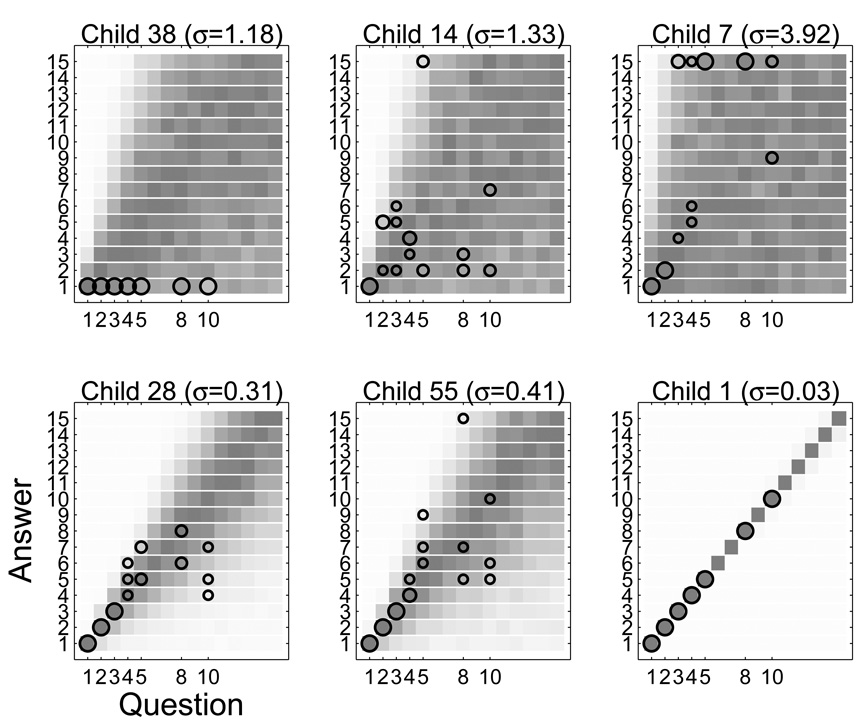
Comparing this approximate representation of number with the knower-level representation is best done at the level of individual children. Figure 6 shows the posterior predictive fit between the knower-level version of the model and the observed behavior of six children, chosen at random with the constraint that one child was chosen from each knower level. Figure 7 shows the fit of the approximate-meanings version of the model to the same six children, together with their estimated coefficient of variation.

Figure 6.

Posterior predictive fit to task behavior of the knower-level version of the model, for six selected children.

Figure 7.

Posterior predictive fit to task behavior of the approximate-meanings version of the model, for six selected children.

Figures 6 and 7 clearly show the superiority of the knower-level theory in accounting for the behavior of the six selected children, and the same conclusion is warranted across the entire data set. It is intuitively obvious that an approximate-meanings account cannot explain why a child might give 15 when asked for 1, without assuming a very large coefficient of variation. The formal modeling summarized in Figure 7 shows that the idea of updating a base-rate does not overcome this deficiency in the approximate-meanings account. To explain why children sometimes give numbers that are very different from the numbers they were asked for—something regularly observed in our data—an approximate-meanings account is forced to allow such huge coefficients of variation that almost any answer would be consistent with the model. Consequently, the model assumes coefficients for three of the six children that are many times larger than coefficients of 0.33 to 0.5 previously reported for children of this age (e.g., Halberda & Feigenson, 2008).

One simple way to quantify the obvious differences in fit seen in Figures 6 and 7 is to calculate the agreement between the observed and predicted behavior for both models. We did this again using Cohen’s kappa, which is suited to the nominal form of the data, for each child separately. For the knower-level model, kappa ranged from 0.45 to 0.99 across all children, with a mean of 0.54. For the approximate-meanings model, kappa ranged from 0.01 to 0.25 with a mean of 0.13. The same pattern held when CP-knowers and non-CP-knowers were analyzed separately. Kappa for CP-knowers ranged from .43 to .99 (mean .52) for the knower-level model, as compared with .02 to .19 (mean .09) for the approximate-meanings model. For non-CP-knowers, kappa ranged from .43 to .69 (mean .53) for the knower-level model, as compared with .28 to .45 (mean .38) for the approximate-meanings model. It would, of course, be possible to consider more advanced Bayesian model comparison measures (e.g. Pitt, Myung, & Zhang, 2002; Shiffrin et al., 2008), but we think these basic results paint a clear picture of the superiority of the knower-level model in describing the current data.

Modeling Knower-Level Accounts of Multiple Tasks

Throughout the empirical sciences, a basic hallmark of a good theory is that it is able to describe observations or make accurate predictions across a wide range of situations. This unification is something that can naturally be achieved within the current Bayesian graphical modeling framework (Lee, 2010). As a first demonstration of this approach, we show how knower-level theory can be evaluated in terms of its ability to account for behavior in two tasks: Give-N and Fast-Cards. The tasks have similar data structure—in one, the child generates a set size to match a number word; in the other, the child generates a number word to match a set size. The tasks are fundamentally different in that only the Give-N task allows counting as a strategy. On Fast-Cards, children are forced to estimate. However, if the knower-level theory is correct, this distinction should not matter for most of the children in this study. These children (the pre-, one-, two-, three- and four-knowers) have not yet acquired the cardinality principle, and so do not use counting to solve the Give-N task in any case. The tasks also make different performance demands. For example, Give-N requires no talking (making it appealing to shy children) whereas Fast-Cards requires verbal responses. Finally, Give-N has a clear maximum response of 15 objects; Fast-Cards has no maximum response, because the child could potentially say any number word at all.

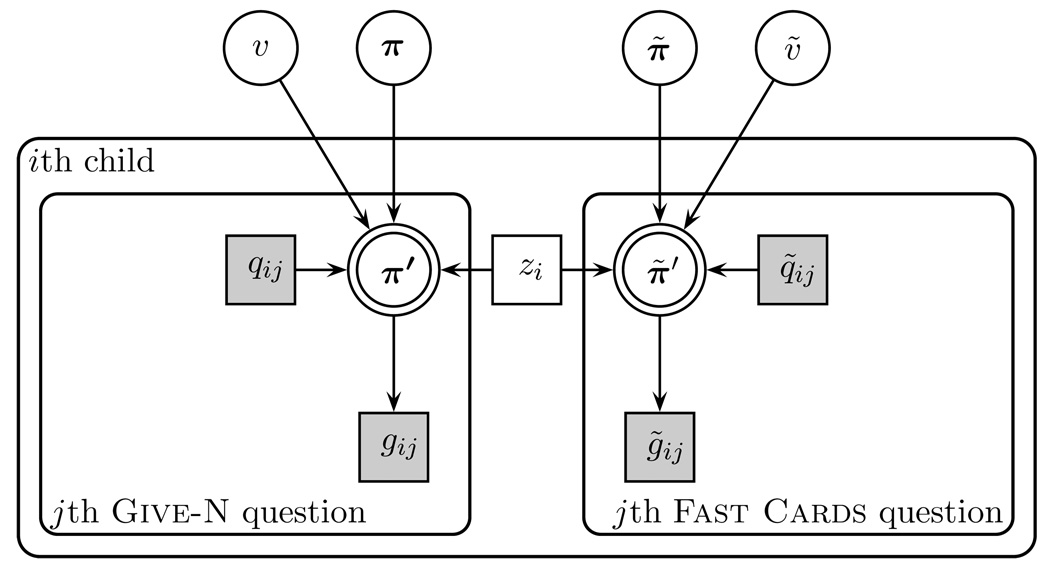
Modeling Give-N and Fast-Cards

Figure 8 presents a graphical model formalizing the integration of the Give-N and Fast-Cards tasks. At the heart of the model is the knower-level, z_i, for the ith child, which plays a key role in generating behavior for all the trials on both tasks. For the Give-N task, the questions and answers continue to be represented by q_ij and g_ij, and the equivalent observations in the Fast-Cards task are represented by q̃_ij and g̃_ij. Each task has its own base-rate, π and π̃, and its own evidence value, υ and υ̃. Updating for both tasks is done exactly as for the Give-N model, as per Equation 1. Thus, the model in Figure 8 assumes that a child’s knower-level is fundamental for both tasks, and variations in the way they answer the same question are due to task-specific base-rates and evidence values.²

Figure 8.

Graphical model using latent knower-level to account for both Give-N and Fast-Cards task behavior simultaneously.

Task Differences

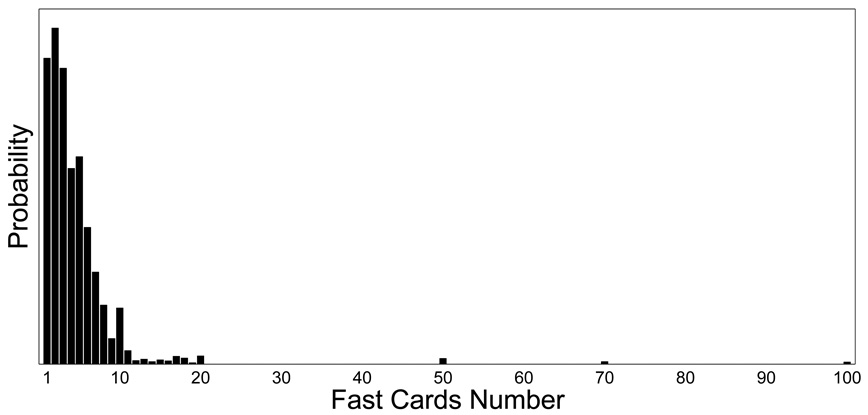
We applied the model in Figure 8 to the within-subjects Give-N and Fast-Cards data. The base-rate for the Give-N task is essentially the same as that shown in Figure 3. The base-rate for the Fast-Cards task is shown in Figure 9, and is very different. It spans a range of possible answers from 1 to 100 (the largest observed answer in the data set). Most of the probability is found for the numbers 1–10, with progressively greater probabilities on the smaller, more common, numbers. There is then a little probability between 10 and 20, with small ‘bumps’ at intuitively reasonable places like 20, 50, 70 and 100, consistent with theories of ‘prominent’ or ‘spontaneous’ numbers (e.g., Albers, 2001).

Figure 9.

Inferred base-rate for the Fast-Cards task.

There was only a small difference in the inferred evidence values for the two tasks, with Fast-Cards being about 20, in comparison to the 23 found for Give-N. This suggests that requesting a number has a similarly large influence in both tasks, and means a more parsimonious model could be considered in which just a single evidence value drives behavior in both tasks.

Combining Knower-Level Information Across Tasks

One basic capability provided by the combined model is a method for estimating knower-levels based on the data from both tasks. This is not easily done by the heuristics usually used. When knower-levels were computed using the heuristic method we described earlier, the knower-level assigned based on Fast Cards agreed with that based on Give-N in only 21 of the 56 cases (38%). In 16 cases (29%), the levels differed by one (e.g., a child might perform as a three-knower on Give-N, but a two-knower on Fast Cards). In 13 cases (23%), the levels differed by two (e.g., a child might be a three-knower on Give-N, but a one-knower on Fast Cards). In five cases (9%), the levels differed by three (one child performed as a three-knower on Fast Cards, but a pre-knower on Give-N; the other four cases were children who performed as CP-knowers on Give-N, but two-knowers on Fast Cards). And there were two cases (4%) of children performing as CP-knowers on Give-N, but pre-knowers or one-knowers on Fast Cards.

Heuristics do not not offer a clear way of interpreting these discrepancies. Some researchers might choose to ignore one dataset altogether. For example, in 78% of discrepant cases, the Give-N knower level was higher than the Fast Cards knower-level, presumably reflecting the fact that Fast Cards was a quick-response task. Thus, researchers might conclude that Give-N provided a more accurate assessment of knower-level. But excluding half the data hardly seems an ideal solution, and does not account for the 22% of cases where the Fast Cards knower-level was actually higher. Of course, it would be possible to extend the heuristics for estimation by defining some sort of rule for combination. But this would require more ad hoc decisions, for procedures that already have several arbitrary components. There is nothing principled about the two-thirds cutoff in correct responding, for example, nor the restriction to one error of commission. In fact, other researchers have used different values within the same heuristics for the same knower-level estimation problem. Most fundamentally, faced with such discrepancies and arbitrariness, researchers might reasonably conclude that knower-levels are not a valid construct at all.

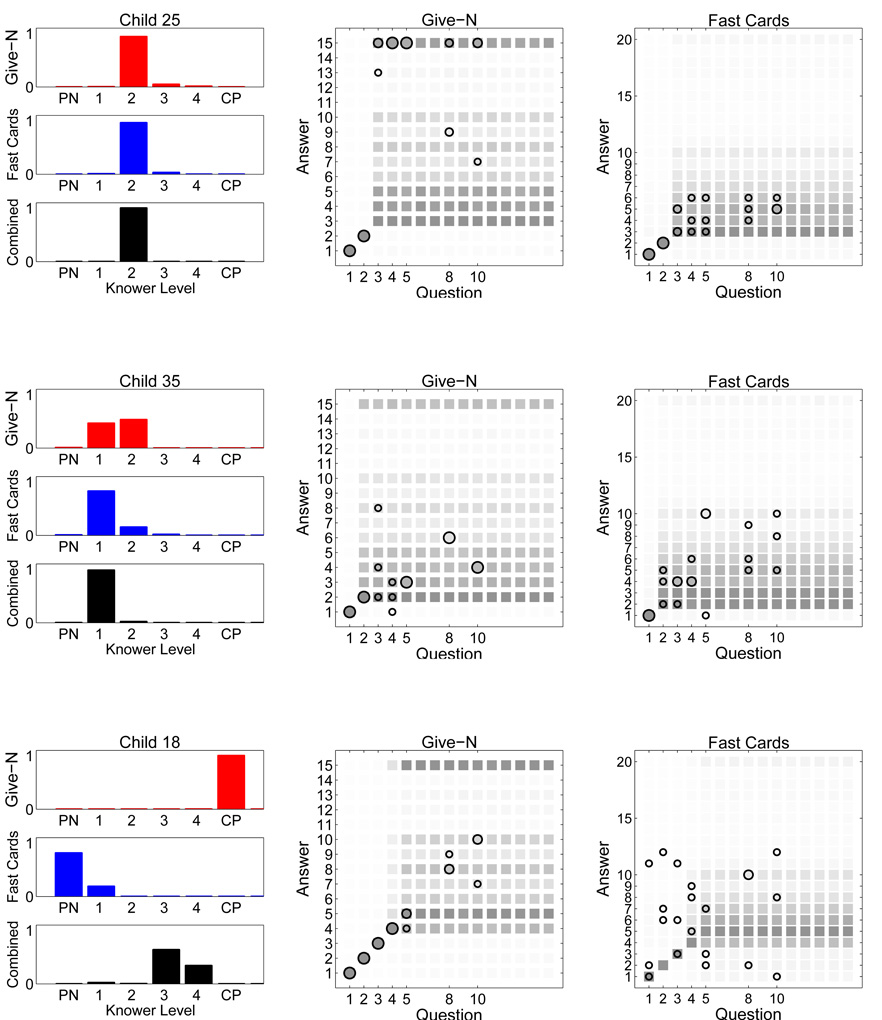
The probabilistic model-based approach offers a more principled way of combining information. Because the model formalizes how knower-levels generate behavior on both tasks, Bayesian inference automatically combines the evidence provided by all of the observed data to estimate knower-levels. Space does not permit us to present a detailed analysis of this simulataneous probabilistic estimation for all 56 children. Figure 10, however. shows results for three children who collectively provide a good characterization of what is observed looking at all children, whose cases we now discuss.

Figure 10.

Knower-level inferences for individual tasks, and Give-N and Fast-Cards tasks combined (left panels), and posterior predictive fits (middle and right panels) for three selected children. See text for details.

Consistent and Clear Estimation

Child 25, in the top row of Figure 10 is typical of the clear and consistent across-task estimation observed for 12 of the 56 children. The left three panels show their inferred knower-level, when modeling just their Give-N behavior, just their Fast-Cards behavior, or both simultaneously. The middle and right panels show the posterior predictive fit between the combined model and all of the child’s data (with the Fast-Cards answers bounded at 20 for legibility, excluding just a few data). The knower-level inferences coming from both tasks independently agree with one another, leading to a near-certain inference for the combined model, which has the benefit of having both sources of task information. The posterior predictive fits show that the individual trial behavior of the child is well described, and the model is able to capture task-specific effects. For example, for Child 25, the model expects the observed answers of 15 to requests above the child’s 2-knower level for the Give-N task, but just expects inaccurate answers a little greater than 2 for the Fast-Cards task.

Consistent but Uncertain Estimation

The results for Child 35 are a good example of what is seen for 27 of the 56 cases. Here, the individual analyses for the tasks separately lead to consistent, but uncertain, inferences about the knower-level. It is possible Child 35 is either a 1-knower or 2-knower, because they make a few mistakes with both numbers, but seem too accurate to be a pre-number knower. But, the combined model, because it models all of the data from both tasks, is able to reduce this uncertainty significantly, and makes a clear inference in favor of 1-knower. The posterior predictive fits again show a good account of the observed behavior, and show intuitively how the ambiguity is resolved. Each task individual has many correct behaviors when asked for “two”, but, cumulatively, there are too many errors, leading to the 1-knower conclusion. For 7 of the 56 children, a different pattern of uncertainty is seen, in which the two tasks separately reach moderately confident, but different, conclusions. Typically, one task gives a knower-level that is one level different from the other task. In these cases, the combined model reflects the uncertainty by giving posterior mass to both neighboring possibilities.

Inconsistent Estimation

In total, the scenarios just discussed apply to 46 of the 56 (82%) of the individual analyses. The analysis of Child 18 in Figure 10 is included to show that, in the 10 remaining cases, the combined model fails to account well for the observed behavior. In one sense, this might be regarded as comforting. It demonstrates by counter-example that the model is not just a fancy, circular way of re-describing the data. For Child 18, the knower-level inferences are very different for the Give-N and Fast-Cards tasks. The compromise reached by the combined model is unsatisfactorily consistent with neither of the individual analyses, and the posterior predictive fit (especially for the Fast-Cards) shows that it fails to provide a good account of the data. We think the inconsistencies in observed behavior for this child can probably be explained in terms of boredom and disengagement from the task.³ This, of course, is just speculation but demonstrates the general point that our model, like all models, is incomplete, and is only useful when applied to data consistent with its theoretical scope. In this case, the model assumes that children are trying to comply with the experimenter’s instructions. Deliberately inconsistent performance results in a pattern for which the model has no explanation.

Discussion

These analyses show how a formal model, grounded in developmental theory, can contribute to our understanding by generating specific and testable predictions about behavior. In this case, the model was useful in two ways. First, it gave us a formal framework for comparing alternative theories about the same behavior. Second, it gave us a principled way of asking whether data from two very different tasks reflected the same underlying knowledge.

First, we used modeling to compare a knower-levels (stage-like) theory of number-word learning to an approximate-meanings (non-stage-like) theory. Both theories were plausible on the surface. For example, both explained why children would perform better on lower numbers than higher numbers, and why childrens performance would gradually improve as they got older. Modeling allowed us to generate and test detailed quantitative predictions for each theory, which led to the finding that the data were actually much more consistent with the knower-levels account.

Second, we used modeling to test the robustness of the knower-levels construct by comparing behavior from two different number tasks: Give-N (where a child hears a number word and produces a set) and Fast Cards (where a child sees a set and produces a number word). If knower-levels are ‘real’ (i.e., if they are a valid psychological construct), then a child’s knower-level should be detectable across a range of tasks. Our combined model formalized the superficial differences between the two tasks. This made it possible to separate task-specific aspects of behavior from those that reflect the childs underlying conceptual knowledge. To the extent that knower-levels are an accurate way of representing this knowledge, the model should be able to describe, predict and interpret behavior on both tasks simultaneously, at the level of the individual child. The advantage of modeling over more informal, heuristic ways of testing the knower-levels theory is that modeling generates specific quantitative predictions for each individual child across the two different tasks. The fact that our combined model does a good job—in terms of describing the data, inferring the knower-level, and modeling the details of the tasks themselves—provides a powerful form of evidence for knower-levels as a valid construct.

The arguments here have been about number, but this type of modeling could be equally useful in other areas of cognitive and developmental science. Investigators in every domain are faced with alternative explanations for the same data, and every branch of psychology must test the validity of its constructs. We think that probabilistic generative models offer researchers a powerful tool for solving these problems.