Proportional odds model for dose finding clinical trial designs with ordinal toxicity grading

SUMMARY

Currently many dose finding clinical trial designs, including the continual reassessment method (CRM) and the standard ‘3+3’ design, dichotomize toxicity outcomes based on pre-specified dose-limiting toxicity criteria. This loss of information is particularly inefficient due to the small sample sizes in phase I trials. Common Toxicity Criteria (CTCAEv3.0) classify adverse events into grades 1 through 5, which range from 1 as a mild adverse event to 5 as death related to an adverse event. In this paper, we extend the CRM to include ordinal toxicity outcomes as specified by CTCAEv3.0 using the proportional odds model and compare results with the dichotomous CRM. A sensitivity analysis of the new design compares various target dose-limiting toxicity rates, sample sizes, and cohort sizes. This design is also assessed under various dose-toxicity relationship models including proportional odds models as well as those that violate the proportional odds assumption. A simulation study shows that the proportional odds CRM performs as well as the dichotomous CRM on all criteria compared (including safety criteria such as percentage of patients treated at highly toxic or suboptimal dose levels) and with improved estimation of the MTD when the PO assumption is not violated. These findings suggest that it is beneficial to incorporate ordinal toxicity endpoints into phase I trial designs.

1. INTRODUCTION

The main objective of dose finding trials for cytotoxic agents in cancer and other severe diseases is to accurately estimate the maximum tolerated dose (MTD) in addition to assessing the safety of an investigational drug for further research in phase II and phase III efficacy trials [1–2]. The maximum tolerated dose is the highest dose at which a pre-specified percentage of patients experience a dose-limiting toxicity (DLT). What constitutes a DLT, as well as the targeted DLT rate, must be agreed upon prior to the start of a trial. DLT rates often range between 20–33% depending on the disease setting, and common DLTs often include severe or life-threatening adverse events directly attributed to the treatment [3].

Finding optimal doses of drugs or transitioning existing drugs as treatment in various diseases requires a reliable and efficient phase I design [4]. There are many phase I trial designs currently implemented in research, including the standard ‘3+3’ design and O’Quigley’s continual reassessment method (CRM) [5]. These dose finding trial designs dichotomize toxicity based on pre-specified dose-limiting criteria; therefore, much information is lost by not accounting for ordinal toxicity grading. General guidelines by Common Toxicity Criteria (CTCAE v3.0) classify adverse events (AE) into grades 1 through 5, which range from 1 as a “mild AE” to 5 as “death related to an AE” [6]. This comprehensive toxicity grading scale is already established and used in clinical practice, which suggests that a binary response may inappropriately ignore various levels of toxicity severity [7]. Less severe grade 1 or 2 toxicities (often classified as sub-DLTs in trials) can still impact dose-escalation in phase I trials. These sub-DLTs can still be clinically significant in their own right, and we may want to limit the number of a particular sub-DLTs type in a trial [8–9]. For this reason, including individual toxicity grades could be advantageous in a phase I trial. Secondly, sub-DLTs could also be indicative of an increased probability of experiencing a DLT with further dose-escalation [8–9]. A design that only incorporates a binary toxicity response would miss the increased information gained by including sub-DLTs. By incorporating all toxicity grades into a dose finding trial design, any toxicity experienced during a phase I trial will influence the next dose selected for testing; therefore, the toxicity information used to estimate the MTD is a more accurate representation of the true drug behavior in the test population.

Since most phase I trials are non-randomized and test small sample sizes, until relatively recently statistical considerations have been largely ignored [7]. The recommended dose obtained from a dose finding trial is often inaccurate due to the large variability of patient responses, and the data tends to provide unreliable estimates of the risk of toxicity for any dose studied [1, 10]. With improved designs, more investigational drugs could potentially show efficacy when they otherwise could be labeled as ineffective or too toxic due to testing at the inappropriate dose in later phases of drug development.

While designs such as the standard ‘3+3’ and its variations remain popular, this is often due to the simplicity of these designs. The ‘3+3’ design is still favored by many investigators because it is algorithmic, does not require any computation to use in clinical trials, and does not depend on a statistician. However, this design tends to treat many patients at low, suboptimal doses, and a critical limitation in the dose escalation process is it only considers the last cohort tested to decide how the study should proceed [3–4, 11]. There is often much uncertainty regarding the MTD as it is not truly associated with a target toxicity, it greatly depends on the individual patients and the order they were treated, and tends to have large variability [2, 12]. This standard design cannot specify a DLT rate prior to the start of a trial, and therefore is not necessarily intended to produce a very accurate estimate of the MTD; instead its main purpose to assess safety quickly and identify a dose that is not too toxic for use in efficacy trials [7].

In recent years, there has been some research to design dose finding trials to incorporate multiple toxicity grades. Wang et al [13] suggest improvements to both the standard ‘3+3’ design and the CRM to include a severity level of toxicity for “dose-limiting” grades 3 and 4. While the specifics of the design will not be discussed in this paper, this design does distinguish between grade 3 and 4 toxicities, but still does not incorporate milder toxicities of grades 1 and 2. It also requires clinical investigators to assign a weight to describe the severity of grade 4 as compared to grade 3 toxicities. The Bekele and Thall method [9] differs substantially from traditional phase I designs by modeling patient outcome as a vector of correlated, ordinal-valued toxicities using the Bayesian multivariate ordinal probit regression model of Chen and Dey [14], which was extended to allow different toxicities to have multiple severity levels [9]. Investigators must list all possible toxicities with corresponding severity levels as well as specify a severity weight for each toxicity level prior to the start of the trial. Investigators must also construct hypothetical cohorts with ranges of toxicity severities, and then a dose-escalation scheme must be agreed upon for each hypothetical cohort. Simulations show that this method works well under various scenarios, and while this complicated design may not appeal to all investigators, it certainly has advantages over traditional designs that reduce several toxicities to one binary outcome [14]. However, due to its complicated setup and the requirement of much investigator input prior to the trial, this method is rarely implemented as a phase I design.

Yuan et al [8] developed a Quasi-CRM, which uses severity weights to convert toxicity grades to numerical scores. Toxicity grades are represented using an “equivalent toxicity (ET) score” where grade 3 toxicities are assigned a value of 1, grades 2 are assigned to 0.5, and grades 4 are assigned to 1.5. They consider an ET score equal to 1 as the cutoff grade for DLT [8]. A quasi-Bernoulli likelihood incorporates these continuous ET scores into the CRM, and the recommended dose for the next patient is the dose level with estimated score closest to the target score, obtained from a pre-specified toxicity profile at the MTD [8]. Simulations show that this Quasi-CRM design performs better than the traditional CRM and is comparable to the Bekele and Thall method. However, the ET score has not been proven to be an effective measure of toxicity severity, and it may be beneficial to consider toxicity grades as ordinal endpoints since CTCAEv3.0 is the current standard for classifying various toxicity severities.

Current designs attempting to include multiple toxicity grades can be somewhat difficult to implement, computationally intensive, and require clinical investigators to assign weights to possible toxicities seen in a trial. While intimate involvement of clinicians in trial design is certainly a benefit, it may not be practical in many settings and many investigators may have difficulty providing the quantitative information requested of them. Other common trial designs such as the standard ‘3+3’ and CRM still dichotomize toxicity based on dose-limiting criteria and can be improved. The proportional odds model (POM) design extends the modified CRM to include ordinal toxicity grading criteria already implemented in clinical practice, thus incorporating more toxicity information than traditional dichotomous designs.

A motivating example for this POM design is the situation where a cohort of patients all experience a grade 2 (i.e., moderate) toxicity in a dose finding clinical trial that pre-specified DLTs as grade 3 or 4 CTCAE toxicity prior to the start of the trial. True phase I trials can vary the definition of DLTs to include some grade 2 toxicities such as permanent late consequences of radiotherapy and/or exclude specific grade 3 toxicities such as neutropenia depending on the disease setting [8–9]. However, many trials often classify DLTs as grade 3 or 4 CTCAE toxicities; therefore in this example, all three patients in this particular cohort experience grade 2 sub-DLTs. Consequently, all patients in this cohort would be classified as not experiencing a DLT and the trial would continue by escalating the dose for the next cohort of patients. Under the assumption that the probability of toxicity increases as dose increases, the last cohort of patients with grade 2 toxicities is most likely indicative of more severe and dose-limiting toxicities at higher dose levels. While the dichotomous design would not take these moderate toxicities into consideration, the ordinal proportional odds design would better utilize the information from patients with moderate toxicities and would restrict how much the dose would increase. Therefore, the ordinal design could potentially prevent patients from being exposed to more highly toxic dose levels by incorporating all ordinal toxicity information into the design.

2. METHODS

2.1. The Original CRM

The CRM was first developed by O’Quigley to address certain types of dose finding trial design challenges often seen in oncology studies [5]. This Bayesian design was motivated by trials where patients are at a high risk of death in the short term, low doses are expected to have no efficacy, little is known about the appropriate dose range for efficacy with tolerable toxicity, and proposed therapies at high doses often have severe or fatal toxicities [5]. The many strengths of the CRM make this dose finding trial design an appealing alternative to the standard ‘3+3’ design. The CRM treats significantly fewer patients at suboptimal doses and more accurately estimates the MTD [1, 3, 13, 15]. This method has also been shown to be efficient and unbiased, and the target DLT rate can be specified in the CRM, unlike the standard ‘3+3’ [5, 16–17]. The CRM may not accurately estimate the entire dose-toxicity model, but it has been shown to be robust and accurate in estimating the MTD, even when the selected dose-toxicity model is not correct [3, 15, 18]. Most importantly, the CRM makes use of all patient information with each treated cohort to influence the next dose studied [19–20].

2.2 Practical CRM using pseudo-data with continuous doses

Modifications to the CRM also allow investigators to add safety and stopping rules into a dose finding trial, and most restrict steep dose escalations between treated cohorts [3]. The CRM is often implemented in trials using discrete dose levels; however, the CRM can also accommodate continuous dose ranges. A modified procedure for the CRM [5] as described by Piantadosi [4] for continuous dose ranges which we will use for comparisons to the POM design is as follows:

1. Doses can take values from a continuous range: x_i; (a ≤ x_i ≤ b)

2. DLT is collected from the i^th patient during the trial:

   $$Y_i=\{\begin{array}{ll}1\hfill & \text{experiences}\text{a}“\text{dose}-\text{limiting}”\text{toxicity}\hfill \\ 0\hfill & \text{has}\text{no}“\text{dose}-\text{limiting}”\text{toxicity}\hfill \end{array}(i=1,\dots ,n)$$

   Prior to the start of the trial, obtain pre-clinical information about drug characteristics as well as expectations of drug behavior at high and low doses. For example, select doses that would be expected to produce 10% and 90% DLT rates. Some of this information may come from prior studies of the investigational drug in other disease settings, animal studies, and/or clinical impressions of the class of drugs tested [2]. This is defined as pseudodata and is described in more detail in section 2.3.

3. Specify a model ψ (x,α,β) for the dose-toxicity association. For example, one can consider a standard 2-parameter logistic model:

   $$\psi (x,\alpha ,\beta )=Pr[Y=1\mid x]=\frac{1}{1+exp[-(\alpha +\beta x)]}$$

4. Use maximum-likelihood (ML) to obtain estimates of parameters (i.e., α and β in the two-parameter model above) by fitting the model to the pseudodata.

5. Invert the fitted model to calculate the starting dose for a pre-defined DLT rate, π_d usually set between 20–33% [3]. For the standard 2-parameter logistic model:

   $$\widehat{x}=\frac{log\left[{\pi }_d/1-{\pi }_d\right]-\widehat{\alpha }}{\widehat{\beta }}$$

6. The initial cohort of patients is treated at x̂. Toxicity outcomes are collected.

7. Repeat steps 4–6, including the pseudodata and all observed data, until a pre-specified sample size is met. Note that pseudodata may be downweighted relative to observed data.

8. The final re-fitted dose is considered the MTD for use in future efficacy trials.

2.3 Using pseudodata for model estimation

Many CRM approaches are Bayesian in their estimation. The approach described by Piantadosi, however, uses ML, but requires data “anchors” to be provided to identify initial doses and to stabilize the estimation. A benefit of the Bayesian approach is even when no patients have experienced DLTs, a posterior distribution can be estimated. In a standard ML approach, a model cannot be estimated until at least one DLT is observed. Piantadosi’s practical CRM has the benefit of incorporating investigator elicited information in practical way and also stabilizing estimation. The practical CRM treats the investigator elicited predicted toxicity and DLT combinations as data in the estimation. For example, x = (500, 3500); y = (0.10, 0.90) are vectors of dose and outcome information that are used to obtain an initial dose and represent the pseudodata. However, this pseudodata can be included in each dose estimation. Or, it can be dropped or downweighted, as described by Piantadosi et al. [4].

2.4. Modified CRM with Ordinal Endpoints

This modified design classifies ordinal toxicity grading by Common Toxicity Criteria (CTCAE v3.0). General guidelines for all possible adverse events describe grade 1 as a “mild AE,” 2 as a “moderate AE,” 3 as a “severe AE,” 4 as a “life-threatening or disabling AE,” and 5 as a “death related to AE” [6]. Deaths strictly related to an AE tend to be rare, and if one did occur in a trial the safety review board must be notified and the trial temporarily suspended until the board decides how to proceed. Therefore, grade 5 toxicities will not be considered in this ordinal dose finding trial design, although it could be easily extended to do so. In the situation where clinical investigators are unwilling to assign importance to grade 1 toxicities, as they are often not clinically significant as compared to experiencing no toxicity, this design does have the option of combining toxicity grades 0 and 1 into one category.

While the design is very similar to the original CRM described in section 2.2, now a proportional odds model is implemented to incorporate ordinal toxicity endpoints. The procedure is as follows:

1. Doses can take values from a continuous range: x_i; (a ≤ x_i ≤ b)

2. DLT is collected from the i^th patient during the trial:

   $$Y_i=\{\begin{array}{ll}0\hfill & \text{has no toxic response}\hfill \\ 1\hfill & \text{experiences}\text{toxicity}\text{grade}1\hfill \\ 2\hfill & \text{experiences}\text{toxicity}\text{grade}2\hfill \\ 3\hfill & \text{experiences}\text{toxicity}\text{grade}3\hfill \\ 4\hfill & \text{experiences}\text{toxicity}\text{grade}4\hfill \end{array}(i=1,\dots ,n)$$

   Note that each patient may incur more than one toxicity. The toxicity response is categorized according to the most severe grade experienced. Prior to the start of the trial, consider toxicity grades 3 and 4 as “dose-limiting”. In a similar way as Piantadosi’s practical CRM, obtain pre-clinical information about drug characteristics as well as expectations of drug behavior at high and low doses (e.g., select doses that are expected to produce 10% and 90% DLT rates). This defined as pseudodata and is described in more detail in section 2.5.

3. Specify a model ψ (x,α,β) incorporating pre-clinical expectations at high and low doses to describe clinical investigator opinions of the dose-response relationship prior to the start of the trial using a proportional odds model. The POM is often selected to characterize the dose-toxicity relationship for ordinal response data, and it assumes a common slope β and ordered intercepts α₁ ≥ α₂ ≥ … ≥ α_k [21]. Toxicity grades 1, 2, 3, and 4 versus dose are fitted using the proportional odds model [22] shown in the following equation:

   $$\psi (x,\alpha ,\beta )=Pr[Y\ge j\mid x]=\frac{1}{1+exp\left[-({\alpha }_j+\beta x)\right]},j=1,2,3,4$$

4. Use ML to obtain estimates of parameters (i.e., α and β in the two- parameter model above) by fitting the model to the pseudodata.

5. Toxicity grades 3 and 4 are considered as “dose-limiting”; therefore, the cutoff to estimate the dose will be the probability of observing a toxicity grade 3 or higher according to the clinical POM. Invert the fitted model to estimate the starting dose for a pre-defined DLT rate, π_d usually set between 20–33%. For the proportional odds model:

   $$\widehat{x}=\frac{log\left[\frac{{\pi }_d}{1-{\pi }_d}\right]-{\widehat{\alpha }}_3}{\widehat{\beta }}$$

6. The initial cohort of patients is treated at x̂. Toxicity outcomes are collected.

7. Repeat steps 4–6, including the pseudodata and all observed data, until a pre-specified sample size is met. Note that pseudodata may be downweighted relative to observed data.

8. The final re-fitted dose is considered the MTD for use in future efficacy trials.

2.5 Pseudodata generation in ordinal CRM

Similar to the approach described in section 2.3, we use a method similar to that described by Piantadosi, which uses maximum-likelihood but requires data “anchors” to be provided to identify initial doses and to stabilize the estimation. The ordinal CRM also treats the investigator elicited predicted toxicity and DLT combinations as data in the estimation. For example, x = (200, 3000); y = (0.10, 0.90) are vectors of dose and outcome information that are used to obtain an initial dose and represent part of the pseudodata. The ordinal CRM differs from the original CRM in that there must be a distribution of toxicity grades at the dose levels selected for 10% and 90% DLT prior to the start of the trial; e.g. at 200 mg, we expect 60% no toxicity, 20% grade 1, 10% grade 2, 6% grade 3, and 4% grade 4. Similarly at 3000 mg, we expect 2% no toxicity, 3% grade 1, 5% grade 2, 45% grade 3, and 45% grade 4. The combination of information from the expected doses that will produce a 10% and 90% DLT rate in addition to the distribution of toxicity grades at these dose levels selected gives enough information to build a proportional odds model with the pseudodata.

The POM is unstable at the beginning of the trial when data accrued is sparse just like any model based on few data points; however, given the number of parameters in the POM, the predicted doses could be illogical. In order to help stabilize the POM, the probability of each toxicity grade is evaluated at an estimated 50% DLT rate according to the POM fit prior to the start of the trial as described above. These points are added to the pseudodata in addition to the information at 10% and 90% DLT rates. This information for an estimated 50% DLT rate will also be incorporated into the binary CRM pseudodata for design comparison purposes.

It is important to note that this pseudodata can be included in each dose estimation. Or, it can be dropped, downweighted or even changed as the trial progresses, as described by Piantadosi et al. [4]. However, when estimating a POM using ML, to obtain an estimate of the full-model (i.e., an intercept for each grade and the slope), there must be at least one occurrence of each level of toxicity. Otherwise, the model is unidentified. Using pseudodata, the model will be identifiable regardless of the distribution of observed toxicities. Because Phase I studies tend to have small sample sizes, it may be such that the trial will be near completion (or completed) without having observed all grades of toxicity. This is not a limitation of our approach: it would be seen as a strength if the goal is to estimate the MTD with no patients experiencing a grade 4 toxicity.

3. SIMULATION STUDY

3.1. Approach

All simulation scenarios were conducted with 2000 datasets using the statistical package R [23], and simulations were run for a continuous dose range of 0 mg to 3600 mg (although the scale chosen is arbitrary). Two weighting schemes for pseudodata were implemented to determine sensitivity to trial conduct and final dose selection. Specifically, the weight of the pseudodata relative to the observed data was explored under two situations, referred to as the 50-50 (pseudodata has initial weight equal to one cohort) and 75-25 (pseudodata has initial weight equal to one individual patient) for a trial with a sample size of 30 with a cohort size equal to 3. The 50-50 weighting scheme starts with 50% weight on the pseudodata and 50% weight on the first cohort of patients and results in only 9% weight on the pseudodata and 91% weight on the 30 patients at the end of the trial. Similarly, the 75-25 weighting scheme starts with 25% weight on the pseudodata and concludes with only 4% weight on the pseudodata after a total sample size of 30 is met.

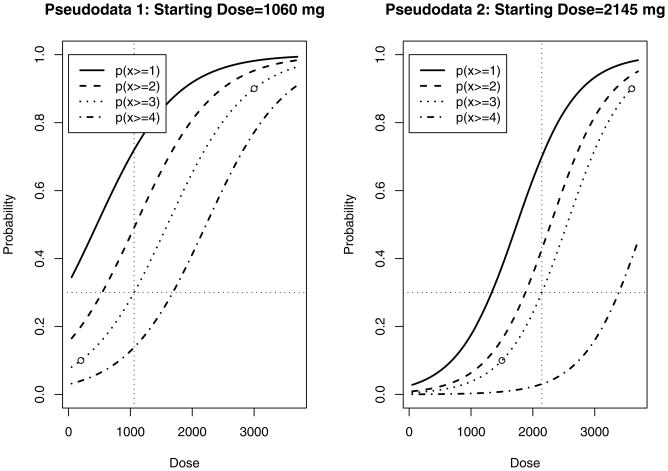
Four scenarios were considered to assess the performance of the ordinal proportional odds CRM compared to the dichotomous CRM. For each scenario, both the 50-50 and 75-25 weighting scheme and cohort size/sample size combinations of 3/30, 2/20, and 3/21 were explored. All simulations assumed a 30% target DLT rate. Figure 1 display the pseudodata proportional odds models utilized in various simulation scenarios. The leftmost figure is pseudodata POM 1, and this model is implemented in Scenarios A and C. Specifically, it is a POM with β = 0.001569, α₁ = −0.719265, α₂ = −1.70009, α₃ = −2.51102, and α₄ = −3.49185. For a specified DLT rate equal to 30%, the starting dose is 1060 mg. The right graph in figure 1 illustrates pseudodata POM 2 used in Scenarios B and D, and this model represents a situation where clinical investigators feel that the investigational drug is not as toxic at lower dose levels and therefore is shifted to the right as compared to pseudodata POM 1. Pseudodata POM 2 is specified by β = 0.002092595, α₁ = −3.64152, α₂ = −4.78181, α₃ = −5.33612, and α₄ = −7.93881, and the starting dose for a 30% DLT rate is now 2145 mg.

Figure 1.

From left to right: pseudodata POM 1 is utilized in Scenarios A and C and has a starting dose of 1060 mg for a 30% DLT rate, and pseudodata POM 2 is utilized in Scenarios B and D and has a starting dose equal to 2145 mg for a 30% DLT rate

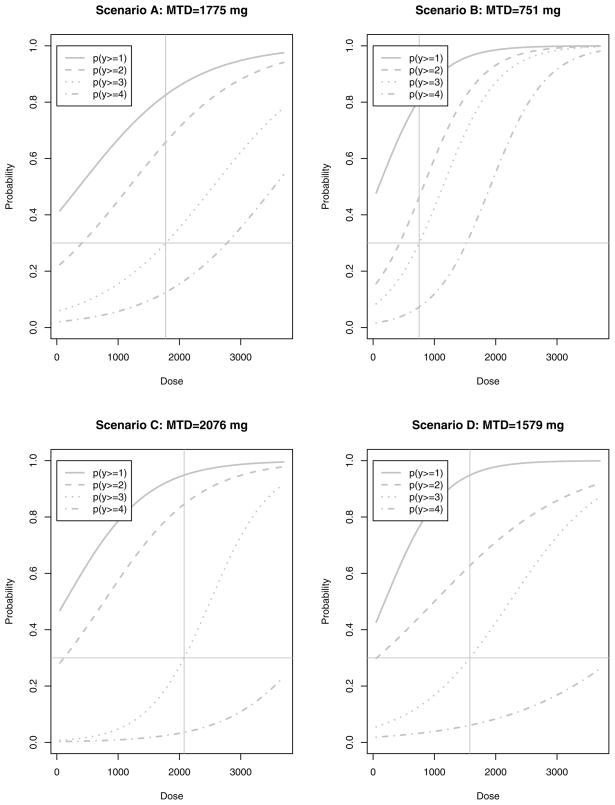
Figure 2 displays the 4 underlying dose-toxicity relationship models used in Scenarios AD. The top two images from left to right represent Scenario A and B respectively. Both underlying dose-toxicity models are POMs and scenario A is specified by β = 0.0011, α₁ = −0.4, α₂ = −1.3, α₃ = −2.8, and α₄ = −3.9, and scenario B is specified by β = 0.0022, α₁ = −0.2, α₂ = −1.8, α₃ = −2.5, and α₄ = −4.2. Scenarios C and D are displayed in the bottom left and right graphs of figure 2 respectively and these two scenarios represent true underlying dose-toxicity relationships that violate the PO assumption. C is specified by β₁ = 0.0020, α₁ = −5.0, β₂ = 0.0013, α₂ = −1.0, β₃ = 0.0020 α₃ = −5.0, β₄ = 0.0013, and α₄ = −6.0. D is specified by β₁ = 0.0021, α₁ = −0.4, β₂ = 0.0009, α₂ = −0.9, β₃ = 0.0013 α₃ = −2.9, β₄ = 0.0008, and α₄ = −4.0. Scenarios A and C have pseudodata that overestimate the true dose-toxicity relationship, which results in starting the trial at a dose smaller than the MTD. Scenarios B and D have pseudodata that underestimate the true dose-toxicity relationship, thus resulting in starting the trial at a dose higher than the MTD.

Figure 2.

From top left: Underlying true dose toxicity models for scenarios A-D with the corresponding MTD specified for a 30% DLT rate. Scenario A and B models are POMs and Scenario C and D models violate the proportional odds assumption

For comparisons to the dichotomous CRM, a standard two-parameter logistic regression model is used. The corresponding pseudodata and true dose-response model for the dichotomous CRM comparisons are the same as observing a grade 3 or 4 “dose-limiting” toxicity as seen in the proportional odds models. For all scenarios, safety checks were put into the ordinal design as well as the comparison binary design similar to prior CRM simulation studies [3–4]. One safety rule does not allow dose to increase by more than 400 mg after each completed cohort. Also, if the updated dose is estimated to be less than 0 mg, the design resets the next dose at 200 mg (unless 200mg was already explored). A safety stopping rule ends the trial early if the next dose is estimated to be very small, i.e. doses less than 200 mg. These estimated low doses suggest sufficient toxicity concerns and the possibility of no true MTD for this particular trial. However, since the pseudodata specified prior to the start of the trial could potentially begin the trial at a dose too toxic for the true dose-toxicity relationship, the trial will not stop after the first cohort of patients tested regardless of the next estimated dose.

One additional safety constraint included in this design requires the next dose after any cohort of patients that experience 2 or more DLTs (toxicity grades 3 or 4) to be at least 5% less than the last dose tested. This constraint ensures that selected doses are logical even if the pseudodata inaccurately reflect the truth. This rule will be unlikely to come into play when sufficient data have been collected, but would only take effect in the very early stages of the trial in cases where the pseudodata overestimate the true MTD.

Summary statistics collected include median final dose estimated over the 2000 datasets, percent difference between the true MTD and final estimated dose, and expected DLT rate according to the underlying dose-toxicity model for the final dose selected. Additionally, we calculated the percentage of trials selecting a final dose within 10% and 20% of the true MTD. Other safety measures such as the percentage of trials stopped early due to safety concerns, and the median percentage of patients treated at suboptimal or highly toxic doses were collected along with the percentage of trials that resulted in a final dose at excessively high or low doses as compared to the true MTD.

3.2. Results

Results from the simulation study show that regardless of scenario or model specification, results did not greatly change based on the cohort size and sample size combinations of 3/30, 2/20, and 3/21. Results also did not greatly differ between the 50/50 and 75/25 pseudodata weighting schemes, therefore simulation-based results will only be displayed for the cohort size and sample size combination of 3/30 with a 50/50 pseudodata weighting scheme.

Table 1 displays selected design performance statistics for simulation scenarios A-D for a sample size/cohort size combination of 3/30 and a 50/50 pseudodata weighting scheme. Scenario A utilizes the Pseudodata POM 1 as displayed in the left graph of figure 1 as well as a true underlying dose-toxicity POM in the top left image of figure 2. In this scenario, both the pseudodata and true dose-toxicity models are proportional odds and the pseudodata underestimates the MTD. The ordinal POM design estimates the median final dose closer to the true MTD than the dichotomous CRM; therefore we see a median percent difference between the estimated final dose and true MTD closer to 0 in the ordinal model. We do see slight improvements in the binary model in terms of percent of trials estimating the final dose within 20% of the true MTD, as well as the percentage of trials with a recommended dose greater than 40%; however, these differences are minimal between the ordinal and binary designs. Interestingly, we did see an increase in the proportion of trials that implemented a constraint to estimate the final dose in the binary CRM as compared to the ordinal design.

Table 1.

All scenarios have a targeted 30% DLT rate, cohort size = 3, sample size = 30, and 50/50 pseudodata weighting scheme. All statistics below are calculated for trials that reached the total sample size and were not stopped early due to safety concerns.

	Scenario A		Scenario B		Scenario C		Scenario D
	POM*	CRM**	POM	CRM	POM	CRM	POM	CRM
Percent of Trials Stopped Early	2.00	1.10	48.40	62.45	0.10	0.35	8.75	7.90
Percent of Trials That Used a Constraint to Estimate the Final Dose	3.93	10.57	0.29	0.80	12.81	13.15	12.82	13.74
True MTD	1775	1775	751	751	2076	2076	1579	1579
5% Quantile Dose	1123	1100	445	526	1648	1657	1102	1223
Median Dose	1646	1625	802	842	1999	2002	1675	1730
95% Quantile Dose	2232	2226	1118	1179	2344	2351	2144	2150
Median Percent Difference Between Estimated Dose and MTD	−7.27	−8.48	6.79	12.12	−3.71	−3.56	6.08	9.56
Median Expected DLT for the Final Estimated Dose	27.10	26.64	32.40	34.35	26.85	26.97	32.68	34.28
% of trials with recommended dose within 20% of MTD	65.97	67.34	53.00	48.20	93.24	93.53	63.67	66.18
% of trials with recommended dose at DLT rate of >40%	6.84	5.97	21.90	33.29	7.66	7.68	22.36	24.38
% of trials with recommended dose at DLT rate of <20%	13.47	14.81	8.62	4.39	18.57	18.01	6.41	3.80
Median % of patients treated at doses with >40% DLT rate	0.00	0.00	30.00	60.00	0.00	0.00	30.00	30.00
Median % of patients treated at doses with <20% DLT rate	20.00	10.00	10.00	10.00	20.00	20.00	0.00	0.00
Median % of patients with a DLT (grade 3 or 4)	26.67	23.33	36.67	43.33	26.67	26.67	36.67	36.67
Median % of patients in trials with a non-DLT (grade 1 or 2)	53.33	NA	43.33	NA	66.67	NA	60.00	NA

^*Proportional Odds Model

^**Binary Continual Reassessment Method

Scenario B exemplifies a situation where the clinical investigators specify pseudodata that represent a dose-toxicity relationship prior to the start of the trial at a level less toxic than the actual dose-toxicity relationship. Therefore, the pseudodata greatly overestimate the MTD. As shown in the second graph of Figure 1, the starting dose for a pre-specified 30% DLT rate is 2145 mg, which is much higher than the true MTD of 751 mg as seen in the top right image in figure 2. As a result, more patients are initially exposed to higher dose levels and experiencing more severe toxicities. It is important to mention that many of the trials in this scenario were stopped early due to safety concerns, with over 48% of trials stopped early in the ordinal model as compared to over 62% stopped trials in the binary CRM. In addition, the median dose for those trials that did not stop early due to safety concerns was closer to the true MTD for the ordinal design as compared to the original CRM and the estimates for the ordinal design were slightly conservatively lower than the true MTD as compared to the original CRM. Interestingly, the median percentage of patients treated at highly toxic dose levels was 30% in the ordinal design versus 60% in the binary design, which resulted in a decrease of patients experiencing DLTs in the ordinal design at a median of 36.67% as compared to 43.33% in the binary CRM.

Scenario C implements pseudodata POM 1 and represents the situation where the true underlying dose-toxicity relationship violates the proportional odds assumption as shown in the bottom left image of figure 2. In this scenario, the pseudodata underestimate the MTD. For this particular scenario, the ordinal and binary designs performed similarly, with no significant differences between the two designs. Scenario D represents one more example where the true underlying dose-toxicity relationship violates the proportional odds assumption as shown in the bottom right image in figure 2. Similar to scenario B, the pseudodata POM 2 overestimates the MTD prior to the start of the trial and a larger percentage of trials are stopped early due to safety concerns as compared to scenarios A and C. In this scenario, the binary CRM performs slightly better; however, it is arguably no different from the ordinal model.

4. DISCUSSION

Through this simulation study, we were able to incorporate ordinal toxicity endpoints in the CRM by using the proportional odds model. In situations where the starting dose range is excessively toxic, the ordinal design was able to reach optimal levels more quickly and treat fewer patients at highly toxic dose levels. When the true underlying dose-toxicity relationship violates the proportional odds assumption, the ordinal design performs similarly to the binary CRM.

This proportional odds model for phase I trials with ordinal toxicity grading has many strengths that make this new design easy to implement and an appealing alternative to other dose finding trial designs. Since this design incorporates all potential toxicity grades in the proportional odds model, it utilizes more information than a design that dichotomizes toxicity based on pre-specified dose-limiting criteria. Most phase I trials do not accrue a large number of patients due to small eligible patient population, general difficulties in accrual to phase I trials and the desire to move quickly into a phase II trial to speed up the drug development process, and this design has the advantage of utilizing all toxicity information to influence the selection of dose. This current design accommodates continuous dose ranges, but it could be easily adjusted to allow for a discrete set of doses simply by assigning rounding criteria to transform the continuous dose selected to a discrete dose level for the next tested cohort.

Another strength of this proposed design is that it is an extension of the CRM, which has already been shown to more efficient and accurate than standard ‘3+3’ designs [3]. This design has the same flexibility as the CRM and can still accommodate different sample sizes, cohort sizes, target DLT rates, stopping rules and safety rules to limit the amount a dose can increase or decrease between cohorts. Results from this simulation study show that the incorporation of ordinal toxicity grades do show improvement especially in situations where the clinical investigators mistakenly expect less toxicity than the true dose-toxicity relationship indicates. In these situations, we find that the ordinal design moves more quickly into a safe and effective range after starting with a dose too toxic, and therefore results in fewer patient DLTs.

While the results of this project will have significant clinical application for new dose finding trials, one limitation of this design and of dose finding trial designs in general is that it would be beneficial to obtain more dose-toxicity information from a clinician prior to the start of the trial. For the traditional CRM, Piantadosi suggests to obtain drug behavior at high and low doses [4]. This requires a clinician to provide the expected dosage for 10% and 90% DLT, even if the clinician is not confident about the estimate. However, since this new design incorporates ordinal toxicity grading, in addition to the two requirements from the traditional CRM it would also be advantageous to predict the probability of each toxicity grade for the investigational drug. This could be obtainable if the drug has been previously tested in other diseases or in pre-clinical experiments. Another limitation of this current simulation study is that we only compared this POM design to the binary CRM. There are other methods that incorporate individual grades or toxicity score schemes that we have yet to compare to the POM design. We plan to address performance to these other designs in future work.

We are currently developing an R library package to run this ordinal POM design as well as the binary CRM based on Piantadosi’s likelihood method for continuous dose levels. This package will be freely accessible for biostatisticians to use in clinical trials. We plan to incorporate options to allow clinical investigators to specify DLT rates, cohort size/sample size combinations, and any safety constraints such as not allowing a dose increase after 2 or more patients in a cohort experience a DLT and/or not allowing a dose to increase past a certain percentage or value between tested cohorts. Although this paper focuses on designs utilizing continuous doses values, we do plan on incorporating discrete dose options into the R library. We also plan to allow clinical investigators the option to combine grade 0 and 1 toxicities into one category. This R package is currently in development, and we plan to make it available soon.