Abstract
The long wavelength, low-frequency modes of motion are the relevant motions for understanding the continuum mechanical properties of biomolecules. By examining these low-frequency modes, in the context of a spherical harmonic basis set, we identify four elastic moduli that are required to describe the two-dimensional elastic behavior of capsids. This is in contrast to previous modeling and theoretical studies on elastic shells, which use only the two-dimensional Young's modulus (Y) and the bending modulus (κ) to describe the system. Presumably, the heterogeneity of the structure and the anisotropy of the biomolecular interactions lead to a deviation from the homogeneous, isotropic, linear elastic shell theory. We assign functional relevance of the various moduli governing different deformation modes, including a mode primarily sensed in atomic force microscopy nanoindentation experiments. We have performed our analysis on the T = 3 cowpea chlorotic mottle virus and our estimate for the nanoindentation modulus is in accord with experimental measurements.
Understanding the mechanical properties of virus capsids is important for deciphering the viral life cycle and for the design of nanoscale devices. Several viruses undergo shape transitions during maturation to become infectious particles (1,2). Some viruses exhibit a remarkable ability to resist high internal pressures due to genome packaging (3,4). Furthermore, atomic force microscopy (AFM) nanoindentation experiments have shown capsids to exhibit elastic behavior and can withstand large deformations and recover (5,6). These phenomena are related to the capsid material properties. By examining the equilibrium dynamics of capsids, we observe that different stiffness characteristics are attributable to different modes of deformation. To first order, we can assign these modes and their respective moduli to describe 1), resistance to uniform pressure, 2), resistance to AFM nanoindentation, and 3), local fluctuations, which the capsid primarily samples at equilibrium. The moduli related to the local fluctuations are relevant for understanding the equilibrium capsid shape as predicted from the buckling transition theory (7).
May and Brooks recently developed a model and methodology to calculate two-dimensional (2D) elastic properties of viral capsids from first principles (8). In brief, the method involves computing a dynamics trajectory of an entire capsid along a set of low-frequency normal modes, which are determined from an elastic network model (ENM) representation of the capsid. From this trajectory the capsid is represented as a 2D surface and radial deformations (from the mean surface) are decomposed in a spherical harmonic basis set. This decomposition yields an analytic expression for the elastic energy
| (1) |
with the definitions b = λ + μ and where λ and μ are the Lamé constants, κ is the bending modulus, R is the capsid radius, and alm is the coefficient of the spherical harmonic Ylm. Because the energy is quadratic in the coefficients, equipartition can be employed and the following relationship can be used to fit the spectral intensities and estimate values for b and κ
| (2) |
The 2D Young's modulus, Y, can be calculated from b via the relationships λ = σY/(1 − σ2), and μ = Y/(2 + 2σ), when a value for the Poisson ratio (σ) is assumed. This method was applied to a T = 1 mutant of the Sesbania mosaic virus (SeMV), where the above model was adequate to describe part of the spectrum, (l = 2,…,6) but the lowest modes (l = 0,1) showed a different behavior (8).
In this work, we assign physical relevance to these lowest modes, and show that they can be connected to experimental measurements. The system we examine is cowpea chlorotic mottle virus (CCMV), because its mechanical properties have been well studied (6,9,10). The most direct method for probing the mechanics of capsids is through AFM nanoindentation experiments (5,6). Although imaging of undeformed and broken capsids is possible with this technique, visualizing the deformation mechanism is not possible. These studies rely on finite element methods (FEM) to inform the experimental measurements and to provide estimates of the three-dimensional Young's modulus (E).
To understand which mode(s) are being deformed in AFM experiments in the context of a spherical harmonic mode spectrum, we analyze a FEM nanoindentation simulation of CCMV. We perform the same analysis on the FEM simulation as we do for equilibrium trajectories, except that we define the undeformed state as the initial state (as opposed to the average structure in an equilibrium simulation). In Fig. 1 A the initial undeformed capsid is shown, during the nanoindentation simulation the capsid is deformed to the configuration shown in Fig. 1 B. The deformation was performed as a quasistatic displacement-controlled indentation using a rigid 20 nm radius spherical probe with rough frictional contact. As in (6,9,10), the capsid was modeled with a uniform, isotropic, large-deformation, neo-Hookean elastic constitutive law. Twenty-five snapshots along the deformation trajectory were used to compute the spherical harmonic spectrum shown in Fig. 1 D. It is clear that the nanoindentation is primarily directed along a single mode, the l = 1 harmonic. On the basis of this evidence, we anticipate that, in general, AFM nanoindentation experiments impose an l = 1 deformation and sense the resistance to this specific mode of deformation.
Figure 1.
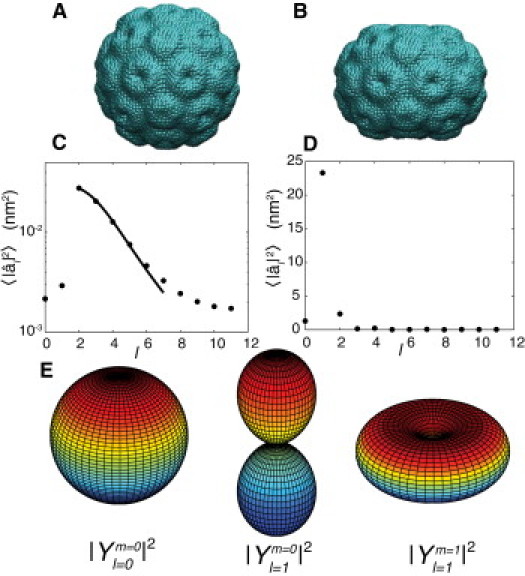
Equilibrium and nanoindentation spectra of CCMV. (A) Undeformed state of CCMV. (B) Final deformed state of CCMV from FEM modeling. (C) Spherical harmonic spectra of equilibrium fluctuations of undeformed capsid. (D) Spherical harmonic spectra of the nanoindentation simulations. (E) Shapes of the lowest wavenumber spherical harmonics.
The shapes of the l = 0 and l = 1 spherical harmonics are shown in Fig. 1 E. Because the -values are summed over the m-components, captures both the m = 0 and m = ±1 deformations. Although one might intuitively think the m = 1 (donut) mode primarily describes the AFM deformation, the m = 0 (dumbbell) mode is the dominate mode describing the deformation. To understand this recall that we are not decomposing the shape of the virus, but rather are decomposing the surface of deformation, which is the difference between the undeformed (Fig. 1 A) and deformed (Fig. 1 B), surfaces. The largest deformations occur in the polar regions, whereas the equatorial regions undergo smaller deformations, analogous to the shape of l = 1, m = 0 harmonic.
To evaluate our assertion that the l = 1 stiffness is a predictor of AFM measurements, we performed an equilibrium simulation of the wild-type unswollen form of CCMV (pdbid: 1CWP) including three calcium ions bound at each quasi-threefold symmetry site (see, Fig. S1 in the Supporting Material) (11). The equilibrium dynamics were generated with a multiscale approach (8), using the normal modes of an ENM (12) to provide initial values for the -values. Our ENM is nondimensional; the spring constants are uniform but have an arbitrary spring constant. To renormalize the network, we also performed an icosahedrally constrained (13) molecular dynamics (MD) simulation of the three protein asymmetric unit of CCMV. The simulation was carried out for 28 ns at 300 K, with the GBSW implicit solvent model (14), the final 10 ns were analyzed to compute the-values. The initial ENM -values were renormalized such that the sum of the -values match between the ENM and the MD systems, to enforce a consistent temperature (see Eq. 2). A more complete description of the computational methods is available in the Supporting Material.
These renormalized coefficients are shown in Fig. 1 C, along with a fit to the elastic model described (Eq. 2). The model describes the spectrum in the range 2 ≤ l ≤ 6, and values of κ = 13 kBT and Yeq = 6 kBT/nm2 are obtained (assuming σ = 0.3), which are consistent with previous theoretical estimates of κ ∼10 kBT and Yeq ∼10 kBT/nm2 (15). We denote the stretching modulus as Yeq, because the fit is performed on the modes that have the largest amplitude at equilibrium. These modes are presumably soft, low-energy modes that the capsid can easily access from thermal energy, and characterize equilibrium motions. At high wavenumbers (l > 6) continuum theory breaks down; these motions are dominated by (sub)molecular scale interactions as was also observed in our earlier study on SeMV (8). The Föppl-von Kármán number (γ = YR2/k, where R is the radius) is a dimensionless parameter that predicts whether an elastic shell will adopt a rounded (γ < 250) or faceted (γ > 250) shape (15) in buckling transition theory (7). We calculate an average radius of 10.6 nm and γ = 51, which indicates the shell should adopt a rounded shape, and CCMV clearly does adopt a rounded shape (Fig. 1 A).
The three-dimensional Young's modulus (E) of CCMV has been estimated from uniform isotropic finite element models of experimental nanoindentation to be in the range of 0.14–0.28 GPa (6,9,16). Using the thin shell approximation E = Y/t, where t is the shell thickness, we can calculate E from our Yeq value. Using a t value of 2.8 nm, we calculate E = 0.009 GPa, which is more than an order of magnitude lower than the experimental measurements. Alternatively, we can calculate Y based only on the l = 1 mode (note the bending term vanishes for l = 0,1 in Eq. 2), which we believe is the mode that the AFM tip is primarily sensing. This calculation results in YAFM = 60 kBT/nm2, from which we calculate E = 0.09 GPa, on the order of the experimental measurements. To further support the notion that multiple stretching moduli are required, we used YAFM to calculate a Föppl-von Kármán number, and we obtained γ > 500. This value of γ would predict a faceted shape, which is inconsistent with the observed spherical shape of CCMV and supports our position that Yeq is the relevant modulus for calculating γ.
The l = 0 mode is even stiffer than the l = 1 mode, and we can directly calculate a Y value based solely on the magnitude of the l = 0 mode. This results in Ypress = 81 kBT/nm2. The l = 0 mode is a uniform spherical mode (Fig. 1 E). This type of deformation could result from a hydrostatic or osmotic pressure gradient between the inside and outside of the capsid. The stiffness of this mode provides mechanical integrity to the capsid allowing it to withstand the pressure exerted by an encapsidated genome and the osmotic environments encountered during the virus life cycle.
We do not believe that the qualitative features of our mode spectrum, namely that the l = 0 and l = 1 modes are stiffer than the l = 2 mode, are a system- or method-specific feature. In our previous work, we observed the same qualitative behavior for the SeMV T = 1 capsid (8), regardless of whether the equilibrium dynamics were generated from an ENM or from an MD simulation of the entire capsid in explicit solvent. In another ENM-based study on capsids, the lowest frequency normal modes were identified to be of type l = 2 for satellite tobacco mosaic virus and brome mosaic virus (17). In both of those capsid systems l = 2, 3, and 4 modes had lower frequencies than the lowest frequency l = 0 or l = 1 normal mode, qualitatively consistent with our findings. In that work, the authors also speculate that the stiffness of the l = 0 modes provides the virus with a natural resistance to internal or external pressures. However, they propose that the AFM deformation is coupled to the l = 2 mode, and hence is a soft mode. Our analysis indicates AFM is sensing the stiff l = 1 mode. Further evidence supporting the heterogeneity and anisotropy in mechanical properties and stiffness of the l = 0 modes comes from Brillouin light scattering experiments on satellite tobacco mosaic virus (18). In that work, the frequencies of an l = 0 and l = 2 mode were measured and the l = 0 mode was observed to be of considerably higher frequency than the l = 2 mode.
In this work, we illustrate the complexity of the mechanical properties of virus capsids. The uniform isotropic linear elastic theory we used to describe the capsid mechanics breaks down for both short and long wavelength motions, and highlights the need for a more complex theory to describe these systems. However, even within this framework we can gain insights into the different modes of deformation and provide semiquantitative estimates of the elastic moduli relevant to viral maturation, genome packaging and release, as well as informing AFM experiments.
Acknowledgments
This work has been supported by the National Institutes of Health to C.L.B. (RR012255) and by the National Science Foundation to E.R.M. (DBI-0905773) and W.S.K. (DMR-1006128).
Supporting Material
References and Footnotes
- 1.Jiang W., Li Z., Chiu W. Coat protein fold and maturation transition of bacteriophage P22 seen at subnanometer resolutions. Nat. Struct. Biol. 2003;10:131–135. doi: 10.1038/nsb891. [DOI] [PubMed] [Google Scholar]
- 2.Wikoff W.R., Liljas L., Johnson J.E. Topologically linked protein rings in the bacteriophage HK97 capsid. Science. 2000;289:2129–2133. doi: 10.1126/science.289.5487.2129. [DOI] [PubMed] [Google Scholar]
- 3.Smith D.E., Tans S.J., Bustamante C. The bacteriophage straight phi29 portal motor can package DNA against a large internal force. Nature. 2001;413:748–752. doi: 10.1038/35099581. [DOI] [PubMed] [Google Scholar]
- 4.Evilevitch A., Castelnovo M., Gelbart W.M. Measuring the force ejecting DNA from phage. J. Phys. Chem. B. 2004;108:6838–6843. [Google Scholar]
- 5.Ivanovska I.L., de Pablo P.J., Wuite G.J. Bacteriophage capsids: tough nanoshells with complex elastic properties. Proc. Natl. Acad. Sci. USA. 2004;101:7600–7605. doi: 10.1073/pnas.0308198101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Michel J.P., Ivanovska I.L., Schmidt C.F. Nanoindentation studies of full and empty viral capsids and the effects of capsid protein mutations on elasticity and strength. Proc. Natl. Acad. Sci. USA. 2006;103:6184–6189. doi: 10.1073/pnas.0601744103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lidmar J., Mirny L., Nelson D.R. Virus shapes and buckling transitions in spherical shells. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2003;68:051910–051919. doi: 10.1103/PhysRevE.68.051910. [DOI] [PubMed] [Google Scholar]
- 8.May E.R., Brooks C.L., III Determination of viral capsid elastic properties from equilibrium thermal fluctuations. Phys. Rev. Lett. 2011;106:188101. doi: 10.1103/PhysRevLett.106.188101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gibbons M.M., Klug W.S. Influence of nonuniform geometry on nanoindentation of viral capsids. Biophys. J. 2008;95:3640–3649. doi: 10.1529/biophysj.108.136176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Klug W.S., Bruinsma R.F., Wuite G.J. Failure of viral shells. Phys. Rev. Lett. 2006;97:228101. doi: 10.1103/PhysRevLett.97.228101. [DOI] [PubMed] [Google Scholar]
- 11.Konecny R., Trylska J., McCammon J.A. Electrostatic properties of cowpea chlorotic mottle virus and cucumber mosaic virus capsids. Biopolymers. 2006;82:106–120. doi: 10.1002/bip.20409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Tirion M.M, Large amplitude elastic motions in proteins from a single-parameter, atomic analysis. Phys. Rev. Lett. 1996;77:1905–1908. doi: 10.1103/PhysRevLett.77.1905. [DOI] [PubMed] [Google Scholar]
- 13.Cagin T., Holder M., Pettitt B.M. A method for modeling icosahedral virions: rotational symmetry boundary-conditions. J. Comp. Chem. 1991;12:627–634. [Google Scholar]
- 14.Im W., Lee M.S., Brooks C.L., 3rd Generalized born model with a simple smoothing function. J. Comput. Chem. 2003;24:1691–1702. doi: 10.1002/jcc.10321. [DOI] [PubMed] [Google Scholar]
- 15.Nguyen T.T., Bruinsma R.F., Gelbart W.M. Elasticity theory and shape transitions of viral shells. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005;72:051923. doi: 10.1103/PhysRevE.72.051923. [DOI] [PubMed] [Google Scholar]
- 16.Gibbons M.M., Klug W.S. Nonlinear finite-element analysis of nanoindentation of viral capsids. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2007;75:031901. doi: 10.1103/PhysRevE.75.031901. [DOI] [PubMed] [Google Scholar]
- 17.Yang Z., Bahar I., Widom M. Vibrational dynamics of icosahedrally symmetric biomolecular assemblies compared with predictions based on continuum elasticity. Biophys. J. 2009;96:4438–4448. doi: 10.1016/j.bpj.2009.03.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Stephanidis B., Adichtchev S., Mermet A. Elastic properties of viruses. Biophys. J. 2007;93:1354–1359. doi: 10.1529/biophysj.107.109033. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


