Cooperative [Ca²⁺]-Dependent Regulation of the Rate of Myosin Binding to Actin: Solution Data and the Tropomyosin Chain Model

Abstract

The regulation of muscle contraction by calcium involves interactions among actin filaments, myosin-S1, tropomyosin (Tm), and troponin (Tn). We have extended our previous model in which the TmTn regulatory units are treated as a continuous flexible chain, and applied it to transient kinetic data. We have measured the time course of myosin-S1 binding to actin-Tm-Tn filaments in solution at various calcium levels with [actin]/[myosin] ratios of 10 and 0.1, which exhibit modest slowing as [Ca²⁺] is reduced and a lag phase at low calcium. These observations can be explained if myosin binds to actin in two steps, where the first step is rate-limiting and blocked by TmTnI at low calcium, and the second step is fast, reversible, and controlled by the neighboring configuration of coupled tropomyosin-troponin units. The model can describe the calcium dependence of the observed myosin binding reactions and predicts cooperative calcium binding to TnC with competition between actin and Ca-TnC for the binding of TnI. Implications for theories of thin-filament regulation in muscle are discussed.

Introduction

The contractility of striated muscle is regulated by calcium-dependent azimuthal movements of tropomyosin-troponin (Tm-Tn) complexes over the surface of the actin filament, which regulate the affinity of myosin for regulated F-actin (1). Each Tm protomer spans seven actin sites on the same strand of the actin double-helix (2), and carries one molecule of troponin, which is composed of TnT which is bound to Tm, TnC which binds calcium, and TnI which binds to actin. Adjacent Tm protomers overlap slightly to form a chain along the actin filament, one for each strand of the double-helix (3). At low calcium, the chain is held in a blocking orientation because most molecules of TnI are bound to actin. Activation by calcium occurs via an allosteric transition in TnC, which transfers a C-terminal region of TnI from actin into the open E-F hands of TnC, allowing the chain to adopt a range of orientations on actin. A prolonged period of research has yielded the structures of the component proteins at near-atomic resolution (4–10) and the azimuthal dispositions of Tm and Tn on F-actin. The central result is the observation of three distinct azimuthal orientations of the chain (11,12), observed, respectively, at high calcium in the absence of myosin (ϕ = 0, the calcium-induced position or C position); at low calcium in the absence of myosin where TnI is bound to actin (ϕ = ϕ_B < 0, the blocked or B position); and at saturating levels of myosin-S1 bound to F-actin (ϕ = ϕ_M > 0, the myosin-induced or M position). These distinct orientations of the chain were predicted by McKillop and Geeves (13) on the basis of equilibrium binding data and were called the blocked, closed, and open states. Typical estimates are ϕ_B = −25° and ϕ_M = +10° (11).

These advances have produced a variety of models based on two or three discrete orientational states of the Tm-Tn complex (14–16), with state-dependent short-range attractive interactions between them (15). However, the chain has also been observed in intermediate orientations (17), which suggests that the overlapping TmTn protomers form a continuous flexible chain rather than a collection of individual regulatory units at discrete orientations (14). A regulatory model of this kind has been formulated in terms of an elastic flexible chain making thermally driven orientational fluctuations in a potential well (18), from which myosin-actin titration data at high and low calcium (19–21) can be predicted using equilibrium statistical mechanics. The continuous-flexible chain (CFC) model is supported by recent molecular modeling which shows that Tm dimers show remarkable uniform dynamic flexibility (22).

The original form of this chain model dealt only with equilibrium binding of myosin heads to actin, with and without Ca. Modeling of the kinetics of myosin binding as a function of calcium concentration will provide a more rigorous test of the model, because transient kinetics contains information on the cooperative activation of thin filaments by calcium and myosin. We have measured the time courses of myosin-S1 binding to actin-Tm-Tn filaments in solution at various calcium levels, with either excess actin or excess myosin. Both data sets display a modest reduction in the initial binding rate as [Ca²⁺] is reduced, also a lag phase at low calcium which is more prominent with excess myosin.

These results can be explained in terms of a continuous chain model where myosin binds to actin in two steps (Fig. 1). The rate of the first step, to a weakly-bound actomyosin, must be rate-limiting and controlled by the fluctuating positions of the chain over the binding site, which accords with the original steric blocking model (1). At low calcium, the chain occupies the blocking position generated by the binding of TnI to every seventh site on each strand of the actin double-helix, so all actin sites for weak myosin-S1 binding must have a similar orientation. The myosin binding rate is therefore proportional to the probability that the chain avoids the weak-binding site.

Figure 1.

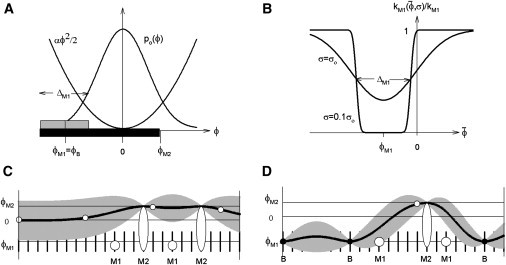
Aspects of a continuous-flexible-chain regulatory model with two-step myosin binding. (A) Azimuthal orientations ϕ of the binding site on actin for weak myosin binding (shaded box of width Δ_M1, centered on ϕ_M1 < 0), followed by a wider site for strong myosin binding (shaded box, out to angle ϕ_M > 0). The weak-binding site can be shared with troponin-I, so ϕ_M1 = ϕ_B, the blocking angle observed for the tropomyosin chain at low calcium. The chain is confined near-zero angle by a quadratic potential so that, at high calcium without bound myosins, the chain fluctuates ∼ϕ = 0 with a Gaussian distribution p_o(ϕ) of width σ_o (the closed state). If the chain is pinned nearby, it will fluctuate about a nonzero mean $\overline{\varphi }$ with a reduced standard deviation σ < σ_o. (B) The myosin binding rate k_M1($\overline{\varphi },$σ) is proportional to the probability that the chain avoids the weak-binding site, which varies with the local mean and SD of the chain as shown. Rate inhibition is most pronounced when the chain is held over the weak site by TnI, when σ will be small (e.g., σ = 0.1σ_o as shown). (C and D) Cartoons of azimuthal chain angles along F-actin (solid line = mean angle, shading = deviations out to ±σ, vertical ticks = weak-binding actin sites). (C) The high-calcium configuration with bound myosins as shown (M1 = weak, M2 = strong). The chain avoids all bound myosins, but M2 myosins trap the chain at angles beyond ϕ_M (the myosin state) because its initial angular distribution lies above ϕ_B. (D) The low calcium configuration, where the chain is pinned at the blocking angle by TnIs bound to actin (open circles on the chain = detached TnI, solid circles = bound TnI). Myosin can bind into state M1 only where the chain has moved to higher angles, firstly by detachment of TnIs and then by M2 myosins. Chain configurations were calculated from formulae in Appendix B in the Supporting Material.

At high calcium, nearly all TnI units are detached from the chain, which in the absence of strongly-bound myosins fluctuates about the closed position; the weak-binding sites are then open for myosin binding. At low calcium, most TnI units on the chain are bound to actin, so the chain is held close to the blocking angle in between bound TnIs and weak myosin binding is strongly inhibited. The quantitative formulation of these ideas is summarized in Fig. 1, A and B. To complete this kinetic description, the subsequent isomerization to strongly-bound myosin must be fast and reversible, and the equilibrium constant of the isomerization must be modulated by the deformation energy of the chain (20,21).

This model can explain why the chain always occupies the M position in the vicinity of strongly-bound myosins. If the B position lies below the range of angular fluctuations of the free chain, then the chain will nearly always be on the high-angle side of any weakly-bound myosin before it isomerizes to the strongly-bound state with a much wider interface on actin (Fig. 1 A). This isomerization is possible only if the chain makes a prior fluctuation to angles beyond the M position, after which the chain is trapped on the high-angle side of the strongly-bound myosin. Fig. 1, C and D, illustrates this principle at high and low calcium, respectively.

Experimental binding transients were fitted to the CFC model by generating simulated transients with the Monte Carlo method. The kinetic parameters of the model are the actin affinity K_M1 and binding rate k_M1 for myosin, the equilibrium constant K_M2, and the actin affinity K_TI of TnI, all defined in the absence of chain distortion. The chain parameters are its persistence length L_P on F-actin, the chain angles ϕ_B, ϕ_M, and Δ_M1, plus the angular standard deviation σ_o of the free chain. The fitting procedure yielded values of K_TI as a function of [Ca²⁺], which can be fitted to a reaction scheme for the allosteric transition on TnC.

Experimental Methods

Transients for the binding of myosin-S1 to actin-Tm-Tn in solution were obtained from rapid-mixing experiments over a wide range of calcium levels (pCa from 4.6 to 8.9), under pseudo-first-order conditions either with excess actin ([A] = 2.5 μM, [M] = 0.25 μM) or excess myosin ([A] = 0.5 μM, [M] = 5.0 μM).

Protein preparations (pyrene-labeled actin, myosin-S1, TmTn)

Rabbit actin was prepared according to Spudich and Watt (23) and labeled with pyrene to >90% at CyS374 (24). Rabbit skeletal muscle TmTn was prepared by the method of Ebashi et al. (25), and rabbit skeletal myosin subfragment 1 (S1) by chymotryptic digestion of myosin (26).

A problem with assembling an active thin filament is to ensure that the filament is fully regulated, so that actin filaments are fully saturated with TmTn and the TmTn units are 100% active. A damaged or inactive TnC can result in a regulatory unit that is turned off, independent of the calcium concentration. A damaged or inactive TnI can result in a regulatory unit that is turned on independent of the calcium. We attempted to maximize the presence of fully active regulatory units by a two-step process. The addition of TmTn to actin results in an inhibition of the observed rate constant (k_obs) of S1 binding to an excess of actin by a maximum of 75%. Saturation of the effect required addition of TmTn at a ratio of 1.5 ± 0.3 TmTn per 7 actin monomers. We therefore routinely added 2 mol of TmTn per 7 actin monomers and rejected any TmTn preparation which inhibited the k_obs by <70% and which could not subsequently be activated by calcium to within 10% of the k_obs for unregulated actin.

Rapid mixing experiments

All data were collected in a model No. SF61 stopped flow fluorimeter (HiTech Scientific, www.hitechscientific.com) which has a dead time of 1.5 ms. The pyrene fluorescence from labeled actin was monitored by excitation at 365 nm (Xe/Hg lamp with wavelength section via a monochromator) and detection through a KV389 filter which cuts off light below 389 nm. All experiments were carried out in a buffer containing 100 mM KCl, 5 mM MgCl₂, 1 mM NaN₃, 20 mM MOPS, pH 7.0, 20°C. The calcium concentration was maintained by mixing a solution of EGTA and calcium-saturated EGTA at 2 mM to give the required free calcium concentration (27).

Characterization of data

The characteristic rate constant k_obs of each myosin-binding transient is calcium-dependent, as shown in Fig. 2. Kinetic regulation by calcium is quite modest: for the excess-actin condition there is a factor of four between the values of k_obs at high and low calcium, and for the excess-myosin condition a factor of two. The binding transients at high, intermediate, and low calcium are shown in Fig. 3 for each condition. Transients with excess actin can be fitted by a single exponential rise, although a slight lag is discernible at low calcium. The excess-myosin transients show a pronounced lag at low calcium, which provides a better test of kinetic models, but these transients also show steric slowing as the actin sites fill up with myosins. This slowing effect complicates data-fitting with the CFC model; additional experiments described in the Supporting Material show that this effect is present with pure actin filaments and hence independent of the regulatory mechanism. Steric slowing was incorporated into Monte Carlo simulations by reducing the rate of myosin binding by a factor of γ for each occupied nearest-neighbor site, where γ was determined by fitting the high-calcium transient.

Figure 2.

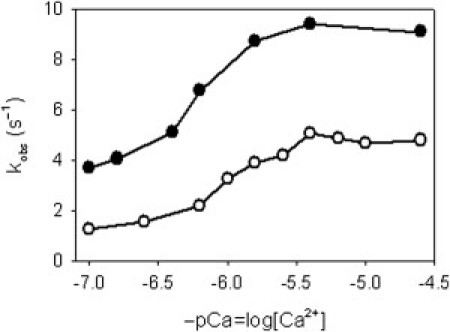
Calcium dependence of the rate constant k_obs for myosin binding transients to regulated actin in solution-mixing experiments, for excess-actin (○) and excess myosin (●). Values of k_obs were obtained by fitting to a single exponential rise 1–exp(−k_obst), which ignores any lag phase and provides a one-parameter description of the transients.

Figure 3.

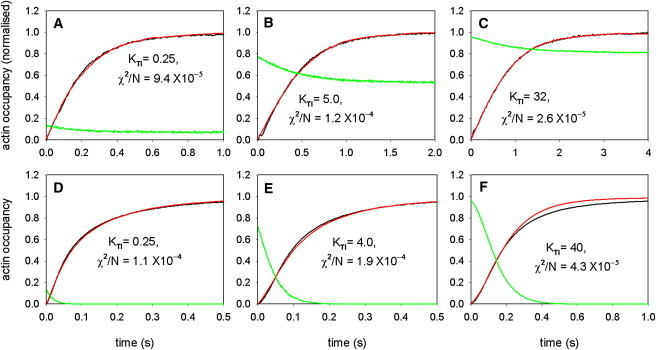
Time courses of the occupancy of actin sites by myosin, measured in solution-mixing experiments with apo-myosin-S1 at high and low calcium (black lines), and their simulation by repeated Monte Carlo runs with the two-step chain model (red lines). The simulations also gave the occupancy of every seventh actin site by TnI (green lines). The ratio [A]/[S1] was 10 for the excess-actin data (A–C) and 0.1 for the excess-myosin data (D–F). (A and D) High calcium (pCa = 4.5), (B and E) intermediate (pCa = 6.2), and (C and F) low calcium (pCa = 7.0). With excess actin, the occupancy of actin sites saturates at just under 0.1, and was renormalized to unity at long times. Simulations at different calcium levels were fitted to the data by adjusting the actin-TnI affinity K_TI to minimize the least-squares deviation χ²/N per data-point over the whole transient in panels A–C, and over the first 50% of the rise in D–F to avoid overshooting in the approach to saturation at low calcium (see main text). The optimal parameters of the model are shown in Table 1.

Mathematical Methods

Overlapping units of tropomyosin-troponin on actin can be modeled as a continuous flexible chain (20). The governing equation is the expression

$$E\left\{\varphi \left(s\right)\right\}=\frac{1}{2}{\int }_0^{\text{L}}\left\{\kappa {\varphi }^{″}{\left(s\right)}^2+\alpha \varphi {\left(s\right)}^2\right\}ds$$ (1)

for the elastic distortion energy of a chain of length L with azimuthal angular displacement ϕ(s) at position s. The parameters κ and α specify the bending stiffness of the chain and the curvature of the quadratic potential which confines the chain to the groove between the strands of the actin double-helix. The resting chain sits at ϕ = 0. In thermal equilibrium, the chain fluctuates about this mean angle, with a standard deviation σ_o = (k_BTL_P³/8κ)^1/2, where L_P = (4κ /α)^1/4 is the persistence length of the chain on F-actin (20). Here k_B is Boltzmann's constant and T is the absolute temperature.

When an isolated troponin-I is bound to actin, the chain is locally pinned at the blocking angle ϕ_B and is displaced from zero angle over a region of width L_P on either side, generating an umbrella of width 2L_P. The resulting distortion energy of the chain is A(ϕ_B), where A(ϕ)/k_BT = ϕ²/2σ_o². A strongly-bound myosin is assumed to pin the chain locally at angle ϕ_M, because the average energy cost A(ϕ_M) is very similar to that of a chain trapped by fluctuations at angles above ϕ_M, as argued in the Introduction. When the chain is pinned at two places by M2 myosin or bound TnI, the distortion energy of the chain depends on their separation x. When x >> L_P, the distortion energy is the sum of the energies of the individual umbrellas. When x << L_P, the umbrellas have merged and the homo-pair distortion energy is that for a single umbrella (20), whereas the hetero-pair energy is large because the chain is forced to adopt different angles over a small distance (18,21).

The chain model is complicated by the need to keep track of the mean and standard deviation of chain angles at any putative binding site, which determine the distribution of chain fluctuations, and this can be done in terms of nearest-neighbor pinning sites. Thus the affinities of myosin and TnI for regulated actin can be quantified in terms of the energy ΔE_mn(ϕ | X,Y) required to move the chain from its equilibrated mean angle to angle ϕ, when nearest-neighbor pinning centers of type m,n are at distances X = x/L_P, Y = y/L_P on either side. The indices m,n are bivalued, say m = 2 for M2 myosin and m = −1 for bound TnI. The net myosin affinity to state M2 and the actin affinity of TnI are

$$K_{\text{M}}^{\left(\text{mn}\right)}\left(X,Y\right)=K_{\text{M}1}{K}_{\text{M}2}\exp \left(-\beta \Delta E_{\text{mn}}\left({\varphi }_{\text{M}2}|X,Y\right)\right),$$ (2a)

$$K_{\text{TI}}^{\left(\text{mn}\right)}\left(X,Y\right)=K_{\text{TI}}\exp \left(-\beta \Delta E_{\text{mn}}\left({\varphi }_{\text{B}}|X,Y\right)\right),$$ (2b)

by Gibbs' thermodynamic identity, where β =1/k_BT, whereas the myosin affinity K_M1 to state M1 is assumed to be unregulated for actin sites not occupied by TnI. Now ΔE_mn(ϕ | X,Y) is quadratic in ϕ because Eq. 1 for chain energy is harmonic in ϕ(s), so

$$\Delta E_{\text{mn}}\left(\varphi |X,Y\right)=k_{\text{B}}T\frac{{\left(\varphi -{\overline{\varphi }}_{\text{mn}}\left(X,Y\right)\right)}^2}{2{\sigma }_{\text{mn}}{\left(X,Y\right)}^2}.$$ (3)

The values ${\overline{\varphi }}_{\text{mn}}(X,Y)$ and σ_mn(X,Y) are the mean and SD of chain angle at the binding site, because the chain is subject to thermal fluctuations and the distribution of chain angles is proportional to the Boltzmann factor exp(−βΔE_mn(ϕ |X,Y)), which is seen to be a Gaussian distribution. Closed formulae for the mean and SD as functions of m, n, X, and Y are given in the Supporting Material. This Boltzmann factor can be used to calculate the myosin binding rate into state M1, in terms of the probability that the chain avoids the weak-binding site. Thus

$$k_{\text{M}1}^{\left(\text{mn}\right)}\left(X,Y\right)=k_{\text{M}1}P\left({\overline{\varphi }}_{\text{mn}}\left(X,Y\right),{\sigma }_{\text{mn}}\left(X,Y\right)\right),$$ (4)

where k_M1 is the equivalent first-order binding rate to unregulated actin and

$$P\left(\overline{\varphi },\sigma \right)=1-\frac{1}{\sqrt{2\pi {\sigma }^2}}{\int }_{{\varphi }_{\text{M}1}-{\Delta }_{\text{M}1}/2}^{{\varphi }_{\text{M}1}+{\Delta }_{\text{M}1}/2}\exp \left(-\frac{{\left(\varphi -\overline{\varphi }\right)}^2}{2{\sigma }^2}\right)d\varphi$$

$$=1-\frac{1}{2}\sum _{\pm }\pm \text{erf}\left(\frac{{\varphi }_{\text{M}1}\pm {\Delta }_{\text{M}1}/2-\overline{\varphi }}{\sqrt{2}\sigma }\right)$$ (5)

in terms of the error function, with ϕ_MI = ϕ_B (Fig. 1 A). As a function of mean chain angle, the extent of inhibition when the chain covers the binding site is controlled by the local standard deviation of the chain (Fig. 1 B). When $\overline{\varphi }={\varphi }_{\text{M}1},$ P attains its minimum value of $1-\text{erf}\left({\Delta }_{\text{M}1}/2\sqrt{2}\sigma \right)$ and substantial inhibition (P_min < 0.32) is achieved when Δ_M1/σ > 2. Rate inhibition is required at low calcium where the chain is pinned by TnI and σ < σ_o. Between two adjacent bound TnIs, the value of σ is typically ∼0.5σ_o (Fig. 1 D), so that calcium regulation of myosin kinetics requires that

$${\Delta }_{\text{M}1}/{\sigma }_{\text{o}}>1.$$ (6)

Equations 2–5 are the defining formulae of the two-state chain model under conditions where the M1→M2 transition and the actin binding of TnI are both rapid with respect to myosin binding to M1. These reversible transitions can then be equilibrated at every stage of the myosin binding transient, for which it suffices to know the affinities in Eq. 2. Myosin transitions to or from state M2 must occur via state M1. The myosin detachment rate from state M1 is equal to $k_{\text{M}1}^{\left(\text{mn}\right)}(X,Y)/K_{\text{M}1}.$

To simplify the mathematics, it was necessary to assume that no chain distortion energy is associated with M1 myosins, which implies that their affinity is not regulated by the chain. This approximation neglects the exclusion of the chain from the weak-binding site. Except in the vicinity of bound TnIs, the energy cost of this exclusion is subthermally small if Δ_M1 << σ_o, and also small if |ϕ_B| > σ_o when most configurations of the free chain lie at angles nearer zero. The first condition is violated by Eq. 6, but the second condition is satisfied by our final value of ϕ_B. Although this approximation breaks down near bound TnIs where the chain is held near the blocking angle, the error involved is limited to the population of weakly-bound myosins, which is very low in this study where K₂ >>1. For strongly-bound myosins, the net energy cost is incorporated correctly in Eq. 2a for the net affinity. The important point is that the net rate of myosin binding is limited by the weak-binding step, as in Eq. 4.

Monte Carlo Simulations with the Chain Model

The chain model with two-step myosin binding was tested by fitting Monte Carlo simulations to the measured binding transients (Fig. 3). The quantity computed was the fractional occupancy of actin sites by myosin. For the case of excess actin, this fraction was normalized to unity by dividing by the steady-state fraction approached at long times, which was always slightly below 0.1. Simulations were computed for one strand of regulated actin, using uniform random deviates in (0,1) to generate myosin attachment events from transition probabilities in the step time δ t. The current state of the system was specified by occupation numbers (n_i; i = 1,….,N) for actin sites, where n_i = 0 for free sites, +1 or +2 when occupied by myosin in states M1 or M2, or –1 when occupied by TnI. Only every seventh site is accessed by TnI, and this formulation implies that myosin and TnI compete for these sites.

To allow for the progressive depletion of free myosin-S1 during binding, k_M1 is proportional to [M] = [M_tot]−[A.M] = [M_tot]−p[A_tot], where p is the fraction of actin sites occupied by myosin, so the binding probability becomes time-dependent, namely $k_{\text{M}1}^{\left(\text{mn}\right)}\left(X,Y\right)\left(1-\lambda p\left(t\right)\right)\delta t$ at time t, where λ = [A_tot]/[M_tot]. The probability of detaching the bound myosin is constant in time and equal to $\left(k_{\text{M}1}^{\left(\text{mn}\right)}\left(X,Y\right)/K_{\text{M}1}\right)\delta t$ The M1-to-M2 transition was equilibrated at each time step by comparing another random deviate with the equilibrium occupancy $K_{\text{M}2}^{\left(\text{mn}\right)}\left(X,Y\right)/\left(K_{\text{M}2}^{\left(\text{mn}\right)}\left(X,Y\right)+1\right)$ of the M2 state, with an analogous procedure for the actin binding of TnI. This method enabled rapid repeated passes of a strand of regulated actin with N = 500, corresponding to a filament length of 2.65 μm. Although filaments of various lengths were present in the solution experiments, the simulation results were not sensitive to filament length as such but only to the product MN where M is the number of passes. For the excess-actin data, M = 40 at high calcium, rising to 200 at low calcium, generated standard errors of 0.07–0.09 in the normalized binding fraction at half-saturation; this accuracy enabled data-fitting which did not change significantly when much higher values of M were used. With excess myosin, the same M values gave standard errors of 0.02 at half-saturation. A time step of 1 ms was used for the excess-actin simulations, and 0.1 ms for the excess-myosin case.

The computational load was much reduced by fixing the values of various parameters, as described in Table 1, and expressing all chain angles as fractions of the free-chain SD σ_o. For a particular choice of pinning angles, the excess-actin transient at high calcium (pCa = 4.6) was first fitted by varying the myosin binding rate k_M1, keeping K_TI = 0.l (Fig. 3 A). Fits to the excess-actin data at all calcium levels were then sought by keeping k_M1 constant and varying the actin-TnI affinity K_TI. Saturation levels of the experimental transients were normalized to unity, so the simulations were scaled accordingly. The excess-actin fits were refined by varying the notional saturation level of the simulation between 0.09 and 0.1 to minimize χ² over the time to 98% saturation, for example as in Fig. 3, B and C.

Table 1.

Optimal values of fitting parameters with the two-step chain model

Chain persistence length	LP = 20 (nm)
M1,TnI pinning angle	ϕB /σo = −1.0
M2 myosin pinning angle	ϕM/σo = 0.4
Myosin binding rate	k−M1 = 0.9, 18 (s−1)
Steric slowing factor	γ = 0.39
TnI affinity, pCa = −4.6	KTI = 0.25, 0.25
TnI affinity, pCa = −7.0	KTI = 32, 40
Ca affinity for TnC	${\tilde{K}}_{\text{c}}=$ 23, 18 (μM−1)
Allosteric TnC parameter	ɛ = 0.034, 0.033

Bivalued parameters refer to excess actin and excess myosin, respectively. Other parameters of the model were fixed as follows. There were N = 500 actin monomers in the putative actin-Tm-Tn filament. Myosin and actin concentrations before mixing were [M] = 0.25, 5.0 μM and [A] = 2.5, 0.5 μM, respectively, for the excess actin and excess myosin experiments. Basal myosin affinities (with no chain distortion) were fixed at values derived from the experimental data—namely, K_M1= 0.05, 1.0, respectively, and K_M2 = 100 (14). The actin-TnI affinity K_TI at high calcium (pCa = 4.6) was initially set to 0.1 to reduce TnI-actin attachment to a low level. The model only requires pinning angles ϕ_B, ϕ_M as fractions of the angular SD. The σ_o of the free chain, and the reduced width Δ_M1/σ_o of the weak-binding site was set at 2.0 (see main text). The simulations suggest that these values are optimal for fitting the experimental binding transients.

The excess-myosin data could only be fitted by incorporating steric slowing, by multiplying the myosin attachment rate k_M1 by 1−γ or (1−γ)², respectively, when one or both nearest-neighbor sites were occupied by myosins. The high-calcium transient was best fitted when γ = 0.39, with the previous value of k_M1 multiplied by 20, the ratio of the myosin concentrations (Fig. 3 D). Fits to the excess-myosin data at all calcium levels were then attempted by varying K_TI, keeping k_M1 and γ constant. At low calcium, the simulated transient showed the pronounced lag seen experimentally, but also rose above the data as binding approached saturation (Fig. 3 F). Hence, the fits were refined with respect to K_TI by minimizing χ² over the first 50% of the transient rise, a procedure which is not sensitive to overshooting.

The values of the reduced pinning angles (ϕ_B/σ_o = −1.0, ϕ_M/σ_o = 0.4 in Table 1) agree with cryo-EM determinations of the angles themselves, namely ϕ_B = −25°, ϕ_M = +10° (8), if σ_o = 25°. This quantity can also be estimated from the formula σ_o = (k_BTL_P³/8κ)^1/2, where L_P is the persistence length of tropomyosin on F-actin (19) and L_PS = (κ /R²)/k_BT is the persistence length in solution. A recent determination of the latter, which includes the curved equilibrium shape of the tropomyosin protomer, gives L_PS ≈ 460 nm (28,29), so κ = 3.03 × 10⁻⁴⁴ N.m⁴ if R = 5.0 nm for the radius of tropomyosin on F-actin. Thus, σ_o = 0.44 radians or 25° if L_P = 22.8 nm. In the McKillop-Geeves model (13,14), an n-site regulatory unit can be reproduced by the chain model if n = 2L_P/c + 1 where c = 5.54 nm is the actin monomer spacing (20), giving n = 9.2. Experimentally, n = 8 for skeletal A-Tm and 12 for A-TmTn at high Ca (14,19). The values of σ_o and L_P used for modeling are broadly consistent with these numbers.

The key result of this fitting procedure is the calcium dependence of K_TI, which is a strongly decreasing function of the free calcium-ion concentration (Fig. 4). This function can be fitted to an allosteric reaction scheme which couples K_TI to the occupancy of the two low-affinity Ca²⁺ sites on skeletal TnC. This scheme is similar to others in the literature (30,31), but has been simplified by assuming that the first and second Ca²⁺ ions bind with the same affinity per site. Hence

where

$$K_{\text{TI}}\left(C\right)={\left(\frac{1+{\tilde{K}}_{\text{c}}C}{\varepsilon +{\tilde{K}}_{\text{c}}C}\right)}^2\frac{1}{\lambda }$$ (7)

and

$$C=\left[\mathrm{C}{\mathrm{a}}^{2+}\right]\text{and}\varepsilon <1.$$

Determinations of K_TI(C) obtained by fitting the chain model to the data were fitted by Eq. 7, and are shown in Fig. 4 for the excess-actin and excess-myosin experiments. The two fits are qualitatively similar, which suggests that the parameters ${\tilde{K}}_{\text{c}}$ and ɛ of TnC-TnI-actin interaction are not much affected by the different solution conditions of the two experiments; this result is the strongest evidence for the viability of the kinetic chain model.

Figure 4.

Actin affinity K_TI(C) of TnI as a function of calcium level C for excess-actin (○) and excess-myosin conditions (●) in Table 1, determined by fitting the myosin binding transients of Fig. 3. (Solid and dashed lines) Corresponding fits to the allosteric function of Eq. 7. For the excess-actin data, ${\tilde{K}}_{\text{C}}$ = (2.31 ± 0.10) × 10⁵ M⁻¹ and ɛ = 0.034 ± 0.0015. Similar values were found for the excess-myosin data, namely ${\tilde{K}}_{\text{C}}$ = (1.77 ± 0.16) × 10⁵ M⁻¹ and ɛ = 0.0327 ± 0.0019. Both fits were obtained with K_TI(∞) ≡ 1/λ = 0.1.

Monte Carlo simulations provide explicit illustrations of the chain model by generating instantaneous chain configurations as myosins and TnIs bind and detach from actin. Four examples are shown in Fig. 5. The amount of clustering evident in these plots can be interpreted in terms of chain-induced cooperativity between neighboring myosins and also between neighboring TnIs, plus chain-induced inhibition between myosin and TnI, as explained in the figure caption.

Figure 5.

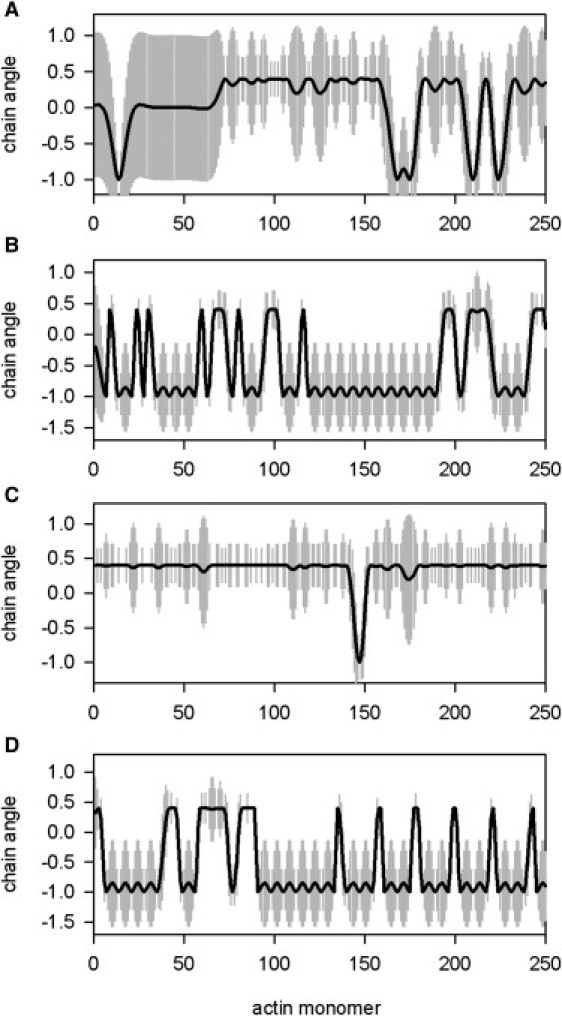
Four instantaneous configurations of the tropomyosin chain generated by Monte Carlo simulation in the course of myosin binding, with chain angles as fractions of the standard angular deviation σ_o. (A) Excess actin and high calcium, sampling the quasi-steady state reached after 2 s with myosins occupying 10% of actin sites. Bound myosins occurred in clusters of 5–10 sites (25–50 nm), whose widths are consistent with chain umbrellas of width 2L_P = 40 nm, each opened by a single myosin. (B) Excess actin and low calcium after 5 s, showing much greater clustering of bound TnIs. The 10% occupancy by myosins was insufficient to disrupt the 14% concentration of bound TnIs which protect intermediate actin sites by holding the chain near the blocking angle ϕ_B (TnI-TnI cooperativity). This cooperative inhibition requires the persistence length to be at least half of the 38.5 nm TnI spacing. (C) Excess myosin and high calcium after 12 ms, which also gave 10% occupancy by myosins. In this case, the myosins moved nearly all the chain to the myosin angle ϕ_M, because the 53-nm average spacing between bound myosins is comparable with the 40-nm span of a single umbrella. Hence these umbrellas overlapped to form a giant cluster of bound myosins (myosin-myosin cooperativity) punctuated by occasional unoccupied sites and just one bound TnI. (D) Excess myosin and low calcium at 10% myosin occupancy, achieved after 47 ms. Here the tendency to myosin clustering is overridden by the clustering of bound TnIs (cooperative myosin-TnI inhibition), just as with excess actin at a much later time.

Discussion

The experimental myosin binding transients show two key properties of kinetic regulation by calcium: the observed binding rate is an increasing function of calcium level, and at low calcium there is an initial lag phase which is more pronounced at high myosin concentrations. These properties follow naturally from a chain model where the rate of myosin binding is regulated by the mean azimuthal position of the chain. As the calcium level is increased, TnIs detach from actin and allow the chain to move away from the blocked position, exposing the weak-binding site for myosin binding. The rate of the initial rise is limited by the number of sparse regions where a molecule of TnI has detached from actin and the chain has moved toward the C-position: this initial rate is a decreasing function of the angular width Δ_M1 of this site (Fig. 1). Strongly-bound myosins open the chain cooperatively to the M position, ending the lag phase; the subsequent rate of binding is limited by the myosin concentration rather than the number of unblocked actin sites. Thus, the lag phase is more pronounced with a high concentration of myosins in solution.

With excess actin, the chain model generated excellent fits to the experimental binding transients, over calcium levels ranging from strong inhibition to full activation (Fig. 4 A). With excess myosin, the fits were affected by steric slowing as saturation approaches, and are of similar quality when restricted to site occupancies below 50%. To understand in detail how the model works, we made a systematic study of the effects of changing the pinning angles and the chain persistence length. This study confirmed that the values assigned in Table 1 are close to optimal, as explained below, and that the overshoot generated by the model with excess myosin at low calcium (Fig. 3 F) could not be removed.

When the magnitude of the blocking angle ϕ_B is increased, the lag phase is reduced because of the increased energy of chain distortion required to hold the blocked state. To counter this effect, TnI must be able to bind more tightly to actin at low calcium: the excess-actin value of K_TI at low calcium (pCa = 7) increases from 40 to 200 when |ϕ_B| is increased from 1.0 to 1.4. Similarly, when ϕ_M is increased, the distortion energy of the chain is increased when myosins bind, and the increased curvature between blocked and open positions of the chain makes it more difficult for the chain to stay pinned in the blocked position by bound TnIs unless K_TI is increased again. For example, when ϕ_B = −1.0 and ϕ_M = 1.0, the required values of K_TI at low calcium increase to 100 and 350 for the excess-actin and excess-myosin data, respectively, and the rough equivalence between these forms of K_TI(C) is lost, although the data can still be simulated. Major differences between the excess-actin and excess-myosin forms are not expected; the conditions are carefully matched, although the measurements are not completed at the same time.

The effects of changing the chain persistence length are more pronounced. If L_P is lowered from 20 nm to 17 nm, the value of K_TI required for the excess-actin data at low calcium exceeds 300. This is a consequence of reducing chain-induced cooperativity between adjacent TnIs, which acts to stabilize the blocked state by holding the chain near the blocking angle in the intervening regions. Values of L_P in excess of 20 nm allow weaker actin-TnI binding at low calcium. In this way, the 22.8 nm estimate from the persistence length L_PS of Tm in solution might be accommodated. Note that L_P << L_PS because lateral displacements of Tm on actin must be constrained by electrostatic interactions.

The fraction of the tropomyosin chain which lies in the blocked state ϕ ≤ ϕ_B is an interesting property of the chain model. For skeletal A-Tm-Tn at high calcium with no myosin, this quantity was estimated at 20% by Pirani et al. (17) from cryo-EM studies with improved axial resolution. For the free chain, Gaussian statistics apply at each point, so the blocked fraction is equal to $\text{erfc}\left(\right|{\varphi }_{\text{B}}|/\sqrt{2}{\sigma }_{\text{o}})/2$= 0.2, giving ϕ_B/σ_o = −0.84, which is close to the optimal value (−1.0) for simulations. More generally, Pirani's observation is cogent evidence for a range of angles of the free chain in the closed state, rather than the single angle implied by rigid-cooperative-unit theories of muscle regulation.

The fitting of myosin binding transients by the kinetic chain model passes a final test: the calcium-dependent actin affinity K_TI(C) of TnI conforms to an allosteric model of TnC-TnI-actin interaction, with very similar parameter values for excess actin and excess myosin. The value of ${\tilde{K}}_{\text{C}}$ is similar to those reported for the low-affinity Ca²⁺ sites (30,31); however, the value ɛ = 0.033 is smaller than that used for pressure-jump studies on a mutant of isolated TnC (32). Equation 7 implies that the actin affinity of TnI at zero calcium is K_TI(0) = K_TI(∞)/ɛ ², which is of ∼100; a value of 50 was used in Smith and Geeves (21). This value is not achieved at submicromolar calcium levels—$C_{\text{o}}=\varepsilon /{\tilde{K}}_{\text{c}}$ is the calcium sensitivity such that K_TI(C_o) = 0.5K_TI(0), and C_o ≈ 1.5 × 10⁻⁷ M here. The allosteric function of Eq. 7 may be too simple: the two calcium binding steps may have different affinities apart from site degeneracy, and the factor ɛ which controls the Ca-dependence of actin-TnI binding may be different for singly and doubly-bound Ca states (31). However, the fits are indifferent to such refinements.

Monte Carlo simulations also predicted the time course of TnI-actin attachments (Fig. 3). At high calcium, most TnIs are initially detached from actin, and the rest are detached as myosin-binding proceeds (Fig. 3, A and D). At low calcium, most TnIs are initially bound. With excess actin (Fig. 3 C), the extent of TnI detachment by myosins is relatively modest, and the time course of TnI detachment follows that of myosin binding. With excess myosin (Fig. 3 F), the detachment of TnIs proceeds to completion and is approximately twofold faster than the time course of myosin binding. The twofold increase reflects a faster overall change in chain configuration, driven by the cooperativity of chain movements caused by many myosin-binding events.

This effect has been observed by monitoring the time course of fluorescent-labeled tropomyosin movements during myosin binding with excess myosin (33). In these experiments, the Tm signal was 5–6 times faster than the myosin signal, consistent with n = 6 and L_P = 14 nm. Although the unit size used here is larger, we conclude that the effective rate of TnI detachment is slower than the rate of chain movements induced by myosin binding, but is still faster than the effective myosin binding rate. Some TnIs stay attached to actin even when myosin binding is well under way and the chain has moved accordingly.

The model presented here should be directly applicable to thin-filament regulation of muscle contraction, except for the consequences of tethering myosins to thick filaments. In frog muscle, which has a 2:1 actin/myosin lattice, there are 150 myosin dimers (pairs of myosin-S1 heads bound to S2) per myosin filament per half-sarcomere and 260 actin monomers on the 720-nm overlap length of an actin filament, so the apparent [S1]/[A] ratio is 1.15. However, axial and azimuthal constraints allow only ∼60% of dimers to interact with actin (34), and only one head of each such dimer can bind strongly to actin. Thus, 90 heads per F-myosin are capable of interaction with the six surrounding F-actins, which means that each F-actin can interact with 45 heads from the three surrounding F-myosins. Hence, 22.5 heads address one strand of the F-actin double-helix, with 130 monomers in the overlap length, which is regulated by a single tropomyosin chain. The effective [S1]/[A] ratio is therefore 22.5:130 = 0.173, and the average spacing between these myosins is 32 nm, not much less than twice the chain persistence length of 20 nm.

At first glance, chain-induced cooperativity between myosins would be rather limited. However, the myosin-myosin spacing is not uniform, being made up of interacting myosins at multiples of the 14.3-nm myosin repeat distance. Islands of cooperatively-bound myosins with an open chain will exist where the predominant spacing is 14.3 nm, linked more weakly by the chain where the local spacing is two or three times that period. It remains to be seen if such a model can reproduce the observed regulation of the rate of force development in striated muscle.