Abstract
Latent variable modeling methods have demonstrated utility for understanding the structure of executive control (EC) across development. These methods are utilized to better characterize the relation between EC and mathematics achievement in the preschool period, and to understand contributing sources of individual variation. Using the sample and battery of laboratory tasks described in Wiebe, Espy and Charak (2008), latent EC was related strongly to emergent mathematics achievement in preschool, and was robust after controlling for crystallized intellectual skills. The relation between crystallized skills and emergent mathematics differed between girls and boys, although the predictive association between EC and mathematics did not. Two dimensions of the child’s social environment contributed to mathematics achievement: social network support through its relation to EC and environmental stressors through its relation with crystallized skills. These findings underscore the need to examine the dimensions, mechanisms, and individual pathways that influence the development of early competence in basic cognitive processes that underpin early academic achievement.
Introduction
Children acquire considerable knowledge of numbers and numeracy before beginning kindergarten. This numerical knowledge that kindergartners bring to school is critical, as it is related to mathematics learning in the early school years (Duncan, Dowsett, Claessens, Magnuson, Huston, Klebanov, Pagani, Feinstein, Engel, Brooks-Gunn, Sexton, Duckworth & Japel, 2007; Jordan, Kaplan, Locuniak & Ramineni, 2007; Locuniak & Jordan, 2008), which in turn provides the grounding for more complex mathematical skills as the child progresses through schooling. Unfortunately, many children from low-income backgrounds enter school with less knowledge than peers from middle-income backgrounds, and the achievement gap in mathematical knowledge progressively widens throughout their school career (National Mathematics Advisory Panel, 2008). Kindergarten children from middle-income homes are reported to engage in more math-related activities than their low-income peers (Jordan, Kaplan, Olah & Locuniak, 2006), and the amount of informal instruction children receive at home on number concepts is a good predictor of the number skills shown by children as they enter school (Saxe, Guberman, Gearhart, Gelman, Masey & Rogoff, 1987). Griffin, Case and Siegler (1994) report that middle-income children enter kindergarten with better developed number knowledge (e.g. discriminating which of two numbers is bigger) than low-income children, and this along with other basic aspects of numeracy strongly predicts subsequent arithmetic achievement in Grade 1 (Jordan et al., 2007) and calculation fluency in Grade 2 (Locuniak & Jordan, 2008). Therefore, factors related to socioeconomic status clearly place some children at greater risk of subsequent mathematical difficulties in early formal schooling (see also Jordan, Huttenlocher & Levine, 1992, 1994).
Skills such as the ability to identify numbers, counting, and understanding of quantity (or in the language domain, identifying letters and the development of vocabulary) have been referred to as crystallized knowledge or crystallized intelligence (gC; see Blair, 2006, for a review; Cattell, 1963; Horn & Cattell, 1966) and are strongly predictive of mathematics and literacy abilities in later school years. As many of these basic skills develop prior to formal schooling, experiences that differ across SES will influence the acquisition of this crystallized knowledge. SES is associated with a number of indices of children’s cognitive ability and achievement, including IQ, achievement test performance, and grade retentions (e.g. Bradley & Corwyn, 2002; Espy, Molfese & DiLalla, 2001; Gottfried, Bathurst, Guerrin & Parramore, 2003; Liaw & Brooks-Gunn, 1994; Noble, McCandliss & Farah, 2007). However, early opportunities for acquiring crystallized knowledge also interact with a basic cognitive capacity for learning that facilitates complex cognitive operations, also known as fluid cognitive skills or fluid intelligence. Gathercole, Pickering, Knight and Stegman (2004) note that it is essential to assess these fluid cognitive capacities; as these skills are not knowledge based, tests of fluid cognitive skills are equally unfamiliar to all children, and some have argued that these skills are impervious to substantial differences in socioeconomic background, including demographic factors and maternal education (Alloway & Alloway, 2010; Engel, Santos & Gathercole, 2008; Gathercole et al., 2003 cited in Gathercole, Brown & Pickering, 2003). Fluid skills involve the active or effortful maintenance of information for purposes of planning and executing goal-directed behavior. Many of these fluid skills also fall under the rubric of executive control (EC).
In classic (Baddeley, 1996) and recent (Miyake, Friedman, Emerson, Witzki, Howerter & Wager, 2000) reports, a ‘central executive’ is conceptualized as discrete executive functions, some of which are related more strongly to general fluid abilities (or gF) than others (Tillman, Nyberg & Bohlin, 2008). These distinct executive functions include inhibition (suppression of dominant action tendencies in favor of more goal-appropriate behavior), shifting (disengagement of an irrelevant task set or strategy and the subsequent activation of a more appropriate one), and updating (encoding and evaluation of incoming information for relevance, and subsequent revision of the information held in memory, most closely associated with complex span tasks). In preschool children, however, a unitary factor structure of executive abilities (rather than one of discrete executive functions) appears the most parsimonious, that is two- and three-factor models do not contain additional information about the latent structure beyond that described by a one-factor model (Wiebe et al., 2008). As EC skills continue to develop and reach maturity in late adolescence, EC skills are thought to become increasingly differentiated, yet still inter-related, constructs (see Garon, Bryson & Smith, 2008, for a review).
Many studies have revealed a direct association between EC and children’s concurrent, early emerging, and later developing complex mathematic skills across the preschool to adolescent age ranges in both cross-sectional (e.g. Andersson & Lyxell, 2007; Bull, Johnston & Roy, 1999; Bull & Scerif, 2001; Espy, McDiarmid, Cwik, Stalets, Hamby & Senn, 2004; Gathercole & Pickering, 2000; Gathercole et al., 2004; Lee, Ng & Ng, 2009; McLean & Hitch, 1999; Passolunghi & Siegel, 2001; St Clair-Thompson & Gathercole, 2006; van der Sluis, de Jong & van der Leij, 2004) and longitudinal analyses (Alloway & Alloway, 2010; Bull, Espy & Wiebe, 2008; De Smedt, Janssen, Bouwens, Verschaffel, Boets & Ghesquiere, 2009; Duncan et al., 2007; Welsh, Nix, Blair, Bierman & Nelson, 2010). Although robust relations between EC and mathematics have been reported consistently, many of these studies have accepted the three-factor structure of EC without empirical evaluation, or have examined only one aspect of EC with a single task (typically working memory or inhibitory control). This limits the precision of EC measurement, given that any single task includes variance related to the EC process of interest but also to the modular content that is being controlled and has a variable relation with math. While a number of these studies have attempted to control for IQ or verbal reasoning by having matched groups or by only including children performing within ‘normal’ IQ limits, the few studies that have statistically evaluated the contribution of gC to the EC–math relation (e.g. Alloway & Alloway, 2010; Andersson & Lyxell, 2007; Bull & Scerif, 2001; Espy et al., 2004) reveal that this relation is independent of gC.
While many studies show a relation between SES and early emerging math skills that may reflect opportunities for learning crystallized knowledge, few of these studies have considered whether socioeconomic factors play a role in EC or mediate the relation between EC and math. While there is evidence for high genetic heritability of EC (Friedman, Miyake, Young, DeFried, Corley & Hewitt, 2008) which may place limits on the environmental mutability of EC, the protracted development of the prefrontal cortex means that there is a large window of plasticity/vulnerability during which environmental factors can impact these developing skills. Evidence is accumulating that the social environment and home context play a role in the development of EC in children (e.g. Farah, Shera, Savage, Betancourt, Gianetta, Brodsky, Malmud & Hurt, 2006; Mezzacappa, 2004; NICHD Early Child Care Research Network, 2003; NICHD Early Child Care Research Network, 2005), although the unique environmental and genetic influences cannot been disentangled without behavior genetic designs. However, low-SES kindergartners have been found to show poorer EC (compared to middle-SES children) on tasks requiring selective responding to targets amongst distractors (Noble, Norman & Farah, 2005) and tasks requiring working memory and inhibitory control (Farah et al., 2006). Quality of physical and social resources available to children in the home, along with greater maternal sensitivity and cognitive stimulation, have been found to predict children’s proficiency in sustaining attention and exerting inhibitory control, which in turn partially mediates the relation between the quality of the home environment and school readiness (NICHD Early Child Care Research Network, 2003).
The impact of SES on skill development is mediated through other proximal variables, such as impoverished learning environment, inadequate physical environment, negative life events, family stressors, family discord, and poorer parental responsiveness. Prefrontal systems that support EC are highly sensitive both to early positive experiences of responsive parenting and enriched home environment in the preschool period (Chase-Lansdale, Gordon, Brooks-Gunn & Klebanov, 1997) and deleterious experiences such as negative life events and stressors that often accompany low SES (Casey, Giedd & Thomas, 2000), because of experience-dependent neural plasticity and the prolonged postnatal development of the prefrontal cortex. Responsive parenting (e.g. sensitivity, autonomy support on tasks) has been linked to a promotion of the child’s interest and willingness to explore the environment, increased regulation of affect, and improved attentional and cognitive skills (Bernier, Carlson & Whipple, 2010; Landry, Smith & Swank, 2006). Parents who are appropriately responsive are thought to provide information and assistance to support children’s immature attention, memory, and language, which may include strategies to focus or maintain the child’s attention to critical elements of a task. Through this scaffolding, or external regulation, children gradually learn to take more responsibility for the task and internalize skills that allow them to solve problems independently (i.e. self regulation; Landry, Miller-Loncar, Smith & Swank, 2002; Landy, Smith, Swank & Miller-Loncar, 2000). Thus far, it is not clear which specific proximal factors in the home environment contribute to EC difficulties, and which might impact academic learning through fewer opportunities to develop a crystallized knowledge base, although there is no question that the interplay between the home environment and the developing child has a profound impact on global cognitive indices such as IQ, school readiness, and school achievement, and also more basic processes such as EC.
Sex differences in mathematics
Studies of sex differences in early mathematics achievement have revealed largely null findings (e.g. Carr, Steiner, Kyser & Biddlecomb, 2008; Lachance & Mazzocco, 2006), with sex differences apparent only at older ages (e.g. Baenninger & Newcombe, 1995; although see Hyde, Lindberg, Linn, Ellis & Williams, 2008) or in high achieving groups (e.g. Carr & Davis, 2001). However, the lack of sex difference in math achievement may mask differences between boys and girls in how they approach mathematical tasks. For example, Carr and Jessup (1997; see also Carr et al., 2008) found that while there were no overall math performance differences, boys and girls differed in the strategies used to solve arithmetical problems. Boys developed a preference for retrieval and decomposition to known facts, even though they were initially less able to use retrieval correctly and consistently. Boys were also concerned with the competitive nature of strategies, specifically retrieval. In contrast, girls were much less likely to use retrieval, instead using overt counting strategies and manipulatives. Furthermore, girls evidenced a better awareness of their own arithmetical skills, with boys’ over-confidence in skills correlated negatively with their actual performance.
Differences in the practices that parents use with girls and boys, or genotypic differences in preferences that invoke different responses from parents (i.e. child evocative effects), may foster differences in how the two sexes regulate their progress towards goals, such that girls regulate their progress more closely than boys (Kenney-Benson, Pomerantz, Ryan & Patrick, 2006; Pomerantz & Eaton, 2001). Boys show a greater willingness to take risks, which within the context of mathematics may be reflected in a higher rate of retrieval/guessing and faster responses (Ben-Shakhar & Sinai, 1991). Such preferences may then be reinforced by parents who are more likely to let boys take such risks, rather than more carefully monitoring their progress towards goals (Lytton & Romney, 1991). Such practices and beliefs may communicate to girls the importance of exerting heightened attention as a way to increase knowledge and understanding, while communicating to boys that a reliance on retrieval from an established knowledge base will suffice. Generally, girls report greater use of strategies involving self-regulated learning, for example, making greater use of record keeping and monitoring, seeking assistance when necessary, and goal setting and planning (e.g. Zimmerman & Martinez-Pons, 1990), strategies that also could be described as appropriate use of EC or self-regulation.
Sex differences in EC and its subsequent role in mathematic achievement may also be the result of differences in rate of biological maturation. Lenroot et al. (Lenroot, Gogtay, Greenstein, Wells, Wallace, Clasen, Blumenthal, Lerch, Zijdenbos, Evans, Thompson & Giedd, 2007) report that grey and white matter volumes in the frontal lobes peak approximately 1 year earlier in females than males, and that trajectories of frontal lobe development differ significantly between males and females. Functional imaging studies also suggest a more mature pattern of frontal activation in females while engaged in tasks of cognitive control (Christakou, Halari, Smith, Ifkovits, Brammer & Rubia, 2009). Again, evidence of girls showing greater attentional control may lead parents to reinforce this type of behavior in girls more so than boys. Based on both biological and socialization factors, we might predict better EC skills in girls, and sex differences in the strength of the relation between age and EC (stronger in girls), between EC and math (stronger in girls), and between gC and math (stronger in boys).
Our purpose was to integrate emergent mathematics, EC, crystallized skills, and individual differences related to sex and SES to better characterize the fundamental relation between EC and early mathematics achievement and its sources of variation. In keeping with our focus on individual differences, we utilize standardized math achievement as our dependent measure to identify the sources of variation that determine why some children outperform others relative to their like-aged peers across the preschool period; our purpose was not to determine relations to discrete aspects of mathematical and numerical understanding such as subitizing, cardinal relations, etc. We hypothesized that EC in the preschool period would be related to a fundamental outcome, emergent mathematic achievement. Given evidence of the dissociation between gC and EC, the relation between EC and emergent mathematics was expected to remain robust even when gC was considered. Second, we evaluated whether the relations between EC, math skills, and gC differ as a function of age during the preschool period, as well as sex. Third, we assessed whether SES dimensions of social network support resources or environmental stressors impact the EC–math achievement relation. Typically, studies addressing SES factors have focused on parental education, occupation, and income, which are considered distal, proxy indicators for other variables that are the more proximal sources of influence, including physical health, home environment, social network support, stress and negative life events, early education, and neighborhood characteristics (Bornstein & Bradley, 2003). Here we focus on some of these proximal factors that encompass positive and negative life events, financial and neighborhood resources and stressors, and the amount and quality of social network support from family and friends relationships to better characterize the relations of EC, crystallized skills, and emergent mathematics achievement.
Method
Participants
The sample included 186 typically developing preschool children (109 girls and 77 boys), the subset of the sample used in Wiebe et al. (2008) that was administered the math achievement measure described below. Participants were recruited through birth announcements, local preschools, the local health department, and by word of mouth. Based on initial screening, children with known developmental or language delays or diagnosed learning or behavioral disorders (e.g. ADHD) were excluded from further participation. Participating children’s age ranged from 2.33 to 6 years (M = 4 years, 1 month; SD = 11 months). The sample included 130 Caucasian, 32 African American, nine Asian American, one Native American, four Hispanic, and nine multi-racial children. Race was not reported for one child. Maternal education of the sample ranged from 8 years to 20 years (M = 14 years, 3 months; SD = 2 years, 3 months).
Procedure
Participating children completed the EC battery and measures of emergent mathematics achievement and verbal intelligence in a single session during which the child’s parent (typically the mother) was present, completing questionnaires. Trained graduate students administered and scored all child assessments. The preschool EC battery varied in format and response demands, and included Delayed Alternation (Espy, Kaufmann, McDiarmid & Glisky, 1999; Goldman, Rosvold, Vest & Galkin, 1971), Six Boxes (Diamond, Prevor, Callender & Druin, 1997), the Digit Span subtest of the Differential Abilities Scale (DAS; Elliott, 1990), Delayed Response (Diamond & Doar, 1989; Goldman, Rosvold & Mishkin, 1970), NEPSY Statue and Visual Attention subtests (Korkman, Kirk & Kemp, 1998), Shape School Inhibit condition (Espy, 1997; Espy, Bull, Martin & Stroup, 2006), Child Continuous Performance Test (CPT; Kerns & Rondeau, 1998), and Tower of Hanoi (TOH; Simon, 1975). Scores from two tasks, Shape School and Towers of Hanoi, were reflected so that higher values indicated better performance to be consistent in direction with the other EC tasks. A brief description of each task is provided in Table 1. For more detail see Wiebe et al. (2008).
Table 1.
Summary of executive control tasks
| Task | Description | Dependent variable |
|---|---|---|
| Delayed Alternation (DA) | Keep location of last reward in mind over delay to retrieve reward in alternate location | # of correct retrievals |
| Continuous Performance Test (CPT) | Press button to target amidst distractors, distractors make sounds that conflict with identity | # correct/# total responses |
| DAS Digit Span (DSP) | Recall progressively increasing strings of digits | Max. length of digit string recalled |
| Delayed Response (DR) | Retrieve reward from hidden location | # of correct retrievals |
| Six Boxes (6B) | Keep location of previously searched boxes in mind to find reward in unsearched location | # correct searches/# total searches |
| Shape School (SSI)† | State name of cued figure and suppress naming figures previously named. | completion time |
| NEPSY Statue (ST) | Maintain a fixed posture in light of examiner induced distractions | # 5-second epochs without movement |
| NEPSY Visual Attention (VA) | Stamp relevant target amidst distractors, with target in view as fast as possible. | # correct targets/completion time |
| Tower of Hanoi (TOH)† | Reproduce configuration by moving rings towards and away from target on progressively more difficult and complex configurations. | # illegal moves/# total moves |
Higher score indicates poorer performance. Measure was reflected to ease factor loading interpretations.
To assess emergent mathematics achievement, children completed the Applied Problems subscale of the Woodcock-Johnson Revised Test of Achievement (WJ-R; Woodcock & Johnson, 1989), a commonly used, norm-referenced, individually administered, standardized instrument of academic achievement. Applied Problems is the only subscale among the WJ-R broad math composite that is suitable for administration across the age span studied here. The specific item content of the Applied Problems scale includes subitizing, ordinal counting, counting relevant object items among mixed object groups, and simple subtraction and addition calculations. Items from the WJ-R Applied Problems subscale are graded in difficulty and empirically determined by Rasch item analyses, and thus are well suited to the present study purposes to understand individual differences in mathematic achievement across the preschool period. Reliability for the Applied Problems subscale ranges from .84 to .97 for children aged 2 to 6 years (McGrew, Werder & Woodcock, 1991), and was .85 for the current sample. According to the standardized administration, the preschool child is shown the pictorial math problem and then points to, or says, the answer. The resulting standard score was used as the dependent variable in the analyses.
With the preschool age range and large number of EC tasks, administration of a complete measure of intellectual ability was not feasible. Because vocabulary is most highly correlated, and is the single best estimate of intellectual ability (Sattler, 1992), a standardized vocabulary measure, the WJ-R Picture Vocabulary subtest (Woodcock & Johnson, 1989), was included as an estimate of gC. Using vocabulary as the gC estimate, rather than assessments with numerical content, also ensured a separation of skill from the content of the task. Reliability for the Picture Vocabulary subscale ranges between .70 and .89 for children aged 2 to 6 years (McGrew et al, 1991) and is .79 for the current sample. In this subtest, children are presented with a word and must identify the correct picture by pointing. The resultant standard score was used in the statistical models.
During child testing, the parent completed the Life Stressors and Social Resources Inventory-Adult Form (LISRES; Moos & Moos, 1994). The LISRES is a standardized questionnaire assessing negative and positive life events, life stressors, and social resources, and was included to gain insight into the parent’s levels of stress and support, which are known to influence both parenting style and child outcomes (e.g. Anhalt, Telzrow & Brown, 2007; Kliewer & Kung, 1998; Meyers, 1999). The following scales were used: Family Resources (e.g. ‘Can you count on [mother/father] when you need it?’), Family Stressors (e.g. ‘How often does [mother/father] disagree with you about important things?’), Friend Resources (e.g. ‘How many clubs and organizations do you belong to?’), Friend Stressors (e.g. ‘Do any of your friends disagree with you about important things?’), Financial Stress (e.g. ‘Do you have enough money to afford good medical and dental care when you (your family) need it?’), Financial Resources (e.g. ‘What is your total annual family income?’), Home and Neighborhood Stressors (e.g. ‘Is [your home] well kept up (e.g. painting, repairs)?’), and Negative Life Events (e.g. ‘Have you had any of these medical conditions in the past 12 months?’). Internal consistency across the scales was good to high (.77–.93).
Because there was interest in contextual variables and there were no a priori predictions of the measurement structure of the LISRES scales for how they index the child’s early experiences, exploratory factor analysis with oblique (Promax) rotation was conducted to reduce the scale data into meaningful factors (see supplementary information Table S1). The first factor was termed ‘Social Network Support’, consisting of the Family Resources, Family Stress (reflected), Friend Resources, and Friend Stress (reflected) subscales. Factor 2 was labeled ‘Environmental Stressors’, and consisted of the Financial Stress, Financial Resources (reflected), Home Stress and Negative Life Events subscales.
Statistical methods
Statistical analyses were conducted using SAS version 9.1.3 (SAS Institute, Cary, NC) for descriptive analyses and exploratory factor analysis, as well as Mplus version 5.1 (Muthén & Muthén, 2006) for structural equation modeling. Mplus uses maximum likelihood estimation to fit models to the observed means and covariances (Muthén & Muthén, 2006). Because the mathematics achievement measure was added to the study protocol after data collection had already begun, the data from children who were excluded in the present study were missing the pertinent math achievement scores purely as a function of the order in which they participated in data collection (and not of their ability level), which is consistent with the Missing at Random (MAR) assumption (Schafer & Graham, 2002). In support of this assumption, missing a math score was unrelated both to EC (B = .000, p = .378) and to gC (B = .396, p = .861), meaning that the results among the subset of children included are not biased as a function of whether children completed the math achievement measure. Therefore, the pattern of missing data was considered MAR, which maximized subject inclusion in each pairwise element of the observed covariance matrix using Mplus (Muthén & Muthén, 2006; see Little & Rubin, 1987, for description of EM algorithm). Prior to conducting the analyses of interest, all EC indicator scores were converted to z scores to minimize the influence of different variable scaling on testing model invariance.
The first step was to determine whether a single-factor EC latent structure (identified in Wiebe et al., 2008) remained the preferred model to best describe EC in the current subsample. Consistent with the procedure described in Wiebe et al. (2008), we compared the fit of alternative models with different configurations of the EC measures derived a priori according to hypotheses. The unitary model fit well and equivalently to other two- and three-factor solutions, χ2 (27, N = 186) = 29.50, p = .34, RMSEA = .022 (.00; .06), CFI = .99. Because the unitary model described the latent structure in the least number of paths and fit the obtained data as well as the more complex models, it was retained as the preferred model for the present sample (Bollen, 1989).
The second step was to model the relations between latent EC and emergent mathematic achievement. Estimated crystallized intellectual skill (gC) was added as a covariate to determine whether the relation between latent EC and math achievement was robust. The relation between gC and latent EC was modeled as a correlation as the direction of the association is not clear (e.g. Blair, 2006). The sample then was divided into subgroups based on age (younger vs. older than 4 years) and sex (boys vs. girls) to assess model invariance. Model invariance was tested through two series of nine nested models (one series of models each for age and sex groups), which allowed for model comparison using χ2 difference tests. Non-significant χ2 difference tests indicate that the more restrictive model fits no worse than the less restrictive model. In this case, the more restrictive model is preferred because fewer paths are being estimated without significantly reducing model fit. A significant χ2 difference test indicates poorer fit of the more restrictive model, and the less restrictive model is retained as the best fitting. The initial configural invariance models included the same model structure but no equality constraints between groups. Next, two sequential models tested measurement invariance of the EC latent factor across groups, including metric invariance (equal factor loadings between groups) and scalar invariance (equal factor indicator intercepts between groups). If measurement invariance of the EC latent factor was tenable, structural invariance was tested in the fourth and fifth models by examining invariance of the factor variance and factor mean across groups, respectively. The sixth models tested invariance of the latent EC-Age path. The seventh models tested invariance of the math achievement-latent EC path by constraining this path to be equal between groups. The eighth and ninth models tested the invariance of the estimated gC-latent EC path and the invariance of the estimated gC-math achievement path, respectively, by constraining the paths to be equal between groups.
The final step was to examine the influence social network support and environmental stressors have as predictors in the math achievement–latent EC relation. One model was estimated including social network support and environmental stressors using the final math achievement–estimated gC model. A critical α of .05 was used for all statistical tests.
Results
Descriptive statistics for the EC task performance scores, age, WJ-R Applied Problems score and the WJ-R Picture Vocabulary score are available in Table S2 of the supplementary information. All manifest variables displayed adequate distributional characteristics, with the exception of the Shape School latency scores. Shape School scores were log-transformed, and outlier scores more than 3 standard deviations from the mean were trimmed. Sex-related performance differences are depicted in Table S2. Girls, on average, significantly outperformed boys in the Child Continuous Performance Test, Six Boxes, NEPSY Statue and Visual Attention subtests, as well as on the WJ-R Applied Problems subscale. Levene’s tests for homogeneity of variance revealed no significant sex differences. Correlations between the EC tasks, age, WJ-R Applied Problems subscale and the WJ-R Picture Vocabulary subscale are also available in the supplementary information (Table S3). There were significant correlations between the EC tasks, with a few exceptions (i.e. Tower of Hanoi was uncorrelated with Delayed Alternation and Shape School; Delayed Response was uncorrelated with Shape School). All EC tasks were correlated with age; as expected, as age increases children exhibit better performance. All of the EC tasks, except the Shape School Inhibit condition, also were correlated with the WJ-R Applied Problems subscale. Fewer EC tasks were correlated with the WJ-R Picture Vocabulary subscale than with the WJ-R Applied Problems subscale, and these significant correlations were smaller in magnitude than the correlations with the WJ-R Applied Problems subscale.
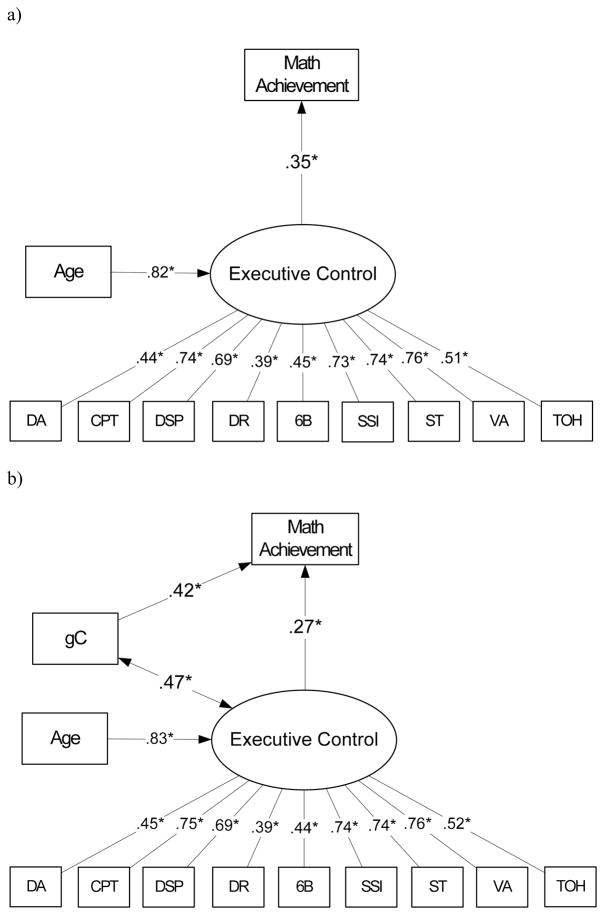
Predicting emergent math achievement from executive control
Latent EC predicted math achievement in preschool children, as depicted in Figure 1a. A child who scored 1 standard deviation higher than the mean level of latent EC scored .35 standard deviations, on average, above his/her peers on the WJ-R Applied Problems scale. Notably, the effect of the age covariate on latent EC was large, reaffirming the substantial developmental differences in EC across the preschool period. This baseline model for the overall sample had inadequate model fit, χ2 (44, N = 186) = 113.72, p < .001, RMSEA = .092 (.07; .11), CFI = .87. When estimated gC was added to the model (Figure 1b), the emergent math achievement–latent EC relation was reduced only slightly in magnitude. The correlation between estimated gC and latent EC, as well as the path between estimated gC and math achievement, both differed from zero. Including gC in the model improved model fit substantially, χ2 (53, N = 186) = 107.41, p <.001, RMSEA = .074 (.05; .09), CFI = .91.
Figure 1.
Emergent math-latent EC models without and with gC.
Tests of invariance
The sample was divided into groups by age and by sex, and model invariance was evaluated using χ2 difference tests. Results from the invariance tests by age group (younger vs. older than 4 years) are presented in the upper panel of Table 2. Metric invariance of the indicator loadings was not supported, meaning that at least one of the EC task loadings onto the latent EC construct was unequal between younger and older preschool children. To explore the sources of age-related metric variance, the equality constraints on the indicator loadings were added to the baseline configural model one at a time (Byrne, Shavelson & Muthen, 1989; Meade & Bauer, 2007). This process revealed that the 6 Boxes task was the source of metric variance, while the loadings of the other eight tasks were found to be invariant. When allowed to vary freely, the indicator loading for 6 Boxes was greater in the younger group (β = .41) than in the older group (β = .31), meaning that 6 Boxes better related to the latent EC factor among younger, compared to older, preschool children. This may simply reflect the task becoming too easy as children get older. A partial metric invariance model (where the loading for 6 Boxes was allowed to vary by age, but all other loadings were constrained to be equal for younger and older children) was fit to the data so that successive invariance constraints could then be added to the model (Byrne et al., 1989; Meade & Bauer, 2007). Scalar invariance constraints were found to be tenable, meaning that all indicator intercepts were found to be equal across both age groups. The EC factor variance was also invariant across age groups. However, the EC factor mean differed significantly between younger and older preschool groups. When allowed to vary freely, the EC factor mean was higher in the older group compared to the younger group. On average, the latent EC score for older children in the sample was .561 standard deviations higher than that of younger children. This age difference is consistent with the single group model presented above, in which age was a significant covariate.
Table 2.
Tests of Invariance by age and sex
| Model | χ2 | Df | P | RMSEA | CFI | BIC | χ2 difference | df difference | p difference |
|---|---|---|---|---|---|---|---|---|---|
| Baseline | 107.41 | 53 | .0000 | 0.07 | 0.91 | 8122.46 | – | – | – |
| Tests of invariance by age | |||||||||
| M1 | 166.31 | 106 | .0002 | 0.08 | 0.83 | 8029.67 | – | – | – |
| M2^ | 178.99 | 113 | .0001 | 0.08 | 0.81 | 8005.77 | 12.68 | 7 | 0.080 |
| M3 | 189.96 | 121 | .0001 | 0.08 | 0.80 | 7974.93 | 10.97 | 8 | 0.203 |
| M4 | 191.00 | 122 | .0001 | 0.08 | 0.80 | 7970.75 | 1.04 | 1 | 0.308 |
| M5* | 196.21 | 123 | .0000 | 0.08 | 0.79 | 7970.74 | 5.21 | 1 | 0.023 |
| M6 | 194.35 | 123 | .0000 | 0.08 | 0.80 | 7968.87 | 3.35 | 1 | 0.067 |
| M7 | 194.49 | 124 | .0001 | 0.08 | 0.80 | 7963.78 | 0.14 | 1 | 0.708 |
| M8 | 196.37 | 125 | .0000 | 0.08 | 0.80 | 7960.44 | 1.88 | 1 | 0.170 |
| M9 | 196.90 | 126 | .0001 | 0.08 | 0.80 | 7955.75 | 0.53 | 1 | 0.467 |
| Tests of invariance by sex | |||||||||
| M1 | 176.23 | 106 | .0000 | 0.08 | 0.88 | 8259.98 | – | – | – |
| M2 | 183.43 | 114 | .0000 | 0.08 | 0.88 | 8225.38 | 7.2 | 8 | 0.515 |
| M3 | 190.31 | 122 | .0001 | 0.08 | 0.88 | 8190.45 | 6.88 | 8 | 0.550 |
| M4 | 190.37 | 123 | .0001 | 0.08 | 0.89 | 8185.28 | 0.06 | 1 | 0.807 |
| M5 | 190.50 | 124 | .0001 | 0.08 | 0.89 | 8180.18 | 0.13 | 1 | 0.718 |
| M6† | 204.68 | 125 | .0000 | 0.08 | 0.86 | 8189.14 | 14.18 | 1 | 0.002 |
| M7 | 190.60 | 125 | .0001 | 0.08 | 0.89 | 8175.06 | 0.10 | 1 | 0.752 |
| M8 | 192.12 | 126 | .0001 | 0.08 | 0.89 | 8171.35 | 1.52 | 1 | 0.218 |
| M9 | 199.46 | 127 | .0000 | 0.08 | 0.88 | 8173.47 | 7.34 | 1 | 0.007 |
Partial Metric Invariance. Indicator loading for 6 Boxes was allowed to vary between age groups due to non-invariance.
EC factor means were allowed to vary due to non-invariance. M6 model fit statistics are compared to M4 model fit statistics.
The latent EC-age path was allowed to vary due to non-invariance. M7 model fit statistics are compared to M5 model fit statistics.
Baseline = entire sample model; M1 = configural invariance; M2 = metric invariance; M3 = scalar invariance; M4 = factor variance invariance; M5 = factor means invariance; M6 = latent EC-Age invariance; M7 = emergent math-EC path invariance; M8 = estimated gC-EC path invariance; M9 = emergent math-estimated gC path invariance.
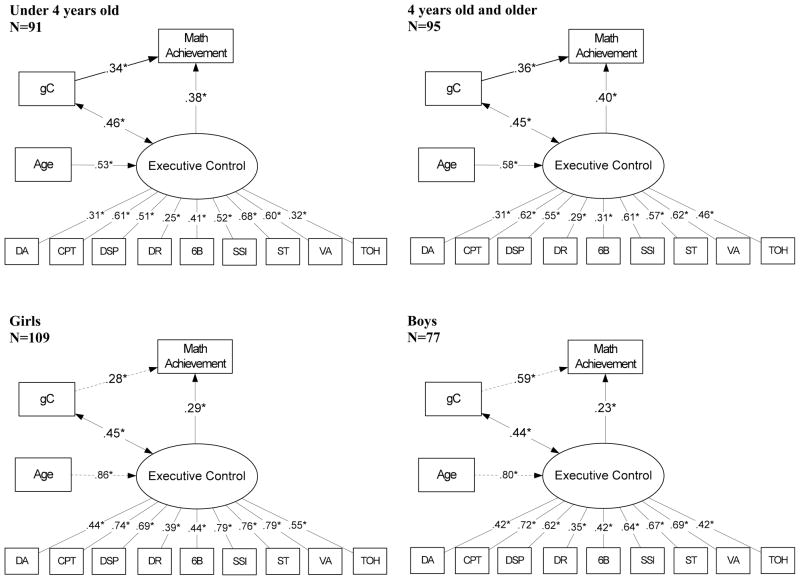
After establishing partial measurement invariance in the EC latent factor between the two age groups of younger and older preschoolers, the key comparison of the invariance of the structural relations among EC, gC, and math achievement was evaluated. The strengths of each of these respective paths were invariant between the two age groups, meaning that the relations among these constructs did not differ significantly between younger and older preschool children (see Table 2 and Figure 2). Importantly, the central relation between EC and math achievement is comparable in the earlier and later parts of the preschool period. The final model for the younger and older age groups is presented in Figure 2, where all paths are constrained to be equal between the age groups except the indicator loading for 6 Boxes and the EC factor mean. As recommended when partial metric invariance is found (Meade & Bauer, 2007; Vandenberg & Lance, 2000), another set of models in which the 6 Boxes task was excluded altogether was run comparing age-related measurement and structural invariance. The pattern of results was the same as that presented with the freely varying 6 Boxes loading included.
Figure 2.
Final emergent math-latent EC models with gC for younger and older preschool children and boys and girls. All model paths are constrained to be equal between the age groups except the indicator loading for 6 Boxes and EC factor means. All model paths are constrained to be equal between boys and girls except for the latent EC-age path and the gC-emergent math achievement path, which are distinguished by dashed lines. The standardized coefficients are reported. Standardized loadings for the constrained paths are not exactly the same between the age groups and between boys and girls because of differences in standard errors between groups.
Upon establishing age-related structural invariance of the key relations among EC, math achievement, and gC, we then turned to evaluating sex differences in how these constructs relate. Results from the invariance tests by sex are presented in the lower panel of Table 2. Measurement and structural invariance of latent EC for boys and girls was supported. The math achievement-latent EC path and the estimated gC-latent EC path were also invariant for boys and girls. Invariance of the latent EC-Age path and the estimated gC-math achievement path, however, were not supported, indicating that the magnitude of the paths differed significantly between girls and boys. When allowed to vary freely, the latent EC-Age path coefficient was greater in girls (β = .86) than in boys (β = .80). The estimated gC-math achievement path coefficient was greater in boys (β = .59) than in girls (β = .28). The final model for boys and girls is presented in Figure 2, where all paths are constrained to be equal across sex except the latent EC-Age path and the estimated gC-math achievement path.
Impact of social network support and environmental stressors
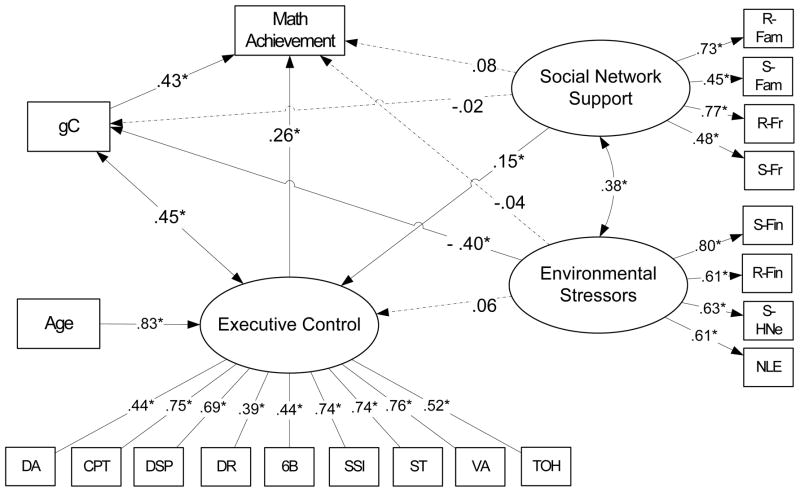
Descriptive statistics for the LISRES subscales are available in Table S1, and correlations between the LISRES subscales and the EC tasks are presented in Table S3. All but the LISRES Family Resources scale were correlated with at least one of the EC tasks. To examine the impact of social network support and environmental stressors these latent factors were included in the final emergent math achievement–EC model as predictors of emergent math, gC, and EC. This model is presented in Figure 3. The social network support latent significantly predicted latent EC, such that 1 standard deviation increment of social network support was associated with a .15 standard deviation increase in the level of latent EC. Social network support did not directly predict emergent math achievement or gC. Unlike the social network support latent, the environmental stressors–latent predicted estimated gC, but not math achievement or latent EC. The environmental stressors–gC relation was in the expected direction, where a 1 standard deviation increase in environmental stressors was associated with a −.40 standard deviation decrement in estimated gC. The significant correlation between the social network support latent and the environmental stressors latent was moderate in magnitude (r = .38).
Figure 3.
Social network support and environmental stressors model.
Discussion
We hypothesized that latent EC in the preschool period would be related to a fundamental outcome, emergent mathematic achievement. Second, we evaluated whether the relation between EC and math achievement might differ as a function of child age and sex. Finally, the contribution of SES contextual characteristics, such as social support from family relationships and friend networks, and life stressors in the home environment, were evaluated.
As predicted, EC was related to emergent mathematic achievement in preschoolers, consistent with numerous extant findings (e.g. Bull et al., 2008; Bull et al., 1999; Bull & Scerif, 2001; Duncan et al., 2007; Gathercole et al., 2004; St Clair-Thompson & Gathercole, 2006; van der Sluis et al., 2004; Welsh et al., 2010). This relation appears fundamental, as it was robust and was not mediated by crystallized intellectual skills. These findings, although important in their own right, also contribute to the theoretical distinction between gC and more general fluid abilities (as some consider executive functions, self-regulation skills, and working memory) that allow individuals to engage in novel tasks (Blair, 2006). Of course, the relative strength of the contributions of EC and gC may differ in older children who are acquiring more complex mathematical skills. However, the current findings show that even when assessing relatively simple numerical and mathematical skills in young children, both EC and gC already make an important contribution to mathematical achievement.
Inclusion of age as a significant covariate of EC in single group models, and invariance testing comparing younger and older preschool children, revealed that older preschool children displayed better developed EC compared to younger children, an expected finding well supported by previous literature pointing to the preschool period as important for the development of EC skills (Garon et al., 2008). The age–EC relation was also found to be significantly higher in girls than boys, which may reflect sex differences in the developmental trajectories of frontal lobe development (Lenroot et al., 2007). Despite the developmental and measurement differences in EC across this age range, the relations among latent EC, math achievement, and gC remained constant in strength throughout the preschool period. The constancy of the relation of EC to math achievement among our 2- to 6-year-old sample points to the reliability of the WJ-III Applied Problems subtest in this age range. However, future work should aim to develop and integrate even more fine-grained assessment of discrete math skills (e.g. informal vs. formal operational/procedural mathematic abilities) among young children, to determine whether additional measures further contribute to the measurement and understanding of specific, early emerging math abilities.
Though no age-related differences were revealed in the relations among EC, math achievement, and gC, there were substantive individual differences related to sex in the predictors of emergent math achievement. For girls, the magnitude of the EC-mathematics achievement path and the estimated gC-mathematics path were comparable. For boys, the gC-mathematics achievement path was stronger than in girls. At least two alternatives can produce this pattern of results. First, boys may have acquired more crystallized knowledge that can be brought to bear on mathematic problems. Because there were no sex differences in the WJ-R Picture Vocabulary normative referenced standard score, there is no clear evidence of more proficient crystallized ability in boys, at least in terms of their acquired vocabulary. The limits of testing preschool-aged children led to obvious limits in the amount of testing that children could withstand, without compromising the reliability of the data, and this finding requires replication with a richer measure of gC. An alternative explanation is that preschool boys draw more heavily on their crystallized skills to support achievement in mathematics tests than do girls, and we can speculate on biological and socialization influences that might support this argument. Although the magnitude of the EC-mathematics achievement path did not differ significantly between preschool girls and boys and the latent EC constructs of boys and girls were found to be invariant, girls were found to have better EC skills on a number of the measures, commensurate with findings from previous studies showing girls to have a small but significant advantage in executive abilities in this age range (Wiebe et al., 2008; Klenberg, Korkman & Lahti-Nuuttila, 2001; Pascualvaca, Anthony, Arnold, Rebok, Ahearn, Kellam & Mirsky, 1997), and to show a more mature pattern of frontal activation when engaged in tasks requiring cognitive control (Christakou et al., 2009). Lower EC skills coupled with phenotypic preferences for risk taking (Ben-Shakhar & Sinai, 1991) that are reinforced by parents (child evocative effects) may mean that boys are more likely to rely on retrieval of information from an established knowledge base (gC), hence accounting for the stronger estimated gC–math achievement relation in boys that girls. While a direct association cannot be drawn, such differences may impact the types of strategies used on mathematical tasks, e.g. boys’ more frequent retrieval of facts from long-term memory (i.e. a form of crystallized knowledge), even when resulting in increased errors, while girls are more likely to use alternative strategies that utilize executive skills, such as mental counting as a check (e.g. Siegler, 1988; Carr & Jessup, 1997).
Besides sex, individual differences in both environmental stressors and social network support contributed differentially to the relations among EC, gC, and emergent mathematics achievement. Although there is a large literature on the relation of SES factors with intelligence and academic achievement, consideration of the role of EC is more recent, as is the focus on individual differences in pathways to academic performance. The first SES factor, social network support, was related to emergent mathematic achievement indirectly through its relation with EC, consistent with findings from the NICHD Study of Early Child Care (2003 (2005) that showed family environment (availability of physical and psychological resources and parental sensitivity and stimulation) to predict children’s ability to regulate their attention in the preschool years, which in turn predicted achievement (composite measure of math and reading), language, and social outcomes for those children (see also Gottfried et al., 2003; Espy et al., 2001; Farah et al., 2006; Liaw & Brooks-Gunn, 1994; Mezzacappa, 2004). The social network support factor included LISRES scales assessing family and friends resources and support (e.g. availability, emotional support, expectations), where parents who reported less supportive and more stressful family relationships and friend networks had preschool children with poorer EC.
At this point it is unclear why and how family/friend support and stress to the parent impacts on child development. Bernier et al. (2010) speculate that in some low-SES families parenting stress may limit the opportunities for joint cognitive activities, leaving less room for competent caregiving to foster development of the child’s neural structures and self-regulatory capacities. A number of studies report that family environments characterized by fewer emotional resources and support foster more adverse, less responsive parenting practices (e.g. Anhalt et al., 2007; Kliewer & Kung, 1998; Meyers, 1999), independent of distal factors such as family income. Responsive parenting is characterized by emotional engagement (warm, sensitive, and contingent responding to child behavior; Landry et al., 2006; Zeanah, 2000) and proactive strategies that guide and structure depending on the child’s needs to promote competence (Dishion & McMahon, 1998; Pettit & Bates, 1989). Bernier et al. (2010) report that autonomy support (mainly scaffolding) is the aspect of parenting which most robustly relates to age-specific indices of child EC. In our view, responsive parenting likely facilitates the development of EC by (a) enabling the child to maintain relevant information through parental provision of clear directions, (b) enhancing response selection by parent provision of feedback on outcomes of differing choices, (c) facilitating attention to salient cues and encoding predictable rules by parental follow through on consequences, and (d) fostering the flexible adjustments in action and attention in response to feedback via both constructive discipline and parental warmth/sensitivity that signal unconditional acceptance. The current findings highlight the link between family/friend support structure and child EC, but we have not directly assessed responsive parenting as the likely mediator of this relation; this clearly will be a productive line of future research.
The second factor identified from the LISRES scales, environmental stressors, included indices assessing financial resources and support (e.g. family income, affordability of medical care and other daily requirements such as clothing and food), home and neighborhood stressors (e.g. adequacy of housing, safety and upkeep of the neighborhood), and negative life events within the family (e.g. mental and physical health, accidents and personal assaults, changes to financial situation, job loss, relationship breakdown). Previous studies that have failed to find a relation between SES and EC have used distal indicators of SES such as family income (e.g.Alloway & Alloway, 2010; Engel et al., 2008). This association was replicated in the current study where no direct relation was found between environmental stressors and EC. However, a direct relation was observed between environmental stressors and gC, which in turn was related to emergent mathematic achievement. This factor likely reflects the family’s access to varied enriching materials, experiences, and education-related services that allow children the opportunities to develop domain-specific knowledge such as basic numeracy and literacy rather than directly impacting domain-general skills such as EC or fluid intelligence.
The latent factors of social network support and environmental stressors were significantly interrelated, and while each impacts mathematics achievement through a different route (via EC and gC, respectively), any influence on one of these routes will have some indirect influence on the other because of the strong relation between EC and gC. The academic and cognitive skills developed by young children certainly are impacted by parenting behaviors, which in turn are influenced by the stresses of the wider social environment. Chronic strains that accompany economic disadvantage (potentially measured through our environmental stressors factor) adversely affect parents’ capacity to respond to their children’s needs in material, emotional, and developmentally tuned ways (Mezzacappa, 2004), which have been linked to children’s IQ (Linver, Brooks-Gunn & Kohen, 2002), school readiness (NICHD, 2003), and EC (Noble et al., 2007). Better characterization of the more specific causal factors in the social and familial environments of children that preferentially support the development of executive, academic and intellectual skills is an important future endeavor, particularly unpacking the rich interplay and impacts of parenting strategies and responsiveness under various social contexts.
While we have speculated on possible heritable and environmental influences on EC and gC, only a behavioral genetics approach will provide a more definitive answer to their true respective contributions and interactions. However, results from the present study build on those from previous investigations showing a link between EC and early mathematics achievement by revealing that when considered in light of gC, the relation is moderated by sex and may be mediated by proximal social network support characteristics. Particularly in early development where the prefrontal system and resultant executive processes are in a rapid phase of development, the relation between EC and experiences in the home likely will be particularly strong, reflecting the heightened susceptibility to both developmentally advantageous and deleterious experiences. The child’s social environment has a critical impact on academic learning via the provision of materials and experiences that provide the stimulation necessary to establish the core domain specific skills (crystallized knowledge), as well as through responsive parenting that provides children with the controlled direction of skills for effective learning, and which allow the child to discern what stimuli are relevant to the task at hand, maintaining focus on those relevant stimuli, and modifying strategies as required. Also highlighted here are sex differences in the relation of age and EC, and in gC and mathematics achievement which may reflect differences in (a) rates of biological maturation, such that (b) girls show evidence of better self regulation/EC earlier in development which (c) produces an evocative effect whereby adults foster self-regulation behaviors in girls and riskier behaviors in boys. This process could manifest itself as differences in approaches to schoolwork where boys are more likely to use riskier strategies (direct retrieval from an established knowledge base) compared to girls’ use of checking and back-up strategies (e.g. counting). These findings underscore the need to examine the dimensions, mechanisms, and individual pathways that influence the development of competence in basic cognitive processes that underpin more complex academic skills.
Supplementary Material
Acknowledgments
This research was supported in part by National Institutes of Health grants R01 MH065668, HD038051, HD050309, DA023653, DA014661, and DA015223. The authors gratefully acknowledge the participating families and project personnel who made this work possible.
References
- Alloway TP, Alloway RG. Investigating the predictive roles of working memory and IQ in academic attainment. Journal of Experimental Child Psychology. 2010;106:20–29. doi: 10.1016/j.jecp.2009.11.003. [DOI] [PubMed] [Google Scholar]
- Andersson U, Lyxell B. Working memory deficit in children with mathematical difficulties: a general or specific deficit? Journal of Experimental Child Psychology. 2007;96:197–228. doi: 10.1016/j.jecp.2006.10.001. [DOI] [PubMed] [Google Scholar]
- Anhalt K, Telzrow CF, Brown CL. Maternal stress and emotional status during the perinatal period and childhood adjustment. School Psychology Quarterly. 2007;22:74–90. [Google Scholar]
- Baddeley AD. Exploring the central executive. Quarterly Journal of Experimental Psychology. 1996;49A:5–28. [Google Scholar]
- Baenninger M, Newcombe N. Environmental input to the development of sex-related differences in spatial and mathematical ability. Learning and Individual Differences. 1995;7:363–379. [Google Scholar]
- Ben-Shakhar G, Sinai Y. Gender differences in multiple-choice tests: the role of differential guessing tendencies. Journal of Educational Measurement. 1991;28:23–35. [Google Scholar]
- Bernier A, Carlson SM, Whipple N. From external regulation to self-regulation: early parenting precursors of young children’s executive functioning. Child Development. 2010;81:326–339. doi: 10.1111/j.1467-8624.2009.01397.x. [DOI] [PubMed] [Google Scholar]
- Blair C. How similar are fluid cognition and general intelligence? A developmental neuroscience perspective on fluid cognition as an aspect of human cognitive ability. Behavioral and Brain Sciences. 2006;29:109–160. doi: 10.1017/S0140525X06009034. [DOI] [PubMed] [Google Scholar]
- Bollen K. Structural equation models with latent variables. New York: Wiley and Son; 1989. [Google Scholar]
- Bornstein MH, Bradley RH. Socioeconomic status, parenting, and child development. Mahwah, NJ: Lawrence Erlbaum Associates; 2003. [Google Scholar]
- Bradley R, Corwyn R. Socioeconomic status and child development. Annual Review of Psychology. 2002;53:371–399. doi: 10.1146/annurev.psych.53.100901.135233. [DOI] [PubMed] [Google Scholar]
- Bull R, Espy KA, Wiebe S. Short-term memory, working memory and executive functioning: longitudinal predictors of mathematics achievement at age 7. Developmental Neuropsychology. 2008;33:205–228. doi: 10.1080/87565640801982312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bull R, Johnston RS, Roy JA. Exploring the roles of the visual-spatial sketch pad and central executive in children's arithmetical skills: views from cognition and developmental neuropsychology. Developmental Neuropsychology. 1999;15:421–442. [Google Scholar]
- Bull R, Scerif G. Executive functioning as a predictor of children’s mathematics ability: inhibition, switching, and working memory. Developmental Neuropsychology. 2001;19:273–293. doi: 10.1207/S15326942DN1903_3. [DOI] [PubMed] [Google Scholar]
- Byrne BM, Shavelson RJ, Muthen B. Testing for the equivalence of factor covariance and mean structures: the issue of partial measurement invariance. Psychological Bulletin. 1989;105:456–466. [Google Scholar]
- Carr M, Davis H. Gender differences in arithmetic strategy use: a function of skill and preference. Contemporary Educational Psychology. 2001;26:330–347. doi: 10.1006/ceps.2000.1059. [DOI] [PubMed] [Google Scholar]
- Carr M, Jessup DL. Gender differences in first-grade mathematics strategy use: social and metacognitive influences. Journal of Educational Psychology. 1997;89:318–328. [Google Scholar]
- Carr M, Steiner HH, Kyser B, Biddlecomb B. A comparison of predictors of early emerging gender differences in mathematics competency. Learning and Individual Differences. 2008;18:61–75. [Google Scholar]
- Casey BJ, Giedd JN, Thomas KM. Structural and functional brain development and its relation to cognitive development. Biological Psychology. 2000;54:241–257. doi: 10.1016/s0301-0511(00)00058-2. [DOI] [PubMed] [Google Scholar]
- Cattell RB. Theory of fluid and crystallized intelligence: a critical experiment. Journal of Educational Psychology. 1963;54:1–22. doi: 10.1037/h0024654. [DOI] [PubMed] [Google Scholar]
- Chase-Lansdale PL, Gordon R, Brooks-Gunn J, Klebanov P. Neighborhood and family influences on the intellectual and behavioral competence of preschool and early school-age children. In: Brooks-Gunn J, Aber J, editors. Neighborhood poverty: Context and consequences for development. Vol. 1. New York: Russell Sage; 1997. pp. 79–118. [Google Scholar]
- Christakou A, Halari R, Smith AB, Ifkovits E, Brammer M, Rubia K. Sex-dependent age modulation of frontostriatal and temporo-parietal activation during cognitive control. NeuroImage. 2009;48:223–236. doi: 10.1016/j.neuroimage.2009.06.070. [DOI] [PubMed] [Google Scholar]
- De Smedt B, Janssen R, Bouwens K, Verschaffel L, Boets B, Ghesquiere P. Working memory and individual differences in mathematics achievement: a longitudinal study from first grade to second grade. Journal of Experimental Child Psychology. 2009;103:186–201. doi: 10.1016/j.jecp.2009.01.004. [DOI] [PubMed] [Google Scholar]
- Diamond A, Doar B. The performance of human infants on a measure of frontal cortex function, the delayed response task. Developmental Psychobiology. 1989;22:271–294. doi: 10.1002/dev.420220307. [DOI] [PubMed] [Google Scholar]
- Diamond A, Prevor M, Callender G, Druin D. Prefrontal cortex cognitive deficits in children treated early and continuous for PKU. Monographs of the Society for Research in Child Psychology. 1997;62(4) Serial No. 252. [PubMed] [Google Scholar]
- Dishion T, McMahon R. Parental monitoring and the prevention of child and adolescent problem behaviour: a conceptual and empirical formulation. Clinical Child and Family Psychology Review. 1998;1:61–75. doi: 10.1023/a:1021800432380. [DOI] [PubMed] [Google Scholar]
- Duncan GJ, Dowsett CJ, Claessens A, Magnuson K, Huston AC, Klebanov P, Pagani LS, Feinstein L, Engel M, Brooks-Gunn J, Sexton H, Duckworth K, Japel C. School readiness and later achievement. Developmental Psychology. 2007;43:1428–1446. doi: 10.1037/0012-1649.43.6.1428. [DOI] [PubMed] [Google Scholar]
- Elliot C. Differential ability scales: Administration and scoring manual. San Antonio, TX: Harcourt Brace Jovanovich; 1990. [Google Scholar]
- Engel PMJ, Santos FH, Gathercole SE. Are working memory measures free of socioeconomic influence? Journal of Speech, Language, and Hearing Research. 2008;51:1580–1587. doi: 10.1044/1092-4388(2008/07-0210). [DOI] [PubMed] [Google Scholar]
- Espy KA. The shape school: assessing executive function in preschool children. Developmental Neuropsychology. 1997;13:495–499. doi: 10.1207/s15326942dn2601_3. [DOI] [PubMed] [Google Scholar]
- Espy KA, Bull R, Martin J, Stroup W. Measuring the development of executive control with the Shape School. Psychological Assessment. 2006;18:373–381. doi: 10.1037/1040-3590.18.4.373. [DOI] [PubMed] [Google Scholar]
- Espy KA, Kaufmann PM, McDiarmid MD, Glisky ML. Executive functioning in preschool children: performance on A-not-B and other delayed response format tasks. Brain and Cognition. 1999;41:178–199. doi: 10.1006/brcg.1999.1117. [DOI] [PubMed] [Google Scholar]
- Espy KA, McDiarmid MM, Cwik MF, Stalets MM, Hamby A, Senn TE. The contribution of executive functions to emergent mathematical skills in preschool children. Developmental Neuropsychology. 2004;26:465–486. doi: 10.1207/s15326942dn2601_6. [DOI] [PubMed] [Google Scholar]
- Espy KA, Molfese VJ, DiLalla LF. Effects of environmental measures on intelligence in young children: growth curve modeling of longitudinal data. Merrill-Palmer Quarterly. 2001;47:42–73. [Google Scholar]
- Farah MJ, Shera DM, Savage JH, Betancourt L, Giannetta JM, Brodsky NL, Malmud EK, Hurt H. Childhood poverty: specific associations with neurocognitive development. Brain Research. 2006;1110:166–174. doi: 10.1016/j.brainres.2006.06.072. [DOI] [PubMed] [Google Scholar]
- Friedman NP, Miyake A, Young SE, DeFries JC, Corley RP, Hewitt JK. Individual differences in executive functions are almost entirely genetic in origin. Journal of Experimental Psychology: General. 2008;137:201–225. doi: 10.1037/0096-3445.137.2.201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garon N, Bryson SE, Smith IM. Executive function in preschoolers: a review using an integrative framework. Psychological Bulletin. 2008;134:31–60. doi: 10.1037/0033-2909.134.1.31. [DOI] [PubMed] [Google Scholar]
- Gathercole SE, Brown L, Pickering SJ. Working memory assessments at school entry as longitudinal predictors of National Curriculum attainment levels. Educational and Child Psychology. 2003;20:109–122. [Google Scholar]
- Gathercole SE, Pickering SJ. Working memory deficits in children with low achievements in the national curriculum at 7 years of age. British Journal of Educational Psychology. 2000;70:177–194. doi: 10.1348/000709900158047. [DOI] [PubMed] [Google Scholar]
- Gathercole SE, Pickering SJ, Knight C, Stegman Z. Working memory skills and educational attainment: evidence from National Curriculum assessments at 7 and 14 years of age. Applied Cognitive Psychology. 2004;18:1–16. [Google Scholar]
- Goldman P, Rosvold E, Mishkin M. Evidence for behavioural impairment following prefrontal lobectomy in the infant monkey. Journal of Comparative and Physiological Psychology. 1970;70:454–463. doi: 10.1037/h0028701. [DOI] [PubMed] [Google Scholar]
- Goldman P, Rosvold E, Vest B, Galkin T. Analysis of the delayed-alternation deficit produced by dorsolateral prefrontal lesions in the rhesus monkey. Journal of Comparative and Physiological Psychology. 1971;77:212–220. doi: 10.1037/h0031649. [DOI] [PubMed] [Google Scholar]
- Gottfried AW, Bathurst K, Guerin DW, Parramore MM. Socioeconomic status in children’s development and family environment: infancy through adolescence. In: Bornstein MH, Bradley RH, editors. Socioeconomic status, parenting, and child development. Mahwah, NJ: Lawrence Erlbaum Associates; 2003. pp. 189–207. [Google Scholar]
- Griffin SA, Case R, Siegler RS. Classroom lessons: integrating cognitive theory and classroom practice. In: McGilly K, editor. Rightstart: Providing the central conceptual prerequisites for first formal learning of arithmetic to students at risk for school failure. Cambridge, MA: MIT Press; 1994. pp. 25–49. [Google Scholar]
- Horn JL, Cattell RB. Refinement and test of the theory of fluid and crystallized general intelligences. Journal of Educational Psychology. 1966;57:253–270. doi: 10.1037/h0023816. [DOI] [PubMed] [Google Scholar]
- Hyde JS, Lindberg SM, Linn MC, Ellis AB, Williams CC. Gender similarities characterize math performance. Science. 2008;321:494–495. doi: 10.1126/science.1160364. [DOI] [PubMed] [Google Scholar]
- Jordan NC, Huttenlocher J, Levine SC. Differential calculation abilities in young children from middle- and low-income families. Developmental Psychology. 1992;28:644–653. [Google Scholar]
- Jordan NC, Huttenlocher J, Levine SC. Assessing early arithmetic abilities: effects of verbal and nonverbal response types on calculation performance of middle- and low-income children. Learning and Individual Differences. 1994;6:413–432. [Google Scholar]
- Jordan NC, Kaplan D, Locuniak MH, Ramineni C. Predicting first grade math achievement from developmental number sense trajectories. Learning Disabilities: Research and Practice. 2007;22:36–46. [Google Scholar]
- Jordan NC, Kaplan D, Olah L, Locuniak MH. Number sense growth in kindergarten: a longitudinal investigation of children at risk for mathematical difficulties. Child Development. 2006;77:153–175. doi: 10.1111/j.1467-8624.2006.00862.x. [DOI] [PubMed] [Google Scholar]
- Kenney-Benson GA, Pomerantz EM, Ryan AM, Patrick H. Sex differences in math performance: the role of children’s approach to schoolwork. Developmental Psychology. 2006;42:11–26. doi: 10.1037/0012-1649.42.1.11. [DOI] [PubMed] [Google Scholar]
- Kerns K, Rondeau L. Development of a continuous performance test for preschool children. Journal of Attention Disorders. 1998;2:229–238. [Google Scholar]
- Klenberg L, Korkman M, Lahti-Nuuttila P. Differential development of attention and executive functions in 3- to 12-year-old Finnish children. Developmental Neuropsychology. 2001;20:407–428. doi: 10.1207/S15326942DN2001_6. [DOI] [PubMed] [Google Scholar]
- Kliewer W, Kung E. Family moderators of the relation between hassles and behavior problems in inner-city youth. Journal of Clinical Child Psychology. 1998;27:278–292. doi: 10.1207/s15374424jccp2703_5. [DOI] [PubMed] [Google Scholar]
- Korkman M, Kirk U, Kemp S. Developmental neuropsychological assessment. San Antonio, TX: Psychological Corporation; 1998. [Google Scholar]
- Lachance JA, Mazzocco MMM. A longitudinal analysis of sex differences in math and spatial skills in primary school age children. Learning and Individual Differences. 2006;16:195–216. doi: 10.1016/j.lindif.2005.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landry SH, Miller-Loncar CL, Smith KE, Swank PR. The role of early parenting in children’s development of executive processes. Developmental Neuropsychology. 2002;21:15–41. doi: 10.1207/S15326942DN2101_2. [DOI] [PubMed] [Google Scholar]
- Landry S, Smith K, Swank P. Responsive parenting: establishing foundations for social, communication, and independent problem-solving skills. Developmental Psychology. 2006;42:327–642. doi: 10.1037/0012-1649.42.4.627. [DOI] [PubMed] [Google Scholar]
- Landry S, Smith K, Swank P, Miller-Loncar C. Early maternal and child influences on children’s later independent cognitive and social functioning. Child Development. 2000;71:358–375. doi: 10.1111/1467-8624.00150. [DOI] [PubMed] [Google Scholar]
- Lee K, Ng EL, Ng SF. The contributions of working memory and executive functioning to problem representation and solution generation in algebraic word problems. Journal of Educational Psychology. 2009;101:373–387. [Google Scholar]
- Lenroot RK, Gogtay N, Greenstein DK, Wells EM, Wallace GL, Clasen LS, Blumenthal JD, Lerch J, Zijdenbos AP, Evans AC, Thompson PM, Giedd JN. Sexual dimorphism of brain developmental trajectories during childhood and adolescence. NeuroImage. 2007;36:1065–1073. doi: 10.1016/j.neuroimage.2007.03.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liaw F-R, Brooks-Gunn J. Cumulative familial risks and low-birthweight children’s cognitive and behavioral development. Journal of Clinical Child Psychology. 1994;23:360–372. [Google Scholar]
- Linver MR, Brooks-Gunn J, Kohen DE. Family processes as pathways from income to young children’s development. Developmental Psychology. 2002;38:719–734. [PubMed] [Google Scholar]
- Little R, Rubin D. Statistical analysis with missing data. New York: Wiley and Son; 1987. [Google Scholar]
- Locuniak MH, Jordan NC. Using kindergarten number sense to predict calculation fluency in second grade. Journal of Learning Disabilities. 2008;41:451–459. doi: 10.1177/0022219408321126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lytton H, Romney DM. Parents’ differential socialization of boys and girls: a meta-analysis. Psychological Bulletin. 1991;109:267–296. [Google Scholar]
- McGrew KS, Werder JR, Woodcock RW. WJ-R technical manual. Itasca: IL: Riverside Publishing; 1991. [Google Scholar]
- McLean JF, Hitch GJ. Working memory impairments in children with specific arithmetic learning difficulties. Journal of Experimental Child Psychology. 1999;74:240–260. doi: 10.1006/jecp.1999.2516. [DOI] [PubMed] [Google Scholar]
- Meade AW, Bauer DJ. Power and precision in confirmatory factor analytic tests of measurement invariance. Structural Equation Modeling. 2007;14:611–635. [Google Scholar]
- Meyers S. Mothering in context: ecological determinants of parent behavior. Merrill- Palmer Quarterly. 1999;45:332–357. [Google Scholar]
- Mezzacappa E. Alerting, orienting, and executive attention: developmental properties and sociodemographic correlates in an epidemiological sample of young, urban children. Child Development. 2004;75:1373–1386. doi: 10.1111/j.1467-8624.2004.00746.x. [DOI] [PubMed] [Google Scholar]
- Miyake A, Friedman NP, Emerson MJ, Witzki AH, Howerter A, Wager TD. The unity and diversity of executive functions and their contributions to complex frontal lobe tasks: a latent variable analysis. Cognitive Psychology. 2000;41:49–100. doi: 10.1006/cogp.1999.0734. [DOI] [PubMed] [Google Scholar]
- Moos R, Moos B. LISRES-A, Life Stressors and Social Resources Inventory-Adult form. Odesa, FL: PAR; 1994. [Google Scholar]
- Muthen L, Muthen B. Mplus user’s guide. Los Angeles, CA: Authors; 2006. [Google Scholar]
- National Mathematics Advisory Panel. Foundations for success: The final report of the National Mathematics Advisory Panel. Washington, DC: US Department of Education; 2008. [Google Scholar]
- NICHD Early Child Care Research Network. Do children’s attention processes mediate the link between family predictors and school readiness? Developmental Psychology. 2003;39:581–593. doi: 10.1037/0012-1649.39.3.581. [DOI] [PubMed] [Google Scholar]
- NICHD Early Child Care Research Network. Predicting individual differences in attention, memory, and planning in first graders from experience at home, child care, and school. Developmental Psychology. 2005;41:99–114. doi: 10.1037/0012-1649.41.1.99. [DOI] [PubMed] [Google Scholar]
- Noble KG, McCandliss BD, Farah MJ. Socioeconomic gradients predict individual differences in neurocognitive abilities. Developmental Science. 2007;10:464–480. doi: 10.1111/j.1467-7687.2007.00600.x. [DOI] [PubMed] [Google Scholar]
- Noble KG, Norman MF, Farah MJ. Neurocognitive correlates of socioeconomic status in kindergarten children. Developmental Science. 2005;8:74–87. doi: 10.1111/j.1467-7687.2005.00394.x. [DOI] [PubMed] [Google Scholar]
- Pascualvaca DM, Anthony BJ, Arnold LE, Rebok GW, Ahearn MB, Kellam SG, Mirsky AF. Attention performance in an epidemiological sample of urban children: the role of gender and verbal intelligence. Child Neuropsychology. 1997;3:13–27. [Google Scholar]
- Passolunghi CM, Siegel LS. Short-term memory, working memory, and inhibitory control in children with difficulties in arithmetic problem solving. Journal of Experimental Child Psychology. 2001;80:44–57. doi: 10.1006/jecp.2000.2626. [DOI] [PubMed] [Google Scholar]
- Pettit G, Bates J. Family interaction patterns and children’s behavior problems from infancy to 4 years. Developmental Psychology. 1989;25:413–420. [Google Scholar]
- Pomerantz E, Eaton M. Maternal intrusive support in the academic context: transactional socialization processes. Developmental Psychology. 2001;37:174–186. doi: 10.1037/0012-1649.37.2.174. [DOI] [PubMed] [Google Scholar]
- Sattler J. Assessment of children. San Diego, CA: Author; 1992. [Google Scholar]
- Saxe GB, Guberman SR, Gearhart M, Gelman R, Massey CM, Rogoff B. Social processes in early number development. Monographs of the Society for Research in Child Development. 1987;52(2) Serial No. 216. [Google Scholar]
- Schafer JL, Graham JW. Missing data: our view of the state of the art. Psychological Methods. 2002;7:147–177. [PubMed] [Google Scholar]
- Siegler RS. Individual differences in strategy choices: good students, not-so-good students, and perfectionists. Child Development. 1988;59:833–851. [PubMed] [Google Scholar]
- Simon H. The functional equivalence of problem solving skills. Cognitive Psychology. 1975;7:268–288. [Google Scholar]
- St Clair-Thompson HL, Gathercole SE. Executive functions and achievements in school: shifting, updating, inhibition, and working memory. Quarterly Journal of Experimental Psychology. 2006;59:745–759. doi: 10.1080/17470210500162854. [DOI] [PubMed] [Google Scholar]
- Tillman CM, Nyberg L, Bohlin G. Working memory components and intelligence in children. Intelligence. 2008;36:394–402. [Google Scholar]
- Vandenberg RJ, Lance CE. A review and synthesis of the measurement invariance literature: suggestions, practices, and recommendations for organizational research. Organizational Research Methods. 2000;3 (1):4–69. [Google Scholar]
- van der Sluis S, de Jong PF, van der Leij A. Inhibition and shifting in children with learning deficits in arithmetic and reading. Journal of Experimental Child Psychology. 2004;87:239–266. doi: 10.1016/j.jecp.2003.12.002. [DOI] [PubMed] [Google Scholar]
- Welsh JA, Nix RL, Blair C, Bierman KL, Nelson KE. The development of cognitive skills and gains in academic school readiness for children from low-income families. Journal of Educational Psychology. 2010;102:43–53. doi: 10.1037/a0016738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiebe SA, Espy KA, Charak D. Using confirmatory factor analysis to understand executive control in preschool children: I. Latent structure. Developmental Psychology. 2008;44:573–587. doi: 10.1037/0012-1649.44.2.575. [DOI] [PubMed] [Google Scholar]
- Woodcock RW, Johnson MB. Woodcock-Johnson revised test of achievement. Itasca: IL: Riverside Publishing; 1989. [Google Scholar]
- Zeanah CH. Disturbances of attachment in young children adopted from institutions. Journal of Developmental and Behavioral Pediatrics. 2000;21:230–236. [PubMed] [Google Scholar]
- Zimmerman BJ, Martinez-Pons M. Student differences in self-regulated learning: relating grade, sex, and giftedness to self-efficacy and strategy use. Journal of Educational Psychology. 1990;82:51–59. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.