The Use of Sample Weights in Hot Deck Imputation

Abstract

A common strategy for handling item nonresponse in survey sampling is hot deck imputation, where each missing value is replaced with an observed response from a “similar” unit. We discuss here the use of sampling weights in the hot deck. The naive approach is to ignore sample weights in creation of adjustment cells, which effectively imputes the unweighted sample distribution of respondents in an adjustment cell, potentially causing bias. Alternative approaches have been proposed that use weights in the imputation by incorporating them into the probabilities of selection for each donor. We show by simulation that these weighted hot decks do not correct for bias when the outcome is related to the sampling weight and the response propensity. The correct approach is to use the sampling weight as a stratifying variable alongside additional adjustment variables when forming adjustment cells.

1 Introduction

Missing data are often a problem in large-scale surveys, arising when a sampled unit does not respond to the entire survey (unit nonresponse) or to a particular question (item nonresponse). We consider here imputation for item nonresponse, a common technique for creating a complete data set that can then be analyzed with traditional analysis methods. In particular we consider use of the hot deck, an imputation strategy in which each missing value is replaced with an observed response from a “similar” unit (Kalton and Kasprzyk 1986). The hot deck method does not rely on model fitting for the variable to be imputed, and thus is potentially less sensitive to model misspecification than an imputation method based on a parametric model, such as regression imputation. It preserves the distribution of item values, unlike mean imputation which leads to a spike of values at the respondent mean. Additionally, only plausible values can be imputed, since values come from observed responses in the donor pool.

The most common method of matching donor to recipient is to divide responding and nonresponding units into imputation classes, also known as adjustment cells or donor pools, based on variables observed for all units (Brick and Kalton 1996). To create cells, any continuous variables are categorized before proceeding. Imputation is then carried out by randomly picking a donor for each nonrespondent within each cell. These classes historically have been formed a priori based on knowledge of the subject matter and choosing variables that are associated with the missing values. In addition, variables that are predictive of nonresponse may be used to define imputation classes.

Once imputation has created a filled-in data set, analysis can proceed using the sampling weights determined by the sample design. Unlike weighting for nonresponse, where sample weights must be combined with nonresponse weights for subsequent analysis, no adjustment to the weights is necessary. However, ignoring sample weights effectively imputes using the unweighted sample distribution of respondents in an adjustment cell, which may cause bias if these respondents have differing sampling weights. In this paper we consider several ways for using the survey weights in creating donor pools and carrying out hot deck imputation. Section 2 reviews methods developed for incorporating sample weights into the hot deck. In Section 3 a simulation study compares estimators of a population mean using these methods. Section 4 demonstrates these methods on data from the third National Health and Nutrition Examination Survey (NHANES III).

2 Methods for Incorporating Sample Weights

Two approaches to selection from hot deck donor pools have been used: sequential and random. Sequential selection first sorts all units within a donor pool and then imputes for each missing value the closest preceding respondent value, a variant of nearest neighbor imputation. The sort order can be random, or sorting variables can be auxiliary variables presumed related to the item being imputed. In contrast, random selection imputes each missing value with a random draw from the donor pool for each nonrespondent. Neither of these methods necessarily incorporate survey design weights into donor selection.

A modification to the sequential procedure to incorporate sample weights was proposed by Cox (1980) and called the weighted sequential hot deck (WSHD). The procedure preserves the sorting methodology of the unweighted procedure, but allows all respondents the chance to be a donor and uses sampling weights to restrict the number of times a respondent value can be used for imputation. Respondents and nonrespondents are first separated into two files and sorted (randomly, or by auxiliary variables). Sample weights of the nonrespondents are rescaled to sum to the total of the respondent weights. The algorithm can be thought of as aligning both these rescaled weights and the donors’ weights along a line segment, and determining which donors overlap each nonrespondent along the line (Williams and Folsom 1981). Thus the set of donors who are eligible to donate to a given nonrespondent is a function of the sort order, the nonrespondent’s sample weight, and the sample weights of all the donors. The algorithm is designed so that, over repeated imputations, the weighted mean obtained from the imputed values is equal in expectation to the weighted mean of the respondents alone within imputation strata. If response probability is constant within a cell then the WSHD leads to an unbiased estimator. “Similarity” of donor to recipient is still controlled by the choice of sorting variables.

Adjustments to the random selection method that incorporate the sample weights include inflating the donated value by the ratio of the sample weight of the donor to that of the recipient (Platek and Gray 1983) or selecting donors via random draw with probability of selection proportional to the potential donor’s sample weight (Rao and Shao 1992; Rao 1996). The former method has drawbacks, particularly in the case of integer-valued imputed values, since the imputations may no longer be plausible values. The latter method does not suffer from this inconsistency problem and yields an asymptotically unbiased estimator, assuming constant response probability within an adjustment cell. Note that in contrast to the weighted sequential hot deck, the sample weights of nonrespondents are not used in determining the selection probabilities of donors. We refer to this method as the weighted random hot deck (WRHD) to distinguish it from the weighted sequential hot deck (WSHD).

We suggest that neither WRHD nor WSHD are appropriate ways of incorporating design weights into the hot deck. Specifically, both the WSHD and WRHD fail to remove bias if outcome is related to the design weights and response propensity is not constant within an adjustment cell. The correct approach is to create donor pools based on stratification by auxiliary variables and design variables that determine the sampling weights. The goal should be to create imputation cells that are homogeneous with respect to both the outcome and the propensity to respond. Creating cells by cross-classification of both auxiliary and design variables is the best way to achieve this goal, in so far as these variables are associated with outcomes and nonresponse. With adjustment cells created in this way, draws proportional to sample weights are unnecessary and inefficient. One concern with this method is that if response is not related to the design variables, excess noise is added by over-stratifying without an accompanying bias reduction. However, simulations in Collins, Schafer, and Kam (2001) suggest that the benefits of reduction in bias outweigh the increase in variance. Little and Vartivarian (2003) demonstrated by simulation that when weighting for nonresponse adjustment, computing the unweighted response rate applied within cells defined by auxiliary and design variables was the correct approach, and that weighting the nonresponse rates using the sampling weights does not remove bias in all cases. In the next section we describe a simulation study, which shows that a similar scenario holds for the hot deck estimators.

3 Simulation Study

A simulation study was conducted to compare the performance of the various forms of the hot deck under a variety of population structures and nonresponse mechanisms. We build on the simulation in Little and Vartivarian (2003) which compared weighting estimators for the population mean. Categorical variables were simulated to avoid distributional assumptions such as normality.

3.1 Description of the Population

As in Little and Vartivarian (2003), a population of size 10000 was generated on a binary stratifier Z known for all population units, a binary adjustment variable X observed for the sample, and a binary survey outcome Y observed only for respondents. Taking S to be the sampling indicator and R the response indicator, the joint distribution of these variables, say [Z, X, Y, S, R] can be factorized as follows:

$$[X,Z,Y,S,R]=[X,Z][Y\mid X,Z][S\mid X,Z,Y][R\mid X,Z,Y,S]$$

The distributions on the right side was then defined as follows:

1. Distribution of X and Z.

   • The joint distribution of [X, Z] was multinomial, with Pr(X = 0, Z = 0) = 0.3, Pr(X = 1, Z = 0) = 0.4, Pr(X = 0, Z = 1) = 0.2, and Pr(X = 1, Z = 1) = 0.1.
2. Distribution of Y given X and Z.

   • Population values of the survey variable Y were generated according to the logistic model
   • $$\mathrm{logit}\left(\mathrm{Pr}(Y=1\mid X,Z)\right)=0.5+{\gamma }_X(X-\stackrel{‒}{X})+{\gamma }_Z(Z-\stackrel{‒}{Z})+{\gamma }_{XZ}(X-\stackrel{‒}{X})(Z-\stackrel{‒}{Z})$$
   • for five choices of γ = (γ_X, γ_Z, γ_XZ) chosen to reflect different relationships between Y and X and Z. These choices are displayed in Table 1 using conventional linear model notation. For example, the additive logistic model [X + Z]^Y sets the interaction γ_XZ to zero, whereas the model [XZ]^Y sets this interaction equal to 2. The models [X]^Y and [Z]^Y allow the outcome to depend on X only and Z only. The null model, where outcome is independent of X and Z, is denoted [ϕ]^Y.
3. Distribution of S given Z, X, and Y.

   • The sample cases were assumed to be selected by stratified random sampling, so S is independent of X and Y given Z, that is [S|X, Z, Y] = [S|Z]. Two different sample sizes were evaluated. A sample of n₀ = 125 was drawn from the stratum with Z = 0 and size n₁ = 25 from the stratum with Z = 1, yielding a total sample size of 150. A larger sample of size 600 was then obtained by sampling n₀ = 500 and n₁ = 100 from the strata with Z = 0 and Z = 1 respectively.
4. Distribution of R given Z, X, Y , and S.

   • Since the response mechanism is assumed ignorable and the selection was by stratified random sampling, R is independent of Y and S given X and Z, i.e. [R|Z, X, Y, S] = [R|Z, X]. The latter was generated according to the logistic model
   • $$\mathrm{logit}\left(\mathrm{Pr}(R=1\mid X,Z)\right)=0.5+{\beta }_X(X-\stackrel{‒}{X})+{\beta }_Z(Z-\stackrel{‒}{Z})+{\beta }_{XZ}(X-\stackrel{‒}{X})(Z-\stackrel{‒}{Z})$$
   • where β = (β_X, β_Z, β_XZ) took the same values as γ, found in Table 1. As with the distribution of Y given X and Z, this yielded five models for the distribution of R given X and Z. For example, [X + Z]^R refers to an additive logistic model for R given X and Z. This produced an average response rate over all simulations of 60%.

Table 1.

Models for Y given X, Z

	γX	γZ	γXZ
[XZ]Y	2	2	2
[X + Z]Y	2	2	0
[X]Y	2	0	0
[Z]Y	0	2	0
[ϕ]Y	0	0	0

There were a total of 5 × 5 = 25 combinations of population structures and nonresponse mechanisms in the simulation study and two different sample sizes. A total of 1000 replicate populations of (X, Z, Y, S, R) were generated for each of the 25 × 2 combinations.

3.2 Estimators

A total of seven methods for estimating the population mean were employed. Four versions of the hot deck were used to impute missing values, followed by computing the usual sample-weighted Horvitz-Thompson estimator for the population mean. The four hot deck methods are summarized in Table 2. All hot deck methods stratify on X, that is, perform imputation separately for units with X = 0 and X = 1. The weighted hot deck methods, wrhd(x) and wshd(x), use information in Z in determining donor probabilities, in contrast to uhd(xz), which imputes within cells additionally defined by Z, and uhd(x), which ignores the information in Z. We implemented the wshd(x) in both a sorted (by Z, within adjustment cells) and unsorted form, the results were similar and we report only the unsorted results. In addition, three weighting estimators were used to estimate the population average without imputation, shown in Table 3. The weighting estimators wrr(x) and urr(xz) are analogous to the hot deck methods wrhd(x) and uhd(xz), respectively. We expected to see higher variance with the hot deck methods, but parallel results in terms of bias. For each replicate we also calculated the complete-case estimate using the Horvitz-Thompson estimator, with weights unadjusted for nonresponse. Finally, for comparison purposes we calculated the before-deletion estimate using the Horvitz-Thompson estimator, that is, before sampled units with R = 0 had their Y values deleted. This captures simulation variance in measures of bias and acts as a benchmark for evaluating increases in root mean square error due to nonresponse.

Table 2.

Hot Deck Methods

Method		Adjustment Cells	Draws
wrhd(x)	Weighted Random Hot Deck	X	Proportional to sample weight
wshd(x)	Weighted Sequential Hot Deck	X	n/a
uhd(x)	Unweighted Hot Deck	X	Equal probability
uhd(xz)	Unweighted Hot Deck	X and Z	Equal probability

Table 3.

Weighting Methods

Method		Adjustment Cells	Response Rate
wrr(x)	Weighted Response Rate	X	Weighted
urr(x)	Unweighted Response Rate	X	Unweighted
urr(xz)	Unweighted Response Rate	X and Z	Unweighted

Empirical bias and root mean square error (RMSE) for each method M were calculated as follows:

$$\mathrm{EBias}=\frac{1}{1000}\sum _{i=1}^{1000}({\widehat{\theta }}_{Mi}-{\theta }_i)$$ (1)

$$\mathrm{RMSE}=\sqrt{\frac{1}{1000}\sum _{i=1}^{1000}{({\widehat{\theta }}_{Mi}-{\theta }_i)}^2}$$ (2)

where ${\widehat{\theta }}_{Mi}$ is the estimate of the population mean using method M for the ith replicate and θ_i is the full population mean for the ith replicate. Selected pairs of hot deck estimators were compared to determine if differences in performance were statistically significant. The average difference between a pair of estimators was calculated as

$$\stackrel{‒}{d}=\frac{1}{1000}\sum _{i=1}^{1000}\mid {\widehat{\theta }}_{BDi}-{\widehat{\theta }}_{1i}\mid -\mid {\widehat{\theta }}_{BDi}-{\widehat{\theta }}_{2i}\mid$$ (3)

where for the ith replicate ${\widehat{\theta }}_{BDi}$ is the estimated sample mean before-deletion of cases due to non-response and ${\widehat{\theta }}_{1i}$ and ${\widehat{\theta }}_{2i}$ are estimates found after imputation with the two different hot deck methods being compared.

3.3 Results

Tables 4 and 5 display the empirical bias for all seven methods as well as the complete case and before-deletion estimates for the smaller and larger sample sizes. Tables 6 and 7 show the percent increase in RMSE for each method over the before-deletion method for sample sizes n = 150 and n = 600 respectively. Table 8 displays $\stackrel{‒}{d}(\times 10,1000)$ for the comparison of uhd(xz) with each of the other three hot deck methods for the smaller sample size; results were similar for the larger sample size and are not shown. Differences that are statistically significant from zero based on a t-test are asterisked (* = p < 0.05, ** = p < 0.01).

Table 4.

1,000 x (Average Empirical Bias) of 1000 replicate samples (n=150)

Generated Model for Y and R			Hot deck estimators				Weighting estimators			Complete case	Before deletion
	[]Y	[]R	wrhd(x)	wshd(x)	uhd(x)	uhd(xz)	wrr(x)	urr(x)	urr(xz)
1	XZ	XZ	22	22	4	− 4	21	17	−4	66	0
2	XZ	X + Z	37	37	21	1	37	27	2	71	2
3	XZ	X	− 2	− 2	−13	− 2	−2	−2	−1	57	0
4	XZ	Z	30	28	14	− 1	29	27	−1	21	−1
5	XZ	ϕ	0	0	−13	1	0	0	0	0	1
6	X + Z	XZ	37	37	10	0	37	33	1	78	2
7	X + Z	X + Z	59	59	34	2	59	51	1	87	0
8	X + Z	X	−3	−3	−27	− 1	−3	−2	−1	59	−1
9	X + Z	Z	39	41	21	1	41	39	2	33	0
10	X + Z	ϕ	0	−1	−18	−1	−1	0	0	0	0
11	X	XZ	0	1	0	1	0	−6	0	65	−1
12	X	X + Z	0	−1	0	−1	0	−16	0	54	−1
13	X	X	1	0	−1	1	0	1	0	84	0
14	X	Z	− 1	− 1	− 1	−2	−1	−4	−1	−13	1
15	X	ϕ	−1	0	0	−1	−1	−1	−1	−1	1
16	Z	XZ	36	37	11	− 1	36	38	0	20	0
17	Z	X + Z	52	52	29	− 2	52	58	−3	33	−2
18	Z	X	−2	− 1	−25	− 1	−2	−1	0	−17	0
19	Z	Z	43	41	20	− 2	41	42	−2	44	0
20	Z	ϕ	− 3	−4	−23	−3	−4	−3	−3	−3	−2
21	ϕ	XZ	−2	−1	1	0	−1	−1	0	−1	−1
22	ϕ	X + Z	− 2	−3	−2	−3	−3	−3	−3	−2	−1
23	ϕ	X	0	−1	−2	−2	−2	−2	−1	−1	−1
24	ϕ	Z	1	1	2	2	1	1	1	1	1
25	ϕ	ϕ	4	4	4	4	4	4	4	4	2
Mean			14	14	2	−1	14	12	0	30	0
Mean absolute average empirical bias			15	15	12	2	15	15	1	33	1

Smallest absolute empirical average bias among hot deck methods shown in italics.

Table 5.

1,000 x (Average Empirical Bias) of 1000 replicate samples (n=600)

Generated Model for Y and R			Hot deck estimators				Weighting estimators			Complete case	Before deletion
	[]Y	[]R	wrhd(x)	wshd(x)	uhd(x)	uhd(xz)	wrr(x)	urr(x)	urr(XZ)
1	XZ	XZ	26	25	8	0	25	21	1	68	1
2	XZ	X + Z	35	35	20	0	35	25	0	68	0
3	XZ	X	2	1	−14	2	1	2	2	59	−1
4	XZ	Z	32	31	16	1	31	29	1	23	0
5	XZ	ϕ	−1	−1	−13	0	0	0	0	0	0
6	X + Z	XZ	36	37	9	1	37	33	0	78	0
7	X + Z	X + Z	57	58	32	0	58	49	0	86	0
8	X + Z	X	−1	−1	−26	0	−1	0	0	62	0
9	X + Z	Z	40	40	21	0	40	38	0	32	0
10	X + Z	ϕ	0	0	−18	0	0	0	0	0	−1
11	X	XZ	2	1	0	0	1	−5	1	67	1
12	X	X + Z	0	0	0	−1	0	−17	−1	55	0
13	X	X	0	0	−1	−1	0	0	0	84	1
14	X	Z	2	2	2	2	2	−2	2	−10	1
15	X	ϕ	1	1	1	1	1	1	1	1	1
16	Z	XZ	37	37	11	1	37	39	1	21	0
17	Z	X + Z	56	56	31	1	56	61	2	36	1
18	Z	X	−1	−1	−25	0	−1	−1	0	−16	0
19	Z	Z	43	43	22	1	43	44	0	46	1
20	Z	ϕ	− 1	− 1	−20	− 1	−1	−1	−1	−1	0
21	ϕ	XZ	0	0	0	0	0	0	0	0	0
22	ϕ	X + Z	−1	−1	−1	0	0	0	0	−1	0
23	ϕ	X	1	1	1	1	1	1	1	1	0
24	ϕ	Z	0	0	0	0	0	0	0	0	0
25	ϕ	ϕ	1	0	1	1	1	1	1	1	1
Mean			14	14	2	−1	14	12	0	30	0
Mean absolute average empirical bias			15	15	12	2	15	15	1	33	1

Smallest absolute empirical average bias among hot deck methods shown in italics.

Table 6.

Percent increase in RMSE compared to before deletion estimate, 1000 replicate samples (n=150)

Generated Model for Y and R			Hot deck estimators				Weighting estimators			Complete Case
	[]Y	[]R	wrhd(x)	wshd(x)	uhd(x)	uhd(xz)	wrr(x)	urr(x)	urr(xz)
1	XZ	XZ	66	56	49	53	55	53	39	108
2	XZ	X + Z	77	71	57	45	68	62	35	115
3	XZ	X	60	52	59	63	48	48	48	89
4	XZ	Z	55	45	37	29	45	43	22	42
5	XZ	ϕ	40	31	42	37	26	26	25	29
6	X + Z	XZ	83	78	58	49	75	71	38	139
7	X + Z	X + Z	116	109	74	40	108	97	31	159
8	X + Z	X	57	49	67	52	47	43	43	91
9	X + Z	Z	61	60	36	26	56	53	18	49
10	X + Z	ϕ	43	33	51	39	30	29	26	31
11	X	XZ	57	48	49	47	45	50	37	107
12	X	X + Z	50	42	44	48	39	51	35	82
13	X	X	53	41	47	55	39	40	44	132
14	X	Z	33	28	28	26	24	26	17	34
15	X	ϕ	34	27	29	38	21	22	23	26
16	Z	XZ	90	82	70	62	78	84	50	50
17	Z	X + Z	99	93	65	51	90	105	38	53
18	Z	X	74	59	89	65	55	56	50	47
19	Z	Z	80	73	52	39	68	70	29	74
20	Z	ϕ	50	40	68	47	35	35	32	35
21	ϕ	XZ	59	48	53	53	46	48	40	32
22	ϕ	X + Z	47	41	46	46	39	43	34	28
23	ϕ	X	63	49	53	61	46	46	50	30
24	ϕ	Z	37	33	32	34	28	29	22	29
25	ϕ	ϕ	43	32	38	46	29	29	30	29
Mean Percent			61	53	52	46	50	50	34	65

Lowest percent increase in RMSE among hot deck methods shown in italics.

Table 7.

Percent increase in RMSE compared to before deletion estimate, 1000 replicate samples (n=600)

Generated Model for Y and R			Hot deck estimators				Weighting estimators			Complete case
	[]Y	[]R	wrhd(x)	wshd(x)	uhd(x)	uhd(xz)	wrr(x)	urr(x)	urr(xz)
1	XZ	XZ	102	91	58	53	90	78	37	259
2	XZ	X + Z	130	124	77	40	123	93	33	257
3	XZ	X	65	53	73	63	52	51	48	215
4	XZ	Z	105	98	55	34	96	88	23	71
5	XZ	ϕ	37	31	51	34	24	24	21	26
6	X + Z	XZ	143	138	59	50	136	122	39	312
7	X + Z	X + Z	241	237	129	42	237	200	32	375
8	X + Z	X	71	57	112	59	53	49	44	243
9	X + Z	Z	153	149	74	30	147	137	20	113
10	X + Z	ϕ	43	30	65	35	26	25	22	28
11	X	XZ	57	44	52	46	43	49	35	256
12	X	X + Z	51	41	46	42	39	64	32	191
13	X	X	60	49	54	57	47	47	47	320
14	X	Z	29	26	28	24	22	22	16	37
15	X	ϕ	40	34	37	39	26	27	27	31
16	Z	XZ	169	163	79	60	160	170	44	86
17	Z	X + Z	238	232	124	52	230	261	41	135
18	Z	X	76	59	129	64	56	57	47	70
19	Z	Z	179	178	89	45	174	178	28	186
20	Z	ϕ	54	38	93	44	34	34	29	34
21	ϕ	XZ	57	48	47	52	43	45	34	33
22	ϕ	X + Z	57	49	49	50	45	49	37	35
23	ϕ	X	66	51	56	63	47	47	48	32
24	ϕ	Z	45	37	37	37	32	32	24	32
25	ϕ	ϕ	40	32	38	43	26	26	26	26
Mean Percent			92	84	68	46	80	79	33	136

Lowest percent increase in RMSE among hot deck methods shown in italics.

Table 8.

Pairwise comparisons of average absolute error $(\stackrel{‒}{d}\times 10,1000)$ of hot deck methods (n=150)

Generated model for Y and R			uhd(xz) and wrhd(x)	uhd(xz) and wshd(x)	uhd(xz) and uhd(x)
	[ ]Y	[ ]R
1	XZ	XZ	−5.2**	−1.7	0.7
2	XZ	X + Z	−11.2**	−8.1**	−2.9**
3	XZ	X	−0.4	3.4**	0.2
4	XZ	Z	−10.0**	−6.5**	−2.6**
5	XZ	ϕ	0.3	4.6**	−2.4**
6	X + Z	XZ	−12.9**	−10.9**	−3.2**
7	X + Z	X + Z	−31.2**	−29.3**	−11.9**
8	X + Z	X	−2.1	0.8	−7.2**
9	X + Z	Z	−17.1**	−16.9**	−4.8**
10	X + Z	ϕ	−2.0*	3.0**	−5.6**
11	X	XZ	−0.4	3.2**	0.6
12	X	X + Z	2.2*	5.1**	3.5**
13	X	X	1.1	6.3**	2.2*
14	X	Z	−0.5	3.0**	0.7
15	X	ϕ	1.5	4.6**	1.2
16	Z	XZ	−11.6**	−8.3**	−3.0**
17	Z	X + Z	−23.6**	−21.9**	−8.5**
18	Z	X	−5.7**	−0.1	−10.3**
19	Z	Z	−18.0**	−14.8**	−6.4**
20	Z	ϕ	−2.7**	2.6**	−7.7**
21	ϕ	XZ	−1.1	4.1**	0.2
22	ϕ	X + Z	4.3**	6.8**	3.4**
23	ϕ	X	−1.2	4.3**	1.6
24	ϕ	Z	0.2	3.2**	1.7*
25	ϕ	ϕ	0.0	4.8**	1.0

Negative value: First estimator does better

Positive value: Second estimator does better

^*Signi cance at the 5 percent level

^**Signi cance at the 1 percent level

As shown in Table 4, the unweighted hot deck using cells based on X and Z, uhd(xz), has small empirical bias in all population structures. With this method, the expected outcome and response propensity are constant within a cell, regardless of the model for Y and R, so imputation leads to an unbiased estimate of the population mean. This is similar to the weighting estimator that uses unweighted response rates but stratifies on both X and Z, urr(xz), which also has low empirical bias over all populations. Not surprisingly, the hot deck estimator that ignores Z, uhd(x), is biased for situations where Y depends on Z, since the dependence on Z cannot be ignored. However, the weighted hot decks (wrhd(x) and wshd(x)) do not correct the bias for all these cases. When the response propensity does not depend on Z, both wrhd(x) and wshd(x) have low bias, since the response propensity is constant within their adjustment cells (based on X only). If the response propensity is not constant within adjustment cells, as in populations where R depends on Z, then wrhd(x) and wshd(x) are biased and in fact have larger bias than the method that ignores Z, though we believe this to be an artifact of the simulation design and cannot conclude that uhd(x) would always outperform wrhd(x) and wshd(x) in these situations. This parallels the performance of the weighting methods that stratify on X only (wrr(x), urr(x)), which have similar performance with two exceptions. As noted in Little and Vartivarian (2003), wrr(x) outperforms urr(x) where R depends on both X and Z and Y depends on X but not Z (specifically rows 11 and 12 of Table 4). This is not seen with the hot deck methods; all hot deck methods have low bias for populations where the outcome Y does not depend on Z, regardless of the model for R. When Y depends only on X, both the weighted and unweighted respondent means are unbiased within cells defined by X. Thus the hot deck methods are all unbiased, as over repeated imputations they impute the (weighted) respondent mean to the nonrespondents. For the weighting methods, using unweighted response rates as in urr(x) yields biased estimates of the response rate, and thus biased estimates of the overall mean, and weighting the response rates as in wrr(x) corrects this bias.

All hot deck and weighting methods perform well in terms of bias when the outcome is independent of X and Z, regardless of the response model. Of note, in comparing the average absolute errors, wshd(x) has statistically significantly lower empirical bias than uhd(xz) when Y does not depend on Z, though the size of the difference is small compared to the differences seen when uhd(xz) outperforms the weighting methods.

When missingness is independent of X and Z, that is, missingness is completely at random (Rubin 1976), the complete case estimator is unbiased. Nonresponse adjustment via any of these methods is unnecessary but not harmful in almost all cases. All hot deck and weighting methods produce unbiased estimates with one exception: the unweighted hot deck that ignores Z, uhd(x), induces bias when the outcome is dependent on Z (populations 5, 10, and 20). In this case the nonresponse compensation has an adverse effect and is dangerous, demonstrating the need to condition on as much auxiliary data as is available.

A crude summary of the overall performance of the methods is the average of the percent increase in RMSE over all populations, shown at the bottom of Tables 6 and 7. The best overall hot deck method under both sample sizes is uhd(xz), which as expected has higher RMSE than the best overall weighting method, urr(xz). Differences between uhd(xz) and other hot deck methods follow similar patterns for both sample sizes but are exaggerated with the larger sample size (n = 600). The worst hot deck method is the weighted random hot deck, with a higher overall RMSE than the sequential version. Somewhat surprisingly, the unweighted hot deck showed lower overall RMSE than both the weighted hot decks and two of the weighting methods (wrr(x), urr(x)). Though uhd(x) is biased in more scenarios, the magnitude of the bias is much lower than wrhd(x), wshd(x), wrr(x), and urr(x), and this difference drives the difference in RMSE. We reiterate that this finding is likely an artifact of the simulation design, and in fact though the bias is smaller, uhd(x) is biased for a larger number of populations than the weighted hot deck methods. The sequential version of the weighted hot deck (wshd(x)) has lower RMSE than wrhd(x) in all populations for both sample sizes, and in fact has the lowest (or in one case just slightly larger than the lowest) RMSE among hot deck methods when Y does not depend on X or Z.

Overall, the unweighted hot deck that stratifies on both design and covariate information is robust under all scenarios, and the expected increase in RMSE when response does not depend on the design variable was not severe. In fact uhd(xz) had very similar RMSE to the unweighted method that stratified on X only, uhd(x), in the ten populations where Y did not depend on Z, demonstrating that over-stratifying at least in this case did not lead to a notable increase in variance. Of the weighted hot deck methods, the sequential version performed slightly better than the method using weighted draws from the donor pools.

4 Application

The third National Health and Nutrition Examination Survey (NHANES III) was a large-scale stratified multistage probability sample of the noninstitutionalized U.S. population conducted during the period from 1988 to 1994 (U.S. Department of Health and Human Services 1994). NHANES III collected data in three phases: (a) a household screening interview, (b) a personal home interview, and (c) a physical examination at a mobile examination center (MEC). The total number of persons screened was 39,695, with 86% (33,994) completing the second phase interview. Of these, only 78% were examined in the MEC. Previous imputation efforts for NHANES III focused on those individuals who had completed the second phase; weighting adjustments are used to compensate for non-response at this second stage. Since the questions asked at both the second and third stage varied considerably by age we chose to select only adults age 20 and older who had completed the second phase interview for the purposes of our example, leaving a sample size of 18,825. Design variables that were fully observed for the sample included age, gender, race, and household size.

In order to demonstrate the hot deck methods on a continuous outcome we used systolic blood pressure measured at the MEC examination (SBP, defined as the average of three recorded measurements). The nonresponse rate was 16%. As our stratification variable (X) we chose a self-reported health status variable (Excellent/Very Good/Good/Fair/Poor) from the household interview. Since only 6% of subjects reported the lowest level of health status, the lowest two categories (Fair/Poor) were combined, leaving 4 strata. The Z variables were the design variables: gender (2 levels), race (3 levels), age (3 levels), and household size (3 levels). The goal was to estimate the population mean of SBP.

In order to demonstrate the effect of larger nonresponse rates we increased the missingness as follows. First, we fit a logistic regression model on an indicator for missingness of SBP using the entire sample (n=18,825), using main effects for health status and all design variables as predictors, leaving the variables age and log(household size) as continuous. This created predicted probabilities of non-response mimicking the actual propensities observed in the NHANES data and ranging from 0.05 to 0.39. The mean probability for respondents was 0.15; in order to double the missingness to 32% we required an additional 19% of the respondents to have missing values, so each predicted probability was increased by 0.04. Nonresponse indicators for each respondent were then independently drawn from a Bernoulli distribution with these predicted probabilities and values were subsequently deleted from the sample to create a second data set.

The four different imputation strategies implemented in the simulation study were applied to each of the two data sets. The weighted hot deck methods, wrhd(x) and wshd(x), stratified by health status and used the sample weights to determine donor probabilities within the donor pools. The most naive hot deck method, uhd(x) stratified by health status and ignored the sample weights, and the fully stratified method, uhd(xz) stratified by both health status and the design variables for a total of 215 donor cells (one cell was empty). Complete case estimates were also calculated. In order to obtain measures of variability and better compare estimates, imputation was via the Approximate Bayesian Bootstrap (Rubin and Schenker 1986). Within each adjustment cell the respondent values were resampled with replacement to form a new pool of potential donors and the imputation method (wrhd(x), wshd(x), uhd(x), uhd(xz)) was then applied to this bootstrapped donor pool. This method is easy to compute, and repeated applications yield proper multiple imputations. A total of 10 multiply imputed data sets were created for each method, the Horvitz-Thompson estimator of the mean SBP calculated for each data set, and resulting inference obtained using the combining rules of Rubin (1987).

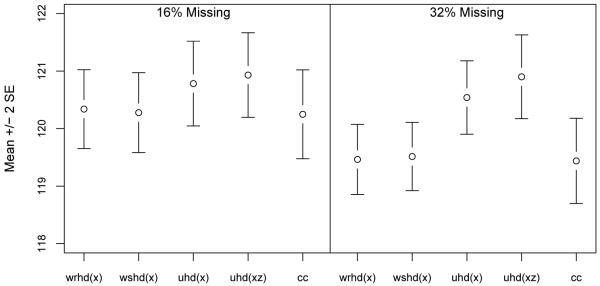
Resulting mean estimates and 95% confidence intervals are displayed in Figure 1 for both the original 16% missingness and the induced 32% missingness. The larger level of nonresponse showed more exaggerated differences in performance between the methods. For both scenarios the weighted hot deck methods (wrhd(x) and wshd(x)) lead to intervals that are close to the complete case estimates. The uhd(xz) method generates estimates that are higher than those of the weighted methods, with the difference becoming more exaggerated with the larger amount of nonresponse. The mean estimate for uhd(xz) is the same across moth missingness scenarios, which is comforting since the overall mean should be the same in both cases, while both wrhd(x) and wshd(x) parallel the complete case estimate and show a downward shift under 32% missingness. The unweighted hot deck that ignores the weights (uhd(x)) also shows a downward shift as missingness increases. One feature that is evident with these data that did not appear in the simulations is the increase in variance with uhd(xz) – for the larger amount of missingness the confidence interval for uhd(xz) is larger than that of the weighted methods, though the difference is minimal. Though the “truth”’ is not available for this real data set, the performance of uhd(xz) appears to be the most robust as it produces similar estimates under both missingness mechanisms.

Figure 1.

Estimates of mean SBP for NHANES III data, after imputation with different hot deck methods. Original missingness was 16%; artificially increased missingness was 32%. Results from 10 multiply-imputed data sets. cc=Complete Case.

5 Conclusion

The simulation study suggests strongly that the two forms of sample-weighted hot deck (WSHD and WRHD) do not correct for bias when the outcome is related to the sampling weight and the response propensity, and are inferior to the method that uses the sampling weight as a stratifying variable when forming adjustment cells. The simulation study focused on estimating a mean and was deliberately kept simple, but it varied systematically the key elements of the problem, namely the relationship between the outcome and the response propensity and the sampling stratum and adjustment cell variable. It seems to us unlikely that more complex simulations will lead to different conclusions, although admittedly this possibility cannot be ruled out. The conclusions parallel similar results for weighting nonresponse adjustments in Little and Vartivarian (2003). Weighting adjustments are a bit more efficient than the hot deck, since the latter is effectively adding noise to the estimates to preserve distributions. However, the hot deck is a more flexible approach to item nonresponse than weighting, and the added noise from imputing real values from donors can be reduced by applying the hot deck repeatedly to generate multiply-imputed data sets (Rubin 1987). Since a benefit of the hot deck is the preservation of associations among variables, future evaluation of these methods when estimating a second order relation such as a correlation or regression coefficient would be of interest. However we conjecture that methods that condition on the design information would outperform sample-weighted hot deck methods for these kinds of estimands, as they do for the mean.

The main drawback to creating adjustment cells that stratify on sampling strata as well as other covariate information is that it may lead to a large number of cells, and hence some cells where there are no donors for a case with missing values. With an extensive set of covariates X and Z, imputation based on the multiple regression of Y on X and Z maintains the logic of the suggested approach while accommodating extensive sets of covariates. Specifically, a hot deck approach is to create adjustment cells based on the predicted means from the regression of Y on X and Z, or to generate donors for incomplete cases based on predictive mean matching (Little 1986). For a review of recent extensions of hot deck adjustment cell methods, including predictive mean matching, see Andridge and Little (2008).