Abstract
The present work develops and implements a biomathematical statement of how reciprocal connectivity drives stress-adaptive homeostasis in the corticotropic (hypothalamo-pituitary-adrenal) axis. In initial analyses with this interactive construct, we test six specific a priori hypotheses of mechanisms linking circadian (24-h) rhythmicity to pulsatile secretory output. This formulation offers a dynamic framework for later statistical estimation of unobserved in vivo neurohormone secretion and within-axis, dose-responsive interfaces in health and disease. Explication of the core dynamics of the stress-responsive corticotropic axis based on secure physiological precepts should help to unveil new biomedical hypotheses of stressor-specific system failure.
The stress-responsive hypothalamo-adrenocorticotropic (ACTH)-adrenal (cortisol) axis is critical in initiating life-sustaining adaptive reactions to internal (disease) and external (environmental) stressors. This neuroendocrine ensemble exhibits prominent time-dependent dynamics reflected in vividly pulsatile (ultradian) and 24-h rhythmic (circadian) output (1, 2). Episodic secretion is driven by hypothalamic neuronal pacemakers, which secrete the pituitary signaling peptides CRH (ACTH-releasing hormone) and AVP (arginine vasopressin) (3, 4). These agonists singly and synergistically stimulate ACTH synthesis and secretion (feedforward), which in turn promotes the time-lagged and dose-responsive biosynthesis of cortisol. Cortisol feeds back to inhibit CRH/AVP and ACTH production via time-delayed concentration-dependent (integral) and rapid, rate-sensitive (differential) mechanisms (5). These core physiological linkages mediate a homeostatic (servocontrol) system governed by nonlinear and time-delayed feedforward and feedback signal interchanges. We postulate that such interactive properties generate the observed complex dynamics of this dynamics.
A network-like notion of joint feedforward and feedback control of the ACTH-adrenal axis was adumbrated by Keller-Wood and Yates nearly two decades ago (5), and reinforced subsequently by Liu et al.'s credible indirect estimates of in vivo CRH, ACTH, and cortisol half-lives (6). Here, we extend these fundamental concepts to a multivalent, interactive, dose-responsive, and time-delayed biomathematical model that achieves coupling of circadian and pulsatile outputs. Thereby, we explore six a priori hypotheses of coupling mechanisms to link 24-h periodic (circadian) rhythmicity to pulsatile (ultradian) secretion, and illustrate the utility of a network-like biostatistical formalism to assess dynamic interfaces within an integrative neuroendocrine system.
Methods
Based on a statistically validated interactive model for the feedback/feedforward control of the male reproductive axis (7), here we implement an extended formulation to encompass the unique interactions inherent in the HPA axis (see Appendix). The system-specific details are highlighted below and illustrated schematically in Fig. 1.
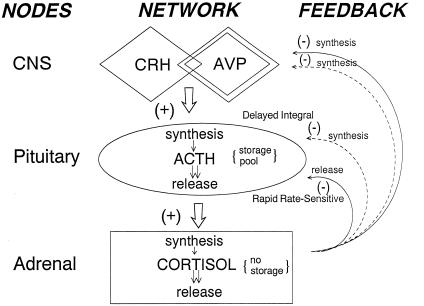
Figure 1.
Schematized core model of the interconnected CRH/AVP (hypothalamo)-ACTH (pituitary)-cortisol (adrenal) stress-adaptive axis. Feedforward and feedback interfaces 1–7 are incorporated via nonlinear dose-responsive (H) functions, which mediate time-lagged rate-sensitive (differential) and concentration-dependent (integral) internodal signaling. In principle, circadian inputs could modulate any of the foregoing interface functions, time-delays, and/or signaling kinetics (see Methods).
CRH/AVP Pulse Generator.
We envision that hypothalamic pulse generators for CRH and AVP drive episodic ACTH release after a slight time delay and poststimulus refractory interval (ref. 8; see Appendix). For simplification, we consider CRH and AVP as a combined feedforward signal, wherein corticotropic synergy is achieved by modifying the joint CRH/AVP dose-response curve (below).
Overview of Model.
Let [XC/V(t), XA(t), XC(t)] designate the evolving hormone concentrations at time t and [ZC/V(t), ZA(t), ZC(t)] denote the corresponding instantaneous hormone secretion rates for CRH/AVP (C/V), ACTH (A), and cortisol (C). Structurally, we also define instantaneous rates of hormone synthesis [SC/V(t), SA(t), SC(t)] and of ACTH release from new synthesis [RA(t)].
Feedback and feedforward between the hormones is incorporated by mathematical interface or dose-response “H” functions. The latter designate (at any instant in time t) how the rate of synthesis of each hormone [e.g., SA(t)] depends in a nonlinear manner on pertinent input by prior concentrations (delayed concentration-sensitive or integral feedback) or prior rates of change of concentrations (rate-sensitive or differential feedback). We use logistic functions to approximate such dose-responsive behavior, assuming a one-dimensional version given by:
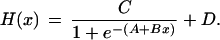 |
Integral feedback is implemented here for CRH/AVP's stimulation of ACTH, ACTH's stimulation of cortisol, and cortisol's inhibition of ACTH synthesis and CRH/AVP synthesis/secretion, whereas rate-sensitive feedback is used to incorporate cortisol's inhibition of ACTH and CRH/AVP release (5).
Pituitary: Feedback- and Feedforward-Controlled Release of ACTH.
To model ACTH production, we assume that (i) the hypothalamo-pituitary portal blood CRH/AVP concentration (pg/ml) exerts a positive time-delayed (0.5–1.5 min before onset) feedforward effect, and the blood cortisol concentration (μg/dl) exerts a negative slow (time-delayed) (30–60 min) feedback effect, on the rate of ACTH synthesis (pg/ml per h; ref. 5); and (ii) the hypothalamo-pituitary portal blood CRH/AVP concentration (pg/ml) exerts a potentially steep time-delayed (0.5–1.5 min before onset) feedforward effect, and the rate of change of blood cortisol concentration exerts a rapid (time-delayed) (5–30 min) feedback action on pituitary ACTH release (pg/ml per h; Fig. 1).
The synergistic effect of CRH and AVP on ACTH synthesis is manifested as an elevation in the upper asymptote of the corresponding H (feedforward) dose-response function. A rapid succession of CRH/AVP pulses outside the refractory window would thus exert both a combined and a supraadditive effect on ACTH synthesis [SA(t)] and release [RA(t)].
Adrenal Gland: Feedforward by ACTH.
We envision a nearly continuous basal rate of cortisol secretion. Blood ACTH concentrations (pg/ml) superimpose time-delayed (10–20 min) feedforward to elevate the rate of adrenal cortisol (C) synthesis and diffusive release (μg/dl per h; Fig. 1). Because ACTH evokes a complex facilitative cascade of second and more distal messengers in the adrenal zona fasciculata, we render such priming by way of a short-lived (5–10 min) left-shift of the ACTH-cortisol dose-response function H5 (increased adrenal sensitivity) with an elevation in its upper asymptote (rise in ACTH efficacy). The delayed sustained effect of ACTH is incorporated via multiplication of the ACTH input into H5 by a linear combination of exponential functions [ΓA(⋅)], as described in ref. 7. Thereby, we emulate the adrenal secretory response observed experimentally.
Hypothalamus: Feedback on CRH/AVP.
The interval-averaged blood cortisol concentration (μg/dl) exerts time-delayed (60–80 min) integral feedback, and the rate of change of blood cortisol concentration imposes rapid (5–30 min) rate-sensitive feedback, on CRH/AVP synthesis/secretion (pg/ml per h; ref. 5, Fig. 1).
The foregoing primary connections do not exclude the existence of other within-axis interactions: e.g., the blood cortisol concentration (μg/dl) might also exert slow (integral) negative feedback on basal ACTH release or the CRH/AVP pulse-firing rate(s) (see Discussion).
Parameters for the Population and Individual.
To represent the diversity among individuals, we allow for variations in in vivo hormone elimination rates, the degree of CRH/AVP synergism and ACTH priming of cortisol synthesis/secretion, the amplitude and phase of the circadian rhythm, and dose-response parameters. Conversely, we consider structural mechanisms, such as the pulse shapes for CRH/AVP and ACTH secretion as populationally defined and relatively consistent among subjects.
Linking Circadian Rhythms to Pulsatile Output.
The above core model addresses (ultradian) pulsatility and feedback/feedforward connections. To explore mechanisms that link the circadian rhythm to such short-term secretory activities, we consider a 24-h periodic internal neural clock (e.g., residing in the suprachiasmatic nucleus), the phase of which is set by relevant internal and environmental cues. Relevant circadian inputs might couple to the pulsatile network via 24-h rhythmic control of: (model 1) the time-delayed negative feedback of cortisol concentrations on hypothalamic CRH and/or AVP synthesis/release (8); (model 2) the rapid rate-sensitive negative feedback of cortisol on the CRH/AVP-stimulated release of ACTH (5); (model 3) ACTH or cortisol's basal secretion rates; (model 4) the feedforward of CRH/AVP on the rate of accumulation of ACTH pulse mass (8, 9); (model 5) the sensitivity and/or maximum of CRH/AVP's dose-responsive stimulation of ACTH secretion, thereby encapsulating changing synergism between AVP and CRH (9, 10); and (model 6) the dose-responsive feedforward of ACTH on adrenal cortisol secretion (11)(see Fig. 1). Other hypotheses could include 24-h variations in cortisol's rapid feedback on CRH/AVP release and/or its integral feedback on hypothalamic CRH/AVP pulse frequency or pituitary ACTH synthesis.
Results
The complex physiological output of the corticotropic axis is illustrated for three healthy men in Fig. 2 (Left column, Top to Bottom), which displays concurrent plasma ACTH and cortisol concentration profiles obtained by sampling blood at 7-min intervals for 24 h. Fig. 2 (Right column, Top to Bottom) depicts computer-assisted simulations using the circadian model of diurnally varying CRH/AVP synergy (model 5 above) to recapitulate both ultradian (pulsatile) and circadian (rhythmic) features.
Figure 2.
(Left Top to Bottom) Paired plasma ACTH (Top) and cortisol (Bottom) concentration time series in three of six healthy young men monitored by sampling blood every 7 min for 24 h. (Right) Computer-assisted simulations of analogously paired ACTH and cortisol concentration profiles, assuming a diurnal variation in hypothalamic CRH/AVP's joint (synergistic) feedforward on pituitary ACTH secretion (see Methods, circadian model 5).
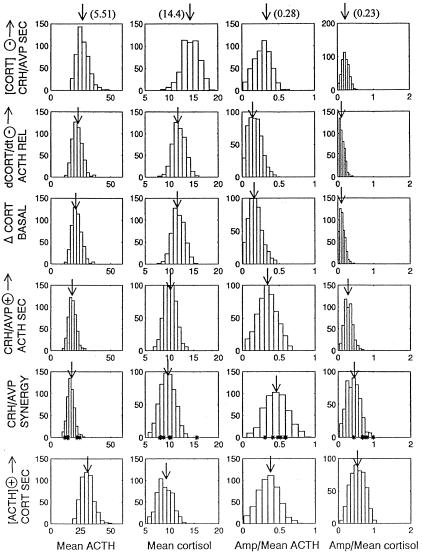
To evaluate circadian-pulsatile linkages (hypotheses 1–6 above) systematically, we shifted the sensitivity of each corresponding H (feedback or feedforward) dose-response curve by smoothly varying the coefficient B in the relevant logistic (interface) functions. Fig. 3 summarizes model-specific histogram predictions (each based on the same initial randomization seed) for 500 realizations. Asterisks in the subpanel for circadian model 5 mark the clinically observed values in six healthy young men. Circadian model 5 (24-h varying CRH/AVP drive on ACTH secretion) and model 6 (a diurnal rhythm in ACTH's feedforward on cortisol production) each predict observed rhythmic properties of this axis (see Discussion).
Figure 3.
Illustrative predictions of six circadian-pulsatile linkage models, represented by 24-h variations in the following: model 1, integral feedback of cortisol on hypothalamic CRH/AVP secretion; model 2, rate-sensitive feedback by cortisol on CRH/AVP-driven pituitary ACTH release; model 3, basal (nonpulsatile) ACTH and cortisol secretion; model 4, CRH/AVP's feedforward drive of corticotrope ACTH accumulation; model 5, CRH/AVP's synergistic stimulation of ACTH secretion; and model 6, ACTH's feedforward on cortisol production. Five hundred simulations were performed at a “sampling” rate of 7 min for 24 h for each model: rows 1–6 (Top to Bottom). Each row of histograms gives the forecasted (24-h) ACTH and cortisol concentrations and their relative (fractional) 24-h variations (ratio of amplitude to mean). Arrows indicate the histogram means. In model 5, asterisks at the base of the histograms mark the individual values observed in six healthy young men (see ACTH and cortisol profiles in Figs. 2, 4, and 5). In parentheses at the top of each column are the means for the six values.
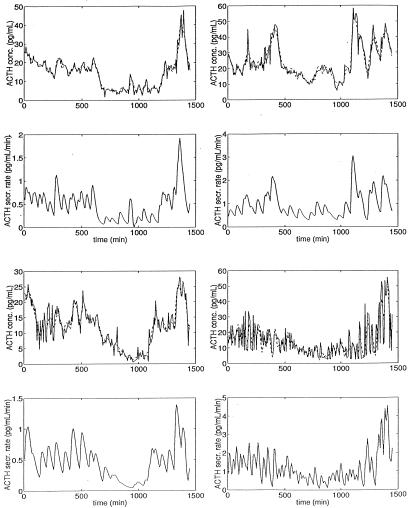
Fig. 4 illustrates model-based fitting of observed plasma ACTH concentration profiles in four young men. Table 1 summarizes predictions of ACTH kinetics and secretory dynamics for all six men so analyzed. Fig. 5 presents an illustrative computer-assisted estimate of the unobserved CRH/AVP pulse signal based on analyzing simultaneously observed plasma ACTH and cortisol concentration time series in one healthy male.
Figure 4.
Illustrative computer-assisted fits (interrupted lines) of four observed diurnal plasma ACTH concentration profiles (top subpanels in each pair) and the corresponding predicted underlying ACTH secretory activity (lower subpanel) in healthy young men sampled every 7 min, as computed by using a linear monohormonal version of pulsatile hormone secretion (see Methods). The rapid half-life of ACTH was approximated as its minimally determinable value, given a sampling rate of 7 min (7 × loge(2) = 4.85 min). Results for all six subjects are summarized in Table 1.
Table 1.
Model-predicted ACTH secretion and kinetics
| Subject no. | Pulse freq., no./24 h | Total secr., ng/liter | Daily basal, ng/liter | Daily pulsatile, ng/liter | Percent basal, % | Mass/pulse, ng/liter | Half-life, min |
|---|---|---|---|---|---|---|---|
| A | 35 | 710 | 40 | 676 | 5.6 | 19 | 28 |
| (250) | (149) | (259) | (7.4) | (21) | (16) | ||
| B | 28 | 1,380 | 350 | 1,020 | 26 | 36 | 24 |
| (900) | (310) | (670) | (13) | (24) | (23) | ||
| C | 30 | 680 | 54 | 630 | 7.8 | 21 | 23 |
| (330) | (170) | (360) | (25) | (12) | (18) | ||
| D | 48 | 1,760 | 2.1 | 1,750 | 0.1 | 37 | 9.8 |
| (690) | (200) | (700) | (12) | (15) | (9.5) | ||
| E | 30 | 1,260 | 490 | 780 | 39 | 26 | 24 |
| (390) | (204) | (220) | (7.4) | (7.5) | (11) | ||
| F | 38 | 1,040 | 126 | 915 | 12 | 24 | 17 |
| (370) | (150) | (390) | (15) | (10) | (10) |
Based on observed plasma ACTH concentration profiles measured by immunoradiometric assay of samples collected every 7 min for 24 h in six healthy young men (Figs. 2 and 4). Half-lives reflect the calculated slow component only. Data are expressed per unit (L) ACTH distribution volume. Parentheses contain the estimated parameter SD (see Methods).
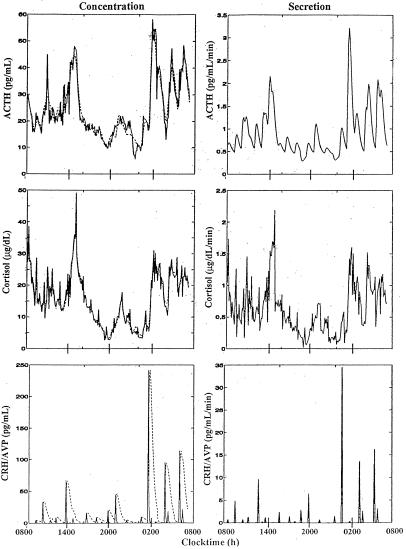
Figure 5.
(Left column) Fitted (observed) plasma ACTH (Top) and cortisol (Middle) concentrations and predicted (unobserved) CRH/AVP (Bottom) concentrations in one healthy young male, sampled every 7 min for 24 h. The dotted line in the Left Bottom subpanel shows the effective CRH/AVP feedforward signal on ACTH synthesis (the effect of ΓC/V). (Right column) Corresponding secretion rates are estimated for ACTH (Top), cortisol (Middle), and the conjoint CRH/AVP signal (Bottom).
Discussion
The present formalism explores the thesis that neuroendocrine ensembles operate homeostatically via organ-specific and time-delayed dose-responsive facilitative or inhibitory interactions (7). To this end, we embody dynamics of the corticotropic axis via a biomathematical model, wherein relevant dose-response interfaces serve to couple changing hypothalamic-pituitary portal venous CRH/AVP concentrations to time-delayed stimulation of corticotrope ACTH biosynthesis and secretion. In turn, varying systemic blood ACTH concentrations drive nonlinear dose-responsive oscillations in cortisol secretion by steroidogenically responsive adrenal zona-fasciculata cells. Biologically available cortisol feeds back on hypothalamic CRH/AVP and pituitary ACTH outputs by way of both delayed (time-integrated) and rapid (rate-sensitive) inhibitory mechanisms (see Methods). We incorporate these dynamic relationships in a core biostatistical construct of coupled stochastic differential equations along with biological variability. The resultant network-like formulation affords an objective, statistically valid, and conceptually tractable basis for predicting corticotropic-axis regulation (below).
To examine the putative neurointegrative mechanisms subserving commingled circadian and ultradian rhythmicity, we first simulated the outcomes of six plausible circadian-pulsatile coupling hypotheses based on earlier studies of the CRH/AVP-ACTH-cortisol feedback axis (1, 2, 5, 6, 8–10). Computer-assisted experiments predicted that 24-h variability in the coupling strength of pituitary ACTH's drive of adrenal cortisol secretion (circadian model 6) can generate diurnal rhythmicity of both cortisol and ACTH release (Fig. 3). CRH/AVP's joint stimulation of ACTH synthesis and secretion (circadian model 5) also engendered nyctohemeral variations in both cortisol and ACTH output. The latter model would accord with preserved circadian ACTH rhythmicity in severely cortisol-deficient (Addisonian) patients (12), and in transgenic CRH knockout mice administered a constant exogenous CRH stimulus (presumptively accompanied by diurnally variable endogenous AVP release) (10). Unvarying CRH stimulation in healthy humans or patients with postoperative Cushing's Disease also sustains cortisol rhythmicity, as plausibly mediated via circadian models 5 or 6. In contrast, four other postulated circadian-ultradian linkage mechanisms (e.g., 24-h rhythmic changes in cortisol's rapid or delayed negative feedback on CRH/AVP or ACTH production) failed to capture expected nyctohemeral ACTH and cortisol changes. Because the foregoing analyses evaluated single linkage mechanisms only, further study of joint coupling models and their presumptive pathophysiological disruptions will also be important hereafter.
The current statistically founded network-like ensemble (Fig. 1) recreates stable and pulsatile and circadian patterns of ACTH and cortisol secretion (Fig. 2). The resultant output also exhibits subordinate (higher frequency) variations, which emerge from the complex dynamics of nonlinear and time-varying feedback and feedforward signaling among regulatory nodes, as predicted from simpler reductionistic mathematical models (13).
The present biomathematical construct also allows estimation of ACTH and cortisol secretion rates and their respective in vivo kinetics, conditional on the inferred pulse times (Fig. 4, Table 1). To extend this notion, we illustrate the combined assessment of ACTH and cortisol secretory behavior and CRH/AVP pulse times based on simultaneous measurements of two of the three signals (Fig. 5). Thereby, one could begin to estimate in vivo dose-response interface functions, while accounting correctly for full-system interactions and variability (7).
The complexity of corticotropic-axis control includes putative gender differences in the ACTH-cortisol dose-response relationship, hypothalamic CRH/AVP rhythmicity, and cortisol feedback sensitivity (14). A formalized combined feedback and feedforward model should offer the basis for further exploration of the network-level implications of such sex differences. Analogously, semiquantitative modeling should aid in appraising the causes and consequences of disruption of selected neuroendocrine dose-response functions in infancy, aging, stress, and disease by complementing clinical intuition. Indeed, intuitive perspectives of dynamic axis behavior are difficult to validate or refute otherwise, given the multivalent, time-lagged, nonlinear dose-responsive and integral and rate-sensitive feedback properties of this homeostatic system. Such statistical analyses will pose new analytical challenges and may require novel experimental data (5–7, 15).
Whereas the current biostatistical construct of CRH/AVP-ACTH-adrenal dynamics incorporates certain core feedback interactions as presently understood, further hypothalamic and extrahypothalamic regulatory inputs will also be important to consider later; e.g., independent CRH and AVP feedforward signaling, autofeedback by CRH and/or AVP, corticolimbic feedback inputs, and intrapituitary or intraadrenal paracrine regulation (3, 4, 8, 9–12, 16). A practicable and valid model structure is essential in considering such enhancements. Second, certain stressors applied during the neonatal period influence responsivity of the adult CRH/AVP-ACTH-adrenal axis; e.g., maternal separation during a critical interval in infancy strongly modulates later stress reactivity in the adult (17). A suitable basic model formulation should aid in the later exploration of mechanisms underlying such longer-term neuroregulatory adaptations. Third, the corticotropic axis often exhibits different homeostatic adjustments to an acute versus chronic stressor (18, 19). This plasticity could point to time-dependent “resetting” of selected physiological feedforward or feedback parameters. A relevant interactive model should find utility in examining such hypotheses. Fourth, neuroendocrine axes that regulate stress, growth, reproduction, and metabolism typically interact; e.g., AVP and CRH also negatively regulate the reproductive-axis neuronal pulse generator or somatotropin secretion (20). Such between-axis linkages likely facilitate organismic adaptations to environmental stressors, but their mechanistic coupling has been difficult to formalize. Fifth, certain stress contexts unmask threshold-like responses of the ACTH-adrenal axis, whereas others unveil gradual neurointegrative changes (5, 8). Understanding putative “jump” mechanisms (rather than continuous dose-responsiveness) is stymied currently by limited quantitative undergirdings. And, lastly (ultra), short-loop feedback interactions are implicit in many biological systems, including the corticotropic axis; e.g., ACTH and/or beta-endorphin can inhibit, whereas enkephalins can stimulate, CRH secretion (21). A more comprehensive biomathematical formalism should aid in examining the physiological implications of such short-loop regulatory effects.
In summary, the present analyses implement and explore the dynamics of an interactive (network-like) biomathematical formulation of the complex but autonomously regulated CRH/AVP-ACTH-adrenal axis, as inferred clinically and experimentally from studies of single components in isolation. This new formalism embodies expected within-axis physiological linkages via time-delayed, nonlinear, dose-responsive, rate-sensitive, and integral feedforward and feedback controls. The ensemble features generate realistic pulsatile, 24-h rhythmic and subordinate (pattern-sensitive) modes of ACTH, cortisol, and CRH/AVP secretion, and allow computer-assisted predictions and hypothesis testing. The foregoing biostatistical encapsulation predicts that certain putative mechanisms of ultradian-circadian coupling are more likely than others to generate the jointly 24-h rhythmic release of ACTH and cortisol observed in vivo. Accordingly, biostatistical tools of this evolving genre should help fuel novel insights into the adaptive physiology and pathophysiology of the CRH/AVP-ACTH-cortisol axis and other complex homeostatic neuroendocrine systems.
Acknowledgments
Support for this work was provided by the University of Virginia Center for Biomathematical Technology, National Institutes of Health General Clinical Research Center Grant M01 RR00847, National Institute on Aging Grant R01 AG14799, and the Specialized Cooperative Center for Reproduction Research (U54 National Institute of Child Health and Human Development Grant HD28934).
Abbreviations
- ACTH
adrenocorticotropic hormone
- CRH
ACTH-releasing hormone
- AVP
arginine vasopressin
Appendix
We assume that CRH/AVP signaling dictates the pulse times
for ACTH after a finite time delay τA,
reflecting hypothalamo-pituitary portal blood transit, and a
poststimulus refractory interval, rA,
when further CRH/AVP inputs are ignored. Thus, there will be two
corresponding sets of pulse times:
T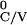 ,
T
,
T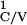 ,
T
,
T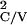 , … and
T
, … and
T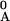 , T
, T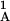 ,
T
,
T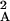 , … , where
T
, … , where
T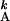 = [Minj
{T
= [Minj
{T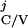 |T
|T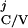 ≥ T
≥ T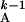 +
rA}] + τA,
with T
+
rA}] + τA,
with T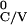 ≤ 0,
T
≤ 0,
T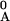 =
T
=
T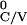 +
τA. Let N(t) denote the
counting process associated with the ACTH pulse times. Here, we view
the pulse times as a Weibull renewal process (15), where λ is a rate
parameter (number of pulses/day) parameter and γ controls the
regularity of interpulse interval lengths. Then, the conditional
probability densities for
T
+
τA. Let N(t) denote the
counting process associated with the ACTH pulse times. Here, we view
the pulse times as a Weibull renewal process (15), where λ is a rate
parameter (number of pulses/day) parameter and γ controls the
regularity of interpulse interval lengths. Then, the conditional
probability densities for
T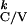 given
T
given
T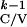 are given by:
are given by:
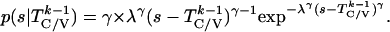 |
We denote a time-averaged feedback signal at time t with time delay (l1,l2) by:
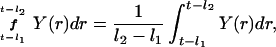 |
where Y(r) is either a hormone concentration or its rate of change at time r. In what follows, the subscripted numerics 1–7 for the interface (H) functions denote corresponding feedback/feedforward interactions (see Fig. 1): viz., ACTH synthesis (subscript 1,2) and release (subscript 3,4) are each joint functions of time-delayed CRH/AVP feedforward and slow and rapid cortisol feedback signals, respectively. CRH/AVP synthesis is analogously controlled jointly by respectively rapid and slow cortisol feedback (subscript 6,7). In refs. 7 and 15, we show that the mathematical effect of cascading target-tissue reactions to a signal input is the multiplication of the initial feedback/feedforward signal by a linear combination of exponential functions, denoted by ΓC/V(⋅) and ΓA(⋅), which allows ongoing glandular responses after the signal is withdrawn. Let ψA(·) and ψC/V(·) represent the normalized rates of secretion per unit mass per unit distribution volume per unit time; these rates are presently modeled as 3-parameter generalized gamma densities (7, 15). Accordingly, synthesis (S), release (R), accumulation (A), and fractional mass remaining for later secretion (Ψ) are given as:
 |
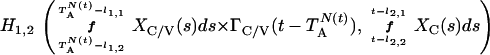 |
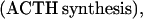 |
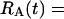 |
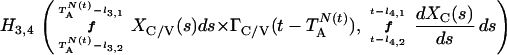 |
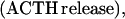 |
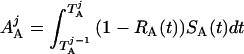 |
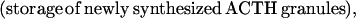 |
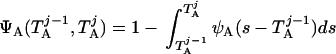 |
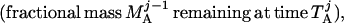 |
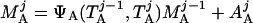 |
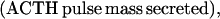 |
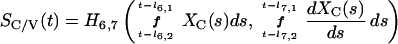 |
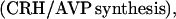 |
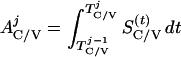 |
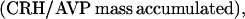 |
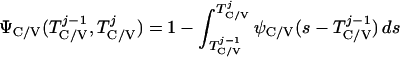 |
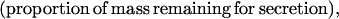 |
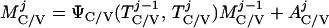 |
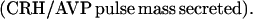 |
Based on the above constructions, the corresponding interactively controlled rates of secretion are given as:
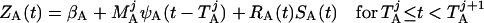 |
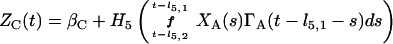 |
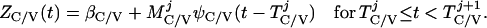 |
Secreted molecules undergo combined diffusion and advection in the
bloodstream at very rapid rates (short half-life component,
α1) and are removed more slowly but
irreversibly (long half-life component, α2). If
Vi is the assumed distribution volume for hormone i
(i = C/V, A, C), we here approximate Vi in
the human as: 1/2 ml for each of CRH and AVP, 3.5–5 liters for ACTH,
and 7–8 liters for cortisol. If incremental secretion
ViZi(t)dt
enters two (statistical) compartments with respective distributional
volumes of V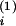 and
V
and
V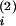 (Vi =
V
(Vi =
V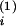 +
V
+
V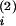 and
a
and
a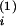 and proportional contents
a
and proportional contents
a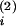 = 1 −
a
= 1 −
a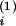 , then
V
, then
V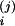 Z
Z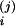 (t)dt
=
a
(t)dt
=
a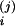 ViZi(t)dt,
(j = 1,2, i = C/V, A, C). Here, we
approximate a
ViZi(t)dt,
(j = 1,2, i = C/V, A, C). Here, we
approximate a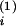 = 0.33,
a
= 0.33,
a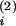 = 0.67, i =
C/V, A, C (1, 3, 16–18). The solution of the above (assuming
V
= 0.67, i =
C/V, A, C (1, 3, 16–18). The solution of the above (assuming
V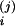 X
X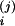 (0)
=
a
(0)
=
a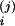 Xi(0),
with Xi(0) being specified (initial condition) for
i = C/V, A, C) is:
Xi(0),
with Xi(0) being specified (initial condition) for
i = C/V, A, C) is:
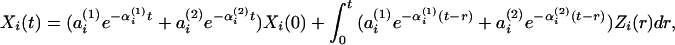 |
which takes the form of a biexponential elimination rate. In the context of the above formulation, we have explicitly modeled the secretion rates Zi(⋅), i = C/V, A, C, based on known physiological structure (Fig. 1). One can allow for additional biological variability as, e.g., because of within- and among-cell heterogeneities in the instantaneous rate of production of each hormone, as well as turbulent admixing and diffusion of hormone molecules in the blood, by including relevant terms for such variabilities (7).
What one then observes is a discrete-time sampling of these processes, plus joint uncertainty because of blood withdrawal, sample processing, and hormone measurement errors, ɛi(k):
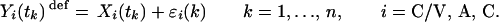 |
References
- 1.Weitzman E D, Fukushima D, Nogeire C, Roffwarg H, Gallagher T F, Hellman L. J Clin Endocrinol. 1971;33:14–22. doi: 10.1210/jcem-33-1-14. [DOI] [PubMed] [Google Scholar]
- 2.Loudon A S I, Wayne N L, Krieg R J, Iranmanesh A, Veldhuis J, Menaker M. Endocrinology. 1994;135:712–718. doi: 10.1210/endo.135.2.8033819. [DOI] [PubMed] [Google Scholar]
- 3.Rivier J, Spiess J, Vale W W. Proc Natl Acad Sci USA. 1983;80:4851–4855. doi: 10.1073/pnas.80.15.4851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Vale W W, Spiess J, Rivier C, Reivier J. Science. 1981;213:1394–1397. doi: 10.1126/science.6267699. [DOI] [PubMed] [Google Scholar]
- 5.Keller-Wood M E, Yates F E. Endocr Rev. 1984;5:1–24. doi: 10.1210/edrv-5-1-1. [DOI] [PubMed] [Google Scholar]
- 6.Liu B, Zhao Z, Chen L. J Biol Phys. 1980;7:221–233. [Google Scholar]
- 7.Keenan D, Sun W, Veldhuis J D. Soc Ind Appl Math J Appl Math. 2000;61:934–965. [Google Scholar]
- 8.Alexander S L, Irvine C H, Donald R A. Front Neuroendocrinol. 1996;17:1–50. doi: 10.1006/frne.1996.0001. [DOI] [PubMed] [Google Scholar]
- 9.De Bold D R, Jackson R V, Sheldon W R, Jr, Island D P, Orth D N. J Clin Endocrinol Metab. 1986;61:273–279. doi: 10.1210/jcem-61-2-273. [DOI] [PubMed] [Google Scholar]
- 10.Muglia L J, Jacobson L, Weninger S C, Luedke C E, Bae D S, Jeong K H, Majzoub J A. J Clin Invest. 1997;99:2923–2929. doi: 10.1172/JCI119487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kaneko M, Kaneko K, Shinsako J, Dallman M F. Endocrinology. 1981;109:70–75. doi: 10.1210/endo-109-1-70. [DOI] [PubMed] [Google Scholar]
- 12.Graber A L, Givens J R, Nicholson W E, Island D P, Liddle G W. J Clin Endocrinol Metab. 1965;25:804–807. doi: 10.1210/jcem-25-6-804. [DOI] [PubMed] [Google Scholar]
- 13.Pincus S M. Math Biosci. 1994;122:161–181. doi: 10.1016/0025-5564(94)90056-6. [DOI] [PubMed] [Google Scholar]
- 14.Roelfsema F, Van den Berg G, Frolich M, Veldhuis J D, van Eijk A, Buurman M M, Etman B H B. J Clin Endocrinol Metab. 1993;77:234–240. doi: 10.1210/jcem.77.1.8392084. [DOI] [PubMed] [Google Scholar]
- 15.Keenan D M, Veldhuis J D. Am J Physiol. 1997;275:E157–E176. doi: 10.1152/ajpendo.1998.275.1.E157. [DOI] [PubMed] [Google Scholar]
- 16.Hiroshige T, Abe K, Wada S, Kaneko M. Neuroendocrinology. 1973;11:306–320. doi: 10.1159/000122142. [DOI] [PubMed] [Google Scholar]
- 17.Plotsky P M, Meaney M J. Brain Res Mol Brain Res. 1993;18:195–200. doi: 10.1016/0169-328x(93)90189-v. [DOI] [PubMed] [Google Scholar]
- 18.Rivier C, Vale W W. Endocrinology. 1987;121:1320–1328. doi: 10.1210/endo-121-4-1320. [DOI] [PubMed] [Google Scholar]
- 19.Plotsky P M, Bruhn T O, Vale W W. Endocrinology. 1985;117:323–329. doi: 10.1210/endo-117-1-323. [DOI] [PubMed] [Google Scholar]
- 20.Rivier C, Vale W W. Endocrinology. 1984;114:914–919. doi: 10.1210/endo-114-3-914. [DOI] [PubMed] [Google Scholar]
- 21.Plotsky P M. Fed Proc. 1985;44:207–213. [PubMed] [Google Scholar]