Abstract
Motivation: Pinpointing genes that underlie human inherited diseases among candidate genes in susceptibility genetic regions is the primary step towards the understanding of pathogenesis of diseases. Although several probabilistic models have been proposed to prioritize candidate genes using phenotype similarities and protein–protein interactions, no combinatorial approaches have been proposed in the literature.
Results: We propose the first combinatorial approach for prioritizing candidate genes. We first construct a phenome–interactome network by integrating the given phenotype similarity profile, protein–protein interaction network and associations between diseases and genes. Then, we introduce a computational method called MAXIF to maximize the information flow in this network for uncovering genes that underlie diseases. We demonstrate the effectiveness of this method in prioritizing candidate genes through a series of cross-validation experiments, and we show the possibility of using this method to identify diseases with which a query gene may be associated. We demonstrate the competitive performance of our method through a comparison with two existing state-of-the-art methods, and we analyze the robustness of our method with respect to the parameters involved. As an example application, we apply our method to predict driver genes in 50 copy number aberration regions of melanoma. Our method is not only able to identify several driver genes that have been reported in the literature, it also shed some new biological insights on the understanding of the modular property and transcriptional regulation scheme of these driver genes.
Contact: ruijiang@tsinghua.edu.cn
1 INTRODUCTION
Although the past few decades have evidenced many successful stories of identifying genetic variants that underlie human inherited diseases through statistical methods such as linkage analysis and association studies (Botstein and Risch, 2003), uncovering genes that are truly associated with these diseases from susceptibility genetic regions obtained by these statistical analyses still remain as a great challenge and appeal for the development of effective computational methods (Glazier et al., 2002; Lander and Schork, 1994).
To tackle this problem, several approaches have been proposed from the viewpoint of one-class novelty learning. For example, the ‘guilt-by-direct-association’ principle suggests ranking candidate genes in a susceptibility region according to their relevance to genes that are already known as associated with the disease under investigation. Based on this principle, a wide variety of information, including protein sequences (Adie et al., 2005; Aerts et al., 2006), gene expression profiles (Aerts et al., 2006; Franke et al., 2006; van Driel et al., 2003), functional annotations (Franke et al., 2006; Freudenberg and Propping, 2002; Perez-Iratxeta et al., 2002; Turner et al., 2003), literature descriptions (Aerts et al., 2006; Gaulton et al., 2007; van Driel et al., 2003), protein–protein interactions (PPI) (Aerts et al., 2006; Franke et al., 2006; Kohler et al., 2008; Oti et al., 2006) and many others (Oti and Brunner, 2007), has been used to facilitate the prioritization of candidate genes.
Recently, a number of studies have also suggested the ‘guilt-by-indirect-association’ principle, which resorts to the modular nature of human genetic diseases (Goh et al., 2007; Lim et al., 2006; Oti and Brunner, 2007; van Driel et al., 2006; Wagner et al., 2007; Wood et al., 2007) and utilizes PPI information and similarities between disease phenotypes with a variety of computational models to infer genes that are truly associated with diseases (Lage et al., 2007; Li and Patra, 2010; Vanunu et al., 2010; Wu et al., 2008, 2009). For example, Lage et al. proposed a Bayesian model to integrate PPI and phenotype similarities (Lage et al., 2007). Wu et al. developed a regression model to explain phenotype similarities using gene proximities (Wu et al., 2008). Wu et al. (2009) also proposed to align the phenotype network against the PPI network. Li and Patra utilized a random walk model called an RWRH to simulate the stationary distribution of the strength of associations for genes (Li and Patra, 2010). Vanunu et al. (2010) proposed a network propagation method called PRINCE to mimic the sharing of disease status among genes. These recent methods not only exhibit the state-of-the-art performance, but also open the possibility of identifying genes that are responsible for diseases, whose genetic bases are completely unknown.
The success of the above methods relies largely on the use of PPI networks for estimating functional similarities between genes (Wu et al., 2008). The functional similarities between a pair of genes are typically measured by using the shortest path between genes in a PPI network (Dezso et al., 2009; Managbanag et al., 2008; Sharan et al., 2007; Sun and Zhao, 2010). Since the shortest path measure considers only a single optimal path between a pair of genes and overlooks all other paths, the reliability of the optimal path and the robustness of the resulting method may therefore be adversely affected. Moreover, most of the above methods are based on probabilistic models, which are typically very computation intensive. On the other hand, although it has been demonstrated before that the effect of a gene on its associated diseases may ‘propagate’ through connections in a PPI network to other genes and eventually contribute to the status of associations between these genes and the diseases (Schadt, 2009; Taylor et al., 2009; Vanunu et al., 2010), systematic studies on this notion from the viewpoint of combinatorial optimization have not yet been reported in the literature.
Motivated by these observations, we propose a novel combinatorial approach for prioritizing candidate disease genes in this paper. Our approach first constructs a phenome–interactome network by integrating the given phenotype similarity profile, PPI network and associations between diseases and genes. Then, we model the strength of association between a query disease and a candidate gene using the amount of information that can flow from the disease to the gene, and we develop a method called MAXIF that maximizes the information flow in the phenome–interactome network to prioritize candidate genes in susceptibility genetic regions. We show the competitive performance of our method through a series of carefully designed cross-validation experiments and comparison with the state-of-the-art methods in the literature, and we demonstrate its robustness to the parameters introduced. As an example case study, we describe a successful application of our method in predicting driver genes in 50 copy number aberration (CNA) regions of melanoma.
2 METHODS
2.1 Construction of the phenome–interactome network
The phenome–interactome network is constructed by integrating a phenotype similarity profile, a PPI network and known associations between genes and diseases.
First, the phenotype similarity profile, represented as a matrix of similarity scores between 5080 human disease phenotypes, is obtained from the literature (van Driel et al., 2006). Since most small similarity scores in this profile are likely to be noise and only high scores have clear biological meanings (van Driel et al., 2006), we introduce a threshold α and only keep similarity scores that are greater than or equal to this threshold. Consequently we obtain a weighted phenotype similarity network, in which vertices are disease phenotypes and weighted edges indicate similarity scores between the vertices incident to the edge. We refer to this phenotype similarity network as the phenome. Second, the PPI network is obtained from release 9 of the Human Protein Reference Database (HPRD) (Peri et al., 2003). After removing duplications and self-linked interactions, we obtain 37 064 manually curated interactions between 9515 human genes. We refer to this PPI network as the interactome. Third, we use the tool BioMart (Smedley et al., 2009) to extract 2496 known associations that involve 1460 genes in the interactome and 1609 diseases in the phenome.
With these data sources, we construct the phenome–interactome network as a heterogeneous network, whose vertices include all diseases in the phenome and all genes in the interactome, and whose edges include all edges in the phenome, all interactions in the interactome and all known associations between diseases in the phenome and genes in the interactome. We further specify for each edge in the phenome–interactome network a capacity value, a real number that indicates our confidence on the connection between the vertices incident to the edge. For each edge in the phenome, we define its associated similarity score as its capacity. For each edge between the phenome and the interactome, we define its capacity as β , a real number ranging from 0 to the positive infinity. For each edge in the interactome, we define its capacity as γ, a real number ranging from 0 to the positive infinity. By default, we set the values of the parameters as α=0.3, β=10 000 (in lieu of the positive infinity) and γ=1. With these definitions, the phenome–interactome network is denoted as an undirected graph G=(V,E), where V is the set of vertices and E is the set of edges. Each edge (u, v) has a positive capacity value c(u, v) as defined above.
2.2 Maximizing the information flow to prioritize candidate genes
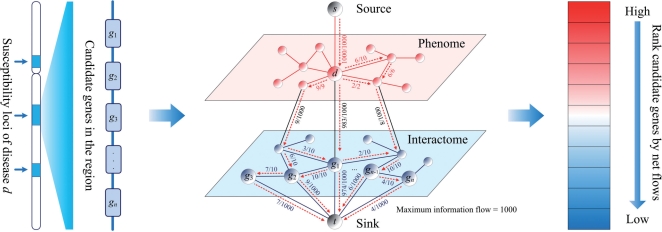
Our objective is to uncover genes that are associated with a query disease of interest from a set of candidate genes. For this purpose, we introduce a method called MAXimum Information Flow (MAXIF) that makes use of the phenome–interactome network to calculate an association score for each candidate gene, and then ranks the candidate genes according to their scores. We illustrate MAXIF in Figure 1 and present the details below.
Fig. 1.
Illustration of the MAXIF method. The phenome–interactome network is constructed by integrating the given phenotype similarity profile, PPI network and associations between diseases and genes. By maximizing the information flow in the phenome–interactome network, the strength of association between a query disease and a candidate gene is calculated as the net flow leaving the gene. Candidate genes are then prioritized according to their association strength scores. The numbers on each edge indicate the flow/capacity values of the edge. Only flows with positive values are shown.
The input of our method includes a query disease d, a set of candidate genes S and the phenome–interactome network G=(V, E) with capacity c(u, v) assigned to each pair of vertices. We first convert the undirected network G into a directed graph G′ by treating each undirected edge (u, v)∈E as two distinct directed edges (u, v) and (v, u). The resulting directed graph is then G′=(V, E′) with E′={(u, v):(u, v)∈E}∪{(v, u):(u, v)∈E} being the set of directed edges. We further define the capacity function c′ in this directed graph as c′(u, v)=c′(v, u)=c(u, v) if (u, v)∈E. Then, we incorporate a source vertex s and introduce a directed edge of infinite capacity pointing from the source sto the vertex corresponding to the query disease (i.e. d). Similarly, we incorporate a sink vertex t and introduce for each candidate gene u∈S, a directed edge of infinite capacity pointing from vertex u to the sink t. Finally, we obtain a directed graph G″=(V″, E″), where V″=V∪{s,t} and E″=E′∪{(s, d)}∪{(u, t): u∈S}. We further define the capacity function c″ as c″(u, v)=c′(u, v) for all (u, v)∈E′, c″(s, d)=∞ and c″(u, t)=∞ for all u∈S.
It is obvious that the graph G″=(V″, E″) is a flow network if both the phenome and interactome are connected, and there is at least one known association between each gene in the interactome and some disease in the phenome (in order to ensure that every vertex lies on some path from the source to the sink). Specially, we refer to G″ as an information flow network, and we define an information flow in such a network as a real-valued function f:V″×V″→ℝ. We interpret an information flow f as a scheme of distributing the total amount of information injected from the source s over all edges in the flow network G″ such that the total amount of information leaving the source is equal to the total amount of information entering the sink. In other words, |f|=Σv∈V″f(s,v)=Σu∈V″f(u,t), where |f| is referred to as the value of flow f. Moreover, we require that an information flow f should satisfy (i) capacity constraint [i.e. f(u,v)≤c″(u,v) for all u, v∈V″]; (ii) skew symmetry [i.e. f(u,v)=−f(v,u) for all u, v∈V″] and (iii) flow conservation [i.e. Σv∈V″ f(u,v)=0 for all u∈V″−{s, t}]. It is clear that the total information that can be injected from the source is determined by the value of the information flow [i.e. |f|=Σv∈V″f(s,v)] in the network. Therefore, the flow with the maximum value is of particular interest, because such a flow allows the maximal possible injection of information from the source. Following the literature (Andrew and Goldberg, 1998), a flow with the maximum value can be efficiently calculated using the push-relabel or the binary blocking flow algorithm. Note that when using this algorithm, we have to multiply all capacities in the flow network by a large number (e.g. 10 000) and round the resulting capacities to integers.
Once the maximum information flow f* has been calculated, we define for each candidate gene vertex u∈S the total amount of net flow leaving u as |fu+|=Σv∈V″,f(u,v)>0f*(u,v) and we use the value of this positive flow as a score to indicate the strength of the association between u and the query disease d. Furthermore, we can rank all candidate genes according to their scores to obtain a ranked list.
The proposed MAXIF method can be easily modified to meet the requirement of other applications in the study of relationships between diseases and genes. For example, as an inverse problem of prioritizing candidate genes, biologists may be interested in fixing a query gene and ranking a set of candidate diseases according to the possibility that the query gene is associated with the diseases. To solve this problem, we can simply construct the information flow network from the phenome–interactome network by again introducing a source, a sink, a directed edge of infinite capacity pointing from the source to the query gene and a set of directed edges of infinite capacity pointing from candidate diseases to the sink. With this construction and the efficient algorithm for solving the maximum-flow problem, we can conveniently obtain association scores for candidate diseases as the total amount of net flow leaving the diseases and then rank the diseases according to their scores.
2.3 Validation methods and evaluation criteria
We perform two leave-one-out cross-validation experiments to examine the capability of our method in uncovering genes that are known to be associated with certain diseases (i.e. disease genes) from a set of candidates. First, in the validation against random genes, we take a known association between a gene and a disease in each run, assume the association is unknown and prioritize the gene against a set of 99 control genes that are selected at random from all genes in the interactome. Second, in the validation against a linkage interval, we select control genes in each validation run as all genes that are located within the 10 Mb region centered around the disease gene under consideration.
It is possible that a disease is associated with multiple genes. This situation is common for complex diseases. Intuitively, the inclusion of known relationships between a query disease and all its associated genes may facilitate the identification of novel genes that are associated with the disease. To eliminate such a confounding factor, we perform ab initio predictions to examine the capability of our method in discovering genes that are associated with a disease whose genetic basis is completely unknown. Specifically, in an ab initio prediction, we consider a known association between a gene and a disease, assume the association is unknown and prioritize the gene against a set of control genes. In this procedure, we also remove all known associations between the disease and other genes. Similar to the leave-one-out cross-validation experiments, we also use two control sets, random genes and a linkage interval.
To examine the performance of our method in prioritizing candidate diseases for a fixed query gene, we perform the following leave-one-out cross-validation experiment. In each validation run, we take a known association between a gene and a disease, assume the association is unknown and prioritize the disease against a set of 99 diseases that are selected at random from all diseases in the phenome. Again, to eliminate the potential confounding factor caused by known associations between a disease and multiple genes, we also perform the ab initio prediction experiment.
We will use three measures to evaluate the performance of the proposed method. Taking the cross-validation against random genes as an example, after each validation run, we are able to obtain a ranked list. We then calculate rank ratios of genes by dividing their ranks with the number of genes in the list. For a set of validation runs, we can then calculate the following measure. First, we calculate the proportion of top ranking disease genes and call this measure the precision (PRE). Second, we calculate the mean rank ratio (MRR) of all disease genes as the average of rank ratios of all disease genes in the validation runs. Third, given a threshold of rank ratio, we calculate the sensitivity as the fraction of disease genes ranked above the threshold and the specificity as the fraction of control genes ranked below the threshold. Varying the threshold value from 0.0 to 1.0, we are able to draw a receiver operating characteristic (ROC) curve and further calculate the area under this curve (AUC). Obviously, larger PRE/AUC values and smaller MRR value indicate higher performance of a prioritization method.
3 RESULTS
3.1 Performance of the proposed method
Under the default parameter setting (α=0.3, β=10 000 and γ=1), we obtain a heterogeneous phenome–interactome network that is composed of 1609 diseases, 9515 genes and 209 983 edges (169 973 between diseases, 37 064 between genes and 2946 between diseases and genes). Using this network, we examine the performance of the proposed method in uncovering disease genes from a set of candidate genes.
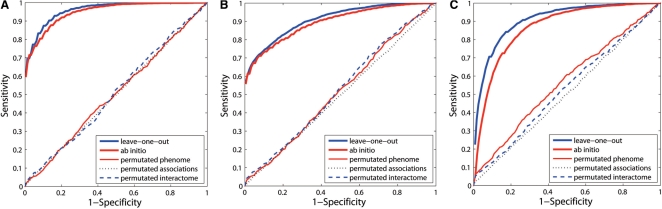
We perform leave-one-out cross-validation experiments against random genes and a linkage interval, and evaluate the results in terms of AUC, PRE and MRR as described above. The results are presented in Figure 2A and B and Table 1 (the column under 0.3), from which we can see that the proposed method is effective in uncovering known associations between genes and diseases. For example, in the leave-one-out cross-validation against a linkage interval, an AUC score is as high as 95.66%, PRE is as high as 60.14% and an MRR is as low as 3.88%. In the validation against random genes, the AUC score is 90.76%, PRE is 56.89% and the MRR is 10.02%.
Fig. 2.
Performance of the proposed method. (A) ROC curves for validation experiments against a linkage interval. (B) ROC curves for validation experiments against random genes. (C) ROC curves for validation experiments against random diseases.
Table 1.
Robustness of the method with respect to the parameter α (with β=10 000 and γ=1) in leave-one-out cross-validation experiments
| 0.1 (%) | 0.2 (%) | 0.3 (%) | 0.4 (%) | 0.5 (%) | |
|---|---|---|---|---|---|
| Linkage interval | |||||
| AUC | 94.56 | 94.57 | 95.66 | 94.68 | 95.57 |
| PRE | 65.06 | 65.06 | 60.14 | 64.38 | 64.46 |
| MRR | 5.15 | 5.15 | 3.88 | 4.84 | 4.20 |
| Random genes | |||||
| AUC | 88.73 | 89.64 | 90.76 | 88.49 | 82.93 |
| PRE | 63.03 | 62.96 | 56.89 | 51.18 | 47.76 |
| MRR | 12.03 | 11.12 | 10.02 | 12.27 | 14.84 |
| Random diseases | |||||
| AUC | 87.76 | 87.73 | 90.65 | 88.45 | 86.07 |
| PRE | 17.95 | 19.03 | 22.44 | 23.52 | 22.24 |
| MRR | 12.84 | 12.20 | 9.47 | 11.61 | 12.98 |
To eliminate the potential confounding effect caused by the association between a disease and multiple genes, we perform ab initio prediction experiments against random genes and a linkage interval, and present the results in Figure 2A and B. We can see from this figure that the proposed method is also effective in uncovering known associations between genes and diseases, even for diseases whose genetic basis is completely unknown. (Recall that in the ab initio prediction, we completely remove all known associations between the query disease and other genes.) For example, in the ab initio prediction against a linkage interval, the AUC score is as high as 94.60%, PRE is as high as 59.46% and the MRR is as low as 4.67%. In the validation against random genes, the AUC score is 89.26%, PRE is 55.69 and MRR is as low as 13.57%. It is not surprising that the performance of the ab initio results are somewhat lower than the corresponding leave-one-out cross-validation results, since the inclusion of genes that are already known to be associated with the query disease should facilitate the discovery of additional genes associated with the disease. However, we can still see the effectiveness of the proposed method in this (more strict) ab initio prediction experiments. In other words, the proposed method is capable of uncovering genes that are associated with diseases, whose genetic bases are completely unknown. This is important because, according to the OMIM database, the genetic bases for about half of the diseases are completely unknown. Our method can then be used to predict potential associations between genes and these diseases.
To meet the requirement of the applications whose objective is to identify for a fixed query gene all diseases with which the gene might be associated, we perform both the leave-one-out cross-validation and ab initio prediction against random diseases. The results are presented in Figure 2C, from which we can see the effectiveness of the proposed method in identifying diseases that are associated with the given query gene. For example, in the leave-one-out cross-validation, the AUC score is as high as 90.65%, PRE is as high as 22.44% and the MRR is as low as 9.47%.
The above validation results demonstrate that the proposed method can successfully rank the gene that is truly associated with the query disease at the top among all the candidates. It would be interesting to know if the correct prioritization is really due to the connectivity information included in the phenome–interactome network (instead of some biases present in the network). For this purpose, we perform three permutation experiments by (i) shuffling interactions in the phenome while fixing the degree (i.e. number of neighbours of each vertex) distribution of the network, (ii) shuffling interactions between diseases and genes while fixing the number of associated genes for each of the diseases and (iii) shuffling the interactome while fixing the degree distribution of the network. We repeat the leave-one-out cross-validation experiments using the shuffled networks and present the results in Figure 2. The AUC scores are all around 50% in the figure, and we therefore conclude that the above successful prioritization of candidate genes is indeed due to the informative interactions that are included in the phenome–interactome network.
3.2 Robustness of the proposed method
There are three parameters in the process of constructing the phenome–interactome network. The parameter α , ranging from 0 to 1, determines the minimum meaningful similarity score between two diseases, and thus controls the sparsity of the phenome. The parameter β , ranging from 0 to the positive infinity, determines the capacity values corresponding to associations between diseases and genes and thus controls the amount of information that can be pumped from the phenome to the interactome, or vice versa. The parameter γ , ranging from 0 to the positive infinity, determines the capacity of each edge in the interactome and thus controls the information that can flow from genes to genes. Obviously, enumerating all possible combinations of these parameters is prohibitive. We therefore study the effect of each parameter individually, while fixing the other parameters in a test.
We first plot the histogram of the similarity scores between diseases and find that the probability density of the similarity scores has a clear positive skewness, indicating that most scores tend to be small. Hence, we conclude that the parameter α should not be set too small for the purpose of filtering out noise in the phenome. We then perform a grid search on α from 0.1 to 0.5 with step 0.1, and present the results in Table 1. From the table, we can see that the proposed method is robust with respect to this parameter. For example, when different values of α are applied, the AUC score fluctuates within a 1.1% band in the leave-one-out cross-validation against a linkage interval. In the validation against random genes, the AUC score fluctuates within a 2.3% band when α is <0.5. However, it shows a significant drop of about 8% when α reaches 0.5. In the validation against random diseases, we observe the similar trend. From these observations, we conclude that the parameter α should not be set too large either. Therefore, we recommend to set α=0.3 in our method.
The parameter β determines the capacity of each edge going from the phenome to the interactome or in the reverse direction. Intuitively, this parameter should be set at a large value in order to ensure that all information injected from the source can be pumped from the phenome to the interactome. In our studies, we perform a grid search on five values of β : 1, 10, 100, 1000 and 10 000 (in lieu of the positive infinity), and we present the results in Table 2. From the table, we can see that our proposed method is quite robust with respect to this parameter. For example, when different values of β are applied, the AUC score fluctuates within a 2.4% band in the leave-one-out cross-validation against a linkage interval. In the validation against random genes, the AUC score fluctuates within a 2.9% band with different values of β being applied. In the validation against random diseases, the AUC score fluctuates within a 1.9% band with different values of β being applied. From these observations, we conclude that the parameter β can be set in a wide range without affecting the performance of our method very much. Therefore, we recommend to set β=10 000 (in lieu of the positive infinity) in our method for the sake of simplicity.
Table 2.
Robustness of method with respect to the parameter β (with α=0.3 and γ=1) in leave-one-out cross-validation experiments
| 1 (%) | 10 (%) | 100 (%) | 1000 (%) | 10 000 (%) | |
|---|---|---|---|---|---|
| Linkage interval | |||||
| AUC | 93.52 | 95.35 | 95.84 | 95.66 | 95.66 |
| PRE | 34.90 | 55.05 | 59.46 | 60.14 | 60.14 |
| MRR | 3.96 | 3.57 | 3.76 | 3.88 | 3.88 |
| Random genes | |||||
| AUC | 88.28 | 89.7 | 91.12 | 90.76 | 90.76 |
| PRE | 35.02 | 53.73 | 55.53 | 56.89 | 56.89 |
| MRR | 8.67 | 8.52 | 9.62 | 10.02 | 10.02 |
| Random diseases | |||||
| AUC | 92.39 | 92.53 | 91.04 | 90.65 | 90.65 |
| PRE | 22.20 | 23.76 | 22.76 | 22.44 | 22.44 |
| MRR | 8.13 | 7.49 | 9.13 | 9.47 | 9.47 |
In the construction of the phenome–interactome network, we convert an undirected association between diseases and genes into two directed edges in opposite directions to allow for unrestricted information transmission in both directions. It might be argued that edges between the phenome and the interactome should all point from diseases to genes but not vice versa, since information is injected from the source and should flow towards the genes. To study the difference of these two different connection schemes, we remove all edges linking genes to diseases in the phenome–interactome network and repeat the leave-one-out cross-validation experiment against random genes. The results show that the AUC score is 90.71%, with PRE being 49.98% and the MRR being 10.14%. When compared with the previous results, where edges go from both diseases to genes and genes to diseases (AUC=95.66%, PRE=56.89% and MRR=10.02%), we see only a slight drop in performance. Therefore, we conclude that the proposed method is robust with respect to the scheme of constructing the phenome–interactome network.
The parameter γ determines the capacity of each edge between genes in the interactome. To study the effect of this parameter, we perform a grid search on 11 values of γ , including 1 and the values from 10 to 100 with step 10. The results are presented in Table 3, which exhibit a very small effect of the parameter on the performance of the proposed method in the leave-one-out cross-validation. Nevertheless, we still observe that the method usually achieves the best performance when γ is equal to 1. Therefore, we use γ=1 as the default setting in our method.
Table 3.
Robustness of the method with respect to the parameter γ (with α=0.3 and β=10 000) in leave-one-out cross-validation experiments
| 1 (%) | 10 (%) | 20 (%) | 30 (%) | 40 (%) | 50 (%) | 60 (%) | 70 (%) | 80 (%) | 90 (%) | 100 (%) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Linkage interval | |||||||||||
| AUC | 95.66 | 94.91 | 94.59 | 94.51 | 94.55 | 94.69 | 94.63 | 94.60 | 94.59 | 94.57 | 94.57 |
| PRE | 60.14 | 63.82 | 64.38 | 64.66 | 64.66 | 64.74 | 64.94 | 64.98 | 65.06 | 65.06 | 65.06 |
| MRR | 3.88 | 4.51 | 4.83 | 4.95 | 5.02 | 5.06 | 5.10 | 5.12 | 5.12 | 5.14 | 5.14 |
| Random genes | |||||||||||
| AUC | 90.76 | 88.30 | 86.85 | 86.20 | 85.97 | 85.76 | 85.57 | 85.44 | 85.44 | 85.40 | 85.40 |
| PRE | 56.89 | 61.50 | 62.26 | 62.54 | 62.66 | 62.78 | 62.86 | 63.02 | 63.06 | 63.02 | 63.02 |
| MRR | 10.02 | 12.46 | 13.90 | 14.54 | 14.77 | 14.98 | 15.17 | 15.30 | 15.30 | 15.34 | 15.34 |
| Random diseases | |||||||||||
| AUC | 90.65 | 91.9 | 91.75 | 91.67 | 91.63 | 91.61 | 91.58 | 91.56 | 91.55 | 91.54 | 91.54 |
| PRE | 22.44 | 22.84 | 22.88 | 22.80 | 22.80 | 22.76 | 22.80 | 22.72 | 22.72 | 22.72 | 22.72 |
| MRR | 9.47 | 8.18 | 8.31 | 8.38 | 8.41 | 8.43 | 8.46 | 8.47 | 8.48 | 8.49 | 8.49 |
3.3 Comparison with existing methods
There have been several methods developed to prioritize candidate genes using both the phenotype similarity profile and the PPI network. Among these methods, PRINCE (Vanunu et al., 2010) and RWRH (Li and Patra, 2010) have the state-of-the-art performance. We therefore repeat leave-one-out cross-validation experiments against random genes for these two methods (using programs provided by the authors) and compare their performance with an MAXIF.
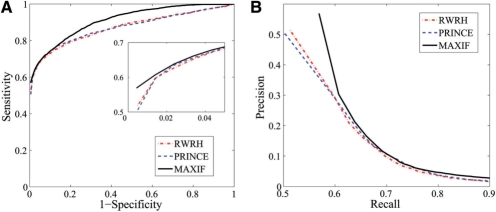
We evaluate the performance using the AUC score and present the results in Figure 3A. The figure shows that the ROC curve of MAXIF lies clearly above those of PRINCE and RWRH. More specifically, the AUC scores are 90.76% for MAXIF, 86.84% for PRINCE and 86.94% for RWRH. In addition, the PRE values are 56.89% for MAXIF, 50.02% for PRINCE and 50.18% for RWRH and the MRR values are 10.03% for MAXIF, 13.80% for PRINCE and 13.81% for RWRH.
Fig. 3.
Comparison with existing methods on leave-one-out cross-validation experiments against random genes. (A) The ROC curve. (B) The precision-recall curve.
Another standard method for evaluating the performance of a prioritization method is to consider the precision–recall curve (Vanunu et al., 2010). Given the association scores calculated for candidate genes, we define positive calls as all genes whose association scores are higher than a certain threshold and define the precision as the proportion of disease genes among the positive calls. We define the recall as the proportion of positively called disease genes among all disease genes. By varying the threshold value, we can obtain a series of precision and recall values, which give rise to a precision–recall curve. We present the precision-recall curves for MAXIF, PRINCE and RWRH in Figure 3B. The figure shows that the curve of MAXIF lies above those of PRINCE and RWRH. We therefore conclude that the performance of MAXIF is superior to both PRINCE and RWRH.
We also compare the computational times of the three methods. It takes 237 s for MAXIF to finish the leave-one-out cross-validation experiment against random genes on a workstation with dual AMD Opteron 2212 CPUs and 4 GB DDR2 memory. In contrast, it takes 840 s for RWRH and more than a day for PRINCE to finish the same experiment. We therefore conclude that the MAXIF is faster than the other two methods.
3.4 Identification of driver genes in 50 copy number aberration regions of melanoma
Copy number aberrations (CNAs), as a typical type of genomic variation, occur frequently in cancers due to genomic instability and have great influence on biological processes involved in many diseases (Ley et al., 2008; Stratton et al., 2009). Although there have been quite a few CNA regions predicted in the literature (Craddock et al., 2010; Kidd et al., 2010), only a small number of genes in these regions has been examined, suggesting a substantial gap between genomic aberrations and the understanding of how these aberrations contribute to diseases (Goldstein, 2009; Kan et al., 2010; Manolio et al., 2009; McClellan and King, 2010). For example, an aberrant region of colon cancer in 11q23.1 includes 17 genes, among which only one gene, DIXDC1, is confirmed to be involved in the induction of colon cancer (Wang et al., 2009). It has also been shown that some genes located in CNA regions are causally implicated in oncogenesis. These genes, known as ‘driver genes’, are different from ‘passenger genes’ that have no contribution to the development of diseases (Akavia et al., 2010; Stratton et al., 2009). Very recently, a method called CONEXIC has been proposed to scan CNA regions to uncover driver genes using gene expression data (Akavia et al., 2010). Since genes in CNA regions can be collected to form a candidate gene set, we could prioritize these genes using MAXIF to distinguish driver genes from passenger genes in CNA regions.
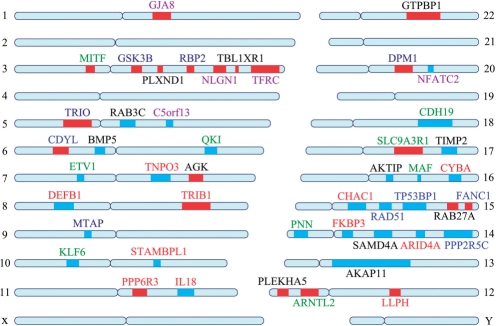
We demonstrate the capability of an MAXIF in predicting driver genes by a case study on a CNA data set concerning melanoma. Specifically, we generate 50 CNA regions, including 23 amplified regions and 27 deleted regions, from 62 cultured melanomas (Lin et al., 2008) using the JISTIC method (Sanchez-Garcia et al., 2010). Then, for each of these regions, we extract all genes in the region as candidate driver genes. Finally, we apply MAXIF to prioritize the candidates, and we predict genes with the top rank as driver genes. Our prediction has resulted in 47 distinct driver genes from a total of 428 distinct candidates, as shown in Table 4 and illustrated in Figure 4.
Table 4.
Detailed information of the 47 predicted driver genes in the 50 CNA regions of melanoma
| ID | Chr | Start | End | #(Genes) | Symbol | OMIM | Predicted transcriptional factor binding sites in the promoter region of the gene |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 147226092 | 150596000 | 20 | GJA8 | 116200 601885 | SREBP-1a, SREBP-1b, SREBP-1c, E47, c-Myc, Max, USF1, Max1, PPAR-gamma1, PPAR-gamma2 |
| 2 | 3 | 70107048 | 70229264 | 6 | MITF | 103500 193510 | CREB, deltaCREB, Sox9, p300, STAT3, GATA-2, C/EBPbeta, PPAR-gamma1, PPAR-gamma2, GATA-3 |
| 3 | 3 | 120500072 | 120923376 | 19 | GSK3B | CREB, deltaCREB, NF-kappaB1, FOXO1a, NF-kappaB, SREBP-1b, SREBP-1c, SREBP-1a, HNF-4alpha2, FOXO4 | |
| 4 | 3 | 129929104 | 130624856 | 9 | PLXND1 | GATA-2, PPAR-gamma2, PPAR-gamma1, MEF-2A, AhR, Arnt, RFX1, MZF-1, Egr-3, GR-beta | |
| 5 | 3 | 139476272 | 139507824 | 4 | RBP2 | XBP-1, PPAR-gamma2, PPAR-gamma1, HNF-4alpha2, COUP-TF1, TFIID, TBP, RORalpha1, NF-1, FOXJ2 (long isoform) | |
| 6 | 3 | 139674960 | 141259840 | 15 | RBP2 | XBP-1, PPAR-gamma2, PPAR-gamma1, HNF-4alpha2, COUP-TF1, TFIID, TBP, RORalpha1, NF-1, FOXJ2 (long isoform) | |
| 7 | 3 | 173931152 | 174312880 | 3 | NLGN1 | MEF-2A, HNF-1A, Pax-2, Pbx1a, Tal-1beta, ITF-2, C/EBPalpha, IRF-7A, FOXL1, CUTL1 | |
| 8 | 3 | 175468448 | 175633120 | 1 | TBL1XR1 | NF-kappaB1, NF-kappaB, POU2F1, MEF-2A, POU3F2 (N-Oct-5b), POU3F2, POU3F2 (N-Oct-5a), FOXC1, GR-alpha, c-Myb | |
| 9 | 3 | 192266400 | 199124224 | 52 | TFRC | ATF, p53, NF-kappaB, NF-kappaB1, YY1, Pbx1a, E47, GATA-1, ARP-1, USF1 | |
| 10 | 5 | 11347004 | 14472551 | 3 | TRIO | NF-kappaB1, NF-kappaB, p53, FOXO1a, Egr-3, Egr-2, Egr-1, HNF-1A, PPAR-gamma2, PPAR-gamma1 | |
| 11 | 6 | 3859295 | 5698904 | 9 | CDYL | Hlf, Pbx1a, POU3F2 (N-Oct-5b), POU3F2 (N-Oct-5a), POU3F2, GATA-1, E4BP4, CREB, deltaCREB, AREB6 | |
| 12 | 6 | 57103452 | 57277264 | 5 | BMP5 | Sox9, IRF-7A, POU3F2 (N-Oct-5b), POU3F2 (N-Oct-5a), POU3F2, RSRFC4, Nkx6-1, MEF-2A, NF-kappaB, RelA | |
| 13 | 7 | 139232720 | 140249792 | 10 | AGK | NRSF form 1, NRSF form 2, ROU2F2 (Oct-2.1), POU2F2B, POU2F2C, Oct-B2, oct-B2, oct-B3, POU2F1, POU2F1a | |
| 14 | 8 | 121760777 | 128993129 | 31 | TRIB1 | 612797 | C/EBPbeta, NF-kappaB1, NF-kappaB, Bach2, ATF-2, AREB6, c-Myc, Max, FOXD1, Max1 |
| 15 | 11 | 68953208 | 69754234 | 8 | PPP6R3 | ||
| 16 | 12 | 18722300 | 19574988 | 5 | PLEKHA5 | FOXO3b, FOXO3a, FOXC1, Pax-2, FOXO4, FOXO1a, FOXF2, AhR, Arnt, POU2F2B | |
| 17 | 12 | 24388521 | 32822550 | 45 | ARNTL2 | PPAR-gamma1, PPAR-gamma2, MEF-2A, CUTL1, AP-1, Sox9, E47, Bach2, Nkx2-2, c-Fos | |
| 18 | 12 | 67491552 | 67636136 | 3 | LLPH | Cdc5, EIK-1, HNF-1, HNF-1A, c-Ets-1, AREB6, ISGF-3, NCX/Ncx, MRF-2, NRF-2 | |
| 19 | 15 | 53109188 | 58337128 | 33 | RAB27A | 607624 | Bach1, Chx10, SRF, RFX1, Tal-1beta, ITF-2, STAT3, Cart-1, Tal-1, E47 |
| 20 | 15 | 87547925 | 89038234 | 23 | FANCI | 609053 | Sox9, Amef-2, MEF-2A, EIK-1, ZID, NRF-2, Sox5, Roaz, ATF6 |
| 21 | 17 | 68172496 | 73084144 | 92 | SLC9A3R1 | 612287 | NF-kappaB1, HNF-4alpha2, COUP-TF1, NF-kappaB, NRSF form 2, NRSF form 1, FOXD1, PPAR-gamma2, PPAR-gamma1, GATA-1 |
| 22 | 20 | 47893352 | 49179608 | 16 | DPM1 | 608799 | STAT5A, ATF-2, ATF6, CUTL1, E4BP4, XBP-1, POU2F2C, POU2F2B, POU2F2 (Oct-2.1), POU2F2 |
| 23 | 22 | 39399572 | 40948612 | 36 | GTPBP1 | ATF, Bach1, Arnt, AhR, POU2F1, Bach2, SREBP-1b, SREBP-1c, SREBP-1a, POU3F2 | |
| 24 | 5 | 58445032 | 58683084 | 1 | RAB3C | POU3F2, POU3F2 (N-Oct-5a), POU3F2 (N-Oct-5b), Lmo2, Nkx3-1 v2, Nkx3-1, Nkx3-1 v1, Nkx3-1 v3, Nkx3-1 v4, Pax-2 | |
| 25 | 5 | 59075480 | 59432304 | 1 | RAB3C | POU3F2, POU3F2 (N-Oct-5a), POU3F2 (N-Oct-5b), Lmo2, Nkx3-1 v2, Nkx3-1, Nkx3-1 v1, Nkx3-1 v3, Nkx3-1 v4, Pax-2 | |
| 26 | 5 | 112049568 | 112105816 | 1 | C5orf13 | E4BP4, IRF-1, RREB-1, RP58, POU2F2C, oct-B2, Oct-B1, POU2F2B, oct-B3, POU2F1 | |
| 27 | 6 | 162494042 | 163637213 | 2 | QKI | 180300 | Max, c-Myc, MEF-2A, CUTL1, HNF-1A, FOXJ2 (long isoform), Max1, Arnt, AhR, SREBP-1a |
| 28 | 8 | 6333250 | 9359366 | 28 | DEFB1 | NF-kappaB, NF-kappaB1, C/EBPalpha, p53, GR-alpha | |
| 29 | 9 | 21999960 | 22009732 | 2 | MTAP | HNF-4alpha2, COUP-TF1, p53, Nkx3-1 v3, Nkx3-1 v2, Nkx3-1 v1, Nkx3-1 v4, Nkx3-1, HNF-1A, YY1 | |
| 30 | 10 | 89436437 | 89908984 | 3 | STAMBPL1 | CHOP-10, C/EBPalpha, E4BP4, GATA-1, Pbx1a, RORalpha2, STAT5B, Hlf, YY1, NF-AT1 | |
| 31 | 11 | 111213008 | 111961672 | 17 | IL18 | 180300 | p300, AP-1, c-Fos, c-Jun, STAT1, STAT1alpha, STAT1beta, IRF-1, GR-alpha, NF-kappaB |
| 32 | 13 | 19867988 | 96252808 | 203 | AKAP11 | GATA-1, Max1, c-Myc, MyoD, Pbx1a, RFX1, USF1, ATF, POU3F1, RORalpha1 | |
| 33 | 14 | 38302632 | 38988776 | 7 | PNN | p53, Pax-6, FOXO3b, FOXO3a, YY1, GATA-1, Meis-1, HOXA9B, C/EBPalpha, POU2F1 | |
| 34 | 14 | 45505796 | 46786096 | 2 | FKBP3 | FOXJ2 (long isoform), MEF-2A, YY1, LCR-F1, Nkx3-1 v4, Nkx3-1 v3, Nkx3-1 v1, Nkx3-1, Nkx3-1 v2, POU3F2 | |
| 35 | 14 | 102319430 | 103810789 | 19 | PPP2R5C | HNF-1A,HSF1 (long), HSF2,NF-kappaB1, NF-kappaB, NF-kappaB2, POU2F1, c-Rel, CP1C, NF-YA | |
| 36 | 15 | 39444436 | 39948236 | 13 | CHAC1 | FOXD1, FOXF2, STAT1beta, STAT1, STAT1alpha, FOXO1a, STAT4, STAT2, STAT6, STAT5B | |
| 37 | 15 | 40049072 | 40114644 | 4 | CHAC1 | FOXD1, FOXF2, STAT1beta, STAT1, STAT1alpha, FOXO1a, STAT4, STAT2, STAT6, STAT5B | |
| 38 | 15 | 40603172 | 40933120 | 7 | RAD51 | 114480 | C/EBPbeta, NF-kappaB1, p53, POU2F1, NF-kappaB, Arnt, AhR, Nkx3-1, Nkx3-1 v1, Nkx3-1 v2 |
| 39 | 15 | 41605345 | 43473384 | 30 | TP53BP1 | AP-1, STAT1alpha, STAT1beta, STAT1, c-Jun, c-Fos, NF-kappaB1, NF-kappaB, PPAR-gamma1, PPAR-gamma2 | |
| 40 | 16 | 52162032 | 52621120 | 3 | AKTIP | NF-1, NF-1/L, SRF, SRF(504 AA), E4BP4, ATF-2, P53, USF-1, USF1, SREBP-1a | |
| 41 | 16 | 77264113 | 78880878 | 2 | MAF | 608983 610202 | AP-1, p53, c-Fos, c-Jun, YY1, c-Rel, POU3F2 (N-Oct-5b), POU3F2 (N-Oct-5a), POU3F2, Chx10 |
| 42 | 16 | 87889112 | 87959104 | 2 | CYBA | AP-1, NF-kappaB1, NF-kappaB, PPAR-gamma1, PPAR-gamma2, STAT5A, Sp1, c-Jun, c-Fos, XBP-1 | |
| 43 | 18 | 62719491 | 76117153 | 33 | CDH19 | CUTL1, C/EBPbeta, GATA-1, p53, MEF-2A, FOXD3, SRY | |
| 44 | 7 | 129619320 | 130330138 | 6 | TNPO3 | 601744 | STAT1, STAT1alpha, STAT1beta, E47, STAT3, ATF6, LUN-1, LCR-F1, C/EBPalpha, CHOP-10 |
| 45 | 7 | 12105143 | 13052351 | 2 | ETV1 | Elk-1, Chx10, ATF, CUTL1, Cart-1, FOXF2, FOXC1, HNF-1A, GATA-3, GATA-1 | |
| 46 | 17 | 74741058 | 77061186 | 24 | TIMP2 | AP-1, c-Jun, c-Fos, STAT1, C/EBPbeta, p53, Sp1, STAT1beta, STAT1alpha, ATF | |
| 47 | 20 | 49142876 | 50443163 | 4 | NFATC2 | NF-kappaB1, NF-kappaB, Elk-1, p300, c-Rel, GATA-3, GATA-1, GATA-2, STAT5A, GR-alpha | |
| 48 | 10 | 2552329 | 4073842 | 3 | KLF6 | 137215 176807 | NF-kappaB1, AP-1, c-Fos, c-Jun, C/EBPbeta, NF-kappaB, SRF, Egr-1, STAT3, Sp1 |
| 49 | 14 | 55290464 | 55652536 | 2 | SAMD4A | SRF, E4BP4, Pbx1a, Nkx6-1, MEF-2A, POU3F2 (N-Oct-5b), POU3F2, POU3F2 (N-Oct-5a), RSRFC4, Nkx3-1 v1 | |
| 50 | 14 | 57178720 | 57588888 | 2 | ARID4A | Sp1,FOXO3a,FOXO3b,FOXO4,FOXC1,CUTL1,Pbx1a,FOXO1a,YY1,Elk-1 |
Fig. 4.
The 47 predicted driver genes. Red lines denote amplified regions and blue lines denote deleted regions. The genes are involved in several functions, such as transcriptional regulation (green), DNA damage and chromosomal instability (blue), metabolism process (deep blue), immune response (deep red), gap junction transport and signaling (black), neuron differentiation and development of the nervous system (purple) and others (red).
We first analyze functional enrichment of these 47 predicted driver genes using DAVID (Huang da et al., 2009). The analysis shows that these genes are involved in a wide variety of biological processes in melanoma, including transcriptional regulation (including both activation and suppression), response to DNA damage and chromosomal instability, metabolic processes, gap junction transport and signaling and so on. For example, FANC1, TP53BP1 and RAD51, located on chromosome 15, are all enriched in the function of response to DNA damage and chromosome instability (Fig. 4).
Among the 47 predicted driver genes, MITF and KLF6 are known as driver genes in the literature (Akavia et al., 2010; Hoek et al., 2008; Huh et al., 2010). Specifically, MITF (the microphthalmia-associated transcription factor) has been found to act as a master regulator of the development, function and survival of melanocyte by modulating various differentiation and cell cycle progression genes. It has also been demonstrated that an MITF is an amplified oncogene in a fraction of human melanomas, and this gene also plays an oncogenic role in human clear cell sarcoma (Hoek et al., 2008; Levy et al., 2006). The other gene, KLF6, has recently been proposed as a tumour suppressor gene in chromosome 10. This gene is involved in hematopoiesis and adipocyte differentiation and could potentially promote melanocyte differentiation (Huh et al., 2010; Santiago-Walker and Herlyn, 2010). Our method also predicts RAB3C and RAB27A as driver genes. These two genes are members of the RAS oncogene family, which is involved in melanoma signaling through the RAS–MAPK pathway (Levy et al., 2006). Moreover, it has been shown that the silencing of the MITF leads to a dramatic decrease in the expression of RAB27A (Chiaverini et al., 2008; Jordens et al., 2006).
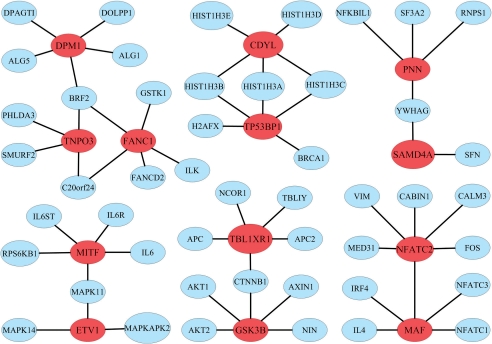
In addition, we find that 14 of the predicted driver genes are reported as associated with some diseases in the OMIM database, and 40 are reported as associated with some diseases in GeneCards (Safran et al., 2003). We also find that these predicted driver genes often interact with other genes to form gene modules, i.e. connected components composed of driver genes and their direct interacting partners. For example, FANC1, TNPO3 and DPM1 interact with other 11 genes to form a large module. Interestingly, these three proteins all interact with protein BRF2, which is one of the multiple subunits of the RNA polymerase III transcription factor complex (Fig. 5). As an illustration, we also include five other large predicted modules in Figure 5.
Fig. 5.
Six large predicted gene modules. The modules are constructed by extracting genes that directly interact with the 47 predicted driver genes from GeneCards and then identifying connected components. Predicted driver genes are marked in red.
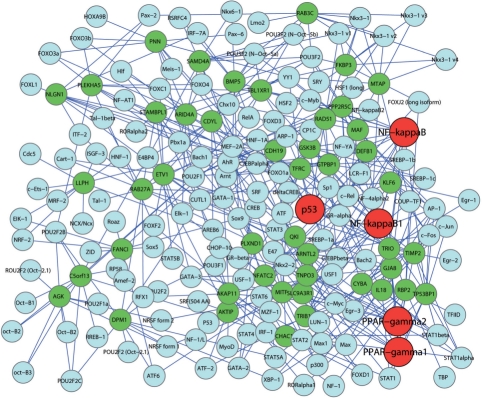
Next, we extract transcription factors of the 47 predicted driver genes from DAVID and examine whether these genes are co-regulated. We find that these genes and their transcription factors form a dense transcriptional regulatory network (Fig. 6). The most enriched transcription factors are P53, NF-kappaB1, NF-kappaB, PPAR-gamma1 and PPAR-gamma2, each of which regulates nine or more genes, suggesting that they are critical in melanoma.
Fig. 6.
Transcriptional network of the 47 predicted driver genes. The predicted genes are marked green and their transcriptional factors are marked blue. The most enriched transcriptional factors, p53, NF-kappaB1, NF-kappaB, PPAR-gamma1and PPAR-gamma2, are marked red.
The above results demonstrate the success of the MAXIF in the prediction of driver genes for CNA regions. Our findings, such as the predicted driver genes involved in response to the DNA damage, the predicted gene modules and the predicted transcriptional regulatory network, may also shed new biological insights on the understanding of melanoma.
4 CONCLUSIONS AND DISCUSSION
In this article, we have proposed a combinatorial approach that integrates the given phenotype similarity profile, PPI network and associations between diseases and genes into a phenome–interactome network, and prioritizes disease genes by maximizing the information flow in the network. We have demonstrated the effectiveness and robustness of this method through a series of cross-validation experiments. As a case study, we presented a successful application of this method in predicting driver genes for a number of CNA regions of melanoma.
The novelty of our method and the key to its success lie in the information flow model which is based on the premise that the relationship between a query disease and the candidate genes can be captured by the maximum information flow sent from the query disease to the genes. Although the shortest path measure has been widely used to calculate the proximity between genes in the previous methods (Wu et al., 2008), the measure considers only a single optimal path while overlooking all other paths. The information flow method, however, considers implicitly all paths between diseases and genes, and can thus overcome the limitation of the methods that rely on the shortest path measure. Moreover, the intrinsic global optimality of the maximum information flow also makes our method superior to existing approaches that rely on local search, such as RWRH and PRINCE (Li and Patra, 2010; Vanunu et al., 2010).
The success of our method also relies on the integration of multiple data sources (i.e. phenotype similarity and PPI). For example, when we ran the method without the phenome and performed the leave-one-out cross-validation against random genes with only the PPI network and known associations between diseases and genes, we got an AUC score of 76.19%, which indicates the indispensible contribution of the phenotype similarity profile.
Our method can be extended in the following aspects. First, as we have seen the power of integrating the phenome and the interactome, the integration of other genomic information, such as gene expression, functional annotations and pathway membership, may further improve the performance of our method. Technically, this can be done by either introducing multiple edges in the network, one for each type of data, between each pair of genes, or by combining all data sources into a single network using statistical methods such as the one in (Guan et al., 2008).
Second, our method can also be extended to uncover associations between protein complexes or biological pathways and human diseases. This can be done by first calculating the total positive flow leaving all members of a complex (or pathway) as an association score to indicate the strength of association between the complex (or pathway, respectively) and the query disease, and then prioritizing candidate complexes (or pathways, respectively) according to their scores.
Funding: National Science Foundation of China (60805010, 60928007, 60934004, 10926027 and 6107030); Tsinghua University Initiative Scientific Research Program, Tsinghua National Laboratory for Information Science and Technology (TNLIST) Cross-discipline Foundation, China Postdoctoral Science Foundation (20090450396 and 2010003119); Scientist Research Fund of Shandong Province (BS2009SW044); Doctor Research Fund from University of Jinan (XBS0914) and NIH (2R01LM008991).
Conflict of Interest: none declared.
REFERENCES
- Adie E.A., et al. Speeding disease gene discovery by sequence based candidate prioritization. BMC Bioinformatics. 2005;6:55. doi: 10.1186/1471-2105-6-55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aerts S., et al. Gene prioritization through genomic data fusion. Nat. Biotechnol. 2006;24:537–544. doi: 10.1038/nbt1203. [DOI] [PubMed] [Google Scholar]
- Akavia U.D., et al. An integrated approach to uncover drivers of cancer. Cell. 2010;143:1005–1017. doi: 10.1016/j.cell.2010.11.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrew V., Goldberg S.R. Beyond the flow decomposition barrier. J. ACM. 1998;45:783–797. [Google Scholar]
- Botstein D., Risch N. Discovering genotypes underlying human phenotypes: past successes for mendelian disease, future approaches for complex disease. Nat. Genet. 2003;33:228–237. doi: 10.1038/ng1090. [DOI] [PubMed] [Google Scholar]
- Chiaverini C., et al. Microphthalmia-associated transcription factor regulates RAB27A gene expression and controls melanosome transport. J. Biol. Chem. 2008;283:12635–12642. doi: 10.1074/jbc.M800130200. [DOI] [PubMed] [Google Scholar]
- Craddock N., et al. Genome-wide association study of CNVs in 16 000 cases of eight common diseases and 3000 shared controls. Nature. 2010;464:713–720. doi: 10.1038/nature08979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dezso Z., et al. Identifying disease-specific genes based on their topological significance in protein networks. BMC Syst. Biol. 2009;3:36. doi: 10.1186/1752-0509-3-36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franke L., et al. Reconstruction of a functional human gene network, with an application for prioritizing positional candidate genes. Am. J. Hum. Genet. 2006;78:1011–1025. doi: 10.1086/504300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freudenberg J., Propping P. A similarity-based method for genome-wide prediction of disease-relevant human genes. Bioinformatics. 2002;18(Suppl. 2):S110–S115. doi: 10.1093/bioinformatics/18.suppl_2.s110. [DOI] [PubMed] [Google Scholar]
- Gaulton K.J., et al. A computational system to select candidate genes for complex human traits. Bioinformatics. 2007;23:1132–1140. doi: 10.1093/bioinformatics/btm001. [DOI] [PubMed] [Google Scholar]
- Glazier A.M., et al. Finding genes that underlie complex traits. Science. 2002;298:2345–2349. doi: 10.1126/science.1076641. [DOI] [PubMed] [Google Scholar]
- Goh K.I., et al. The human disease network. Proc. Natl Acad. Sci. USA. 2007;104:8685–8690. doi: 10.1073/pnas.0701361104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldstein D.B. Common genetic variation and human traits. N. Engl. J. Med. 2009;360:1696–1698. doi: 10.1056/NEJMp0806284. [DOI] [PubMed] [Google Scholar]
- Guan Y., et al. A genomewide functional network for the laboratory mouse. PLoS Comput. Biol. 2008;4:e1000165. doi: 10.1371/journal.pcbi.1000165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoek K.S., et al. Novel MITF targets identified using a two-step DNA microarray strategy. Pigment Cell Melanoma Res. 2008;21:665–676. doi: 10.1111/j.1755-148X.2008.00505.x. [DOI] [PubMed] [Google Scholar]
- Huang da,W., et al. Systematic and integrative analysis of large gene lists using DAVID bioinformatics resources. Nat. Protoc. 2009;4:44–57. doi: 10.1038/nprot.2008.211. [DOI] [PubMed] [Google Scholar]
- Huh S.J., et al. KLF6 gene and early melanoma development in a collagen I-rich extracellular environment. J. Natl Cancer Inst. 2010;102:1131–1147. doi: 10.1093/jnci/djq218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jordens I., et al. Rab7 and Rab27a control two motor protein activities involved in melanosomal transport. Pigment Cell Res. 2006;19:412–423. doi: 10.1111/j.1600-0749.2006.00329.x. [DOI] [PubMed] [Google Scholar]
- Kan Z., et al. Diverse somatic mutation patterns and pathway alterations in human cancers. Nature. 2010;466:869–873. doi: 10.1038/nature09208. [DOI] [PubMed] [Google Scholar]
- Kidd J.M., et al. A human genome structural variation sequencing resource reveals insights into mutational mechanisms. Cell. 2010;143:837–847. doi: 10.1016/j.cell.2010.10.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kohler S., et al. Walking the interactome for prioritization of candidate disease genes. Am. J. Hum. Genet. 2008;82:949–958. doi: 10.1016/j.ajhg.2008.02.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lage K., et al. A human phenome–interactome network of protein complexes implicated in genetic disorders. Nat. Biotechnol. 2007;25:309–316. doi: 10.1038/nbt1295. [DOI] [PubMed] [Google Scholar]
- Lander E.S., Schork N.J. Genetic dissection of complex traits. Science. 1994;265:2037–2048. doi: 10.1126/science.8091226. [DOI] [PubMed] [Google Scholar]
- Levy C., et al. MITF: master regulator of melanocyte development and melanoma oncogene. Trends Mol. Med. 2006;12:406–414. doi: 10.1016/j.molmed.2006.07.008. [DOI] [PubMed] [Google Scholar]
- Ley T.J., et al. DNA sequencing of a cytogenetically normal acute myeloid leukaemia genome. Nature. 2008;456:66–72. doi: 10.1038/nature07485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y., Patra J.C. Genome-wide inferring gene-phenotype relationship by walking on the heterogeneous network. Bioinformatics. 2010;26:1219–1224. doi: 10.1093/bioinformatics/btq108. [DOI] [PubMed] [Google Scholar]
- Lim J., et al. A protein–protein interaction network for human inherited ataxias and disorders of Purkinje cell degeneration. Cell. 2006;125:801–814. doi: 10.1016/j.cell.2006.03.032. [DOI] [PubMed] [Google Scholar]
- Lin W.M., et al. Modeling genomic diversity and tumor dependency in malignant melanoma. Cancer Res. 2008;68:664–673. doi: 10.1158/0008-5472.CAN-07-2615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Managbanag J.R., et al. Shortest-path network analysis is a useful approach toward identifying genetic determinants of longevity. PLoS One. 2008;3:e3802. doi: 10.1371/journal.pone.0003802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manolio T.A., et al. Finding the missing heritability of complex diseases. Nature. 2009;461:747–753. doi: 10.1038/nature08494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClellan J., King M.C. Genetic heterogeneity in human disease. Cell. 2010;141:210–217. doi: 10.1016/j.cell.2010.03.032. [DOI] [PubMed] [Google Scholar]
- Oti M., Brunner H.G. The modular nature of genetic diseases. Clin. Genet. 2007;71:1–11. doi: 10.1111/j.1399-0004.2006.00708.x. [DOI] [PubMed] [Google Scholar]
- Oti M., et al. Predicting disease genes using protein–protein interactions. J. Med. Genet. 2006;43:691–698. doi: 10.1136/jmg.2006.041376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perez-Iratxeta C., et al. Association of genes to genetically inherited diseases using data mining. Nat. Genet. 2002;31:316–319. doi: 10.1038/ng895. [DOI] [PubMed] [Google Scholar]
- Peri S., et al. Development of human protein reference database as an initial platform for approaching systems biology in humans. Genome Res. 2003;13:2363–2371. doi: 10.1101/gr.1680803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Safran M., et al. Human Gene-Centric Databases at the Weizmann Institute of Science: GeneCards, UDB, CroW 21 and HORDE. Nucleic Acids Res. 2003;31:142–146. doi: 10.1093/nar/gkg050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanchez-Garcia F., et al. JISTIC: identification of significant targets in cancer. BMC Bioinformatics. 2010;11:189. doi: 10.1186/1471-2105-11-189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santiago-Walker A., Herlyn M. The ups and downs of transcription factors in melanoma. J. Natl Cancer Inst. 2010;102:1103–1104. doi: 10.1093/jnci/djq267. [DOI] [PubMed] [Google Scholar]
- Schadt E.E. Molecular networks as sensors and drivers of common human diseases. Nature. 2009;461:218–223. doi: 10.1038/nature08454. [DOI] [PubMed] [Google Scholar]
- Sharan R., et al. Network-based prediction of protein function. Mol. Syst. Biol. 2007;3:88. doi: 10.1038/msb4100129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smedley D., et al. BioMart–biological queries made easy. BMC Genomics. 2009;10:22. doi: 10.1186/1471-2164-10-22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stratton M.R., et al. The cancer genome. Nature. 2009;458:719–724. doi: 10.1038/nature07943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun J., Zhao Z. A comparative study of cancer proteins in the human protein–protein interaction network. BMC Genomics. 2010;11(Suppl. 3):S5. doi: 10.1186/1471-2164-11-S3-S5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor I.W., et al. Dynamic modularity in protein interaction networks predicts breast cancer outcome. Nat. Biotechnol. 2009;27:199–204. doi: 10.1038/nbt.1522. [DOI] [PubMed] [Google Scholar]
- Turner F.S., et al. POCUS: mining genomic sequence annotation to predict disease genes. Genome Biol. 2003;4:R75. doi: 10.1186/gb-2003-4-11-r75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Driel M.A., et al. A text-mining analysis of the human phenome. Eur. J. Hum. Genet. 2006;14:535–542. doi: 10.1038/sj.ejhg.5201585. [DOI] [PubMed] [Google Scholar]
- van Driel M.A., et al. A new web-based data mining tool for the identification of candidate genes for human genetic disorders. Eur. J. Hum. Genet. 2003;11:57–63. doi: 10.1038/sj.ejhg.5200918. [DOI] [PubMed] [Google Scholar]
- Vanunu O., et al. Associating genes and protein complexes with disease via network propagation. PLoS Comput. Biol. 2010;6:e1000641. doi: 10.1371/journal.pcbi.1000641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner G.P., et al. The road to modularity. Nat. Rev. Genet. 2007;8:921–931. doi: 10.1038/nrg2267. [DOI] [PubMed] [Google Scholar]
- Wang K., et al. Genome-wide identification of post-translational modulators of transcription factor activity in human B cells. Nat. Biotechnol. 2009;27:829–839. doi: 10.1038/nbt.1563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wood L.D., et al. The genomic landscapes of human breast and colorectal cancers. Science. 2007;318:1108–1113. doi: 10.1126/science.1145720. [DOI] [PubMed] [Google Scholar]
- Wu X., et al. Network-based global inference of human disease genes. Mol. Syst. Biol. 2008;4:189. doi: 10.1038/msb.2008.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu X., et al. Align human interactome with phenome to identify causative genes and networks underlying disease families. Bioinformatics. 2009;25:98–104. doi: 10.1093/bioinformatics/btn593. [DOI] [PubMed] [Google Scholar]