Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2011 Jun 14;27(13):i275–i282. doi: 10.1093/bioinformatics/btr209

PhyloCSF: a comparative genomics method to distinguish protein coding and non-coding regions

Michael F Lin 1,2,*, Irwin Jungreis 1,2, Manolis Kellis 1,2,*
PMCID: PMC3117341  PMID: 21685081

Abstract

Motivation: As high-throughput transcriptome sequencing provides evidence for novel transcripts in many species, there is a renewed need for accurate methods to classify small genomic regions as protein coding or non-coding. We present PhyloCSF, a novel comparative genomics method that analyzes a multispecies nucleotide sequence alignment to determine whether it is likely to represent a conserved protein-coding region, based on a formal statistical comparison of phylogenetic codon models.

Results: We show that PhyloCSF's classification performance in 12-species Drosophila genome alignments exceeds all other methods we compared in a previous study. We anticipate that this method will be widely applicable as the transcriptomes of many additional species, tissues and subcellular compartments are sequenced, particularly in the context of ENCODE and modENCODE, and as interest grows in long non-coding RNAs, often initially recognized by their lack of protein coding potential rather than conserved RNA secondary structures.

Availability and Implementation: The Objective Caml source code and executables for GNU/Linux and Mac OS X are freely available at http://compbio.mit.edu/PhyloCSF

Contact: mlin@mit.edu; manoli@mit.edu

1 INTRODUCTION

High-throughput transcriptome sequencing (mRNA-Seq) is yielding precise structures for novel transcripts in many species, including mammals (Guttman et al., 2010). Accurate computational methods are needed to classify these transcripts and the corresponding genomic exons as protein coding or non-coding, even if the transcript models are incomplete or if they only reveal novel exons of already-known genes. In addition to classifying novel transcript models, such methods also have applications in evaluating and revising existing gene annotations (Butler et al., 2009; Clamp et al., 2007; Kellis et al., 2003; Lin et al., 2007; Pruitt et al., 2009), and as input features for de novo gene structure predictors (Alioto and Guigó, 2009; Brent, 2008). We have previously (Lin et al., 2008) compared numerous methods for determining whether an exon-length nucleotide sequence is likely to be protein coding or non-coding, including single-sequence metrics that analyze the genome of interest only and comparative genomics metrics that use alignments of orthologous regions in the genomes of related species.

Among the comparative methods benchmarked in our previous study, one of our original contributions was the Codon Substitution Frequencies (CSF) metric, which assigns a score to each codon substitution observed in the input alignment based on the relative frequency of that substitution in known coding and non-coding regions. We showed that CSF is highly effective, performing competitively with a phylogenetic modeling approach with much less computational expense, and indeed we have applied it successfully in flies (Lin et al., 2007; Stark et al., 2007), fungi (Butler et al., 2009) and mammals (Clamp et al., 2007; Guttman et al., 2009; 2010). However, as discussed in our previous work, CSF has certain drawbacks arising from its ad hoc scheme for combining evidence from multiple species. For example, it makes only partial use of the evidence available in a multispecies alignment, and it produces a score lacking a precise theoretical interpretation, meaningful only relative to its empirical distributions in known coding and non-coding regions.

This article introduces a rigorous reformulation of CSF, which frames the evaluation of a given alignment as a statistical model comparison problem, choosing between phylogenetic models estimated from known coding and non-coding regions as the best explanation for the alignment. This new ‘PhyloCSF’ method fully leverages multiple alignments in a phylogenetic framework, produces meaningful likelihood ratios as its output and rests upon the sweeping theoretical foundation for statistical model comparison. Benchmarking on the classification datasets from our original study, we show that PhyloCSF outperforms all the other methods we had previously considered.

PhyloCSF is applicable for assessing the coding potential of transcript models or individual exons in an assembled genome that can be aligned to one or more informant genomes at appropriate phylogenetic distances. To estimate parameters in the underlying statistical models, the approach also requires that the genome of interest, or one of the informant genomes, have existing coding gene annotations of reasonably good quality. We describe several initial applications of the method in such settings, which illustrate how it can contribute to new genome annotation strategies based on mRNA-Seq.

2 APPROACH

PhyloCSF is based on the well-established theoretical framework for statistical phylogenetic model comparison. In this context, phylogenetic models are generative probabilistic models that produce alignments of molecular sequences, based on a prior distribution over a common ancestral sequence, the topology and branch lengths of a phylogenetic tree relating the descendants, and a substitution process along each branch giving the rates (per unit branch length) at which each character changes to any other. In phylogenetic model comparison, we wish to choose between two competing models as the better explanation for a given alignment. A standard approach is to decide based on the likelihood ratio between the two models, which quantifies how much more probable the alignment is under one model than under the other. This general approach has been used to explore many different aspects of the evolution of protein-coding genes, as recently reviewed in Anisimova and Kosiol (2008) and Delport et al. (2008).

To distinguish coding and non-coding regions, we design one phylogenetic model to represent the evolution of codons in protein-coding genes, and another to represent the evolution of nucleotide triplet sites in non-coding regions. These models may have one or more parameters θ that adjust them to the genomic region of interest, e.g. the neutral substitution rate or G+C content. To analyze a given alignment A of extant sequences, we first determine the probability of the alignment under the maximum likelihood estimate (MLE) of the parameters for the coding model, pC=maxθC Pr(A|Coding,θC). We similarly estimate the alignment's probability under the non-coding model, pN=maxθN Pr(A|Noncoding,θN). Finally, we decide if the alignment is more likely to represent a protein-coding region or a non-coding region based on the log-likelihood ratio 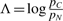Inline graphic. The cutoff can be chosen to achieve a certain level of statistical significance, based on known asymptotic convergence properties of the log-likelihood ratio statistic (Ota et al., 2000; Vuong, 1989; Whelan and Goldman, 1999), or it can be chosen empirically based on classification performance in a test set; we use the latter strategy in this work.

2.1 The dN/dS test

A standard method for detecting purifying selection on protein-coding sequences is to test for evidence that non-synonymous substitutions occur at a slower rate than synonymous substitutions. In the widely used PAML implementation of this test (Yang, 2007; Yang and Nielsen, 1998), the vector of codon frequencies π and the ratio of transition to transversion rates κ are the only parameters used to determine all triplet substitution rates in the background/non-coding model, while the coding model additionally supposes that non-synonymous codon substitution rates are reduced relative to synonymous rates by a scale factor ω (also called dN/dS). PAML takes the phylogenetic tree topology as input, and estimates the branch lengths, π, κ and ω for each alignment. The log-likelihood ratio between the coding and non-coding models can then be obtained from PAML's output. (For detecting purifying selection, the log-likelihood ratio is set to zero if the estimated ω≥1.)

Our previous work (Lin et al., 2008) showed this to be one of the best comparative methods for distinguishing coding and non-coding regions, outperforming our CSF metric according to standard classification error measures. Notably however, the dN/dS test performed worse than CSF for short regions (≤180 nt). This is not surprising since PAML was designed for evolutionary analysis of complete open-reading frames (ORFs), not short exon-length regions, which probably provide too little information to reliably estimate both the branch lengths and codon frequencies in addition to the two rate parameters.

2.2 PhyloCSF

PhyloCSF differs from the standard dN/dS test in two main ways. First, it takes advantage of recent advances in phylogenetic codon models that enable much more detailed representations of coding and non-coding sequence evolution. Specifically, while the dN/dS test uses only a few parameters to model the rates of all possible codon substitutions (Yang and Nielsen, 1998), PhyloCSF uses empirical codon models (ECMs) based on several thousand parameters modeling these rates (Kosiol et al., 2007)—one ECM estimated from alignments of many known coding regions and another ECM from non-coding regions. By comparing these two rich evolutionary models, PhyloCSF can observe many additional informative features of a given alignment compared with the dN/dS test. For example, the coding ECM captures not only the decreased overall rate of non-synonymous substitutions, but also the different rates of specific non-synonymous substitutions reflecting the chemical properties of the amino acids. [Earlier codon modeling approaches also incorporate amino acid distances, e.g. Goldman and Yang (1994), but to our knowledge, these are not widely used for distinguishing coding and non-coding regions.] Also, our ECMs explicitly model the extreme difference in the rates of nonsense substitutions (giving rise to stop codons) in coding and non-coding regions.

Second, PhyloCSF also takes advantage of genome-wide training data to provide prior information about the branch lengths in the phylogenetic tree and the codon frequencies, rather than attempting to reestimate these a priori in each individual alignment. PhyloCSF assumes a fixed tree ‘shape’ based on the genome-wide MLEs of the branch lengths, and estimates only two scale factors ρC and ρN, applied uniformly to all the branch lengths in the coding and non-coding models, respectively, for each individual region analyzed. This allows PhyloCSF to accomodate some region-specific rate variation and reduces its sensitivity to the absolute degree of conservation—without needing to estimate many parameters for each alignment, which may be difficult for short regions.

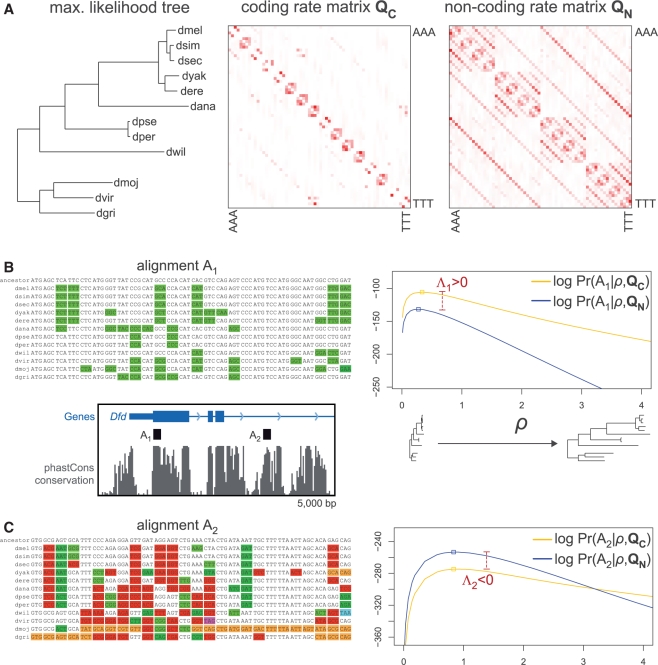
In summary (Fig. 1), PhyloCSF relies on two ECMs fit to genome-wide training data, which include estimates for the branch lengths, codon frequencies and codon substitution rates for known coding and non-coding regions. To evaluate a given nucleotide sequence alignment, PhyloCSF (i) determines the MLE of the scale factor ρ on the branch lengths for each of these models, (ii) computes the likelihood of each model (the probability of the alignment under the model) using the MLE of the scale factor, and (iii) reports the log-likelihood ratio between the coding and non-coding models.

Fig. 1.

Fig. 1.

Open in a new tab

PhyloCSF method overview. (A) PhyloCSF uses phylogenetic codon models estimated from genome-wide training data based on known coding and non-coding regions. These models include a phylogenetic tree and codon substitution rate matrices QC and QN for coding and non-coding regions, respectively, shown here for 12 Drosophila species. QC captures the characteristic evolutionary signatures of codon substitutions in conserved coding regions, while QN captures the typical evolutionary rates of triplet sites in non-coding regions. (B) PhyloCSF applied to a short region from the first exon of the D.melanogaster homeobox gene Dfd. The alignment of this region shows only synonymous substitutions compared with the inferred ancestral sequence (green). Using the maximum likelihood estimate of a scale factor ρ applied to the assumed branch lengths, the alignment has higher probability under the coding model than the non-coding model, resulting in a positive log-likelihood ratio Λ. (C) PhyloCSF applied to a conserved region within a Dfd intron. In contrast to the exonic alignment, this region shows many non-synonymous substitutions (red), nonsense substitutions (blue, purple) and frameshifts (orange). The alignment has lower probability under the coding model, resulting in a negative score.

3 METHODS

3.1 PhyloCSF

PhyloCSF's trained parameters include a phylogenetic tree (with branch lengths) and two 64×64 codon rate matrices QC and QN representing coding and non-coding sequence evolution, respectively, as reversible, homogeneous, continuous-time Markov processes. To evaluate a given alignment, we first evaluate the likelihood of the coding model as follows. We define an alignment-specific parameter ρC that operates as a scale factor applied to all of the branch lengths in the predefined tree. Given a setting of ρC, the substitution probability matrix along any branch with length t is given by P=exp(tρCQC). We can then compute the probability of the full alignment using Felsenstein (2004)'s algorithm—assuming independence of the codon sites, using the equilibrium frequencies implicit in QC as the prior distribution over the common ancestral sequence, and marginalizing out any gapped or ambiguous codons. We numerically maximize this probability over ρC to obtain the likelihood of the coding model pC. We then evaluate the likelihood of the non-coding model pN in the same way, using QN and an independent scale factor ρN, and report the log-likelihood ratio 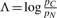Inline graphic as the result.

3.2 Estimation of empirical codon models

To estimate the phylogenetic tree and the empirical rate matrices QC and QN for the species of interest, we rely on sequence alignments of many known coding and random non-coding regions. Given this genome-wide training data, we estimate the parameters for the coding and non-coding models by maximum likelihood, using an expectation–maximization approach. The E-step is carried out as previously described (Holmes and Rubin, 2002; Siepel and Haussler, 2004). In each M-step, we update the ECM exchangeability parameters using a spectral approximation method (Arvestad and Bruno, 1997) and the branch lengths by numerical optimization of the expected log-likelihood function (Siepel and Haussler, 2004). Meanwhile, the codon/triplet frequencies are fixed to their empirical averages in the training examples, and we assume a fixed species tree topology.

3.3 Parameter estimation for Ψ transformation

Below, we introduce a length-based transformation of the PhyloCSF log-likelihood ratio score Λ for an alignment,

graphic file with name btr209um1.jpg

where n is the length of the aligned region in the reference species, 𝒩(x|μ,σ2) is the normal density and the six parameters μC, AC, BC, μN, AN and BN must be estimated from the training dataset. We estimate these parameters by maximum likelihood, i.e. for the known coding regions in the training dataset (indexed by i), we seek

graphic file with name btr209um2.jpg

Setting the gradient of this log-likelihood function to zero yields a system of three equations,

graphic file with name btr209um3.jpg

where the Z-score Zi=(Λi−niμ)/(ACniBC). We solve this system using Newton's method to obtain MLEs of μC, AC and BC. We estimate the corresponding parameters for non-coding regions μN, AN and BN similarly, using the non-coding examples in the training dataset instead of the coding examples.

4 RESULTS

4.1 PhyloCSF outperforms other methods

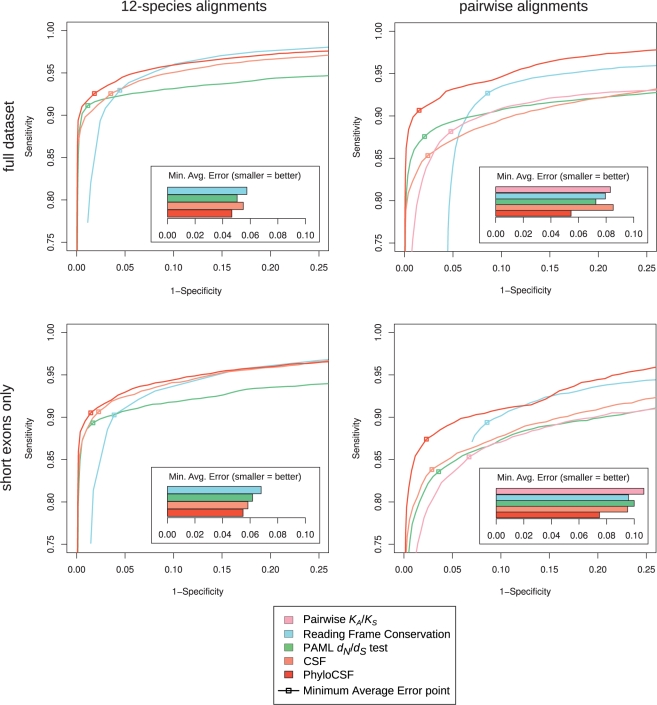
We used the datasets and benchmarks from our previous study (Lin et al., 2008) to evaluate our new method. Briefly, the datasets consist of known protein-coding regions and randomly selected non-coding regions (~50 000 total regions) in the genome of the fruitfly Drosophila melanogaster, aligned with 11 other Drosophila species using MULTIZ (Blanchette et al., 2004; Drosophila 12 Genomes Consortium, 2007; Stark et al., 2007). The lengths of the regions in both the coding and non-coding sets match the length distribution of fly coding exons. Consistent with our previous work, we trained and applied PhyloCSF on this dataset using 4-fold cross-validation to ensure that any observed performance differences are not due to overfitting. We assessed the results by examining ROC curves and computing the minimum average error (MAE), the average false positive and false negative rates at the cutoff that minimizes this average. To compare the power of the methods for short exons specifically, we additionally computed these benchmarks only for the 37% of examples from 30 to 180 nt in length (a range including three-quarters of mammalian coding exons).

These benchmarks show that PhyloCSF outperforms the other comparative methods we previously benchmarked (Fig. 2, left column), effectively dominating them all at good sensitivity/specificity tradeoffs. PhyloCSF's overall MAE is 19% lower than that of the Reading Frame Conservation metric, 15% lower than that of our older CSF method and 8% lower than the dN/dS test's. PhyloCSF also clearly outperforms the other methods for short exons (Fig. 2, bottom row), with an MAE 11% lower than the dN/dS test's. Our previous study (Lin et al., 2008) showed that these comparative methods in turn outperform single-species metrics based on sequence composition [e.g. interpolated Markov models (Delcher et al., 1999) and the Z curve discriminant (Gao and Zhang, 2004)].

Fig. 2.

Fig. 2.

Open in a new tab

PhyloCSF performance benchmarks. ROC plots and error measures for several methods to distinguish known protein-coding and randomly selected non-coding regions in D.melanogaster. The top row of plots shows the results for our full dataset of ~50 000 regions matching the fly exon length distribution, while the bottom row of plots is based on the 37% of these regions between 30 and 180 nt in length. The left-hand plots show the performance of the methods applied to multiple alignments of 12 fly genomes, while the right-hand plots use pairwise alignments between D.melanogaster and D.ananassae. PhyloCSF effectively dominates the other methods.

We also compared PhyloCSF to the other methods using only pairwise alignments between D.melanogaster and D.ananassae, which we previously showed to be the best single informant for this purpose. PhyloCSF also dominates other methods in these pairwise alignments (Fig. 2, right column), with MAE 24% lower than the next-best method's for all aligned regions (dN/dS test) and 21% lower for the short regions (CSF). Some of PhyloCSF's greater relative advantage in the pairwise case arises from its ability to produce an informative score even for regions lacking alignment with D.ananassae, based on the composition of the D.melanogaster region and the codon frequencies included in PhyloCSF's generative ECMs.

Overall, these benchmarks show that PhyloCSF provides superior power to distinguish fly coding and non-coding regions based on either multispecies or pairwise genome alignments.

4.2 Using non-independence of codon sites to increase accuracy

Like most codon modeling approaches, PhyloCSF assumes statistical independence of each codon site from all the others in the alignment (conditional on the model parameters). We next studied the extent to which this assumption is violated in the real alignments in our dataset, and sought to use this to further improve our ability to distinguish the coding and non-coding regions.

One simple way of assessing the dependence of codon sites in a set of alignments is to measure the relationship between the PhyloCSF log-likelihood ratio, Λ, and the number of sites in each alignment, n. For alignments consisting of n truly i.i.d. sites generated from either the coding or non-coding ECM, it can be shown by central limit arguments that the 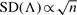Inline graphic (Cox, 1961; 1962; Vuong, 1989; White, 1982). On the other hand, SD(Λ)∝n under complete dependence of the sites in each alignment—that is, where each alignment consists of a single randomly sampled site, repeated n times. We applied a numerical procedure to find MLEs of coefficients A and B in SD(Λ)~AnB based on the real alignments in our dataset. For coding regions, we found BC=0.84 and for non-coding regions, we found BN=0.76. Compared with the expected values of B=0.5 under complete independence and B=1 under complete dependence, these results suggest considerable site-to-site dependencies in the real alignments—stronger in coding regions than non-coding regions.

The differing length-dependent dispersions of Λ for coding and non-coding regions suggest that a better classification rule could be obtained by interpreting the log-likelihood ratio for each example in the context of the alignment's length. This contrasts with the suggestion of the ‘law of likelihood’ that, under the model's independence assumptions, any information pertinent to the decision would already be captured in the likelihood ratio (Hacking, 1974).

We defined a new log-likelihood ratio score Ψ for each alignment by assuming that Λ normally distributes with mean and variance as differing functions of n for coding and non-coding regions:

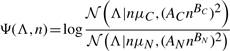graphic file with name btr209um4.jpg

where 𝒩(x|μ,σ2) is the normal density and the six parameters μC, AC, BC, μN, AN and BN are estimated from the training dataset by maximum likelihood (see Section 3).

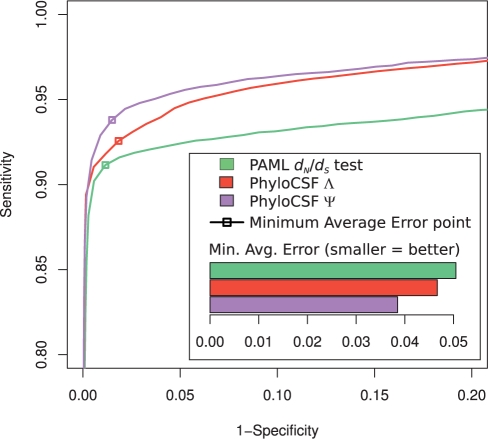
We calculated Ψ for each of the examples in our Drosophila dataset (with 2-fold cross-validation) and found that it indeed provides a superior overall discriminant between the coding and non-coding regions (Fig. 3), with an MAE 17% lower than that of Λ and 24% lower than the dN/dS test's. While Ψ somewhat distorts the formal inferential meaning captured by Λ, this approach exploits information from site-to-site dependencies in a principled way, and at negligible additional computational cost—in contrast to attempts to explicitly capture such dependencies in the generative codon models (Anisimova and Kosiol, 2008; Delport et al., 2008).

Fig. 3.

Fig. 3.

Open in a new tab

Exploiting non-independence of codon sites. The PhyloCSF log-likelihood ratio Λ is transformed based on alignment length into a new log-likelihood ratio score Ψ (see main text). Ψ provides a superior discriminant in the full 12 fly dataset.

5 IMPLEMENTATION

To facilitate the use of PhyloCSF by the community, we provide an implementation that evaluates input sequence alignments in Multi-FASTA format and reports the resulting log-likelihood ratios in units of decibans. We also provide the ECMs and other parameter settings for several phylogenies.

The software provides two additional noteworthy features. First, it can evaluate all ORFs above a given length, in three or six reading frames, within each alignment. Thus, it can delimit likely protein-coding ORFs within transcript models that include untranslated regions. Second, the software also provides a simplified method, similar to the aforementioned dN/dS test, that does not require extensive training data from known coding and non-coding regions. While considerably less accurate than the full ECM comparison presented here, this method can be used in settings where genome alignments are available but high-quality existing gene annotations are lacking, as may increasingly be the case outside of well-studied phylogenies such as mammals and flies.

The Objective Caml source code and executables for GNU/Linux and Mac OS X are available at: http://compbio.mit.edu/PhyloCSF

6 APPLICATIONS IN FUNGI, FLIES AND MAMMALS

We now briefly discuss several initial applications of PhyloCSF in three different phylogenies. While biological results of each of these applications are presented elsewhere in greater detail, together they illustrate PhyloCSF's usefulness in practice.

Recent efforts to reconstruct the transcriptome of the fission yeast Schizosaccharomyces pombe based on mRNA-Seq experiments suggested numerous novel transcript models. We generated whole-genome alignments of S.pombe with S.octosporus, S.japonicus and S.cryophilus, and identified 89 novel protein-coding genes that are highly conserved among these species, even though they do not show primary sequence similarity to known proteins. The mRNA-Seq reconstruction also suggested several hundred revisions to the exon–intron structures of existing gene annotations. PhyloCSF showed that the revised transcript models strongly tend to have higher coding potential than the originals, confirming the quality of the proposed revisions (Rhind et al., in press).

The modENCODE project undertook a comprehensive effort to map the transcriptome of D.melanogaster, identifying 1938 novel transcribed loci in this well-studied genome. Using PhyloCSF with the 12-species whole-genome alignments, we identified 138 of these likely to represent novel coding genes (The modENCODE Consortium, 2010). We also used PhyloCSF in concert with the modENCODE data to identify and characterize 283 known D.melanogaster genes that show high coding potential immediately downstream of their stop codon, suggesting a surprisingly widespread mechanism of stop codon readthrough (Jungreis,J. et al., submitted for publication). PhyloCSF's ability to systematically resolve small regions was especially important in this application, as many of these putative readthrough regions are quite short (mean 67 codons).

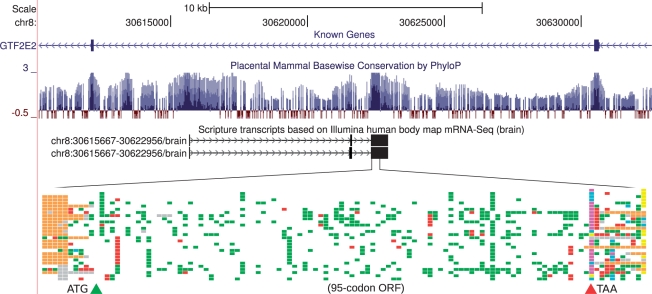
Lastly, we have also used PhyloCSF in the human and mouse genomes, using alignments of 29 placental mammals (Linblad-Toh,K. et al., submitted for publication). We applied PhyloCSF to transcript models reconstructed from mRNA-Seq on 16 human tissues to identify several candidate novel coding genes (Fig. 4), despite the extensive decade-long efforts to annotate the human genome. We also used CSF and PhyloCSF to evaluate coding potential in novel mouse transcripts, helping to identify thousands of long non-coding RNAs with diverse functional roles (Guttman et al., 2010) (Hung et al., in press).

Fig. 4.

Fig. 4.

Open in a new tab

A novel human coding gene found using mRNA-Seq and PhyloCSF. Transcriptome reconstruction by Scripture (Guttman et al., 2010) based on brain mRNA-Seq data provided by Illumina, Inc. produced two alternative transcript models lying antisense to an intron of GTF2E2, a known protein-coding gene. PhyloCSF identified a 95-codon ORF in the third exon of this transcript, highly conserved across placental mammals. The color schematic illustrates the genome alignment of 29 placental mammals for this ORF, indicating conservation (white), synonymous and conservative codon substitutions (green), other non-synonymous codon substitutions (red), stop codons (blue/magenta/yellow) and frame-shifted regions (orange). Despite its unmistakable protein-coding evolutionary signatures, the ORF's translation shows no sequence similarity to known proteins.

7 CONCLUSION

We have introduced PhyloCSF, a comparative genomics method for distinguishing protein-coding and non-coding regions, and shown that it outperforms previous methods. In addition to its superior discriminatory power, PhyloCSF is far more theoretically attractive than our older CSF and other ad hoc metrics, relying on a formal statistical comparison of phylogenetic codon models. However, we note that PhyloCSF and CSF produce highly correlated scores (Pearson coefficient 0.95 in our dataset), and the new method is much more computationally demanding.

As our initial applications illustrate, PhyloCSF can provide an important building block in future computational strategies for genome annotation based on mRNA-Seq. Other pieces of the puzzle include methods to reconstruct transcript models based on short reads, complementary metrics of coding potential based on primary sequence composition or indel patterns, database search tools to identify similarity to known proteins and non-coding RNAs and de novo gene structure predictors that may be able to identify lowly or rarely expressed genes. Major challenges remain in integrating these methods into coherent pipelines, harmonizing the results with existing genome annotation databases, and coping with the uneven coverage and relatively high error rate of current high-throughput sequencing technologies (Ozsolak and Milos, 2011).

ACKNOWLEDGEMENTS

The authors thank Matthew D. Rasmussen and Manuel Garber for helpful comments and discussions.

Funding: National Institutes of Health (U54 HG004555-01); National Science Foundation (DBI 0644282).

Conflict of Interest: none declared.

REFERENCES

  1. Alioto T., Guigó R. State of the art in eukaryotic gene prediction. In: Frishman D., Valencia A., editors. Modern Genome Annotation: the BioSapiens Network. New York: Springer; 2009. pp. 7–40. [Google Scholar]
  2. Anisimova M., Kosiol C. Investigating protein-coding sequence evolution with probabilistic codon substitution models. Mol. Biol. Evol. 2008;26:255–271. doi: 10.1093/molbev/msn232. [DOI] [PubMed] [Google Scholar]
  3. Arvestad L., Bruno W.J. Estimation of reversible substitution matrices from multiple pairs of sequences. J. Mol. Evol. 1997;45:696–703. doi: 10.1007/pl00006274. [DOI] [PubMed] [Google Scholar]
  4. Blanchette M., et al. Aligning multiple genomic sequences with the threaded blockset aligner. Genome Res. 2004;14:708–715. doi: 10.1101/gr.1933104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Brent M.R. Steady progress and recent breakthroughs in the accuracy of automated genome annotation. Nat. Rev. Genet. 2008;9:62–73. doi: 10.1038/nrg2220. [DOI] [PubMed] [Google Scholar]
  6. Butler G., et al. Evolution of pathogenicity and sexual reproduction in eight candida genomes. Nature. 2009;459:657–662. doi: 10.1038/nature08064. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Clamp M., et al. Distinguishing protein-coding and noncoding genes in the human genome. Proc. Natl Acad. Sci. USA. 2007;104:19428–19433. doi: 10.1073/pnas.0709013104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Cox D.R. Tests of separate families of hypotheses. Proc. Fourth Berkeley Symp. Math. Statist. Prob. 1961;1:105–123. [Google Scholar]
  9. Cox D.R. Further results on tests of separate families of hypotheses. J. R. Stat. Soc. Ser. B. 1962;24:406–424. [Google Scholar]
  10. Delcher A.L., et al. Improved microbial gene identification with GLIMMER. Nucleic Acids Res. 1999;27:4636–4641. doi: 10.1093/nar/27.23.4636. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Delport W., et al. Models of coding sequence evolution. Brief. Bioinformatics. 2008;10:97–109. doi: 10.1093/bib/bbn049. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Drosophila 12 Genomes Consortium. Evolution of genes and genomes on the drosophila phylogeny. Nature. 2007;450:203–218. doi: 10.1038/nature06341. [DOI] [PubMed] [Google Scholar]
  13. Felsenstein J. Inferring Phylogenies. Sunderland, MA: Sinauer Associates; 2004. [Google Scholar]
  14. Gao F., Zhang C. Comparison of various algorithms for recognizing short coding sequences of human genes. Bioinformatics. 2004;20:673–681. doi: 10.1093/bioinformatics/btg467. [DOI] [PubMed] [Google Scholar]
  15. Goldman N., Yang Z. A codon-based model of nucleotide substitution for protein-coding DNA sequences. Mol. Biol. Evol. 1994;11:725–736. doi: 10.1093/oxfordjournals.molbev.a040153. [DOI] [PubMed] [Google Scholar]
  16. Guttman M., et al. Chromatin signature reveals over a thousand highly conserved large non-coding RNAs in mammals. Nature. 2009;458:223–227. doi: 10.1038/nature07672. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Guttman M., et al. Ab initio reconstruction of cell type–specific transcriptomes in mouse reveals the conserved multi-exonic structure of lincRNAs. Nat. Biotechnol. 2010;28:503–510. doi: 10.1038/nbt.1633. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Hacking I. Logic of Statistical Inference. Cambridge U.P., London: 1974. [Google Scholar]
  19. Holmes I., Rubin G. An expectation maximization algorithm for training hidden substitution models. J. Mol. Biol. 2002;317:753–764. doi: 10.1006/jmbi.2002.5405. [DOI] [PubMed] [Google Scholar]
  20. Hung T., et al. Extensive and coordinated transcription of noncoding RNAs within cell cycle promoters. Nature Genet. 2011 doi: 10.1038/ng.848. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Kellis M., et al. Sequencing and comparison of yeast species to identify genes and regulatory elements. Nature. 2003;423:241–254. doi: 10.1038/nature01644. [DOI] [PubMed] [Google Scholar]
  22. Kosiol C., et al. An empirical codon model for protein sequence evolution. Mol. Biol. Evol. 2007;24:1464–1479. doi: 10.1093/molbev/msm064. [DOI] [PubMed] [Google Scholar]
  23. Lin M.F., et al. Revisiting the protein-coding gene catalog of drosophila melanogaster using 12 fly genomes. Genome Res. 2007;17:000. doi: 10.1101/gr.6679507. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Lin M.F., et al. Performance and scalability of discriminative metrics for comparative gene identification in 12 drosophila genomes. PLoS Comput. Biol. 2008;4:e1000067. doi: 10.1371/journal.pcbi.1000067. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Ota R., et al. Appropriate likelihood ratio tests and marginal distributions for evolutionary tree models with constraints on parameters. Mol. Biol. Evol. 2000;17:798–803. doi: 10.1093/oxfordjournals.molbev.a026358. [DOI] [PubMed] [Google Scholar]
  26. Ozsolak F., Milos P.M. RNA sequencing: advances, challenges and opportunities. Nat. Rev. Genet. 2011;12:87–98. doi: 10.1038/nrg2934. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Rhind N., et al. Comparative Functional Genomics of the Fission Yeasts. Science. 2011 doi: 10.1126/science.1203357. in press [Epub ahead of print, doi:10.1126/science.1203357] [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Pruitt K.D., et al. The consensus coding sequence (CCDS) project: Identifying a common protein-coding gene set for the human and mouse genomes. Genome Res. 2009;19:1316–1323. doi: 10.1101/gr.080531.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Siepel A., Haussler D. Phylogenetic estimation of context-dependent substitution rates by maximum likelihood. Mol. Biol. Evol. 2004;21:468–488. doi: 10.1093/molbev/msh039. [DOI] [PubMed] [Google Scholar]
  30. Stark A., et al. Discovery of functional elements in 12 drosophila genomes using evolutionary signatures. Nature. 2007;450:219–232. doi: 10.1038/nature06340. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. The modENCODE Consortium. Identification of functional elements and regulatory circuits by drosophila modENCODE. Science. 2010;330:1787–1797. doi: 10.1126/science.1198374. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Vuong Q.H. Likelihood ratio tests for model selection and Non-Nested hypotheses. Econometrica. 1989;57:307–333. [Google Scholar]
  33. Whelan S., Goldman N. Distributions of statistics used for the comparison of models of sequence evolution in phylogenetics. Mol. Biol. Evol. 1999;16:1292. [Google Scholar]
  34. White H. Regularity conditions for cox's test of non-nested hypotheses. J. Economet. 1982;19:301–318. [Google Scholar]
  35. Yang Z. PAML 4: phylogenetic analysis by maximum likelihood. Mol. Biol. Evol. 2007;24:1586–1591. doi: 10.1093/molbev/msm088. [DOI] [PubMed] [Google Scholar]
  36. Yang Z., Nielsen R. Synonymous and nonsynonymous rate variation in nuclear genes of mammals. J. Mol. Evol. 1998;46:409–418. doi: 10.1007/pl00006320. [DOI] [PubMed] [Google Scholar]

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES