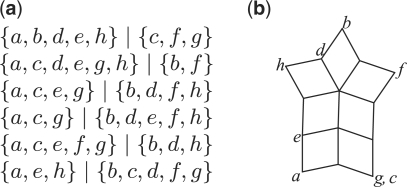Abstract
Motivation: In systematic biology, one is often faced with the task of comparing different phylogenetic trees, in particular in multi-gene analysis or cospeciation studies. One approach is to use a tanglegram in which two rooted phylogenetic trees are drawn opposite each other, using auxiliary lines to connect matching taxa. There is an increasing interest in using rooted phylogenetic networks to represent evolutionary history, so as to explicitly represent reticulate events, such as horizontal gene transfer, hybridization or reassortment. Thus, the question arises how to define and compute a tanglegram for such networks.
Results: In this article, we present the first formal definition of a tanglegram for rooted phylogenetic networks and present a heuristic approach for computing one, called the NN-tanglegram method. We compare the performance of our method with existing tree tanglegram algorithms and also show a typical application to real biological datasets. For maximum usability, the algorithm does not require that the trees or networks are bifurcating or bicombining, or that they are on identical taxon sets.
Availability: The algorithm is implemented in our program Dendroscope 3, which is freely available from www.dendroscope.org.
Contact: scornava@informatik.uni-tuebingen.de; huson@informatik.uni-tuebingen.de
1 INTRODUCTION
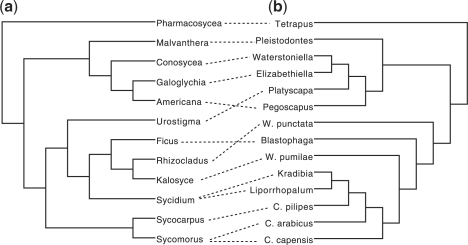
In systematic biology, one is often faced with the task of comparing different phylogenetic trees, in particular in multi-gene analysis or cospeciation studies (Burt and Trivers, 2008; Charleston, 1998; Charleston and Perkins, 2003; Lee and Stock, 2010; Machado et al., 2005; Merkel et al., 2010). One way to visualize similarities and differences is to draw two phylogenetic trees as rooted trees side by side and to draw lines (which we will call connectors) between taxa that correspond to each other in the two trees, see Figure 1. Such a depiction is called a tanglegram and different variations of the problem of computing an optimal tanglegram have been studied in the literature.
Fig. 1.
A tanglegram between a phylogeny of sections of Ficus (a) and that of their associated genera of pollinating wasps (b). Adapted from (Machado et al., 2005).
For example, a number of articles (Bansal et al., 2009; Böcker et al., 2009; Buchin et al., 2009; Fernau et al., 2005; Nöllenburg et al., 2009; Venkatachalam et al., 2010). consider the One-Tree Crossing Minimization (OTCM) and the Two-Tree Crossing Minimization (TTCM) problems that both aim at minimizing the number of crossings between connectors. In the former problem, the layout of one of the trees is fixed and that of the other is mutable whereas in the latter formulation the layout of both trees are allowed to be changed. For binary trees, OTCM is solvable in O(nlogn) time (Venkatachalam et al., 2010), while TTCM is NP-complete (Fernau et al., 2010). In Dwyer and Schreiber (2004), the authors describe a ‘seesaw’ heuristic for the TTCM problem for binary (or bifurcating) trees, which operates by repeatedly solving the OTCM problem, each time switching the roles of the two trees. A branch-and-bound approach for binary trees that works in O(n3) time and gives a 2-approximation for complete binary trees is presented in Buchin et al. (2009). A generalization of the algorithm to unbalanced binary trees is described in Nöllenburg et al. (2009), though in this case the approximation factor does not hold. In addition, this article gives an ILP formulation and an exact branch-and-bound algorithm for binary trees, where the latter has a worst-case running time of O(n2+n·22n). Other approaches use fixed-parameter tractability (FPT) parameterized by the number k of connector crossings (Fernau et al., 2005). A generalization to non-binary trees is discussed in Venkatachalam et al. (2010). The only algorithm that is able to compute tanglegrams for binary trees with many-to-many connections is described in Bansal et al. (2009). Their algorithm requires O(klog2k/loglogk) time (where k is the number of connectors) in the case that one tree is fixed. Additionally, they present some alternating and local search strategies for the TTCM problem.
While evolutionary histories are usually described by rooted phylogenetic trees, in some cases rooted phylogenetic networks may provide a more accurate evolutionary scenario, especially when mechanisms such as horizontal gene transfer, hybridization, recombination, reassortment or incomplete lineage sorting have played a role in shaping the history. There is currently much research on the development of computational methods for computing rooted phylogenetic networks, for an overview see Huson and Scornavacca (2011a); Huson et al. (2011).
The goal of this article is to introduce the concept of a tanglegram for rooted phylogenetic networks and to provide a useful heuristic for computing such tanglegrams. Unlike trees, rooted phylogenetic networks are not necessarily planar and so the definition of an optimal tanglegram is not immediately obvious for them. Our heuristic does not require that the networks are bifurcating or bicombining, or that they both contain the same set of taxa. It can also be used to compare two trees, or to compare a tree and a network, of course. Moreover, the heuristic can also be employed to align the order of leaves for a whole collection of rooted trees or networks. The algorithm is implemented in our Java program Dendroscope 3 (Huson and Scornavacca, 2011b; Huson et al., 2007), which is freely available from www.dendroscope.org.
2 BASICS
Throughout this article, we follow the terminology and notation defined in Huson et al. (2011) and assume that the reader is familiar with graphs and related terminology. In this section we introduce some basic concepts and results.
2.1 Phylogenetic trees and networks
Let 𝒳 be a set of taxa. An unrooted phylogenetic network N on 𝒳 is an unrooted, connected graph whose leaves are bijectively labeled by the taxa in 𝒳. A rooted DAG is defined as a directed graph that is free of directed cycles and contains precisely one node with indegree zero, called the root. A rooted phylogenetic network N on 𝒳 is a rooted DAG whose set of leaves is bijectively labeled by the taxa in 𝒳. A node v in N is said to be a tree node if its indegree is less than two and a reticulate node otherwise. An edge of N is called a tree edge, unless it leads to a reticulate node, in which case it is called a reticulate edge. A (rooted) phylogenetic tree is a (rooted) phylogenetic network for which it is not possible to delete any edge without producing a graph that is not connected.
2.2 Clusters, splits and split networks
Let N be a rooted phylogenetic network on 𝒳. Any tree edge e in N defines a cluster C(e) which is given by the set of all taxa that label leaves that lie below e in N. We use 𝒞(N) to denote the set of all clusters obtainable from N in this way.
Let 𝒳 be a set of taxa. A split A∣B on 𝒳 is a partition of 𝒳 into two non-empty sets. Any edge e in an unrooted phylogenetic tree T on 𝒳 defines a split S(e)=A∣B, where A and B are all taxa that label nodes that lie on one side or the other side of the edge, respectively. A split A∣B is said to separate two taxa x and y if they are contained in different parts of the split, that is, if |{x,y}∩A|=|{x,y}∩B|=1 holds. The restriction of a split S to a set of taxa 𝒳', denoted by S|𝒳′ is defined as the split S′=A′|B′, where A′=A∩𝒳' and B′=B∩𝒳′.
Let Σ be a set of splits on 𝒳. A weighting of Σ is given by a map ω that assigns a non-negative weight ω(S) to each split S∈Σ. Let Σ be a set of weighted splits on 𝒳. We define a distance matrix of split distances D(Σ)={dxy} on 𝒳 by setting dxy=∑S∈Σ(x,y)ω(S), where Σ(x,y) denotes the set of all splits in Σ that separate the taxa x and y. If Σ is unweighted, then we use this definition with ω(S)=1 for all S.
Definition 2.1 (Compatibility). —
Two splits A1∣B1 and A2∣B2 are compatible if at least one of the sets A1∩A2, A1∩B2, B1∩A2 or B1∩B2 is empty. Otherwise they are called incompatible. A collection of splits Σ is compatible if and only if all splits are pairwise compatible.
A set of compatible splits can always be represented by a tree (Buneman, 1971). More generally, any set of splits Σ can always be represented by a split network N (Dress and Huson, 2004). This is an unrooted phylogenetic network with the property that every split S=A∣B in Σ is represented in N by a set of parallel edges, such that deleting all edges in the set will result in exactly two connected components, one labeled by the taxa in A and the other labeled by B.
A class of splits of particular interest are the circular splits.
Definition 2.2 (Circular splits). —
A set of splits Σ on 𝒳 is called circular, if there exists a linear ordering π=(x1,…,xn) of the elements of 𝒳 for Σ such that each split S∈Σ is interval-realizable, that is, has the form
for appropriately chosen 1<p≤q≤n.
Such an ordering π=(x1,…,xn) is called a circular ordering for Σ, as it holds that (x1,…,xn) is a circular ordering for Σ, if and only if the inverse ordering (xn,xn−1,…,x1) and (x2,x3,…,xn,x1) both are.
Circular splits are of particular interest because any set of circular splits can always be represented by a split network that can be drawn in the plane such that no two edges intersect and all labeled nodes lie on the outside of the network, see Figure 2.
Fig. 2.
(a) A set of six circular splits Σ on 𝒳={a,b,…,h}. A circular ordering is given by (a,g,c,f,b,d,h,e). (b) An outer-labeled planar split network representing Σ.
2.3 The Neighbor-Net algorithm
Given a distance matrix D on 𝒳, the Neighbor-Net algorithm (Bryant and Moulton, 2004) computes a circular ordering π of 𝒳 from D and then a set of weighted splits Σ that are interval-realizable with respect to π. A distance matrix D on 𝒳 is said to be circular if and only if there exists a set of circular weighted splits Σ on 𝒳 such that D(Σ)=D. The following result asserts the consistency of the Neighbor-Net method:
Theorem 2.3 [Neighbor-Net consistency (Bryant et al., 2007)]. —
Given a circular distance matrix D on 𝒳, the Neighbor-Net algorithm produces a circular ordering π and a set of weighted splits Σ that are interval-realizable with respect to π such that D=D(Σ).
3 TANGLEGRAMS FOR ROOTED PHYLOGENETIC NETWORKS
In this section, we first develop the concept of a tanglegram for rooted phylogenetic networks and then define what we mean by an optimal tanglegram. We then develop a heuristic for computing an optimal tanglegram for two rooted phylogenetic networks.
Let N be a rooted phylogenetic network on 𝒳. A topological embedding of N is given by a map that assigns to each node v in N an ordering (v1,v2,…,vk) of the set of its children. Note that any concrete drawing θ of N induces such a topological embedding that is given by the order in which edges leave a node. Moreover, such a drawing defines a total order on 𝒳, which we will denote by πθ.
Note that deletion of all reticulate edges in N produces a forest or collection of trees, {T1,…,Tk}, which we denote by ℱ(N). For any tree Ti in ℱ(N), let 𝒳i denote the set of taxa that label leaves of Ti. Note that Ti is not necessarily a phylogenetic tree because some (or even all) of its leaves may be unlabeled.
A topological embedding τ for ℱ(N) is given by specifying a topological embedding for each tree Ti in ℱ(N). Note that τ induces a total ordering of the taxon set 𝒳i for each Ti in ℱ(N). While τ determines a partial ordering <τ of 𝒳, it does not specify a total ordering of 𝒳 because the trees of ℱ(N) are not ordered.
Definition 3.1 (Non-interleaving order). —
Let N be a rooted phylogenetic network on 𝒳 and let τ be a topological embedding of ℱ(N). A total order π on 𝒳 is called non-interleaving with respect to τ if for any two taxa a<πb, we have:
If a,b∈𝒳i for some tree Ti, then a<τb;
If a∈𝒳i and b∈𝒳j (with i≠j), then there exists no taxa c∈𝒳i and d∈𝒳j such that a<πb<πc<πd.
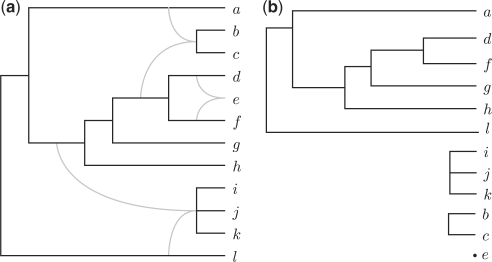
For example, for the phylogenetic network N on 𝒳={a,…,l} and the concrete drawing θ of the forest ℱ(N) in Figure 3, both (a,b,c,d,e,f,g,h,i,j,k,l) and (a,d,f,g,h,l,i,j,k,b,c,e) are non-interleaving total orders on 𝒳 w.r.t. θ, while (a,d,f,g,h,i,j,l,k,b,c,e) is not because it violates condition (2) of Definition 3.1.
Fig. 3.
(a) A phylogenetic network N. (b) A concrete drawing τ of the forest ℱ(N). This drawing induces a partial order of the leaves such that a<τd<τf<τg<τh<τl, i<τj<τk, and b<τc.
What is the relevance of this definition? We want to be able to draw a rooted phylogenetic network N in such a way that we preserve the given topological embedding τ of its forest and also that we place all leaves of the network along a line in the order specified by π and the root occurs on the outside of the drawing. The non-interleaving property ensures that this can be done in such a way that no two tree edges cross.
3.1 Definition of a tanglegram for networks
Let N1 and N2 be two rooted phylogenetic networks on taxon sets 𝒳1 and 𝒳2, respectively. We will use M⊆𝒳1×𝒳2 to denote a set of connectors between 𝒳1 and 𝒳2. If the two networks are on the same taxon set, then M is the set of identity connectors that connects each taxon to itself, which we will denote by MId below for emphasis. In the case of a host-parasite comparison, M will pair hosts and parasites.
Unlike trees, rooted phylogenetic networks are not necessarily planar and so the definition of a tanglegram is not immediately obvious for them:
Definition 3.2 (Tanglegram for networks). —
Let N1 and N2 be two rooted phylogenetic networks on 𝒳1 and 𝒳2, respectively, and let M be a set of connectors between 𝒳1 and 𝒳2. A tanglegram Z for N1, N2 and M is specified by a system (N1,𝒳1,τ1,π1,N2,𝒳2,τ2,π2,M) where τi is a topological embedding of ℱ(Ni) and πi is a non-interleaving total order of 𝒳i with respect to τi, for i=1,2.
Let N be a rooted phylogenetic network on 𝒳. Consider a concrete drawing θ of N in the plane. We call θ a rooted outer-labeled (tree-)planar embedding if all taxon labels are placed on a line, the root node occurs on the outside of the embedded network and no two (tree) edges cross. If N possesses a non-interleaving order π of 𝒳 with respect to a topological embedding τ for ℱ(N), then there exists a rooted outer-labeled tree-planar embedding for N in which the taxa appear along a line in the order specified by π. As mentioned above, the non-interleaving property of π ensures that we can lineup appropriate embeddings of all the trees in ℱ(N) in the order induced by π.
A drawing of a tanglegram Z=(N1,𝒳1,τ1,π1,N2,𝒳2,τ2,π2,M) consists of a rooted outer-labeled tree-planar embedding of both N1 and N2, together with a set of lines representing the connectors between 𝒳1 and 𝒳2. Such a drawing of Z can be obtained in the following steps. First draw all trees in ℱ(N1) and ℱ(N2) in such a way that the two orderings τ1 and τ2 are respected and all the leaves of N1 and N2 are lined up in the order specified by π1 and π2. Second, add all reticulate edges to the diagram. These two steps can always be done in such a way that no two tree edges cross and that the roots of N1 and N2 occur on the outside of the drawing, due to the fact that both π1 and π2 are non-interleaving. Finally, draw lines between the leaves of the two networks so as to connect taxa as specified in M.
Note that, if N1 and N2 are two trees, F(N1) and F(N2) coincide with N1 and N2, respectively. This means that, in this case, a tanglegram between N1 and N2 define univocally the rooted outer-labeled tree-planar embeddings of N1 and N2. Giving an embedding, drawing a tree is straightforward (see Huson et al., 2011), Chapter 13). Therefore, our definition of a tanglegram for two rooted phylogenetic networks generalizes the definition of a tanglegram for two rooted phylogenetic trees, and so, in particular, the problem of computing an optimal tanglegram for networks is NP-complete (Fernau et al., 2010).
Let N be a rooted phylogenetic network on 𝒳, let τ be a topological embedding of ℱ(N) and let π be a non-interleaving total order on 𝒳. We define the reticulation crossing number as the minimum number of crossings involving reticulation edges in any drawing of N respecting τ and π. An optimal tanglegram can now be defined as follows:
Definition 3.3 (Optimal tanglegram). —
Let N1 and N2 be two rooted phylogenetic networks on 𝒳1 and 𝒳2, respectively, and let M be a set of connectors between 𝒳1 and 𝒳2. A tanglegram Z=(N1,𝒳1,τ1,π1,N2,𝒳2,τ2,π2,M) is called optimal if the crossings between connectors in M is minimized by τ1 and τ2 and, among the tanglegrams minimizing this value, it can be drawn so as to minimize the sum of reticulation crossing numbers for N1 and N2.
Let N1 and N2 be two rooted phylogenetic networks on 𝒳1 and 𝒳2, respectively, and let M be a set of connectors between 𝒳1 and 𝒳2. For two linear orderings π1 and π2 of 𝒳1 and 𝒳2, the number of crossings Cr(π1,π2,M) among connectors in M can be calculated as |{(a,b)∈M×M∣a=(p,q),b=(x,y) with (p<πx∧q>πy)ν(p>πx∧q<πx)}|. A heuristic that computes the reticulate crossing number for a drawing of a rooted phylogenetic network is described in (Huson, 2009).
3.2 Neighbor-net heuristic for tanglegrams
Let N1 and N2 be two rooted phylogenetic networks on 𝒳1 and 𝒳2, respectively, and let M be a set of connectors between 𝒳1 and 𝒳2. For the purposes of this paper, we will assume that M pairs the leaves of the two trees in a one-to-one manner. (Note, however, that the example shown in Figure 1 does not have this property.) If M pairs two distinct taxa a and b, as for example in a host/parasite study, then we identify the labels a and b with each other while computing the tanglegram, but then distinguish between the two labels when drawing the tanglegram.
In the following, we present a heuristic for obtaining an optimal tanglegram for N1 and N2. We call this the NN-tanglegram approach.
In our approach, we first compute a distance matrix H on the total set of taxa 𝒳=𝒳1∪𝒳2 that reflects the topology of the two networks N1 and N2, then apply the Neighbor-Net algorithm to H to obtain an ordering π of 𝒳, and finally construct a tanglegram for N1 and N2 based on π. In the following, we will assume that both networks contain a single leaf connected to the root of the network that is labeled by a special taxon ρ, which we will refer to as a formal outgroup.
To compute a distance matrix on 𝒳, we need to construct a set of splits for each of the two networks. We describe the process for the network N1. For each tree edge e in N1 let C1(e) be the set of all taxa that label a leaf that lies below e in N1. We define the split associated with e as C(e)∣𝒳1∖C1(e)). Let Σ(N1) denote the set of all splits obtained in this way. We compute Σ(N2) similarly and we then define Σ=Σ(N1)|X1∩X2∪Σ(N2)|X1∩X2. (The restriction to 𝒳1∩𝒳2 ensures the applicability of Theorem 3.5 if 𝒳1≠𝒳2).
We obtain the distance matrix H on 𝒳 by setting the distance between two taxa x and y equal to the number of splits that separate the two taxa, where any split that occurs both for N1 and N2 is counted twice. In other words, we set H=D(Σ(N1)|X1∩X2)+D(Σ(N2)|X1∩X2).
In the simulation study in Section 5.1, we will also present the results when using H′=Dpath(N1)+Dpath(N2) as distance matrix, where Dpath(Ni)={dxy} such that dxy is the length of the shortest path between x and y in Ni. As we will see, this variant actually performs better on networks than using splits-based distances.
We apply the Neighbor-Net algorithm to the distance matrix H (or H′ in the case that the shortest path distance matrix is used) so as to obtain a circular ordering ζ=(x1,…,xn) of 𝒳. The ordering ζ is computed in this way because this ensures that the NN-tanglegram method returns the optimal solution under optimal conditions (see Theorem 3.5). Let i denote the position of the formal outgroup taxon ρ in ζ. We obtain a linear ordering π of 𝒳 by breaking the ordering ζ at position i, that is, by setting π=(xi,xi+1,…,xn,x1,…,xi−1). Given the ordering π of 𝒳, we now have to compute two embeddings τ1 and τ2 for the forests ℱ(N1) and ℱ(N2) such that π is non-interleaving with respect to τ1 and τ2. Given a rooted phylogenetic network N and a node u of N, we use 𝒳N(u) to denote the set of taxa that label the leaves below u.
To compute τ1, we first delete all reticulate edges in N1 to produce the forest ℱ(N1). Then, for each T*∈ℱ(N1), we determine a topological embedding τ* that minimizes the number of crossings among connectors Cr(ζ*,π,MId), where ζ* is the ordering of 𝒳* induced by the embedding τ*. This optimization is easily solved in a bottom-up traversal of each tree in ℱ(N1). Note that the place that is assigned to a node v such that 𝒳N1(v)=∅ or 𝒳N1(v)|𝒳1∩𝒳2=∅ in the the topological embedding of its parent is not relevant for the computation of the number of crossings among connectors Cr(ζ*,π,MId) and so can be chosen arbitrarily. The set of topological embeddings for all trees T* in ℱ(N1) constitutes τ1. To obtain π1 from τ1, we add the taxa of 𝒳1 to π1 one by one, in such a way that π1 remains non-interleaving w.r.t. τ1 and the value of Cr(π1,π,MId) is minimized. The ordering τ2 is computed in exactly the same way but using the network N2 instead of N1.
Let 𝒞(N) be the set of clusters associated with N. We say that 𝒞(N) is interval-realizable with respect to π=(x1,x2,…,xn) if each cluster C in 𝒞(N) has the form {xp,xp+1,…,xq}, for appropriately chosen 1≤p≤q≤n. We have the following result:
Lemma 3.4 (Interval realizability). —
Let N be a phylogenetic network on 𝒳. If N has a rooted outer-labeled planar embedding θ and πθ is the linear order on 𝒳 that is defined by θ, then 𝒞(N) is interval-realizable with respect to πθ.
This lemma is used to prove the following theorem:
Theorem 3.5 (Zero crossings solution). —
Let N1 and N2 be two rooted phylogenetic networks on 𝒳1 and 𝒳2, respectively and let M be a set of connectors between 𝒳1 and 𝒳2. If a planar drawing exists for the tanglegram of N1, N2 and M, then the NN-tanglegram heuristic will find a solution with zero crossings among connectors.
The proof of both results can be found in Appendix A. Note that Theorem 3.5 ensures that, if an optimal tanglegram with cost zero exists for two trees, then our algorithm will find it, because a tree does not contain any reticulate edges.
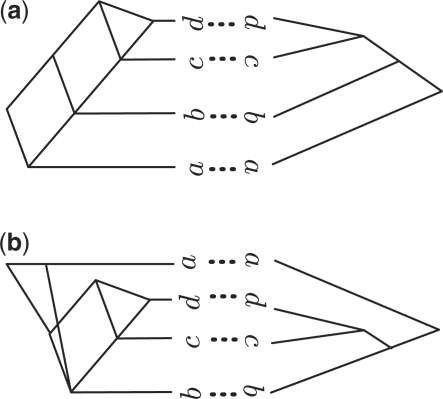
This is not true for networks. Indeed, in this case the Neighbor-Net algorithm may have more than one optimal solution. Theorem 3.5 ensures that any linear ordering π computed as described in Section 3.2 can be realized with zero crossings among connectors, but it does not guarantee that the resulting drawing will have zero crossings involving reticulate edges. For example, for the two networks in Figure 4, both orders (a,b,c,d) and (b,c,d,a) are circular with respect to H=D(Σ(N1))+D(Σ(N2)) and can be obtained from the distance matrix H using Neighbor-Net. Both orderings give a solution with zero crossings among connectors; yet, while a planar drawing for (a,b,c,d) exists [see Fig. 4(a)], a drawing respecting the ordering (b,c,d,a) will contain some crossings involving reticulate edges and thus fail to be optimal [see Fig. 4(b)]. However, if all optimal solutions of Neighbor-Net given H can be considered, then the NN-tanglegram approach will find the solution with cost zero. In such a case, our algorithm can be used to solve the planar layout (Lozano et al., 2008) or drawability problem (Fernau et al., 2010) for two networks [solved in linear time for two binary trees in (Fernau et al., 2010)].
Fig. 4.
A pair of networks for which our approach may fail to find the optimal solution. (a) An optimal ordering and (b) an ordering that needs to be drawn with at least one crossing.
3.3 Minimizing the reticulation crossing number and drawing the tanglegram
The previous section describes a heuristic for computing an optimal tanglegram. This heuristic aims at minimizing the crossings among connectors but it does not try to minimize the reticulation crossing numbers for N1 and N2. For example, if 𝒳1≠𝒳2 then multiple choices of π1 and π2 can exist that minimize the number of crossing among connectors. In such a case, one of them is chosen at random, whether or not it happens to minimize the sum of reticulation crossing numbers for N1 and N2 (see Definition 3.3). In a forthcoming paper (Scornavacca and Huson, 2011), we will describe a heuristic for minimizing this value and a method for computing a concrete drawing of the optimized tanglegram that tries to minimize the crossing involving reticulation edges (as implemented in Dendroscope 3).
4 ALIGNMENT OF PHYLOGENETIC NETWORKS
The heuristic for calculating an optimal tanglegram for rooted phylogenetic networks that we describe in Section 3.2 is easily extended to a set of more than two rooted phylogenetic networks or trees, simply by computing the matrix H based on splits from all the networks or trees under consideration. This is implemented in our program Dendroscope 3 and can be used to ‘align’ the taxa when viewing a whole collection of networks or trees simultaneously.
5 VALIDATION
To validate the approach, we first report on a simulation study that we have undertaken and then apply the algorithm to a published dataset to illustrate how the algorithm may be used in practice.
5.1 Simulation study
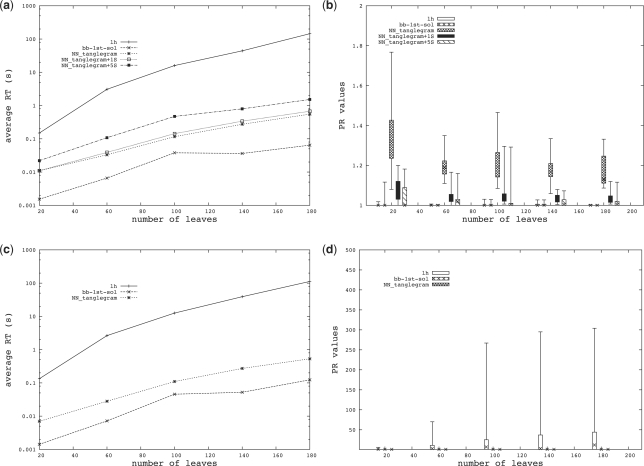
In the first part of the simulation study, we compared our implementation with the best available software for computing tanglegrams of trees. In more detail, we compared against the bb-1st-sol algorithm, as it is the best performing algorithm of the five presented in Nöllenburg et al. (2009), and against the lh algorithm, as it has similar performance to the other algorithms described in Bansal et al. (2009), while being faster. Since these algorithms only accept binary trees, we first restricted our attention to binary trees. We compared these two published methods against our NN-tanglegram heuristic and two variants of it, which we will refer to as NN-tanglegram+1S and NN-tanglegram+5S. These two variants first compute π1 and π2 as described in Section 3.2, then define π as the order π1 restricted to the common taxa and finally use π to compute the new orders π1 and π2 as described in Section 3.2. NN-tanglegram+5S executes this step 5 times, alternating π1 and π2 to compute the new π. Since the NN-tanglegram heuristic performs similarly on trees when using the splits-based distance H or the shortest path distance matrix H′, we will present the results only for the former variant. All runs were executed on a 2.53 GHz processor with 4 GB of RAM.
For the first dataset, which we will refer to as D1, we created 6 random binary trees on the same taxon set for five different sizes, namely on 20, 60, 100, 140 and 180 taxa. This dataset contains 15 instances to solve for each taxon set. Each instance was formulated as an ILP (integer linear program) as described in Nöllenburg et al. (2009) and then solved using lpSolve (freely available from lpsolve.sourceforge.net/5.5/). The number of replicates considered for each parameter setting was limited by the long running time of the ILP solver. In the second dataset, D2, we created 10 random binary trees for each of the 5 sizes listed above, ensuring in each case that a tanglegram with zero crossings among connectors exists. This dataset contains 45 instances to solve for each taxon set.
For each tanglegram and each method, we computed the performance ratio (PR), that is, the ratio (cn+1)/(cnopt+1), where cn and cnopt are the computed and the optimum number of crossings among connectors, respectively. The performance ratio values and the average running time for each method are shown in Figure 5.
Fig. 5.
(a) Average running time (RT) and (b) performance ratio values (PR) for dataset D1. (c) Average running time (RT) and (d) performance ratio values (PR) for dataset D2.
For both datasets, the best-performing method is bb-1st-sol, having the lowest PR values and the lowest average running time. Note that this method is guaranteed to find a solution with zero crossings, if one exists (Nöllenburg et al., 2009), just like our NN-tanglegram heuristic [see Fig. 5(d)]. However, the method is restricted to binary trees, unlike our method, which also applies to multifurcating trees. On the first dataset lh appears to perform well and its PR values are comparable with those of bb-1st-sol. However, when the number of instances per taxon set is increased (as in dataset D2), this method can perform very badly for some instances [see Fig. 5(d)], although the average PR values remain low. Moreover, the average running time of lh is unacceptably high for use in an interactive visualization tool [on average >100 s when the cardinality of the taxon set is 180, see Fig. 5(a,c)].
Our new method, although designed for the general case of networks, also performs well for binary trees, while the average running time is low. Comparing the performance of NN-tanglegram with NN-tanglegram+1S and NN-tanglegram+5S, we can see that the swapping step, as expected, improves the PR values but increases the average running time. However, swapping one time (as done in NN-tanglegram+1S) is highly recommended because the achieved improvement of the PR values is worth the small increase in running time. In our implementation, the user can choose how many times to swap or can abort the swapping procedure after a given amount of time.
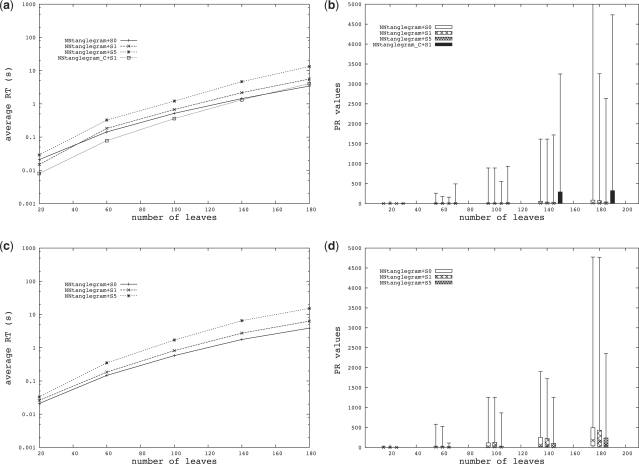
In the second part of the simulation, we studied the performance of our methods on two different network datasets. For both datasets (D3 and D4), we created 15 random binary networks (not necessarily bicombining) on the same taxon set for 5 different sizes, namely on 20, 60, 100, 140 and 180 taxa, ensuring in each case that a tanglegram with zero crossings among connectors exists. This leads to 105 instances to solve for each taxon set. The two datasets differ by the probability to add a reticulate edge between two nodes, which is higher for D4. (This implies that D4 on average contains more reticulations than D3 and thus is a more complicated dataset than the latter.)
For both datasets, we compared the performance of NN-tanglegram with NN-tanglegram+1S and NN-tanglegram+5S. Since the NN-tanglegram heuristic performs a lot better on networks when using the shortest path distance matrix H′ rather than the splits-based distance H [see Figure 6(b), NN-tanglegram+1S vs NN-tanglegram_C+1S], we will discuss the results only for the former variant.
Fig. 6.
(a) Average running time (RT) and (b) performance ratio values (PR) for datasets D3. (c) Average running time (RT) and (d) performance ratio values (PR) for datasets D4.
As expected, the PR values and average running times are higher than for the binary tree datasets but still acceptably low for use in an interactive visualization tool [see Fig. 6]. The PR values increase both with the number of leaves and the number of reticulations in the networks [see Fig. 6(b,d)]. The pattern of relations among NN-tanglegram, NN-tanglegram+1S and NN-tanglegram+5S is the same than for the tree datasets (i.e. the swapping step improves the PR values but increases the average running time).
In general, although the average PR values remain low, the methods can produce tanglegrams with high numbers of crossings among connectors for some instances. Note that, when the number of leaves in the networks is large, the crossing number can easily be very high. For example, if the two networks under consideration have 180 leaves each and if only one taxon is incorrectly placed at the two different ends of the networks, then the crossing number will be at least 179. Nevertheless, in this case the tanglegram may still be useful for visualizing similarities and differences among the two networks.
5.2 Application to published data
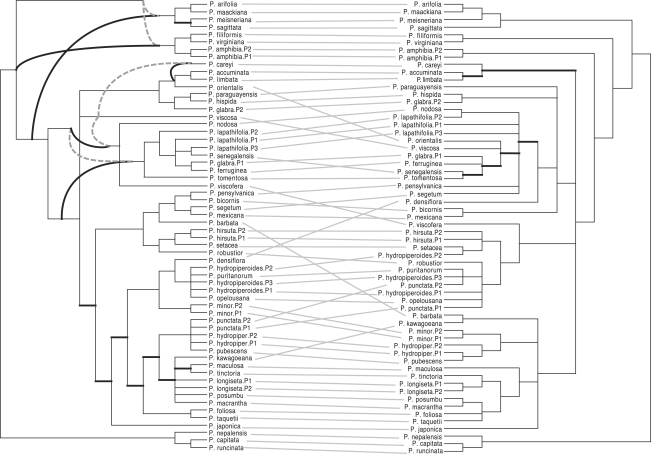
Persicaria is a genus of plants in the family Polygonaceae. In (Kim and Donoghue, 2008), the authors present evidence of hybrid speciations within this genus using cpDNA regions and nuclear ITS sequences. The strict consensus tree from the most parsimonious (MP) trees and the maximum likelihood (ML) tree were computed and drawn superposed on each other for both the cpDNA and nuclear ITS datasets. A tanglegram between the two superposed drawings (one for the cpDNA dataset and nuclear ITS dataset, respectively) with crossing number among connectors 244 was shown. Here, instead of superposing the drawing of the strict consensus MP tree and the ML tree, we show both trees embedded in a network. The tanglegram between the network obtained by combining the strict consensus MP tree and the ML tree for the cpDNA dataset and the one obtained by the nuclear ITS dataset is shown in Figure 7. This tanglegram is much clearer than the original representation see Fig. 1 of(Kim and Donoghue, 2008).
Fig. 7.
A tanglegram between the networks obtained by analyzing the nrITS dataset (left) and the cpDNA dataset (right). For each dataset, the edges present only in the ML tree or in the strict consensus MP tree, are shown as bold black lines, or bold dotted gray lines, respectively. Data from (Kim and Donoghue, 2008).
6 CONCLUSIONS
Tanglegrams are a useful tool for comparing rooted phylogenetic trees. In this article, we have extended them to rooted phylogenetic networks and have described a practical approach to their computation. The simulation study proves that our new method, although designed for the general case of networks, also performs well for binary trees, while the average running time stays low. Moreover, the performance of our method on networks is good enough for use in an interactive visualization tool. Our implementation in the popular tree-drawing program Dendroscope will make tanglegrams for trees and networks easily accessible to biologists and other users.
ACKNOWLEDGEMENTS
The authors would like to thank Mukul S. Bansal and Martin Nöllenburg for providing them with an implementation of their methods.
Conflict of Interest: none declared.
APPENDIX A
A.1 Proof of Lemma 3.4
To obtain a contradiction, assume that 𝒞(N) is not interval-realizable with respect to an order π and there exists a rooted outer-labeled planar embedding θ such that πθ=π. Let C be a cluster in 𝒞(N) that is not interval-realizable with respect to π. Then there exist three taxa a,b,c∈𝒳 such that a,b∈C, c∉C and a<πc<πb. Let v be the target node of a tree edge in N that represents C and let p1 and p2 two paths connecting v to the leaves labeled by a and b, respectively. By definition of a rooted phylogenetic network, there exists a direct path p3 connecting c to the root node ρ. Since any p3 cannot include v, the Jordan curve theorem implies that p3 has to cross p1 or p2, a contradiction.
A.2 Proof of Theorem 3.5
For ease of exposition, assume that 𝒳1=𝒳2 holds. Since both N1 and N2 can be represented by rooted outer-labeled planar graphs, it follows from Lemma 3.4 that 𝒞(N1) and 𝒞(N2) are interval-realizable for some orders π1 and π2 of 𝒳, respectively. From the definition of ∑(·) we have that both ∑(N1) and ∑(N2) fulfill Definition 2.2 with respect to π1 and π2 and thus are circular split systems. Thus, by definition, D(∑(N1)), D(∑(N2)) and D(∑(N1))+D(∑(N2)) are circular. It follows, from the consistency of Neighbor-Net (Theorem 2.3), that the split set ∑(N1)∪∑(N2) is circular with respect to the circular ordering π computed by the Neighbor-Net algorithm. Note that also ∑(N1) and ∑(N2) are circular with respect to π and thus the linear ordering π is by definition a circular ordering for ∑(N1) and ∑(N2) too. The definitions of ∑(·) and of π imply that the sets 𝒞(N1) and 𝒞(N2) are interval-realizable with respect to π.
It remains to be established that the ordering π1 (similar for π2) returned by the Neighbor-Net tanglegram heuristic is such that π1=π. To establish this, we have to show that, if 𝒞(N1) is interval-realizable with respect to π, then there exists an embedding τ1 of ℱ(N1) such that π is a non-interleaving order w.r.t. τ1. Note that, for each T*∈ℱ(N1) on a taxon set 𝒳*, the cluster set 𝒞(T*) is a subset if 𝒞(N1) and thus is interval-realizable with respect to π; second, 𝒞(T*) is compatible. This implies that we can construct an embedding τ* of T* with 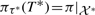 that can be drawn in such a way that no two tree edges cross. Thus, the set of topological embeddings for all trees T* in ℱ(N) constitutes a topological embedding τ1 for ℱ(N1) such that π satisfies condition (1) of Definition 3.1 w.r.t. τ1. But π also satisfies condition (2) of Definition 3.1 w.r.t. τ1, otherwise 𝒞(N1) would not be interval-realizable with respect to π. From these observations, it follows that we can construct an embedding τ1 for the forest ℱ(N1) such that π is a non-interleaving order w.r.t. τ1 as described in Section 3.2. This concludes the proof.
that can be drawn in such a way that no two tree edges cross. Thus, the set of topological embeddings for all trees T* in ℱ(N) constitutes a topological embedding τ1 for ℱ(N1) such that π satisfies condition (1) of Definition 3.1 w.r.t. τ1. But π also satisfies condition (2) of Definition 3.1 w.r.t. τ1, otherwise 𝒞(N1) would not be interval-realizable with respect to π. From these observations, it follows that we can construct an embedding τ1 for the forest ℱ(N1) such that π is a non-interleaving order w.r.t. τ1 as described in Section 3.2. This concludes the proof.
REFERENCES
- Bansal M.S., et al. BICoB '09: Proceedings of the 1st International Conference on Bioinformatics and Computational Biology. Berlin, Heidelberg: Springer; 2009. Generalized binary tanglegrams: Algorithms and applications; pp. 114–125. [Google Scholar]
- Böcker S., et al. 4th International Workshop of Parameterized and Exact Computation. Vol. 5917. Springer; 2009. A faster fixed-parameter approach to drawing binary tanglegrams; pp. 38–49. of LNSC. [Google Scholar]
- Bryant D., Moulton V. Neighbor-net: an agglomerative method for the construction of phylogenetic networks. Mol. Biol. Evol. 2004;21:255–265. doi: 10.1093/molbev/msh018. [DOI] [PubMed] [Google Scholar]
- Bryant D., et al. Consistency of the Neighbor-Net algorithm. Algorithms Mol. Biol. 2007;2:8. doi: 10.1186/1748-7188-2-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buchin K., et al. Proceedings of the 16th International Symposium on Graph Drawing. Vol. 5417. Springer; 2009. Drawing (complete) binary tanglegrams: Hardness, approximation, fixed-parameter tractability; pp. 324–335. of LNCS. [Google Scholar]
- Buneman P. The recovery of trees from measures of dissimilarity. In: Hodson F.R., et al., editors. Mathematics in the Archaeological and Historical Sciences. Edinburgh, UK: Edinburgh University Press; 1971. pp. 387–395. [Google Scholar]
- Burt A., Trivers R. Genes in Conflict: The Biology of Selfish Genetic Elements. 1st. Harvard, USA: Belknap Press of Harvard University Press; 2008. [Google Scholar]
- Charleston M. Jungles: a new solution to the host/parasite phylogeny reconciliation problem. Math. Biosci. 1998;149:191–223. doi: 10.1016/s0025-5564(97)10012-8. [DOI] [PubMed] [Google Scholar]
- Charleston M.A., Perkins S.L. Lizards, malaria, and jungles in the caribbean. In: Page R.D.M., editor. Tangled Trees: Phylogeny, Cospeciation, and Coevolution. Chicago, USA: The University of Chicago Press; 2003. pp. 65–92. [Google Scholar]
- Dress A.W.M., Huson D.H. Constructing splits graphs. IEEE/ACM Trans. Comput. Biol. Bioinformatics. 2004;1:109–115. doi: 10.1109/TCBB.2004.27. [DOI] [PubMed] [Google Scholar]
- Dwyer T., Schreiber F. Australasian Symposium on Information Visualisation. Vol. 35. ACS; 2004. Optimal leaf ordering for two and a half dimensional phylogenetic tree visualisation; pp. 109–115. of CRPIT. [Google Scholar]
- Fernau H., et al. The 25th Conference on Foundations of Software Technology and Theoretical Computer Science. Vol. 3821. Springer; 2005. Comparing trees via crossing minimization; pp. 457–469. of LNSC. [Google Scholar]
- Fernau H., et al. Comparing trees via crossing minimization. J. Comput. Syst. 2010;76:593–608. [Google Scholar]
- Huson D.H. Drawing rooted phylogenetic networks. IEEE/ACM Trans. Comput. Biol. Bioinformatics. 2009;6:103–109. doi: 10.1109/TCBB.2008.58. [DOI] [PubMed] [Google Scholar]
- Huson D.H., Scornavacca C. A survey of combinatorial methods for phylogenetic networks. Genome Biol. Evol. 2011a;3:23–35. doi: 10.1093/gbe/evq077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huson D.H., Scornavacca C. Dendroscope 3 - a program for computing and drawing rooted phylogenetic trees and networks. 2011b In preparation, software available from: www.dendroscope.org. [Google Scholar]
- Huson D.H., et al. Dendroscope: an interactive viewer for large phylogenetic trees. BMC Bioinformatics. 2007;8:460. doi: 10.1186/1471-2105-8-460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huson D.H., et al. Phylogenetic Networks: Concepts, Algorithms and Applications. Cambridge, UK: Cambridge University Press; 2011. [Google Scholar]
- Kim S.-T., Donoghue M.J. Incongruence between cpDNA and nrITS trees indicates extensive hybridization within eupersicaria (polygonaceae) Am. J. Bot. 2008;95:1122–1135. doi: 10.3732/ajb.0700008. [DOI] [PubMed] [Google Scholar]
- Lee M.-M., Stock S. A multilocus approach to assessing co-evolutionary relationships between Steinernemaspp. (nematoda: Steinernematidae) and their bacterial symbionts Xenorhabdusspp. (γ-proteobacteria: Enterobacteriaceae) Syst. Parasitol. 2010;77:1–12. doi: 10.1007/s11230-010-9256-9. [DOI] [PubMed] [Google Scholar]
- Lozano A., et al. Seeded tree alignment. IEEE/ACM Trans. Comput. Biol. Bioinformatics. 2008;5:503–513. doi: 10.1109/TCBB.2008.59. [DOI] [PubMed] [Google Scholar]
- Machado C.A., et al. Critical review of host specificity and its coevolutionary implications in the fig/fig-wasp mutualism. Proc. Natl Acad. Sci. USA. 2005;102(Suppl. 1):6558–6565. doi: 10.1073/pnas.0501840102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merkel V., et al. Distribution and phylogeny of immunoglobulin-binding protein G in Shiga toxin-producing Escherichia coli and its association with adherence phenotypes. Infect. Immun. 2010;78:3625–3636. doi: 10.1128/IAI.00006-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nöllenburg M., et al. Proceedings of the Eleventh Workshop on Algorithm Engineering and Experiments (ALENEX) SIAM; 2009. Drawing binary tanglegrams: an experimental evaluation; pp. 106–119. [Google Scholar]
- Scornavacca C., Huson D. Drawing phylogenetic networks with constraints on the order of taxa. 2011 In preparation. [Google Scholar]
- Venkatachalam B., et al. Untangling tanglegrams: comparing trees by their drawings. IEEE/ACM Trans. Comput. Biol. Bioinformatics. 2010;7:588–597. doi: 10.1109/TCBB.2010.57. [DOI] [PubMed] [Google Scholar]