QAARM: quasi-anharmonic autoregressive model reveals molecular recognition pathways in ubiquitin

Abstract

Motivation: Molecular dynamics (MD) simulations have dramatically improved the atomistic understanding of protein motions, energetics and function. These growing datasets have necessitated a corresponding emphasis on trajectory analysis methods for characterizing simulation data, particularly since functional protein motions and transitions are often rare and/or intricate events. Observing that such events give rise to long-tailed spatial distributions, we recently developed a higher-order statistics based dimensionality reduction method, called quasi-anharmonic analysis (QAA), for identifying biophysically-relevant reaction coordinates and substates within MD simulations. Further characterization of conformation space should consider the temporal dynamics specific to each identified substate.

Results: Our model uses hierarchical clustering to learn energetically coherent substates and dynamic modes of motion from a 0.5 μs ubiqutin simulation. Autoregressive (AR) modeling within and between states enables a compact and generative description of the conformational landscape as it relates to functional transitions between binding poses. Lacking a predictive component, QAA is extended here within a general AR model appreciative of the trajectory's temporal dependencies and the specific, local dynamics accessible to a protein within identified energy wells. These metastable states and their transition rates are extracted within a QAA-derived subspace using hierarchical Markov clustering to provide parameter sets for the second-order AR model. We show the learned model can be extrapolated to synthesize trajectories of arbitrary length.

Contact: ramanathana@ornl.gov; chakracs@pitt.edu

1 INTRODUCTION

Conformational changes in proteins constitute the underlying behavior of cellular regulation. As part of regulating cellular homeostasis, proteins perform a number of functions through native fluctuations at multiple length- and timescales. A variety of experimental techniques have illuminated the linkage between protein dynamics and function; however, resolving the precise spatio-temporal relationships in protein motions which confer biological function remains a long-standing challenge in protein biochemistry (Henzler-Wildman and Kern, 2007).

Governing the protein's rich conformational space is a high-dimensional energy landscape with multiple hills and valleys (Elber and Karplus, 1987; Frauenfelder et al., 1988, 1991). To characterize this energy surface, theoretical and computational modeling of protein dynamics have been widely used (Agarwal, 2006; Bahar and Cui, 2003), as have molecular dynamics (MD) and Monte Carlo techniques to provide atomistic insights into protein fluctuation (Karplus and McCammon, 2002). These techniques are now being extensively used to investigate various biophysical and biochemical processes including protein-ligand binding (Simonson et al., 2002), protein folding (Balbach et al., 1995; Bowman G. and Pande, 2010) and enzyme catalysis (Agarwal, 2006).

As the timescales accessible to all-atom MD (and other coarse-grained approaches) continue to reach the micro- and milli-second timescales, the data generated from such simulations can potentially reach O(petabytes). The availability of large datasets that cover the native-state dynamics and folding and unfolding pathways of the entire foldome, called Dynameomics (van der Kamp et al., 2010), has allowed scientists to simulate over 2000 proteins with a combined timescale of 340 μs. Projects such as Folding@home (Beberg et al., 2009) have also accelerated the availability of large datasets of protein folding trajectories as have specialized hardware, such as Anton (Shaw et al., 2007), field-programmable gate-arrays (FPGA; Alam et al., 2007), and GPUs (Harvey et al., 2009).

The availability of such datasets, while useful, has created new challenges in (i) extracting low-dimensional, biophysically relevant coordinates that elucidate how the protein functions (for example, how a protein recognizes its binding partner), (ii) separating the landscape spanned by the simulations (or even groups of simulations) into a coherent set of conformational substates, (iii) quantifying the intrinsic structural and dynamical properties within a substate and finally, (iv) determining transition rates between these conformational substates. Indeed, important dynamical phenomena within simulated trajectories must be extracted from an enormous quantity of non-specific, ambient fluctuations. Clustering techniques for mining this noisy conformational space often use structural similarity measures, such as root-mean square deviation (RMSD) which quantifies an average value of structural deviation. However, functional motions need not elicit large global RMSD values; indeed, localized protein regions commonly exhibit small but important flexibility.

These observations motivated us to examine the statistical nature of atomic fluctuations from long timescale simulations (Ramanathan et al., 2009; 2011b). Our studies across multiple simulations (and multiple force-fields) reveal that functionally relevant motions generally occur rarely. These events are reflected in higher-order correlations, manifested in long-tailed spatial (fluctuation) distributions (Mao et al., 1982). Techniques reliant on second-order statistics (variance) are poorly suited to resolve such higher-order correlations in the data, and we have observed that linear orthogonal bases (as in principal component analysis (Amadei et al., 1993)) poorly describe some energy landscapes. Thus, the current frameworks to analyze long timescale trajectories do not guarantee that identified substates are correlated with biophysically relevant events.

We recently put forward a low-dimensional representation of protein motions at long timescales using a novel technique, quasi-anharmonic analysis (QAA; Ramanathan et al., 2011a). QAA partitions the conformational landscape using fourth-order spatial-fluctuation statistics and detects substates with energetic coherence. Each region contains conformers that show similarity with respect to biophysically relevant order parameters. The insights gained from QAA were effectively used to resolve higher-order dependencies in spatial fluctuations in the context of molecular recognition and enzyme catalysis.

While QAA effectively captures spatial correlations, it lacks a stochastic model of the underlying dynamics and substate transitions. To address this shortcoming, we build autoregressive (AR) models to both encode local protein dynamics accessible within energetically coherent substates and permit transitions between connected regions in the landscape. We call this method the quasi-anharmonic autoregressive model (QAARM). Within a QAA-derived subspace, metastable states and their transition rates are extracted using hierarchical Markov clustering which provides parameter sets for the second-order AR model. We show that the learned AR model can be extrapolated to synthesize trajectories of arbitrary length. We exploit the time-invariant statistical regularities within protein motions to investigate equilibrium fluctuations of ubiquitin, a widely studied protein involved in the proteosomal degradation pathway. We show that QAARM can extract and synthesize pathways by which ubiquitin adapts its binding surface to recognize a variety of substrates.

2 RELATED WORK

Previous studies have focused on the use of AR models in the frequency domain to understand memory functions in MD simulations (Kneller and Hinsen, 2001). The approach has been used to interpret quasi-elastic neutron scattering experiments (Kneller, 2005) and to accelerate MD simulations (Brutovsky et al., 2003). Using principal component analysis (PCA), Alakent et al. (2005a) pursued time-series analysis of MD simulations (Alakent et al., 2004, 2005b, 2007) to hierarchically describe the energy landscape and analyze explicit solvent effects on protein dynamics. However, PCA-based representations and their extensions are limited in their description of the conformational landscape (Balsera et al., 1996; Tai et al., 2008) due to assumed Gaussian fluctuations, and hence such approaches may not sufficiently describe conformational diversity (Lange and Grubmuller, 2006, 2008).

More recent kinetic modeling, based on Markov state models (MSM), can describe the kinetics associated with protein folding (Bowman G. and Pande, 2010; Chodera et al., 2007; West et al., 2007). MSMs commonly use RMSD values to first cluster simulation conformations into kinetically accessible micro-states and then iteratively merge these micro-states into several macro-states. MSMs can provide insights into macro-state dwell times (residence time) and can characterize mean first passage times. However, structure-based clustering need not result in energetically coherent substates. Our complementary but generative approach here explicitly pursues energetically coherent substates clusters which correspond intuitively to separated energy wells. (Chiang et al., 2010) recently developed a related approach based on Markov dynamic models (MDM), which includes a set of hidden states to capture conformational dependencies. The generative models resulting from MDM were applied on small systems such as alanine dipeptide. In comparison, we illustrate our results on real proteins such as ubiquitin and also demonstrate the utility of our approach to reveal molecular recognition pathways.

3 APPROACH

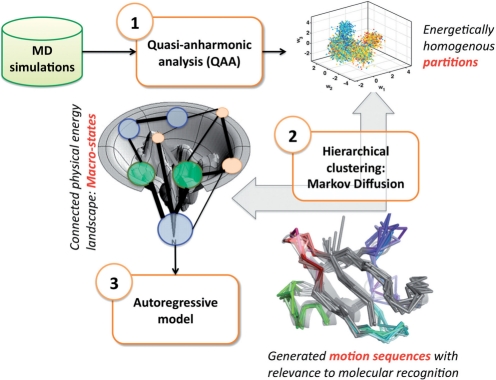
An overview of QAARM is shown in Figure 1. MD simulation data is first processed to remove rotational and translational degrees of freedom. QAA is then applied (Section 5) which outputs a reduced dimensional representation of the original MD data. Motivated to detect biophysically relevant energy wells, or highly populated regions, in the low-dimensional QAA space, we next use a simple Markov diffusion model to cluster the conformations into meta-stable substates (Section 6). Local dynamics within each substate are then captured by a linear, second-order AR model (Section 7) which explicitly models spatial fluctuations. The AR model thus extends the time-insensitive QAA model by considering temporal relationships between successive MD frames.

Fig. 1.

Overview of QAARM: We use MD simulations as input to QAA. The output of QAA is a reduced dimensional space, in which conformers clustered together represent micro-states. This reduced-dimensional space is then input into a Markov diffusion framework to identify clusters of conformations that are kinetically accessible. These clusters represent metastable macro-states. We then build second order AR models for each substate to identify pathways between metastable states.

4 MOLECULAR DYNAMICS SIMULATION OF HUMAN UBIQUITIN

Ubiquitin, a small globular protein, is involved in the proteosomal degradation pathway. It consists of 76 residues and folds into a well defined β-grasp fold. Ubiquitin's structure is evolutionarily conserved across all eukaryotes, consisting of five anti-parallel β-strands (β₁−β₅) as well as two α-helices. The primary binding surface (R1 in Fig. 3) of ubiquitin is composed of a small number of residues proximal to the flexible β₁−β₂ and β₃−β₄ loops. A secondary binding interface consists of the β₄−α₂ region. Ubiquitin binds to over 300 or more targets in the human cell and naturally has been the focus of many experimental and computational efforts to characterize molecular recognition (Meisenberg et al., 2006). With a large number of crystal structures and NMR conformers available (both substrate-free and substrate-bound), ubiquitin provides an ideal platform for studying protein dynamics in the context of biomolecular recognition.

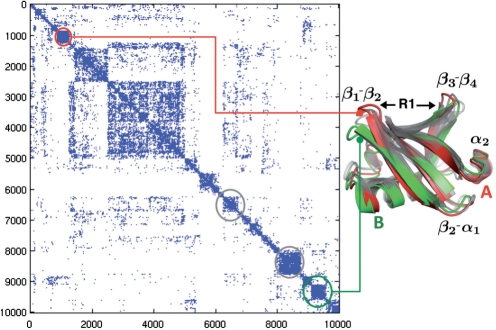
Fig. 3.

Markov diffusion clustering of QAA shows ubiquitin motions involved in binding substrates: The 30 dimensional space determined form QAA is used to construct a set of meta-stable states that are energetically accessible. From a group of 10 000 conformers, we show how the network is modeled with the adjacency matrix C₀ shown here. The Markov diffusion produces a total of 78 macro-states at level 4 of the hierarchy. To illustrate the extremum points in the network, we depict two representative clusters (A and B shown in red and green respectively) representing changes within the binding regions of ubiquitin. The primary binding region is indicated by R1.

The protocol for simulating ubiquitin in solution has been described in detail in Ramanathan and Agarwal (2009). Briefly, eight crystal structures of ubiquitin (PDB codes: 1UBQ, 1P3Q, 1S1Q, 1TBE, 1YIW, 2D3G, 2G45 and 2FCQ) were used for our simulation. Each simulation was carried out using the AMBER suite of tools, and each production run lasted a total of 62.5 ns. Hydrogen atoms were simulated using SHAKE algorithm, while electrostatics were evaluated using the particle mesh-ewald (PME) technique. A cut-off of 10 Å was used for long-range interactions (electrostatic and van der Waals). Conformations were stored every picosecond resulting in a total of 62,500 conformations per simulation. The simulations cumulatively constitute 0.5 μs of sampling in the ubiquitin landscape. For analyses only C^α atoms were used. All trajectory processing was performed with MATLAB.

5 QUASI-ANHARMONIC REPRESENTATION OF PROTEIN DYNAMICS

QAA is a general, statistically rigorous approach to identify non-Gaussian and rare behavior within extensive atomistic MD trajectories. It utilizes higher-order statistics of protein motions and is not restricted to orthogonal basis directions, a major compromise of existing techniques. QAA identifies energetically coherent substates in the conformational hierarchy and also possible transitions between these substates, consistent with the understanding that proteins sample from a hierarchical, multi-level energy landscape, with minima/maxima separated by energy barriers (Frauenfelder et al., 1988, 1991). Internal protein motions, driven by thermal energy in the solvent, enable proteins to explore this rugged landscape.

Here, we summarize quasi-anharmonic representation of protein motions in long timescale simulation trajectories based on diagonalization of a tensor of fourth-order statistics. This tensor describes positional fluctuations and their couplings. We use an efficient algebraic technique called joint-diagonalization of cumulant matrices (JADE), a well known algorithm in the machine learning literature for analyzing multi-variate data (Cardoso, 1999).

First, we assume that overall rotation/translation degrees of freedom have been removed and hence that positional fluctuations 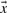are centered around the origin. Second, second-order correlations are removed from the fluctuation data. In particular, a covariance matrix G is estimated: 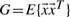, which is then diagonalized by orthogonal eigenvectors B and eigenvalues Σ using G=BΣB^T, followed by elimination of second-order correlations in with 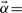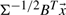, leaving 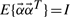, an identity matrix of size 3N×3N for N atoms under consideration.

Third, a fourth order cumulant tensor 𝒦 is estimated comprising both auto- and cross-cumulants given by

(1)

and

(2)

respectively. This expression is further simplified because 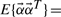, and hence E{α_iα_j}=1 when i=j and 0 when i≠j. The cumulant tensor will have a total 3N×(3N+1)/2 matrices each of size 3N×3N accounting for auto- and cross-cumulant terms.

Fourth, the fourth order dependencies denoted by the sum of the cross-cumulant terms are minimized, a procedure equivalent to diagonalizing the tensor 𝒦. No closed form solution exists for diagonalizing a tensor, however an approximate solution can be found using efficient algebraic techniques, such as Jacobi rotations (Golub and Van Loan, 1996). Just as the eigenbasis B diagonalizes the covariance matrix G, a rotation matrix J can be found which approximately diagonalizes the cumulant tensor 𝒦, leading to:

(3)

Substituting for 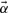from above:

(4)

and thus 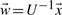implying

(5)

Thus, U represents anharmonic modes of motion derived by minimizing the fourth-order dependencies in positional fluctuations, in addition to eliminating the second-order correlations (as is the case with quasi-harmonic analysis). Unlike in approaches that use principal component analysis, U can be non-orthogonal and hence intrinsically coupled. The anharmonic modes of motion U_i, each a column vector of matrix U, are sorted decreasingly by amplitude (‖U_i‖).

Finally, we paint each conformer in the QAA subspace by internal energy, the sum of electrostatic and Van der Waals interactions (computed with NAMDenergy; Phillips et al., 2005) over each conformation. We emphasize that resultant energy coherence within observed substates is an emergent property of the method, that is, conformer internal energies are not considered during the projection onto the QAA subspace.

5.1 Results: organizing ubiquitin conformational landscape into energetically homogenous regions

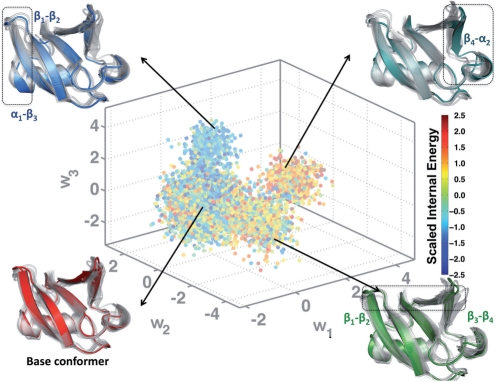
From the original simulation consisting of nearly 500 000 conformations (0.5 μs), 10 000 equally spaced conformations were collected for training the QAA basis. We performed QAA within a 30-dimensional subspace which covers 95% of the input variance. The anharmonic modes of motion reveal the exquisite ability of ubiquitin to modulate both the primary and secondary binding surfaces (β₁−β₂ and β₃−β₄; β₄−α₂), as shown in Figure 2. In addition, the distances between β₁−β₂ and β₃−β₄ can also serve as order parameters to describe the anharmonic landscape spanned by our simulations. Motions along each of the anharmonic modes permits ubiquitin to adopt a conformation that resembles the substrate-bound conformation. Our AR models will be deemed successful if they can recover this property.

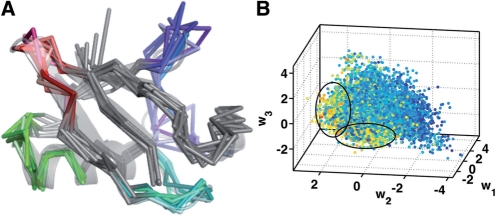
Fig. 2.

Organizing the conformational landscape of ubiquitin into energetically homogenous regions: Projections (w₁−w₃) of the conformations from the ubiquitin simulation onto the top three anharmonic basis vectors are colored according to the scaled internal energy values of the conformers. Also shown are the results from hierarchical clustering (Section 6), where a total of 78 clusters were identified. The arrows indicate portions of the landscape from where some of the clusters originated. Illustrative examples of cluster centers are shown as colored cartoons; overlaps with the other cluster centers are shown as transparent gray cartoons. In each of the example cluster centers, the region that undergoes the maximal conformational change is highlighted using a dotted rectangle. The corresponding secondary structures are marked for ease of identification.

6 HIERARCHICAL CLUSTERING FOR METASTABLE SUBSTATES

Energy wells in the 30-dimensional QAA-space determine biophysically relevant substates; the structure and dynamics of each can be characterized through clustering. Neighboring conformers in QAA-space have similar internal energies (cf. Fig. 2) and thus are dynamically and kinetically related. To facilitate clustering, we model the MD trajectory as an undirected network where edges connect energetically adjacent conformers in QAA-space. We can then cluster this network using a hierarchical Markov diffusion framework. This approach is an adaptation of our earlier work developing spectral graph partitioning algorithms for segmenting natural images (Chennubhotla and Jepson, 2003, 2005), understanding protein dynamics and allosteric propagation (Chennubhotla and Bahar, 2006, 2007a), and relating signal propagation on a protein structure to its equilibrium dynamics (Chennubhotla and Bahar, 2007b).

We begin hierarchical clustering by constructing a Markov transition matrix using edge weights between conformer pairs. Weights are chosen according to distance within QAA-space between connected conformers.

We then initiate a Markov chain (or random walk) on the weighted undirected network. As Markov transition probabilities homogenize through diffusion, an implicit clustering emerges from the network. First, a set of nodes representing the putative clusters are identified. Then, a Markov transition matrix is newly constructed using this reduced representation. The principle behind this construction is that upon reaching a stationary distribution at the coarsest hierarchy level, the Markov chain has also converged at finer (more local) network levels. This consistency regulates the overall topology of the network and helps build a multi-resolution representation of metastable states.

We expect that fine-grained hierarchy levels will produce many small clusters containing close neighbors in QAA space; that is, most cluster members will be from the same time-window (and single trajectory). As Markov diffusion progresses (fine-grained to coarse), conformers that are more distant neighbors will be connected by edges in the diffused network, and will therefore be assigned to the same cluster. Thus, the hierarchical clustering can highlight dynamical connections between conformers at different timescales.

6.1 Markov diffusion framework

Initiation: the MD simulation is modeled as an undirected graph by placing an edge with weight 1 from each data point to its six nearest Euclidean neighbors in the QAA space. At hierarchy level t=0, each data point is considered a node. Let n_o be the number of trajectory frames. The n₀×n₀ adjacency matrix C₀ gives the edge weights between each data point pair and the n₀×n₀ diagonal degree matrix D₀ (Step 1) gives the connectivity at each node in that D_t(i,i) contains the total number of connections to node i at hierarchy level t. Nodes with high degrees can be seen as hubs, and nodes with very low degrees can be seen as isolates. The stationary distribution of the Markov chain is given by the normalized degree vector 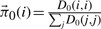, and represents the probability of a Markov Chain residing in a particular node after infinite iterations.

Iteration: for t=1 until done:

1. Compute the diagonal degree matrix D_t−1, with entries

   

   and the Markov transition matrix M_t−1=C_t−1D_t−1⁻¹.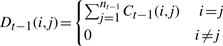

2. Diffuse the Markov transition matrix by repeated multiplication M^d_t−1=M_t−1×M_t−1 to reveal distant connectivity.

3. Determine the (n_t−1×n_t) kernel matrix K_t to carry network information from hierarchy level (t−1) to level (t). The kernel matrix is made up of a subset of n_t≪n_t−1 columns of M^d_t−1, which are selected so that all n_t−1 points have some probability.

4. Solve 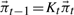for 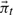with an expectation-maximization algorithm to find a low-dimensional representation 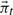of the stationary distribution .

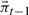5. Compute C_t using 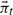: 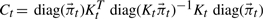where K_t^T denotes the transpose of K_t and 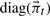indicates the diagonal matrix formed from the vector .

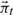6. t→t+1.

Termination: end if n_t≤2. At this point, the network has been divided into one or two clusters.

Backwards iteration along the hierarchy allows computation of an (n_t−1×n_t) ownership matrix O_t for each hierarchy level t, in which O_t(i,j) gives the probability that data point i belongs to cluster j at level t of the hierarchy:

where ∑_j=1^n_t O_t(i,j)=1. The ownership matrix gives the probability distribution for the likelihood that a data point belongs to any metastable state of the trajectory, providing a soft partitioning of the data. A hard partitioning is determined by assigning each data point to the cluster to which it has maximal ownership probability.

6.2 Results: characterizing metastable substates in the ubiquitin landscape

The connectivity matrix C₀ at clustering initialization is shown in Figure 3. The connectivity matrix shows several regions of high cross-talk. Iterative diffusion of the Markov chain derived from this connectivity matrix, followed by kernel selection, results in six hierarchy levels with 10 000, 4486, 978, 78, 11, and 2 clusters at each respective level.

To provide parameters for the AR model (Section 7), a membership threshold must be chosen that is fine enough to capture local dynamics, but still coarse enough to allow flexibility. We chose a membership threshold such that all cluster members were reachable from the cluster center within 50 ps, where a substate's center is defined as the closest conformer to the mean of that substate. The mean QAA-space distance between conformers in successive frames is 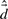, and the standard deviation is σ_d. The hierarchy level at which 99.7% of the conformers are within 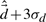of their substate center is selected for further processing. Following this criterion, AR analysis was pursued using statistics from level 4 of the hierarchy.

Four cluster centers from the connectivity matrix are shown for example clusters in Figure 3. Clusters can be mapped from QAA-space onto the connectivity matrix to visualize accessibility between substates. As an example, dynamically distant clusters are illustrated in Figure 3 by the red and green enclosed regions. The metastable substates identified share significant similarities in both conformational and energetic space, however, they do not interact directly in QAA-space. This produces a partitioning of the landscape that is quite unique from the perspective of understanding ubiquitin's equilibrium fluctuations: the landscapes's extrema represent distinct conformations of ubiquitin's binding regions. Note that while β₁−β₂ and β₃−β₄ adapt an ‘open’ conformation in the structure shown in green (average separation of over 18 Å), the red structure shows the binding regions ‘close’ to each other (average separation of 13.5 Å). Thus, the inherent motions of ubiquitin involve sampling the two metastable states with almost exclusively no cross-talk. However, note that both the red and green structures can interconvert between the metastable states highlighted in gray. These metastable states represent the so-called intermediates which are necessarily visited before sampling either open or close conformations. Intermediate metastable states also highlight the importance of ancillary structural changes that ubiquitin might have to undergo in order to sample either the open or close conformations. These changes are predominantly located along β₂−α₁ and the C-terminal tip of α₁ helix. Thus, for the opening and closing of the binding region in ubiquitin, our pathways deduced from the Markov transition matrices reveal that it is energetically more favorable to undergo conformational changes along the two regions highlighted in gray.

7 BUILDING AR MODELS

Motivated by the need for a compact, linear and generative model of ubiquitin's dynamics, we extend our findings from QAA and hierarchical clustering with a stochastic AR model inspired by problems in control theory and signal processing (Blake and Isard, 1998). Understood as a second-order stochastic differential equation that has been sampled at regular intervals, the model relates each successive protein conformation to the previous two. It consists of an appearance model and a dynamic model, which can be conceptualized, respectively, as encoding the protein in a meaningful low-dimensional (embedded) space and modeling characteristic motions within that subspace. Because we learn summarizing parameters for the protein's dynamics in the model, we can synthesize extrapolated trajectories of arbitrary length. As a contrast to molecular dynamics methods, where the system and environment are simulated and dynamics result, the approach here models dynamics explicitly and exploits the statistical regularities intrinsic to a natively fluctuating protein. Within this approach, time-evolution of the protein's conformation 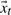results from coupling the appearance and dynamics models:

(6)

(7)

where weights 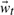constitute the projection of 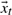onto the subspace spanned by U, or its state. Determining a physically meaningful subset of basis vectors, and the vectors themselves, is frustrated by the enormous conformational space accessible to a fluctuating protein. A poor choice of basis vectors (or selecting too few) would increase the reconstruction error 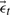upon mapping each embedded state back to full conformational space. The basis chosen here, U,ins the first 30 anharmonic modes which are extracted using QAA and which span the conformational subspace available to the dynamic model. Both deterministic and stochastic elements are contained in the model's dynamic component [Equation (7)]. The deterministic element is a second order Markov model in which the state at time t, 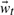, is a linear combination of states 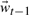and 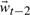. Stochasticity is introduced by the Gaussian driving distribution 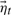, which quantifies motions that are not fully captured by the linear model. More temporal information is available to this model than to a first order model; we show that this permits characterization of complex motion patterns that extend over several timeframes (or MD conformations during training). Distinct from the connectivity matrix in Section 4, the transition matrices A₁ and A₂ here constitute the second-order transition matrices of the stochastic process and must be learned from training simulation data. In the following subsections we address learning these dynamical model parameters and generating synthetic trajectories.

7.1 Learning the dynamical model

The dynamical model, Equation (7), exploits our knowledge of past states (conformations) to propose a future state. Before we can compute transition matrices A₁ and A₂ from training data, we first project the ubiquitin simulation into the embedded 30-dimensional QAA-space to yield training states :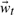

(8)

where columns of X, , are 3N vectors carrying the protein's coordinates (for N residues). Following the derivation put forward in Hyndman (2007) the AR model is defined sequentially over the weights:

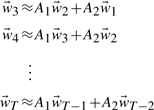(9)

with unknowns A₁ and A₂. We concatenate state vectors and transition matrices with the notation 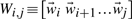and A≡[A₁  A₂] to express the system in matrix form:

(10)

The total squared error between the true states and the predicted states is minimized with the Frobenius norm ‖·‖_F:

(11)

Generally the state subspace is much smaller than the number of observations (training simulation frames), so W_i,j is rarely square. The solution to (11) then follows:

(12)

where F*≡F^T(FF^T)⁻¹ denotes the pseudo-inverse of a matrix F. Representative A₁ and A₂ matrices are shown in Figure 4A. The stochastic term, 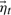, represents those dynamics that are inadequately captured by the second-order linear model, and is drawn from a Gaussian distribution with covariance equal to that of the prediction error averaged over the training sequence. That is,

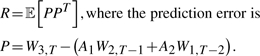(13)

Interpreted physically, each A₁ and A₂ pair encodes the local, time invariant dynamics. The eigen-decomposition of 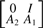yields the exponential decay constants 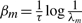for these local dynamics, where λ_m<1 denotes any positive eigenvalue (Fig. 4B).

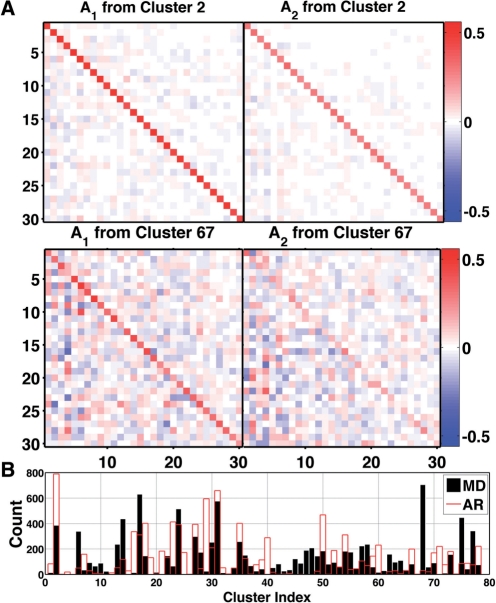
Fig. 4.

Representative transition matrices are highly diagonal: (A) A₁ and A₂ for the most populated cluster, cluster 2, which contained 29 108 structures or 5.84% of the entire 0.5 μs simulation. Cross correlations between QAA modes are highly reduced, yielding low off-diagonal elements. Distinctions between A₁ and A₂ indicate the constituent structures (from cluster 2) carried dynamic information across multiple frames. The lower two panels show less strongly diagonal transition matrices for a less populated cluster, 67, which contained 627 structures. Elements of A₁ and A₂ range from −0.84 to 0.72 over all clusters (−0.33 to 0.5597 over clusters 2 and 67). (B) Cluster memberships for MD training data (black) and AR-synthesized (red) ubiquitin conformations, 10 000 frames each.

7.2 Synthesizing new motion sequences

The learned transition matrices A₁ and A₂, unique to each cluster, can be used to generate novel structure sequences of arbitrary length. That is, 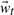and 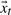now constitute the unknowns in Equations (6) and (7). Starting from a randomly selected frame from our training trajectory, we propagate the model using only the learned transition matrices. Within the QAA space defined by the column vectors of U, we compare each generated conformer to the mean structure of every cluster. At every step, the nascent trajectory is assigned to the cluster center with nearest Euclidean distance, and permitted to evolve according to that cluster's A₁, A₂, and 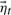until it moves closer to a different cluster center. We generated a synthetic trajectory of 25 000 frames, during which the protein visited 76 of the 78 clusters present in the training data (cluster membership for 10 000 training and testing frames is shown in Fig. 4). Other than error/transition parameters and the determined local mean of each cluster, no temporal information from the training data was necessary for the time-evolution of ubiquitin's dynamics. Additionally, it should be noted that the entirety of the generative process is carried out in the embedded QAA subspace, and the appearance model, Equation (6), is only used in post processing to return to full, 3N conformation space. We can conceptualize each substate's transition matrices as linearly encoding local dynamics, whereas reconstruction information from embedded to full conformational space is carried in the QAA basis vectors U. Far less storage and computing resources are required to propagate the AR-derived dynamics than with conventional sampling. Temporally, the synthetic trajectory employs the same time step found in the training data; the 25 000 synthetic trajectory frames compares with approximately 25 ns of MD simulation.

7.3 Results: predicted pathways of molecular recognition in ubiquitin

The underlying stochastic dynamical model allows us to synthesize new conformations of arbitrary length. This is particularly useful when one has to predict the binding mode of ubiquitin with another protein. Note that in our simulations, ubiquitin was simulated in its substrate-free form. Hence, no explicit knowledge of the substrate-bound form was available. However, when we synthesize 25 000 conformers from QAARM, its utility becomes quite evident. The conformers show remarkable fluctuations along the flexible regions of ubiquitin (highlighted in Fig. 5A). Further, these motions are largely similar to the fluctuations in the ubiquitin simulations, as evidenced by projecting the synthesized conformations back onto the QAA basis vectors.

Fig. 5.

Synthesized conformations from QAARM reveal novel binding modes of ubiquitin substrate. (A) A movie-like representation of the fluctuations in ubiquitin synthesized from the QAARM model. Note that regions undergoing large conformational changes include the binding regions and the ancillary regions of ubiquitin. These motions have a direct implication on binding a variety of substrates. (B) Synthetically generated 25 000 conformers are projected back onto the QAA bases to reveal the number of potential contacts that each of the synthesized conformer can make with a known substrate, Rabex 5. Note that the substate highlighted by the ellipse consists of a small number of conformers in the synthesized data that can form a large number of contacts with Rabex 5.

It is also interesting to note that the projection of the synthesized conformers onto the QAA basis space reveals novel pathways of ubiquitin binding. To illustrate this, we chose the PDB id: 2FIF where ubiquitin interacts with Rabex-5 along the secondary binding site of ubiquitin (β₂−α₁ and β₃−β₄ interface). We computed the estimated number of contacts each synthesized conformer would form if it were to be superimposed onto the crystal structure. Since we use only C^α atoms to generate the conformers, we consider two atoms to be in contact whenever they are separated by less than 7.3 Å (a standard practice in coarse-graining literature (Bahar and Cui, 2003)). The results of this computation are illustrated in Figure 5B. By projecting the synthesized conformers onto the QAA basis space, we discover that a small number of conformers (highlighted by the ellipse) form a large number of contacts with the substrate. Furthermore, the other parts of the landscape (in QAA) show meager contacts with the substrate. This allows us to pin-point a specific mechanism by which only a small number of the generated conformers can bind to ubiquitin in a specific manner. Although it remains to be seen if these conformations are also energetically favorable, we believe that QAARM has allowed one to predict complex formation by exploiting the statistical regularities in the substrate-free simulations of ubiquitin. Thus, in line with previous studies that proposed conformational selection to be a predominant pathway for recognizing binding partners in ubiquitin (Lange et al., 2008), our studies also predict a similar mechanism (at least at the C^α resolution).

8 DISCUSSION AND CONCLUSION

Well-sampled conformational space is more useful with organizational principles which can describe and characterize it. Methods for extracting meaningful features and events must cope with longer simulations of increasingly larger and more complicated systems, and should eventually be used for validating and error-checking MD simulations themselves. The trajectory studied here samples many of the unique binding poses ubiquitin must adopt for specific recognition of diverse ligands, providing a rich platform for studying functionally relevant structural transitions. However, ubiquitin's structural shifts are subtle when compared to those of hinge or multidomain proteins; that these motions and connecting pathways are distinctly resolved with our method speaks to the utility and suitability of higher-order statistics for decomposing conformational space.

We exploited long-tail spatial distributions in former work (QAA), and we extended it in this article with linear stochastic models which account for temporal dependencies. This allows us to explore specific, local dynamics accessible to a protein within energetically homogeneous wells. Clustering to determine substates was performed here within the 30-dimensional QAA subspace, and we plan to compare our identified substates to those from other clustering methods in the future. Additionally, increasingly subtle or energetically local behaviors can be encoded by learning AR models at successive clustering levels; how we couple AR-models at potentially disparate hierarchical levels to give a coherent picture of protein fluctuations is a topic of future work. In addition, we plan to apply maximum entropy methods to enable the dynamics of even poorly-sampled energy wells to be incorporated into the AR-model. While we demonstrated our framework on ubiquitin, we have already used QAA on several other protein systems where we expect QAARM to be useful as well.